| | | |
|
Шифровка - 2
Строки
Для кодирования сообщения используют следующие действия: сообщение записывают, опуская пробелы, в прямоугольник заданной высоты по столбцам, а затем прочитывают строки в заданном порядке.
1 P R I
2 R A N
3 O M G
4 G M
а затем, если выбрать порядок строк 3, 1, 2, 4, получают закодированное сообщение OMGPRIRANGM.
Требуется написать программу, которая по заданным высоте прямоугольника и порядке прочтения строк при кодировке декодирует заданное сообщение.
Входные данные
Входные данные содержат: в первой строке высоту прямоугольника H (2 ≤ H ≤ 10), во второй – порядок прочтения строк (числа записаны через пробел), в третьей – закодированное сообщение, длина которого составляет от 1 до 200 символов. Закодированное сообщение состоит из заглавных и строчных латинских букв и цифр.
Выходные данные
В выходные данные записывается декодированное сообщение.
|
Ввод |
Вывод |
4
3 1 2 4
OMGPRIRANGM |
PROGRAMMING |
| |
![]()
|
|
Строка - 4
Строки
Напишите программу, которая выводит строчку.
[:|/||\|:]
| |
![]()
|
|
Строка - 3
Строки
Напишите программу, которая выводит строчку.
\\||//\\||//||\\||//
| |
![]()
|
|
Строка - 2
Строки
Напишите программу, которая выводит строчку.
(:)]-/\-\/
| |
![]()
|
|
Строка - 5
Строки
Напишите программу, которая выводит строчку.
(-["|-|-|"]-)
| |
![]()
|
|
Рыбка
Строки
Напишите программу, которая выводит рыбку в виде рисука ASCII-арт (рисунок в виде строки 1х10 символов).
<@(/\/\)><
| |
![]()
|
|
Клад
Циклы
Строки
Путь к кладу задан в виде указаний, какое количество шагов нужно пройти в одном из четырёх направлений: север (N), юг (S), запад (W), восток (E). Весь маршрут записан в виде строки, содержащей последовательность из чисел и следующих за числами букв, указывающих направление перемещения. Например, строка «7N5E2S3E» означает "пройти 7 шагов на север, 5 шагов на восток, 2 шага на юг, 3 шага на восток». В маршруте может быть много команд перемещения, поэтому каждый такой маршрут можно сократить.
Например, ранее приведённый маршрут можно сократить до «5N8E". По данному маршруту до клада сократите его до строки минимальной длины.
Программа получает на вход строку, состоящую из целых неотрицательных чисел, не превосходящих 107 каждое, и одной буквы (N, S, W, E ) следующей за каждым
числом. Других символов (в том числе пробелов), кроме цифр и букв направлений, в строке нет. Длина строки не превосходит 250 символов. Гарантируется, что начальная
и конечная точки маршрута различаются.
Программа должна вывести маршрут, ведущий в ту же точку, записанный в таком же виде, как во входных данных, используя минимальное число символов. Если ответов
несколько, программа должна вывести один (любой) из них.
| Ввод |
Вывод |
Примечание |
| 7N5E2S3E |
5N8E |
Правильным ответом будет также «8E5N» |
| 10N30W20N |
30N30W |
Правильным ответом будет также «30W30N» |
| |
![]()
|
|
Стрела
Строки
Напишите программу, которая рисует картинку размером 11х7 символов.
(
\
)
##-------->
)
/
(
| |
![]()
|
|
Гномик
Строки
Напишите программу, которая рисует картинку размером 7х5 символов.
/_\
{~._.~}
( Y )
()~*~()
(/)-(\)
| |
![]()
|
|
Собачка
Строки
Напишите программу, которая рисует картинку размером 13х4 символов.
_ _ ;;
.~.~~;;;;;;;
\_/-\|----\\
' "" ""
| |
![]()
|
|
Увеличение чисел - 1
Строки
В первой строке входных данных записано число N (от 1 до 100).
В каждой из последующих N строк записано сначала некоторое целое число (из диапазона от 0 до 10000), затем пробел, и затем некоторый текст (не более 20 символов).
Требуется вывести информацию в том же формате, увеличив число в каждой строке (кроме первой, где записано число N) на 1.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2
14 Start
42 Stop
|
2
15 Start
43 Stop
|
| |
![]()
|
|
И.О. Фамилия
Строки
Ввести имя, отчество и фамилию. Преобразовать их к формату «инициалы-фамилия».
Входные данные: в первой строке задается предложение. Слова разделены одном пробелом, вначале и в конце текста лишних пробелов нет.
Выходные данные: необходимо вывести модифицированную строку.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
Inav Ivanovich Ivanov |
I. I. Ivanov |
| |
![]()
|
|
Замена подстроки
Строки
Найти в строке указанную подстроку и заменить ее на новую. Строка s, ее подстрока s1 для замены и новая подстрока s2 вводятся.
P.S. Искомые подстроки в исходной строке не пересекаются.
P.P.S. В строках не содержатся пробелы.
P.P.P.S. Искомая подстрока может встречаться неоднократно.
P.P.P.P.S. Все буквы строчные.
P.P.P.P.P.S. Нет символов помимо строчных латинских букв.
На вход подаются 3 строки: s, s1, s2. Длина всех строк не превосходит 100.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
abcde
ab
fg |
fgcde |
| 2 |
ababc
ab
c
|
ccc |
| |
![]()
|
|
Редактор скобочной последовательности
Строки
Задана строка, состоящая только из:
• прописных и строчных букв английского алфавита;
• символов подчёркивания (они используются в качестве разделителей);
• круглых скобок (как открывающих, так и закрывающих).
Гарантируется, что каждая открывающая скобка имеет парную закрывающую, идущую следом. Аналогично, каждая закрывающая скобка имеет парную открывающую, которая расположена до неё. Для каждой пары соответствующих скобок верно, что между ними нет каких-либо других скобок. Иными словами, каждая скобка в строке входит в пару «открывающая-закрывающая», и такие пары не вкладываются друг в друга.
Например, допустимой строкой является: _Hello_Vasya(and_Petya)__bye_(and_OK)
Словом называется нерасширяемая последовательность подряд идущих букв, то есть последовательность букв, где слева и справа от неё находится скобка или символ подчёркивания, или соответствующий символ отсутствует.
Приведенный пример содержит семь слов: «Hello», «Vasya», «and», «Petya», «bye», «and» и «OK».
Напишите программу, которая найдет:
• длину самого длинного слова вне скобок (выведите 0, если слов вне скобок нет),
• количество слов внутри скобок (выведите 0, если слов внутри скобок нет).
Входные данные: в первой строке записано целое число n (\(1 <= n <= 255\)) — длина заданной строки. Во второй строке записана строка, состоящая только из строчных и прописных английских букв, открывающих и закрывающих скобок, а также символов подчёркивания.
Выходные данные: выведите два числа:
• длину самого длинного слова вне скобок (выведите 0, если слов вне скобок нет);
• количество слов внутри скобок (выведите 0, если слов внутри скобок нет).
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
37
_Hello_Vasya(and_Petya)__bye_(and_OK) |
5 4 |
| 2 |
37
_a_(_b___c)__de_f(g_)__h__i(j_k_l)m__
|
2 6 |
| 3 |
27
(LoooonG)__shOrt__(LoooonG)
|
5 2 |
| 4 |
5
(___)
|
0 0 |
Примечание
В первом примере слова «Hello», «Vasya» и «bye» записаны вне скобок, а слова «and», «Petya», «and» и «OK» — внутри. Обратите внимание, что слово «and» встречается дважды, и учитывать в ответе его тоже следует два раза.
| |
![]()
|
|
Шифр Юлия
Строки
Юлий Цезарь использовал свой способ шифрования текста. Каждая буква заменялась на следующую по алфавиту через K позиций по кругу. Необходимо по заданной шифровке определить исходный текст.
Входные данные: в первой строке дана шифровка, состоящая из заглавных латинских букв. Во второй строке число K (\(1 <= K <= 10\)).
Выходные данные: требуется вывести результат расшифровки.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
XPSE
1 |
WORD |
| 2 |
ZABC
3 |
WXYZ |
| |
![]()
|
|
Арифметическое выражение
Строки
В первой строке входных данных записано арифметическое выражение в виде:
<число> <операция> <число> =
<Число> - это натуральное число, не превышающее 10000.
<Операция> - один из знаков +, -, *.
В начале строки, в конце строки, а также между числами и знаком операции, числом и символом =, может быть любое число пробелов (а может пробелов и не быть).
Гарантируется, что длина строки не превышает 200 символов.
Выведите результат вычисления выражения.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
154 +3 = |
157 |
| |
![]()
|
|
Арифметическое выражение-1
Строки
Напишите программу, которая вычисляет выражение, состоящее из трех чисел и двух знаков (допускаются только знаки «+» или «–»). На вход подается символьная строка, представляющая собой арифметическое выражение. Все числа целые.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
12+3+45 |
60 |
| 2 |
12-45+3 |
-30 |
| |
![]()
|
|
Арифметическое выражение-3
Строки
Напишите программу, которая вычисляет выражение, состоящее из трех чисел, трех знаков арифметических операций (допускаются знаки «+», «–», «*» и «/») и круглых скобок. На вход подается символьная строка, представляющая собой арифметическое выражение. Все числа - целые. Операция «/» выполняется как целочисленное деление.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2*(3+45)+4 |
100 |
| 2 |
2*3/(5-2) |
2 |
| |
![]()
|
|
Украшение елки
Строки
В преддверии Нового Года Вася купил ёлку и решил её украсить. Для этого он должен достать с верхней полки шкафа самые красивые украшения. К сожалению, ставить стул на стул было плохой идеей… Теперь у него вместо коробки украшений – куча, состоящая из украшений, осколков и вещей из других коробок. Конечно же, её нужно разобрать. Но Вася так хочет смотреть новогодние фильмы! Помогите ему написать программу, которая разберёт кучу мусора за него.
Входные данные
На вход подаётся две строки. Первая – примеры украшений. Вторая – собственно куча.
Выходные данные
Нужно вывести количество украшений каждого вида, а также количество разбитых (обозначены точкой) украшений.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
60oQ
484QQQQ.Qhu.6.oodnh...ddh76762..300ojha.
|
6: 3
0: 2
o: 3
Q: 5
Broken: 9
|
| 2 |
80
..7.8.7.8.9.8
|
8: 3
0: 0
Broken: 7
|
| |
![]()
|
|
Шифр Цезаря
Строки
Гай Юлий Цезарь (13 июля, или из других источников, 12 июля 100 или 102 гг. до н. э. — 15 марта 44 г. до н. э.) — древнеримский государственный и политический деятель, диктатор, полководец, писатель. Своим завоеванием Галлии Цезарь расширил Римскую державу. Деятельность Цезаря коренным образом изменила культурный и политический облик Западной Европы и оставила неизгладимый след в жизни следующих поколений европейцев. Гай Юлий Цезарь, обладая блестящими способностями военного стратега и тактика, одержал победу в сражениях гражданской войны и стал единовластным повелителем Pax Romana.
Цезарь часто брал бумагу и писал письма во время гладиаторских боёв. Его спросили, мол, как вы и на гладиаторов можете смотреть и письма писать. На что Цезарь ответил: «Цезарь может делать три дела одновременно: и писать, и смотреть, и слушать».
Юлий Цезарь, чтобы скрыть информацию от врагов, использовал свой способ шифрования текста. Каждая буква заменялась на следующую по алфавиту через K позиций по кругу.
Используя современные компьютерные технологии, определите по заданной шифровке исходный текст.
Входные данные
В первой строке дана шифровка, состоящая из заглавных латинских букв. Во второй строке число K (\(1 <= K <= 10\)).
Выходные данные
Требуется вывести результат расшифровки.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
XPSE
1 |
WORD |
| |
![]()
|
|
Сочинения Гай Юлия Цезаря
Строки
Избрав путь политика и полководца, Цезарь имел немного времени для творческой работы, однако написал сочинения разных жанров: эпическую поэму "Геркулес", трагедию "Царь Эдип", поэму "Путешествие", "Записки о галльской войне" и "Записки о гражданской войне". Были изданы сборники его сентенций, речей, писем. Кроме того, великий полководец интересовался филологией.
Отвлекшись от написания поэмы, Цезарь записал одну под другой две строчки и задумался. Затем он посмотрел на написанные строчки и понял, что первая строка (S) может содержать в себе несколько раз вторую строку (T). Гай Юлий Цезарь решил подсчитать все вхождения строки T в строку S. Помогите ему, напишите соответствующую программу.
Входные данные
Первые две строки входных данных содержат строки S и T, соответственно. Длины строк больше 0 и меньше 50000, строки содержат только строчные латинские буквы.
Выходные данные
Выведите номера символов, начиная с которых строка T входит в строку S, в порядке возрастания (по одному значению в строке).
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
ababbababa
aba |
0
5
7 |
| |
![]()
|
|
Задача
Строки
Ученики, посещавшие школы в Древнем Риме решали на занятиях различные задачи. Вот одна из задач:
101=1
8181515=4
1111112=0
8888888=14
1010101=3
7000007=?
Пусть первое число x, а соответствующее ему n.
Напишите программу, которая по числу x определяет n.
Входные данные
Единственное неотрицательное число x, не превышающее 101001.
Выходные данные
Выведите n.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
689 |
4 |
| |
![]()
|
|
Распаковка строчки
Строки
Всем известно, что Цезарь пользовался иногда тайнописью, т. е. неким шифром, изобретенным им самим.
Иногда, чтобы сократить время написания, Цезарь использовал упаковку, принцип которой заключается в удалении повторяющихся букв и замены их на числа, определяющих количество повторений.
Будем рассматривать только строчки, состоящие из заглавных латинских букв. Например, рассмотрим строку AAAABCCCCCDDDD. Данная строка может быть представлена как 4AB5C4D.
Напишите программу, которая берет упакованную строчку и восстанавливает по ней исходную строку.
Входные данные
Входные данные содержат одну упакованную строку. В строке могут встречаться только конструкции вида nA, где n — количество повторений символа (целое число от 2 до 99), а A — заглавная латинская буква, либо конструкции вида A, то есть символ без числа, определяющего количество повторений. Максимальная длина строки не превышает 80.
Выходные данные
Выведите восстановленную строку. При этом строка должна быть разбита на строчки длиной ровно по 40 символов (за исключением последней, которая может содержать меньше 40 символов).
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
ABC |
ABC |
| 2 |
O2A3O2AO |
OAAOOOAAO |
| 3 |
A2B3C4D5E6F7G |
ABBCCCDDDDEEEEEFFFFFFGGGGGGG |
| |
![]()
|
|
Финальная стоимость - 1
Строки
Представьте, что вас наняли в IT отдел сетевого продуктового магазина. Со следующего месяца планируется ввести скидку в 20% на некоторые товары. От вас требуется написать программу расчета финальной стоимости покупки с учетом всех скидок.
Покупка задается в виде списка товаров, где каждый товар описывается в формате <НазваниеТовара> <цена> x<количество>. Если название товара заканчивается на подстроку «sale», то цена на товар при финальном расчете покупки уменьшается на 20% с округлением до целого числа в меньшую сторону. Так, например, если цена товара была 12 рублей, с учетом скидки она составит 9 рублей. На остальные товары скидка не распространяется.
Суммарная стоимость каждого товара вычисляется по формуле finalPrice⋅x, где finalPrice - финальная цена, возможно, с учетом скидки и округлением, а x - количество товара в списке покупок.
Ваша задача - вычислить итоговую стоимость покупки.
Входные данные
В первой строке дано число n - число наименований товаров в покупке (1≤n≤1000).
В следующих n строках заданы описания товаров в покупке в формате: <НазваниеТовара> <цена> x<количество>.
Название товара состоит из не более чем 20 строчных латинских букв. Цена - натуральное число, которое строго больше 1, но не больше 1000. Количество - натуральное число не больше 100.
Выходные данные
Выведите одно число - итоговую стоимость покупки.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
5
bananassale 10 x2
breadfixed 5 x5
colafixed 20 x2
gumsale 9 x10
tea 2 x15 |
181 |
В тесте из примера итоговые стоимости товаров составят: 8, 5, 20, 7 и 2 соответственно. Итоговая стоимость покупки: 8⋅2+5⋅5+20⋅2+7⋅10+2⋅15=181. |
| |
![]()
|
|
Финальная стоимость - 2
Строки
Представьте, что вас наняли в IT отдел сетевого продуктового магазина. Со следующего месяца планируется ввести скидку в 20% на некоторые товары. От вас требуется написать программу расчета финальной стоимости покупки с учетом всех скидок.
Покупка задается в виде списка товаров, где каждый товар описывается в формате <НазваниеТовара> <цена> x<количество>. Если название товара не заканчивается на подстроку «fixed», то цена на товар при финальном расчете покупки уменьшается на 20% с округлением до целого числа в меньшую сторону. Так, например, если цена товара была 12 рублей, с учетом скидки она составит 9 рублей. На товары, название которых заканчивается на подстроку «fixed», скидка не распространяется.
Суммарная стоимость каждого товара вычисляется по формуле finalPrice⋅x, где finalPrice - финальная цена, возможно, с учетом скидки и округлением, а x - количество товара в списке покупок.
Ваша задача - вычислить итоговую стоимость покупки.
Входные данные
В первой строке дано число n - число наименований товаров в покупке (1≤n≤1000).
В следующих n строках заданы описания товаров в покупке в формате: <НазваниеТовара> <цена> x<количество>.
Название товара состоит из не более чем 20 строчных латинских букв. Цена - натуральное число, которое строго больше 1, но не больше 1000. Количество - натуральное число не больше 100.
Выходные данные
Выведите одно число - итоговую стоимость покупки.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
5
bananassale 10 x2
breadfixed 5 x5
colafixed 20 x2
gumsale 9 x10
tea 2 x15 |
166 |
В тесте из примера итоговые стоимости товаров составят: 8, 5, 20, 7 и 1 соответственно.
Итоговая стоимость покупки: 8⋅2+5⋅5+20⋅2+7⋅10+1⋅15=166$. |
| |
![]()
|
|
Количество слов
Строки
На вход программы поступает строка текста, в которой могут встречаться:
— прописные и строчные (т.е. большие и маленькие) латинские буквы;
— пробелы;
— знаки препинания: точка, запятая, восклицательный и вопросительный знак;
— символ –, обозначающий в некоторых случаях тире, а в некоторых — дефис.
Слово — это последовательность подряд идущих латинских букв и знаков дефис, ограниченная с обоих концов. В качестве ограничителей могут выступать начало строки, конец строки, пробел, знак препинания, тире. Тире отличается от дефиса тем, что слева и справа от знака дефис пишутся буквы, а хотя бы с одной стороны от тире идет либо начало строки, либо конец строки, либо пробел, либо какой-либо знак препинания, либо еще одно тире.
Напишите программу, определяющую, сколько слов в данной строке текста.
Входные данные
Вводится строка длиной не более 200 символов.
Выходные данные
Выведите одно число — количество слов, которые содержатся в исходной строке.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
Hello , world! |
2 |
| 2 |
www.olympiads.ru |
3 |
| 3 |
Gyro-compass - this is a ... |
4 |
| |
![]()
|
|
Негласный палиндром
Строки
Возьмем произвольное слово и проделаем с ним следующую операцию: поменяем местами его первую согласную букву с последней согласной буквой, вторую согласную букву с предпоследней согласной буквой и т.д. Если после этой операции мы вновь получим исходное слово, то будем называть такое слово негласным палиндромом. Например, слова sos, rare, rotor, gong, karaoke являются негласными палиндромами.
Вам требуется написать программу, которая по данному слову определяет, является ли оно негласным палиндромом.
Входные данные
Вводится одно слово.
Выходные данные
Программа должна вывести YES, если введенное слово является негласным палиндромом, и NO в противном случае.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
tennete |
YES |
| |
![]()
|
|
Число
Цикл for
Условный оператор
Строки
Вводится натуральное число. Требуется разделить запятыми тройки его цифр (считая справа).
Входные данные
Вводится одно натуральное число, не превышающее 10100.
Выходные данные
Вывести то же число, разделяя тройки цифр запятыми.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1000 |
1,000 |
| 2 |
12345678 |
12,345,678 |
| 3 |
999 |
999 |
| |
![]()
|
|
«У моего папы больше денег»
Строки
Двое играют в такую игру. Первый называет число, затем второй называет число. Если число второго больше, то он выиграл, в противном случае (даже если числа равны), выиграл первый. Помогите второму игроку – напишите программу, которая будет за него успешно играть в эту игру.
Входные данные
Вводится натуральное число A, которое назвал первый игрок (в числе А не больше 100 цифр).
Выходные данные
Выведите одно натуральное число – какой-нибудь (любой!) выигрышный ход второго игрока.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1 |
2 |
| 2 |
1000000000000000 |
1000000000000009 |
| |
![]()
|
|
Считалочка
Строки
Дети решили поиграть в догонялки, и, чтобы выбрать водящего, встали в круг и стали считаться. Для этого они использовали считалочку. Показывая пальцем по очереди на каждого стоящего в кругу, считающий произносит одно слово, и тот, на кого придется последнее слово, и будет водить. Требуется по данной считалочке определить, кто же будет водить.
Входные данные
В первой строке вводится считалочка. Она состоит из слов, записанных латинскими буквами. Слова разделены одним пробелом. Знаков препинания нет, строка начинается и заканчивается буквой. В считалочке не менее двух слов, а длина строки не превосходит 100.
Во второй строке в том же формате вводится список имен школьников в том порядке, в котором они стоят по кругу. Считать начинают с первого школьника. Детей не менее двух, а длина строки не превосходит 100.
Выходные данные
Выведите имя школьника, которому предстоит водить.
| № |
Входные данные |
Выходные данные |
| 1 |
To be or not to be
John Mary Ann Kate |
Mary |
| 2 |
Na zolotom kryltse sideli
Vasya Vasya Vasya |
Vasya |
| |
![]()
|
|
Хорошие стихи
Строки
Вы когда-нибудь задумывались над тем, как отличить хорошие стихи от посредственных?
Нет? А вот редактор литературного журнала занимается этим каждый день, получая тонны корреспонденции от молодых авторов, желающих стать известными поэтами. Благо, в последнее время большая часть стихов присылается по электронной почте, поэтому у редактора возникла мысль автоматизировать процесс. Он твердо уверен, что стихи тем лучше, чем точнее в них рифма. Он считает две строки зарифмованными, если у них совпадает несколько последних букв. И чем больше букв совпадает, тем лучше зарифмованы строки. Например, у строк “палка” и “веревка” совпадают только пары последних букв “ка”, а у строк “олимпиада” и “рая и ада” совпадают четыре буквы (пробелы мы пропускаем). Поэтому вторая рифма лучше. Редактор считает, что в четверостишии (четыре строки) первая строка должна рифмоваться с третьей, а вторая – с четвертой. Для каждой из этих двух пар строк он считает количество совпадающих последних символов и из этих двух чисел выбирает наибольшее. Полученное число он называет коэффициентом качества стихотворения – чем он выше, тем больше шансов у стихотворения быть опубликованным. Помогите редактору – напишите программу, которая определяет качество стихотворения. И кто знает, может быть, благодаря вашим усилиям, мир познакомится с гениальными стихами (см. первый пример).
Входные данные
На вход подается 4 непустые строки, каждая из которых состоит из не более чем 100 строчных латинских букв (стихотворение уже подверглось предварительной обработке: из него удалили все пробелы и знаки препинания, а заглавные буквы сделали строчными).
Выходные данные
Выведите одно число – коэффициент качества стихотворения.
| № |
Входные данные |
Выходные данные |
| 1 |
yapomnyuchudnoemgnovenje
peredomnojyavilasty
kakmimoletnoevidenje
kakgenijchistoykrasoty |
4 |
| 2 |
eto
vovse
ne
stihi |
0 |
| 3 |
etootlichnyestihi
etootlichnyestihi
etootlichnyestihi
etootlichnyestihi |
17 |
| |
![]()
|
|
Буквы по кругу
Строки
Перебор
По кругу записано несколько букв (возможно, повторяющихся). Петя интересуется, сможет ли он прочитать некоторое слово, если будет двигаться по кругу (в каком-либо направлении), не пропуская буквы (откуда начинать, и в какую сторону двигаться, он может выбрать сам).
Входные данные
В первой строке записаны строчные латинские буквы в том порядке, в котором они расставлены по кругу по часовой стрелке. Буквы записаны без пробелов, их количество не меньше 1 и не больше 100.
Во второй строке записано слово, которое хочет найти Петя. Оно также состоит из строчных латинских букв и имеет длину от 1 до 100.
Выходные данные
Выведите YES заглавными латинскими буквами, если такое слово можно прочитать, двигаясь по кругу, и NO в противном случае.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
abcdefg
abd |
NO |
| 2 |
abcdg
bag |
YES |
| 3 |
a
aaa |
YES |
| |
![]()
|
|
Умножения
Строки
Дано алгебраическое выражение, состоящее из натуральных чисел, переменных (a, b, c, ..., z) записанных строчной латинской буквой, знаков арифметических операций + , - , * (умножение) и * * (возведение в степень). При этом если после числа идет переменная, то знак умножения может быть пропущен.
Требуется подсчитать, сколько в данном выражении умножений и сколько возведений в степень.
Входные данные
Ввдится строка, состоящая не более чем из 200 символов, и не менее, чем из одного символа. Она представляет собой корректное алгебраическое выражение.
Выходные данные
Выведите два числа через пробел: количество умножений и количество возведений в степень.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2x+5 |
1 0 |
| 2 |
x**y**2z*3*5 |
3 2 |
| |
![]()
|
|
Шпионские штучки
Строки
Алиса и Боб — очень опытные шпионы. Лучше всего им удается находить пароли для доступа к различным секретным данным. Вот и в этот раз Алиса получила от Боба сообщение, в котором говорилось, что ключом является число и далее шло само это число. Также Боб писал, что число-ключ должно делиться на 9. Когда Алиса попробовала ввести полученный пароль, то оказалось, что он не подходит. Алиса очень доверяет Бобу, и поэтому она решила, что Боб мог ошибиться только в одной цифре пароля. Поскольку у Алисы не так много времени, она решила не выяснять у Боба правильный ответ, а перебрать все числа, которые могли бы быть паролем, т.е. все такие числа, которые могут быть получены из того числа, которое прислал Боб, заменой ровно одной из его цифр и делятся на 9. За помощью Алиса обратилась к вам. Напишите программу, которая предложит Алисе все возможные варианты пароля.
Входные данные
Во входных данных содержится единственное число P (1 ≤ P ≤ 109) — то число, которая Алиса получила в сообщении от Боба. Гарантируется, что оно не начинается с нуля.
Выходные данные
Выведите в столбик все возможные варианты паролей, которые нужно перебрать Алисе, в произвольном порядке. Ни одно из полученных вами чисел не должно начинаться с нуля. Все возможные варианты паролей должны содержать столько же цифр, сколько и исходное число, полученное Алисой.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
256 |
756
216
252 |
| |
![]()
|
|
Слишком много кофеина
Строки
Цикл while
Артур всегда очень боялся знакомиться с девушками. Дело даже не в природной стеснительности Артура, и даже не столько в том, что Артур не знает, о чем говорить с девушками. Просто Артур с детства не выговаривает букву «р» и очень этого стесняется. Поэтому Артур старается не произносить лишний раз слова, в которых есть эта ненавистная ему буква.
Однажды друзья познакомили Артура с девушкой по имени Нина (о, какое прекрасное имя!). Она была очаровательна и очень болтлива, поэтому Артуру почти не нужно было подбирать слова — она заполняла неловкую тишину за него. Разумеется, он пригласил ее в кафе выпить чашечку кофе. Артур даже продумал все свои реплики заранее: «Счастлив тебя видеть», «Ты сегодня восхитительна», «Да, конечно, я внимательно тебя слушаю», «И что дальше?», «Счет, пожалуйста» и, конечно, «Я позвоню тебе на днях, не скучай».
Но, как известно, не бывает идеальных планов. Все шло как по маслу, но вдруг, сидя за столиком в кафе, Нина сказала, что ужасно не выспалась и не отказалась бы от N чашек кофе. И тут Артур понял, что он не обдумал заранее, как он будет делать заказ. Понятно, что нужно сказать что-то вроде: «Сколько-то чашек кофе, пожалуйста», но вот сколько же чашек нужно, чтобы Нина так и не поняла, что Артур не выговаривает букву «р»? Явно нужно заказать не меньше, чем N + 1 чашку — чтобы и Нине досталось N чашек, и самому выпить, но вот сколько точно — Артур не знает. Денег у него не слишком много, поэтому заказывать больше, чем жизненно необходимо для того, чтобы избежать разоблачения, Артур не хочет.
Помогите Артуру — посчитайте, сколько чашек кофе он должен заказать.
Входные данные
Вводится одно целое число N (1 ≤ N ≤ 2999).
Выходные данные
Выведите одно число — количество чашек кофе, которое должен заказать Артур.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1 |
2 |
| 2 |
12 |
15 |
| |
![]()
|
|
Телеграммы Матроскина
Строки
Когда Дядя Фёдор уехал домой в город, следить за хозяйством остались Матроскин и Шарик. Но поскольку Дядю Фёдора очень волновали дела в Простоквашино, они договорились, что каждую неделю Матроскин будет писать письмо с отчетом о делах. Довольно скоро Матроскин понял, что письма идут слишком долго, поэтому решил отправлять телеграммы. Обычно отчеты очень длинные, поэтому Матроскину пришлось отправлять несколько телеграмм. Чтобы Дяде Фёдору было удобнее разобраться в пришедших телеграммах, Матроскин следует следущим правилам:
В каждой телеграмме должно быть не более 140 символов, включая пробелы и знаки препинания.
Исходный текст должен быть разбит на телеграммы по пробелам, при этом пробел, по которому разбивается телеграмма, уничтожается.
Если телеграмма не является последней, в её конец нужно дописать три точки.
Если телеграмма не является первой, в её начало нужно дописать три точки.
Чтобы сэкономить деньги на отправке телеграмм, Матроскин хочет разбить текст на как можно меньшее количество.
Помогите Матроскину разбить исходный текст на как можно меньшее количество телеграмм по приведенным выше правилам.
Входные данные
На вход подается строка из маленьких латинских букв и пробелов. Она не начинается и не заканчивается пробелами и никакие два пробела в ней не идут подряд. Длина строки не превышает 10000.
Выходные данные
В первой строке выведите число N – количество телеграмм, на которое надо разбить исходную строку. В следующих N строках выведите сами телеграммы. Если текст передать заданным способом невозможно, выведите −1.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
deesecnj vmguhee xhled rrr dfjhj fdytiaf baulvovt kvhygzhv wfaocftf scugmcqsk wadi bjeiq coesxqgnry tmlko gpmwns rcf dtdey bvirmlv gzl bwuoio |
2
deesecnj vmguhee xhled rrr dfjhj fdytiaf baulvovt kvhygzhv wfaocftf scugmcqsk wadi bjeiq coesxqgnry tmlko gpmwns rcf dtdey bvirmlv gzl...
...bwuoio |
| |
![]()
|
|
Cлова не пройдут
Строки
Дети, как известно, все раньше и раньше начинают пользоваться интернетом. Теперь, когда у них возникают вопросы, они не бегут к родителям, а заходят в свою любимую поисковую систему и узнают ответ в интернете. Но вдруг они случайно найдут что-нибудь, что им знать пока рановато? Или, может быть, лучше не знать вообще никогда?
В одной стране эту проблему решили очень просто: был создан список запрещенных для использования в интернете слов. Ведь очевидно, что статья, в которой упоминается какое-нибудь нехорошее слово, не может научить ребенка ничему хорошему. Любой сайт, содержащий хотя бы одно слово из этого списка, теперь подлежит мгновенной блокировке. Невинный ребенок никогда не натолкнется на что-нибудь, про что ему еще рановато знать — такой статьи просто не найдется в интернете. Но злобные сайтовладельцы придумали способ обойти этот запрет: если вместо некоторых букв написать внешне похожие на них цифры, то прочитать этот текст все равно будет можно, а робот, проверяющий сайты на пригодность, не распознает в слове запрещенное — ведь формально его нет на сайте.
Ваша задача — помочь правительству этой страны защитить детей от вредной информации. Напишите программу, которая будет проверять, нет ли в данной строке запрещенного слова, учитывая возможное коварство сайтовладельцев. Известно, что сайтовладельцы иногда делают следующие замены: e 3, o 0, i 1, t 7, a 4, s 5.
Входные данные
В первой строке входных данных дана строка — текст с сайта. Во второй строке входных данных дана другая строка — запрещенное слово. Первая строка состоит из маленьких латинских букв и цифр, вторая строка состоит только из маленьких латинских букв. Длина каждой строки не превышает 100.
Выходные данные
Выведите «YES», если запрещенное слово встречается как подстрока в строке с сайта, и «NO» иначе. Возможно, в строке с сайта некоторые буквы изначально были заменены на цифры в соответствии с приведенными выше правилами.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
inah0leinthegroundthereliv3dah0bb1t
hobbit |
YES |
| 2 |
whath4v3igotinmypocket
handses |
NO |
| 3 |
whath4veig0t1nmyp0ck37
knife |
NO |
| 4 |
wh4thav31go71nmyp0ck3t
stringofnothing |
NO |
| |
![]()
|
|
Подстрока-палиндром
Строки
Марина очень любит палиндромы. Палиндром — это строка, которая одинаково читается слева направо и справа налево, например « noon », « rotator » или « radar ».
Марина написала на доске строку s , состоящую из n строчных латинских букв s1 s2 ... sn . Подстрокой строки s называется строка s ls l + 1 ... sr для некоторых 1 ≤ l ≤ r ≤ n . Марина ищет в строке s как можно более длинную подстроку, которая является палиндромом. Например, в строке « rotateradars » такой подстрокой будет « radar ».
Вова хочет изменить написанную Мариной строку, чтобы подстрока-палиндром была как можно длиннее. Он может либо оставить строку нетронутой, либо изменить в ней ровно одну букву на другую. Например, если в строке « rotateradars » изменить шестую букву на « o », получится строка « rotatoradars », в которой максимальная подстрока-палиндром « rotator » имеет длину 7 . Подстроку-палиндром большей длины получить нельзя.
Помогите Вове определить, какую максимальную длину подстроки-палиндрома он сможет получить.
Входные данные
Первая строка входных данных содержит натуральное число n — длину строки, которую написала Марина ( 1 ≤ n ≤ 100 ).
Во второй строке входных данных содержится сама строка, состоящая из n строчных латинских букв.
Выходные данные
В выходной файл выведите одно число — максимальную длину подстроки-палиндрома, которую может получить Вова.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
12
rotateradars |
7 |
| |
![]()
|
|
Метод бутерброда
Строки
Секретное агентство «Super-Secret-no» решило для шифрования переписки своих сотрудников использовать «метод бутерброда». Сначала буквы слова нумеруются в таком порядке: первая буква получает номер 1, последняя буква - номер 2, вторая – номер 3, предпоследняя – номер 4, потом третья … и так для всех букв (см. рисунок). Затем все буквы записываются в шифр в порядке своих номеров. В конец зашифрованного слова добавляется знак «диез» (#), который нельзя использовать в сообщениях.
Например, слово «sandwich» зашифруется в «shacnidw#».
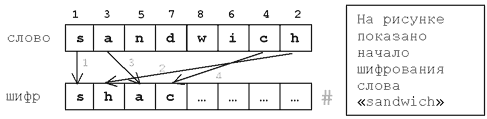
К сожалению, программист «Super-Secret-no», написал только программу шифрования и уволился. И теперь агенты не могут понять, что же они написали друг другу. Помогите им.
Входные данные
Вводится слово, зашифрованное методом бутерброда. Длина слова не превышает 20 букв.
Выходные данные
Выведите расшифрованное слово.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
Aabrrbaacda# |
Abracadabra |
| |
![]()
|
|
Благозвучное слово
Цикл for
Строки
Все буквы латинского алфавита делятся на гласные и согласные. Гласными буквами являются: a, e, i, o, u, y. Остальные буквы являются согласными.
Слово называется благозвучным, если в этом слове не встречается больше двух согласных букв подряд и не встречается больше двух гласных букв подряд. Например, слова abba, mama, program — благозвучные, а слова aaa, school, search — неблагозвучные.
Вводится слово. Если это слово является неблагозвучным, то разрешается добавлять в любые места этого слова любые буквы. Определите, какое минимальное количество букв можно добавить в это слово, чтобы оно стало благозвучным.
Входные данные
Вводится слово, состоящее только из маленьких латинских букв. Длина слова не превышает 30 символов.
Выходные данные
Выведите минимальное число букв, которые нужно добавить в это слово, чтобы оно стало благозвучным.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
program |
0 |
Слово уже является благозвучным. |
| 2 |
school |
1 |
Достаточно добавить одну гласную букву, например, между буквами s и с |
| |
![]()
|
|
Телефонные номера
Строки
Обработка текста
Телефонные номера в адресной книге мобильного телефона имеют один из следующих форматов:
+7<код><номер>
8<код><номер>
<номер>
где <номер> — это семь цифр, а <код> — это три цифры или три цифры в круглых скобках. Если код не указан, то считается, что он равен 495. Кроме того, в записи телефонного номера может стоять знак “-” между любыми двумя цифрами (см. пример).
На данный момент в адресной книге телефона Васи записано всего три телефонных номера, и он хочет записать туда еще один. Но он не может понять, не записан ли уже такой номер в телефонной книге. Помогите ему!
Два телефонных номера совпадают, если у них равны коды и равны номера. Например, +7(916)0123456 и 89160123456 — это один и тот же номер.
Входные данные
В первой строке входных данных записан номер телефона, который Вася хочет добавить в адресную книгу своего телефона. В следующих трех строках записаны три номера телефонов, которые уже находятся в адресной книге телефона Васи.
Гарантируется, что каждая из записей соответствует одному из трех приведенных в условии форматов.
Выходные данные
Для каждого телефонного номера в адресной книге выведите YES (заглавными буквами), если он совпадает с тем телефонным номером, который Вася хочет добавить в адресную книгу или NO (заглавными буквами) в противном случае.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
8(495)430-23-97
+7-4-9-5-43-023-97
4-3-0-2-3-9-7
8-495-430 |
YES
YES
NO |
| |
![]()
|
|
Строки
Строки
Конструктив
Даны три строки, состоящие из строчных латинских букв. С этими строками можно производить следующие операции: либо заменить один символ строки на два таких же символа (например, заменить символ «a» на «aa»), либо, наоборот, заменить два подряд идущих одинаковых символа на один такой же символ.
Необходимо при помощи этих операций сделать все три строки равными какой-то другой общей строке S либо определить, что это сделать невозможно. При этом нужно минимизировать общее количество операций.
Входные данные
Программа получает на вход три строки, состоящие из строчных букв латинского алфавита. Длина каждой строки не превышает 100 символов.
Выходные данные
Если при помощи указанных операций возможно сделать все три строки равными, выведите такую строку S , что суммарное число операций, необходимых для преобразования всех трёх данных строк к строке S , будет минимальным. Если этого сделать нельзя, программа должна вывести одно слово IMPOSSIBLE (заглавными буквами).
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
aaaza
aazzaa
azzza |
aazza |
| 2 |
xy
xxyy
yx |
IMPOSSIBLE |
| |
![]()
|
|
Вопль
Строки
Вожди известного племени Мумба-Юмба решили придумать новый боевой вопль для своих воинов. При этом они решили, что вопль должен состоять ровно из N букв (всего в алфавите племени M букв). Также, после долгих исследований было выяснено, что если в вопле встречается слово si (слово – это последовательность букв алфавита, не длиннее трех символов), то этот вопль вселяет во врага fi единиц страха. Если в вопль входит несколько слов, то их “страшность” суммируется. Например, если вопль содержит слова si и sj, то вопль вселяет fi+fj единиц страха.
Требуется по заданным N, M, алфавиту и списку слов si составить максимально страшный вопль.
Входные данные:
В первой строке записано три числа – N, M и К (0<N≤100, 0<M<25, 0 ≤ K ≤ 100), где K – количество страшных слов. В следующей строке записан алфавит – строка из M строчных латинских букв. Далее в K строках записана информация о словах – само слово и через пробел одно число, обозначающее страшность этого слова (0 < fi ≤ 10000).
Выходные данные:
В выходной файл необходимо вывести страшность полученного вопля и на следующей строке – сам вопль.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 5 4
abcde
abc 10
ab 5
be 7
e 4 |
16
abe |
| |
![]()
|
|
Неправильный палиндром
Строки
Палиндромом называется слово, которое одинаково читается как слева направо, так и справа налево, например, в английском языке такими словами являются «radar» и «racecar».
Света изучает английский язык и решила принять участие в дистанционном конкурсе знатоков английского языка. Но, когда она писала ответ на задание «найдите самое длинное слово, которое является палиндромом», ошиблась и нажала на клавиатуре одну лишнюю клавишу.
Определите, какую букву нужно удалить в набранном Светой слове, чтобы это слово стало палиндромом.
Входные данные
Программа получает на вход строку из строчных английских букв, содержащую не менее 2 и не более 100 000 символов.
Выходные данные
Программа должна вывести единственное число – номер буквы в строке, при удалении которой слово становится палиндромом. Если при удалении любой буквы слово не станет палиндромом, программа должна вывести число 0.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
raceczar |
6 |
| 2 |
car |
0 |
| |
![]()
|
|
Ироха любит строки
Строки
Алгоритмы сортировки
У Ирохи есть последовательность из N строк s1, s2, .., sN. Каждая строка длиной L. Ироха хочет объединить все строки, чтобы получить очень длинную строку. Среди всех строк, которые она может получить таким образом, найдите лексикографически наименьшую.
Будем считать, что строка s = s1s2...sn лексикографически меньше строки t = t1t2...tm, если выполняется одно из следующих условий:
- существует индекс i (\(1<=i<=min(n,m)\)), такой что \(s_j =t_j \), для всех индексов j (\(1<=j<=i\)), и \(s_i <t_i \);
- \(s_i=t_j\) для всех i (\(1<=i<=min(n,m)\)), и \(n<m\).
Входные данные
В первой строке задаются числа N и L. Далее идут строки s1, s2, .., sN, каждая в отдельной строке.
Выходные данные
Выведите лексикографически наименьшую строку, которую может создать Ироха.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 3
dxx
axx
cxx |
axxcxxdxx |
| |
![]()
|
|
Клавиатура Громозеки
Строки
Громозека построил собственную клавиатуру. Эта клавиатура разработана для максимальной простоты, на ней всего 3 клавиши: клавиша 0, клавиша 1 и клавиша backspace.
Тестировать собственную клавиатуру Громозека решил в текстовом редакторе. Этот редактор всегда отображает одну строку (возможно, пустую). При запуске редактора эта строка пуста. При нажатии каждой клавиши на клавиатуре в строке происходят следующие изменения:
- клавиша 0: символ 0 будет вставлен справа от строки;
- клавиша 1: символ 1 будет вставлен справа от строки;
- клавиша backspace: если строка пуста, ничего не происходит. В противном случае удаляется крайняя правая буква строки.
Громозека запустил редактор и несколько раз нажал эти клавиши. Вам дана строке s, которая является записью нажатий клавиш по порядку. В этой строке символ 0 обозначает клавишу 0, символ 1 обозначает клавишу 1, а символ B обозначает клавишу backspace. Определите какая строка теперь отображается в редакторе?
Входные данные
На вход подается строка s (\(1 <= len(s) <=10\)). Строка состоит из символов 0, 1 или B.
Выходные данные
Выведите на экран ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
01B0
|
00
|
| 2 |
0BB1
|
1
|
| |
![]()
|
|
Красивая строка
Строки
Пусть s - строка, состоящая из строчных букв. Мы будем называть строку s красивой, если каждая строчная буква английского алфавита встречается в ней четное количество раз. По заданной строке s, определите, красива ли она.
Входные данные
На вход подается строка. Длина строки не нулевая и не более 100 символов. Строка состоит только из строчных английских букв (a-z).
Выходные данные
Выведите Yes если s красива, в противном случае, выведите No.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
abaccaba |
Yes |
| 2 |
hthth |
No |
| |
![]()
|
|
Тонкий рисунок
Символы
Строки
Другое
Есть изображение высотой H пикселей и шириной W пикселей. Каждый пиксель представлен либо символом . или *. Символ, представляющий пиксель в i-й строке сверху и j-м столбце слева, обозначается Ci,j. Растяните это изображение по вертикали так, чтобы его высота увеличилась вдвое. То есть напечатайте изображение высотой 2H пикселей и шириной W пикселей, где пиксель в i-й строке и j-м столбце равен C(i+1)/2,j (результат деления округляется в меньшую сторону).
Входные данные
В первой строке записаны два целых числа H и W (\(1 <= H, W <=100\)). Затем идут H строк по W символов в строке, где каждый символ либо . либо *.
Выходные данные
Выведите на экран растянутое изображение.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 2
*.
.*
|
*.
*.
.*
.*
|
| 2 |
1 4
***.
|
|
| 3 |
9 20
.....***....***.....
....*...*..*...*....
...*.....**.....*...
...*.....*......*...
....*.....*....*....
.....**..*...**.....
.......*..*.*.......
........**.*........
.........**.........
|
.....***....***.....
.....***....***.....
....*...*..*...*....
....*...*..*...*....
...*.....**.....*...
...*.....**.....*...
...*.....*......*...
...*.....*......*...
....*.....*....*....
....*.....*....*....
.....**..*...**.....
.....**..*...**.....
.......*..*.*.......
.......*..*.*.......
........**.*........
........**.*........
.........**.........
.........**.........
|
| |
![]()
|
|
Мечта
Строки
У Громозеки есть любимая строка S, состоящая из строчных английских букв и пустая строка T. В конец строки T он хочет добавить произвольное количество раз одно из следующих слов: dream, dreamer, erase и eraser. Помогите Громозеке определить, сможет ли он получить S = T.
Формат входных данных
На вход подается строка S (1<= длина строки S <=105), состоящая из строчных английских букв (a-z).
Формат выходных данных
Если возможно получить S = T, выведите YES. В противном случае выведите NO.
| |
![]()
|
|
Хайку
Строки
В качестве новогоднего подарка Громозека получил строку s длиной 19 следующего формата:
[пять строчных английских букв], [семь строчных английских букв], [пять строчных английских букв].
Громозека хочет преобразовать строку s, разделенную запятыми, в строку, разделенную пробелами. Напишите программу для выполнения преобразования за него.
Входные данные
На вход подается одна строка s, длина строки ровно 19 символов. Шестой и четырнадцатый символы в s - это ,. Остальные символы - строчные буквы английского алфавита (a-z).
Выходные данные
Выведите строку после преобразования
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
happy,newyear,enjoy
|
happy newyear enjoy
|
| |
![]()
|
|
Уменьшим-увеличим
Строки
Циклы
У вас есть целочисленная переменная x. Первоначально \(x = 0\). Кто-то дал вам строку S длины N, и, используя эту строку, вы выполнили следующую операцию N раз. В i-й операции вы увеличили значение x на 1, если Si = I, и уменьшили значение x на 1, если Si = D. Найдите максимальное значение, которое принимает x во время операций (в том числе до первой операции и после последней операции).
Формат входных данных
В первой строке задается число N (\(1<=N<=100\)), во второй - строка S. Длина строки N. Строка содержит только символы I и D.
Формат выходных данных
Выведите максимальное значение x, полученное во время операций.
| |
![]()
|
|
A-Z строка
Строки
Громозека решил построить строку, которая начинается с A и заканчивается Z, извлекая подстроку строки s (то есть последовательную часть s). Найдите наибольшую длину строки, которую может построить Громозека. Гарантируется, что всегда существует подстрока s, которая начинается с A и заканчивается Z.
Формат входных данных
На вход подается строка s (1 <= длина строки s <= 2·105 ), состоящая из больших английских букв (A-Z).
Формат выходных данных
Выведите на экран ответ на задачу.
Пояснение к примерам
1. В первом примере, убрав символы с седьмого по одиннадцатый, можно построить строку ASDFZ, которая начинается с A и заканчивается Z.
| |
![]()
|
|
Две одинаковые буквы
Строки
Символы
Дана строка. Известно, что она содержит ровно две одинаковые буквы. Найдите эти буквы. Гарантируется, что повторяются буквы только одного вида.
Входные данные
На вход подается 1 строка.
Выходные данные
Необходимо вывести букву, которая встречается в строке дважды.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
fif |
f |
| |
![]()
|
|
Арифметические печеньки. Очень легкая задача
Условный оператор
Строки
Символы
В уме Громозеки всегда есть целое число. Первоначально в уме Громозеки целое число равно 0. Теперь Громозека собирается съесть четыре печеньки, на каждой из которых написан символи либо + либо -. Когда он ест печеньку с символом +, целое число в его уме увеличивается на 1; когда он ест печеньку с символом -, целое число в его уме уменьшается на 1. Печеньки, которые Громозека собирается съесть, даются вам в виде строки S, i-й символ в S - это i-я печенька, которую он ест. Найдите целое число в уме Громозеки после того, как он съест все печеньки.
Входные данные
На вход подается строка из 4-х символов, каждый из которых равен + или -.
Выходные данные
Выведите целое число в уме Громозеки после того, как он съест все печеньки.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
+-++
|
2 |
| 2 |
-+--
|
-2 |
| 3 |
----
|
-4 |
| |
![]()
|
|
Множество формул
Простые задачи на перебор
Строки
Вам дана строка S, состоящая из цифр от 1 до 9 включительно. Вы можете вставить символ + в некоторые позиции (возможно, ни в одну) между двумя цифрами в этой строке. Здесь знак + не должен появляться последовательно после вставки (т.е. не должно быть два и больше знака + подряд). Все строки, которые можно получить таким образом, можно оценить как формулы. Оцените все возможные формулы и распечатайте сумму результатов, полученных при вычислении всех возможных формул.
Входные данные
На вход подается непустая строка S, состоящая из цифр от 1 до 9 включительно. Длина строки не более 10 символов.
Выходные данные
Выведите сумму результатов, полученных при вычислении всех возможных формул.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
125 |
176 |
Всего можно получить 4 формулы: 125, 1 + 25, 12 + 5 и 1 + 2 + 5.
Результат после вычисления каждой формулы:
125
1 + 25 = 26
12 + 5 = 17
1 + 2 + 5 = 8
Таким образом, сумма 125 + 26 + 17 + 8 = 176. |
| 2 |
9999999999 |
12656242944 |
|
| |
![]()
|
|
Статистика
Строки
Дан текст. Напишите программу, которая посчитает статистику - сколько раз встречается буква A, сколько - B и т.д. При этом большие и маленькие латинские буквы считать одинаковыми. В тексте могут быть сколь угодно длинные строки. Длина текста не превышает 100 Кб.
Входные данные
На вход подается текст, состоящий из английских букв (больших и маленьких), знаков препинания, цифр и т.д.
Выходные данные
Выведите 26 строк. Каждая строка должна соответствовать латинской букве, буквы должны идти в алфавитном порядке.Каждая строка должна содержать сначала большую латинскую букву, которой она соответствует, пробел, символ - (тире), пробел и число: сколько раз буква встречается во входном файле.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
Ab - a |
A - 2
B - 1
C - 0
D - 0
<...здесь в выходном файле перечисляются все буквы...>
Z - 0
|
| |
![]()
|
|
Средний балл по предметам - 2
Структуры
Строки
Определите средний балл всех учащихся по каждому предмету.
Входные данные
В первой строке задается количество учащихся n (\(0 < n <=100\)). Далее идет n строк, каждая из которых содержит фамилию, имя и три числа (оценки по трем предметам: математике, физике, информатике). Данные в строке разделены одним пробелом. Оценки принимают значение от 1 до 5.
Выходные данные
Выведите три действительных числа, разделяя их одним пробелом: средний балл всех учащихся по математике, по физике, по информатике.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2
Markov Valeriy 4 5 2
Kozlov Georgiy 5 1 2
|
4.5 3 2 |
| |
![]()
|
|
Учащиеся без троек
Строки
Структуры
Выведите фамилии и имена учащихся, не имеющих троек (а также двоек и колов).
Входные данные
Заданы сначала количество учащихся n, затем n строк, каждая из которых содержит фамилию, имя и три числа (оценки по трем предметам: математике, физике, информатике). Данные в строке разделены одним пробелом. Оценки принимают значение от 1 до 5.
Выходные данные
Необходимо вывести пары фамилия-имя по одной на строке, разделяя фамилию и имя одним пробелом. Выводить оценки не нужно. Порядок вывода должен быть таким же, как в исходных данных.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
Babat Anna 5 4 3
Belova Galina 4 3 5
Moroz Yaroslav 3 5 4 |
|
| |
![]()
|
|
Трое лучших
Строки
Структуры
Определите трех учащихся с наилучшим средним баллом по трем предметам. Выведите фамилии и имена этих учащихся. Если при этом у нескольких учащихся средний балл совпадает со средним баллом учащегося, "занявшего 3-е место", то необходимо вывести их всех.
Входные данные
Заданы сначала количество учащихся n, затем n строк, каждая из которых содержит фамилию, имя и три числа (оценки по трем предметам: математике, физике, информатике). Данные в строке разделены одним пробелом. Оценки принимают значение от 1 до 5.
Выходные данные
Необходимо вывести пары фамилия-имя по одной на строке, разделяя фамилию и имя одним пробелом. Выводить оценки не нужно. Порядок вывода должен быть таким же, как в исходных данных.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
Yakovlev Ivan 5 5 5
Yapryntsev Aleksey 5 5 5
Kozlov Georgiy 5 5 5 |
Yakovlev Ivan
Yapryntsev Aleksey
Kozlov Georgiy |
| |
![]()
|
|
Отсортировать по среднему баллу
Строки
Структуры
Выведите фамилии и имена учащихся в порядке убывания их среднего балла.
Входные данные
Заданы сначала количество учащихся n, затем n строк, каждая из которых содержит фамилию, имя и три числа (оценки по трем предметам: математике, физике, информатике). Данные в строке разделены одним пробелом. Оценки принимают значение от 1 до 5.
Общее число учащихся не превосходит 100001.
Выходные данные
Необходимо вывести пары фамилия-имя по одной на строке, разделяя фамилию и имя одним пробелом. Выводить оценки не нужно. Если несколько учащихся имеют одинаковые средние баллы, то их нужно выводить в порядке, заданном во входных данных.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2
Markov Valeriy 1 1 1
Ivanov Ivan 2 2 2 |
Ivanov Ivan
Markov Valeriy |
| 2 |
3
Markov Valeriy 5 5 5
Sergey Petrov 1 1 1
Petrov Petr 3 3 3 |
Markov Valeriy
Petrov Petr
Sergey Petrov |
| |
![]()
|
|
Скучная лекция
Строки
Лёша сидел на лекции. Ему было невероятно скучно. Голос лектора казался таким далеким и незаметным...
Чтобы окончательно не уснуть, он взял листок и написал на нём свое любимое слово. Чуть ниже он повторил своё любимое слово, без первой буквы. Ещё ниже он снова написал своё любимое слово, но в этот раз без двух первых и последней буквы.
Тут ему пришла в голову мысль — времени до конца лекции все равно ещё очень много, почему бы не продолжить выписывать всеми возможными способами это слово без какой-то части с начала и какой-то части с конца?
После лекции Лёша рассказал Максу, как замечательно он скоротал время. Максу стало интересно посчитать, сколько букв каждого вида встречается у Лёши в листочке. Но к сожалению, сам листочек куда-то запропастился.
Макс хорошо знает любимое слово Лёши, а ещё у него не так много свободного времени, как у его друга, так что помогите ему быстро восстановить, сколько раз Лёше пришлось выписать каждую букву.
Входные данные
На вход подаётся строка, состоящая из строчных латинских букв — любимое слово Лёши.
Длина строки лежит в пределах от 5 до 100 000 символов.
Выходные данные
Для каждой буквы на листочке Лёши, выведите её, а затем через двоеточие и пробел сколько раз она встретилась в выписанных Лёшей словах (см. формат вывода в примерах). Буквы должны следовать в алфавитном порядке. Буквы, не встречающиеся на листочке, выводить не нужно.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
hello |
e: 8
h: 5
l: 17
o: 5 |
| 2 |
abacaba |
a: 44
b: 24
c: 16 |
Примечание
Пояснение к первому примеру. Если любимое Лёшино слово — "hello", то на листочке у Лёши будут выписаны следующие слова:
"hello"
"hell"
"ello"
"hel"
"ell"
"llo"
"he"
"el"
"ll"
"lo"
"h"
"e"
"l"
"l"
"o"
Среди этих слов 8 раз встречается буква "e", 5 раз — буква "h", 17 раз — буква "l" и 5 раз буква "o".
| |
![]()
|
|
Получите OK
Строки
Префиксные суммы(минимумы, ...)
Дана строка S длины N, состоящая из символов S, T, O и K. Дайте ответ на Q запросов следующего вида.
Запрос i(1 <= i <= Q): для заданных целых чисел li и ri (1 <= li< ri <= N), рассматривается подстрока S, начинающаяся с индекса li и заканчивающася индексом ri (оба включительно). Необходимо определить, сколько раз в этой строке втречается OK как подстрока?
Пояснение
Подстрока строки - это строка, полученная удалением нуля или более символов из начала и конца строки исходной строки. Например, для строки KOTS подстроками будут строки KO, KOT, OT, OTS, (пустая строка) и другие, но не OK.
Входные данные
В первой строке записаны два числа N (2<=N<=105) и Q (1<=Q<=105). Во второй строке записана строка S длины N. Каждый символ строки это S, T, O или K. Далее идут Q строк по 2 числа в каждой: li и ri (1 <= li< ri <= N).
Выходные данные
Выведите Q строк. I-я строка должна содержать ответ на i-й запрос.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
8 3
OKOKTOKS
3 7
2 3
1 8 |
2
0
3 |
| |
![]()
|
|
Голодная пешка
Строки
Условный оператор
Вывод формулы
Громозека уважает игры на шахматной доске. На обычной доске размером 8х8 у Громозеки стоит голодная пешка. Голодная пешка каждым ходом съедает какую-либо фигуру соперника (т.е. она может пойти по диагонали вперед на 1 клетку вправо или влево, назад пойти она не может). Громозека, не глядя на доску, научился определять, может ли голодная пешка попасть с одной клетки доски на другую. Превращаться в ферзя голодной пешке нельзя.
Напишите программу, с помощью которой вы могли бы также легко проверить Громозеку.
Входные данные
Программа получает на вход две клетки шахматной доски в шахматной нотации. Сначала клетка, где стоит голодная пешка, а затем, через пробел, клетка, куда голодная пешка должна попасть.
Выходные данные
Выведите слово YES (заглавными буквами), если голодная пешка может попасть из первой клетки во вторую, и NO в противном случае.
Доска имеет размер 8x8, вертикали нумеруются маленькими латинскими буквами от a до h, горизонтали - числами от 1 до 8. Исходная и конечная клетки не совпадают.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
a1 b2 |
YES |
| 2 |
b2 a1 |
NO |
| 3 |
a1 h7 |
NO |
| |
![]()
|
|
Коровий алфавит
Перебор
Строки
Малоизвестен тот факт, что у коров свой алфавит "cowphabet". Он состоит из тех же 26 букв от 'a' до 'z', но в другом порядке.
Чтобы скоротать время, Беси бормочет cowphabet опять и опять. Фермеру Джону интересно, сколько раз она его пробормотала.
По заданной строке букв, которые ФД расслышал из бормотания Беси, определите минимальное количество раз, которое Беси должна пробормотать cowphabet, чтобы ФД услышал заданную строку. ФД не всегда обращает внимание на бормотание Беси, поэтому он может не расслышать некоторые буквы из бормотания Беси. Данная Вам строка содержит только те буквы, которые он услышал.
Входные данные
Первая строка ввода содержит 26 маленьких латинских букв от 'a' до 'z' в порядке их появления в cowphabet. Следующая строка содержит строку из маленьких латинских букв, которые услышал ФД. Эта строка имеет длину от 1 до 1000.
Выходные данные
Выведите минимальное количество раз, которое Беси пробормотала алфавит.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
abcdefghijklmnopqrstuvwxyz
mood
|
3 |
В этом примере cowphabet упорядочен как нормальный алфавит.
Бесси пробормотала cowphabet как минимум 3 раза. Ниже показано, как Беси бормотала, и большими буквами - какие буквы услышал ФД.
abcdefghijklMnOpqrstuvwxyz abcdefghijklmnOpqrstuvwxyz abcDefghijklmnopqrstuvwxyz
|
| |
![]()
|
|
Анализ файла
ЕГЭ_информатика
Строки
Текстовый файл состоит не более чем из 106 символов и содержит только заглавные буквы латинского алфавита (ABC…Z). Текст разбит на строки различной длины. Назовем подпоследовательность оригинальной, если она ограничена слева подстрокой AВ, а справа подстрокой BA (данные подстроки также входят в подпоследовательность) и при этом в этой подпоследовательности нет других букв А и B. Оригинальная подпоследовательность не может начинаться в одной строке, а заканчиваться в другой.
Определите, сколько всего оригинальных подпоследовательностей во всем файле, а также длину максимальной из них.
В ответе укажите слитно два целых числа, сначала количество оригинальных подпоследовательностей, затем - длину максимальной из них.
Пример
Исходный файл:
AAABCAABCBAA
ZZABZZZBABCBA
QRABUTUUBA
В этом примере всего 4 оригинальных подпоследовательности (AВСВА, ABZZZBA, ABCBA, ABUTUTBA)
Самая длинная подпоследовательность (ABUTUTBA) имеет длину 8.
Ответ: 48
Файл к заданию
| |
![]()
|
|
Индексы и срезы
Символы
Строки
На вход программы поступает строка s. Используя обращения к символам по индексу и срезы строк выведите следующие подстроки:
- все символы, начиная с индекса 3, до середины строки включительно (при нечетной длине строки, средний символ не брать);
- последний символ;
- все символа с четными индексами (0, 2, ...);
- все символы с нечетнымы индексами (1, 3, ...);
- все символы, кроме последнего;
- все символы, кроме первого;
- все символы в обратном порядке;
- все символы в обратном порядке, начиная с 3 с конца, и кроме первых двух;
- все символы первой половины в обратном порядке, кроме первого (при нечетной длине строки, средний символ не брать);
- скопировать срезом всю строку s в строку
s2.
Допишите строчки в программе.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
Hallo, World! |
lo,
!
Hlo ol!
al,Wrd
Hallo, World
allo, World!
!dlroW ,ollaH
lroW ,oll
,olla
Hallo, World! |
| |
![]()
|
|
Строки с гласными и согласными
Задачи на процедуры и функции
Строки
Символы
Напишите функцию vowels_count, которая принимает строку и подсчитывает количество английских гласных в ней.
Английские гласные буквы: a, e, i, o, u, y.
Используя данную функцию, определите две строки:
s1 - строку с самым большим числом гласных букв (если таких строк несколько, взять ту, которая встретится раньше).
s2 - строку с самым маленьким числом согласных букв (если таких строк несколько, взять ту, которая встретится раньше).
Входные данные
В первой строке подается натуральное число n (1 < n <= 10) - количество строк. Далее идут n строк. Каждая строка состоит из английских маленьких букв и пробелов.
Выходные данные
Выведите на экран две строки: сначала строку s1, затем, с новой строки - s2. Наименьшую из данных строк выровняйте по длине с наибольшей, добавив слева строки символы '*'.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4
mama papa
doughter son
brother sister
grandmama grandpa |
grandmama grandpa
********mama papa |
| |
![]()
|
|
Чего не хватает?
Строки
Символы
Вам дается строка S длиной ровно 9 символов. Каждый символ в строке - это любая из цифр от 0 до 9. Все символы в строке различны. Выведите цифру, которой не хватает в строке.
Входные данные
На вход подается строка, состоящая из цифр.
Выходные данные
Выведите на экран ответ на задачу
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
023456789
|
1
|
| 2 |
459230781
|
6
|
| |
![]()
|
|
Шаг вправо
Строки
Есть 4 квадрата, нарисованных горизонтально в ряд.
Вам дана строка S длиной 4, состоящие из 0 и 1.
Если i-й символ S равен 1, в i-м квадрате слева есть человек;
если i-й символ S равен 0, в i-м квадрате слева нет человека.
Теперь все одновременно делают шаг вправо. То есть переходят на следующую клетку справа. При этом перемещении человек, который изначально находился в крайнем правом квадрате, выбывает.
Определите, останется ли человек на каждой клетке после хода.
Выведите результат в виде строки в том же формате, что и S. (Для наглядности см. пример ввода / вывода).
Входные данные
На вход подается строка S длиной 4, состоящие из 0 и 1.
Выходные данные
Выведите строку длиной 4. i-й символ должен быть равен 1, если в i-м квадрате слева после перемещения будет человек, и 0 в противном случае.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1011
|
0101
|
| 2 |
1111
|
0111
|
| |
![]()
|
|
Когда же суббота
Строки
Условный оператор
Однажды, устав от похода в школу, Томми захотел узнать, сколько дней осталось до субботы. Мы знаем, что этот день был будним, и название дня недели было S (по-английски).Сколько дней оставалось до первой субботы после этого дня (считая саму субботу, но не считая день S)?
Входные данные
На вход подается строка S (S может быть Monday, Tuesday, Wednesday, Thursday или Friday).
Выходные данные
Выведите на экран ответ на задачу
Используйте вложенные условия (конструкцию elif для языка Python и else if для других языков).
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
Wednesday
|
3
|
| |
![]()
|
|
Символы перед запятой
Строки
Символы
Дано предложение. Напечатать все его символы, предшествующие первой запятой. Если запятых в предложении нет, то вывести все предложение.
Решите задачу, не используя встроенные функции работы со строками, за исключением функции, возвращающей длину строки.
Входные данные: в первой строке задается исходное предложение.
Выходные данные: необходимо вывести все символы предложения, которые предшествуют первой запятой, если запятых нет - вывести все предложение
Пример входных и выходных данных
| № теста |
Входные данные |
Выходные данные |
| 1 |
fore, s t.
|
fore |
| 2 |
fore s t. |
fore s t. |
| |
![]()
|
|
Первая "e"
Строки
Символы
Дано предложение, в котором имеется несколько букв 'e' (англ.). Найти порядковый номер первой из них.
Решите задачу, не используя встроенные функции работы со строками, за исключением функции, возвращающей длину строки.
Входные данные: в первой строке задается исходное предложение.
Выходные данные: необходимо вывести номе первой буквы "е" (англ) в предложении
Пример входных и выходных данных
| № теста |
Входные данные |
Выходные данные |
| 1 |
foresete |
4 |
| |
![]()
|
|
Найди "a"
Символы
Строки
Дано предложение. Определить, есть ли в нем буква " a" (англ.). В случае положительного ответа вывести порядковый номер первой из них. В случае отрицательного - вывести слово NO.
Решите задачу, не используя встроенные функции работы со строками, за исключением функции, возвращающей длину строки.
Входные данные: в первой строке задается исходное предложение.
Выходные данные: выведите ответ на задачу.
Пример входных и выходных данных
| № теста |
Входные данные |
Выходные данные |
| 1 |
foresete |
NO |
| 2 |
forast |
4 |
| |
![]()
|
|
Перевертыш
Строки
Символы
Дано слово. Проверить, является ли оно "перевертышем", (то есть читается одинаково как сначала, так и с конца).
Решите задачу, не используя встроенные функции работы со строками, за исключением функции, возвращающей длину строки.
Входные данные: в первой строке задается слово.
Выходные данные: необходимо вывести слово "YES", если слово является перевертышем, и слово "NO" - в противном случае
Пример входных и выходных данных
| № теста |
Входные данные |
Выходные данные |
| 1 |
foresete |
NO |
| 2 |
halah |
YES |
| |
![]()
|
|
Сколько "i"
Строки
Символы
Дана строка, разбитая на предложения. Все предложения заканчиваются знаком точка. Определить количество букв 'i' в первом предложении.
Решите задачу, не используя встроенные функции работы со строками, за исключением функции, возвращающей длину строки.
Входные данные: программа получает на вход строку.
Выходные данные: необходимо вывести количество букв 'i' в первом предложении.
Пример входных и выходных данных
| № теста |
Входные данные |
Выходные данные |
| 1 |
foresete. forest. |
0 |
| 2 |
firist. forist |
2 |
| |
![]()
|
|
Сколько "o"
Строки
Символы
Дано предложение, в котором нет символа "-". Определить количество букв "o" (англ.) в первом слове. В начале предложения могут быть пробелы.
Решите задачу, не используя встроенные функции работы со строками, за исключением функции, возвращающей длину строки.
Входные данные: в единственной строке задается исходное предложение.
Выходные данные: необходимо вывести количество букв "о" (англ.) в первом слове.
Пример входных и выходных данных
| № теста |
Входные данные |
Выходные данные |
| 1 |
fore sete. |
1 |
| 2 |
hal ah. |
0 |
| |
![]()
|
|
Префикс
Символы
Строки
Дано два слово. Определить, сколько начальных букв первого слова совпадает с начальными буквами второго слова
Решите задачу, не используя встроенные функции работы со строками, за исключением функции, возвращающей длину строки.
Входные данные: в первой строке задается два слова через пробел
Выходные данные: необходимо вывести количество совпадающих с начала букв
Пример входных и выходных данных
| № теста |
Входные данные |
Выходные данные |
| 1 |
fore forest |
4 |
| 2 |
forest torest |
0 |
| |
![]()
|
|
Сколько "n" перед запятой
Символы
Строки
Дано предложение. Определить количество букв "n", предшествующих первой запятой предложения. Если запятой нет, то считать до конца предложения.
Решите задачу, не используя встроенные функции работы со строками, за исключением функции, возвращающей длину строки.
Входные данные: в первой строке задается исходное предложение.
Выходные данные: выведите одно число - ответ на задачу
Примеры
| № теста |
Входные данные |
Выходные данные |
| 1 |
fore, sete. |
0 |
| 2 |
hanah. |
1 |
| |
![]()
|
|
Первые одинаковые
Строки
Символы
Дано предложение. Определить порядковые номера первой пары одинаковых соседних символов. Если таких символов нет, то вывести на экран слово NO.
Решите задачу, не используя встроенные функции работы со строками, за исключением функции, возвращающей длину строки.
Входные данные
В первой строке задается предложение длиной не более 255 символов (в начале и конце предложения нет пробелов).
Выходные данные
Необходимо вывести через пробел порядковые номера первой пары одинаковых соседних символов, или слово "NO" - если такой пары соседних символов нет (первый символ в предложении имеет порядковый номер 1).
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
foresete |
NO |
| 2 |
haah |
2 3 |
| |
![]()
|
|
Одинаковые в начале
Символы
Строки
Дана последовательность символов, в начале которой имеется некоторое количество одинаковых символов. Определить это количество.
Решите задачу, не используя встроенные функции работы со строками, за исключением функции, возвращающей длину строки.
Входные данные: в первой строке задается последовательность символов.
Выходные данные: необходимо вывести количество одинаковых симвлов в начале строки.
Пример входных и выходных данных
| № теста |
Входные данные |
Выходные данные |
| 1 |
foresete |
0 |
| 2 |
ааав |
3 |
| |
![]()
|
|
Сколько слов в предложении
Строки
Символы
В строке записано предложением. Напишите программу, которая будет определять количество слов в нем. В предложении между словами только один пробел, в конце и в начале пробелов нет.
Пример входных и выходных данных
| № теста |
Входные данные |
Выходные данные |
| 1 |
test |
1 |
| 2 |
test test |
2 |
| |
![]()
|
|
Измени регистр
Символы
Строки
Измените регистр символа. Если он был строчной английской буквой сделайте его заглавной буквой; если он был заглавной английской буквой - строчной.
Входные данные
Задан единственный символ c.
Выходные данные
Необходимо вывести получившийся символ.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
a |
A |
| 2 |
B |
b |
| |
![]()
|
|
Замени символы
Символы
Строки
В одной строке записаны символ и некторый текст. Напишите программу, которая заменяет все символы текста, стоящие на четных местах, заданным символом. Нумерация символов начинается с 1.
Пример входных и выходных данных
| № теста |
Входные данные |
Выходные данные |
| 1 |
t slovo |
stoto |
| 2 |
a test test |
tasa aeat |
| |
![]()
|
|
Замена одного на другой
Символы
Строки
В одной строке через пробел заданы два символа и некоторый текст. Напишите программу, которая заменить в тексте все буквы, совпадающие с первым символом, на второй.
Пример входных и выходных данных
| № теста |
Входные данные |
Выходные данные |
| 1 |
a b slovo |
slovo |
| 2 |
r t rr rr |
tt tt |
| |
![]()
|
|
Символы на нужных местах
Символы
Строки
В одной строке через пробел записаны число и некоторый текст. Напишите программу, которая выводит из текста те символы, номера которых кратны заданному числу (нумерация начинается с 1).
Пример входных и выходных данных
| № теста |
Входные данные |
Выходные данные |
| 1 |
2 slovo |
lv |
| 2 |
3 test test |
stt |
| |
![]()
|
|
Считаем цифры
Символы
Строки
Дана строка. Напишите программу, которая определяет, есть ли в заданной строке цифры.
Пример входных и выходных данных
| № теста |
Входные данные |
Выходные данные |
| 1 |
test |
NO |
| 2 |
Ocenka-5 |
YES |
| |
![]()
|
|
Слово с нужной буквой на конце
Символы
Строки
В одной строке через пробел записаны символ и предложение. Напишите программу, которая подсчитывает сколько в предложении слов, оканчивающихся на заданный символ. В предложении между словами только один пробел, в конце и в начале пробелов нет.
Пример входных и выходных данных
| № теста |
Входные данные |
Выходные данные |
| 1 |
a b |
0 |
| 2 |
t test slovo |
1 |
| |
![]()
|
|
Строковый сдвиг
Алгоритмы сортировки
Строки
В непустой строке сдвиг влево перемещает первый символ в конец строки, а сдвиг вправо перемещает последний символ в начало строки. Например, сдвиг влево на строке abcde приводит к bcdea, а два сдвига вправо на abcde приводят к deabc.
Дана непустая строка S, состоящая из строчных латинских букв. Среди строк, которые можно получить, выполнив ноль или более сдвигов влево и ноль или более сдвигов вправо, найдите лексикографически наименьшую строку и лексикографически наибольшую строку.
Входные данные
На вход подается одна строка S. S состоит из строчных английских букв. 1 <= |S| <= 1000, где |S| - длина строки S.
Выходные данные
Выведите в первой строке лексикографически наименьшу строку, во второй - лексикографически наибольшую строку.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
aaba |
aaab
baaa |
| 2 |
z |
z
z |
| 3 |
abracadabra |
aabracadabr
racadabraab |
| |
![]()
|
|
БОльшие цифры
Строки
Типы данных
Пусть S(n) - сумма цифр в десятичной системе счисления целого числа n. Например, S(123)=1+2+3=6.
Для двух трехзначных целых чисел A и B, найдите большее из S(A) и S(B).
Входные данные
На вход подается одна строка, содержащая два целых числа A и B (100 <= A, B <= 999).
Выходные данные
Выведите значение большего из значений S(A) и S(B). Если они равны, выведите S(A).
Обратите внимание, что при решении задачи нельзя пользоваться операциями деления.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
123 234 |
9 |
| |
![]()
|
|
Копирование n-ok
Типы данных
Строки
Пусть \(N(n,k) = n+\overline{nn}+\overline{nnn} + ... +\underbrace{\overline{n..n}}_{k}\). По заданному значению n и k посчитайте значение N(n, k).
Входные данные
Программа получает на вход две строки. В первой строке записано натуральное число n (1<=n<=9), во второй строке - натуральное число k (1 <= k <= 10).
Выходные данные
Выведите на экран N(n, k) в виде выражения и ответа.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1
3
|
1+11+111=123
|
| |
![]()
|
|
Подстрока
Бинарный поиск по ответу
Строки
"Два указателя"
В этой задаче Вам требуется найти максимальную по длине подстроку данной строки, такую что каждый символ встречается в ней не более k раз.
Входные данные
В первой строке даны два целых числа n и k (1 ≤ n ≤ 100000, 1 ≤ k ≤ n ) , где n – количество символов в строке. Во второй строке n символов – данная строка, состоящая только из строчных латинских букв.
Выходные данные
В выходной файл выведите два числа – длину искомой подстроки и номер её первого символа. Если решений несколько, выведите любое.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 1
abb |
2 1 |
| 2 |
5 2
ababa |
4 1 |
| |
![]()
|
|
Когда же Новый год?
Строки
Условный оператор
Томми очень любит Новый год! 31 декабря в этом году приходится на субботу. Томми захотел узнать, сколько дней осталось до 31 декабря. Мы знаем, что сегодня будний день S (по-английски) и 31 декабря уже на этой неделе в субботу. Помогите Томми определить сколько дней оставалось до 31 декабря после сегодня (считая день 31 декабря, но не считая сегодняшний день S)?
Входные данные
На вход подается строка S (S может быть Monday(понедельник), Tuesday(вторник), Wednesday(среда), Thursday(четверг) или Friday(пятница)).
Выходные данные
Выведите на экран ответ на задачу
Используйте вложенные условия (конструкцию elif для языка Python и else if для других языков).
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
Wednesday
|
3
|
| |
![]()
|
|
Летовец пакует строчки
Строки
Летовец не любит много писать. Поэтому, чтобы сократить свои записи, он использует упаковку, принцип которой заключается в удалении повторяющихся букв и замены их на числа, определяющих количество повторений.
Будем рассматривать только строчки, состоящие из заглавных латинских букв. Например, рассмотрим строку AAAABCCCCCDDDD. Данная строка может быть представлена как 4AB5C4D.
Напишите программу, которая поможет Летовцу восстановить по упакованной строке исходную.
Входные данные
Входные данные содержат одну упакованную строку. В строке могут встречаться только конструкции вида nA, где n — количество повторений символа (целое число от 2 до 99), а A — заглавная латинская буква, либо конструкции вида A, то есть символ без числа, определяющего количество повторений. Максимальная длина строки не превышает 80.
Выходные данные
Выведите восстановленную строку. При этом строка должна быть разбита на строчки длиной ровно по 40 символов (за исключением последней, которая может содержать меньше 40 символов).
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
ABC |
ABC |
| 2 |
O2A3O2AO |
OAAOOOAAO |
| 3 |
A2B3C4D5E6F7G |
ABBCCCDDDDEEEEEFFFFFFGGGGGGG |
| |
![]()
|
|
Цветочек
Строки
Напишите программу, которая рисует картинку размером 7х5 символов.
0 0
0 " 0
0 0
\/\
\/
| |
![]()
|
|
Первый уникальный
Строки
Сортировка подсчетом
Символ называется уникальным, если он встречается в строке один раз. Первый уникальный символ - это уникальный символ с наименьшим индексом.
Дана строка s. Найдите первый уникальный символ в данной строке. Выведите его индекс. Если в строке нет уникальных символов, выведите -1.
Входные данные
Программа получает на вход последовательность непробельных символов s.
Ограничения
'a' <= s[i] <= 'z'
0 <= i <= 255
Выходные данные
Выведите ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
silvertests
|
1 |
| 2 |
sstt
|
-1 |
| |
![]()
|
|
Сортировка строки по частоте букв
Строки
Сортировка подсчетом
Дана строка s. Отсортируйте символы данной строки в порядке убывания частоты встречаемости. Частота встречаемости символа - это количество раз, которое данный символ встречается в строке.
Выведите отсортированную строку. Если два символа встречаются одинаковое количество раз, то они должны идти в лексикографическом порядке.
Входные данные
Программа получает на вход
Ограничения
1 <= s.length <= 5 * 105 (s.length - длина строки s)
s содержит большие и маленькие английские буквы и цифры.
Выходные данные
Выведите отсортированную строку.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
tree
|
eert
|
| 2 |
cccaaa
|
aaaccc
|
| 3 |
Aabb
|
bbAa
|
| |
![]()
|
|
(C++) Обращение к символам строки
Строки
На вход программе подаются две строки:
- в первой строке задается слово s;
- во второй - три целых числа a, b, c (каждое число находится в диапазоне [0; len(s)-1])
Выведите на экран новое слово, образованное символами с индексами a, b, c (в указанном порядке)
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
информатика
2 3 4 |
фор |
| |
![]()
|
|
Судьба Королевства
Символы
Строки
Условный оператор
В далеком царстве жил могущественный маг по имени Эльдрик, который был помешан на шахматах. В башне Эльдрика была волшебная шахматная доска, о которой говорили, что она предсказывает будущее королевства. Но был казус. Шахматные фигуры двигались только по белым клеткам, а черные клетки хранили секреты прошлого.
Однажды молодой оруженосец по имени Леон решил узнать все секреты прошлого и пошел к башне. Маг Эльдриг дал оруженосцу пергамент, на котором были написаны координаты одной клетки шахматной доски. Эльдриг сказал, что если он сумеет не глядя на доску определить какой цвет у данной клетки шахматной доски, то ему откроются все секреты прошлого!
Леон не был так помешан на шахматах, но все же смог определить цвет клетки правильно! Сможете ли это сделать и вы?
Шахматная доска выглядит таким образом

Формат входных данных
Программа получает на вход одну строку, в которой записана координата шахматной клетки.
Ограничения
длина строки == 2'a' <= первый символ строки <= 'h''1' <= второй символ строки <= '8'
Формат выходных данных
Выведите слово white, если клетка белого цвета и black - если черного.
| |
![]()
|
|
Чемпионат по поиску в сети Меганет
Структуры данных
Строки
Динамическое программирование
Конструктив
Задача на реализацию
Для проведения чемпионата мира по поиску в сети Меганет организаторам необходимо ограничить доступ к некоторым адресам. Адрес в сети Меганет представляет собой строку, состоящую из имени сервера и имени раздела.
Имя сервера представляет собой строку, содержащую от одной до пяти частей включительно. Каждая часть представляет собой непустую строку, состоящую из строчных букв латинского алфавита. Части разделены точкой. Примеры корректных имен сервера: «a», «ab.cd», «abacaba», «a.b.c.d.e».
Имя раздела представляет собой строку, которая может быть либо пустой, либо содержать от одной до пяти частей включительно. Каждая часть начинается с символа «/», после которого следует одна или несколько строчных латинских букв. Примеры корректных имен разделов: «», «/a», «/aba», «/a/b/c/d/e». Адрес формируется приписыванием имени раздела в конец имени сервера. Например, корректными адресами являются строки: «a», «aba/d/f/g/h», «a.b», «aba.caba/def/g», «c.d.e.f.g/a/b/c/d/e».
Для ограничения доступа к некоторым адресам сети Меганет организаторы чемпионата подготовили несколько фильтров. Фильтр, как и адрес, состоит из двух частей: фильтра сервера и фильтра раздела.
Фильтр сервера состоит из имени сервера, перед которым может также идти строка «*.». Если фильтр сервера представляет собой только имя сервера, то этому фильтру соответствует только сервер, имеющий точно такое же имя. Если фильтр сервера представляет собой строку «*.S », где S — имя сервера, то ему соответствуют сервера, удалением нуля или более начальных частей от имени которых можно получить строку S.
Аналогично, фильтр раздела представляет собой имя раздела, после которого может идти строка «/*». Фильтру раздела, который представляет собой просто имя раздела R, соответствуют только разделы, в точности совпадающие с R. Если фильтр раздела представляет собой строку «R/*», то ему соответствуют все разделы, удалением от имен которых нуля или более конечных частей можно получить строку R. Адрес соответствует фильтру, если его имя сервера соответствует фильтру сервера, а его имя раздела соответствует фильтру раздела.
Примеры фильтров и соответствующих им адресов приведены в таблице ниже.
| ab.c/d/e |
ab.c/d/e |
| *.a |
a ax.a efg.a |
| *.a/b/c |
a/b/c x.a/b/c e.fg.a/b/c |
| x.yz/a/* |
x.yz/a x.yz/a/b/c x.yz/a/xyz |
| *.a/* |
a x.a e.fg.a
a/b/c x.a/ddd/c e.fg.a/b/c/g/haha/i |
| *.a/b/c/* |
a/b/c x.a/b/c e.fg.a/b/c
a/b/c/xxx e.fg.a/b/c/d/e/f |
| |
|
Требуется написать программу, которая по заданному набору фильтров и списку адресов определяет для каждого адреса, какому числу фильтров соответствует этот адрес.
Пример:
Ввод:
2 0
a.bb/c
bb/c/d
4
a.bb
bb/c/d
a.bb/c/d
bb/c
Вывод:
0
1
0
0
Вывод:
4 0
*.bb/c
*.bb/c/*
bb/c/*
bb/c/*
6
bb
bb/c
bb/c/d
a.bb
a.bb/c
a.bb/c/d
Вывод:
0
4
3
0
2
1
| |
![]()
|
|
Британские учёные и Василий
Z-функция. Префикс-функция
Строки
По рзелульаттам илссеовадний одонго анлигйсокго унвиертисета, не иеемт занчнеия, в кокам пряокде рсапожолены бкувы в солве. Галвоне, чотбы преавя и пслоендяя бквуы блыи на мсете. Осатьлыне бкувы мгоут селдовтаь в плоонм бсепордяке, все-рвано ткест чтаитсея без побрелм. Пичрионй эгото ялвятеся то, что мы чиатем не кдаужю бкуву по отдльенотси, а все солво цликеом.
Вдохновившись исследованием британских учёных о восприятии человеком текста, Вася решил, что современная письменность нуждается в серьёзном упрощении. В частности, в лексиконе Васи все слова состоят только из букв a, b и c. Кроме того, память у Васи плохая, поэтому Вася помнит лишь слова, которые содержат не более L букв.
Более того, с тех пор как наш юный друг пролил кофе на свой любимый ноутбук, он не утруждает себя нажатием клавиши пробел (объясняя это тем, что и отсутствие пробелов в тексте совершенно не мешает его пониманию). Однако остальные клавиши клавиатуры работают исправно, что позволяет Васе набирать все известные ему слова без единой орфографической ошибки.
Британские учёные очень заинтересовались исследованиями Васи. Они вступили с молодым учё- ным в активную переписку, однако, получив очередное Васино сообщение были несколько озадачены тем, что же он имел ввиду. Так как разобраться они так и не смогли, а очередное революционное открытие уже было проанонсировано в СМИ, они решили как-то оценить уровень гениальности автора. Для этого они решили понять, а из какого минимального количества слов может состоять словарный запас Василия?
Формат входных данных
В первой строке входных данных содержится целое число L — максимальная длина слова, кото- рое может содержаться в лексиконе Васи (1 <= L <= 10 000). В следующей строке содержится непустое сообщение, полученное учеными. Длина сообщения не превосходит 20 000 символов.
Формат выходных данных
В первой строке выведите единственное число K — минимальное количество слов, которые дол- жен знать Василий, чтобы написать данное сообщение. В следующих K строках выведите сами сло- ва, каждое из которых должно иметь длину не превосходящую L. В случае, если ответов несколько, разрешается выдать любой из них.
Пример
Ввод:
3
ababaabab
Вывод:
2
aba
ab
Замечание
В первом примере из условия одним из возможных способов проинтерпретировать Васино сооб- щение является: ab aba ab ab.
| |
![]()
|
|
Consonant Fencity
Конструктив
Строки
There are two kinds of sounds in spoken languages: vowels and consonants. Vowel is a sound, produced with an open vocal tract; and consonant is pronounced in such a way that the breath is at least partly obstructed. For example, letters a and o are used to express vowel sounds, while letters b and p are the consonants (e.g. bad, pot).
Some letters can be used to express both vowel and consonant sounds: for example, y may be used as a vowel (e.g. silly) or as a consonant (e.g. yellow). The letter w, usually used as a consonant (e.g. wet) could produce a vowel after another vowel (e.g. growth) in English, and in some languages (e.g. Welsh) it could be even the only vowel in a word.
In this task, we consider y and w as vowels, so there are seven vowels in English alphabet: a, e, i, o, u, w and y, all other letters are consonants.
Let’s define the consonant fencity of a string as the number of pairs of consecutive letters in the string which both are consonants and have different cases (lowercase letter followed by uppercase or vice versa). For example, the consonant fencity of a string CoNsoNaNts is 2, the consonant fencity of a string dEsTrUcTiOn is 3 and the consonant fencity of string StRenGtH is 5.
You will be given a string consisting of lowercase English letters. Your task is to change the case of some letters in such a way that all equal letters will be of the same case (that means, no letter can occur in resulting string as both lowercase and uppercase), and the consonant fencity of resulting string is maximal.
Input
The only line of the input contains non-empty original string consisting of no more than 106 lowercase English letters.
Output
Output the only line: the input string changed to have maximum consonant fencity.
| Input |
Output |
| consonants |
CoNsoNaNts |
| destruction |
dEsTrUcTiOn |
| strength |
StRenGtH |
| |
![]()
|
|
СКОБКИ
Строки
Задача на реализацию
Дано корректное математическое выражение, состоящее из переменных, обозначаемых строчными латинскими буквами, инфиксных бинарных операций и круглых скобок для группировки подвыражений. Все операции имеют ассоциативность слева направо и приоритеты, указанные в таблице:
| Приоритет |
Операции |
| 1 (наибольший) |
*, / |
| 2 |
+, - |
| 3 |
& |
| 4 |
^ |
| 5 (наименьший) |
| |
Требуется удалить из выражения все лишние пары скобок, не влияющие на порядок операций в нём (операции трактовать абстрактно, без какого-либо математического смысла, опираясь только на формальный порядок операций). Приоритет определяет, в каком порядке выполняются операции в цепочке, а ассоциативность определяет направление вычислений в цепочке операций одного приоритета.
| Ввод |
Вывод |
Замечания |
| a+(b*c) |
a+b*c |
(у ‘*’ приоритет выше, чем у ‘+’, поэтому она и так выполняется первой,- скобки лишние); |
| ((a+b)+(c+d)) |
a+b+(c+d) |
(Скобки вокруг всего выражения допустимы, но никогда не влияют на порядок вычисления внутри. Поскольку ассоциативность всех операций слева направо, первые внутренние скобки лишние, а вторые – нет, без них выражение было бы эквивалентно (((a+b)+c)+d)); |
| ((a)+b)&c^d |
a+b&c^d |
(скобки вокруг переменной всегда лишние). |
| (((a)&b^c|((d)))) |
a&b^c|d |
|
| a |
a |
|
Формат входного файла:
Одна строка, содержащая исходное математическое выражение не длиннее 100 символов.
Формат выходного файла:
Одна строка с математическим выражением без лишних скобок.
| |
![]()
|
|
Опять двойка (В, В')
Строки
Задача на реализацию
Пете нравится цифра 2. Он считает число красивым, если в его десятичной записи ровно две цифры 2. Петя хочет получить большой список красивых чисел и повесить его на стенку.
ПомогитеПете и выведите все красивые числа, не превосходищие n.
Формат входных данных
В первой и единственной строке записано одно целое число n (1 <= n <= 106).
Формат выходных данных
Выведите все целые положительные числа, не превосходящие n, в десятичной записи которых ровно две цифры 2. Числа следует выводить в порядке возрастания, по одному на строке.
Замечание
Обратите внимание, что список может быть пустым, в этом случае ничего выводить не нужно.
| |
![]()
|
|
Головасты
Целые числа
Строки
Арифметические алгоритмы (Теория чисел)
Находясь на планете Малого Арктура, Алиса и Громозека отправились в зоопарк. Этот зоопарк известен тем, что в нем можно увидеть головастов - рептилий, которые обитают только на этой планете. Чтобы получить доступ к рептилиям, им необходимо ввести код на входе в зоопарк. Однако, код постоянно меняется и всегда равен минимальному числу, не меньшему, чем записанное на экране перед входом и состоящему только из цифр 3, 6 или 9.
Помогите Алисе и Громозеке определить код доступа к рептилиям.
Входные данные
Ввод содержит одно число n (1 <= n <= 1018).
Выходные данные
Выведите одно число - код доступа к рептилиям.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2007
|
3333
|
| 2 |
97
|
99
|
| |
![]()
|
|
Артефакты Максимуса
Строки
У Магистра Максимуса в руках три артефакта с последовательностями символов. Чтобы раскрыть их тайны, нужно открыть все три артефакта одновременно с помощью одинаковых последовательностей символов. Для этого Максимус может удалять только самый правый символ из каждой последовательности сколько угодно раз. Обратите внимание, что для того, чтобы Максимус мог удалить символ из последовательности, ее длина должна быть не менее двух символов.
Определите минимальное количество операций, которые необходимо выполнить Максимусу, чтобы привести три последовательности к одинаковому виду. Если такое невозможно, ответ должен быть -1.
Входные данные
Программа получает на вход три строки s1, s2, s3 - последовательности символов, записанные на каждом из артефактов.
Constraints:
1 <= |s1|, |s2|, |s3| <= 100
s1, s2 и s3 состоят только из строчных английских букв
|s| означает длину последовательности s
Выходные данные
Выведите ответ на задачу.
| |
![]()
|
|
Bovine Genomics
Строки
Хеш
Множества
У Фермера Джона NN коров с пятнами и NN коров без пятен. Пройдя курс генетики, ФД убеждён, что пятна у коров вызваны мутацией генов.
За большие деньги ФД зафиксировал геномы своих коров. Каждый геном это строка длиной MM, состоящая из символов A, C, G, T. Когда он выписал все геномы у него получилась такая таблица, N=3 и M=8:
Позиция : 1 2 3 4 5 6 7 8
Пятнистая корова 1: A A T C C C A T
Пятнистая корова 2: A C T T G C A A
Пятнистая корова 3: G G T C G C A A
Корова без пятен 1: A C T C C C A G
Корова без пятен 2: A C T C G C A T
Корова без пятен 3: A C T T C C A T
Посмотрев внимательно на эту таблицу, он заметил, что последовательность от позиции 2 до позиции 5 успешна, чтобы объяснять пятнистость. То есть, рассматривая символы в этих позициях (2…5), ФД может предсказать какие из его коров пятнистые, а какие нет. Например, если он видит символы GTCG в этих позициях, он знает, что корова будет пятнистая.
Помогите ФД определить длину кратчайшей последовательности позиций, которая может объяснить пятнистость.
ФОРМАТ ВВОДА:
Первая строка ввода содержит N (1≤N≤500) и M (3≤M≤500). Каждая из N следующих строк содержит по M символов. Эти символы описывают геномы пятнистых коров. Следующие N строк описывают геномы коров без пятен. Никакая пятнистая корова на имеет точно такой же геном, как корова без пятен.
ФОРМАТ ВЫВОДА:
Пожалуйста, выведите длину кратчайшей последовательности позиций, достаточной для объяснения пятнистости. Последовательность позиций объясняет пятнистость, если по ней можно предсказывать абсолютно точно пятнистая или нет любая из коров ФД.
| Ввод |
Вывод |
|
3 8
AATCCCAT
ACTTGCAA
GGTCGCAA
ACTCCCAG
ACTCGCAT
ACTTCCAT
|
4 |
| |
![]()
|
|
Palindromic Paths
Динамическое программирование
Динамическое программирование: два параметра
Комбинаторика
Строки
Ферма Джона представлена решёткой N×N полей (1≤N≤500). Каждое поле представлено символом латинского алфавита. Например:
ABCD
BXZX
CDXB
WCBA
Каждый день корова Беси прогуливается из верхнего левого угла в правый нижний, каждый раз двигаясь на один шаг вправо или вниз. Беси записывает в строку буквы, по которым прошлась. Она огорчится, если у неё получится палиндром (слово, которое читается одинаково слева направо и справа налево), поскольку тогда она запутается, в каком направлении двигалась.
Пожалуйста, помогите Беси определить количество различных маршрутов которыми она может получить палиндромы. Различные пути, которыми получаются одинаковые палиндромы учитывать множество раз. Выведите свой ответ по модулю 1,000,000,007.
ФОРМАТ ВВОДА:
Первая строка ввода содержит N, и последующие N строк содержат N строк решётки, описывающей поля. Каждая строка содержит N символов в интервале A..Z.
ФОРМАТ ВЫВОДА:
Выведите количество различных путей Беси, формирующих палиндромы по модулю 1,000,000,007.
| Ввод |
Вывод |
|
4
ABCD
BXZX
CDXB
WCBA
|
12 |
Беси может сделать следующие палиндромы:
1 x "ABCDCBA"
1 x "ABCWCBA"
6 x "ABXZXBA"
4 x "ABXDXBA"
| |
![]()
|
|
Censoring
Строки
Хеш
Структуры данных
Фермер Джон купил подписку журнала Good Hooveskeeping для своих коров. К сожалению, последний номер содержит неподходящую статью - как приготовить бифштекс. ФД не хочет, чтобы его коровы её читали.
ФД взял текст журнала, создал строку S длиной не более чем 10^5 символов. У него есть список слов t_1, t_2, ..., t_N, которые он хочет удалить из S. Поэтому ФД находит ближайшее вхождение слова из списка T (то есь с наименьшим индексом) и удаляет его из S. Затем он продолжает это процесс опять, пока в S не останется слов из T. Заметим, что удаление слова может создавать новое вхождение свлоа из T, которое не существовало ранее.
ФД заметил, что слова из списка T обладают таким свойством, что никакое из них не является подстрокой другого слова из T. В частности, это означает, что ранее вхождение слова из T в S всегда определено однозначно. Пожалуйста, помогите ФД определить финальное содержание строки S.
INPUT FORMAT:
Первая строка содержит S. Вторая строка содержит N - количество удаляемых слов. Последующие N строк содержат строки t_1, t_2, ..., t_N. Каждая строка содержит только маленькие латинские буквы (a..z) и суммарная длина всех строк не превысит 10^5.
OUTPUT FORMAT:
Строка S после всех удалений. Гарантируется, что S не станет пустой.
| Ввод |
Вывод |
|
begintheescapexecutionatthebreakofdawn
2
escape
execution
|
beginthatthebreakofdawn |
| |
![]()
|
|
Самая длинная подстрока
Поиск подстроки в строке
Строки
ЕГЭ_информатика
Дана строка s Определите длину самой длинной подцепочки, состоящей из одинаковых символов. В ответе укажите сначала символ, из которого строится данная подцепочка, затем, слитно без разделителей, длину данной подцепочки. Если таких подцепочек несколько, то укажите ту, в которой буква стоит раньше в алфавите.
Формат входных данных
Программа получает на вход строку s (10 <= s <= 106). Строка состоит из символов английского алфавита, записанных в верхнем регистре (от A до Z).
Формат выходных данных
Выведите ответ на задачу.
| |
![]()
|
|
Гласная подстрока
Строки
Поиск подстроки в строке
Дана строка s. Определите длину самой длинной подстроки, состоящей только из гласных букв. В ответе укажите длину данной подцепочки.
Формат входных данных
Программа получает на вход строку s (10 <= s <= 106). Строка состоит из символов английского алфавита, записанных в верхнем регистре (от A до Z). Гласные буквы английского алфавита: AEIOUY.
Формат выходных данных
Выведите ответ на задачу.
| |
![]()
|
|
Строка Громозеки
Строки
У Громозеки есть его любимая строка S и другая строка T. Он внимательно посмотрел на свои строки и понял, что первая строка (S) может содержать в себе несколько раз вторую строку (T). Громозека подсчитал все вхождения строки T в строку S и написал себе в порядке возрастания список индексов, начиная с которых строка T входит в строку S. Однако, путешествуя по Галактике, Громозека потерял этот список и пришел в уныние. Помогите Громозеке восстановить потерянный список.
Формат входных данных
Первые две строки входных данных содержат строки S и T, соответственно. Длины строк больше 0 и меньше 50000, строки содержат только строчные латинские буквы.
Формат выходных данных
Выведите в порядке возрастания индексы символов, начиная с которых строка T входит в строку S (в одной строке должно быть записано одно число).
| |
![]()
|
|
Телефонный справочник
Линейный поиск
Задача на реализацию
Строки
Саша недавно начала регистровать компанию по разработке чат ботов и уже подала необходимые документы. Но добрые люди рассказали Саше, что в телефонном справочнике компании располагаются в лексикографически возрастающем порядке их названий. Что такое телефонный справочник, Саша не знает, но решила учесть рекомендации и поменять название своей компании, чтобы оно было как можно раньше в телефонном справочнике. Поскольку Саша уже подала документы, она не может полностью поменять название компании, но может сказать, что допустила опечатку, и поменять любые две буквы в названии местами. Помогите Саше выбрать новое название компании или оставить текущее.
Формат входных данных
В единственной строке содержится одно слово, состоящее из строчных латинских букв от "a" до "z" (2 ≤ n ≤ 106)
Формат выходных данных
Выведите одно слово - новое название компании. Если название не~изменилось, выведите изначальное название.
| |
![]()
|
|
Вордл наоборот
Строки
Задача на реализацию
Перебор
Камила и Динара играют в <<Wordle>>. Камила загадала слово длины \(n\), состоящее из различных латинских букв. Динара сделала одну попытку угадать и назвала слово длины \(n\), также состоящее из различных латинских букв. Камила раскрасила буквы в догадке Динары в соответствии со следующими правилами:
-
Буква, совпадающая с буквой в загаданном слове, красится в зеленый цвет и обозначается G.
-
Буква, которая присутствует в загаданном слове, но стоит не своей позиции, красится в жёлтый цвет и обозначается Y.
-
Буква, отсутствующая в загаданном слове, красится в белый цвет и обозначается W.
Например, если было загадано слово ALERT, а догадка была ALONE, то буквы будут раскрашены в цвета GGWWY. Первые две буквы в словах совпадают, поэтому они зеленые. Буква E есть в загаданном слове, но находится на другой позиции, поэтому она жёлтая. Остальные буквы белые, так как их нет в загаданном слове.
Проснувшись следующим утром, Динара увидела, что буквы в ее слове не разобрать, так как они закрашены гуашью. Динара поняла, что забыла свою догадку. Помогите ей и определите, существует ли слово из различных букв, которое было бы раскрашено таким образом, и если существует, выведите любое такое слово.
В первой строке вводится одно целое число \(n\) \((1 \le n \le 10)\) — длина загаданного слова.
Во второй строке вводится строка длины \(n\), состоящая из заглавных латинских букв — загаданное слово. Гарантируется, что все буквы в нем различны.
В третьей строке вводится строка длины \(n\), состоящая из букв G, Y, W — цвета, в которые были раскрашены буквы в слове Динары.
Если подходящих слов не существует, выведите No.
Если хотя бы одно подходящее слово существует, в первой строке выведите Yes, во второй — любое подходящее слово.
Разберем первый пример из условия.
Буквы H и G не встречаются в загаданном слове, поэтому они белые.
Буквы E и B встречаются, но на других позициях, поэтому они жёлтые
Буквы C и D совпадают с буквами на соответствующих позициях в загаданном слове, поэтому они зелёные.
Есть и другие ответы, любой правильный ответ будет зачтен.
Обратите внимание, что строка HECDBH не является ответом, так как в ней есть совпадающие буквы.
| |
![]()
|
|
Палиндромные числа
Строки
Задача на реализацию
Участникам, использующим язык Python3, рекомендуется отправлять решения на проверку с использованием интерпретатора PyPy3.
Однажды во время прогулки Алина увидела длинное число, которое кто-то написал на асфальте. Алина захотела найти положительное число такой же длины без ведущих нулей, чтобы сумма этих двух чисел была палиндромом.
Число называется палиндромом, если оно читается одинаково справа налево и слева направо. Например, числа \(121, 66, 98989\) являются палиндромами, а \(103, 239, 1241\) — нет.
После некоторых размышлений Алина поняла, что такое число всегда можно найти. Помогите Алине найти подходящее число!
Формат входных данных
В первой строке вводится одно целое число \(n\) (\(2 \leq n \leq 100\,000\)) — длина числа, которое увидела Алина.
Во второй строке вводится одно положительное целое число длины \(n\). Гарантируется, что оно не содержит ведущих нулей.
Формат выходных данных
Выведите ответ на задачу — положительное целое число без ведущих нулей длины \(n\), такое что его сумма с числом из входных данных будет палиндромом.
Если таких чисел несколько, вы можете вывести любое из них.
В первом примере из условия \(99 + 32 = 131\) — палиндром. Число \(12\) также будет являться ответом, так как \(99 + 12 = 111\).
Во втором примере из условия \(1023 + 8646 = 9669\).
В третьем примере из условия \(385 + 604 = 989\).
| |
![]()
|
|
Ввод и вывод строки
Типы данных
Строки
Python
Вам дана строчка. Прочитайте её,сохраните в переменную и выведите её на экран.
| |
![]()
|
|
Телефонные номера
Разбор случаев
Задача на реализацию
Строки
Неотъемлемой частью программного обеспечения любого мобильного телефона является записная книжка. В самых первых мобильных телефонах в ней можно было хранить лишь имена абонентов и их телефонные номера. В более современных моделях в ней можно также хранить множество другой полезной информации — электронный адрес человека, его фотографию, ссылки на его страницы в социальных сетях и дату его рождения. Однако, при реализации даже самой простой версии этой программы, позволяющей работать только с телефонными номерами, разработчики иногда сталкиваются с некоторыми сложностями.
Будем считать, что любой телефонный номер состоит из 11 цифр и делится на три части, каждая из которых является числом без ведущих нулей. Первая часть состоит из одной, двух или трех цифр и является кодом страны, в которой этот телефон зарегистрирован. Вторая часть может состоять из трех, четырех или пяти цифр, и может являться или кодом региона, в котором зарегистрирован номер, или кодом мобильного оператора, которому этот номер принадлежит. Третья часть состоит из всех оставшихся цифр номера и является номером конкретного абонента.
При отображении телефонного номера на экране телефона, части этого номера принято отделять друг от друга различными символами так, чтобы номер было проще прочитать и запомнить. Так, перед кодом страны обычно ставится символ «+», код региона или оператора берется в скобки, номер абонента разделяется символами «-» на несколько частей. При этом, то, на сколько частей он разбивается, напрямую зависит от количества цифр в нем:
• если номер абонента состоит из трех цифр, то он представляет собой одну часть, состоящую из трех цифр;
• если номер абонента состоит из четырех цифр, то он разбивается на две части, каждая из которых состоит из двух цифр;
• если номер абонента состоит из пяти цифр, то он разбивается на две части, первая из которых состоит из трех цифр, а вторая — из двух;
• если номер абонента состоит из шести цифр, то он разбивается на три части, каждая из которых состоит из двух цифр;
• если номер абонента состоит из семи цифр, то он разбивается на три части, первая из которых состоит из трех цифр, а все остальные — из двух.
Естественно, что человек, заносящий новый номер в записную книжку своего телефона, не станет задумываться об этих правилах, а просто введет его как последовательность из 11 цифр. Однако, перед отображением номера на экране, программное обеспечение телефона должно выяснить, какая часть этого номера является кодом страны, какая — кодом региона или оператора, а какая — номером абонента, и отформатировать номер по правилам, описанным выше. Чтобы сделать эту задачу разрешимой, в память телефона записывается информация о том, какие в данный момент существуют коды государств и какие в этих государствах существуют коды операторов или регионов. Вам необходимо реализовать программу, которая, имея эту информацию, будет правильно форматировать номера, сохраненные в записной книжке телефона.
Формат входных данных
Первая строка файла содержит одно целое число n (1 ≤ n ≤ 100) — количество государств, информация про телефонные коды которых записана в память телефона. Далее следуют n описаний этих государств, разделенных переводами строк. Первая строка описания каждого государства содержит два целых числа c и k (1 ≤ c ≤ 999, 1 ≤ k ≤ 100) — телефонный код этого государства и количество операторов или регионов, существующих в этом государстве. Следующие k строк описания этого государства содержат целые числа, каждое из которых не меньше 100 и не больше 99999 — коды операторов или регионов, зарегистрированных в этом государстве.
Следующая строка входного файла содержит одно целое число m (1 ≤ m ≤ 10 000) — количество телефонных номеров, которые необходимо отформатировать. Следующие m строк содержат сами номера — строки, состоящие ровно из 11 цифр.
Гарантируется, что ни один данный вам номер невозможно разбить на код государства, код оператора или региона и номер абонента более, чем одним способом.
Формат выходных данных
Выведите номера, данные вам во входном файле, отформатированными по правилам, описанным в условии. Каждый номер необходимо вывести в отдельной строке. Номера необходимо выводить в том же порядке, в котором они были перечислены во входном файле. Вместо номеров, корректного разбиения которых на код государства, код оператора или региона и номер абонента не существует, необходимо вывести слово «Incorrect».
| Ввод |
Вывод |
2
7 3
981
3517
812
351 3
34712
1234
963
8
79818266456
35196328463
78122472557
01234567890
73517960326
35134712239
35112342013
78120203040 |
+7(981)826-64-56
+351(963)284-63
+7(812)247-25-57
Incorrect
+7(3517)96-03-26
+351(34712)239
+351(1234)20-13
Incorrect |
| |
![]()
|
|
Мониторинг труб
Деревья
Алгоритмы на графах
Строки
Динамическое программирование
Газораспределительная система одного региона устроена следующим образом. Она
содержит n узлов, пронумерованных от 1 до n, некоторые узлы соединены односторонними
трубами. Узел с номером 1 соответствует центральному газохранилищу.
Система узлов описывается числами от p2, p3, …, pn. Для всех i от 2 до n узел с
номером pi соединен односторонней трубой с узлом i, газ по этой трубе передается от узла pi
к узлу i. Известно, что возможно доставить газ по трубам от центрального газохранилища до
любого узла системы (возможно, с использованием промежуточных узлов). В системе
используются трубы различных типов, тип трубы обозначается буквой английского алфавита
от «a» до «z». Труба, соединяющая узел pi с узлом i, имеет тип ci.
Для проверки качества труб используется специальный робот. Он помещается в
систему труб в одном из узлов и перемещается по трубам, каждый раз проверяя трубу, по
которой он перемещается. Робот может перемещаться по трубам только в том же
направлении, в котором по трубе передается газ. Совершив одно или несколько
перемещений по трубам между узлами, робот извлекается из системы труб.
Каждый запуск робота должен соответствовать одной из m заданных спецификаций,
пронумерованных от 1 до m. Спецификация с номером t представляет собой строку st,
состоящую из строчных букв английского алфавита. Запуск соответствует спецификации st,
если количество перемещений робота по трубам во время запуска совпадает с длиной st, и
для всех j от 1 до длины st на j-м шаге робот перемещается по трубе, тип которой совпадает с
st[j] —символом на позиции j в спецификации.
Если запуск робота соответствует спецификации с номером t, то стоимость этого
запуска составляет wt. Оператору системы необходимо проверить все трубы, для этого
можно запускать робот несколько раз. Каждый раз выбирается спецификация и маршрут
робота по трубам, соответствующие выбранной спецификации. Необходимо проверить все
трубы так, чтобы суммарная стоимость запусков робота для проверки качества труб была
минимальна. Одну и ту же трубу можно проверять несколько раз.
Требуется написать программу, которая по описанию системы труб и списку
спецификаций определяет минимальную суммарную стоимость запусков робота, в
результате которых все трубы будут проверены, а также список необходимых для этого
запусков (по требованию).
Формат входных данных
В первой строке входных данных находятся три целых числа n, m и t — количество
узлов системы труб, количество спецификаций запусков робота и параметр, указывающий,
требуется ли вывести список запусков робота или только их минимальную суммарную
стоимость (1 ≤ n ≤ 500, 1 ≤ m ≤ 105, t равно 0 или 1).
В последующих (n – 1) строках содержится информация о трубах, (i – 1)-я из этих
строк содержит разделенные пробелом значения pi и ci, где pi — целое число, задающее
номер узла, из которого ведет труба в i-й узел, а ci — строчная буква английского алфавита,
задающая тип этой трубы (1 ≤ pi ≤ i – 1).
В последующих m строках содержится информация о спецификациях, i-я из этих
строк содержит разделенные пробелом целое число wi — стоимость запуска робота в
соответствии с этой спецификацией, и состоящую из строчных букв английского алфавита
строку si — саму спецификацию (1 ≤ wi ≤ 10 9). Суммарная длина строк si не превышает 10 6.
Формат выходных данных
Первая строка выходных данных должна содержать одно число — минимальную
суммарную стоимость запусков робота, в результате которых все трубы будут проверены.
Если проверить все трубы невозможно, требуется вывести «–1».
Если t = 0, то больше ничего выводить не требуется.
Если t = 1 и проверить трубы возможно, то далее следует вывести список описаний
запусков робота. В этом случае вторая строка выходных данных должна содержать
число k — количество запусков робота, которое необходимо выполнить для проверки труб. В
следующих k строках необходимо вывести по три целых числа ai, bi и ci — номер узла, в
котором начинается запуск, номер узла, в котором заканчивается запуск, и номер
спецификации, которой соответствует запуск.
Если оптимальных способов проверки несколько, требуется вывести любой из них.
| Ввод |
Вывод |
|
3 3 0
1 a
2 b
3 a
4 b
2 a
|
6 |
|
7 3 1
1 a
2 a
3 b
3 b
1 b
6 b
3 aab
5 b
2 ab
|
15
4
1 4 1
2 5 3
1 6 2
6 7 2
|
Пояснение к примеру
Система труб, заданная во втором примере входных данных, и оптимальный способ
проверки всех труб для этого случая приведены на рисунке ниже.
Необходимо обратить внимание на следующие моменты:
- трубу можно проверять несколько раз, так в приведенном примере дважды
проверена труба из узла 2 в узел 3;
- одну и ту же спецификацию разрешается использовать несколько раз, в
приведенном примере вторая спецификация используется дважды, для
проверки труб из узла 1 в узел 6 и из узла 6 в узел 7;
- робот может перемещаться по трубам только в том же направлении, по
которому по трубе передается газ, спецификацию «ab» нельзя использовать
для проверки труб по маршруту 2→1→6, так как робот не может
переместиться из узла 2 в узел 1.
| |
![]()
|
|
Римские числа
Задача на реализацию
Разбор случаев
Строки
Один древнеримский торговец брал несколько раз ссуду в древнеримском банке. Каждый раз банкир записывал размер выданной ссуды на листе пергамента, используя римские числа. Но ввиду дороговизны пергамента запись производилась плотно и все числа оказались записанными подряд, без разделителей. Когда торговец пришёл возвращать ссуду, оказалось, что невозможно установить разбиение записи на числа.
Например, если на пергаменте записана строка «XIIV», её можно разбить на римскиечисла разными способами, например, XI + IV = 11 + 4 = 15 или XII + V = 12 + 5 = 17, возможны и другие варианты разбиения.
Торговец хочет вернуть как можно меньше денег, поэтому он хочет так разбить строку цифр на римские числа, чтобы сумма всех чисел была как можно меньше.
Программа получает на вход строку, длина которой не превосходит 250 символов. Строка состоит только из заглавных латинских букв I, V, X, L, С, D, M.
Программа должна вывести единственное число – минимально возможную сумму, которую можно получить при разбиении данной строки на последовательность корректных римских чисел. Ответ нужно вывести арабскими цифрами в десятичной системе счисления.
Правила записи римских чисел
Римскими цифрами можно записать целые числа от 1 до 3999. Число представляется в виде суммы тысяч, сотен, десятков и единиц. Далее из следующей таблицы берётся по одному элементу, соответствующему тысячам, сотням, десяткам, единицам ровно в таком порядке.
Если число тысяч, сотен, десятков, единиц равно 0, то из соответствующего столбца ничего не берётся. Например, число 1990 записывается, как 1000 + 900 + 90 = MCMXС.
| |
![]()
|
|
50096
Строки
Требуется разделить заданный текст на английском языке на 3 группы слов по их первой букве так, чтобы количество слов в группах отличалось на минимальную величину. Группы могут формироваться только на основе алфавитного порядка латинских букв и задаются в виде диапазонов, например a-i, j-o, p-z.
Входные данные
В первой строке записано число N, не превышающее 106 - количество строк в тексте. Далее записано N строк текста, в каждой из которых не более 1000 символов. Текст состоит из латинских букв разного регистра, пробелов и знаков препинания ".", ",", "!", "?", ":".
После каждого знака препинания обязательно ставится пробел либо строка заканчивается.
Переносы слов с одной строки на другую отсутствуют.
Выходные данные
Одно число - величина, на которую отличается количество слов в группе, где их больше всего, от количества слов в группе, где их меньше всего.
Примеры
| № |
Входные данные |
Выходные данные |
Примечание |
| 1 |
3
Above all zoo the blue bird
soars. Hippopotamus hopes high
honey
hotel? |
2 |
Слова можно разбить на 3
группы:
1-я - 4 слова на буквы a и b;
2-я - 5 слов на букву h;
3-я - 3 слова на буквы s-z. |
| 2 |
2
A a a a, o.
O o o! A? |
5 |
Слова можно разбить на 2
группы:
1-я - все слова на букву a;
2-я - все слова на букву o;
3-я - пустая. |
| |
![]()
|
|
Новое --- это хорошо забытое старое
Строки
Задача на реализацию
Московские библиотеки имеют электронный сервис, с помощью которого можно бесплатно получить издание, несколько лет не востребованное читателями. Андрея заинтересовала красочная энциклопедия, правда изданная в прошлом веке на неизвестном ему языке.
Получив желаемое издание, он стал его изучать, открывая в произвольных местах. На одной из открытых страниц было всего две статьи, название первой из них можно было легко прочитать, так как оно было записано английскими буквами, а буквы в названии второй из них оказались практически затертыми. Легко определить было только что остались следы от \(k\) букв. Очевидно также, что второе название стоит в алфавитном порядке позже, чем первое. Это означает, что либо первая не совпадающая в написании двух слов буква в первом слове стоит в алфавите раньше, чем соответствующая буква второго слова, либо начало второго слова полностью совпадает с первым словом, но при этом второе слово длиннее первого (содержит еще какие то буквы).
Андрей не знает язык, на котором написана энциклопедия, поэтому он предположил, что второе слово состоит из тех же букв, что и первое. Чтобы проверить свое предположение, он собирается искать предполагаемое слово в интернете.
Помогите Андрею найти первое следующее в алфавитном порядке слово, состоящее из тех же букв, что и заданное слово, и состоящее ровно из \(k\) букв. Гарантируется, что такое слово существует.
Формат входных данных
В первой строке задано целое число \(n\) (\(1 \leq n \leq 100\,000\)) — количество букв в первом слове.
Во второй строке задано слово, состоящее из \(n\) строчных букв английского алфавита.
В третьей строке задано целое число \(k\) (\(1 \leq k \leq 100\,000\)) — количество букв в искомом слове.
Формат выходных данных
Выведите искомое слово, состоящее из \(k\) букв, входящих в первое слово.
Примечание
В первом тестовом примере требуемое слово должно состоять из букв a, b и c. Следующим после abc в алфавитном порядке будет слово abca, но оно состоит из 4 букв, а не из 3. Следующим после abc в алфавитном порядке состоящим из букв a, b и c и имеющим длину 3 будет слово aca.
В данной задаче \(50\) тестов, помимо тестов из условия.
Не менее чем в 15 тестах первое слово будет состоять только из букв abc, причем каждая из трех букв будет встречаться.
Решения, работающие при \(1 \leq n, k \leq 3\) будут набирать не менее \(10\) баллов.
Решения, работающие при \(1 \leq n, k \leq 10\) будут набирать не менее \(30\) баллов.
Решения, работающие при \(1 \leq n, k \leq 5\,000\) будут набирать не менее \(60\) баллов.
| |
![]()
|
|
Древний английский
Строки
Символы
Онуфрий изучает древний английский язык. Поскольку он делает это в рамках домашнего задания на завтра, он не успевает детально изучить его грамматику, поэтому он решил для простоты применить следующие правила для перевода современных английских слов в свой вариант древнего английского.
-
Все буквы <<s>>, после которых не идет <<h>> и которые не являются первыми в слове, заменяются на комбинацию <<th>>.
-
Если первая буква в слове <<e>>, то она заменяется на <<ae>>.
-
Комбинация <<oo>> заменяется на <<ou>>, причем если в слове идет подряд более двух букв <<o>>, то из них заменяются только первые две.
Помогите Онуфрию перевести несколько слов на свою версию древнего английского языка.
Формат входных данных
Первая строка ввода содержит \(n\) — количество слов, которые требуется перевести (\(1 \le n \le 100\)). Далее следует \(n\) строк, каждая из которых состоит только из букв латинского алфавита. Все буквы каждого слова строчные, кроме, возможно первой, которая может быть заглавной. Длина каждого слова не превышает 30.
Формат выходных данных
Выведите \(n\) строк — результат перевода. Если первая буква исходного слова была заглавной, то такой же должна быть и первая буква переведенного слова. Иначе все буквы должны остаться строчными.
| |
![]()
|
|
Искусство ASCII
Строки
Символы
Давным давно, еще когда не было персональных компьютеров, люди использовали печатные машинки для создания текстов, а самые умельцы создавали картинки из символов.
Некоторые из таких картинок удалось найти в закодированном виде. Восстановите картинку по строке с кодом.
Формат входных данных
Программа получает на вход строку с кодом. Части кода разделены пробелом.
Каждый фрагмент кода это либо:
nl означает NewLine (переход на новую строку)
либо
Количество символа и какой символ
В качестве символов может быть любой печатаемый символ ASCII кода (до символа с кодом 127) либо специальные символы, закодированные следующим образом:
sp - пробел
bS - бэкслеш \
sQ - апостроф '
Количество символа - натуральное число, не превышающее 100.
Формат выходных данных
Выведите получившуюся картинку.
| |
![]()
|
|
Лучшие учащиеся
Строки
Структуры
Определите учащихся с наилучшей успеваемостью, то есть с максимальным средним баллом по трем предметам. Выведите всех учащихся, имеющих максимальный средний балл.
Входные данные
Заданы сначала количество учащихся n, затем n строк, каждая из которых содержит фамилию, имя и три числа (оценки по трем предметам: математике, физике, информатике). Данные в строке разделены одним пробелом. Оценки принимают значение от 1 до 5.
Выходные данные
Необходимо вывести пары фамилия-имя по одной на строке, разделяя фамилию и имя одним пробелом. Выводить оценки не нужно. Порядок вывода должен быть таким же, как в исходных данных.
| |
![]()
|
|
Вполоборота
Строки
Словом считается непустая последовательность больших и маленьких латинских букв. Вам необходимо развернуть все слова во входном файле задом наперед.
Входные данные
Во входном файле записано все что угодно. Его размер не превышает 1 Мб.
Выходные данные
В выходном файле должен содержаться входной файл, в котором все слова развернуты. Все прочие символы, в том числе переводы строк, должны остаться нетронутымию.
| |
![]()
|
|
Слишком вложенные скобки
Строки
Дана правильная последовательность из круглых скобок. Требуется удалить из неё все скобки, находящиеся на глубине вложенности N и более. Например, в последовательности (()((()(())())))(((()))) выделены скобки, вложенные на 3 и более уровней.
Входные данные
Первая строка входного файла содержит число N (1 <= N <= 5000). Вторая строка содержит правильную скобочную последовательность длиной от 2 до 10000 символов.
Выходные данные
Выходной файл должен содержать укороченную скобочную последовательность.
| |
![]()
|
|
Изображение таблицы
Строки
Задачи на моделирование
При разработке программ для просмотра веб-страниц одной из наиболее сложных задач является корректное отображение таблиц. Компания <<Kozilla>>, в которой вы работаете, планирует разработать новую версию браузера <<Waterrat>> для работы в терминальном режиме, и просит вас написать фрагмент ядра отображения веб-страниц, ответственный за формирование структуры таблиц.
Фрагмент, который вы должны написать, получает на вход информацию о количестве строк таблицы и ячейках этих строк и должен сгенерировать структуру таблицы и передать ее модулю, который занимается отображением таблицы на экране.
Таблица состоит из строк, каждая строка состоит из одной или нескольких ячеек, \(j\)-я ячейка \(i\)-й строки имеет ширину \(a_{i,j}\).
По заданным параметрам таблицы постройте символическое изображение ее структуры.
Формат входных данных
Первая строка содержит \(n\) — количество строк в таблице (\(1 \le n \le 100\)). Следующие \(n\) строк входного файла содержат описание строк таблицы.
Описание каждой строки включает число \(m_i\) — количество ячеек этой строки, и \(m_i\) целых чисел \(a_{i,1}, a_{i,2}, \dots, a_{i,m_i}\) — ширину каждой из ячеек строки (\(1 \le m_i \le 10\), \(1 \le a_{i,j} \le 20\)).
Формат выходных данных
Выведите символическое изображение структуры таблицы.
Изображение \(i\)-й строки таблицы должно начинаться изображением горизонтальной линии, составленным из символов <<+>> (плюс) и <<->> (минус). Затем должна следовать строка, содержащая пробелы и символы <<|>> (вертикальная черта). Первым символом строки должна быть вертикальная черта, затем \(a_{i,1}\) пробелов, затем вертикальная черта, затем \(a_{i,2}\) пробелов, и так далее, всего \(m_i\) блоков пробелов. После последнего блока должна следовать вертикальная черта. После последней строки таблицы также должно следовать изображение горизонтальной линии.
В изображении горизонтальной линии используйте символ <<+>>, если сверху или снизу от этой позиции находится вертикальная черта, и <<->> в противном случае. Горизонтальная линия должна иметь минимальную возможную длину, чтобы над каждым символом вертикальной черты следующей строки и под каждым символом вертикальной черты предыдущей строки были символы <<+>>.
| |
![]()
|
|
Календарь
Дата и время
Строки
Неудовлетворенный стандартным календарем своей операционной системы, Витя решил написать программу, которая будет выводить красиво отформатированный календарь. Он разработал формальные требования к календарю, но понял, что сам не способен написать соответствующую программу. Помогите ему.
Календарь состоит из блоков, каждый из которых соответствует одному месяцу. Блоки расположены в виде таблицы из \(k\) столбцов и \(12/k\) строк (\(k\) выбирается делителем числа 12). Месяцы выводятся в следующем порядке: первая строка содержит блоки, соответствующие месяцам с первого по \(k\)-ый, следующая — с \((k + 1)\)-го по \(2k\)-ый, и т. д.
Ширина всех блоков в столбце должна быть одинакова, высота всех блоков равна семи (числу дней в неделе). Между блоками различных строк таблицы выводится пустая строка, в каждой строке между соседними блоками из разных столбцов выводится три пробела.
Блок, соответствующий месяцу, устроен следующим образом. Каждой (в том числе неполной) неделе данного месяца в блоке соответствует столбец, имеющий ширину равную двум. Между двумя соседними столбцами в каждой строке выводится один пробел. Если несколько блоков располагаются в одном столбце в календаре, то для выравнивания ширины в те блоки, которые содержат меньше недель, в конец добавляется необходимое число пустых столбцов-недель. При этом разные столбцы календаря могут иметь разную ширину.
Все числа месяца заносятся в блок, соответствующий этому месяцу. Число заносится в ту строку блока, которая соответствует дню недели, на который приходится число в этом месяце. Число заносится в столбец блока, соответствующий неделе, в которой находится данное число. Однозначные числа дополняются слева одним пробелом. Таким образом, числа в столбце оказываются выравнены по правому краю.
Формат входных данных
Входной файл содержит описание года, календарь для которого следует вывести — три числа: \(d\) — день недели, на который приходится первое января (\(1 \le d \le 7\)), \(l\) — является ли год високосным (\(l = 1\) означает, что год является високосными, \(l = 0\) — что не является) и \(k\) — количество столбцов в календаре (\(k\) — одно из чисел \(1, 2, 3, 4, 6, 12\)).
Напомним, что високосный год отличается от обычного тем, что в високосном году февраль содержит 29 дней.
Формат выходных данных
Выведите календарь, отформатированный как описано в условии задачи. Проверяющая программа в этой задаче игнорирует пробелы в конце строк. В остальном календарь должен быть отформатирован в точности в соответствии с условием.
Для наглядности в примере вместо пробелов выведены точки. Ваша программа должна выводить пробелы.
| |
![]()
|
|
Криптостойкий пароль. Встроенные методы
Строки
Пароль называется криптостойким, если он включает в себя и строчные латинские буквы, и заглавные латинские буквы, и цифры, при этом его длина должна быть не менее 8 символов.
Требуется по данному паролю определить, является ли он криптостойким.
Входные данные
Вводится одна строка, состоящая только из латинских букв и цифр. Количество символов в строке не превышает 100.
Выходные данные
Выведите слово YES, если указанный пароль является криптостойким, и NO – в противном случае.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
e |
NO |
| 2 |
AAAbbb123 |
YES |
| |
![]()
|
|
Найди и замени
Строки
В текстовом редакторе Microsoft Word имеется достаточно мощный механизм поиска и замены, который доступен после установки флажка Подстановочные знаки (Use wildcards). При этом некоторые символы в строке поиска получают особый смысл.
Так, знаком вопроса в шаблоне поиска можно задать ровно один любой символ. Кроме того, в шаблоне поиска на месте одного из символов в квадратных скобках можно перечислить сразу несколько символов, никак их при этом не разделяя (поиск будет считаться успешным, если на этом месте стоит один из символов, указанных в [ ]). В квадратных скобках можно вместо любого символа указывать и диапазоны символов. Мы будем использовать только три следующих диапазона: 0–9, a–z и A–Z (других диапазонов не будет). В этом случае будет искаться один любой символ из указанного диапазона (диапазонов). Если же первый символ в квадратных скобках – “!”, то, наоборот, искаться будет любой символ, из не перечисленных после восклицательного знака в квадратных скобках (например, [!.a-z,] означает один любой символ кроме точки, запятой, и строчных латинских букв). Если же искать надо один из специальных символов !, ?, [, ], (, ), –, \ то, как в квадратных скобках, так и без скобок перед таким символом ставится \.
Еще одно замечательное свойство строки поиска – выражения. Выражением считается часть строки поиска, взятая в круглые скобки. Пар скобок может быть до 9, но вложенность не допускается. В строке замены выражения представляются в виде \n, где n – порядковый номер выражения в шаблоне поиска (от 1 до 9). Например, по шаблону поиска (k)(?)t и шаблону замены t\2\1 произойдут например, следующие замены:
kot -> tok
kit -> tik
Таким образом, в строке замены существует только один специальный символ – \ , после которого обязательно должна идти цифра. Причем, например, цифра 5 может идти только если в строке поиска было не менее пяти выражений в скобках. При этом символы !, ?, [, ], (, ), – в строке замены указываются без предшествующего символа , а символ \ используется только перед цифрой и обозначает номер выражения. В качестве символа, который должен попасть в конечный текст, символ \ в строке замены не может быть использован.
Поиск начинается с первого символа текста. Находится первый фрагмент, который соответствует шаблону поиска, и производится его замена в соответствии с шаблоном замены. После этого поиск продолжается с символа, следующего за замененным фрагментом. Если снова находится фрагмент, соответствующий шаблону поиска, то он снова заменяется, и так далее до тех пор, пока поиск не достигнет конца текста.
Требуется по данному образцу поиска и образцу замены, произвести все замены в заданном тексте.
Входные данные
В первой строке входных данных расположен текст, в котором требуется произвести все необходимые замены. Длина текста не превышает 100 символов. Во второй строке записан шаблон для поиска. Шаблон является корректным: каждой открывающей скобке соответствует закрывающая, восклицательный знак как спецсимвол употребляется только сразу за символом [ и т.д. В третьей строке расположен шаблон для замены. Выражения в шаблоне для замены также корректны. Длины шаблонов не превышают 100 символов. Коды всех символов, встречающихся как в тексте, так и в шаблонах находятся в диапазоне от 32 до 126. Символы перевода строки в сами шаблоны и в текст не входят.
Выходные данные
Выведите одну строку – текст после всех произведенных замен.
| |
![]()
|
|
Шифровка
Строки
Шпион Коля зашифровал и послал в центр радиограмму. Он использовал такой способ шифровки: сначала выписал все символы своего сообщения (включая знаки препинания и т.п.), стоявшие на четных местах, в том же порядке, а затем – все символы, стоящие на нечетных местах. Напишите программу, которая расшифровывает сообщение.
Входные данные
Вводится одна непустая строка длиной не более 250 символов – зашифрованное сообщение. Строка может состоять из любых символов, кроме пробельных.
Выходные данные
Выведите одну строку – расшифрованное сообщение.
| |
![]()
|
|
ЕГЭ
Строки
В ЕГЭ по математике было решено не давать задач, в которых используются числа, большие 5, например, 6, 10 и т.п. (они теперь считаются трудными и не обязательными для изучения). Вводится уравнение. Требуется определить, можно ли его давать в ЕГЭ (в уравнении могут присутствовать любые символы-нецифры, а также натуральные числа).
Входные данные
Вводится одна строка без пробелов, состоящая из не более чем 100 символов.
В строке могут встречаться натуральные числа, а также нецифровые символы.
Выходные данные
Выведите слово YES заглавными латинскими буквами, если такое уравнение можно дать в ЕГЭ и NO в противном случае.
| |
![]()
|
|
Контрольная по ударениям
Строки
Бинарный поиск в массиве
Учительница задала Пете домашнее задание — в заданном тексте расставить ударения в словах, после чего поручила Васе проверить это домашнее задание. Вася очень плохо знаком с данной темой, поэтому он нашел словарь, в котором указано, как ставятся ударения в словах. К сожалению, в этом словаре присутствуют не все слова. Вася решил, что в словах, которых нет в словаре, он будет считать, что Петя поставил ударения правильно, если в этом слове Петей поставлено ровно одно ударение.
Оказалось, что в некоторых словах ударение может быть поставлено больше, чем одним способом. Вася решил, что в этом случае если то, как Петя поставил ударение, соответствует одному из приведенных в словаре вариантов, он будет засчитывать это как правильную расстановку ударения, а если не соответствует, то как ошибку.
Вам дан словарь, которым пользовался Вася и домашнее задание, сданное Петей. Ваша задача — определить количество ошибок, которое в этом задании насчитает Вася.
Входные данные
Вводится сначала число N — количество слов в словаре (0≤N≤20000).
Далее идет N строк со словами из словаря. Каждое слово состоит не более чем из 30 символов. Все слова состоят из маленьких и заглавных латинских букв. В каждом слове заглавная ровно одна буква — та, на которую попадает ударение. Слова в словаре расположены в алфавитном порядке. Если есть несколько возможностей расстановки ударения в одном и том же слове, то эти варианты в словаре идут в произвольном порядке.
Далее идет упражнение, выполненное Петей. Упражнение представляет собой строку текста, суммарным объемом не более 300000 символов. Строка состоит из слов, которые разделяются между собой ровно одним пробелом. Длина каждого слова не превышает 30 символов. Все слова состоят из маленьких и заглавных латинских букв (заглавными обозначены те буквы, над которыми Петя поставил ударение). Петя мог по ошибке в каком-то слове поставить более одного ударения или не поставить ударения вовсе.
Выходные данные
Выведите количество ошибок в Петином тексте, которые найдет Вася.
Примечание
1) В слове cannot, согласно словарю возможно два варианта расстановки ударения. Эти варианты в словаре могут быть перечислены в любом порядке (т.е. как сначала cAnnot, а потом cannOt, так и наоборот).
Две ошибки, совершенные Петей — это слова be (ударение вообще не поставлено) и fouNd (ударение поставлено неверно). Слово thE отсутствует в словаре, но поскольку в нем Петя поставил ровно одно ударение, признается верным.
2) Неверно расставлены ударения во всех словах, кроме The (оно отсутствует в словаре, в нем поставлено ровно одно ударение). В остальных словах либо ударные все буквы (в слове PAGE), либо не поставлено ни одного ударения.
| |
![]()
|
|
Контрольная по ударениям
Строки
Бинарный поиск в массиве
Учительница задала Пете домашнее задание — в заданном тексте расставить ударения в словах, после чего поручила Васе проверить это домашнее задание. Вася очень плохо знаком с данной темой, поэтому он нашел словарь, в котором указано, как ставятся ударения в словах. К сожалению, в этом словаре присутствуют не все слова. Вася решил, что в словах, которых нет в словаре, он будет считать, что Петя поставил ударения правильно, если в этом слове Петей поставлено ровно одно ударение.
Оказалось, что в некоторых словах ударение может быть поставлено больше, чем одним способом. Вася решил, что в этом случае если то, как Петя поставил ударение, соответствует одному из приведенных в словаре вариантов, он будет засчитывать это как правильную расстановку ударения, а если не соответствует, то как ошибку.
Вам дан словарь, которым пользовался Вася и домашнее задание, сданное Петей. Ваша задача — определить количество ошибок, которое в этом задании насчитает Вася.
Входные данные
Вводится сначала число N — количество слов в словаре (0≤N≤100).
Далее идет N строк со словами из словаря. Каждое слово состоит не более чем из 30 символов. Все слова состоят из маленьких и заглавных латинских букв. В каждом слове заглавная ровно одна буква — та, на которую попадает ударение. Слова в словаре расположены в алфавитном порядке. Если есть несколько возможностей расстановки ударения в одном и том же слове, то эти варианты в словаре идут в произвольном порядке.
Далее идет упражнение, выполненное Петей. Упражнение представляет собой строку текста, суммарным объемом не более 30000 символов. Строка состоит из слов, которые разделяются между собой ровно одним пробелом. Длина каждого слова не превышает 30 символов. Все слова состоят из маленьких и заглавных латинских букв (заглавными обозначены те буквы, над которыми Петя поставил ударение). Петя мог по ошибке в каком-то слове поставить более одного ударения или не поставить ударения вовсе.
Выходные данные
Выведите количество ошибок в Петином тексте, которые найдет Вася.
Примечание
1) В слове cannot, согласно словарю возможно два варианта расстановки ударения. Эти варианты в словаре могут быть перечислены в любом порядке (т.е. как сначала cAnnot, а потом cannOt, так и наоборот).
Две ошибки, совершенные Петей — это слова be (ударение вообще не поставлено) и fouNd (ударение поставлено неверно). Слово thE отсутствует в словаре, но поскольку в нем Петя поставил ровно одно ударение, признается верным.
2) Неверно расставлены ударения во всех словах, кроме The (оно отсутствует в словаре, в нем поставлено ровно одно ударение). В остальных словах либо ударные все буквы (в слове PAGE), либо не поставлено ни одного ударения.
| |
![]()
|
|
Таймер
Дата и время
Условный оператор
Строки
Таймер - это часы, которые умеют подавать звуковой сигнал по прошествии некоторого периода времени. Напишите программу, которая определяет, когда должен быть подан звуковой сигнал.
Входные данные:
В первой строке записано текущее время в формате ЧЧ:ММ:СС (с ведущими нулями). При этом оно удовлетворяет ограничениям: ЧЧ - от 00 до 23, ММ и СС - от 00 до 60.
Во второй строке записан интервал времени, который должен быть измерен. Интервал записывается в формате Ч:М:С (где Ч, М и С - от 0 до 109, без ведущих нулей). Дополнительно если Ч=0 (или Ч=0 и М=0), то они могут быть опущены. Например, 100:60 на самом деле означает 100 минут 60 секунд, что то же самое, что 101:0 или 1:41:0.
А 42 обозначает 42 секунды. 100:100:100 - 100 часов, 100 минут, 100 секунд, что то же самое, что 101:41:40.
Выходные данные:
В ответе выведите в формате ЧЧ:ММ:СС время, когда прозвучит звуковой сигнал. При этом если сигнал прозвучит не в текущие сутки, то дальше должна следовать запись +<кол-во> days. Например, если сигнал прозвучит на следующий день - то +1 days.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
01:01:01
48:0:0
|
01:01:01+2 days |
| 2 |
01:01:01
58:119
|
02:01:00 |
| 3 |
23:59:59
1
|
00:00:00+1 days |
| |
![]()
|
|
Многочлен
Строки
Условный оператор
Васе задали несколько однотипных задач по математике: «найти значение многочлена». Он хочет написать программу, которая по заданному многочлену и значению x находила бы ответ. Напишите такую программу!
Входные данные
В первой строке входного файла записан многочлен в виде суммы одночленов. Между одночленами находится знак + или –. Перед первым одночленом может быть знак –. Одночлен записывается как
[<Коэффициент>*]x[^<Степень>]
или
<Коэффициент>
где <Коэффициент> — натуральное число, не превосходящее 100, x — символ переменной (всегда маленькая латинская буква x), <Степень> — натуральное число, не превосходящее 4. Параметры, взятые в квадратные скобки, могут быть опущены. Во второй строке записано одно целое число — значение x.
Выходные данные
В выходной файл нужно записать одно число — значение данного многочлена при данном значении x.
Ограничения
Все числа в исходном файле по модулю не превосходят 100. Количество одночленов не более 10 (могут быть одночлены одинаковой степени).
| |
![]()
|
|
Найди пару
Строки
Использование сортировки
Друзья играют в интересную игру со словами, суть которой заключается в разбиении слов на пары.
У друзей есть \(n\) слов одинаковой длины. Они хотят выбрать такое наибольшее число \(k\), чтобы можно было разбить слова на пары так, чтобы в каждой паре у слов совпадало хотя бы \(k\) первых букв.
Помогите друзьям найти искомое максимальное значение \(k\).
Формат входных данных
В первой строке входных данных находится целое число \(n\) — количество слов (\(1 \leqslant n \leqslant 2\cdot 10^5\), \(n\) — четное).
В следующих \(n\) строках заданы слова, которые есть у друзей. Гарантируется, что все строки имеют одинаковую длину и суммарная длина строк не превышает \(2 \cdot 10^6\).
Формат выходных данных
В единственной строке выведите число \(k\) — искомое максимальное значение.
| |
![]()
|
|
65984
Строки
Циклы
Условный оператор
Прибор передает результаты измерений блоками информации. Каждый блок представляет собой набор цифр в шестнадцатеричной системе счисления (0123456789ABCDEF). Последняя цифра пятеричной записи суммы цифр блока показывает код ошибки, где 0 означает корректную передачу данных. Предпоследняя цифра пятеричной записи суммы цифр блока показывает тип результата:
0: «Излучение»
1: «Вспышка»
2: «Нагрев»
3: «Охлаждение»
4: «Перегрузка»
Определите количество результатов «Перегрузка», которые были переданы без ошибок после приема n блоков данных.
Формат ввода
В первой строке программе подается на вход число натуральное число n, не превышающее 1000.
Далее в каждой из n строк идет блок данных – набор цифр в шестнадцатеричной системе счисления (0123456789ABCDEF), длина блока не превышает 100 знаков.
Формат вывода
Вывести одно число – количество результатов «Перегрузка», которые были переданы без ошибок после приема n блоков данных.
| |
![]()
|
|
65985
Строки
Разные системы счисления
В ходе игры «Зарница» Саша и Женя пересылают друг другу важные сообщения. Но для того, чтобы противник не смог их понять, сообщения кодируются. Для кодирования информации ребята используют латинский алфавит из 26 букв, все буквы заглавные. Слова кодируются следующим образом. Каждая буква в слове заменяется ее порядковым номером в алфавите, записанном в системе счисления с основанием Sys (2 <= Sys <= 36). Все полученные числа записываются подряд без пробелов. Если числа (порядковые номера букв) в заданной системе счисления могут иметь разную длину, то более короткие числа дополняются слева нулями до требуемой длины. Например, в десятичной системе счисления порядковый номер буквы A будет равен 1, а буквы Z – 26. Соответственно, при шифровании, к единице слева будет дописан ноль. То есть код буквы A будет 01, а код буквы Z – 26. Для усложнения возможной расшифровки сообщения противником, для кодирования букв, стоящих на разных местах в слове, используются различные системы счисления. Основание использованной системы счисления выбирается исходя из порядкового номера буквы в кодируемом сообщении. Для кодирования первой буквы сообщения используется двоичная система счисления, для второй – троичная, для третьей – четверичная и т.д., до системы счисления с основанием 36 включительно. Далее основания систем счисления повторяются циклически – 2, 3, 4, …36, 2, 3, … Например, слово AZ, будет закодировано как 00001222.
Напишите программу, которая будет расшифровывать закодированные сообщения.
На вход программе подается одно закодированное сообщение. Длина сообщения не более 200 символов. Программа должна вывести исходное слово.
| |
![]()
|
|
65995
Строки
Разные системы счисления
В ходе игры «Зарница» Витя и Паша пересылают друг другу важные сообщения. Но для того, чтобы противник не смог их понять, сообщения кодируются. Для кодирования информации ребята используют латинский алфавит из 26 букв, все буквы заглавные. Слова кодируются следующим образом. Каждая буква в слове заменяется ее порядковым номером в алфавите, записанном в системе счисления с основанием Sys (2 <= Sys <= 36). Все полученные числа записываются подряд без пробелов. Если числа (порядковые номера букв) в заданной системе счисления могут иметь разную длину, то более короткие числа дополняются слева нулями до требуемой длины. Например, в десятичной системе счисления порядковый номер буквы A будет равен 1, а буквы Z – 26. Соответственно, при шифровании, к единице слева будет дописан ноль. То есть код буквы A будет 01, а код буквы Z – 26. Для усложнения возможной расшифровки сообщения противником, при кодировании разных слов, могут использоваться различные системы счисления. Основание использованной системы счисления, выраженное двухзначным десятичным числом дописывается справа к коду всего слова.
Например, слово AZ, при использовании десятичной системы счисления, будет закодировано как 012610, а при использовании троичной системы счисления будет закодировано как 00122203.
Напишите программу, которая будет расшифровывать закодированные сообщения.
На вход программе подается одно закодированное сообщение. Длина сообщения не более 100 символов. Программа должна вывести исходное слово.
| |
![]()
|
|
Задача 1
Строки
Строки
Вася недавно изучил индексы и пока в них путается. В программе у него есть строка string, символ s и индекс index. Вася считает, что по индексу index в string стоит символ s. Прав ли он? Выведите "ДА" или "НЕТ".
Дано такое число index, что символ по нему всегда найдётся.
| |
![]()
|
|
Задача 1
Строки
Строки
Вася недавно изучил индексы и пока в них путается. В программе у него есть строка string, символ s и индекс index. Вася считает, что по индексу index в string стоит символ s. Прав ли он? Выведите "ДА" или "НЕТ".
Дано такое число index, что символ по нему всегда найдётся.
| |
![]()
|
|
Задача 2
Строки
На уроке Соня пишет в прописи. Писать всё синей ручкой очень скучно, тем более что Соне подарили набор гелевых ручек. Для каждого слова девочка загадывает число n и пишет это слово тремя цветами: первые n букв красным, последние n букв зелёным, а средние — фиолетовым.
Дано слово и число n. Выведите первую и последнюю букву фиолетовой части.
| |
![]()
|
|
Задача 3
Строки
Вася с сестрой Соней играли в морской бой. Вася вспомнил, что должен помочь Соне с домашним заданием по русскому. Теперь они играют в морской бой со сложными словами. Вася загадывает слово. Соня придумывает произвольные числа, и Вася называет ей буквы слова по индексам — этим числам. В конце Соня должна отгадать слово.
Дана строка с Васиным словом и набор чисел, которые назвала Соня, а потом строка "стоп". Выведите все буквы, которые назвал Вася.
| |
![]()
|
|
Задача 4
Строки
Первоклассник Петя учится писать и считать. Чтобы быстрее закончить, он совмещает эти два занятия: берёт n слов из n букв и выписывает в столбик первую букву первого слова, вторую букву второго слова, третью третьего и так далее.
Дано число n и n слов из n букв. Выведите, что записал Петя.
| |
![]()
|
|
Задача 5
Строки
Вася и Соня играют в города: Вася пишет название одного города, Соня — другого. Это второе название начинается на последнюю букву первого. Названия они пишут с маленькой буквы. Правильно ли Соня придумала город? Выведите "ДА" или "НЕТ".
| |
![]()
|
|
Задача 6
Строки
Вася взял строку символов, выбрал один, поставил курсор слева от него, подвинул курсор на 5 символов вправо, потом на 7 влево, потом опять на n символов вправо — и дошёл до конца строки. Дана строка и число n. Выведите символ, который выбрал Вася.
| |
![]()
|
|
Задача 7
Строки
Соня раскрашивает Васин учебник. Красным карандашом она красит буквы, оставляя между ними одинаковые промежутки. Количество букв между каждыми двумя покрашенными равно количеству букв перед первой покрашенной и после последней покрашенной. Соня покрасила n букв.
Дано слово и число n. Выведите раскрашенные буквы в столбик.
| |
![]()
|
|
Задача 8
Строки
Вася разделяет две части предложения либо двоеточием («текст: текст»), либо точкой с запятой («текст; текст»), либо тире («текст — текст»). Длина частей одинаковая (в предложении «текст: таков» длина строки "текст" равна длине строки "таков").
Дано предложение. Выведите знак препинания, которым Вася разделил предложение.
| |
![]()
|
|
Задача 9
Строки
У редактора школьной газеты Кости опять проблемы. Авторов мало, тексты слишком короткие. Костя предложил авторам увеличить каждое слово до n символов.
Дана строка и число n, которое больше длины строки. Продублируйте первый и последний символы строки столько раз, чтобы длина строки была равна n. Этих добавленных в начале и в конце слова символов должно быть поровну. Если невозможно добавить равное количество символов так, чтобы длина строки стала равна n, справа можно добавить точку.
| |
![]()
|
|
Задача 10
Строки
У Сони есть n карандашей разных цветов. Она снова взялась за Васин учебник. Каждый следующий символ она красит карандашом другого цвета. Через каждые n символов она возвращается к первому карандашу.
Дана строка с текстом, раскрашенным Соней. Первый символ в строке покрашен красным. Выведите последний красный символ в строке.
Примечание: в строке "сегодня" будет две полные тройки: "сег" и "одн" и «остаток» из строки "я". Красным будет символ "я". В строке "КАРТОН" символов столько же, сколько у Сони карандашей. Поэтому красный символ только один: это "К".
| |
![]()
|
|
Задача 11
Строки
Назовём углом из слова «аксолотль» такую запись:
л
о о
с т
к л
а ь
Дано слово нечётной длины. Выведите угол из этого слова.
| |
![]()
|
|
Задача 12
АА
Строки
Соня продолжает раскрашивать Васин учебник. Красным карандашом она красит буквы не подряд, а в определённом порядке. Одну букву красит, одну пропускает, снова красит одну, пропускает две буквы, красит одну букву, пропускает три буквы и т. д.
Дано слово. Соня покрасила в нём несколько букв. Первая — красная. Выведите все покрашенные буквы (слитно, в одну строку).
| |
![]()
|
|
Задача 1
Строки
Вася с папой решили поздравить маму с днём рождения. Они сделали картонные буквы и повесили их на видном месте. Васин папа нечаянно передвинул первые n букв в конец поздравления.
Дана строка и число n. Поменяйте местами начало строки из n символов и её конец.
| |
![]()
|
|
Задача 2
Строки
Илья забыл покормить черепашку. В ответ она обглодала его список покупок. Из первого пункта в списке исчезли первые и последние n символов (n ≥ 1).
Дана строка с первым пунктом и число n. Выведите то, что осталось в списке.
| |
![]()
|
|
Задача 3
Строки
Вася с Эмилией играют в слова. Вася записывает слово, а Эмилия угадывает. Буквы, которые Эмилия еще не отгадала, Вася помечает точками. В разгар игры в начале и в конце слова было ровно по n угаданных букв, а все буквы в середине были помечены точками.
Дано Васино слово и число n. Выведите, как оно было записано в разгар игры.
| |
![]()
|
|
Задача 4
Строки
Вася с Эмилией продолжают играть в слова. Эмилии осталось угадать совсем немного букв.
Дано Васино слово, последовательность индексов, символы по которым ещё отмечены точками, и строка "стоп" в конце. Выведите, что записано у Васи.
| |
![]()
|
|
Задача 5
Строки
Костя записывает важные цифры на листке бумаги. Цифр много, а бумаги мало. Костя решил записывать цифры не через запятую, а слитно.
Дана строка с цифрами через запятую. Выведите их слитно.
| |
![]()
|
|
Задача 6
Строки
Сонины родители пишут друг другу записки. Соня нашла записку и сложила её так, что видны первые n и последние n символов. Девочке показалось, что эти части записки зеркальные: если написать одну задом наперёд, получится другая. Права ли Соня? Выведите "ДА" или "НЕТ".
| |
![]()
|
|
Задача 7
Строки
Соня пишет подружке секретные сообщения. Она взяла слово, количество букв в котором кратно 4, разделила его на 4 части и записала буквы по периметру фигуры, чтобы читать по часовой стрелке. Например, слово «аббревиатура» выглядит так:
абб
а р
р е
у в
таи
Дано слово. Выведите его так, как у Сони.
| |
![]()
|
|
Задача 8
Строки
Вася учит Соню языку Python. Он рассказал сестре, как складывать и умножать переменные, велел ей написать программу, которая складывает и перемножает несколько трёхзначных чисел, и подготовил тест. Когда Вася с Соней ужинали, к компьютеру подлетел коварный попугай и постучал по клавиатуре клювом. Теперь Васины числа записаны в одну строчку. Между каждыми двумя — один произвольный символ.
Дана строка с числами. Выведите их сумму и произведение.
| |
![]()
|
|
Задача 9
Строки
Гриша с Яной поспорили. Гриша говорит, что слово word было в Янином сообщении message, а Яна считает, что слова word она не писала.
Даны word и message. Прав ли Гриша? Выведите "ДА" или "НЕТ".
| |
![]()
|
|
Задача 10
Строки
Петя с Васей играют: придумывают вместе число n, затем каждый в своём блокноте пишет строку длиной 2n из пробелов и минусов. Свои строки они друг другу не показывают.
Потом Петя называет n чисел от 0 до 2n - 1. Если в Васиной строке на местах по этим индексам стоят минусы, он зачёркивает их так, что получаются плюсы. Затем они меняются: Вася называет числа, а Петя зачёркивает минусы.
Даны две строки (Петина и Васина), Петины числа в столбик и Васины числа в столбик. Выведите две строки (сначала Петину, потом Васину), какими они стали после всех зачеркиваний.
| |
![]()
|
|
Задача 11
Строки
Строки
Васина программа раз за разом выдаёт синтаксическую ошибку. Вася подозревает, что где-то не так поставил кавычки. Он придумал алгоритм исправления этой ошибки:
- • если кавычек нет, ставить двойные,
- • если с одной стороны кавычки нет, добавить правильную,
- • если кавычки разные, поменять закрывающую на открывающую,
- • если кавычки есть и одна соответствует другой, оставить так.
Дана строка из Васиной программы. Выведите её с Васиными исправлениями.
| |
![]()
|
|
Задача 11
Строки
Строки
Васина программа раз за разом выдаёт синтаксическую ошибку. Вася подозревает, что где-то не так поставил кавычки. Он придумал алгоритм исправления этой ошибки:
- • если кавычек нет, ставить двойные,
- • если с одной стороны кавычки нет, добавить правильную,
- • если кавычки разные, поменять закрывающую на открывающую,
- • если кавычки есть и одна соответствует другой, оставить так.
Дана строка из Васиной программы. Выведите её с Васиными исправлениями.
| |
![]()
|
|
Задача 12
Строки
Оля вырезает трафареты для надписей на футболке. У неё есть две надписи. Чтобы сэкономить время, она отрезала конец первого трафарета, добавила к нему справа недостающие буквы и так получила второй трафарет. Общая часть должна быть максимально возможной длины.
Даны две строки с первой и второй надписью. Выведите общую часть.
| |
![]()
|
|
Задача 1
Строки
Учительница Анна Николаевна смотрит на список присутствующих и вызывает первого по списку к доске.
Даны две строки в произвольном порядке, в каждой — имя и фамилия ученика из списка. Кого из них Анна Николаевна вызовет к доске, если её список в алфавитном порядке?
| |
![]()
|
|
Задача 2
Строки
Когда играют в «шляпу» или в «крокодил», Василий всегда загадывает слова, которые начинаются на букву с В до Й (включительно).
Дано слово с большой буквы. Согласится ли Вася загадать его? Выведите "ДА" или "НЕТ".
| |
![]()
|
|
Задача 3
Строки
Соня купила две шоколадки: в красной упаковке и в синей. В чеке названия шоколадок идут по алфавиту. Сначала Соня съела шоколадку, которая шла в чеке первой.
Даны названия красной и синей шоколадок. Какую шоколадку Соня съела первой? Выведите "красная" или "синяя".
| |
![]()
|
|
Задача 4
Строки
Вася подготовил для Сони мини-диктант из четырёх слов. Он сказал, что расставил их в алфавитном порядке. Прав ли Вася? Выведите "ДА" или "НЕТ".
| |
![]()
|
|
Задача 5
Строки
Юная разведчица Соня расшифровывает «секретное сообщение» — набор букв, который оставила кошка, пройдясь по клавиатуре. Соня загадывает букву и выписывает в одну строчку те буквы кошкиного сообщения, которые идут в алфавите раньше её буквы, а во вторую строчку — те, что позже.
Дано сообщение и Сонина буква. Выведите две Сониных строчки.
| |
![]()
|
|
Задача 6
Строки
Первоклассник Петя вечно путает строчные буквы с прописными. Мама помогает ему разобраться.
Дана строка с одной буквой русского алфавита. Выведите "прописная" или "строчная".
| |
![]()
|
|
Задача 7
Строки
Анна захотела расставить свои книги в алфавитном порядке. На верхней полке стоят три её любимые книги.
Даны три строки с названиями книг. Выведите их в столбик в алфавитном порядке.
| |
![]()
|
|
Задача 8
Строки
Композитор Пьер написал гениальную мелодию. Надо отправить её дирижеру, чтобы он выступил с ней на концерте. Пьер боится, что мелодию коварно перехватят конкуренты. Он зашифровал её буквами. Чем позже буква в алфавите, тем выше нота. Буквы для простой мелодии без аккордов Пьер записывает слитно, в строчку.
Дана строка с зашифрованной мелодией. Будет ли каждая нота выше (или равна) предыдущей? Выведите "ДА" или "НЕТ".
| |
![]()
|
|
Задача 9
Строки
Композитор Пьер продолжает шифровать простые мелодии буквами. Чем позже буква по алфавиту, тем выше нота.
Дана строка с зашифрованной мелодией. Выведите символ, который обозначает самую низкую ноту.
| |
![]()
|
|
Задача 10
Строки
Соня устала от Васиных попыток «подтянуть» её по русскому. В отместку она нашла файл с Васиным сочинением по литературе и добавила туда произвольные английские буквы. Теперь Вася правит текст. Чтобы найти лишние символы, он каждое слово пропускает через специальную программу.
Вася не любит букву «Ё», поэтому никогда её не пишет.
Дано строка со словом (только буквы). Состоит ли она только из русских букв? Выведите "ДА" или "НЕТ".
| |
![]()
|
|
Задача 11
Строки
Петя пишет диктант. Ему не нравится ставить знаки препинания, поэтому он их пропускает.
Дана строка с текстом из диктанта. В ней только русские буквы, пробелы и знаки препинания. Удалите из неё все знаки препинания, оставив только буквы и пробелы.
| |
![]()
|
|
Задача 12
Строки
Гоше не понравился лексикографический порядок, поэтому он придумал свой: одно слово меньше другого, если каждый его символ меньше символа другого слова по тому же индексу. Если слова разной длины, короткое слово Гоша дополняет справа пробелами.
Даны две строки со словами. Выведите "Первое меньше", "Второе меньше" или "Невозможно определить".
| |
![]()
|
|
Задача 1
Строки
Редактор школьной газеты Костя прочитал новую заметку, покраснел, побледнел и велел автору Асе: «Всё до слова word — удалить!» Ася удалила всё до последнего (крайнего справа) слова word (не включительно).
Дано слово word и строка со статьей. Выведите, что получилось у Аси.
| |
![]()
|
|
Задача 2
Строки
У редактора газеты Кости непонимание с автором Асей. Ася удалила из заметки весь текст до последнего слова word, а надо было до первого. Костя сердится, а Ася жалуется друзьям.
Дано слово word и строка со статьей. Выведите строку "Удалить «»", но между кавычками-ёлочками добавьте часть статьи до первого слова word.
| |
![]()
|
|
Задача 3
Строки
Вася попросил Алису помочь ему с сочинением. Алиса читает сочинение и пишет Васе, что нужно поправить. Её сообщение выглядит так:
Я бы в месте «(предложение)» исправила «(слово)» на «(новое слово)». Получилось бы «(новое предложение)»
Кавычки — это часть сообщения Алисы, а скобки — нет.
Дано предложение, старое слово и новое слово. Выведите Алисино сообщение.
| |
![]()
|
|
Задача 4
Строки
Соня любит цифры 4 и 2. Дан текст на несколько строк, а в конце — строка "стоп". В тексте есть разные числа. Выведите, сколько раз в тексте встречаются Сонины любимые цифры.
| |
![]()
|
|
Задача 5
Строки
Вася пишет сочинения по литературе на компьютере и отправляет файлы учительнице. Пока никто не видит, его сестра Соня может приписать что-нибудь в конце. Прежде чем отправить файл, Вася смотрит, не пошалила ли Соня. К счастью, он знает, что Соня никогда не ставит точек, и поэтому может определить, где закончилось его сочинение: там, где стоит последняя точка.
Дана строка с Васиным сочинением. Выведите сочинение, убрав Сонино дополнение.
| |
![]()
|
|
Задача 6
Строки
В сочинениях Алиса ставит много скобок (например, вот так (или даже вот так)). Иногда Алиса может ошибиться — поставить лишнюю скобку или не поставить нужную.
Дана строка. Скобки стоят в правильном порядке. Строка не может быть равна, например, ")(".
Поставила ли Алиса нужное число скобок? Выведите "ДА" или "НЕТ".
| |
![]()
|
|
Задача 7
Строки
Вася подозревает, что сестра Соня открыла файл с его сочинением по литературе и что-то приписала в конце. Он знает, что Соня никогда не ставит точек.
Убедитесь, что после последней точки в тексте — только пробелы. Если это правда, то выведите "Всё хорошо!". Иначе выведите "Лишние символы!".
| |
![]()
|
|
Задача 8
Строки
Вася написал пост и решил заменить одно слово в нём (обозначим его old) на другое (new). Для этого Вася написал небольшую программу, но она поменяла в Васином посте все найденные слова old, а ему нужно было только первое.
Даны три строки: string, old, new. Замените первое old в строке string на строку new.
| |
![]()
|
|
Задача 9
Строки
Редактор школьной газеты Костя подготовил слишком много заметок. Они не помещаются в номер. Костя решил их все немного сократить. Он удалил из всех заметок одно и то же выражение, и они поместились.
Даны две строки. Удалите из первой строки все вхождения второй строки.
| |
![]()
|
|
Задача 10
Строки
Люба рисует красивые граффити. Она любит число 3, поэтому в надписях какое-то слово или символ часто повторяет трижды. Второе слово из трёх она всегда выводит золотой краской.
Даны две строки. Известно, что вторая строка встречается в первой 3 раза. Выведите индекс второго вхождения.
| |
![]()
|
|
Задача 11
Строки
Вася написал большую программу с разными строками. Он присваивал строки переменным, использовал их в выражениях. Внутри строк он никогда не ставил кавычек.
Дана Васина программа, а в конце "стоп". Сколько значений типа «строка» в Васиной программе?
| |
![]()
|
|
Задача 12
Строки
Дана строка с текстом на русском языке. В ней могут быть русские буквы (строчные и прописные), пробелы, запятые и точки. Текст написан правильно, в нём нет лишних пробелов или знаков препинания помимо точек и запятых.
Выведите, сколько в тексте слов.
| |
![]()
|
|
Задача 1
Строки
Макс учит детей играть в футбол. Дети полюбили Макса и стали бегать к нему с разными вопросами, чаще всего почему-то с математикой. У Макса по алгебре тройка, но с задачами для начальной школы он вполне справляется.
Петя попросил Макса помочь посчитать выражение: a разделить на b и умножить на c.
Даны числа a, b, c. Выведите a // b * c.
| |
![]()
|
|
Задача 2
Строки
Макс распределил маленьких футболистов по четырём командам и велел всем носить футболки цвета своей команды. У первой команды цвет оранжевый, у второй — белый, у третьей — синий, а у четвертой — зелёный.
Дан цвет. Выведите номер команды (цифрой). Обратите внимание, что слово «зелёный» пишется через «ё».
| |
![]()
|
|
Задача 3
Строки
Макс не понял, как так вышло, но теперь он учит первоклассников считать. Ему помогают футбольные мячи. Сегодня Макс объясняет деление на три. Он сложил мячи в две корзины. Сколько мячей класть в каждую, он решил с помощью генератора случайных чисел.
Числа должны быть положительные. Хотя бы одно должно делиться на 3.
Генератор выдал два числа. Подойдут ли они Максу? Выведите "ДА" или "НЕТ".
| |
![]()
|
|
D. Слово - не воробей
*особая задача
Строки
*1500
В наши дни средства массовой информации распространяют много слухов. Однажды Аида захотела узнать, как создаются слухи. Она попросила n своих друзей помочь ей. Все друзья собрались в круг и Аида поведала человеку справа от неё некоторую новость, представленную простой строкой. Затем каждый человек пересказал строку человеку справа. Однако они не пересказали строку в том самом виде, в каком слышали её: каждый человек произвел не более чем одну из приведенных ниже двух видов операций: - удалил один символа с конца услышанной строки,
- добавил один символ в конец услышанной строки.
В итоге, когда слух был пересказан ровно n раз (то есть прошел один полный круг), Аида услышала совсем не то, что ожидала услышать от человека слева. Она считает, что кто-то сжульничал и произвел изменения, отличные от изменений, приведенных выше. Теперь она хочет, чтобы вы проверили, возможно ли что строка пришедшая к ней получена по описанным выше правилам. Выходные данные Выведите единственное слово — YES или NO. Выведите YES только в том случае, если можно получить конечную строку из начальной. Примечание Регистр во входных данных учитывается, в выходных — нет. | |
![]()
|
|
F. Аббревиация
дп
Строки
хэши
*2200
Дан текст, состоящий из \(n\) слов, разделённых пробелами. Между каждой парой соседних слов ровно один пробел. Перед первым словом и после последнего слова нет пробелов. Длина текста — это количество букв и пробелов в нём. \(w_i\) обозначает \(i\)-е слово текста. Все слова состоят только из строчных букв латинского алфавита. Определим отрезок слов \(w[i..j]\) как последовательность слов \(w_i, w_{i + 1}, \dots, w_j\). Два отрезка слов \(w[i_1 .. j_1]\) и \(w[i_2 .. j_2]\) считаются одинаковыми, если \(j_1 - i_1 = j_2 - i_2\), \(j_1 \ge i_1\), \(j_2 \ge i_2\), и для каждого \(t \in [0, j_1 - i_1]\) \(w_{i_1 + t} = w_{i_2 + t}\). Например, в тексте "to be or not to be" отрезки \(w[1..2]\) и \(w[5..6]\) одинаковы, они соответствуют последовательности слов "to be". Аббревиация — это замена некоторых слов в тексте их первыми заглавными буквами. Чтобы использовать аббревиацию, вы должны выбрать хотя бы два непересекающихся одинаковых отрезка слов и заменить каждый из выбранных отрезков на строку, состоящую из первых букв этих слов (буквы в новой строке являются заглавными). К примеру, в тексте "a ab a a b ab a a b c" можно заменить отрезки слов \(w[2..4]\) и \(w[6..8]\) аббревиацией "AAA" и получить текст "a AAA b AAA b c", или заменить \(w[2..5]\) и \(w[6..9]\) на аббревиацию "AAAB" и получить текст "a AAAB AAAB c". Чему равна минимальная длина текста после использования не более чем одной аббревиации? Выходные данные Выведите одно целое число — минимальную длину текста после использования не более чем одной аббревиации. Примечание В первом примере можно получить текст "TB or not TB". Во втором примере можно получить текст "a AAAB AAAB c". В третьем примере можно получить текст "AB aa AB bb". | |
![]()
|
|
B. Удаляй слева
Перебор
реализация
Строки
*900
Заданы две строки \(s\) и \(t\). За один ход можно выбрать произвольную из двух строк и удалить её первый (самый левый) символ. При этом длина строки уменьшается на \(1\). Например: - применив ход к строке «where», в результате получится строка «here»,
- применив ход к строке «a», в результате получится пустая строка «».
Требуется сделать две строки равными, выполнив наименьшее количество ходов, применяя каждый раз ход к любой из двух строк. Это допустимо, что в итоге обе строки окажутся равны пустой строке и равны между собой. В этом случае, очевидно, ответ — это сумма длин заданных строк. Напишите программу, которая найдет минимальное количество ходов, чтобы сделать две заданные строки \(s\) и \(t\) равными. Выходные данные Выведите искомое наименьшее количество ходов. Возможно, что в итоге обе строки окажутся равны пустой строке и равны между собой. В этом случае, очевидно, ответ — это сумма длин заданных строк. Примечание В первом примере следует один раз применить ход к первой строке и один раз применить ход ко второй строке. В результате обе строки будут равны «est». Во втором примере ход следует применить \(8\) раз к «codeforces». В результате будет получена строка «codeforces» \(\to\) «es». К строке «yes» ход следует применить один раз. В результате будет получена такая же строка «yes» \(\to\) «es». В третьем примере строки можно сделать равными только полностью их удалив. То есть в итоге обе строки получатся пустыми. В четвёртом примере следует удалить первый символ второй строки. | |
![]()
|
|
A. Ромадзи
реализация
Строки
*900
Витя начал учить берляндский язык. Известно, что в Берляндии используют латинский алфавит. Буквы «a», «o», «u», «i» и «e» являются гласными. Остальные буквы — согласные. В берляндском языке после каждой согласной буквы обязательно идёт гласная буква, а после гласной — может идти любая. Единственным исключением является согласная буква «n» — после неё может идти любая буква (не только гласная), а может и не идти буква вообще. Например, слова «harakiri», «yupie», «man» и «nbo» являются берляндскими, а слова «horse», «king», «my» и «nz» — нет. Помогите Вите понять, является ли слово \(s\) берляндским. Выходные данные Выведите «YES» (без кавычек), если идет гласная после каждой согласной кроме «n», иначе выведите «NO». Вы можете выводить каждую из букв в любом регистре (строчную или заглавную). Примечание В первом и втором примерах после каждой согласной кроме «n» идёт гласная, поэтому слово является берляндским. В третьем примере после согласной «r» идёт другая согласная «c», а согласная «s» стоит в конце, поэтому слово не является берляндским. | |
![]()
|
|
D. AB-Строки
Конструктив
Строки
*2800
Даны две строки s и t, состоящие только из букв a и b. Вы можете несколько раз совершить следующую операцию: выбрать префикс строки s, префикс строки t и поменять их местами. Префиксы могут быть пустыми, также префикс может совпадать со всей строкой. Ваша задача — найти последовательность операций, после которой одна из строк будет состоять только из букв a, а другая — только из букв b. Число операций нужно минимизировать. Выходные данные Первая строка вывода должна содержать число n (0 ≤ n ≤ 5·105) — количество операций. Каждая из последующих n строк должна содержать два числа ai, bi, разделённых пробелом — длины префиксов s и t для обмена, соответственно. Если существует несколько возможных решений, вы можете вывести любое. Гарантируется, что решение с заданными ограничениями существует. Примечание В первом примере вы можете решить задачу в две операции: - Обменять префикс первой строки длины 1 и префикс второй строки длины 0. После этого обмена вы получите ab и bbb.
- Обменять префикс первой строки длины 1 и префикс второй строки длины 3. После этого обмена вы получите bbbb и a.
Во втором примере строки уже подходящие, поэтому операции не нужны. | |
![]()
|
|
F. Скобочная подстрока
дп
Строки
*2300
Задана скобочная последовательность \(s\) (не обязательно правильная). Скобочная последовательность — это строка, состоящая только из символов '(' и ')'. Правильная скобочная последовательность — это скобочная последовательность, которая может быть преобразована в корректное арифметическое выражение при помощи вставки символов '1' и '+' между изначальными символами последовательности. Например, скобочные последовательности «()()» и «(())» являются правильными (полученные выражения выглядят следующим образом: «(1)+(1)» и «((1+1)+1)»), а «)(», «(» и «)» — нет. Ваша задача — посчитать количество правильных скобочных последовательностей длины \(2n\), содержащих заданную скобочную последовательность \(s\) как подстроку (последовательность подряд идущих символов) по модулю \(10^9+7\) (\(1000000007\)). Выходные данные Выведите одно целое число — количество правильных скобочных последовательностей, содержащих заданную скобочную последовательность \(s\) как подстроку. Так как это число может быть очень большим, выведите его по модулю \(10^9+7\) (\(1000000007\)). Примечание Все правильные скобочные последовательности, удовлетворяющие ограничениям, описанным выше, для первого тестового примера: - «(((()))())»;
- «((()()))()»;
- «((()))()()»;
- «(()(()))()»;
- «()((()))()».
Все правильные скобочные последовательности, удовлетворяющие ограничениям, описанным выше, для второго тестового примера: - «((()))»;
- «(()())»;
- «(())()»;
- «()(())».
В третьем примере не существует правильных скобочных последовательностей длины \(4\), содержащих «(((» как подстроку. | |
![]()
|
|
E. Сверхзвуковая ракета
геометрия
Строки
хэши
*2400
После войны сверхзвуковая ракета стала самым популярным видом общественным транспортом. Каждая сверхзвуковая ракета состоит из двух «двигателей». Каждый двигатель представляет собой множество из «источников питания». Первый двигатель состоит из \(n\) источников питания, а второй из \(m\). Источник питания можно представить как точку \((x_i, y_i)\) на 2-D плоскости. Все точки в каждом двигателе различные. Вы можете влиять на каждый двигатель отдельно. Есть два действия, которые вы можете делать с каждым двигателем. Вы можете делать каждое действие столько раз, сколько хотите. - Каждый источник питания двигателя \((x_i, y_i)\) станет \((x_i+a, y_i+b)\), где \(a\) и \(b\) могут быть любыми действительными числами. Другими словами, все источники питания будут смещены.
- Каждый источник питания двигателя \((x_i, y_i)\) станет \((x_i \cos \theta - y_i \sin \theta, x_i \sin \theta + y_i \cos \theta)\), где \(\theta\) может быть любым действительным числом. Другими словами, все источники питания будут повернуты.
Двигатель работает следующим способом: после того, как оба двигателя будут заряжены, их источники питания объединяются вместе (координаты источников питания разных двигателей могут совпадать). А именно, если есть две точки питания \(A(x_a, y_a)\) и \(B(x_b, y_b)\), то для каждого действительного числа \(k\), такого что \(0 \lt k \lt 1\), будет сгенерирован новый источник питания \(C_k(kx_a+(1-k)x_b,ky_a+(1-k)y_b)\). Эта процедура будет повторена еще раз со всеми новыми и старыми источниками. После этого будет сгенерировано «силовое поле» из всех источников питания. Сверхзвуковая ракета будет «безопасна» тогда и только тогда, когда после всех ваших действий на генераторы, уничтожение любого источника питания не изменит силовое поле (в сравнении со случаем, когда ни один источник питания не был уничтожен). Два силовые поля считаются одинаковыми тогда и только тогда, когда каждый источник питания в одном силовом поле принадлежит и второму. У вас есть сверхзвуковая ракета, проверьте безопасна ли она. Выходные данные Выведите «YES», если сверхзвуковая ракета безопасна, иначе выведите «NO». Вы можете выводить каждую букву в любом регистре (строчную или заглавную). Примечание  Те точки, которые находятся близко друг к другу, на самом деле совпадают. Те точки, которые находятся близко друг к другу, на самом деле совпадают. Сначала, вы можете использовать второе действие над первым двигателем, где \(\theta = \pi\) (вы поверните все точки на \(180\) градусов). После операции источники питания в первом двигателе будут иметь координаты \((0, 0)\), \((0, -2)\) и \((-2, 0)\).  Потом, вы можете использовать первое действие над вторым двигателем, где \(a = b = -2\). После операции источники питания во втором двигателе будут иметь координаты \((-2, 0)\), \((0, 0)\), \((0, -2)\) и \((-1, -1)\).  Можно заметить, что, уничтожая любую точку, силовое поле будет всегда выпуклым треугольником с координатами \((0, 0)\), \((-2, 0)\), \((0, -2)\). Во втором примере не имеет значения как вы будете менять, во втором двигателе всегда будет источник питания, который изменит силовое поле, если будет уничтожен. | |
![]()
|
|
A. Соответствие шаблону с одним джокером
Перебор
реализация
Строки
*1200
Задано две строки \(s\) и \(t\). Строка \(s\) состоит из строчных букв латинского алфавита и не более одного символа звездочки '*', строка \(t\) состоит только из строчных букв латинского алфавита. Длина строки \(s\) равна \(n\), длина строки \(t\) равна \(m\). Символ зведочки '*' в строке \(s\) (если он есть) можно заменить на произвольную последовательность символов (возможно, пустую) строчных латинских букв. Другие символы строки \(s\) ни на что заменять нельзя. Если после такой замены в \(s\) можно получить строку \(t\), то говорят, что строка \(t\) соответствует шаблону \(s\). Например, если \(s=\)«aba*aba», то такому шаблону соответствуют строки «abaaba», «abacaba», «abazzzzaba», но не соответствуют строки «ababa», «abcaaba», «codeforces», «aba1aba», «aba?aba». Если строка \(t\) из соответствует шаблону \(s\), выведите «YES», иначе выведите «NO». Выходные данные Выведите «YES» (без кавычек), если можно получить строку \(t\) из строки \(s\). В противном случае выведите «NO» (без кавычек). Примечание В первом тестовом примере символ звездочки '*' может быть заменен строкой «force». Таким образом, строка \(s\) после этой замены будет равна «codeforces», а ответ «YES». Во втором тестовом примере символ звездочки '*' может быть заменен пустой строкой. Таким образом, строка \(s\) после этой замены будет равна «vkcup», а ответ «YES». В третьем тестовом примере нет символа звездочки '*', а строки «v» и «k» не равны, таким образом ответ «NO». В четвертом тестовом примере не существует такой замены символа звездочки '*', что вы сможете получить строку \(t\), таким образом ответ «NO». | |
![]()
|
|
A. Палиндромная замена
реализация
Строки
*1000
Задана строка \(s\), состоящая из \(n\) строчных букв латинского алфавита. \(n\) всегда четно. Для каждой позиции \(i\) (\(1 \le i \le n\)) в строке \(s\) вам необходимо заменить букву на этой позиции либо на предыдущую в алфавитном порядке, либо на следующую (для букв 'a' и 'z' доступен только один вариант). Буква на каждой позиции должна быть изменена ровно один раз. Например, буква 'p' должна быть изменена либо на 'o', либо на 'q', буква 'a' должна быть изменена на 'b', и буква 'z' должна быть изменена на 'y'. Таким образом, строка «codeforces», например, может быть изменена на «dpedepqbft» ('c' \(\rightarrow\) 'd', 'o' \(\rightarrow\) 'p', 'd' \(\rightarrow\) 'e', 'e' \(\rightarrow\) 'd', 'f' \(\rightarrow\) 'e', 'o' \(\rightarrow\) 'p', 'r' \(\rightarrow\) 'q', 'c' \(\rightarrow\) 'b', 'e' \(\rightarrow\) 'f', 's' \(\rightarrow\) 't'). Строка \(s\) называется палиндромом, если она читается одинаково как слева направо, так и справа налево. Например, строки «abba» и «zz» — палиндромы, а строки «abca» и «zy» — нет. Ваша задача — проверить, что можно сделать строку \(s\) палиндромом, применив выше приведенные замены к каждой позиции. Выведите «YES», если строку \(s\) можно сделать палиндромом. В противном случае выведите «NO». Каждый тест содержит несколько строк, для каждой из них необходимо решить задачу независимо. Выходные данные Выведите \(T\) строк. \(i\)-я строка должна содержать ответ для \(i\)-й строки входных данных. Выведите «YES», если \(i\)-ю строку можно сделать палиндромом, применив выше приведенные замены к каждой позиции. В противном случае выведите «NO». Примечание Первая строка примера может быть изменена на «bcbbcb», две самых левых буквы и две самых правых буквы заменяются на соответствующие следующие по алфавиту буквы, две центральные заменяются на предыдущие. Вторая строка может быть изменена на «be», «bg», «de», «dg», но ни одна из этих строк не является палиндромом. Третья строка может быть изменена на палиндром «beeb». Пятая строка может быть изменена на «lk», «lm», «nk», «nm», но ни одна из этих строк не является палиндромом. Также обратите внимание, что нельзя оставить букву без изменений, поэтому нельзя получить строки «ll» или «mm». | |
![]()
|
|
A. Много одинаковых подстрок
реализация
Строки
*1300
Задана строка \(t\) длины \(n\), состоящая из строчных букв латинского алфавита, и целое число \(k\). Определим подстроку какой-либо строки \(s\) с индексами от \(l\) до \(r\) как \(s[l \dots r]\). Ваша задача — составить такую строку \(s\) минимальной возможной длины, что в ней существует ровно \(k\) позиций \(i\) таких, что \(s[i \dots i + n - 1] = t\). Другими словами, ваша задача — составить такую строку \(s\) минимальной возможной длины, что ровно \(k\) подстрок строки \(s\) равны \(t\). Гарантируется, что существует один возможный ответ. Выходные данные Выведите такую строку \(s\) минимально возможной длины, что ровно \(k\) подстрок строки \(s\) равны \(t\). Гарантируется, что существует один возможный ответ. | |
![]()
|
|
C. Добиться равенства
дп
жадные алгоритмы
Строки
*1300
Вам даны две бинарные строки \(a\) и \(b\) равной длины. Вы можете производить над строкой \(a\) следующие операции: - Поменять два бита на позициях \(i\) и \(j\) соответственно (\(1 \le i, j \le n\)), стоимость этой операции составляет \(|i - j|\), то есть модуль разницы \(i\) и \(j\).
- Выбрать произвольную позицию \(i\) (\(1 \le i \le n\)) и инвертировать (заменить \(0\) на \(1\) или \(1\) на \(0\)) значение бита на этой позиции. Стоимость этой операции равна \(1\)
Найдите минимальную стоимость, которую нужно потратить, чтобы сделать строку \(a\) равной строке \(b\). Менять строку \(b\) не разрешается. Выходные данные Выведите минимальную стоимость, которая требуется, чтобы превратить строку \(a\) в \(b\). Примечание В первом примере одним из оптимальных способов является следующий: нужно инвертировать позицию \(1\), а затем позицию \(3\). Тогда строка \(a\) меняется следующим образом: «100» \(\to\) «000» \(\to\) «001». Стоимость составляет \(1 + 1 = 2\). Другим оптимальным решением является следующее: можно поменять местами позиции \(1\) и \(3\), тогда строка \(a\) меняется как «100» \(\to\) «001», стоимость также равна \(|1 - 3| = 2\). Во втором примере оптимальным решением является следующее: нужно поменять местами позиции \(2\) и \(3\), тогда строка \(a\) меняется как «0101» \(\to\) «0011». Стоимость равна \(|2 - 3| = 1\). | |
![]()
|
|
A. Равенство
реализация
Строки
*800
Вам дана строка \(s\) длины \(n\), которая содержит только первые \(k\) букв латинского алфавита. Все буквы в строке \(s\) заглавные. Строка называется подпоследовательностью строки \(s\), если она получается удалением из \(s\) нескольких символов без изменения порядка остальных символов. Например, «ADE» и «BD» являются подпоследовательностями «ABCDE», а «DEA» — нет. Подпоследовательность \(s\) называется хорошей, если каждая из первых \(k\) букв алфавита встречается одинаковое число раз. Найдите длину самой длинной хорошей подпоследовательности \(s\). Выходные данные Выведите одно целое число — длину самой длинной хорошей подпоследовательности строки \(s\). Примечание В первом примере, подпоследовательность «ACBCAB» («ACAABCCAB») является одной из подпоследовательностей содержащей одинаковое число 'A', 'B' и 'C'. Подпоследовательность «CAB» тоже содержит одинаковое число этих букв, но не является максимальной по длине. Во втором примере, ни одна из подпоследовательность не может содержать 'D', а значит ответ равен \(0\). | |
![]()
|
|
F. Поворот строки
дп
Строки
*2900
Вам дана строка \(s\) над бинарным алфавитом. Посчитайте количество различных циклических строк длины \(n\) над бинарным алфавитом, которые содержат \(s\) как подстроку. Циклическая строка \(t\) содержит \(s\) как подстроку если существует какой-то циклический сдвиг строки \(t\), такой что \(s\) является подстрокой этого циклического сдвига строки \(t\). Например, циклическая строка «000111» содержит подстроки «001», «01110» и «10», но не содержит «0110» и «10110». Две циклические строки называются различными, если они отличаются как строки. Например, две различные строки, которые отличаются друг от друга циклическим сдвигом, являются различными циклическими строками. Выходные данные Выведите одно число — количество различных циклических строк \(t\) над бинарным алфавитом, которые содержат \(s\) как подстроку. Примечание В первом примере есть три циклических строки, которые содержат "0" — "00", "01" и "10". Во втором примере есть только две такие строки — "1010", "0101". | |
![]()
|
|
G. Пестрая лента
разделяй и властвуй
Строки
строковые суфф. структуры
Структуры данных
хэши
*3500
Ильдар взял ленточку и покрасил её в несколько цветов. Формально, ленточка разбита на \(n\) клеточек, каждую из которых он покрасил в один из \(26\) цветов, которые можно обозначить строчными буквами латинского алфавита. Ильдар решил, что он выберет отрезок ленточки \([l, r]\) (\(1 \le l \le r \le n\)), который ему нравится, и вырежет его из ленточки. Таким образом получится новая ленточка, которую можно условно представить как строку \(t = s_l s_{l+1} \ldots s_r\). Теперь Ильдар играет в следующую игру — разрезает ленточку \(t\) на несколько новых ленточек и смотрит, сколько среди них различных. Формально, Ильдар выбирает \(1 \le k \le |t|\) индекcов \(1 \le i_1 < i_2 < \ldots < i_k = |t|\) и разрезает \(t\) на \(k\) ленточек-строк \(t_1 t_2 \ldots t_{i_1}, t_{i_1 + 1} \ldots t_{i_2}, \ldots, {t_{i_{k-1} + 1}} \ldots t_{i_k}\) и считает среди них количество различных. Внезапно Ильдара заинтересовал вопрос — а какое минимальное количество различных как строк из них может получиться, при условии что среди этих кусочков хотя бы один вид ленточек повторяется хотя бы два раза? Результатом игры Ильдар считает это число. Если не существует ни одного способа разрезать \(t\) таким образом, то результатом игры будет число -1. К сожалению, Ильдар ещё не выбрал, какой именно отрезок ему нравится, но у него есть \(q\) отрезков-предпочтений \([l_1, r_1]\), \([l_2, r_2]\), ..., \([l_q, r_q]\). Посчитайте для каждого из отрезков какой будет результат игры нём. Выходные данные Выведите \(q\) строк, где \(i\)-я из них содержит результат игры на строке \([l_i, r_i]\). Примечание Рассмотрим первый пример. Если Ильдар выберет отрезок \([1, 6]\), то он вырежет строку \(t = abcabc\). Если разрезать \(t\) на два кусочка \(abc\) и \(abc\), то строка \(abc\) повторится два раза, а количество различных строк из разрезания будет равно \(1\). Поэтому результат этой игры \(1\). Если Ильдар выберет отрезок \([4, 7]\), то он вырежет строку \(t = abcd\). Эту строку невозможно разрезать на строки так, что будет хотя бы строка, повторяющаяся хотя бы два раза. Поэтому результат этой игры \(-1\). Если Ильдар выберет отрезок \([3, 6]\), то он вырежет строку \(t = cabc\). Если разрезать \(t\) на три кусочка \(c\), \(ab\) и \(c\), то строка \(c\) повторится два раза, а количество различных строк будет равно \(2\). Поэтому результат этой игры \(2\). | |
![]()
|
|
I. Палиндромные пары
Строки
хэши
*1600
Узнав много нового об освоении космоса, маленькая девочка по имени Ана хочет сменить тему исследования. Ана это девушка, которая любит палиндромы (строки, которые читаются одинаково слева-направо и справа-налево). Она научилась проверять данную строку на палиндромность, но вскоре ей надоела эта задача, она придумала более интересную и теперь ей нужна ваша помощь, чтобы ее решить: Дан массив строк, состоящих из строчных букв латинского алфавита. Ваша задача — найти сколько палиндромных пар в массиве. Палиндромная пара — это пара строк, такая, что выполняется следующее условие: по крайней мере одна перестановка букв в конкатенации двух строк является палиндромом. Другими словами, если у вас есть две строки, скажем, «aab» и «abcac», мы объединяем их в «aababcac», и должны проверить, существует ли такая перестановка букв этой новой строки, что получится палиндром (в этом случае можно переставить буквы так, чтобы получить «aabccbaa»). Две пары строк считаются разными, если строки находятся на разных позициях. Пара строк \((i,j)\) считается совпадающей с парой \((j,i)\). Выходные данные Выведите одно целое число, описывающее сколько палиндромных пар есть в этом массиве. Примечание Первый пример: - aa \(+\) bb \(\to\) abba.
Второй пример: - aab \(+\) abcac \(=\) aababcac \(\to\) aabccbaa
- aab \(+\) aa \(=\) aabaa
- abcac \(+\) aa \(=\) abcacaa \(\to\) aacbcaa
- dffe \(+\) ed \(=\) dffeed \(\to\) fdeedf
- dffe \(+\) aade \(=\) dffeaade \(\to\) adfaafde
- ed \(+\) aade \(=\) edaade \(\to\) aeddea
| |
![]()
|
|
J. Moonwalk challenge
Деревья
Строки
Структуры данных
*2600
Поскольку астронавты из миссии BubbleCup XI закончили свою миссию на Луне и являются большими поклонниками известного певца, они решили провести некоторое время перед возвращением на Землю, и, таким образом, создали так называемую игру «Moonwalk challenge». Командам астронавтов выдаются карты кратеров на Луне и прямых двунаправленных путей от одних кратеров к другим, безопасные для «лунной походки». Каждый из этих прямых путей окрашен в один цвет, и есть единственный путь между каждым из двух кратеров. Цель игры заключается в том, чтобы найти два кратера, такие, что заданный массив цветов появляется чаще всего как непрерывный подотрезок на пути между этими двумя кратерами (пересекающиеся вхождения должны быть учтены как два различных). Чтобы помочь любимой команде одержать победу, необходимо составить программу, которая по заданной карте отвечает на запросы следующего типа: для двух кратеров и массива цветов ответит, сколько раз заданный массив появляется как непрерывный подотрезок на пути от первого кратера ко второму. Все цвета являются строчными буквами латинского алфавита. Выходные данные Для каждого запроса выведите количество вхождений S (представленного в виде строки) на пути между \(u\) и \(v\). | |
![]()
|
|
A. Вася и пароль
жадные алгоритмы
реализация
Строки
*1200
Для регистрации на сайте EatForces Вася придумал пароль — строку \(s\). Пароль на сайте EatForces — это строка, состоящая из строчных и заглавных латинских букв, а также цифр. Но так как EatForces заботится о безопасности своих пользователей, пароли пользователей должны содержать минимум одну цифру, минимум одну заглавную латинскую букву и минимум одну строчную латинскую букву. Например пароли «abaCABA12», «Z7q» и «3R24m» допустимы, а пароли «qwerty», «qwerty12345» и «Password» — нет. Подстрока строки \(s\) — строка \(x = s_l s_{l + 1} \dots s_{l + len - 1} (1 \le l \le |s|, 0 \le len \le |s| - l + 1)\). \(len\) — длина подстроки. Обратите внимание, что пустая строка так же считается подстрокой строки \(s\), и имеет длину \(0\). Возможно, пароль, придуманный Васей, не соответствует правилам безопасности EatForces. Однако, так как Васе он очень нравится, он хочет заменить некоторую его подстроку на подстроку такой же длины таким образом, чтобы пароль удовлетворял описанным выше условиям. При том, данная операция должна быть совершена ровно один раз, а выбранная подстрока должна быть минимально возможной длины. Обратите внимание, что длина строки \(s\) после замены подстроки не должна измениться, а сама строка должна состоять только из строчных и заглавных латинских букв, а также цифр. Выходные данные Для каждого теста в отдельной строке выведите новый пароль, который удовлетворяет описанным выше условиям. Длина замененной подстроки подсчитывается следующим способом: выпишем все измененные позиции. Если таких нет, то длина равна \(0\). В противном случае длина равна разности первой и последней измененной позиции плюс один. Например, длина измененной подстроки между паролями "abcdef" \(\rightarrow\) "a7cdEf" равна \(4\), потому что измененные позиции — это \(2\) и \(5\), соответственно, длина \((5 - 2) + 1 = 4\). Гарантируется, что всегда существует подходящий пароль. Если существует несколько подходящих паролей, разрешается вывести любой из них. Примечание В первом тестовом примере в Васином пароле не хватает цифры, он заменяет подстроку «C» на «4», и получает пароль «abcD4E». Таким образом, он заменил подстроку длины 1. Во втором тестовом примере Васин пароль изначально подходящий, и ничего не нужно менять. Таким образом, мы заменили подстроку длины 0 (пустую подстроку). | |
![]()
|
|
E. Вася и длинные числа
Бинарный поиск
дп
Строки
Структуры данных
хэши
*2600
У Васи есть три длинных числа — \(a, l, r\). Назовем разбиением длинного числа \(x\) такую последовательность строк \(s_1, s_2, \dots, s_k\), что \(s_1 + s_2 + \dots + s_k = x\), где \(+\) означает конкатенацию строк. При этом \(s_i\) называется \(i\)-м элементом разбиения. Например, для числа \(12345\) существуют следующие разбиения: ["1", "2", "3", "4", "5"], ["123", "4", "5"], ["1", "2345"], ["12345"] и многие другие. Назовем разбиение числа \(a\) хорошим, если каждый его элемент не содержит лидирующих нулей. Вася хочет знать количество хороших разбиений числа \(a\), где каждый элемент разбиения \(s_i\) будет удовлетворять условию \(l \le s_i \le r\). Обратите внимание, что сравнение происходит по правилам сравнения целых чисел, а не сравнения строк. Помогите Васе! Сообщите ему количество разбиений числа \(a\), удовлетворяющих описанным выше условиям. Полученное число может быть достаточно велико, поэтому выведите его по модулю \(998244353\). Выходные данные Выведите одно целое число — количество разбиений числа \(a\), удовлетворяющих описанным выше условиям, по модулю \(998244353\). Примечание В первом тестовом примере существует два хороших разбиения \(13+5\) и \(1+3+5\). Во втором тестовом примере существует одно хорошее разбиение \(1+0+0+0+0\). | |
![]()
|
|
D. Рефакторинг
жадные алгоритмы
реализация
Строки
*2400
Алиса написала программу, и теперь всячески работает над улучшением её читаемости. Один из способов улучшить читаемость — давать переменным подходящие имена, поэтому Алиса хочет переименовать часть переменных в своей программе. В её среде разработке есть команда под названием «масштабный рефакторинг», которая позволяет менять сразу имена многим переменным. Для этого нужно выбрать две строки \(s\) и \(t\), после чего для всех переменных выполняется следующий алгоритм: если название переменной содержит \(s\) как подстроку, то первое (и только первое) вхождение \(s\) заменяется на \(t\), а если не содержит \(s\), то оно остаётся прежним. Дан список переменных, для каждой из которых известно её исходное название и название, на которое Алиса хочет его заменить. Известно, что у каждой переменной длины этих двух названий совпадают (это связано с тем, что выравнивание блоков может «поехать», если длины названий переменных изменятся). Требуется произвести переименование всех переменных за ровно один вызов команды масштабного рефакторинга, или сказать, что это невозможно сделать. Выходные данные Если произвести переименование всех переменных за один вызов команды «масштабный рефакторинг» невозможно, выведите «NO» (без кавычек). Иначе на первой строке выведите «YES» (без кавычек), а на следующих строках \(s\) и \(t\) (\(1 \le |s|, |t| \le 5000\)), которые необходимо использовать для замены. Строки \(s\) и \(t\) должны состоять только из строчных букв латинского алфавита. Если существует несколько способов провести «масштабный рефакторинг», то можно воспользоваться любым из них. | |
![]()
|
|
F. Дерево и XOR
Деревья
Строки
*2900
Дан связный неориентированный граф без циклов (то есть дерево) на \(n\) вершинах, при этом на каждом ребре написано какое-то целое неотрицательное число. Рассмотрим все пары вершин \((v, u)\) (то есть всего \(n^2\) таких пар) и для каждой пары посчитаем побитовое исключащее ИЛИ (xor) всех чисел на рёбрах на простом пути между \(v\) и \(u\). Если путь состоял только из одной вершины, то xor всех чисел на рёбрах этого пути считается равным \(0\). Предположим, мы отсортировали полученные \(n^2\) значений по неубыванию. Требуется вывести \(k\)-е из них. Операция xor определяется следующим образом: Пусть даны два целых неотрицательных числа \(x\) и \(y\), рассмотрим их двоичные записи (возможно с ведущими нулями): \(x_k \dots x_2 x_1 x_0\) и \(y_k \dots y_2 y_1 y_0\) (где \(k\) любое число, что все биты \(x\) и \(y\) могут быть представлены). Здесь \(x_i\) это \(i\)-й бит числа \(x\), а \(y_i\) это \(i\)-й бит числа \(y\). Пусть \(r = x \oplus y\) — результат операции xor над числами \(x\) и \(y\). Тогда двоичной записью \(r\) будет \(r_k \dots r_2 r_1 r_0\), где: \(\) r_i = \left\{ \begin{aligned} 1, ~ \text{если} ~ x_i \ne y_i \\ 0, ~ \text{если} ~ x_i = y_i \end{aligned} \right. \(\) Выходные данные Выведите одно целое число — \(k\)-й по возрастанию xor пути в дереве. Примечание Дерево во втором тесте выглядит следующим образом: 
В таком дереве существует \(9\) путей: - \(1 \to 1\) со значением \(0\)
- \(2 \to 2\) со значением \(0\)
- \(3 \to 3\) со значением \(0\)
- \(2 \to 3\) (проходит через \(1\)) со значением \(1 = 2 \oplus 3\)
- \(3 \to 2\) (проходит через \(1\)) со значением \(1 = 2 \oplus 3\)
- \(1 \to 2\) со значением \(2\)
- \(2 \to 1\) со значением \(2\)
- \(1 \to 3\) со значением \(3\)
- \(3 \to 1\) со значением \(3\)
| |
![]()
|
|
E. Проверь транскрипцию
Перебор
Строки
Структуры данных
хэши
*2100
Один из друзей Аркадия работает на огромном радиотелескопе. Несколько десятилетий назад телескоп послал сигнал \(s\) в соседнюю галактику. Кто бы мог подумать, но недавно от инопланетян пришёл ответ — сигнал \(t\)! Учёные хотят проверить, есть ли сходство между сигналами \(s\) и \(t\) или нет. Исходный сигнал \(s\) был последовательностью нулей и единиц (все знают, что битовая запись является межгалактическим стандартом). Но полученный сигнал \(t\), однако, выглядит более замысловато, чем \(s\). Однако учёные не сдались и представили \(t\) как последовательность латинских букв. Учёные считают, что \(s\) и \(t\) похожи, если можно заменить все нули в \(s\) на некоторую строку \(r_0\), а все единицы в \(s\) на некоторую иную строку \(r_1\) так, что получится строка \(t\). Строки \(r_0\) и \(r_1\) должны быть различными и не пустыми. Помогите другу Аркадия и посчитайте количество возможных замен нулей и единиц (то есть количество пар строк \(r_0\) и \(r_1\)), которые превращают \(s\) в \(t\). Выходные данные Выведите одно целое число — количество пар строк \(r_0\) и \(r_1\), которые переводят \(s\) в \(t\). В случае, если ни одной подходящей пары нет, выведите \(0\). Примечание В первом примере возможные пары \((r_0, r_1)\) выглядят следующим образом: - «a», «aaaaa»
- «aa», «aaaa»
- «aaaa», «aa»
- «aaaaa», «a»
Пара «aaa», «aaa» не разрешена, так как \(r_0\) и \(r_1\) должны быть различными. Во втором примере возможны следующие пары: - «ko», «kokotlin»
- «koko», «tlin»
| |
![]()
|
|
H. Определи робота
Строки
Структуры данных
*3200
Вы успешно предсказали станцию, на которой выйдет бедный Аркадий и нашли его. Вы отправили его домой на такси и внезапно задумались над следующим вопросом. В вашем городе есть \(n\) перекрёстков и несколько двусторонних дорог, их соединяющих. Назовём путь из одного перекрёстка в другой поездкой на такси, если он не проезжает ни один перекрёсток более одного раза. Вы собрали коллекцию поездок, которую совершил один водитель и теперь размышляете, может ли этот водитель быть роботом, или он точно человек. Вы считаете, что водитель может быть роботом, если для любой пары перекрёстков \(a\) и \(b\) этот водитель всегда едет по одному и тому же пути, когда едет из \(a\) в \(b\). Обратите внимание, что \(a\) и \(b\) не обязательно должны являться началом и концом поездки, кроме того, путь из \(b\) в \(a\) может отличаться. Напротив, если водитель выбрал два разных маршрута из какого-то \(a\) в какое-то \(b\), то он однозначно человек. Вы знаете карту города и описание всех поездок, совершённых водителем. Выясните, может ли водитель быть роботом или нет. Выходные данные Для каждого тестового случая выведите «Robot», если водитель может быть роботом и «Human» иначе. Вы можете выводить каждую букву в любом регистре (строчную или заглавную). Примечание В первом примере водитель использовал два разных пути, чтобы добраться из перекрёстка \(1\) в перекрёсток \(3\). Он однозначно человек. Во втором примере водитель всегда едет по циклу \(1 \to 2 \to 3 \to 4 \to 1\) пока не доезжает до точки назначения. | |
![]()
|
|
A. Ох уж эти палиндромы
Конструктив
Строки
*1300
Назовём палиндромом непустую строку, которая читается одинаково справа налево и слева направо. Например, «abcba», «a» и «abba» являются палиндромами, а «abab» и «xy» не являются. Назовём подстрокой строки строку, полученную отбрасыванием некоторого (возможно, нулевого) количества символов с начала и с конца строки. Например, «abc», «ab» и «c» являются подстроками строки «abc», а «ac» и «d» не являются. Назовем палиндромностью строки количество её подстрок, которые являются палиндромами. Например, палиндромность строки «aaa» равна \(6\), так как все её подстроки являются палиндромами, а палиндромность строки «abc» равна \(3\), так как только подстроки длины \(1\) являются палиндромами. Вам дана строка \(s\). Вы можете произвольным образом переставлять символы в ней. Требуется получить строку, имеющую максимальную палиндромность. Выходные данные Выведите строку \(t\), которая состоит из тех же символов (с учётом кратностей), что и \(s\), и имеет максимальную палиндромность среди всех строк, которые могут быть получены из \(s\) перестановкой символов. Если подходящих строк несколько, выведите любую. Примечание В первом примере у строки «ololo» есть \(9\) подстрок-палиндромов: «o», «l», «o», «l», «o», «olo», «lol», «olo», «ololo». Обратите внимание, что некоторые подстроки совпадают, но учитываются несколько раз. Во втором примере палиндромность строки «abccbaghghghgdfd» равна \(29\). | |
![]()
|
|
E. Преобразования краев
Комбинаторика
Строки
*2300
Рассмотрим некоторое множество различных символов \(A\) и некоторую строку \(S\), состоящую ровно из \(n\) символов, где каждый символ присутствует в \(A\). Задан массив \(b\) из \(m\) целых чисел (\(b_1 < b_2 < \dots < b_m\)). Разрешено проводить следующую операцию над строкой \(S\): - Выбрать некоторый корректный \(i\) и выставить \(k = b_i\);
- Взять первые \(k\) символов \(S = Pr_k\);
- Взять последние \(k\) символов \(S = Su_k\);
- Заменить первые \(k\) символов \(S\) развернутой \(Su_k\);
- Заменить последние \(k\) символов \(S\) развернутой \(Pr_k\).
Например, рассмотрим строку \(S =\) «abcdefghi» и \(k = 2\). \(Pr_2 =\) «ab», \(Su_2 =\) «hi». Развернутые \(Pr_2 =\) «ba», \(Su_2 =\) «ih». Следовательно, полученная \(S\) равна «ihcdefgba». Данная операция может быть проведена произвольное количество раз (возможно, ноль). Любой \(i\) может быть выбран несколько раз в ходе проведения операций. Назовем строки \(S\) и \(T\) равными тогда и только тогда, когда существует такая последовательность операций, которая преобразовывает строку \(S\) в строку \(T\). Для приведенного выше примера «abcdefghi» и «ihcdefgba» равны. Обратите внимание, что это подразумевает и \(S = S\). Задача проста. Посчитайте количество различных строк. Ответ может быть достаточно велик, поэтому посчитайте его по модулю \(998244353\). Выходные данные Выведите единственное целое число — количество различных строк длины \(n\) с символами из множества \(A\) по модулю \(998244353\). Примечание Приведены все различные строки для первого примера. Выбранные буквы 'a' и 'b' только чтобы показать, что символы в \(A\) различны. - «aaa»
- «aab» = «baa»
- «aba»
- «abb» = «bba»
- «bab»
- «bbb»
| |
![]()
|
|
G. Суффиксы Фибоначчи
Строки
*2700
Давайте введём (ага, опять) последовательность строк Фибоначчи: \(F(0) = \) 0, \(F(1) = \) 1, \(F(i) = F(i - 2) + F(i - 1)\), где плюс обозначает конкатенацию двух строк. Обозначим отсортированную в лексикографическом порядке последовательность суффиксов строки \(F(i)\) как \(A(F(i))\). К примеру, \(F(4)\) — 01101, а \(A(F(4))\) — следующая последовательность: 01, 01101, 1, 101, 1101. Элементы этой последовательности пронумерованы от \(1\). Ваша задача — вывести \(m\) первых символов \(k\)-го элемента \(A(F(n))\). Если в этом суффиксе меньше \(m\) символов, выведите его полностью. Выходные данные Выведите \(m\) первых символов \(k\)-го элемента \(A(F(n))\), или весь этот элемент, если его длина меньше \(m\). | |
![]()
|
|
A. Разнообразная подстрока
реализация
Строки
*1000
Задана строка \(s\), состоящая из \(n\) строчных букв латинского алфавита. Подстрока строки \(s\) — это последовательный отрезок букв из \(s\). Например, «defor» — это подстрока «codeforces», а «fors» — нет. Длина подстроки — это количество букв в ней. Назовем некоторую строку длины \(n\) разнообразной тогда и только тогда, когда никакая буква не встречается в ней строго больше \(\frac n 2\) раз. Например, строки «abc» и «iltlml» разнообразные, а строки «aab» и «zz» — нет. Ваша задача — найти любую разнообразную подстроку строки \(s\) или сообщить, что такой нет. Обратите внимание, что не требуется максимизировать или минимизировать длину полученной подстроки. Выходные данные Выведите «NO», если в строке \(s\) нет разнообразных подстрок. В противном случае первая строка должна содержать «YES». Вторая подстрока должна содержать любую разнообразную подстроку строки \(s\). Примечание В первом примере есть множество правильных ответов. Пожалуйста, избегайте задавать вопросы о правильности конкретного ответа на конкретный тест, такие вопросы всегда приводят к ответу «Без комментариев». | |
![]()
|
|
A. Минимизация строки
жадные алгоритмы
Строки
*1200
Задана строка \(s\), состоящая из \(n\) строчных букв латинского алфавита. Вам необходимо удалить из строки не более одного (то есть ноль или один) символа таким образом, что строка, которую вы получите, будет являться лексикографически минимальной среди всех строк, которые можно получить при помощи этой операции. Строка \(s = s_1 s_2 \dots s_n\) лексикографически меньше строки \(t = t_1 t_2 \dots t_m\), если \(n < m\) и \(s_1 = t_1, s_2 = t_2, \dots, s_n = t_n\) или найдется такое число \(p\), что \(p \le min(n, m)\) и \(s_1 = t_1, s_2 = t_2, \dots, s_{p-1} = t_{p-1}\) и \(s_p < t_p\). Например, «aaa» меньше, чем «aaaa», «abb» меньше, чем «abc», «pqr» меньше, чем «z». Выходные данные Выведите одну строку — минимально возможную лексикографически строку, которая может быть получена при помощи удаления не более одного символа из строки \(s\). Примечание В первом тестовом примере вы можете удалить любой символ строки \(s\), чтобы получить строку «aa». Во втором тестовом примере «abca» < «abcd» < «abcda» < «abda» < «acda» < «bcda». | |
![]()
|
|
A. Время-палиндром
реализация
Строки
*1000
Таттах спит тогда и только тогда, когда он на лекции. Эта шутка популярна среди его однокурсников. В среду утром Таттах был на лекции у профессора NN. В 12:21, как раз перед сном, он созерцал часы на запястье Захира. Таттах обратил внимание, что цифры на часах обозначали одно и то же время будучи прочитанными как справа налево (*), так и слева направо. Иными словами, время на часах было палиндромом. Во сне Таттаху снились те редкие моменты, когда время, показываемое на электронных часах, является палиндромом. Когда он проснулся, он решил во что бы то ни стало написать программу, которая найдет следующий ближайший момент времени, обладающий таким свойством. К сожалению, Таттах пока еще не силен в программировании, и вы должны помочь ему. (*) Как и все египтяне, Таттах читает справа налево. Выходные данные Выведите ближайшее (в будущем по отношению к текущему времени) время-палиндром, которое будут показывать электронные часы. Если введенное на входе время является палиндромом, выведите ближайшее следующее время-палиндром. | |
![]()
|
|
E. Соня и красота матрицы
Строки
*2400
Недавно у Сони был День рождения и ей подарили матрицу размером \(n\times m\), элементы которой маленькие латинские буквы. Будем считать, что строки матрицы пронумерованы сверху вниз от \(1\) до \(n\), а столбцы слева направо от \(1\) до \(m\). Подматрицей \((i_1, j_1, i_2, j_2)\) \((1\leq i_1\leq i_2\leq n; 1\leq j_1\leq j_2\leq m)\) будем называть такие элементы \(a_{ij}\) заданной матрицы, что \(i_1\leq i\leq i_2\) и \(j_1\leq j\leq j_2\). Соня считает подматрицу красивой, если мы можем независимо переупорядочить порядок символов в каждой строке (не в столбце) подматрицы так, чтобы все строки и столбцы подматрицы образовывали палиндромы. Напомним, что строка называется палиндромом, если она одинаково читается как слева направо, так и справа налево. Например, строки \(abacaba, bcaacb, a\) — палиндромы, а строки \(abca, acbba, ab\) — нет. Помогите Соне найти количество красивых подматриц данной матрицы. Подматрицы считаются разными, если существует элемент, что принадлежит только одной из двух подматриц. Выходные данные Выведите одно целое число — количество красивых подматриц данной матрицы. Примечание В первом примере подойдут следующие подматрицы: \(((1, 1), (1, 1)); ((1, 2), (1, 2));\) \(((1, 3), (1, 3)); ((1, 1), (1, 3))\). Во втором примере подойдут все подматрицы состоящие из одного элемента, а также подматрицы: \(((1, 1), (2, 1));\) \(((1, 1), (1, 3)); ((2, 1), (2, 3)); ((1, 1), (2, 3)); ((2, 1), (2, 2))\). Одними из вариантов в третьем примере могут быть подматрицы: \(((1, 1), (1, 5)); ((1, 2), (3, 4));\) \(((1, 1), (3, 5))\). Подматрица \(((1, 1), (3, 5))\) красивая, поскольку можно привести её к виду:
accca
aabaa
accca
Очевидно, что в такой матрице каждая строка и каждый столбец образовывают палиндромы. | |
![]()
|
|
H. Палиндромная магия
Строки
Структуры данных
хэши
*3500
После изучения всяких разных палиндромовых алгоритмов, Chouti решил, что палиндромы это очень интересно, и он решил дать вам следующую задачу. У Chouti есть две строки \(A\) и \(B\). Так как он любит палиндромы, он хочет выбрать \(a\) как непустую палиндромную подстроку строки \(A\), а \(b\) как непустую палиндромную подстроку строки \(B\). Сконкатенировав их, он получит строку \(ab\). Chouti считает, что строки, которые можно получить таким образом, очень интересные, поэтому он хочет знать, скоько различных строк он может так получить. Выходные данные В единственной строка выведите одно целое число — количество возможных строк. Примечание В первом примере можно получить строки - "a" + "a" = "aa",
- "aa" + "a" = "aaa",
- "aa" + "aba" = "aaaba",
- "aa" + "b" = "aab",
- "a" + "aba" = "aaba",
- "a" + "b" = "ab".
Во втором примере можно получить строки "aa", "aaa", "aaaa", "aaaba", "aab", "aaba", "ab", "abaa", "abaaa", "abaaba", "abab", "ba", "baa", "baba", "bb". Обратите внимание, что, не смотря на то, что "a"+"aa"="aa"+"a"="aaa", строка "aaa" учитывается только один раз. | |
![]()
|
|
F. Быстрый набор
Деревья
дп
Строки
*2800
У Поликарпа в записной книжке \(n\) телефонов, про каждый он знает сам номер \(s_i\) и \(m_i\) — сколько раз в день он его набирает. Недавно Поликарп приобрел совершенно новый телефон с инновационной опцией быстрого набора! Более точно, \(k\) его клавишам можно назначить некоторый номер (не обязательно из телефонной книги). Для ввода номера Поликарп может нажать одну из этих \(k\) клавиш, а потом завершить набор номера нажатиями на обычные цифровые клавиши (ввод номера только цифровыми клавишами также возможен). Клавиша быстрого набора может быть нажата только когда ни одной цифры еще не набрано. Нельзя переназначать номера на клавиши быстрого набора. Сколько минимально нажатий цифровых клавиш ему придётся делать в сутки, если он назначит на клавиши быстрого набора номера оптимальным способом? Выходные данные Выведите единственное число — сколько минимально нажатий цифровых клавиш Поликарпу придётся делать в сутки, если он назначит на клавиши быстрого набора номера оптимальным способом. Примечание На единственной клавише цифрового набора в первом примере должно быть записано «0001». Тогда суммарное количество нажатий цифровых клавиш будет равно \(0 \cdot 5\) для первого номера + \(3 \cdot 4\) для второго + \(2 \cdot 1\) для третьего. \(14\) в сумме. На единственной клавише цифрового набора во втором примере должно быть записано «00». Тогда суммарное количество нажатий цифровых клавиш будет равно \(2 \cdot 5\) для первого номера + \(1 \cdot 6\) для второго + \(2 \cdot 1\) для третьего. \(18\) в сумме. | |
![]()
|
|
B. Орехус и строки
жадные алгоритмы
Строки
*2000
Недавно Орехус написал \(k\) строк длины \(n\), состоящих из букв «a» и «b». Он посчитал \(c\) — количество строк, которые являются префиксами хотя бы одной из написанных. Каждая строка была посчитана ровно один раз. Затем, он потерял листочек со строками. Он помнит, что все написанные строки были лексикографически не меньше строки \(s\) и не больше строки \(t\). Ему интересно: какое максимально возможное \(c\) он мог получить. Строка \(a\) лексикографически меньше строки \(b\), если и только если выполняется один из следующих пунктов: - \(a\) — префикс \(b\), но \(a \ne b\);
- в первой позиции, где \(a\) и \(b\) различны, в строке \(a\) находится буква, которая встречается в алфавите раньше, чем соответствующая буква в \(b\).
Выходные данные Выведите одно число — максимально возможное \(c\). Примечание В первом примере Орехус мог записать строки «aa», «ab», «ba», «bb». Тогда эти \(4\) строки являются префиксами одной из записанных, а кроме них ещё строки «a» и «b». Всего \(6\) строк. Во втором примере Орехус мог записать строки «aba», «baa», «bba». В третьем примере есть всего две различные строки, которые мог записать Орехус. Если обе из них написаны, \(c=8\). | |
![]()
|
|
A. Право-левое шифрование
реализация
Строки
*800
Поликарп обожает шифры. Недавно он изобрёл свой собственный, который назвал право-левым. Право-левое шифрование используется для шифрования строк. Чтобы зашифровать строку \(s=s_{1}s_{2} \dots s_{n}\) Поликарп выполняет следующие шаги: - он выписывает \(s_1\),
- к текущему результату приписывает справа \(s_2\),
- к текущему результату приписывает слева \(s_3\),
- к текущему результату приписывает справа \(s_4\),
- к текущему результату приписывает слева \(s_5\),
- и так далее, пока не будут обработаны все символы строки.
Например, если \(s\)="techno", то процесс шифрования будет выглядеть так: "t" \(\to\) "te" \(\to\) "cte" \(\to\) "cteh" \(\to\) "ncteh" \(\to\) "ncteho". Таким образом, для \(s\)="techno" результат шифрования равен "ncteho". Дана строка \(t\) — результат шифрования некоторой строки \(s\). Ваша задача расшифровать, то есть найти строку \(s\). Выходные данные Выведите такую строку \(s\), которая после шифрования равна \(t\). | |
![]()
|
|
E. Вася и паттерны
жадные алгоритмы
реализация
Строки
*2300
У Васи есть три строки \(s\), \(a\) и \(b\), состоящие из первых \(k\) букв латинского алфавита. Назовем паттерном строку длины \(k\), где каждая из первых \(k\) букв латинского алфавита встречается ровно один раз (таким образом, существует ровно \(k!\) различных паттернов). Применение паттерна \(p\) к строке \(s\) — это замена каждой буквы строки \(s\) на \(p_i\), где \(i\) – это порядковый номер этой буквы в латинском алфавите. Например, применив паттерн «bdca» к строке «aabccd» мы получим строку «bbdcca». Васю интересует, существует ли такой паттерн, применив который к строке \(s\), он получит строку, лексикографически больше либо равную строки \(a\) и лексикографически меньше либо равную строки \(b\). Если существует несколько подходящих паттернов, разрешается вывести любой. Строка \(a\) лексикографически меньше строки \(b\), если существует такое \(i\) (\(1 \le i \le n\)), что \(a_i < b_i\), а для любого \(j\) (\(1 \le j < i\)) \(a_j = b_j\). В этой задаче вам необходимо ответить на \(t\) независимых тестовых наборов. Выходные данные На каждый тестовый набор выведите ответ в следующем формате: Если не существует подходящего паттерна, то в первой строке выведите «NO». Иначе в первой строке выведите «YES», а во второй сам паттерн (\(k\) строчных букв, каждая из первых \(k\) букв латинского алфавита должна встретиться ровно один раз). Если существует несколько подходящих паттернов — разрешается вывести любой. | |
![]()
|
|
C. Префиксы и суффиксы
Строки
*1700
Иван хочет сыграть с вами в игру. Он загадал какую-то строку \(s\) длины \(n\), состоящую только из строчных букв латинского алфавита. Вы не знаете эту строку. Иван сообщил вам все ее несобственные префиксы и суффиксы (то есть префиксы и суффиксы всех длин от \(1\) до \(n-1\)), но он не сказал вам, какие из сообщенных им строк являются префиксами, а какие — суффиксами. Иван хочет, чтобы вы угадали, какие из заданных \(2n-2\) строк являются префиксами, а какие — суффиксами. Бывают случаи, когда невозможно угадать строку, которую загадывал Иван (так как несколько разных строк могли иметь одинаковый набор префиксов и суффиксов), но Иван примет ваш ответ, если он будет совпадать с любой подходящей под ограничения строкой. Да начнется игра! Выходные данные Выведите одну строку длины \(2n-2\) — строку, состоящую только из символов 'P' и 'S'. Количество символов 'P' должно быть равно количеству символов 'S'. \(i\)-й символ этой строки должен быть равен 'P', если \(i\)-я входная строка является префиксом, и 'S' иначе. Если существует несколько возможных ответов, вы можете вывести любой. Примечание Единственная строка, которую мог загадать Иван в первом тестовом примере, — «ababa». Единственная строка, которую мог загадать Иван во втором тестовом примере, — «aaa». Ответы «SPSP», «SSPP» и «PSPS» также являются правильными. В третем тестовом примере Иван мог загадать строку «ac» или же строку «ca». Ответ «SP» также является правильным. | |
![]()
|
|
B. Перестановка букв
жадные алгоритмы
Конструктив
сортировки
Строки
*900
Задана строка \(s\), состоящая только из строчных букв латинского алфавита. Вы можете переставлять буквы этой строки так, как угодно. Ваша задача заключается в том, чтобы получить хорошую строку при помощи перестановки букв заданной строки, либо сказать, что это невозможно сделать. Назовем строку хорошей, если она не является палиндромом. Палиндром — это строка, которая читается слева направо также, как и справа налево. Например, строки «abacaba», «aa» и «z» являются палиндромами, а строки «bba», «xd» — нет. Вам необходимо ответить на \(t\) независимых запросов. Выходные данные Выведите \(t\) строк. В \(i\)-й строке выведите ответ на \(i\)-й запрос: -1, если невозможно получить хорошую строку при помощи перестановки букв строки \(s_i\), иначе любую хорошую строку, которую можно получить из заданной (при помощи перестановки букв). Примечание В первом запросе невозможно переставить буквы таким образом, чтобы получить хорошую строку. Другие примеры (не все) корректных ответов на второй запрос: «ababaca», «abcabaa», «baacaba». В третьем запросе необязательно что-то делать, чтобы получить хорошую строку. | |
![]()
|
|
B. Удаление подстроки
Комбинаторика
математика
Строки
*1300
Задана строка \(s\) длины \(n\), состоящая только из строчных букв латинского алфавита. Подстрока строки — это последовательная подпоследовательность этой строки. Таким образом, строка «forces» является подстрокой «codeforces», а строка «coder» — нет. Ваша задача — посчитать количество способов удалить ровно одну подстроку из этой строки таким образом, чтобы все оставшиеся символы были равны между собой (количество различных символов было равно единице или нулю). Гарантируется, что в строке \(s\) существует хотя бы два различных символа. Заметьте, что вы можете удалить всю строку и это является корректным способом. Также заметьте, что вам необходимо удалить хотя бы один символ. Так как ответ может быть довольно большим (хотя не очень большим), выведите его по модулю \(998244353\). Если вы программируете на Python, рассмотрите возможность отправки решения на PyPy, а не на Python, когда будете отправлять свой код. Выходные данные Выведите одно целое число — количество способов по модулю \(998244353\) удалить ровно одну подстроку из \(s\) таким образом, чтобы все оставшиеся символы были равны. Примечание Пусть \(s[l; r]\) — подстрока строки \(s\) с позиции \(l\) по позицию \(r\) включительно. Тогда в первом тестовом примере вы можете удалить следующие подстроки: - \(s[1; 2]\);
- \(s[1; 3]\);
- \(s[1; 4]\);
- \(s[2; 2]\);
- \(s[2; 3]\);
- \(s[2; 4]\).
Во втором тестовом примере вы можете удалить следующие подстроки: - \(s[1; 4]\);
- \(s[1; 5]\);
- \(s[1; 6]\);
- \(s[1; 7]\);
- \(s[2; 7]\);
- \(s[3; 7]\).
В третьем тестовом примере вы можете удалить следующие подстроки: - \(s[1; 1]\);
- \(s[1; 2]\);
- \(s[2; 2]\).
| |
![]()
|
|
H. Матеуш и бесконечная последовательность
битмаски
дп
Перебор
Строки
*3400
Последовательность Туе-Морса-Радецки-Матеуша (Туорса-Радевуша, для краткости) это бесконечная последовательность, получающаяся из конечной последовательности \(\mathrm{gen}\) длины \(d\) и целого числа \(m\), следующим образом: - В начале мы определяем \(M_0=(0)\).
- На \(k\)-м шаге, \(k \geq 1\), мы определяем \(M_k\) как конкатенацию \(d\) копий \(M_{k-1}\). Однако, каждая из них немного изменяется — в \(i\)-й из них (\(1 \leq i \leq d\)) каждый элемент \(x\) заменяется на \((x+\mathrm{gen}_i) \pmod{m}\).
Например, если \(\mathrm{gen} = (0, \color{blue}{1}, \color{green}{2})\) и \(m = 4\): - \(M_0 = (0)\),
- \(M_1 = (0, \color{blue}{1}, \color{green}{2})\),
- \(M_2 = (0, 1, 2, \color{blue}{1, 2, 3}, \color{green}{2, 3, 0})\),
- \(M_3 = (0, 1, 2, 1, 2, 3, 2, 3, 0, \color{blue}{1, 2, 3, 2, 3, 0, 3, 0, 1}, \color{green}{2, 3, 0, 3, 0, 1, 0, 1, 2})\), и так далее.
Как можно заметить, при условии, что первый элемент \(\mathrm{gen}\) равен \(0\), каждый последующий шаг порождает последовательность, префиксом которой является последовательность с предыдущего шага. Тогда мы можем определить бесконечную последовательность Туорса-Радевуша \(M_\infty\) как последовательность, получаемую бесконечным применением шага выше. Например, для параметров выше, \(M_\infty = (0, 1, 2, 1, 2, 3, 2, 3, 0, 1, 2, 3, 2, 3, 0, 3, 0, 1, \dots)\). Матеуш выбрал последовательность \(\mathrm{gen}\) и целое число \(m\), и с помощью них получил последовательность Туорса-Радевуша \(M_\infty\). Затем он выбрал два целых числа \(l\) и \(r\) и записал подпоследовательность этой последовательности: \(A := ((M_\infty)_l, (M_\infty)_{l+1}, \dots, (M_\infty)_r)\). Обратите внимание, что мы используем нумерацию с \(1\) для \(M_\infty\) и \(A\). У Матеуша есть его любимая последовательность \(B\) длины \(n\) и хочет узнать, насколько она большая относительно \(A\). Он говорит, что последовательность \(B\) мажорирует последовательность \(X\) длины \(n\) (обозначим как \(B \geq X\)), если для всех \(i \in \{1, 2, \dots, n\}\) выполняется \(B_i \geq X_i\). Теперь он спрашивает себя, сколько существует целых чисел \(x\) в отрезке \([1, |A| - n + 1]\) таких, что \(B \geq (A_x, A_{x+1}, A_{x+2}, \dots, A_{x+n-1})\). Так как обе последовательности очень большие, то ответить на вопрос, используя только бумагу и ручку, оказалось затруднительно. Не могли бы вы ему помочь? Выходные данные Выведите одно целое число — ответ на задачу. Примечание Последовательность Туорса-Радевуша в первом примере это стандартная последовательность Туе-Морса, так что последовательность \(A\) выглядит следующим образом: \(11010011001011010010\). Места, где \(B\) мажорирует последовательность \(A\) представлены на картинке:  | |
![]()
|
|
F. Ж-функция
Строки
строковые суфф. структуры
*3500
Длиной наибольшего общего префикса двух строк \(s=s_1 s_2 \ldots s_n\) и \(t = t_1 t_2 \ldots t_m\) называется максимальное такое \(k \le \min(n, m)\), что строки \(s_1 s_2 \ldots s_k\) и \(t_1 t_2 \ldots t_k\) равны. Будем обозначать длину наибольшего общего префикса двух строк \(s\) и \(t\) как \(lcp(s,t)\). Z-функция строки \(s_1 s_2 \dots s_n\) — это последовательность чисел \(z_1, z_2, \ldots, z_n\), где \(z_i = lcp(s_1 s_2 \ldots s_n,\ \ s_i s_{i+1} \dots s_n)\). Ж-функцией строки назовем величину \(z_1 + z_2 + \ldots + z_n\). Вам дана строка \(s=s_1 s_2 \ldots s_n\) и \(q\) запросов. Запрос с номером \(i\) описывается двумя числами \(l_i\) и \(r_i\), где \(1 \le l_i \le r_i \le n\). В качестве ответа на запрос посчитайте значение Ж-функции строки \(s_{l_i} s_{l_i +1} \ldots s_{r_i}\). Выходные данные Для каждого запроса выведите единственное число — Ж-функцию соответствующей подстроки. Примечание В первом примере содержатся четыре запроса: - первый запрос соответствует строке bb, Ж-функция которой равна \(2 + 1 = 3\);
- второй запрос соответствует строке abb, Ж-функция которой равна \(3 + 0 + 0 = 3\);
- третий запрос соответствует строке b, Ж-функция которой равна 1;
- четвертый запрос соответствует строке abbd, Ж-функция которой равна \(4 + 0 + 0 + 0= 4\).
| |
![]()
|
|
B. Счастливая строка
Конструктив
Строки
*1100
Петя любит счастливые числа. Всем известно, что счастливыми являются положительные целые числа, в десятичной записи которых содержатся только счастливые цифры 4 и 7. Например, числа 47, 744, 4 являются счастливыми, а 5, 17, 467 — не являются. Недавно Петя научился определять, является ли счастливой строка из маленьких букв латинского алфавита. Для каждой буквы в отдельности выписываются в порядке возрастания все ее позиций в строке. В итоге получается 26 списков чисел, некоторые из них могут быть пусты. Строка считается счастливой тогда и только тогда, когда в каждом списке модуль разности любых двух соседних чисел является счастливым числом. Например, рассмотрим строку «zbcdzefdzc». Списки позиций одинаковых символов: - b: 2
- c: 3, 10
- d: 4, 8
- e: 6
- f: 7
- z: 1, 5, 9
- Списки позиций букв a, g, h, ..., y пусты.
Эта строка счастливая, так как все разности являются счастливыми числами. Для символа z: 5 - 1 = 4, 9 - 5 = 4, для символа c: 10 - 3 = 7, для символа d: 8 - 4 = 4. Заметим, что если какой-то символ встречается в строке только один раз, то после построения списков позиций на счастливость строки он уже не влияет. Строка, в которой нет повторяющихся символов, является счастливой. Найдите лексикографически минимальную счастливую строку длины n. Выходные данные В единственной строке выведите лексикографически минимальную счастливую строку длины n. Примечание Лексикографическое сравнение строк реализует оператор < в современных языках программирования. Строка a лексикографически меньше строки b, если существует такое i (1 ≤ i ≤ n), что ai < bi, а для любого j (1 ≤ j < i) aj = bj. | |
![]()
|
|
D. Сбалансированная троичная строка
жадные алгоритмы
Строки
*1500
Задана строка \(s\), состоящая ровно из \(n\) символов '0', '1' и '2'. Такие строки называются троичными. Ваша задача — заменить минимальное количество символов в строке другими символами, чтобы получилась сбалансированная троичная строка (сбалансированная троичная строка — это троичная строка, в которой количество символов '0' равно количеству символов '1' и количество символов '1' (и, очевидно, '0') равно количеству символов '2'. Среди всех сбалансированных троичных строк вам необходимо получить лексикографически (алфавитно) минимальную. Заметьте, что вы не можете удалять символы из строки и добавлять символы в строку. Также заметьте, что вы можете заменять заданные символы только на символы '0', '1' и '2'. Гарантируется, что ответ существует. Выходные данные Выведите одну строку — лексикографически (алфавитно) минимальную сбалансированную троичную строку, полученную из заданной при помощи минимального количества замен. Так как \(n\) делится на \(3\), то очевидно, что ответ существует. Также очевидно, что существует только один возможный ответ. | |
![]()
|
|
B. Зухаир и строки
Перебор
реализация
Строки
*1100
Задана строка \(s\) длины \(n\) и целое число \(k\) (\(1 \le k \le n\)). Скажем, что строка \(s\) имеет уровень \(x\), если \(x\) это наибольшее неотрицательное целое число, такое что в строке \(s\) можно выбрать: - \(x\) непересекающихся подстрок длины \(k\),
- все символы в этих \(x\) подстроках должны быть одинаковы (т.е. каждая подстрока содержит только один различный символ, который один и тот же для всех выбранных подстрок).
Подстрока — это последовательность подряд идущих символов строки, подстрока определяется парой целых чисел \(i\) и \(j\) (\(1 \le i \le j \le n\)), обозначается как \(s[i \dots j]\) = «\(s_{i}s_{i+1} \dots s_{j}\)». Например, если \(k = 2\), то: - строка «aabb» имеет уровень \(1\) (можно выбрать подстроку «aa»),
- строки «zzzz» и «zzbzz» имеют уровень \(2\) (можно выбрать две непересекающихся подстроки «zz» в каждой их них),
- строки «abed» и «aca» имеют уровень \(0\) (невозможно выбрать хотя бы одну подстроку длины \(k=2\), которая содержит один различный символ).
Зухаир дал вам целое число \(k\) и строку \(s\) длины \(n\). Вам нужно найти \(x\) — уровень строки \(s\). Выходные данные Выведите одно целое число \(x\) — уровень строки. Примечание В первом примере мы можем выбрать \(2\) непересекающиеся строки, состоящей из буквы «a»: «(aa)ac(aa)bb», так что уровень равен \(2\). Во втором примере мы можем выбрать или подстроку «a» или «b» чтобы получить ответ \(1\). | |
![]()
|
|
A. Разбиение последовательности цифр
жадные алгоритмы
Строки
*900
Вам задана последовательность \(s\), состоящая из \(n\) цифр от \(1\) до \(9\). Вам нужно разбить ее на хотя бы два отрезка (отрезок — это последовательность подряд идущих элементов) (другими словами, вам нужно поставить разделители между некоторыми цифрами последовательности) таким образом, что каждый элемент принадлежит ровно одному отрезку и если результирующее разбиение будет представлено в виду последовательности целых чисел, то каждый следующий элемент этой последовательности будет строго больше, чем предыдущий. Более формально: если результирующее разбиение последовательности — это \(t_1, t_2, \dots, t_k\), где \(k\) — количество элементов в разбиении, то для каждого \(i\) от \(1\) до \(k-1\) должно выполняться условие \(t_{i} < t_{i + 1}\) (используется численное сравнение, то есть сравниваются численные интерпретации строк). Например, если \(s=654\), то вы можете разбить ее на части \([6, 54]\) и это будет являться подходящим разбиением. Но если вы разобьете ее на части \([65, 4]\), то это будет являться плохим разбиением, потому что \(65 > 4\). Если \(s=123\), то вы можете разбить его на части \([1, 23]\) и \([1, 2, 3]\), но не на части \([12, 3]\). Ваша задача — найти любое подходящее разбиение для каждого из \(q\) независимых запросов. Выходные данные Если последовательность цифр \(i\)-го запроса не может быть разбита на хотя бы две части способом, описанном в условии задачи, выведите единственную строку «NO» для этого запроса. Иначе в первой строке ответа на этот запрос выведите «YES», во второй строке выведите \(k_i\) — количество элементов в вашем разбиении последовательности \(i\)-го запроса и в третьей строке выведите \(k_i\) строк \(t_{i, 1}, t_{i, 2}, \dots, t_{i, k_i}\) — ваше разбиение. Части должны быть выведены в порядке следования цифр в заданной строке. Это означает, что если записать выведенные подстроки одну за другой, сохранив их порядок, то получится строка \(s_i\). Посмотрите в примеры для лучшего понимания. | |
![]()
|
|
B. Саша и ещё одно имя
Конструктив
Строки
хэши
*1800
Саша очень любит читать книги. При прочтении одной книги он познакомился с необычным персонажем. Персонаж говорит про себя так: «У меня много имён в разных странах. Митрандир среди эльфов, Таркун среди гномов; в юности на давно забытом Западе я был Олорином, на юге — Инканус, на севере — Гэндальф, а на востоке я не бываю.» И тут Саша задумался, а какое имя дали бы герою на Востоке? На Востоке все имена — палиндромы. Строка называется палиндромом, если она одинаково читается слева-направо и справа-налево. Например, строки «kazak», «oo» и «r» — палиндромы, а строки «abb» и «ij» — нет. Саша считает, что героя назвали бы в честь одного из богов Востока. Так как имена не должны повторяться, на Востоке поступают следующим образом: записывают исходное имя как строку, из которой хотят получить новое имя на лист бумаги. Затем разрезают лист минимальное количество раз \(k\), получив при этом \(k+1\) лист с подстроками имени, и склеивают полученные куски в новую строку. Листы при этом нельзя переворачивать, их можно только менять местами. Таким образом, выполнив \(3\) разреза в строке f|de|abc|g, может быть получена строка abcdefg (поменяв местами листы с подстроками f и abc), а строка cbadefg — нет. Более формально, Саша хочет для данного палиндрома \(s\) найти такое минимальное \(k\), что существует способ разрезать исходную строку на \(k + 1\) подстроку, а затем склеить их так, чтобы полученная строка являлась палиндромом и была отлична от исходной строки \(s\). Если решения не существует, выведите «Impossible» (без кавычек). Выходные данные Выведите одно целое число \(k\) — минимальное число разрезов, необходимых для получения нового имени, или «Impossible» (без кавычек), если ответа не существует. Примечание В первом примере можно выполнить разрезы в следующих местах: no|l|on, а затем склеить их как on|l|no. Можно показать, что не существует решения, использующего один разрез. Во втором примере строку можно разрезать посредине и поменять половины местами, получив строку toot. В третьем примере все полученные палиндромы будут совпадать с исходной строкой. В четвёртом примере можно отрезать суффикс nik и добавить его в начало, получив nikkinnikkin. | |
![]()
|
|
H. Скромные подстроки
дп
Строки
*3500
Вам даны два целых числа \(l\) и \(r\). Назовём число \(x\) скромным, если \(l \le x \le r\). Найдите строку длины \(n\), состоящую из цифр, с наибольшим возможным количеством подстрок, являющихся скромными числами. Подстроки, имеющие ведущие нули, не учитываются. Если возможных ответов несколько, найдите лексикографически минимальный. Если одно и то же число встречается несколько раз как подстрока, то при подсчёте количества скромных подстрок, оно будет тоже учитываться несколько раз. Выходные данные В первой строке выведите наибольшее возможное количество скромных подстрок. Во второй строке выведите строку длины \(n\) имеющую ровно такое число скромных подстрок. Если существует несколько таких строк, выведите лексикографически минимальную из них. Примечание В первом примере у строки «101» скромные подстроки «1», «10», «1». Во втором примере у строки «111» скромные подстроки «1» (\(3\) раза) и «11» (\(2\) раза). | |
![]()
|
|
A. Трансформация супергероев
реализация
Строки
*1000
Все знают, что супергерои могут трансформироваться в некоторых других супергероев. Но не любой супергерой может трансформироваться в любого другого супергероя. Супергерой с именем \(s\) может трансформироваться в другого супергероя с именем \(t\), если \(s\) можно превратить в \(t\), выполнив несколько операций по замене одной любой гласной буквы в \(s\) на любую другую гласную букву, а также любой одной согласной буквы в \(s\) на любую другую согласную. Можно производить сколько угодно замен. В этой задаче мы считаем, что гласными являются буквы 'a', 'e', 'i', 'o' и 'u', а согласными — все остальные. По данным двум именам супергероев определите, может ли супергерой с именем \(s\) трансформироваться в супергероя с именем \(t\). Выходные данные Выведите «Yes» (без кавычек), если супергерой с именем \(s\) может трансформироваться в супергероя с именем \(t\), и «No» (без кавычек) иначе. Вы можете выводить каждую букву в любом регистре (строчную или заглавную). Примечание В первом примере, так как буквы «a» и «u» гласные, возможно трансформировать строку \(s\) в \(t\). В третьем примере «k» является согласной, а «a» — гласная, поэтому невозможно преобразовать строку \(s\) в \(t\). | |
![]()
|
|
A. Петя и строки
реализация
Строки
*800
Маленький Петя очень любит подарки. Его мама подарила ему на день рождения две строки равной длины, состоящие из больших и маленьких букв латинского алфавита. Теперь Петя хочет сравнить эти строки лексикографически. При этом регистр букв значения не имеет, то есть большая буква считается эквивалентной соответствующей маленькой букве. Помогите Пете выполнить сравнение. Выходные данные Если первая строка меньше второй, выведите «-1». Если вторая строка меньше первой, выведите «1». Если строки равны, выведите «0». Учтите, что регистр букв не учитывается при сравнении. Примечание Формально про лексикографический порядок (также известный как «порядок слов в словаре» и «алфавитный порядок»): - http://ru.wikipedia.org/wiki/Лексикографический_порядок
- http://en.wikipedia.org/wiki/Lexicographical_order
| |
![]()
|
|
C. Азбука Морзе
Бинарный поиск
дп
сортировки
Строки
строковые суфф. структуры
Структуры данных
хэши
*2400
В азбуке Морзе каждая буква латинского алфавита определена как строка некоторый длины от \(1\) до \(4\), состоящая из точек и тире. В этой задаче мы будем обозначать точку как «0», а тире как «1». Так как существует \(2^1+2^2+2^3+2^4 = 30\) строк длины от \(1\) до \(4\), состоящих только из «0» и «1», не все из них соответствуют какой-то из \(26\) букв латинского алфавита. А именно, все строки из «0» и/или «1» длины не более \(4\) соответствуют разным буквы латинского алфавита, кроме следующих четырех строк, которые ничему не соответствуют: «0011», «0101», «1110» и «1111». Вы работаете на строке \(S\), которая изначально пуста. \(m\) раз далее либо точка, либо тире будут дописаны к \(S\), по одному символу за раз. Ваша задача — после каждого добавления к строке \(S\) найти количество непустых последовательностей букв латинского алфавита, которые представляются в азбуке Морзе как некоторая подстрока \(S\). Так как ответы могут быть очень большим, выводите их по модулю \(10^9 + 7\). Выходные данные Выведите \(m\) строк, \(i\)-я из которых должна содержать ответ после \(i\)-й модификации \(S\). Примечание Рассмотрим первый тестовый пример, после того, как к \(S\) будут дописаны все буквы, т.е. «111». Как вы можете видеть, «1», «11» и «111» соответствуют каким-то буквам латинского алфавита. Более точно, они переводятся в 'T', 'M', и в 'O', соответственно. Все слова, которые переводятся в подстроку строки \(S\) в азбуке Морзе, таким образом, равны: - «T» (переводится в «1»)
- «M» (переводится в «11»)
- «O» (переводится в «111»)
- «TT» (переводится в «11»)
- «TM» (переводится в «111»)
- «MT» (переводится в «111»)
- «TTT» (переводится в «111»)
Хоть это и не нужно в этой задаче, таблица переводов букв латинского алфавита в азбуку Морзе: здесь. | |
![]()
|
|
A. Уроки грамматики
реализация
Строки
*1600
В третьем классе Петя увлекся грамматикой и придумал свой собственный язык, который назвал Петровский. Петя хотел создать максимально простой язык, которого бы хватило для общения с друзьями, поэтому вся грамматика языка описывается следующим набором правил: - Есть три части речи: прилагательное, существительное, глагол. Каждое слово языка является либо прилагательным, либо существительным, либо глаголом.
- Есть два рода: мужской и женский. Каждое слово языка имеет либо мужской, либо женский род.
- Прилагательные мужского рода заканчиваются на -lios, а женского — на -liala.
- Существительные мужского рода заканчиваются на -etr, а женского — на -etra.
- Глаголы мужского рода заканчиваются на -initis, а женского — на -inites.
- Таким образом, каждое слово Петровского языка имеет одно из шести описанных выше окончаний. Других слов в Петровском языке нет.
- Допускается, что слово целиком состоит из окончания. То есть слова «lios», «liala», «etr» и так далее принадлежат Петровскому языку.
- Знаки препинания, времена, числа и прочее в этом языке отсутствуют.
- Предложение — это либо ровно одно слово любой части речи Петровского языка, либо ровно одно словосочетание.
Словосочетание — это любая последовательность слов Петровского языка, удовлетворяющая следующим условиям: - Слова в словосочетании идут в следующем порядке (слева направо): ноль или более прилагательных, затем ровно одно существительное, затем ноль или более глаголов.
- Все части слова в словосочетании должны быть одного рода.
После того, как Петин друг Вася написал instant messenger (программу для быстрого обмена сообщениями) с поддержкой Петровского языка, Пете захотелось добавить в программу подсветку синтаксиса и грамматики. Так как Вася был в деревне, а ждать Пете не хотелось, то он попросил вас помочь ему с этой задачей. Ваша задача — по заданному набору слов определить, верно ли, что данный текст представляет собой ровно одно предложение на Петровском языке. Выходные данные Если какое-то слово заданного текста не принадлежит Петровскому языку, или в тексте содержится более одного предложения, выведите «NO» (без кавычек). В противном случае выведите «YES» (без кавычек). | |
![]()
|
|
B. Petr#
Перебор
Строки
Структуры данных
хэши
*2000
Когда Петя еще учился в школе, он очень увлекался грамматикой языка Petr#. На одном из уроков Петю заинтересовал следующий вопрос: сколько различных подстрок, начинающихся строкой sbegin этого языка и заканчивающихся строкой send (возможно, sbegin = send), существует у заданной строки t. Подстроки называются различными, если различно их содержание, при этом позиции вхождения не имеют значения. В школе Петя не дружил с математикой, поэтому он не смог посчитать это количество. Помогите ему! Выходные данные Выведите единственное число — количество различных подстрок строки t, которые начинаются со строки sbegin и заканчиваются строкой send. Примечание В третьем тесте есть четыре различные подходящие подстроки: ab, abab, ababab, abababab. В четвертом тесте подстроки, соответствующие sbegin и send, пересекаются. | |
![]()
|
|
E. Произведение строк
дп
жадные алгоритмы
Строки
*2300
Рома и Денис отправились на соревнование по программированию. В долгой дороге ребята заскучали, поэтому решили придумать что-нибудь интересное. Рома придумал рецепт вкусной пиццы, а Денис придумал операцию умножения строк. По версии Дениса, произведением строки \(s\) длины \(m\) и строки \(t\) называется строка \(t + s_1 + t + s_2 + \ldots + t + s_m + t\), где \(s_i\) обозначает \(i\)-й символ строки \(s\), а знаком «+» обозначена конкатенация строк. Например, произведением строк «abc» и «de» является строка «deadebdecde», а произведением строк «ab» и «z» является строка «zazbz». Обратите внимание, что, в отличие от умножения чисел, произведение строк \(s\) и \(t\) не всегда равно произведению строк \(t\) и \(s\). Рома позавидовал Денису, что он придумал такую интересную операцию, и тоже решил придумать что-нибудь связанное со строками. Так как Рома — ценитель прекрасного, он решил определить красоту строки как максимальную длину подстроки, состоящей из одинаковых букв. Например, красота строки «xayyaaabca» равна \(3\), так как есть подстрока «aaa», а красота строки «qwerqwer» равна \(1\), потому что все соседние буквы в ней различны. Чтобы развлечь Рому, Денис написал ему на листочке \(n\) строк \(p_1, p_2, p_3, \ldots, p_n\) и попросил его вычислить красоту строки \(( \ldots (((p_1 \cdot p_2) \cdot p_3) \cdot \ldots ) \cdot p_n\), где \(s \cdot t\) обозначает произведение строк \(s\) и \(t\). Рома не до конца понял, как работает умножение Дениса, но не хочет признаваться в этом, поэтому просит посчитать красоту этой строки вас. Денис знает, что Рома слишком впечатлительный, поэтому гарантирует, что красота полученной строки не превосходит \(10^9\). Выходные данные Выведите одно целое число — красоту произведения строк. Примечание В первом примере произведение строк равно «abaaaba». Во втором примере произведение строк равно «abanana». | |
![]()
|
|
B. Расписание смены
жадные алгоритмы
Строки
хэши
*1600
В известной на всю страну Весенней компьютерной школе скоро начнется новая смена, и в связи с этим весь дружный состав преподавателей и кураторов начал составлять ее расписание. В процессе обсуждения они пришли к расписанию \(s\), которое может быть представлено в виде бинарной строки, в которой на \(i\)-й позиции стоит «1», если ученики в \(i\)-й день пишут контест, и «0», если отдыхают. В последний момент на заседание пришел Глеб и заявил, что если смена в школе проходит по расписанию \(t\) (которое может быть описано в таком же формате, что и \(s\)), то ученики особенно хорошо усваивают материал. Поскольку количество дней в грядущей смене может отличаться от количества дней в \(t\), Глеб потребовал, чтобы уже составленное расписание переделали таким образом, чтобы количество вхождений \(t\) в него как подстроки было максимально. При этом количество учебных и выходных дней не должно измениться, может измениться только порядок их следования. Сможете ли вы переставить порядок дней в расписании оптимальным образом? Выходные данные В единственной строке выведите расписание, количество вхождений \(t\) как подстроки в которое максимально. Выведенное расписание должно состоять только из «0» и «1», причём количество нулей должно совпадать с количеством нулей в \(s\), а количество единиц — с количеством единиц в \(s\). Если существует несколько оптимальных расписаний, выведите любое из них. Примечание В первом примере два вхождения, начинающихся с первой и четвертой позиции. Во втором примере всего одно вхождение, и оно начинается с третьей позиции. Заметим также, что ответ не единственен — например, самый первый день (являющийся выходным) можно переместить на последнюю позицию, и кол-во вхождений \(t\) не изменится. В третьем примере добиться даже одного вхождения не получится. | |
![]()
|
|
B. Цирк
жадные алгоритмы
математика
Перебор
Строки
*1800
Это просто цирк какой-то! Поликарп — руководитель труппы небольшого цирка. Всего в труппе \(n\) — четное число — артистов. Про \(i\)-го артиста известно, может ли он на манеже выступить как клоун (если да, то \(c_i = 1\), иначе \(c_i = 0\)), и может ли он выступить на манеже как акробат (если да, то \(a_i = 1\), иначе \(a_i = 0\)). Разделите артистов на два выступления так, чтобы: - каждый артист участвовал ровно в одном выступлении,
- количество артистов в каждом выступлении одинаково (следовательно, равно \(\frac{n}{2}\)),
- количество артистов в первом выступлении, которые могут выступить клоунами, равно количеству артистов во во втором выступлении, которые могут выступить акробатами.
Выходные данные Выведите \(\frac{n}{2}\) различных чисел — номера артистов, которые должны войти в первое выступление, в любом порядке. Если существует несколько решений, выведите любое из них. Если решения не существует, выведите одно целое число \(-1\). Примечание В первом примере одно из подходящих разделений следующее: в первом выступлении выступают артисты \(1\) и \(4\). Тогда в первом выступлении количество артистов, которые могут быть клоунами, равно \(1\). Количество артистов во втором выступлении, которые могут быть акробатами, также равно \(1\). Во втором примере не существует ни одного подходящего разделения. В третьем примере одно из подходящих разделений следующее: в первом выступлении выступают артисты \(3\) и \(4\). Тогда в первом выступлении количество артистов, которые могут быть клоунами, равно \(2\). Количество артистов во втором выступлении, которые могут быть акробатами, также равно \(2\). | |
![]()
|
|
A. Чётные подстроки
реализация
Строки
*800
Вам дана строка \(s=s_1s_2\dots s_n\) длины \(n\), содержащая только цифры \(1\), \(2\), ..., \(9\). Подстрокой \(s[l \dots r]\) строки \(s\) назовём строку \(s_l s_{l + 1} s_{l + 2} \ldots s_r\). Подстрока \(s[l \dots r]\) строки \(s\) называется чётной, если число, которое соответствует этой подстроке является чётным. Найдите количество чётных подстрок строки \(s\). Обратите внимание, что если некоторые подстроки равны как строки, но определены разными числами \(l\), \(r\), то они считаются различными. Выходные данные Выведите одно целое число — количество чётных подстрок в строке \(s\). Примечание В первом примере следующие \([l, r]\) пары задают чётные подстроки: - \(s[1 \dots 2]\)
- \(s[2 \dots 2]\)
- \(s[1 \dots 4]\)
- \(s[2 \dots 4]\)
- \(s[3 \dots 4]\)
- \(s[4 \dots 4]\)
Во втором примере, все \(10\) подстрок строки \(s\) являются чётными. Обратите внимание, что не смотря на то, что строки \(s[1 \dots 1]\) и \(s[2 \dots 2]\) задают подстроку «2», они всё равно считаются как различные подстроки. | |
![]()
|
|
B. Хорошая строка
реализация
Строки
*1200
У вас есть строка \(s\) длины \(n\) состоящая только из символов > и <. Вы можете выполнять операции с этой строкой, для каждой операции вы выбираете какой-то символ этой строки, еще не удаленный из нее. Если вы выбрали символ >, следующий символ удаляется (если выбранный вами символ стоит правее всех остальных — ничего не происходит). Если вы выбрали символ <, то предыдущий символ удаляется (если выбранный вами символ стоит левее всех остальных — ничего не происходит). Например, если мы выберем символ > в строке > > < >, то строка превратится в > > >. А если мы выберем символ < в строке > <, то строка превратится в <. Строка называется хорошей, если существует последовательность операций, после выполнения которой в строке останется ровно один символ. Например строки >, > > хорошие. До применения операций, вы можете удалить какое-то количество символов из строки (возможно, ни одного, возможно, \(n - 1\), но всю строку удалять нельзя). Вам нужно посчитать минимальное количество символов, которые нужно удалить из строки \(s\), чтобы она стала хорошей. Выходные данные Ответ для каждого тестового примера выведите в отдельной строке. Для \(i\)-го тестового примера выведите минимальное количество символов, которые нужно удалить из строки \(s\), чтобы она стала хорошей. Примечание В первом тестовм примере мы можем удалить любой символ из строки <>. Во втором тестовом примере нам не нужно ничего удалять. Строка > < < хорошая, так как мы можем выполнить следующую последовательность операций: > < < \(\rightarrow\) < < \(\rightarrow\) <. | |
![]()
|
|
A. Разнообразные строки
реализация
Строки
*800
Строка называется разнообразной, если она содержит последовательные (соседние) буквы латинского алфавита и каждая бука встречается ровно один раз. Например, следующие строки являются разнообразными:«fced», «xyz», «r» и «dabcef». Следующие строки не являются разнообразными: «az», «aa», «bad» и «babc». Заметьте, что буквы 'a' и 'z' не являются соседними. Более формально: рассмотрим позиции всех букв строки в алфавите. Эти позиции должны образовывать непрерывный отрезок, то есть они должны идти одна за другой без каких-либо пропусков. И все буквы в строке должны быть различны (дубликаты недопустимы). Вам задана последовательность строк. Для каждой строки, если она является разнообразной, выведите «Yes». Иначе выведите «No». Выходные данные Выведите \(n\) строк, по одной на каждую строку из входных данных. Строка должна содержать «Yes», если соответствующая строка из входных данных является разнообразной, и «No», если соответствующая строка из входных данных не является разнообразной. Вы можете выводить каждую букву в любом регистре (нижнем или верхнем). Например, «YeS», «no» и «yES» являются корректными ответами. | |
![]()
|
|
E. Медианная строка
битмаски
математика
Строки
теория чисел
*1900
Заданы две строки \(s\) и \(t\), обе состоят ровно из \(k\) строчных букв латинского алфавита, \(s\) лексикографически меньше \(t\). Рассмотрим список всех строк, состоящих ровно из \(k\) строчных латинских букв, лексикографически не меньших, чем \(s\) и не больше, чем \(t\) (включая \(s\) и \(t\)) в лексикографическом порядке. Например, для \(k=2\), \(s=\)«az» и \(t=\)«bf» список будет равен [«az», «ba», «bb», «bc», «bd», «be», «bf»]. Ваша задача — вывести медиану (средний элемент) этого списка. Для примера выше это будет «bc». Гарантируется, что количество строк, лексикографически не меньших, чем \(s\) и не больших, чем \(t\), нечетно. Выходные данные Выведите одну строку, состоящую ровно из \(k\) строчных букв латинского алфавита — медиану (средний элемент) списка строк длины \(k\), лексикографически не меньших, чем \(s\) и не больших, чем \(t\). | |
![]()
|
|
A. Любите "A"
реализация
Строки
*800
У Алисы есть строка \(s\). Она очень сильно любит букву «a». Она называет строку хорошей, если в ней строго больше половины символов «a». Например, «aaabb», «axaa» — хорошие строки, а «baca», «awwwa», «» (пустая строка) — нет. Алиса может стирать некоторые символы в строке \(s\). Она хотела бы узнать длину самой длинной хорошей строки, которая может остаться, если она сотрет несколько (возможно ноль) символов. Поскольку гарантируется, что в строке всегда есть как минимум одна буква «a», то ответ всегда существует. Выходные данные Выведите одно число — длину самой длинной хорошей строки, которую Алиса может получить, если будет стирать символы из \(s\). Примечание В первом примере достаточно стереть любые четыре буквы «x». Ответ будет \(3\), так как это максимальное количество символов, которые могут остаться. Во втором примере не нужно ничего стирать. | |
![]()
|
|
B. Ненавидьте "A"
реализация
Строки
*1100
У Боба есть строка \(s\), которая состоит из английских букв нижнего регистра. Он определил \(s'\) как строку, которую он получит, удаляя все буквы «a» из строки \(s\) (оставляя все остальные символы в том же порядке). Он сгенерировал новую строку \(t\) путем соединения \(s\) и \(s'\). Другими словами, \(t=s+s'\) (смотрите примеры). Вам дана строка \(t\). Найдите такую строку \(s\), которую использовал Боб, чтобы сгенерировать строку \(t\). Можно показать, что если ответ существует, то он уникальный. Выходные данные Выведите строку \(s\), которую можно использовать для генерации \(t\). Можно показать, что если ответ существует, то он уникальный. Если такой строки нет, то выведите «:(» (без кавычек, между символами нет пробела). Примечание В первом примере \(s = \) «aaaaa», а \(s' = \) «». Во втором примере нет такой строки \(s\), которая может сгенерировать \(t\). В третьем примере \(s = \) «ababacac», а \(s' = \) «bbcc», поэтому \(t = s + s' = \) «ababacacbbcc». | |
![]()
|
|
B. Фигуры Хладни
Перебор
Строки
*1900
У Инаки есть диск, длина окружности которого равна \(n\) единицам. Окружность разделена на равные части \(n\) точками, пронумерованными от \(1\) до \(n\) так, что точки \(i\) и \(i + 1\) (\(1 \leq i < n\)) соседние, кроме того, соседними являются точки \(n\) и \(1\). На диске нарисованы \(m\) хорд, соединяющих некоторые из данных \(n\) точек. Инака хочет понять, имеет ли ее диск вращательную симметрию, т. е. существует ли целое число \(k\) (\(1 \leq k < n\)), такое, что если повернуть все хорды по часовой стрелке на \(k\) единиц, то диск будет выглядеть так же. Выходные данные Выведите «Yes» если диск имеет вращательную симметрию, и «No» в обратном случае (без кавычек). Вы можете выводить каждую букву в любом регистре (строчную или заглавную). Примечание Первые два примера показаны на рисунке ниже. Оба диска совпадают с собой после поворота на \(120\) градусов.  | |
![]()
|
|
B. Три религии
дп
реализация
Строки
*2200
Во время археологических исследований на Ближнем Востоке вы обнаружили следы трёх древних религий: первой религии, второй религии и третьей религии. Вы собрали информацию о развитии каждого из этих верований, и теперь вы думаете, могут ли последователи каждой религии мирно сосуществовать? Слово Вселенной — это длинное слово, содержащее только строчные английские символы. В каждый момент времени каждое из религиозных верований может быть описано словом, состоящим из строчных английских символов. Три религии могут сосуществовать мирно, если их описания являются непересекающимеся подпоследовательностями Слова Вселенной. Формально, религии могут сосуществовать мирно если можно покрасить некоторые символы Слова Вселенной в три цвета: \(1\), \(2\), \(3\), что каждый символ покрашен в не более чем один цвет, и описание \(i\)-й религии может быть построено из Слова Вселенной удалением всех символов, которые не покрашены в цвет \(i\). Однако религии изменяются. Вначале описание каждой религии пусто. Время от времени, в конец описания какой-нибудь из религий добавляется символ или из описания какой-то религии удаляется последний символ. После каждого изменения определите, могут ли три религии сосуществовать мирно. Выходные данные Выведите \(q\) строк. \(i\)-я из них должна содержать «YES» если религии могут мирно сосуществовать после \(i\)-й эволюции, и «NO» иначе. Вы можете выводить каждую букву в любом регистре (верхнем или нижнем). Примечание В первом примере, после 6 изменений описания религий равны: ad, bc, и ab. Следующая иллюстрация показывает, какими подпоследовательностями Слова Вселенной они являются:  | |
![]()
|
|
A. Максим и биология
Перебор
Строки
*1000
Сегодня в научном лицее Королевства Кремляндия был урок биологии. Темой урока были геномы. Назовем геномом строку «ACTG». Максиму было очень скучно сидеть на уроке, поэтому учитель придумал для него задание: по заданной строке \(s\), состоящей из заглавных латинских букв и длины как минимум \(4\), необходимо найти минимальное количество операций которое нужно применить, чтобы в ней появился геном как подстрока. За одну операцию можно заменить любую букву в строке \(s\) на следующую или предыдущую в алфавите. Например, для буквы «D» предыдущей будет «C», а следующей — «E». В этой задаче считаем, что для буквы «A» предыдущей будет буква «Z», а следующей — буква «B», а для буквы «Z» предыдущей будет буква «Y», а следующей — буква «A». Помогите Максиму решить задачу, которую дал ему учитель. Напомним, что строка \(a\) является подстрокой \(b\), если \(a\) может быть получена из \(b\) удалением нескольких (возможно, ни одного или всех) символов из начала и нескольких (возможно, ни одного или всех) символов из конца. Выходные данные Выведите минимальное количество операций, которые нужно применить к строке \(s\), чтобы в ней появился геном как подстрока. Примечание В первом примере следует заменить букву «Z» на «A» за одну операцию, букву «H» — на букву «G» за одну операцию. Получится строка «ACTG», в которой присутствует геном как подстрока. Во втором примере заменим букву «A» на «C» за две операции, букву «D» — на букву «A» за три операции. Получится строка «ZACTG», в которой есть геном. | |
![]()
|
|
C. Сервал и скобочная последовательность
жадные алгоритмы
Строки
*1700
Сервал попрощался с детским садом Джапари и начал свою школьную жизнь в школе Джапари. На его любимом уроке математики учитель рассказал ему следующие интересные определения. Скобочной последовательностью называется строка, состоящая только из символов «(», «)». Правильной скобочной последовательностью называется скобочная последовательность, которую можно преобразовать в корректное арифметическое выражение путем вставок между ее символами символов «1» и «+». Например, скобочные последовательности «()()», «(())» — правильные (полученные выражения: «(1+1)+(1+1)», «((1+1)+1)»), а «)(» и «)» — нет. Пустая строка является правильной скобочной последовательностью по определению. Обозначим за \(|s|\) длину строки \(s\). Собственным префиксом \(s[1\dots l]\) \((1\leq l< |s|)\) строки \(s = s_1s_2\dots s_{|s|}\) назовем строку \(s_1s_2\dots s_l\). Обратите внимание, что пустая строка и вся строка не являются собственными префиксами по определению. Изучив эти определения, он придумал новую задачу. Он выписал строку \(s\), состоящую только из символов «(», «)», «?». Теперь он хочет заменить каждый из «?» в \(s\) независимо на один из символов «(» или «)», чтобы все собственные префиксы строки не являлись правильной скобочной последовательностью, а сама строка являлась. В конце концов Сервал всего лишь ученик начальной школы, поэтому эта задача для него слишком трудная. Как его лучший друг, может быть, вы поможете ему заменить знаки вопроса? Если существует несколько решений, вы можете найти любое. Выходные данные Выведите одну строку, содержащую ответ на задачу. Если возможных решений несколько, вы можете вывести любое. Если решения не существует, выведите единственную строку, содержащую «:(» (без кавычек). Примечание Можно доказать, что не существует ответа на второй тест из примера, поэтому требуется вывести «:(». | |
![]()
|
|
A. Разверни подстроку
реализация
сортировки
Строки
*1000
Вам дана строка \(s\), состоящая из \(n\) строчных букв латинского алфавита. Подстрока строки — это некоторый ее непрерывный подотрезок. Например, «acab» — подстрока строки «abacaba» (она начинается в позиции \(3\) и заканчивается в позиции \(6\)), но «aa» и «d» не являются подстроками этой строки. То есть подстрока строки \(s\) с позиции \(l\) по позицию \(r\) — это строка \(s[l; r] = s_l s_{l + 1} \dots s_r\). Вам нужно выбрать ровно одну подстроку данной строки и развернуть ее (то есть сделать \(s[l; r] = s_r s_{r - 1} \dots s_l\)), чтобы полученная строка оказалась лексикографически меньше исходной. Обратите внимание, что не обязательно минимизировать полученную строку. Если невозможно таким образом развернуть подстроку, выведите «NO». Иначе выведите «YES» и любую подходящую подстроку. Строка \(x\) лексикографически меньше строки \(y\), если либо \(x\) является префиксом \(y\) (и при этом \(x \ne y\)), либо существует такое \(i\) (\(1 \le i \le min(|x|, |y|)\)), что \(x_i < y_i\), и для любого \(j\) (\(1 \le j < i\)) \(x_j = y_j\). Здесь \(|a|\) обозначает длину строки \(a\). Лексикографическое сравнение строк реализует оператор < в современных языках программирования. Выходные данные Если невозможно развернуть подстроку так, чтобы в итоге получилась строка лексикографически меньше исходной, выведите «NO». Иначе выведите «YES» и два индекса \(l\) и \(r\) (\(1 \le l < r \le n\)), обозначающие начало и конец подстроки, которую вы хотите перевернуть. Если ответов несколько, выведите любой из них. Примечание В первом тесте после разворота подстроки получается строка «aacabba». | |
![]()
|
|
B. Противные пары
жадные алгоритмы
поиск в глубину и подобное
реализация
сортировки
Строки
*1800
Задана строка, состоящая из строчных латинских букв. Пара соседних букв в строке считается противной, если данные буквы так же соседние в алфавите. Например, строка «abaca» содержит противные пары на позициях \((1, 2)\) — «'ab» и \((2, 3)\) — «ba». Буквы 'a' и 'z' не считаются соседними в алфавите. Можете ли вы так переставить местами буквы в данном строке, чтобы в ней не было противных пар? Выбирая новый порядок, помните, что нельзя добавлять в строку новые буквы или удалять уже имеющиеся. Также можно сохранить начальный порядок. Если существует несколько ответов, выведите любой из них. Также требуется ответить на \(T\) независимых запросов. Выходные данные Выведите \(T\) строк. В \(i\)-й строке должен быть записан ответ на \(i\)-й запрос. Если ответ на \(i\)-й запрос существует, то выведите строку с новым порядком букв такую, что она не содержит противных пар. Выбирая новый порядок, помните, что нельзя добавлять в строку новые буквы или удалять уже имеющиеся. Также можно сохранить начальный порядок. Если существует несколько ответов, выведите любой из них. Если ответа на запрос нет, выведите «No answer». Примечание В первом примере ответ «bdac» также корректен. Второй пример показывает, что только соседние буквы в алфавите неприемлемы. Одинаковые подходят. В третьем примере множество правильных ответов. | |
![]()
|
|
B. Минимальная уникальная подстрока
Конструктив
математика
Строки
*2200
Пусть у вас есть строка \(s\) из символов "0" и "1". Будем называть строку \(t\) подстрокой строки \(s\), если существует \(1 \leq l \leq |s| - |t| + 1\), такое что \(t = s_l s_{l+1} \ldots s_{l + |t| - 1}\). Будем называть подстроку \(t\) строки \(s\) уникальной, если существует единственное такое \(l\). Например, пусть \(s = \)"1010111". Тогда \(t = \)"010" является уникальной подстрокой \(s\), так как существует единственное подходящее \(l = 2\). Заметим, что \(t = \)"10" не является уникальной подстрокой \(s\), так как подходят \(l = 1\) и \(l = 3\). А, например, \(t =\)"00" вообще не является подстрокой строки \(s\), так как не существует подходящих \(l\). Сегодня Вася на уроке информатики решал такую задачу: дана строка из символов "0" и "1", надо найти длину её кратчайшей уникальной подстроки. Написав решение к этой задаче, он решил его протестировать. Он просит помощи у вас. Вам даны \(2\) таких целых положительных числа \(n\) и \(k\), что \((n \bmod 2) = (k \bmod 2)\), где \((x \bmod 2)\) — это операция взятия остатка числа \(x\) при делении на \(2\). Найдите любую строку \(s\) состоящую из \(n\) символов "0" и "1", такую что наименьшая длина её уникальной подстроки равна \(k\). Выходные данные Выведите строку \(s\) длины \(n\), состоящую из символов "0" и "1". Минимальная длина уникальной подстроки \(s\) должна равняться \(k\). Среди таких строк разрешается вывести любую. Гарантируется, что хотя бы одна подходящая строка существует. Примечание В первом тесте легко видеть, что единственной уникальной подстрокой строки \(s = \)"1111" является вся строка \(s\), длина которой \(4\). Во втором тесте у строки \(s = \)"01010" минимальной по длине уникальной подстрокой является строка \(t =\)"101" длина которой \(3\). Во третьем тесте у строки \(s = \)"1011011" минимальной по длине уникальной подстрокой является строка \(t =\)"110" длина которой \(3\). | |
![]()
|
|
D. Таинственный код
дп
Строки
*2100
Гуляя по лесу, Кэти наткнулась на таинственный код! Однако некоторые символы, к сожалению, оказались нечитаемыми. Кэти записала таинственный код как строку \(c\), состоящую из строчных латинских букв и звёздочек («*»), где звёздочка обозначает нечитаемый символ. Вдохновлённая своим открытием, Кэти хочет восстановить нечитаемые символы, заменив каждую звёздочку произвольной строчной латинской буквой (разные звёздочки можно заменить на разные буквы). Также у Кэти есть любимая строка \(s\) и не очень любимая строка \(t\). Она хочет восстановить таинственный код таким образом, чтобы количество вхождений \(s\) в него было как можно больше, а количество вхождений \(t\) как можно меньше. Формально, обозначим \(f(x, y)\) как количество вхождений строки \(y\) в строку \(x\) (например, \(f(aababa, ab) = 2\)). Кэти хочет восстановить код \(c'\), подходящий под изначальный код \(c\), такой что \(f(c', s) - f(c', t)\) является максимально возможной. Кэти не очень хороша в восстановлении кодов, поэтому она хочет, чтобы вы ей помогли. Выходные данные Выведите одно целое число — максимальное значение \(f(c', s) - f(c', t)\) у восстановленного кода. Примечание В первом примере для \(c'\) равной «katie», \(f(c', s) = 1\) и \(f(c', t) = 0\), тем самым \(f(c', s) - f(c', t) = 1\), что является наибольшим возможным значением. Во втором примере есть лишь одна \(c'\) подходящая под исходный код \(c\): «caat». Соответствующая \(f(c', s) - f(c', t) = 1 - 2 = -1\). В третьем примере есть несколько способов восстановить код, так чтобы \(f(c', s) - f(c', t)\) была максимально возможной, например «aaa», «aac», или «zaz». Величина \(f(c', s) - f(c', t) = 0\) для всех этих способов. В четвёртом примере оптимальным способом восстановить \(c'\) является «ccc». В этом случае \(f(c', s) - f(c', t) = 2\). | |
![]()
|
|
A. Телефонный номер
жадные алгоритмы
Перебор
Строки
*800
Телефонный номер — это последовательность длины ровно 11 из цифр, где первая цифра — это 8. Например, последовательность 80011223388 является телефонным номером, но последовательности 70011223388 и 80000011223388 — не являются телефонными номерами. Вам дана строка \(s\) длины \(n\), состоящая только из цифр. За одну операцию вы можете удалить любой символ из строки \(s\). Например, из строки 1121 вы можете получить строку 112, 111 или 121. Вам нужно определить, существует ли такая последовательность операций (возможно пустая), после которой строка \(s\) станет телефонным номером. Выходные данные Для каждого тестового примера выведите ответ в отдельной строке. Если существует последовательность операций, превращающая строку \(s\) в телефонный номер, выведите YES. Иначе выведите NO. Примечание В первом тестовом примере вам нужно удалить первую и третью цифры. Тогда строка 7818005553535 превратится в 88005553535. | |
![]()
|
|
C. Минус на минус дают плюс
*особая задача
реализация
Строки
Все знают, что два идущих подряд знака «минус» можно заменить на знак «плюс». Вам задана строка \(s\), состоящая исключительно из знаков «плюс» и «минус». С ней можно провести ноль или более операций. Каждая операция состоит в выборе произвольных двух минусов, которые идут подряд, затем эти два минуса заменяются на знак «плюс». Таким образом, за одну операцию длина строки уменьшается на \(1\). Вам заданы две строки \(s\) и \(t\). Определите, можно ли с помощью \(0\) или более операций из строки \(s\) получить строку \(t\). Выходные данные Выведите \(k\) строк: \(i\)-я строка должна содержать YES, если ответ на \(i\)-й набор входных данных положительный, иначе NO. Выводите YES и NO исключительно прописными буквами. | |
![]()
|
|
B. WOW фактор
дп
Строки
*1300
Строка \(a\) является подпоследовательностью строки \(b\), если \(a\) может быть получена из \(b\) удалением нескольких (возможно, ни одного или всех) символов. Например, для строки \(a\)=«wowwo», следующие строки являются подпоследовательностями: «wowwo», «wowo», «oo», «wow», «» и другие, а следующие не являются подпоследовательностями: «owoo», «owwwo», «ooo». Wow фактор строки равен количеству подпоследовательностей, которые равны строке «wow». Боб хотел выписать строку, которая имеет большой wow фактор. Однако кнопка «w» на его клавиатуре сломана, поэтому он пишет вместо нее две буквы «v». Боб неожиданно осознал, что, возможно, в строке можно найти больше букв «w», чем он написал. Например, рассмотрим строку «ww». Боб написал бы ее как «vvvv», но в этой строке можно найти три буквы «w»: Например, wow фактор в слове «vvvovvv» равен четырем, потому что есть четыре способа выбрать «wow»: - «vvvovvv»
- «vvvovvv»
- «vvvovvv»
- «vvvovvv»
Обратите внимание, что подпоследовательность «vvvovvv» не считается, так как буквы «v» должны быть последовательными. Посчитайте wow фактор для строки \(s\) и выведите его. Обратите внимание, что не гарантируется, что возможно получить строку \(s\) из другой строки, заменяя «w» на «vv». Например, \(s\) может быть «vov». Выходные данные Выведите одно целое число — wow фактор строки \(s\). Примечание Первый пример объяснен в легенде. | |
![]()
|
|
E. Археология
жадные алгоритмы
Конструктив
Перебор
Строки
*1900
После того, как Алиса купила подписку на Congo Prime Video, она начала смотреть документальный фильм об археологических находках с острова Фактор на озере Лох Катрин в Шотландии. Археологи нашли книгу, возраст и происхождение которой неизвестны. Возможно Алиса сможет расшифровать ее? В книжке записано только одно слово, которое состоит из символов «a», «b» и «c». Было замечено, что нет двух последовательных одинаковых символов. Так же было предположено, что в этой строке есть длинная подпоследовательность, которая читается слева направо так же, как и справа налево. Помогите Алисе найти любую такую подпоследовательность, которая содержит как минимум половину (округленную вниз) символов из начальной строки. Обратите внимание, что вам не нужно максимизировать ее длину. Строка \(a\) является подпоследовательностью \(b\), если \(a\) может быть получена из \(b\) удалением нескольких (возможно, ни одного или всех) символов. Выходные данные Выведите палиндром \(t\), который является подпоследовательностью строки \(s\) и \(|t| \geq \lfloor \frac{|s|}{2} \rfloor\). Если существует несколько решений, выведите любое из них. Обратите внимание, что вам не нужно максимизировать длину \(t\). Если решения не существует, выведите «IMPOSSIBLE» (без кавычек). Примечание В первом примере другими возможными ответами могут быть «cacac», «caac», «aca» и «ccc». | |
![]()
|
|
A. Упражнение на строки
реализация
Строки
*1000
Петя записался в кружок по программированию. На первом занятии Пете задали написать простую программу. Программа должна делать следующее: в заданной строке, которая состоит из прописных и строчных латинских букв, она: - удаляет все гласные буквы,
- перед каждой согласной буквой ставит символ ".",
- все прописные согласные буквы заменяет на строчные.
Гласными буквами считаются буквы "A", "O", "Y", "E", "U", "I", а согласными — все остальные. На вход программе подается ровно одна строка, она должна вернуть результат в виде одной строки, получившейся после обработки. Помогите Пете справиться с этим несложным заданием. Выходные данные Выведите получившуюся строку. Гарантируется, что эта строка не пуста. | |
![]()
|
|
C. Модный номер
жадные алгоритмы
Перебор
сортировки
Строки
*1900
Номер машины в Берляндии состоит ровно из n цифр. Номер называется красивым, если в нем есть хотя бы k одинаковых цифр. Вася хочет поменять цифры в номере своей машины так, чтобы он стал красивым. За замену одной из n цифр номера нужно заплатить сумму денег, равную модулю разности старой и новой цифры. Помогите Васе: найдите минимальную стоимость замены номера Васиной машины на красивый. Также требуется найти получившийся в итоге красивый номер. Если таких несколько, нужно вывести лексикографически наименьший. Выходные данные В первой строке выведите минимальное количество денег, которые потребуются Васе для замены номера. Во второй строке выведите новый номер машины. Если решений несколько, выведите лексикографически наименьшее. Примечание В первом примере замена второй цифры на «8» стоит |9 - 8| = 1. Замена пятой цифры на «8» стоит столько же. Замена шестой цифры стоит |6 - 8| = 2. В итоге Вася заплатит 1 + 1 + 2 = 4 чтобы получить красивый номер «888188». Лексикографическое сравнение строк реализует оператор < в современных языках программирования. Строка x лексикографически меньше строки y, если существует такое i (1 ≤ i ≤ n), что xi < yi, а для любого j (1 ≤ j < i) xj = yj. Сравниваемые строки в этой задаче всегда имеют длину n. | |
![]()
|
|
B. Разделение числа
жадные алгоритмы
реализация
Строки
*1500
Сегодня Дима целый день старался и выписывал на длинную бумажную ленту своё любимое целое положительное число \(n\), состоящее из \(l\) цифр. К сожалению, лента получилась настолько длинной, что в итоге не влезла в Димин шкаф. Чтобы справиться с этой неприятностью, Дима решил разрезать ленту на две непустые части, на каждой из которых записано целое положительное число без ведущих нулей, после чего сложить числа, написанные на получившихся частях, а полученную сумму записать на новую ленту. Дима хочет, чтобы полученное число было как можно меньше, ведь это повышает шансы на то, что хотя бы сумма в шкаф влезет. Помогите Диме определить, какое минимальное число он может получить. Выходные данные Выведите одно целое число — минимальное число, которое может получить Дима. Примечание В первом примере Дима может разрезать число \(1234567\) на числа \(1234\) и \(567\). Их сумма равна \(1801\). Во втором примере Дима может разрезать число \(101\) на числа \(10\) и \(1\). Их сумма равна \(11\). Обратите внимание, запрещено разрезать число на «1» и «01», так как числа не могут начинаться с нулей. | |
![]()
|
|
B. Плюс из рисунка
поиск в глубину и подобное
реализация
Строки
*1300
Вам дан рисунок с размерами \(w \times h\). Определите, имеет ли данный рисунок одну «+» форму или нет. «+» форма определена ниже: - «+» форма имеет одну центральную заполненную клетку.
- Должно быть несколько (как минимум одна) последовательных заполненных клеток в каждом направлении (влево, вправо, вверх, вниз) от центра, то есть каждый из четырёх лучей должен быть непустым.
- Все остальные клетки незаполненны.
Определите, имеет ли данный рисунок одну «+» форму или нет. Выходные данные Если данное изображение удовлетворяет всем условиям, выведите «YES». Иначе выведите «NO». Вы можете выводить каждую букву в любом регистре (строчную или заглавную). Примечание В первом примере данная картина содержит одну «+» форму. Во втором примере две вертикальные ветви расположены в разных столбцах. В третьем примере есть заполненная точка вне фигуры. В четвертом примере ширина двух вертикальных ветвей составляет \(2\). В пятом примере есть две фигуры. В шестом примере внутри фигуры есть пустое пространство. | |
![]()
|
|
C. Красивые строфы
жадные алгоритмы
Строки
Структуры данных
*1700
Вам дано \(n\) слов, состоящих из строчных букв алфавита. Все слова имеют как минимум одну гласную букву. Вы хотите выбрать некоторые из заданных слов и составить из них как можно больше красивых строф. Каждая строфа состоит из двух строк. Каждая строка состоит из двух слов, разделенных пробелом. Строфа красивая тогда и только тогда, когда строфа удовлетворяет всем условиям ниже. - Количество гласных в первом слове первой строки совпадает с количеством гласных в первом слове второй строки.
- Количество гласных во втором слова первой строки совпадает с количеством гласных во втором слове второй строки.
- Последняя гласная в первой строке совпадает с последней гласной во второй строке. Обратите внимание, что после гласной могут быть согласные.
Буквы «a», «e», «o», «i» и «u» гласные. Обратите внимание, что «y» никогда не является гласной. Пример красивой строфы: "hello hellooowww" "whatsup yowowowow" она красивая, потому что есть две гласные буквы в « hello» и « whatsup», четыре гласные буквы в « hellooowww» и « yowowowow» (не забывайте, что « y» — не гласная), и последняя гласная — это « o». Пример некрасивой строфы: "hey man""iam mcdic" эта строфа некрасивая, потому что слова « hey» и « iam» имеют неодинаковое количество гласных букв и две строки имеют разные последние гласные (« a» в первой и « i» во второй). Сколько красивых строф вы можете написать по заданным словам? Обратите внимание, что вы не можете использовать слово больше раз, чем оно было дано вам. Например, если слово было дано три раза, вы можете использовать это слово максимум три раза. Выходные данные В первой строке выведите \(m\) — максимальное количество красивых строф. В следующих \(2m\) строках выведите \(m\) красивых строф (две строки на строфу). Если существует несколько решений, выведите любое из них. Примечание В первом примере те строфы являют одним из возможных ответов. Посмотрим на первую строфу. «about proud hooray round» — красивая строфа, потому что слова «about» и «hooray» имеют одинаковое количество гласных, «proud» и «round» имеют одинаковое количество гласных и у них последняя гласная совпадает. С другой стороны, вы не можете использовать слово «codeforces», чтобы сформировать красивую строфу. Во втором примере вы не можете составить красивую строфу из заданных слов. В третьем примере вы можете использовать слово «same» до трех раз. | |
![]()
|
|
H. Подпоследовательности (усложненная версия)
дп
Строки
*1900
Единственное отличие между легкой и сложной версиями — ограничения. Подпоследовательность строки может быть получена из другой строки при помощи удаления некоторого (возможно, нулевого) количества символов без изменения порядка оставшихся символов. Удаляемые символы не обязательно должны идти друг за другом, между ними могут быть любые пропуски. Например, для строки «abaca» следующие строки являются ее подпоследовательностями: «abaca», «aba», «aaa», «a» и «» (пустая строка). А следующие строки не являются подпоследовательностями: «aabaca», «cb» и «bcaa». Вам задана строка \(s\), состоящая из \(n\) строчных букв латинского алфавита. За один ход вы можете выбрать любую подпоследовательность \(t\) заданной строки и добавить ее во множество \(S\). Множество \(S\) не может содержать одинаковых элементов. Этот ход стоит \(n - |t|\), где \(|t|\) равно длине добавляемой подпоследовательности (то есть цена равна количеству удаленных символов). Ваша задача — найти минимальную возможную суммарную стоимость получения множества \(S\) размера \(k\) или сообщить, что это сделать невозможно. Выходные данные Выведите одно целое число — если невозможно составить множество \(S\) размера \(k\), выведите -1. Иначе выведите минимально возможную суммарную стоимость составления такого множества. Примечание В первом тестовом примере мы можем составить \(S\) = { «asdf», «asd», «adf», «asf», «sdf» }. Стоимость первого элемента в \(S\) равна \(0\), а стоимости остальных равны \(1\). Таким образом, суммарная стоимость \(S\) равна \(4\). | |
![]()
|
|
B. Письмо от Поликарпа
реализация
Строки
*1200
Мефодий получил от своего друга Поликарпа письмо по электронной почте. Однако у Поликарпа сломалась клавиатура: на его клавиатуре при однократном нажатии на клавишу соответствующий символ может появиться более одного раза (в то время, как на обычной клавиатуре однократное нажатие приводит к появлению ровно одного символа). Например, в результате набора слова «hello» следующие слова могли оказаться набранными: «hello», «hhhhello», «hheeeellllooo», но следующие слова не могли оказаться набранными: «hell», «helo», «hhllllooo». Обратите внимание, что при нажатии на клавишу символ обязательно появляется (возможно, более одного раза). Клавиатура сломана недетерменированным образом, то есть нажатие на одну и ту же клавишу в разные моменты времени может приводить к разному количеству появившихся букв. Для каждого слова в письме Мефодий предположил, какое на самом деле слово хотел написать Поликарп, но он не уверен, что понял написанное правильно, поэтому он просит вас ему помочь. Вам дан список пар слов. Для каждой пары определите, могло ли второе слово быть получено в результате набора первого слова на клавиатуре Поликарпа. Выходные данные Выведите \(n\) строк. В \(i\)-й строке для \(i\)-й пары слов \(s\), \(t\) выведите YES, если при наборе слова \(s\) можно получить слово \(t\). Иначе, выведите NO. | |
![]()
|
|
B. Магазин букв
Бинарный поиск
реализация
Строки
*1300
Витрина магазина букв — это строка \(s\), состоящая из \(n\) строчных латинских букв. Как следует из названия, в магазине продаются буквы. Буквы продают одну за другой последовательно от первой (самой левой) буквы до последней (самой правой). Любой покупатель может купить только некоторый префикс букв из строки \(s\). Есть \(m\) друзей, \(i\)-го из них зовут \(t_i\). Каждый из них хочет оценить следующую величину: если он/а придёт в магазин и будет покупать буквы одну за другой с целью написать своё имя, то сколько букв (длина кратчайшего префикса) ей/ему придётся купить? Своё имя можно написать, если в наличии есть все буквы имени (в количестве равном или большем необходимого). - Например, если \(s\)=«arrayhead», а имя \(t_i\)=«arya», то придётся купить \(5\) букв. («arrayhead»).
- Например, если \(s\)=«arrayhead», а имя \(t_i\)=«harry», то придётся купить \(6\) букв («arrayhead»).
- Например, если \(s\)=«arrayhead», а имя \(t_i\)=«ray», то придётся купить \(5\) букв («arrayhead»).
- Например, если \(s\)=«arrayhead», а имя \(t_i\)=«r», то придётся купить \(2\) буквы («arrayhead»).
- Например, если \(s\)=«arrayhead», а имя \(t_i\)=«areahydra», то придётся купить все \(9\) буквы («arrayhead»).
Гарантируется, что каждый друг может написать свое имя, используя буквы из строки \(s\). Обратите внимание, что ответы для друзей надо находить независимо (друзья только лишь оценивают ситуации, но не покупают буквы). Выходные данные Для каждого друга выведите длину кратчайшего префикса \(s\), которую ей/ему придётся купить, чтобы написать свое имя. Своё имя можно написать, если в наличии есть все буквы имени (в количестве равном или большем необходимого). Гарантируется, что каждый друг может написать свое имя, используя буквы из строки \(s\). | |
![]()
|
|
A. Киану Ривз
Строки
*800
После исполнения роли Нео в легендарной трилогии «Матрица», Киану Ривз начал сомневаться: возможно, мы действительно живем в виртуальной реальности? Чтобы это выяснить, ему нужно решить следующую задачу. Будем называть строку состоящую только из нулей и единиц хорошей, если она содержит различное число нулей и единиц. К примеру, строки 1, 101, 0000 являются хорошими, а 01, 1001 and 111000 не являются хорошими. Дана строка \(s\) длины \(n\) состоящая только из нулей и единиц. Мы должны разрезать \(s\) на минимально возможное количество подстрок \(s_1, s_2, \ldots, s_k\) таким образом, чтобы все они были хорошими. Более формально, мы должны найти минимальную по количеству строк последовательность хороших строк \(s_1, s_2, \ldots, s_k\) такую, что их конкатенация (последовательное склеивание) равно \(s\), то есть \(s_1 + s_2 + \dots + s_k = s\). К примеру, разрезания 110010 на 110 и 010 или на 11 и 0010 удовлетворяют условию, так как 110, 010, 11, 0010 являются хорошими, а на меньшее число разрезать 110010 нельзя, так как 110010 хорошей не является. В то же время, разрезание 110010 на 1100 и 10 не удовлетворяет условию, так как обе строки не являются хорошими. Также, разрезание 110010 на 1, 1, 0010 не удовлетворяет условию, так как не является минимальным, хоть все \(3\) строки и являются хорошими. Можете ли вы помочь Киану? Можно показать, что решение всегда существует. Если существует несколько оптимальных решений, выведите любое из них. Выходные данные В первой строке выведите одно целое число \(k\) (\(1\le k\)) — искомое минимальное количество частей, на которое нужно разрезать \(s\). Во второй строке через пробел выведите \(k\) строк \(s_1, s_2, \ldots, s_k\). Длина каждой строки должна быть положительной. Их конкатенация (последовательное склеивание) должна равняться \(s\), и все они должны быть хорошими. Если существует несколько решений, выведите любое из них. Примечание В первом примере, строка 1 вообще не была разрезана. Она является хорошей, поэтому условие выполнено. Во втором примере, 1 and 0 обе являются хорошими. Строка 10 хорошей не является, поэтому ответ действительно минимальный. В третьем примере, 100 и 011 обе являются хорошими. Строка 100011 хорошей не является, поэтому ответ действительно минимальный. | |
![]()
|
|
D. Преобразование строки
Строки
хэши
*2500
Пусть s — строка длины n, символы которой пронумерованы от 0 до n - 1, i и j — целые числа, 0 ≤ i < j < n. Определим функцию f следующим образом: f(s, i, j) = s[i + 1... j - 1] + r(s[j... n - 1]) + r(s[0... i]). Здесь s[p... q] — подстрока строки s, начинающаяся в позиции p и заканчивающаяся в позиции q (включительно); «+» — операция конкатенации строк; r(x) — строка, полученная записью символов строки x в обратном порядке. Если j = i + 1, то подстрока s[i + 1... j - 1] считается пустой. Заданы две строки a и b. Найдите такие числа i и j, что f(a, i, j) = b. Число i должно быть максимально возможным. Если при этом существует несколько допустимых значений j, выберите минимальное из них. Выходные данные Выведите два целых числа i, j — ответ на задачу. Если решения не существует, выведите «-1 -1» (без кавычек). | |
![]()
|
|
C. От S к T
реализация
Строки
*1300
У вас есть три строки \(s\), \(t\) и \(p\), состоящие из строчных букв латинского алфавита. Вы можете выполнять любое количество (возможно, нулевое) операций над этими строками. Каждая операция выглядит следующим образом: вы выбираете любой символ из строки \(p\), удаляете его из \(p\) и вставляете в любую позицию строки \(s\) (вы можете вставить этот символ куда захотите: в начало \(s\), в конец или между любыми двумя подряд идущими символами). Например, если \(p\) — это aba, и \(s\) — это de, тогда возможны следующие варианты (символ, удаленный из \(p\) и вставленный в \(s\), выделен жирным шрифтом): - aba \(\rightarrow\) ba, de \(\rightarrow\) ade;
- aba \(\rightarrow\) ba, de \(\rightarrow\) dae;
- aba \(\rightarrow\) ba, de \(\rightarrow\) dea;
- aba \(\rightarrow\) aa, de \(\rightarrow\) bde;
- aba \(\rightarrow\) aa, de \(\rightarrow\) dbe;
- aba \(\rightarrow\) aa, de \(\rightarrow\) deb;
- aba \(\rightarrow\) ab, de \(\rightarrow\) ade;
- aba \(\rightarrow\) ab, de \(\rightarrow\) dae;
- aba \(\rightarrow\) ab, de \(\rightarrow\) dea;
Вам нужно выполнить несколько (возможно, ноль) операций так, чтобы строка \(s\) стала равна строке \(t\). Определите, возможно ли это. Обратите внимание, что вам нужно ответить на \(q\) независимых запросов. Выходные данные Для каждого запросы выведите YES, если возможно превратить строку \(s\) в строку \(t\), и NO в противном случае. Ответ можете выводить в любом регистре (например, строки yEs, yes, Yes и YES будут распознаны как положительный ответ на запрос). Примечание В первом запросе возможна следующая последовательность операций: - \(s = \) ab, \(t = \) acxb, \(p = \) cax;
- \(s = \) acb, \(t = \) acxb, \(p = \) ax;
- \(s = \) acxb, \(t = \) acxb, \(p = \) a.
Во втрором запросе возможна следующая последовательность операций: - \(s = \) a, \(t = \) aaaa, \(p = \) aaabbcc;
- \(s = \) aa, \(t = \) aaaa, \(p = \) aabbcc;
- \(s = \) aaa, \(t = \) aaaa, \(p = \) abbcc;
- \(s = \) aaaa, \(t = \) aaaa, \(p = \) bbcc.
| |
![]()
|
|
E. Склеивание слов
Перебор
реализация
Строки
строковые суфф. структуры
хэши
*2000
У Амуга есть предложение, состоящее из \(n\) слов. Он хочет склеить это предложение в одно слово. Амуга не любит повторений, поэтому, когда он склеивает два слова в одно, он удаляет самый длинный префикс второго слова, который совпадает с суффиксом первого слова. Например, слова «sample» и «please» он склеивает в «samplease». Амуга хочет склеить предложение слева направо (т.е. сначала склеить первые два слова, потом склеить результат с третьим, и так далее). Напишите программу, которая найдет полученное после всех склеиваний слово. Выходные данные Выведите результат после всех склеиваний. | |
![]()
|
|
A. Важный экзамен
реализация
Строки
*900
Группа студентов написала экзамен в виде теста. Всего в группе было \(n\) студентов, а тест состоял из \(m\) вопросов, каждый из которых имел \(5\) вариантов ответа (A, B, C, D или Е). На каждый вопрос есть ровно один правильный ответ. Правильный ответ на \(i\)-й вопрос даёт \(a_i\) баллов. Неправильные ответы оцениваются нулём баллов. Студенты помнят, какие ответы они дали на экзамене, но не знают, какие ответы являются правильными. Они настроены достаточно оптимистично, а потому интересуются насколько большим может быть суммарный балл всех студентов группы. Выходные данные Выведите одно целое число — максимальный суммарный балл группы. Примечание В первом примере один из наиболее благоприятных правильных ответов это «ABCD», тогда суммарный балл будет равен \(16\). Во втором примере одним из оптимальных для студентов правильных ответов является «CCC». Тогда на каждый вопрос ответит ровно один студент и суммарный балл будет равен \(5 + 4 + 12 = 21\). | |
![]()
|
|
C. Вам задана WASD-строка...
дп
жадные алгоритмы
математика
Перебор
реализация
Строки
Структуры данных
*2100
У вас есть строка \(s\) — последовательность команд для робота. Робот находится в одной из клеток клетчатого поля. Он может выполнять следующие команды: - 'W' — переместиться на одну клетку вверх;
- 'S' — переместиться на одну клетку вниз;
- 'A' — переместиться на одну клетку влево;
- 'D' — переместиться на одну клетку вправо.
\(Grid(s)\) — прямоугольное поле минимальной площади, такое, что на нем можно выбрать стартовую позицию робота так, что при выполнении всей последовательностей комнад \(s\) робот не выйдет за пределы прямоугольника. Например, если \(s = \text{DSAWWAW}\), то \(Grid(s)\) — это прямоугольник \(4 \times 3\). - вы можете поместить робота в клетку \((3, 2)\);
- робот выполняет команду 'D' и перемещается в \((3, 3)\);
- робот выполняет команду 'S' и перемещается в \((4, 3)\);
- робот выполняет команду 'A' и перемещается в \((4, 2)\);
- робот выполняет команду 'W' и перемещается в \((3, 2)\);
- робот выполняет команду 'W' и перемещается в \((2, 2)\);
- робот выполняет команду 'A' и перемещается в \((2, 1)\);
- робот выполняет команду 'W' и перемещается в \((1, 1)\).
 У вас есть \(4\) дополнительных буквы: одна 'W', одна 'A', одна 'S' и одна 'D'. Вы можете вставить одну из них (либо не вставлять вообще) в любую позицию в строке \(s\) для минимизации площади \(Grid(s)\). Какую минимальную площадь \(Grid(s)\) вы можете получить? Выходные данные Выведите \(T\) строк, по одному числу в каждой строке. На каждый запрос выведите минимальное значение \(Grid(s)\), которое вы можете получить. Примечание В первом запросе вам нужно получить строку \(\text{DSAWW}\underline{D}\text{AW}\). Во втором и третьем запросах вы не можете уменьшить площадь \(Grid(s)\). | |
![]()
|
|
D. Выведите 1337-строку...
Комбинаторика
Конструктив
математика
Строки
*1900
Подпоследовательность — это последовательность, которую можно получить из другой последовательности путем удаления некоторых элементов, не меняя порядок оставшихся элементов. Вам задано число \(n\). Вам нужно найти такую последовательность \(s\), состоящую из цифр \(\{1, 3, 7\}\), что она имеет ровно \(n\) подпоследовательностей \(1337\). Например, последовательность \(337133377\) имеет \(6\) подпоследовательностей \(1337\): - \(337\underline{1}3\underline{3}\underline{3}7\underline{7}\) (нужно удалить второй и пятый символы);
- \(337\underline{1}\underline{3}3\underline{3}7\underline{7}\) (нужно удалить третий и пятый символы);
- \(337\underline{1}\underline{3}\underline{3}37\underline{7}\) (нужно удалить четверты и пятый символы);
- \(337\underline{1}3\underline{3}\underline{3}\underline{7}7\) (нужно удалить второй и шестой символы);
- \(337\underline{1}\underline{3}3\underline{3}\underline{7}7\) (нужно удалить третий и шестой символы);
- \(337\underline{1}\underline{3}\underline{3}3\underline{7}7\) (нужно удалить четвертый и шестой символы).
Обратите внимание, что длина последовательности \(s\) не должна превышать \(10^5\). Вам нужно ответить на \(t\) независимых запросов. Выходные данные На \(i\)-й запрос выведите строку \(s_i\) (\(1 \le |s_i| \le 10^5\)), состоящую из цифр \(\{1, 3, 7\}\). Строка \(s_i\) должна содержать ровно \(n_i\) подпоследовательностей \(1337\). Если подходящих строк несколько, выведите любую из них. | |
![]()
|
|
E. Вам задана строка...
Перебор
Строки
строковые суфф. структуры
*2400
Вам задана строка \(t\) и \(n\) строк \(s_1, s_2, \dots, s_n\). Все строки состоят из строчных букв латинского алфавита. Пусть \(f(t, s)\) равно количеству вхождений строки \(s\) в строку \(t\). Например, \(f('\text{aaabacaa}', '\text{aa}') = 3\), и \(f('\text{ababa}', '\text{aba}') = 2\). Посчитайте значение \(\sum\limits_{i=1}^{n} \sum\limits_{j=1}^{n} f(t, s_i + s_j)\), где \(s + t\) — конкатенация строк \(s\) и \(t\). Обратите внимание, что если есть две пары \(i_1\), \(j_1\) и \(i_2\), \(j_2\), такие что \(s_{i_1} + s_{j_1} = s_{i_2} + s_{j_2}\), вы должны учесть и \(f(t, s_{i_1} + s_{j_1})\), и \(f(t, s_{i_2} + s_{j_2})\). Выходные данные Выведите число — значение \(\sum\limits_{i=1}^{n} \sum\limits_{j=1}^{n} f(t, s_i + s_j)\). | |
![]()
|
|
D1. Кёрк и бинарная строка (лёгкая версия)
жадные алгоритмы
Перебор
Строки
*2000
Единственное отличие между легкой и сложной версиями — длины строк. Вы можете взламывать эту задачу только тогда, когда решите обе задачи. У Кёрка есть бинарная строка \(s\) (строка, содержащая только нули и единицы) длины \(n\), и он просит вас найти бинарную строку \(t\) такой же длины, для которой выполняются следующие условия: - Для любых \(l\) и \(r\) (\(1 \leq l \leq r \leq n\)) длина наибольшей неубывающей подпоследовательности в подстроке \(s_{l}s_{l+1} \ldots s_{r}\) равна длине наибольшей неубывающей подпоследовательности в подстроке \(t_{l}t_{l+1} \ldots t_{r}\);
- Количество нулей в строке \(t\) — максимально возможное.
Неубывающая подпоследовательность в строке \(p\) — это такая последовательность индексов \(i_1, i_2, \ldots, i_k\), что \(i_1 < i_2 < \ldots < i_k\) и \(p_{i_1} \leq p_{i_2} \leq \ldots \leq p_{i_k}\). Число \(k\) называется длиной подпоследовательности. Если существует несколько строк, удовлетворяющих условиям, то выведите любую. Выходные данные Выведите бинарную строку, для которой выполняются указанные условия. Если существует несколько таких строк, выведите любую. Примечание В первом примере: - Для подстрок длины \(1\) длина наибольшей неубывающей подпоследовательности равна \(1\);
- Для \(l = 1, r = 2\) наибольшая неубывающая подпоследовательность для подстроки \(s_{1}s_{2}\) — \(11\), для подстроки \(t_{1}t_{2}\) — \(01\);
- Для \(l = 2, r = 3\) наибольшая неубывающая подпоследовательность для подстроки \(s_{2}s_{3}\) — \(1\), для подстроки \(t_{2}t_{3}\) — \(1\);
- Для \(l = 1, r = 3\) наибольшая неубывающая подпоследовательность для подстроки \(s_{1}s_{3}\) — \(11\), для подстроки \(t_{1}t_{3}\) — \(00\);
Второй пример аналогичен первому. | |
![]()
|
|
D2. Кёрк и бинарная строка (сложная версия)
жадные алгоритмы
математика
Строки
Структуры данных
*2100
Единственное отличие между легкой и сложной версиями — длины строк. Вы можете взламывать эту задачу тогда, когда решите ее. Но предыдущую только тогда, когда решите обе задачи. У Кёрка есть бинарная строка \(s\) (строка, содержащая только нули и единицы) длины \(n\), и он просит вас найти бинарную строку \(t\) такой же длины, для которой выполняются следующие условия: - Для любых \(l\) и \(r\) (\(1 \leq l \leq r \leq n\)) длина наибольшей неубывающей подпоследовательности в подстроке \(s_{l}s_{l+1} \ldots s_{r}\) равна длине наибольшей неубывающей подпоследовательности в подстроке \(t_{l}t_{l+1} \ldots t_{r}\);
- Количество нулей в строке \(t\) — максимально возможное.
Неубывающая подпоследовательность в строке \(p\) — это такая последовательность индексов \(i_1, i_2, \ldots, i_k\), что \(i_1 < i_2 < \ldots < i_k\) и \(p_{i_1} \leq p_{i_2} \leq \ldots \leq p_{i_k}\). Число \(k\) называется длиной подпоследовательности. Если существует несколько строк, удовлетворяющих условиям, то выведите любую. Выходные данные Выведите бинарную строку, для которой выполняются указанные условия. Если существует несколько таких строк, выведите любую. Примечание В первом примере: - Для подстрок длины \(1\) длина наибольшей неубывающей подпоследовательности равна \(1\);
- Для \(l = 1, r = 2\) наибольшая неубывающая подпоследовательность для подстроки \(s_{1}s_{2}\) — \(11\), для подстроки \(t_{1}t_{2}\) — \(01\);
- Для \(l = 2, r = 3\) наибольшая неубывающая подпоследовательность для подстроки \(s_{2}s_{3}\) — \(1\), для подстроки \(t_{2}t_{3}\) — \(1\);
- Для \(l = 1, r = 3\) наибольшая неубывающая подпоследовательность для подстроки \(s_{1}s_{3}\) — \(11\), для подстроки \(t_{1}t_{3}\) — \(00\);
Второй пример аналогичен первому. | |
![]()
|
|
E. Очередная задача на матожидание
Комбинаторика
Строки
*3100
Даны целые числа \(n\), \(k\). Рассмотрим алфавит из \(k\) различных символов. Назовем красотой \(f(s)\) строки \(s\) количество таких индексов \(i\), \(1\le i<|s|\), что префикс \(s\) длины \(i\) равен суфиксу \(s\) длины \(i\). К примеру, красота строки \(abacaba\) равна \(2\), так как для \(i = 1, 3\) префикс и суфикс длины \(i\) совпадают. Рассмотрим все слова длины \(n\) в данном алфавите. Найдите матожидание \(f(s)^2\) выбранного случайно и равновероятно слова алфавита. Можно показать, что ее можно представить в виде \(\frac{P}{Q}\), где \(P\) и \(Q\) взаимно простые, и \(Q\) не делится на \(10^9 + 7\). Выведите \(P\cdot Q^{-1} \bmod 10^9 + 7\). Выходные данные Выведите единственное число — \(P\times Q^{-1} \bmod 10^9 + 7\). Примечание В первом примере, существует \(9\) слов \(2\) в алфавите размера \(3\) — \(aa\), \(ab\), \(ac\), \(ba\), \(bb\), \(bc\), \(ca\), \(cb\), \(cc\). У \(3\) из них красота \(1\) и у \(6\) из них красота \(0\), поэтому среднее значение равно \(\frac{1}{3}\). В третьем примере, существует только одно такое слово, и его красота равна \(99\), поэтому среднее значение равно \(99^2\). | |
![]()
|
|
G. Инди альбом
Деревья
поиск в глубину и подобное
Строки
строковые суфф. структуры
Структуры данных
хэши
*2700
Любимая экспериментальная инди группа Мишки недавно выпустила новый альбом! У песен этого альбома есть одна общая особенность. Название каждой песни \(s_i\) — одно из следующих типов: - \(1~c\) — одна строчная латинская буква;
- \(2~j~c\) — название \(s_j\) (\(1 \le j < i\)) с приписанной к нему справа одной строчной латинской буквой.
Песни пронумерованы от \(1\) до \(n\). Гарантируется, что первая песня всегда типа \(1\). Вове тоже интересен новый альбом, но он никак не может найти время его послушать целиком. Поэтому он решил задать Мишке несколько вопросов о нем, чтобы узнать, достойна ли какая-нибудь песня прослушивания. Все вопросы имеют одинаковый формат: - \(i~t\) — посчитать количество вхождений строки \(t\) в \(s_i\) (название \(i\)-й песни альбома), как подстроки, \(t\) состоит только из строчных латинских букв.
И хотя Мишка не понимает, какая польза от этой информации, он старается помочь Вове. Однако вопросов так много, что он не справляется. Помогите, пожалуйста, Мише ответить на все вопросы Вовы. Выходные данные На каждый вопрос выведите одно целое число — количество вхождений строки вопроса \(t\) в название \(i\)-й песни альбома, как подстроки. Примечание Названия песен из первого примера: - d
- da
- dad
- dada
- dadad
- dadada
- dadadad
- dadadada
- d
- do
- dok
- doki
- dokid
- dokido
- dokidok
- dokidoki
- do
- dok
- doki
- dokidoki
Тогда вхождения для каждого вопроса следующие: - строка «da» начинается в позициях \([1, 3, 5, 7]\) в названии «dadadada»;
- строка «dada» начинается в позициях \([1, 3, 5]\) в названии «dadadada»;
- строка «ada» начинается в позициях \([2, 4, 6]\) в названии «dadadada»;
- строка «dada» начинается в позициях \([1, 3]\) в названии «dadada»;
- нет вхождений строки «dada» в названии «dad»;
- строка «doki» начинается в позиции \([1]\) в названии «doki»;
- строка «ok» начинается в позиции \([2]\) в названии «doki»;
- строка «doki» начинается в позициях \([1, 5]\) в названии «dokidoki»;
- строка «doki» начинается в позиции \([1]\) в названии «dokidok»;
- строка «d» начинается в позиции \([1]\) в названии «d»;
- нет вхождений строки «a» в названии «d»;
- строка «doki» начинается в позициях \([1, 5]\) в названии «dokidoki».
| |
![]()
|
|
F. Коала и блокнот
графы
Деревья
кратчайшие пути
поиск в глубину и подобное
Строки
Структуры данных
*2600
Страна коал состоит из \(n\) городов и \(m\) двусторонних дорог, их соединяющих. Дороги пронумерованы от \(1\) до \(m\) в порядке входных данных. Гарантируется, что можно добраться от каждого города до любого другого города. Коала начинает путешествие из города \(1\). Каждый раз, когда он проходит по дороге, он записывает её номер в блокнот. Он не делает пробелов между числами, так что все записи склеятся в одно большое число. Перед тем как отправится в свой путь, Коала интересуется какое число может получится в блокноте в зависимости от конечного пункта. Для каждого возможного конечного пункта выясните, какое наименьшее число может для него получиться? Так как эти числа могут быть достаточно большими, вычислите их по модулю \(10^9+7\). Обратите внимание, что нужно вычислить остаток минимального возможного числа, не минимально возможный остаток. Выходные данные Выведите \(n - 1\) целое число — ответ для каждого города за исключением первого. \(i\)-е число должно быть равно наименьшему числу, которое получилось бы для конечной точки \(i+1\). Так как это число может быть достаточно большим, выведите его остаток по модулю \(10^9+7\). | |
![]()
|
|
B. Счастливое преобразование
Строки
*1500
Петя любит счастливые числа. Всем известно, что счастливыми являются положительные целые числа, в десятичной записи которых содержатся только счастливые цифры 4 и 7. Например, числа 47, 744, 4 являются счастливыми, а 5, 17, 467 — не являются. У Пети есть число из n цифр без лидирующих нулей. Он представил его в виде массива цифр d (нумерация с 1, начиная от старших цифр). Петя хочет k раз выполнить следующую операцию: найти минимальное x (1 ≤ x < n) такое, что dx = 4 и dx + 1 = 7, если x нечетное, то присвоить dx = dx + 1 = 4, иначе присвоить dx = dx + 1 = 7. Учтите, что если x не нашлось, то операция засчитывается как выполненная, и массив не меняется вообще. Вам дано исходное число (в виде массива цифр) и число k. Помогите Пете узнать результат выполнения k операций. Выходные данные В единственной строке выведите без пробелов результат — число после выполнения k операций. Примечание В первом примере число меняется в следующей последовательности: 4727447 → 4427447 → 4427477 → 4427447 → 4427477. Во втором примере: 4478 → 4778 → 4478. | |
![]()
|
|
F. kotlinkotlinkotlinkotlin...
*особая задача
графы
реализация
Строки
*2300
Поликарпу очень нравится писать слово «kotlin». Он выписал это слово несколько раз подряд без пробелов. Например, у него могла получиться такая строка «kotlinkotlinkotlinkotlin». Полученную строку Поликарп порезал на \(n\) частей и перемешал полученные строки. В результате в настоящий момент у него есть \(n\) строк \(s_1, s_2, \dots, s_n\) таких, что их можно объединить в одну строку вида «kotlinkotlin...kotlin», расположив их в подходящем порядке. Помогите Поликарпу найти такой порядок записи для строк \(s_1, s_2, \dots, s_n\), что если выписать все эти строки в этом порядке, то получится повторённое один или более раз слово «kotlin». Обратите внимание, что необходимо использовать все заданные строки и при этом каждую ровно по одному разу. Выходные данные Выведите \(n\) различных целых чисел \(p_1, p_2, \dots, p_n\) (\(1 \le p_i \le n\)), где \(p_i\) это порядковый номер (индекс) строки, которая должна идти \(i\)-й в искомом объединении. Иными словами, результат конкатенации \(s_{p_1}+s_{p_2}+\dots+s_{p_n}\) должен иметь вид «kotlinkotlin...kotlin». Если решений, выведите любое из них. | |
![]()
|
|
F. Нестабильная сортировка строки
графы
жадные алгоритмы
поиск в глубину и подобное
реализация
снм
Строки
Структуры данных
*2100
Авторы загадали строку \(s\), состоящую из \(n\) строчных букв латинского алфавита. Вам задано две перестановки ее индексов (не обязательно одинаковых) \(p\) и \(q\) (обе длины \(n\)). Напомним, что перестановкой называется массив длины \(n\), содержащий каждое целое число от \(1\) до \(n\) ровно один раз. Для всех \(i\) от \(1\) до \(n-1\) выполняются следующие свойства: \(s[p_i] \le s[p_{i + 1}]\) и \(s[q_i] \le s[q_{i + 1}]\). Это значит, что если вы выпишете все символы \(s\) в порядке индексов в перестановке, результирующая строка получится отсортированной в неубывающем порядке. Ваша задача — восстановить любую строку \(s\) длины \(n\), состоящую хотя бы из \(k\) различных строчных букв латинского алфавита, которая подходит к заданным перестановкам. Если существует несколько возможных ответов, вы можете вывести любой. Выходные данные Если невозможно найти подходящую строку, выведите «NO» в первой строке. Иначе выведите «YES» в первой строке и строку \(s\) во второй строке. Она должна состоять ровно из \(n\) строчных букв латинского алфавита, содержать хотя бы \(k\) различных символов и подходить заданным перестановкам. Если существует несколько возможных ответов, вы можете вывести любой. | |
![]()
|
|
A. Префиксы
Строки
*800
У Николая есть строка \(s\) четной длины \(n\), состоящая из латинских букв 'a' и 'b'. Позиции букв пронумерованы от \(1\) до \(n\). Он хочет изменить свою строку таким образом, чтобы в любом её префиксе четной длины было поровну букв 'a' и 'b'. Для этого Николай может производить следующую операцию любое количество раз (возможно, нулевое): выбрать позицию в своей строке и заменить букву на этой позиции на другую (то есть заменить букву 'a' на букву 'b' или заменить букву 'b' на букву 'a'). Использовать какие-либо другие буквы, кроме 'a' и 'b', Николай не может. Префиксом строки \(s\) длины \(l\) (\(1 \le l \le n\)) называется строка \(s[1..l]\). Например, для строки \(s=\)«abba» существует два префикса чётной длины. Первый из них — это \(s[1\dots2]=\)«ab», второй из них — это \(s[1\dots4]=\)«abba». Оба префикса содержат одинаковое количество букв 'a' и 'b'. Ваша задача — посчитать минимальное количество операций, которое должен сделать Николай со строкой \(s\), чтобы в любом ее префиксе четной длины строки стало поровну букв 'a' и 'b'. Выходные данные В первую строку выведите минимальное количество операций, которые Николай должен произвести со строкой \(s\), чтобы в любом префиксе ее префиксе четной длины стало поровну букв 'a' и 'b'. Во вторую строку выведите строку Николая после проведения им всех операций. Если ответов несколько, разрешается вывести любой из них. Примечание В первом примере Николай должен произвести две операции. Например, он может заменить первую букву 'b' на букву 'a' и заменить последнюю букву 'b' на букву 'a'. Во втором примере не нужно заменять никакие буквы, так как в любом префиксе четной длины исходной строки содержится поровну букв 'a' и 'b'. | |
![]()
|
|
C. Periodic integer number
реализация
Строки
*1700
Alice became interested in periods of integer numbers. We say positive \(X\) integer number is periodic with length \(L\) if there exists positive integer number \(P\) with \(L\) digits such that \(X\) can be written as \(PPPP…P\). For example: \(X = 123123123\) is periodic number with length \(L = 3\) and \(L = 9\) \(X = 42424242\) is periodic number with length \(L = 2,L = 4\) and \(L = 8\) \(X = 12345\) is periodic number with length \(L = 5\) For given positive period length \(L\) and positive integer number \(A\), Alice wants to find smallest integer number \(X\) strictly greater than \(A\) that is periodic with length L. Output One positive integer number representing smallest positive number that is periodic with length \(L\) and is greater than \(A\). Note In first example 124124 is the smallest number greater than 123456 that can be written with period L = 3 (P = 124). In the second example 100100 is the smallest number greater than 12345 with period L = 3 (P=100) | |
![]()
|
|
A. Карточки
реализация
сортировки
Строки
*800
Когда Серёже было три года, ему подарили на день рождения набор карточек с буквами. С их помощью было записано словами любимое число мамы мальчика в двоичной системе счисления. Серёжа тотчас же принялся с ними играть, но так как не умел читать, перемешал их в случайном порядке. Папа решил привести в порядок карточки. Помогите ему восстановить исходное число при условии, что оно было максимально возможным. Выходные данные Выведите максимально возможное число в двоичной системе счисления. Выводите двоичные цифры, разделяя их пробелами. Лидирующие нули допустимы. Примечание В первом примере правильная последовательность букв — это «zero». Во втором примере правильная последовательность букв — это «oneonezero». | |
![]()
|
|
C. Игра в подстроки на уроке
жадные алгоритмы
игры
Строки
*1300
Миша и Аня сидят на скучном уроке. Чтобы хоть как-то скрасить ожидание перемены, они придумали интересную игру. Для игры необходима лишь строка \(s\) и число \(k\) (\(0 \le k < |s|\)). Игра начинается с того, что на строке \(s\) отмечается подстрока длины 1, ее левая граница \(l\) и правая граница \(r\) равны \(k\) (то есть вначале игры \(l=r=k\)). Далее игроки ходят по очереди, расширяя подстроку по следующим правилам: - Игрок выбирает индексы \(l^{\prime}\) и \(r^{\prime}\) такие, что \(l^{\prime} \le l\), \(r^{\prime} \ge r\) и \(s[l^{\prime}, r^{\prime}]\) лексикографически меньше \(s[l, r]\). После этого изменяет значения \(l\) и \(r\) следующим образом: \(l := l^{\prime}\), \(r := r^{\prime}\).
- Аня ходит первой.
- Проигрывает тот, кто не может сделать ход.
Напомним, что подстрокой \(s[l, r]\) (\(l \le r\)) строки \(s\) будем называть непрерывную подпоследовательность символов начинающуюся в позиции \(l\) и заканчивающуюся в позиции \(r\). Например «ehn» — подстрока (\(s[3, 5]\)) строки «aaaehnsvz», а «ahz» — нет. Миша и Аня играли в игру так увлеченно, что не заметили как к ним подошел учитель. К большому удивлению обоих, он не стал их отчитывать, а сказал, что может определить победителя до начала игры, зная лишь \(s\) и \(k\)! К сожалению, Миша и Аня не разбираются в теории игр, поэтому попросили Вас написать программу, которая по заданной \(s\) определяет победителя для всех возможных \(k\). Выходные данные Выходные данные должны содержать \(|s|\) строк. В строке номер \(i\) выведите имя победителя игры (выведите Ann или Mike) со строкой \(s\), для \(k = i\), при условии, что Аня и Миша играют оптимально. | |
![]()
|
|
B. Уравнивание строк
Строки
*1000
Вам заданы две строки \(s\) и \(t\) одинаковой длины, состоящие из строчных букв латинского алфавита. Вы можете выполнять любое (возможно нулевое) количество операций над этими строками. В течении каждой операции вы выбираете два соседних символа в любой строке и присваиваете значение первого символа значению второго или наоборот. Например, если \(s\) равна «acbc» вы можете получить следующие строки за одну операцию: - «aabc» (если выполните присвоение \(s_2 = s_1\));
- «ccbc» (если выполните присвоение \(s_1 = s_2\));
- «accc» (если выполните присвоение \(s_3 = s_2\) или \(s_3 = s_4\));
- «abbc» (если выполните присвоение \(s_2 = s_3\));
- «acbb» (если выполните присвоение \(s_4 = s_3\));
Обратите внимание, что такие же операции вы можете применять и к строке \(t\). Вам нужна выполнить несколько (возможно ноль) таких операций, чтобы строка \(s\) стала равна \(t\). Определите, возможно ли это. Обратите внимание, что вам нужно ответить на \(q\) независимых запросов. Выходные данные На каждый запрос выведите «YES», если возможно сделать строку \(s\) равной \(t\), и «NO» в обратном случае. Вы можете выводить ответ в любом регистре (например, строки «yEs», «yes», «Yes» и «YES» будут учтены как положительный ответ). Примечание В первом запросе вы можете применить две операции \(s_1 = s_2\) (после неё \(s\) превратится в «aabb») и \(t_4 = t_3\) (после нее \(t\) превратится в «aabb»). Во втором запросе строки равны изначально, а значит ответ «YES». В третьем запросе вы не можете сделать строки \(s\) и \(t\) равными. Таким образом, ответ «NO». | |
![]()
|
|
A. Перестановка на простоту
реализация
Строки
теория чисел
*1300
Дана строка s, состоящая из строчных букв латинского алфавита. Будем обозначать длину строки |s|. Нумерация символов в этой строке начинается с 1. Определите, возможно ли в строке s так переставить символы, чтобы для любого простого числа p ≤ |s| и для любого целого i в диапазоне от 1 до |s| / p (включительно) выполнялось условие sp = sp × i. В случае положительного ответа найдите один из способов так переставить символы. Выходные данные Если в строке можно переставить символы так, чтобы выполнялись перечисленные выше условия, то выведите в первой строке «YES» (без кавычек) и во второй — одну из возможных получившихся строк. Если такая перестановка невозможна, выведите одну строку «NO». Примечание В первом примере подойдет любая из шести возможных строк «abc», «acb», «bac», «bca», «cab» или «cba». Во втором примере никакая перестановка букв не будет выполнять условие при p = 2 (s2 = s4). Третий тест — подойдет любая строка, в которой символ «y» не стоит на позиции 2, 3, 4, 6. | |
![]()
|
|
E. Middle-Out
жадные алгоритмы
Конструктив
Строки
*2200
Вдохновением для задачи послужила история компании Pied Piper. После анонса технологии Nucleus со стороны конкурирующей компании Hooli Ричард при содействии друзей изобрёл принципиально новый подход к сжатию: «из середины наружу». Вам даны две строки \(s\) и \(t\) одинаковой длины \(n\). Пронумеруем их символы то \(1\) до \(n\) слева направо (т.е. от начала к концу) За один ход вы можете сделать следующую последовательность действий: - выбрать произвольный индекс \(i\) (\(1 \le i \le n\)),
- передвинуть \(i\)-й символ строки \(s\) с текущей позиции в начало строки или передвинуть \(i\)-й символ строки \(s\) с текущей позиции в конец строки.
Заметим, что длина строки \(s\) в результате хода не поменяется. Вы можете применить ход только к строке \(s\). Например, если \(s=\)«test», то за один ход можно получить: - если \(i=1\) и вы перемещаете символ в начало, то результат будет равен «test» (строка не изменяется),
- если \(i=2\) и вы перемещаете символ в начало, то результат будет равен «etst»,
- если \(i=3\) и вы перемещаете символ в начало, то результат будет равен «stet»,
- если \(i=4\) и вы перемещаете символ в начало, то результат будет равен «ttes»,
- если \(i=1\) и вы перемещаете символ в конец, то результат будет равен «estt»,
- если \(i=2\) и вы перемещаете символ в конец, то результат будет равен «tste»,
- если \(i=3\) и вы перемещаете символ в конец, то результат будет равен «tets»,
- если \(i=4\) и вы перемещаете символ в конец, то результат будет равен «test» (строка не изменяется).
Вы хотите преобразовать строку \(s\) в строку \(t\). Какое минимальное количество ходов для этого потребуется? Если преобразовать \(s\) в \(t\) невозможно, выведите -1. Выходные данные Для каждого набора входных данных выведите минимальное количество ходов, которое нужно чтобы превратить \(s\) в \(t\) или -1, если это сделать невозможно. Примечание В первом примере, ходы в одном из оптимальных ответов выглядят следующим образом: - в первом наборе: \(s=\)«iredppipe», \(t=\)«piedpiper»: «iredppipe» \(\rightarrow\) «iedppiper» \(\rightarrow\) «piedpiper»;
- во втором наборе: \(s=\)«estt», \(t=\)«test»: «estt» \(\rightarrow\) «test»;
- в третьем наборе: \(s=\)«tste», \(t=\)«test»: «tste» \(\rightarrow\) «etst» \(\rightarrow\) «test».
| |
![]()
|
|
D. AB-строка
Бинарный поиск
дп
Комбинаторика
Строки
*1900
Строка \(t_1t_2 \dots t_k\) является хорошей, если каждый символ этой строки принадлежит хотя бы одному палиндрому длины больше 1. Палиндром — это строка, читающаяся одинаково от первого символа к последнему и от последнего символа к первому. Например, строки A, BAB, ABBA, BAABBBAAB являются палиндромами, а строки AB, ABBBAA, BBBA — нет. Например, хорошим являются строки: - \(t\) = AABBB (символы \(t_1\), \(t_2\) принадлежат палиндрому \(t_1 \dots t_2\), а символы \(t_3\), \(t_4\), \(t_5\) — палиндрому \(t_3 \dots t_5\));
- \(t\) = ABAA (символы \(t_1\), \(t_2\), \(t_3\) принадлежат палиндрому \(t_1 \dots t_3\), а символ \(t_4\) — палиндрому \(t_3 \dots t_4\));
- \(t\) = AAAAA (все символы принадлежат палиндрому \(t_1 \dots t_5\));
Вам задана строка \(s\) длины \(n\), состоящая только из букв A и B. Посчитайте количество хороших подстрок строки \(s\). Выходные данные Выведите одно число — количество хороших подстрок строки \(s\). Примечание Первая строка содержит шесть хороших подстрок: \(s_1 \dots s_2\), \(s_1 \dots s_4\), \(s_1 \dots s_5\), \(s_3 \dots s_4\), \(s_3 \dots s_5\) и \(s_4 \dots s_5\). Вторая строка содержит две хороших подстроки: \(s_1 \dots s_2\), \(s_1 \dots s_3\) and \(s_2 \dots s_3\) | |
![]()
|
|
B1. Обмен символов (упрощённая версия)
Строки
*1000
Эта задача отличается от усложнённой версии. В этой версии задачи Уджана сделает ровно один обмен. Вы можете взламывать эту задачу только тогда, когда решите обе задачи. После долгих страданий и многих неуспешных попыток Уджан решил снова попробовать прибраться в своём доме. Вначале он решил привести в порядок свои строки. У Уджана есть две различные строки \(s\) и \(t\) длины \(n\), которые содержат только строчные буквы английского алфавита. Он хочет сделать их одинаковыми. Так как Уджан ленивый, он выполнит следующую операцию ровно один раз: он выбирает два индекса \(i\) и \(j\) (\(1 \le i,j \le n\), значения \(i\) и \(j\) могут как совпадать, так и различаться), и меняет местами буквы \(s_i\) и \(t_j\). Получится ли у него задуманное? Обратите внимание, что он должен применить эту операцию ровно один раз. Он не может ее не cделать. Выходные данные Для каждого набора входных данных выведите «Yes», если Уджан может сделать строки одинаковыми, и «No» в противоположном случае. Вы можете выводить каждую букву в любом регистре (строчную или заглавную). Примечание В первом наборе входных данных примера Уджан может поменять местами буквы \(s_1\) и \(t_4\), получив слово «house». Во втором наборе входных данных примера нельзя сделать строки одинаковыми, сделав ровно один обмен \(s_i\) и \(t_j\). | |
![]()
|
|
B2. Обмен символов (усложнённая версия)
Строки
*1600
Эта задача отличается от упрощённой версии. В этой версии задачи Уджана может сделать не более \(2n\) обменов. Кроме того, \(k \le 1000, n \le 50\) и необходимо вывести сами обмены. Вы можете взламывать эту задачу тогда, когда решите ее. Но предыдущую только тогда, когда решите обе задачи. После долгих страданий и многих неуспешных попыток Уджан решил снова попробовать прибраться в своём доме. Вначале он решил привести в порядок свои строки. У Уджана есть две различные строки \(s\) и \(t\) длины \(n\), которые содержат только строчные буквы английского алфавита. Он хочет сделать их одинаковыми. Так как Уджан ленивый, он выполнит следующую операцию не более \(2n\) раз: он выбирает два индекса \(i\) и \(j\) (\(1 \le i,j \le n\), значения \(i\) и \(j\) могут как совпадать, так и различаться), и меняет местами буквы \(s_i\) и \(t_j\). Цель Уджан сделать строки \(s\) и \(t\) равными. Уджану не нужно минимизировать количество операций. Его устроит любой способ, который содержит \(2n\) или менее операций. Выходные данные Для каждого набора входных данных выведите «Yes», если Уджан может сделать строки одинаковыми за \(2n\) или менее операций, и «No» в противоположном случае. Вы можете выводить каждую букву в любом регистре (строчную или заглавную). В случае положительного ответа в следующую строку выведите целое число \(m\) (\(1 \le m \le 2n\)), где \(m\) — количество операций в ответе. Затем выведите \(m\) строк, где каждая строка содержит два целых числа \(i, j\) (\(1 \le i, j \le n\)), которые обозначают что во время соответствующей операции Уджан обменивает символы \(s_i\) и \(t_j\). Вам не нужно минимизировать количество операций. Любой способ сделать это за \(2n\) или менее операций является корректным ответом. | |
![]()
|
|
A. Сломанная клавиатура
Перебор
Строки
*1000
Недавно Поликарп заметил, что некоторые кнопки на его клавиатуре неисправны. Клавиатура Поликарпа содержит \(26\) кнопок (по кнопке на каждую букву латинского алфавита). Каждая кнопка либо работает исправно, либо сломана. Для проверки исправности клавиатуры Поликарп понажимал на некоторые кнопки и строка \(s\) появилась на экране. Когда Поликарп нажимает на кнопку \(c\), происходит одно из двух событий: - если кнопка работает исправно, то в конец строки просто добавляется символ \(c\);
- если кнопка работает неисправно, то ровно два символа \(c\) добавляется в конец строки.
Например предположим, что кнопки a и c работают корректно, а кнопка b неисправна. Если Поликарп нажмет на кнопки в порядке a, b, a, c, a, b, a, то строка будет меняться следующим образом: a \(\rightarrow\) abb \(\rightarrow\) abba \(\rightarrow\) abbac \(\rightarrow\) abbaca \(\rightarrow\) abbacabb \(\rightarrow\) abbacabba. Вам задана строка \(s\), которая появилась на экране после нажатия некоторых кнопок. Помогите Поликарпу определить, какие кнопки точно работают корректно (что означает, что эта строка не могла появиться на экране, если бы эти кнопки работали некорректно). Обратите внимание, что кнопки не могут ломаться или чиниться в процессе набора текста. Каждая кнопка изначально либо неисправна, либо работает корректно. Выходные данные Для каждого набора входных данных выведите строку \(res\). Эта строка \(res\) должна содержать все кнопки, которые точно работают корректно в алфавитном порядке, без пробелов. Если нет таких кнопок, то строка \(res\) должна быть пустой. | |
![]()
|
|
B. Двоичные палиндромы
жадные алгоритмы
Строки
*1400
Палиндром — это строка \(t\), которая одинаково читается как слева направо, так и справа налево (формально, \(t[i] = t[|t| + 1 - i]\) для всех \(i \in [1, |t|]\)). Здесь и далее \(|t|\) обозначает длину строки \(t\). Например, строки 010, 1001 и 0 — палиндромы. У вас есть \(n\) двоичных строк \(s_1, s_2, \dots, s_n\) (каждая \(s_i\) состоит только из нулей и/или единиц). Вы можете менять местами любую пару символов любое количество раз (возможно, ноль раз). Символы могут быть как из одной строки, так и из разных строк — ограничений нет. Формально, одна операция обмена выглядит следующим образом: - вы выбираете четыре целых числа \(x, a, y, b\), такие что \(1 \le x, y \le n\), \(1 \le a \le |s_x|\) и \(1 \le b \le |s_y|\) (где \(x\) и \(y\) — номера строк, а \(a\) и \(b\) — позиции в соответствующих строках \(s_x\) и \(s_y\)),
- меняете местами символы \(s_x[a]\) и \(s_y[b]\).
Какое максимальное количество строк вы сможете сделать палиндромами одновременно? Выходные данные Выведите \(Q\) чисел — по одному на набор входных данных. \(i\)-е число — это максимальное количество палиндромов, которые вы сможете получить одновременно, применяя операцию обмена символов ноль или более раз на строках из \(i\)-го набора. Примечание В первом наборе \(s_1\) — уже палиндром, поэтому ответ равен \(1\). Во втором наборе вы не можете сделать все три строки палиндромами одновременно, но вы сможете сделать палиндромами любую пару из них. Например, сделаем \(s_1 = \text{0110}\), \(s_2 = \text{111111}\) и \(s_3 = \text{010000}\). В третьем наборе вы можете сделать обе строки палиндромами. Например, \(s_1 = \text{11011}\) и \(s_2 = \text{100001}\). В последнем наборе \(s_2\) — палиндром и вы можете сделать \(s_1\) палиндромом, например, поменяв местами \(s_1[2]\) и \(s_1[3]\). | |
![]()
|
|
D. Find String in a Grid
Деревья
дп
Строки
Структуры данных
*3000
You have a grid \(G\) containing \(R\) rows (numbered from \(1\) to \(R\), top to bottom) and \(C\) columns (numbered from \(1\) to \(C\), left to right) of uppercase characters. The character in the \(r^{th}\) row and the \(c^{th}\) column is denoted by \(G_{r, c}\). You also have \(Q\) strings containing uppercase characters. For each of the string, you want to find the number of occurrences of the string in the grid. An occurrence of string \(S\) in the grid is counted if \(S\) can be constructed by starting at one of the cells in the grid, going right \(0\) or more times, and then going down \(0\) or more times. Two occurrences are different if the set of cells used to construct the string is different. Formally, for each string \(S\), you would like to count the number of tuples \(\langle r, c, \Delta r, \Delta c \rangle\) such that: - \(1 \le r \le R\) and \(r \le r + \Delta r \le R\)
- \(1 \le c \le C\) and \(c \le c + \Delta c \le C\)
- \(S = G_{r, c} G_{r, c + 1} \dots G_{r, c + \Delta c} G_{r + 1, c + \Delta c} \dots G_{r + \Delta r, c + \Delta c}\)
Output For each query in the same order as input, output in a line an integer representing the number of occurrences of the string in the grid. Note Explanation for the sample input/output #1 - There are \(2\) occurrences of "ABC", represented by the tuples \(\langle 1, 1, 1, 1 \rangle\) and \(\langle 1, 1, 0, 2 \rangle\).
- There are \(3\) occurrences of "BC", represented by the tuples \(\langle 1, 2, 0, 1 \rangle\), \(\langle 1, 2, 1, 0 \rangle\), and \(\langle 2, 1, 0, 1 \rangle\).
- There is \(1\) occurrence of "BD", represented by the tuple \(\langle 2, 1, 1, 0 \rangle\).
- There is no occurrence of "AC".
- There are \(2\) occurrences of "A", represented by the tuples \(\langle 1, 1, 0, 0 \rangle\) and \(\langle 3, 2, 0, 0 \rangle\).
| |
![]()
|
|
F. Приравнивание двух строк
Конструктив
сортировки
Строки
*2000
Задано две строки \(s\) и \(t\), обе длины \(n\) и обе состоят из строчных букв латинского алфавита. За один ход вы можете выбрать любую длину \(len\) от \(1\) до \(n\) и выполнить следующую операцию: - Выбрать любую непрерывную подстроку строки \(s\) длины \(len\) и перевернуть ее;
- в тот же момент выбрать любую непрерывную подстроку строки \(t\) длины \(len\) и также перевернуть ее.
Заметьте, что в течение одного хода вы переворачиваете ровно одну подстроку строки \(s\) и ровно одну подстроку строки \(t\). Также заметьте, что границы подстрок, которые вы переворачиваете в \(s\) и в \(t\), могут быть различны, единственное ограничение — вы должны переворачивать подстроки одинаковых длин. Например, если \(len=3\) и \(n=5\), то вы можете перевернуть \(s[1 \dots 3]\) и \(t[3 \dots 5]\), \(s[2 \dots 4]\) и \(t[2 \dots 4]\), но не \(s[1 \dots 3]\) и \(t[1 \dots 2]\). Ваша задача — сказать, можно ли сделать строки \(s\) и \(t\) одинаковыми после какой-то (возможно, пустой) последовательности ходов. Вам необходимо ответить на \(q\) независимых наборов входных данных. Выходные данные Для каждого набора входных данных выведите ответ на него — «YES» (без кавычек), если возможно сделать строки \(s\) и \(t\) равными после какой-то (возможно, пустой) последовательности ходов и «NO» иначе. | |
![]()
|
|
C. Задоминированный подмассив
жадные алгоритмы
реализация
сортировки
Строки
*1200
Назовем массив \(t\) задоминированным значением \(v\) в следующем случае. Во-первых, массив \(t\) должен состоять хотя бы из \(2\) элементов. Теперь, давайте посчитаем количество вхождений каждого числа \(num\) в \(t\) и назовем данное значение \(occ(num)\). Тогда, \(t\) — задоминирована (числом \(v\)) тогда (и только тогда), когда \(occ(v) > occ(v')\) для любого другого числа \(v'\). Например, массивы \([1, 2, 3, 4, 5, 2]\), \([11, 11]\) и \([3, 2, 3, 2, 3]\) задоминированы (числами \(2\), \(11\) и \(3\) соответственно), но массивы \([3]\), \([1, 2]\) и \([3, 3, 2, 2, 1]\) — нет. Небольшая заметка: так как любой массив может быть задоминирован только одним числом, то мы можем не уточнять данное число и просто говорить, что массив либо задоминирован, либо нет. Вам задан массив \(a_1, a_2, \dots, a_n\). Определите его самый короткий задоминированный подмассив, либо скажите, что таких нет. Подмассив массива \(a\) — это последовательная часть массива \(a\), другими словами массив \(a_i, a_{i + 1}, \dots, a_j\) для некоторых \(1 \le i \le j \le n\). Выходные данные Выведите \(T\) чисел — по одному на набор входных данных. Для каждого набора выведите единственное целое число — длину самого короткого задоминированного подмассива либо \(-1\), если таких подмассивов нет. Примечание В первом наборе входных данных, нет подмассивов длины хотя бы \(2\), а потому ответ равен \(-1\). Во втором наборе, весь массив задоминирован (числом \(1\)) и это единственный задоминированный подмассив. В третьем наборе, подмассив \(a_4, a_5, a_6\) — самый короткий задоминированный подмассив. В четвертом наборе, все подмассивы длины больше, чем один, задоминированы. | |
![]()
|
|
B. Пароль
Бинарный поиск
дп
Строки
строковые суфф. структуры
хэши
*1700
Астерикс, Обеликс и их временные спутники Суффикс и Префикс наконец нашли храм Гармонии. Однако его двери были прочно заперты, и даже Обеликсу было не под силу их открыть. Чуть позже они обнаружили строку s, которая была высечена в камне над воротами храма. Астерикс предположил, что это пароль для входа в храм, и громко вслух произнес эту надпись. Однако ничего не произошло. Тогда Астерикс предположил, что паролем является некоторая подстрока t строки s. Префикс считал, что строка t является началом строки s. Суффикс считал, что строки t должна быть концом строки s. Обеликс же посчитал, что t должна находиться где-то внутри строки s, то есть не являться ни ее началом, ни ее концом. Астерикс выбрал подстроку t так, чтобы угодить всем своим спутникам. Кроме того, из всех допустимых вариантов Астерикс выбрал наиболее длинный (потому что Астерикс любит длинные строки). Когда Астерикс произнес строку t — двери храма открылись. Вам известна строка s. Найдите строку t или определите, что таких строк не существует, а все написанное выше — всего лишь легенда. Выходные данные Выведите строку t. Если подходящей строки t не существует — выведите «Just a legend» без кавычек. | |
![]()
|
|
L. Lexicography
Конструктив
Строки
*1800
Lucy likes letters. She studied the definition of the lexicographical order at school and plays with it. At first, she tried to construct the lexicographically smallest word out of given letters. It was so easy! Then she tried to build multiple words and minimize one of them. This was much harder! Formally, Lucy wants to make \(n\) words of length \(l\) each out of the given \(n \cdot l\) letters, so that the \(k\)-th of them in the lexicographic order is lexicographically as small as possible. Output Output \(n\) words of \(l\) letters each, one per line, using the letters from the input. Words must be sorted in the lexicographic order, and the \(k\)-th of them must be lexicographically as small as possible. If there are multiple answers with the smallest \(k\)-th word, output any of them. | |
![]()
|
|
A. Длинное красивое число
жадные алгоритмы
Конструктив
реализация
Строки
*1700
Вам дано положительное целое число \(x\) из \(n\) цифр \(a_1, a_2, \ldots, a_n\), которые составляют его десятичную запись в порядке слева направо. А также, вам дано положительное целое число \(k < n\). Назовем число \(b_1, b_2, \ldots, b_m\) красивым если \(b_i = b_{i+k}\) для всех \(i\), что \(1 \leq i \leq m - k\). Вам необходимо найти минимальное красивое целое число \(y\), что \(y \geq x\). Выходные данные В первой строке выведите одно целое число \(m\): количество цифр в \(y\). В следующей строке выведите \(m\) цифр \(b_1, b_2, \ldots, b_m\) (\(b_1 \neq 0\), \(0 \leq b_i \leq 9\)): цифры \(y\). | |
![]()
|
|
F. Восхитительные подстроки
математика
Строки
*2600
Назовем бинарную строку \(s\) восхитительной, если она содержит по крайней мере \(1\) символ 1 и длина строки делится на количество 1 в ней. К примеру, 1, 1010, 111 являются восхитительными, но 0, 110, 01010 не являются. Вам дана бинарная строка \(s\). Посчитайте количество ее восхитительных подстрок. Строка \(a\) является подстрокой \(b\), если \(a\) может быть получена из \(b\) удалением нескольких (возможно, ни одного или всех) символов из начала и нескольких (возможно, ни одного или всех) символов из конца. Выходные данные Выведите единственное число — количество восхитительных подстрок \(s\). Примечание В первом примере, все подстроки \(s\) являются восхитительными. Во втором примере, есть следующие восхитительные подстроки \(s\): 1 (\(2\) раза), 01 (\(2\) раза), 10 (\(2\) раза), 010 (\(2\) раза), 1010, 0101 В третьем примере, ни одна подстрока не является восхитительной. | |
![]()
|
|
F. Две скобочные последовательности
дп
Строки
*2200
Вам задано две скобочные последовательности (не обязательно правильные) \(s\) и \(t\), состоящие только из символов '(' и ')'. Вы хотите построить кратчайшую правильную скобочную последовательность, которая содержит обе заданные скобочные последовательности в качестве подпоследовательностей (не обязательно подряд идущих). Напомним, что такое правильная скобочная последовательность: - () является правильной скобочной последовательностью;
- если \(S\) является правильной скобочной последовательностью, то (\(S\)) является правильной скобочной последовательностью;
- если \(S\) и \(T\) являются правильными скобочными последовательностями, то \(ST\) (конкатенация \(S\) и \(T\)) тоже является правильной скобочной последовательностью.
Напомним, что подпоследовательностью строки \(s\) называется такая строка \(t\), которая получается из \(s\) при помощи удаления некоторого (возможно, нулевого) количества символов. Например, «coder», «force», «cf» и «cores» являются подпоследовательностями «codeforces», а «fed» и «z» — нет. Выходные данные Выведите одну строку — кратчайшую правильную скобочную последовательность, которая содержит обе заданные скобочные последовательности как подпоследовательности (не обязательно подряд идущие). Если существует несколько возможных ответов, выведите любой. | |
![]()
|
|
A. Хеширование перемешиванием
Перебор
реализация
Строки
*1000
Поликарп недавно создал новый веб сервис. Как в любом современном сервисе, в нем есть возможность авторизации. А это автоматически подразумевает угрозы безопасности. Поликарп решил сохранять хеш пароля, полученный по следующему алгоритму: - получить пароль \(p\), состоящий из строчных латинских букв, и перемешать буквы в нем, чтобы получить \(p'\) (\(p'\) может остаться равным \(p\));
- построить две случайные строки, состоящие из строчных латинских букв, \(s_1\) и \(s_2\) (любая из них может быть пустой);
- полученный хеш \(h = s_1 + p' + s_2\), где сложение — это склеивание строк.
Например, пусть пароль будет \(p =\) «abacaba». Тогда \(p'\) может быть равно «aabcaab». Случайные строки \(s1 =\) «zyx» и \(s2 =\) «kjh». Тогда \(h =\) «zyxaabcaabkjh». Обратите внимание, что нельзя удалять или добавлять буквы в \(p\), чтобы получить \(p'\), можно только менять их порядок. Теперь Поликарп просит вас помочь ему в реализации модуля проверки пароля. По данному паролю \(p\) и хешу \(h\), проверьте, что \(h\) может являться хешом пароля \(p\). Вам нужно ответить на \(t\) наборов входных данных. Выходные данные На каждый набор входных данных выведите «YES», если данный хеш \(h\) может быть получен по данному паролю \(p\), и «NO» в противном случае. Примечание Первый набор входных данных объяснен в условии. Во втором наборе входных данных и \(s_1\), и \(s_2\) пусты, а \(p'=\) «threetwoone» — это перемешанная \(p\). В третьем наборе входных данных хеш нельзя получить из пароля. В четвертом наборе входных данных \(s_1=\) «n», \(s_2\) пуста, а \(p'=\) «one» — это перемешанная \(p\) (даже несмотря на то, что они совпадают). В пятом наборе входных данных хеш нельзя получить из пароля. | |
![]()
|
|
B. Строка
Конструктив
Перебор
реализация
Строки
строковые суфф. структуры
хэши
*2100
Однажды на уроке информатики Аня и Маша прошли лексикографический порядок. Строка x лексикографически меньше строки y, если либо x является префиксом y (и при этом x ≠ y), либо существует такое i (1 ≤ i ≤ min(|x|, |y|)), что xi < yi, и для любого j (1 ≤ j < i) xj = yj. Здесь |a| обозначает длину строки a. Лексикографическое сравнение строк реализует оператор < в современных языках программирования. Учительница задала Ане и Маше домашнее задание. Она выдала им строку длины n. Из этой строки требуется выписать все подстроки, в том числе всю строчку целиком и все одинаковые подстроки (например, из строки «aab» требуется выписать «a», «a», «aa», «ab», «aab», «b»). После этого полученные строки требуется расположить в лексикографическом порядке. А чтобы не проверять все эти строки, хитрая учительница попросила предъявить лишь k-тую строку из этого списка. Помогите Ане с Машей выполнить домашнее задание. Выходные данные Выведите строку, которую требуется выписать Ане с Машей — лексикографически k-ую подстроку заданной строки. Если у строки всего меньше, чем k подстрок, выведите строку «No such line.» (без кавычек). Примечание Во втором тесте перед строкой «bc» идут строки «a», «ab», «abc», «b». | |
![]()
|
|
D. Заколдованный артефакт
интерактив
Конструктив
Строки
*2300
Это интерактивная задача. Пройдя последний уровень зачарованного храма, вы получили могущественный артефакт 255-го уровня. Не стоит спешить радоваться, ведь на данном артефакте установлена мощная руна, которую можно разрушить единственным секретным заклинанием \(s\). Именно это заклинание вам и предстоит найти. Определим заклинание как некоторую непустую строку, состоящую только из букв a и b. В любой момент времени Вы можете произнести произвольное непустое заклинание \(t\), при этом руна на артефакте начнёт сопротивляться. Сопротивлением руны называется редакционное расстояние между строками, задающих произнесённое заклинание \(t\) и искомое секретное заклинание \(s\), при произнесении которого руна разрушается. Редакционным расстоянием двух строк \(s\) и \(t\) называется величина, равная минимальному количеству односимвольных операций замены, вставки и удаления символов в \(s\) для получения \(t\). К примеру, расстояние между ababa и aaa равно \(2\), aaa и aba — \(1\), bbaba и abb — \(3\). Редакционное расстояние равно \(0\) тогда и только тогда, когда строки равны. Также стоит учитывать, что у артефакта есть предел сопротивляемости — если вы произнесёте более чем \(n + 2\) заклинаний, где \(n\) — это длина заклинания \(s\), то руна заблокируется. Таким образом, требуется за \(n + 2\) или меньшее количество заклинаний разрушить руну, находящуюся на Вашем артефакте. Следует учитывать, что искомое разрушающее заклинание \(s\) также должно быть учтено среди этих \(n + 2\) заклинаний. Учтите, что длина \(n\) разрушающего руну заклинания \(s\) вам заранее не известна. Известно только то, что его длина \(n\) не превосходит \(300\). Протокол взаимодействия Взаимодействие происходит с помощью запросов. Каждый запрос состоит из единственной непустой строки \(t\) — заклинания, которое вы хотите произнести. Длина строки \(t\) не должна превышать \(300\). Строка должна состоять только из букв a и b. В ответ на запрос вы получите сопротивление руны — редакционное расстояние между строками, задающих произнесённое заклинание \(t\) и искомое заклинание \(s\), при произнесении которого руна разрушается. Помните, что \(s\) содержит только буквы a и b. После разрушения руны ваша программа должна немедленно завершиться. Руна разрушается, если её сопротивление достигает значения \(0\). После получения значения \(0\) ваша программа должна завершиться штатным образом. В этой задаче интерактор не адаптивный. Это означает, что в рамках одного теста искомое заклинание \(s\) не меняется. При некорректном запросе будет выведено -1. При получении данного значения ваша программа должна немедленно завершиться штатным образом (к примеру, с помощью вызова exit(0)), иначе тестирующая система может выдать произвольный вердикт. При превышении количества заклинаний (то есть числа \(n + 2\), где \(n\) — длина заклинания \(s\), это число вам неизвестно) будет выведен вердикт неправильный ответ. Ваше решение может получить вердикт Решение «зависло», если вы ничего не выведете или забудете сбросить буфер вывода. Чтобы сбросить буфер вывода вам нужно сделать следующее сразу после вывода запроса и символа конца строки: - fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- см. документацию других языков.
Взломы Используйте следующий формат для взломов: В единственной строке выведите строку \(s\) (\(1 \le |s| \le 300\)) из букв a и b, задающую разрушающее заклинание. Взламываемое решение не будет иметь прямого доступа к загаданной строке. | |
![]()
|
|
A. Новый год и названия
реализация
Строки
*800
С новым годом! 2020 год также известен как год Gyeongja (경자년, gyeongja-nyeon) в Корее. Откуда это имя? Кратко рассмотрим систему Gapja, которая традиционно используется в Корее для обозначения лет. Существует две последовательности строк, \(n\) строк \(s_1, s_2, s_3, \ldots, s_{n}\) и \(m\) строк \(t_1, t_2, t_3, \ldots, t_{m}\). Эти строки состоят только из строчных букв алфавита. Среди этих строк могут быть одинаковые. Назовем конкатенацией двух строк \(x\) и \(y\) такую строку, которая получится при последовательной записи сначала \(x\), затем \(y\) друг за другом, не меняя порядок символов в них. Например, конкатенация строк «code» и «forces» равна строке «codeforces». Год 1 начинается с конкатенации двух строк \(s_1\) и \(t_1\). Если год увеличивается на один, то мы берем следующую строку по порядку для каждой соответствующей последовательности. Если используемая в данный момент строка находится в конце массива, то переходим к первой строке. Например, если \(n = 3, m = 4, s = \){«a», «b», «c»}, \(t =\) {«d», «e», «f», «g»}, то строки для лет с 1 по 14 - {«ad», «be», «cf», «ag», «bd», «ce», «af», «bg», «cd», «ae», «bf», «cg», «ad», «be»}. Обратите внимание, что название года может повторяться.  Вам даются две последовательности строк размером \(n\) и \(m\), а также \(q\) запросов. Для каждого запроса вам будет указан год. Можете ли вы найти имена, соответствующие данным годам, согласно системе Gapja? Выходные данные Выведите \(q\) строк. Для каждой строки выведите название года по описанному выше правилу. Примечание Первый пример использует актуальные названия, используемые в системе Gapja. Эти строки обычно означают числа или названия животных. | |
![]()
|
|
D. Dr. Evil Underscores
битмаски
Деревья
дп
жадные алгоритмы
Перебор
поиск в глубину и подобное
разделяй и властвуй
Строки
*1900
Сегодня Бакри в качестве дружеского подарка вручил Бадави \(n\) целых чисел \(a_1, a_2, \dots, a_n\) и дал ему задачку выбрать такой \(X\), что \(\underset{1 \leq i \leq n}{\max} (a_i \oplus X)\) принимает минимальное возможное значение, где \(\oplus\) обозначает операцию побитового исключающего ИЛИ. Бадави, как обычно, ленится, поэтому вы решили помочь ему и найти минимальное возможное значение \(\underset{1 \leq i \leq n}{\max} (a_i \oplus X)\). Выходные данные Выведите одно целое число — минимальное возможное значение \(\underset{1 \leq i \leq n}{\max} (a_i \oplus X)\). Примечание В первом примере можно выбрать \(X = 3\). Во втором примере можно выбрать \(X = 5\). | |
![]()
|
|
E. Гончар Фёдор наносит ответный удар
Строки
Структуры данных
*3200
У Феди есть строка \(S\), изначально пустая, и массив \(W\), тоже изначально пустой. Феде по одному приходят \(n\) запросов к этой строке и этому массиву. Запрос \(i\) состоит из строчной буквы английского алфавита \(c_i\) и целого неотрицательного числа \(w_i\). К строке \(S\) необходимо в конец приписать символ \(c_i\), а к \(W\) в конец добавить \(w_i\). Ответом на запрос является сумма подозрительностей по всем подотрезкам \([L, \ R]\) массива \(W\) \((1 \leq L \leq R \leq i)\). Определим подозрительность подотрезка следующим образом: если подстрока \(S\), соответствующая этому подотрезку (то есть строка из идущих подряд символов от \(L\)-го до \(R\)-го включительно), совпадает с префиксом \(S\) такой же длины (то есть с подстрокой, соответствующей подотрезку \([1, \ R - L + 1]\)), то его подозрительность равна минимуму в массиве \(W\) на том же подотрезке \([L, \ R]\), а иначе она равна \(0\). Помогите Феде ответить на все запросы, пока за ним не приехали санитары! Выходные данные Выведите \(n\) строк, в строке \(i\) должно находиться одно целое число — ответ на запрос \(i\). Примечание Для удобства будем называть «подозрительными» те подотрезки, для которых соответствующие им строки являются префиксами \(S\), то есть те, подозрительность которых может быть не нулевой. В результате расшифровки в первом примере из условия после всех запросов строка \(S\) равна «abacaba», а все \(w_i = 1\), то есть подозрительность всех подозрительных подотрезков просто равна \(1\). Посмотрим, как получается ответ после каждого запроса: 1. \(S\) = «a», у массива \(W\) есть единственный подотрезок — \([1, \ 1]\), и соответствующая ему подстрока равна «a», то есть всей строке \(S\), то есть она является префиксом \(S\), и подозрительность подотрезка равна \(1\). 2. \(S\) = «ab», подозрительные подотрезки: \([1, \ 1]\) и \([1, \ 2]\), всего \(2\). 3. \(S\) = «aba», подозрительные подотрезки: \([1, \ 1]\), \([1, \ 2]\), \([1, \ 3]\) и \([3, \ 3]\), всего \(4\). 4. \(S\) = «abac», подозрительные подотрезки: \([1, \ 1]\), \([1, \ 2]\), \([1, \ 3]\), \([1, \ 4]\) и \([3, \ 3]\), всего \(5\). 5. \(S\) = «abaca», подозрительные подотрезки: \([1, \ 1]\), \([1, \ 2]\), \([1, \ 3]\), \([1, \ 4]\), \([1, \ 5]\), \([3, \ 3]\) и \([5, \ 5]\), всего \(7\). 6. \(S\) = «abacab», подозрительные подотрезки: \([1, \ 1]\), \([1, \ 2]\), \([1, \ 3]\), \([1, \ 4]\), \([1, \ 5]\), \([1, \ 6]\), \([3, \ 3]\), \([5, \ 5]\) и \([5, \ 6]\) всего \(9\). 7. \(S\) = «abacaba», подозрительные подотрезки: \([1, \ 1]\), \([1, \ 2]\), \([1, \ 3]\), \([1, \ 4]\), \([1, \ 5]\), \([1, \ 6]\), \([1, \ 7]\), \([3, \ 3]\), \([5, \ 5]\), \([5, \ 6]\), \([5, \ 7]\) и \([7, \ 7]\) всего \(12\). Во втором примере из условия после всех запросов \(S\) = «aaba», \(W = [2, 0, 2, 0]\). 1. \(S\) = «a», подозрительные подотрезки: \([1, \ 1]\) (подозрительность \(2\)), в сумме \(2\). 2. \(S\) = «aa», подозрительные подотрезки: \([1, \ 1]\) (\(2\)), \([1, \ 2]\) (\(0\)), \([2, \ 2]\) (\(0\)), в сумме \(2\). 3. \(S\) = «aab», подозрительные подотрезки: \([1, \ 1]\) (\(2\)), \([1, \ 2]\) (\(0\)), \([1, \ 3]\) (\(0\)), \([2, \ 2]\) (\(0\)), в сумме \(2\). 4. \(S\) = «aaba», подозрительные подотрезки: \([1, \ 1]\) (\(2\)), \([1, \ 2]\) (\(0\)), \([1, \ 3]\) (\(0\)), \([1, \ 4]\) (\(0\)), \([2, \ 2]\) (\(0\)), \([4, \ 4]\) (\(0\)), в сумме \(2\). В третьем примере из условия после всех запросов \(S\) = «abcde», \(W = [7, 2, 10, 1, 7]\). 1. \(S\) = «a», подозрительные подотрезки: \([1, \ 1]\) (\(7\)), в сумме \(7\). 2. \(S\) = «ab», подозрительные подотрезки: \([1, \ 1]\) (\(7\)), \([1, \ 2]\) (\(2\)), в сумме \(9\). 3. \(S\) = «abc», подозрительные подотрезки: \([1, \ 1]\) (\(7\)), \([1, \ 2]\) (\(2\)), \([1, \ 3]\) (\(2\)), в сумме \(11\). 4. \(S\) = «abcd», подозрительные подотрезки: \([1, \ 1]\) (\(7\)), \([1, \ 2]\) (\(2\)), \([1, \ 3]\) (\(2\)), \([1, \ 4]\) (\(1\)), в сумме \(12\). 5. \(S\) = «abcde», подозрительные подотрезки: \([1, \ 1]\) (\(7\)), \([1, \ 2]\) (\(2\)), \([1, \ 3]\) (\(2\)), \([1, \ 4]\) (\(1\)), \([1, \ 5]\) (\(1\)), в сумме \(13\). | |
![]()
|
|
B. Неприводимые анаграммы
Бинарный поиск
Конструктив
Строки
Структуры данных
*1800
Назовем две строки \(s\) и \(t\) анаграммами друг друга, если можно так переставить символы в строке \(s\), чтобы получить строку, равную \(t\). Рассмотрим две строки \(s\) и \(t\), являющиеся анаграммами друг друга. Будем говорить, что \(t\) это приводимая анаграмма строки \(s\), если существует такое целое число \(k \ge 2\) и \(2k\) непустых строк \(s_1, t_1, s_2, t_2, \dots, s_k, t_k\), которые удовлетворяют следующим условиям: - Если мы запишем в линию строки \(s_1, s_2, \dots, s_k\) в таком порядке, то получившаяся строка будет равна \(s\);
- Если мы запишем в линию строки \(t_1, t_2, \dots, t_k\) в таком порядке, то получившаяся строка будет равна \(t\);
- Для всех целых \(i\) между \(1\) и \(k\) включительно, \(s_i\) и \(t_i\) являются анаграммами.
Если таких строк не существует, тогда \(t\) называется неприводимой анаграммой строки \(s\). Обратите внимание, что этот термин определяется только в случае, когда \(s\) и \(t\) это анаграммы. Например, рассмотрим строку \(s = \) «gamegame». Тогда строка \(t = \) «megamage» это приводимая анаграмма для \(s\), потому что мы можем выбрать, например, \(s_1 = \) «game», \(s_2 = \) «gam», \(s_3 = \) «e» и \(t_1 = \) «mega», \(t_2 = \) «mag», \(t_3 = \) «e»:  С другой стороны, можно показать, что \(t = \) «memegaga» это неприводимая анаграмма для \(s\). Вам будет дана строка \(s\) и \(q\) запросов, каждый представляется двумя целыми числами \(1 \le l \le r \le |s|\) (где за \(|s|\) обозначается длина строки \(s\)). Для каждого запроса, вы должны определить, имеет ли подстрока строки \(s\), с \(l\)-о по \(r\)-й символ, включительно, хотя бы одну неприводимую анаграмму. Выходные данные Для каждого запроса, выведите единственную строку, содержащую «Yes» (без кавычек), если соответствующая запросу подстрока имеет хотя бы одну неприводимую анаграмму и «No» (без кавычек), иначе. Примечание В первом тесте, в первом и третьем запросах, подстрока будет «a» и она имеет саму себя как неприводимую анаграмму, так как две и больше непустые строки, записанные вместе, не смогут дать строку «a». С другой стороны, во втором запросе, подстрока будет «aaa», которая не имеет неприводимых анаграмм: ее единственная анаграмма это она сама и мы можем выбрать \(s_1 = \) «a», \(s_2 = \) «aa», \(t_1 = \) «a», \(t_2 = \) «aa», чтобы показать, что это приводимая анаграмма. Во втором запросе второго тестового случая, подстрока будет «abb» и она имеет, например, неприводимую анаграмму «bba». | |
![]()
|
|
A. Четные, но нечетные
жадные алгоритмы
математика
Строки
*900
Назовем число неопределенным, если сумма его цифр делится на \(2\), тогда как само число не делится на \(2\). Например, числа \(13\), \(1227\), \(185217\) являются неопределенными, а числа \(2\), \(12\), \(177013\), \(265918\) — нет. Для лучшего понимания этого определения посмотрите в пояснения к примерам. Вам дано неотрицательное целое число \(s\), состоящее из \(n\) цифр. Вы можете удалить некоторые его цифры (они не обязательно идут подряд), чтобы получить неопределенное число. Вы не можете менять порядок цифр, то есть после удаления цифр из числа оставшиеся цифры просто схлопываются. Получившееся число должно не содержать ведущие нули. Количество удаляемых цифр может быть любым от \(0\) (вы вообще не удаляете цифры) до \(n-1\). Например, если было задано целое число \(s=\)222373204424185217171912, то один из способов сделать его неопределенным имеет вид: 222373204424185217171912 \(\rightarrow\) 2237344218521717191. Сумма цифр числа 2237344218521717191 равна \(70\) и делится на \(2\), но само число на \(2\) не делится — значит это число является неопределенным. Найдите любое число, которое может получиться таким образом и является неопределенным. Если получить таким способом неопределенное число невозможно, то сообщите об этом. Выходные данные Для каждого набора входных данных выведите ответ в следующем формате: - Если невозможно получить неопределенное число, выведите «-1» (без кавычек).
- Иначе, выведите получившееся число, после удаления некоторых, возможно нуля, но не всех цифр данного числа. Это число должно являться неопределенным. Если существует несколько возможных ответов, вы можете вывести любой из них. Обратите внимание, что числа, содержащие ведущие нули или пустая строка не являются верными ответами. Количество удаленных цифр не нужно минимизировать или максимизировать, вы можете найти любой ответ, подходящий под условие.
Примечание В первом тестовом случае, \(1227\) уже является неопределенным числом (\(1 + 2 + 2 + 7 = 12\). Число \(12\) делится на \(2\), тогда как число \(1227\) не делится на \(2\)), поэтому можно не удалять цифры. Такие ответы, как \(127\) и \(17\) тоже являются верными. Во втором тестовом случае, очевидно, что невозможно получить неопределенное число из данного числа. В третьем тестовом случае, существует много неопределенных чисел, которые мы можем получить с помощью удаления некоторых цифр. Например при удалении \(1\) цифры это числа \(17703\), \(77013\) или \(17013\). Ответы, такие как \(1701\) или \(770\) не будут верными, потому что они не являются неопределенными числами. Ответ \(013\) не является верным, потому что он содержит ведущие нули. Пояснение: - \(1 + 7 + 7 + 0 + 3 = 18\). Так как \(18\) делится на \(2\), а само число \(17703\) не делится на \(2\), мы можем увидеть, что число \(17703\) является неопределенным числом. Тоже самое верно для чисел \(77013\) и \(17013\);
- \(1 + 7 + 0 + 1 = 9\). Так как \(9\) не делится на \(2\), число \(1701\) не является неопределенным числом;
- \(7 + 7 + 0 = 14\). В этот раз, \(14\) делится на \(2\), но само число \(770\) также делится на \(2\), поэтому число \(770\) не является неопределенным.
В последнем наборе входных данных примера продемонстрирован один из множества возможных ответов. Другой возможный ответ: 222373204424185217171912 \(\rightarrow\) 22237320442418521717191 (достаточно удалить одну последнюю цифру). | |
![]()
|
|
B. Бесконечные префиксы
математика
Строки
*1700
Вам задана строка \(s\) длины \(n\), состоящая только из 0 и 1. Построим бесконечную строку \(t\) как конкатенацию бесконечного числа строк \(s\), или \(t = ssss \dots\) Например, если \(s =\) 10010, то \(t =\) 100101001010010... Посчитайте количество префиксов \(t\) с балансом равным \(x\). Баланс строки \(q\) равен \(cnt_{0, q} - cnt_{1, q}\), где \(cnt_{0, q}\) — это количество вхождений 0 в \(q\), а \(cnt_{1, q}\) — количество вхождений 1 в \(q\). Количество таких префиксов может быть бесконечно: в таком случае, вы должны определить это. Префикс — строка, состоящая из нескольких первых букв заданной строки, без изменения их порядка. Пустой префикс тоже является префиксом. Например, у строки «abcd» пять префиксов: пустая строка, «a», «ab», «abc» и «abcd». Выходные данные Выведите \(T\) чисел — по одному на набор входных данных. Для каждого набора выведите количество префиксов или \(-1\), если таких префиксов бесконечное количество. Примечание В первом наборе есть 3 хороших префикса строки \(t\): длины \(28\), \(30\) и \(32\). | |
![]()
|
|
C. Получи строку
дп
жадные алгоритмы
Строки
*1600
Вам заданы две строки \(s\) и \(t\), состоящие из строчных букв латинского алфавита. Также у вас есть строка \(z\), которая изначально пуста. Вы хотите, чтобы строка \(z\) стала равна строке \(t\). Для этого вы можете выполнять следующую операцию: добавить любую подпоследовательность строки \(s\) в конец строки \(z\). Подпоследовательность — это последовательность, которая получается из данной путем удаления нуля или более ее элементов. Например, если \(z = ac\), \(s = abcde\), вы можете превратить \(z\) в следующие строки за одну операцию: - \(z = acace\) (если выберете подпоследовательность \(ace\));
- \(z = acbcd\) (если выберете подпоследовательность \(bcd\));
- \(z = acbce\) (если выберете подпоследовательность \(bce\)).
Обратите внимание, что строка \(s\) не меняется после операций. Посчитайте минимальное количество операций, необходимое для того, чтобы превратить строку \(z\) в строку \(t\). Выходные данные На каждый набор входных данных выведите одно число — минимальное количество операций, необходимое для того, чтобы превратить строку \(z\) в строку \(t\). Если это невозможно выведите \(-1\). | |
![]()
|
|
H. Покраска строки
*особая задача
дп
Строки
Задана строка \(s\) из строчных букв латинского алфавита. Требуется покрасить каждую букву в один из двух цветов (красный или синий) так, что если выписать все красные буквы слева направо и выписать все синие буквы слева направо, то лексикографически максимальная из двух выписанных строк будет как можно лексикографически меньше. Одинаковые буквы могут быть покрашены в разные цвета, то есть для каждого индекса в строке \(s\) можно выбрать любой из двух цветов. Формально, выпишем - строку \(r\) (может быть пустой) — все красные буквы в порядке слева направо (красная подпоследовательность),
- строку \(b\) (может быть пустой) — все синие буквы в порядке слева направо (синяя подпоследовательность).
Ваша задача придумать такую покраску, что \(\max(r, b)\) — минимален. Небольшое напоминание: пустая строка является лексикографически наименьшей. Выходные данные Выведите \(t\) строк, \(i\)-я из них должна содержать ответ на \(i\)-й набор входных данных. Выведите строку длины \(n\), где \(n\) — длина заданной строки \(s\): \(j\)-й символ строки должен быть равен либо 'R', либо 'B' в зависимости от того в красный или синий цвет покрашен \(j\)-й символ строки в найденном решении. Если ответов несколько, выведите любой из них. | |
![]()
|
|
B. Gnikool Ssalg
*особая задача
реализация
Строки
*1400
Вам дана строка. Переставьте ее символы в обратном порядке. Выходные данные Выведите символы заданной строки в обратном порядке. | |
![]()
|
|
A. Три строки
реализация
Строки
*800
Вам даны три строки \(a\), \(b\) и \(c\) одинаковой длины \(n\). Строки состоят только из строчных символов латинского алфавита. Тогда \(i\)-й символ строки \(a\) это \(a_i\), \(i\)-й символ строки \(b\) это \(b_i\), \(i\)-й символ строки \(c\) это \(c_i\). Для всех \(i\) (\(1 \leq i \leq n\)) вы должны поменять символ \(c_i\) либо с \(a_i\), либо с \(b_i\) (это значит поменять его значение в строке со значением другого символа в другой строке). То есть суммарно вы должны выполнить ровно \(n\) замен, каждая из которых это либо \(c_i \leftrightarrow a_i\), либо \(c_i \leftrightarrow b_i\) (для всех целых \(i\) от \(1\) до \(n\), включительно). Например, если \(a\) это «code», \(b\) это «true» и \(c\) это «help», вы можете сделать строку \(c\) равной «crue», меняя \(1\)-й и \(4\)-й символы с соответствующими символами в строке \(a\) и остальные с соответствующими символами в строке \(b\). В этом случае строка \(a\) станет равной «hodp» и строка \(b\) станет равной «tele». Возможно ли так сделать замены, что строка \(a\) станет равна строке \(b\)? Выходные данные Выведите \(t\) строк с ответами на тестовые случаи. Для каждого тестового случая: Если возможно сделать строку \(a\) равной строке \(b\) выведите «YES» (без кавычек), иначе выведите «NO» (без кавычек). Вы можете выводить как строчные, так и заглавные буквы в ответах. Примечание В первом тестовом случае, невозможно так сделать замены, чтобы строка \(a\) стала равной строке \(b\). Во втором тестовом случае, вы можете поменять \(c_i\) с \(a_i\) для всех \(i\). После таких замен \(a\) станет равной «bca», \(b\) станет равной «bca» и \(c\) станет равной «abc». Легко видеть, что строки \(a\) и \(b\) станут равными. В третьем тестовом случае, вы можете поменять \(c_1\) с \(a_1\), \(c_2\) с \(b_2\), \(c_3\) с \(b_3\) и \(c_4\) с \(a_4\). Тогда строка \(a\) станет равной «baba», строка \(b\) станет равной «baba» и строка \(c\) станет равной «abab». Легко видеть, что строки \(a\) и \(b\) станут равными. В четвертом тестовом случае, невозможно так сделать замены, чтобы строка \(a\) стала равной строке \(b\). | |
![]()
|
|
C. Функция Айоуба
Бинарный поиск
жадные алгоритмы
Комбинаторика
математика
Строки
*1700
Айоуб думает, что он очень умный человек, поэтому он придумал функцию \(f(s)\), где \(s\) это бинарная строка (строка, содержащая только символы «0» и «1»). Функция \(f(s)\) равна количеству подстрок строки \(s\), которые содержат хотя бы один символ, равный «1». Более формально, \(f(s)\) равно количеству пар целых чисел \((l, r)\), таких что \(1 \leq l \leq r \leq |s|\) (где \(|s|\) равно длине строки \(s\)), таких что хотя бы один из символов \(s_l, s_{l+1}, \ldots, s_r\) равен «1». Например, если \(s = \)«01010», то \(f(s) = 12\), потому что есть \(12\) таких пар \((l, r)\): \((1, 2), (1, 3), (1, 4), (1, 5), (2, 2), (2, 3), (2, 4), (2, 5), (3, 4), (3, 5), (4, 4), (4, 5)\). Айоуб также думает, что он умнее Махмуда, поэтому дал ему два целых числа \(n\) и \(m\) и следующую задачу. По всем бинарным строкам \(s\) длины \(n\), которые содержат ровно \(m\) символов, равных «1», найдите максимальное значение \(f(s)\). У Махмуда не получилось решить эту задачу, поэтому он попросил вас о помощи. Можете ли вы помочь ему? Выходные данные Для каждого тестового случая выведите единственное целое число — максимальное значение \(f(s)\) по всем строкам \(s\) длины \(n\), которые содержат ровно \(m\) символов, равных «1». Примечание В первом тестовом случае, существует только \(3\) строки длины \(3\), которые содержат ровно \(1\) символ, равный «1». Эти строки это: \(s_1 = \)«100», \(s_2 = \)«010», \(s_3 = \)«001». Значения \(f\) для них это: \(f(s_1) = 3, f(s_2) = 4, f(s_3) = 3\), поэтому максимальное значение это \(4\) и ответ равен \(4\). Во втором тестовом случае, строка \(s\) для которой максимальное значение функции это «101». Во третьем тестовом случае, строка \(s\) для которой максимальное значение функции это «111». В четвертом тестовом случае, единственная строка \(s\) длины \(4\), которая содержит ровно \(0\) символов, равных «1» это «0000» и значение функции \(f\) для этой строки это \(0\), поэтому ответ равен \(0\). В пятом тестовом случае, строка \(s\) с максимальным значением функции это «01010» и она была подробно разобрана в качестве примера в тексте условия задачи. | |
![]()
|
|
A. Удаление нулей
реализация
Строки
*800
Вам задана строка \(s\). Она состоит только из 0 и 1. Вы хотите, чтобы все символы 1 образовывали непрерывный подотрезок. Например, в строках 0, 1, 00111 и 01111100 все символы 1 образуют непрерывный подотрезок, а в строках 0101, 100001 и 11111111111101 — нет. Вы можете удалить какое-то количество (возможно, нулевое) символов 0 из строки. Чему равно минимальное количество символов 0, которое вам нужно удалить? Выходные данные Выведите \(t\) чисел, \(i\)-е число — это ответ на \(i\)-й набор входных данных (минимальное количество символов 0, которое нужно удалить из строки \(s\)). Примечание В первом тестовом примере вам нужно удалить третий и четвертый символы из строки 010011 (она превратится в 0111). | |
![]()
|
|
E. Удаляем подпоследовательности
дп
Строки
*2200
Вам задана строка \(s\). Вы можете построить новую строку \(p\) из \(s\), используя следующую операцию не более двух раз: - выберем любую подпоследовательность \(s_{i_1}, s_{i_2}, \dots, s_{i_k}\), где \(1 \le i_1 < i_2 < \dots < i_k \le |s|\);
- удалим выбранную подпоследовательность из \(s\) (\(s\) может стать пустой);
- присоединим выбранную подпоследовательность справа к \(p\) как строку (другими словами, \(p = p + s_{i_1}s_{i_2}\dots s_{i_k}\)).
Конечно, в начале строка \(p\) является пустой. Например, пусть \(s = \text{ababcd}\). Сначала выберем подпоследовательность \(s_1 s_4 s_5 = \text{abc}\) — в результате мы получим \(s = \text{bad}\) и \(p = \text{abc}\). Потом, выберем \(s_1 s_2 = \text{ba}\) — мы получим \(s = \text{d}\) и \(p = \text{abcba}\). Таким образом, возможно построить \(\text{abcba}\) из \(\text{ababcd}\). Можно ли построить заданную строку \(t\), используя описанный выше алгоритм? Выходные данные Выведите \(T\) ответов — по одному на набор. Выведите YES (регистр не важен), если возможно построить \(t\), и NO (регистр не важен) иначе. | |
![]()
|
|
B. Самый длинный палиндром
жадные алгоритмы
Конструктив
Перебор
реализация
Строки
*1100
Вернувшись к решению задач, Гильдонг взялся за изучение палиндромов. Он выяснил, что палиндром это строка, которая равна своему перевороту. Например, строки «pop», «noon», «x», и «kkkkkk» являются палиндромами, а строки «moon», «tv», и «abab» не являются. Пустая строка также является палиндромом. Гильдонгу очень понравился этот концепт, так что он решил немного с ним поиграть. У него есть \(n\) различных строк равной длины \(m\). Он хочет удалить некоторые из этих строк (возможно, ни одну, или все) и переставить оставшиеся, чтобы их конкатенация была палиндромом. Он также хочет, чтобы палиндром был как можно длиннее. Помогите ему решить эту задачу! Выходные данные В первую строку выведите длину наибольшего палиндрома. Во вторую строку выведите искомый палиндром. Если есть несколько возможных ответов, выведите любой. Если палиндром пуст, то можете как вывести пустую строку, так и не выводить эту строку вообще. Примечание В первом примере «battab» также является корректным ответом. Во втором примере есть 4 разных возможных корректных ответа, включая ответ из примера. Мы не будем давать никаких подсказок, какими являются остальные ответы. В третьем примере единственная возможная строка — пустая. | |
![]()
|
|
B. Курони и простые строки
жадные алгоритмы
Конструктив
Строки
*1200
Теперь, когда Курони исполнилось 10 лет, он большой мальчик и больше не любит массивы целых чисел в качестве подарков. В этом году он хочет получить скобочную последовательность в качестве подарка на день рождения. В частности, он хочет, чтобы последовательность скобок была настолько сложной, что, как бы он ни старался, он не сможет удалить простую подпоследовательность! Назовем строку, образованную \(n\) символами '(' или ')' простой, если ее длина \(n\) четна и положительная, ее первые \(\frac{n}{2}\) символов — это '(', а ее последние \(\frac{n}{2}\) символов — это ')'. Например, строки () и (()) являются простыми, в то время как строки )( и ()() не являются простыми. Курони будет дана строка, образованная символами '(' и ')' (заданная строка не обязательно является простой). Операция состоит из выбора подпоследовательности символов строки, которая образует простую строку, и удаления всех символов этой подпоследовательности из строки. Заметьте, символы подпоследовательности не обязаны идти подряд. К примеру, он может применить операцию к строке ')()(()))', выбрать подпоследовательность из выделенных жирным шрифтом символов, так как они формируют простую строку '(())', удалить эти символы с строки и получить '))()'. Курони должен выполнить минимально возможное количество операций над строкой таким образом, чтобы с оставшейся строкой больше нельзя было выполнить ни одной операции. Результирующая строка не обязана быть пустой. Поскольку заданная строка слишком велика, Курони не может понять, как минимизировать количество операций. Можете ли вы помочь ему сделать это? Последовательность символов \(a\) является подпоследовательностью строки \(b\), если \(a\) может быть получена из \(b\) удалением нескольких (возможно, ни одного или всех) символов. Выходные данные В первой строке выведите единственное целое число \(k\) — минимальное количество операций, которые вы должны применить. Затем выведите \(2k\) строк, описывающих операции в следующем формате: Для каждой операции выведите строку, содержащую целое число \(m\) — количество символов в подпоследовательности, которую вы удалите. Затем выведите строку, содержащую \(m\) целых чисел \(1 \le a_1 < a_2 < \dots < a_m\) — индексы символов, которые вы удалите. Все целые числа должны быть меньше или равны длине текущей строки, а соответствующая подпоследовательность должна образовывать простую строку. Если существует несколько различных последовательностей операций с минимальным \(k\), вы можете вывести любую из них. Примечание В первом примере строка равна '(()(('. Описанная операция соответствует удалению выделенной жирным шрифтом подпоследовательности. Получившаяся строка равна '(((', и над ней больше нельзя выполнить ни одну операцию. Другой правильный ответ — это выбор индексов \(2\) и \(3\), что приводит к той же самой конечной строке. Во втором примере уже невозможно выполнить ни одну операцию. | |
![]()
|
|
C. Корова и сообщение
дп
математика
Перебор
Строки
*1500
Корова Бесси только что перехватила сообщение, которое Фермер Джон отправил Бургер Куин! Бесси уверена, что в нем скрыто секретное сообщение. Сообщение представляет из себя строку \(s\), состоящую из строчных букв латинского алфавита. Бесси считает, что строка \(t\) скрыта в строке \(s\), если \(t\) является подпоследовательностью \(s\), индексы которой формируют арифметическую прогрессию. Например, строка aab скрыта в строке aaabb, потому что она получена в индексах \(1\), \(3\) и \(5\), которые формируют арифметическую прогрессию с шагом \(2\). Бесси считает, что любая скрытая строка, которая имеет наибольшее количество вхождений и является скрытым сообщением. Два вхождения подпоследовательности \(S\) различны, если различаются их множества индексов. Помогите Бесси узнать количество вхождений скрытого сообщения! Например, в строке aaabb, a скрыта \(3\) раза, b скрыта \(2\) раза, ab скрыта \(6\) раз, aa скрыта \(3\) раза, bb скрыта \(1\) раз, aab скрыта \(2\) раза, aaa скрыта \(1\) раз, abb скрыта \(1\) раз, aaab скрыта \(1\) раз, aabb скрыта \(1\) раз и aaabb скрыта \(1\) раз. Количество вхождений скрытого сообщения равно \(6\). Выходные данные Выведите единственное число — количество вхождений секретного сообщения. Примечание В первом примере скрыты следующие строки (с соответствующими множествами индексов): - a встречается как \((1)\), \((2)\), \((3)\);
- b встречается как \((4)\), \((5)\);
- ab встречается как \((1,4)\), \((1,5)\), \((2,4)\), \((2,5)\), \((3,4)\), \((3,5)\);
- aa встречается как \((1,2)\), \((1,3)\), \((2,3)\);
- bb встречается как \((4,5)\);
- aab встречается как \((1,3,5)\), \((2,3,4)\);
- aaa встречается как at \((1,2,3)\)
- abb встречается как \((3,4,5)\)
- aaab встречается как \((1,2,3,4)\);
- aabb встречается как \((2,3,4,5)\);
- aaabb встречается как \((1,2,3,4,5)\);
Заметим, что все множества индексов являются арифметическими прогрессиями. Во втором примере, ни одна скрытая строка не встречается более одного раза. В третьем примере, скрытым сообщением является одна буква l. | |
![]()
|
|
A. cAPS lOCK
реализация
Строки
*1000
зАЧЕМ НУЖНА КЛАВИША cAPS lOCK? Caps Lock — клавиша компьютерной клавиатуры, предназначенная для автоматической (постоянной) смены регистра букв со строчных на прописные. Будучи случайно нажатой, она приводит к последствиям вроде первого абзаца в условии этой задачи. Будем считать, что слово набрано с ошибочно нажатой клавишей Caps Lock, если: - либо оно полностью состоит из прописных букв;
- либо прописными являются все его буквы, кроме первой.
В таком случае, нужно автоматически поменять регистр всех букв на противоположный. Например, регистр букв слов «hELLO», «HTTP», «z» должен быть изменен. Напишите программу, которая применяет описанное выше правило или оставляет слово без изменения, если оно не применимо. Выходные данные Выведите результат обработки данного слова. | |
![]()
|
|
A. cAPS lOCK
реализация
Строки
*1000
зАЧЕМ НУЖНА КЛАВИША cAPS lOCK? Caps Lock — клавиша компьютерной клавиатуры, предназначенная для автоматической (постоянной) смены регистра букв со строчных на прописные. Будучи случайно нажатой, она приводит к последствиям вроде первого абзаца в условии этой задачи. Будем считать, что слово набрано с ошибочно нажатой клавишей Caps Lock, если: - либо оно полностью состоит из прописных букв;
- либо прописными являются все его буквы, кроме первой.
В таком случае, нужно автоматически поменять регистр всех букв на противоположный. Например, регистр букв слов «hELLO», «HTTP», «z» должен быть изменен. Напишите программу, которая применяет описанное выше правило или оставляет слово без изменения, если оно не применимо. Выходные данные Выведите результат обработки данного слова. | |
![]()
|
|
A. cAPS lOCK
реализация
Строки
*1000
зАЧЕМ НУЖНА КЛАВИША cAPS lOCK? Caps Lock — клавиша компьютерной клавиатуры, предназначенная для автоматической (постоянной) смены регистра букв со строчных на прописные. Будучи случайно нажатой, она приводит к последствиям вроде первого абзаца в условии этой задачи. Будем считать, что слово набрано с ошибочно нажатой клавишей Caps Lock, если: - либо оно полностью состоит из прописных букв;
- либо прописными являются все его буквы, кроме первой.
В таком случае, нужно автоматически поменять регистр всех букв на противоположный. Например, регистр букв слов «hELLO», «HTTP», «z» должен быть изменен. Напишите программу, которая применяет описанное выше правило или оставляет слово без изменения, если оно не применимо. Выходные данные Выведите результат обработки данного слова. | |
![]()
|
|
A. cAPS lOCK
реализация
Строки
*1000
зАЧЕМ НУЖНА КЛАВИША cAPS lOCK? Caps Lock — клавиша компьютерной клавиатуры, предназначенная для автоматической (постоянной) смены регистра букв со строчных на прописные. Будучи случайно нажатой, она приводит к последствиям вроде первого абзаца в условии этой задачи. Будем считать, что слово набрано с ошибочно нажатой клавишей Caps Lock, если: - либо оно полностью состоит из прописных букв;
- либо прописными являются все его буквы, кроме первой.
В таком случае, нужно автоматически поменять регистр всех букв на противоположный. Например, регистр букв слов «hELLO», «HTTP», «z» должен быть изменен. Напишите программу, которая применяет описанное выше правило или оставляет слово без изменения, если оно не применимо. Выходные данные Выведите результат обработки данного слова. | |
![]()
|
|
A. cAPS lOCK
реализация
Строки
*1000
зАЧЕМ НУЖНА КЛАВИША cAPS lOCK? Caps Lock — клавиша компьютерной клавиатуры, предназначенная для автоматической (постоянной) смены регистра букв со строчных на прописные. Будучи случайно нажатой, она приводит к последствиям вроде первого абзаца в условии этой задачи. Будем считать, что слово набрано с ошибочно нажатой клавишей Caps Lock, если: - либо оно полностью состоит из прописных букв;
- либо прописными являются все его буквы, кроме первой.
В таком случае, нужно автоматически поменять регистр всех букв на противоположный. Например, регистр букв слов «hELLO», «HTTP», «z» должен быть изменен. Напишите программу, которая применяет описанное выше правило или оставляет слово без изменения, если оно не применимо. Выходные данные Выведите результат обработки данного слова. | |
![]()
|
|
A. cAPS lOCK
реализация
Строки
*1000
зАЧЕМ НУЖНА КЛАВИША cAPS lOCK? Caps Lock — клавиша компьютерной клавиатуры, предназначенная для автоматической (постоянной) смены регистра букв со строчных на прописные. Будучи случайно нажатой, она приводит к последствиям вроде первого абзаца в условии этой задачи. Будем считать, что слово набрано с ошибочно нажатой клавишей Caps Lock, если: - либо оно полностью состоит из прописных букв;
- либо прописными являются все его буквы, кроме первой.
В таком случае, нужно автоматически поменять регистр всех букв на противоположный. Например, регистр букв слов «hELLO», «HTTP», «z» должен быть изменен. Напишите программу, которая применяет описанное выше правило или оставляет слово без изменения, если оно не применимо. Выходные данные Выведите результат обработки данного слова. | |
![]()
|
|
A. cAPS lOCK
реализация
Строки
*1000
зАЧЕМ НУЖНА КЛАВИША cAPS lOCK? Caps Lock — клавиша компьютерной клавиатуры, предназначенная для автоматической (постоянной) смены регистра букв со строчных на прописные. Будучи случайно нажатой, она приводит к последствиям вроде первого абзаца в условии этой задачи. Будем считать, что слово набрано с ошибочно нажатой клавишей Caps Lock, если: - либо оно полностью состоит из прописных букв;
- либо прописными являются все его буквы, кроме первой.
В таком случае, нужно автоматически поменять регистр всех букв на противоположный. Например, регистр букв слов «hELLO», «HTTP», «z» должен быть изменен. Напишите программу, которая применяет описанное выше правило или оставляет слово без изменения, если оно не применимо. Выходные данные Выведите результат обработки данного слова. | |
![]()
|
|
A. cAPS lOCK
реализация
Строки
*1000
зАЧЕМ НУЖНА КЛАВИША cAPS lOCK? Caps Lock — клавиша компьютерной клавиатуры, предназначенная для автоматической (постоянной) смены регистра букв со строчных на прописные. Будучи случайно нажатой, она приводит к последствиям вроде первого абзаца в условии этой задачи. Будем считать, что слово набрано с ошибочно нажатой клавишей Caps Lock, если: - либо оно полностью состоит из прописных букв;
- либо прописными являются все его буквы, кроме первой.
В таком случае, нужно автоматически поменять регистр всех букв на противоположный. Например, регистр букв слов «hELLO», «HTTP», «z» должен быть изменен. Напишите программу, которая применяет описанное выше правило или оставляет слово без изменения, если оно не применимо. Выходные данные Выведите результат обработки данного слова. | |
![]()
|
|
A. cAPS lOCK
реализация
Строки
*1000
зАЧЕМ НУЖНА КЛАВИША cAPS lOCK? Caps Lock — клавиша компьютерной клавиатуры, предназначенная для автоматической (постоянной) смены регистра букв со строчных на прописные. Будучи случайно нажатой, она приводит к последствиям вроде первого абзаца в условии этой задачи. Будем считать, что слово набрано с ошибочно нажатой клавишей Caps Lock, если: - либо оно полностью состоит из прописных букв;
- либо прописными являются все его буквы, кроме первой.
В таком случае, нужно автоматически поменять регистр всех букв на противоположный. Например, регистр букв слов «hELLO», «HTTP», «z» должен быть изменен. Напишите программу, которая применяет описанное выше правило или оставляет слово без изменения, если оно не применимо. Выходные данные Выведите результат обработки данного слова. | |
![]()
|
|
C. Красный мост
Бинарный поиск
дп
Строки
*2800
ВКонтакте открыла второй штаб в Санкт-Петербурге! На фасаде здания, в котором он находится, написана строка \(s\). В процессе проектирования офиса часть офиса вдоль всей этой надписи было принято разделить на \(m\) переговорных комнат таким образом, чтобы стены комнат всегда были точно между символами строки на фасаде. Разумеется, переговорные не должны быть нулевого размера, но вполне могут быть шириной в одну букву. Названием каждой комнаты станет подстрока исходной строки \(s\), находящаяся на соответствующей части фасада.  Для того, чтобы протестировать разные варианты дизайна офиса, для каждой возможной конфигурации из \(m\) переговорных комнат напечатали табличку с названием минимальной в лексикографическом порядке комнаты. Для доставки, типография отсортировала эти таблички в обратном лексикографическом порядке напечатанных названий переговорных. Какое название написано на \(k\)-й табличке? Выходные данные Выведите одну строку — надпись на \(k\)-й табличке из доставки. Примечание В первом примере посылка из типографии состоит из табличек «aba», «ab», «a». В втором примере посылка состоит из \(3060\) табличек, первая из которых — «aupontrougevkof», а последняя — «a». | |
![]()
|
|
E. Конкатенация с пересечением
Строки
Структуры данных
хэши
*2700
У Васи было три строки \(a\), \(b\) и \(s\), состоящие из строчных символов латинского алфавита. Длины строк \(a\) и \(b\) равны \(n\), длина строки \(s\) равна \(m\). Вася решил выбрать подстроку из строки \(a\), затем выбрать подстроку из строки \(b\) и сконцентрировать их. Формально, он выбирает подотрезок \([l_1, r_1]\) (\(1 \leq l_1 \leq r_1 \leq n\)) и подотрезок \([l_2, r_2]\) (\(1 \leq l_2 \leq r_2 \leq n\)), а после конкатенации получает строку \(a[l_1, r_1] + b[l_2, r_2] = a_{l_1} a_{l_1 + 1} \ldots a_{r_1} b_{l_2} b_{l_2 + 1} \ldots b_{r_2}\). Теперь Васю заинтересовал вопрос, сколькими способами он может выбрать пару отрезков так, что выполнены следующие условия: - отрезки \([l_1, r_1]\) и \([l_2, r_2]\) пересекаются, то есть существует хотя бы одно целое число \(x\), такое что \(l_1 \leq x \leq r_1\) и \(l_2 \leq x \leq r_2\);
- полученная Васей в итоге строка \(a[l_1, r_1] + b[l_2, r_2]\) равна строке \(s\).
Выходные данные Выведите одно целое число — количество способов выбрать пару отрезков, удовлетворяющую Васиным условиям. Примечание Перечислим все пары отрезков, которые мог выбрать Вася в первом примере: - \([2, 2]\) и \([2, 5]\);
- \([1, 2]\) и \([2, 4]\);
- \([5, 5]\) и \([2, 5]\);
- \([5, 6]\) и \([3, 5]\);
| |
![]()
|
|
B. Дорога домой
Бинарный поиск
дп
жадные алгоритмы
Строки
*1300
После долгой вечеринки Петя захотел поехать домой, но обнаружил себя в другом конце города. В городе есть \(n\) перекрестков, расположенных в ряд, и на каждом перекрестке есть остановка, на которой можно сесть либо на автобус, либо на троллейбус. Перекрестки можно задать как строку \(s\) длины \(n\), где \(s_i = \texttt{A}\), если на \(i\)-м перекрестке есть автобусная станция, и \(s_i = \texttt{B}\), если на \(i\)-м перекрестке есть троллейбусная станция. Сейчас Петя находится на первом перекрестке (которому соответствует \(s_1\)), и ему нужно попасть на последний перекресток (которому соответствует \(s_n\)). Если для двух перекрестков \(i\) и \(j\) на всех перекрестках \(i, i+1, \ldots, j-1\) есть автобусная остановка, то можно заплатить \(a\) рублей за билет на автобус, и доехать с \(i\)-й остановки до \(j\)-й (на \(j\)-й остановке не обязательно иметь возможность сесть на автобус). Формально, заплатив \(a\) рублей Петя может добраться из \(i\) до \(j\), если \(s_t = \texttt{A}\) для всех \(i \le t < j\). Если для двух перекрестков \(i\) и \(j\) на всех перекрестках \(i, i+1, \ldots, j-1\) есть троллейбусная остановка, то можно заплатить \(b\) рублей за билет на троллейбус, и доехать с \(i\)-й остановки до \(j\)-й (на \(j\)-й остановке не обязательно иметь возможность сесть на троллейбус). Формально, заплатив \(b\) рублей Петя может добраться из \(i\) до \(j\), если \(s_t = \texttt{B}\) для всех \(i \le t < j\). Например, если \(s\)=«AABBBAB», \(a=4\) и \(b=3\), то Петя может:  - купить билет на автобус, чтобы добраться от \(1\) до \(3\),
- купить билет на троллейбус, чтобы добраться от \(3\) до \(6\),
- купить билет на автобус, чтобы добраться от \(6\) до \(7\).
Так, в общем ему нужно потратить \(4+3+4=11\) рублей. Обратите внимание, что остановка на последнем перекрестке (т.е. символ \(s_n\)) не влияет на итоговую стоимость. Сейчас Петя находится на первом перекрестке, и он хочет попасть на \(n\)-й перекресток. После вечеринки у него осталось всего \(p\) рублей, и он хочет попасть домой. Он решил пройти несколько перекрестков пешком, а после этого доехать домой на общественном транспорте. Помогите ему выбрать ближайший перекресток \(i\) к первому так, чтобы ему хватило денег добраться с \(i\)-го перекрестка до \(n\)-го, используя лишь поездки на автобусах и троллейбусах. Выходные данные Для каждого набора входных данных выведите одно целое число — минимальный номер перекрестка \(i\), до которого Пете придется идти пешком. Оставшуюся часть пути (т.е. от \(i\) до \(n\)) он должен ехать на общественном транспорте. | |
![]()
|
|
B. Преобразование строки
Конструктив
Перебор
реализация
сортировки
Строки
*1400
У Васи есть строка \(s\) длины \(n\). Он решает применить к ней следующее преобразование: - Выберите целое \(k\), (\(1 \leq k \leq n\)).
- Для \(i\) от \(1\) до \(n-k+1\), переверните подстроку \(s[i:i+k-1]\) строки \(s\). К примеру, если строка \(s\) равна qwer и \(k = 2\), то строка пройдет следующую последовательность изменений:
- qwer (начальная строка)
- wqer (после переворачивания первой подстроки длины \(2\))
- weqr (после переворачивания второй подстроки длины \(2\))
- werq (после переворачивания последней подстроки длины \(2\))
Следовательно, получившаяся строка после преобразования \(s\) с \(k = 2\) равна werq. Вася хочет выбрать такое \(k\), чтобы строка, полученная в результате преобразования, была лексикографически минимальной возможной среди всех выборов \(k\). Среди всех таких \(k\) он хочет выбрать наименьшее. Так как он занят посещением Felicity 2020, он просит вашей помощи. Строка \(a\) лексикографически меньше строки \(b\), если и только если выполняется один из следующих пунктов: - \(a\) — префикс \(b\), но \(a \ne b\);
- в первой позиции, где \(a\) и \(b\) различны, в строке \(a\) находится буква, которая встречается в алфавите раньше, чем соответствующая буква в \(b\).
Выходные данные Для каждого набора входных данных выведите две строки: В первой строке выведите лексикографически минимально возможную строку \(s'\), получающуюся как результат преобразования. Во второй строке выведите подходящее значение \(k\) (\(1 \leq k \leq n\)), которое вы выбрали для преобрразования. Если несколько значений \(k\) дают лексикографически минимальную строку, выведите минимальное \(k\) среди них. Примечание В первом наборе тестовых данных примера, преобразование строки abab даст следующие результаты: | |
![]()
|
|
C. Удаление соседних
жадные алгоритмы
Конструктив
Перебор
Строки
*1600
Вам задана строка \(s\), состоящая из строчных букв латинского алфавита. Пусть длина \(s\) равна \(|s|\). За один ход вы можете выбрать любой индекс \(i\) и удалить \(i\)-й символ \(s\) (\(s_i\)), если хотя бы один из его соседних символов является предыдущей буквой в латинском алфавите для \(s_i\). Например, для буквы b предыдущей буквой является a, для буквы s предыдущей букой является r, для буквы a предыдущей буквы не существует. Заметьте, что после каждого удаления длина строки уменьшается на единицу. Таким образом, индекс \(i\) должен удовлетворять условию \(1 \le i \le |s|\) в течение каждого хода. Соседними символами для символа \(s_i\) являются символы \(s_{i-1}\) и \(s_{i+1}\). Первый и последний символы \(s\) имеют только один соседний символ (за исключением случая \(|s| = 1\)). Рассмотрим следующий пример. Пусть \(s=\) bacabcab. - В течение первого хода вы можете удалить первый символ \(s_1=\) b, так как \(s_2=\) a. Тогда строка станет равна \(s=\) acabcab.
- В течение второго хода вы можете удалить пятый символ \(s_5=\) c, так как \(s_4=\) b. Тогда строка станет равна \(s=\) acabab.
- В течение третьего хода вы можете удалить шестой символ \(s_6=\) b, так как \(s_5=\) a. Тогда строка станет равна \(s=\) acaba.
- В течение четвертого хода единственным символом, который вы можете удалить, является \(s_4=\) b, так как \(s_3=\) a (или \(s_5=\) a). Строка станет равна \(s=\) acaa, и вы больше не сможете ничего с ней сделать.
Ваша задача — найти максимальное количество символов, которые вы можете удалить, если вы выберете последовательность ходов оптимально. Выходные данные Выведите одно целое число — максимально возможное количество символов, которые вы можете удалить, если вы выберете последовательность ходов оптимально. Примечание Первый тестовый пример разобран в условии задачи. Заметьте, что последовательность ходов, представленная в условии, не является единственной, но можно показать, что максимально возможный ответ на этот тест равен \(4\). Во втором тестовом примере вы можете удалить все символы \(s\), кроме одного. Единственный возможный ответ описан ниже. - В течение первого хода следует удалить третий символ \(s_3=\) d, \(s\) станет равна bca.
- В течение второго хода следует удалить второй символ \(s_2=\) c, \(s\) станет равна ba.
- Наконец, в течение третьего хода следует удалить первый символ \(s_1=\) b, \(s\) станет равна a.
| |
![]()
|
|
B. Еще одна задача про палиндромы
Перебор
Строки
*1100
Вам задан массив \(a\), состоящий из \(n\) целых чисел. Ваша задача — определить, содержит ли \(a\) какую-то подпоследовательность длины хотя бы \(3\), которая является палиндромом. Напомним, что массив \(b\) называется подпоследовательностью массива \(a\), если \(b\) может быть получен удалением некоторого (возможно, нулевого) количества элементов из \(a\) (не обязательно подряд идущих) без изменения порядка оставшихся элементов. Например, \([2]\), \([1, 2, 1, 3]\) и \([2, 3]\) являются подпоследовательностями \([1, 2, 1, 3]\), а \([1, 1, 2]\) и \([4]\) — нет. Также напомним, что палиндром — это массив, который читается одинаково как слева направо, так и справа налево. Другими словами, массив \(a\) длины \(n\) является палиндромом, если \(a_i = a_{n - i - 1}\) для всех \(i\) от \(1\) до \(n\). Например, массивы \([1234]\), \([1, 2, 1]\), \([1, 3, 2, 2, 3, 1]\) и \([10, 100, 10]\) являются палиндромами, а массивы \([1, 2]\) и \([1, 2, 3, 1]\) — нет. Вам необходимо ответить на \(t\) независимых наборов тестовых данных. Выходные данные Для каждого набора тестовых данных выведите ответ — «YES» (без кавычек), если \(a\) содержит какую-то подпоследовательность длины хотя бы \(3\), которая является палиндромом, и «NO» в противном случае. Примечание В первом наборе тестовых данных из примера массив \(a\) содержит подпоследовательность \([1, 2, 1]\), которая является палиндромом. Во втором наборе тестовых данных из примера массив \(a\) содержит две подпоследовательности длины \(3\), которые являются палиндромами: \([2, 3, 2]\) и \([2, 2, 2]\). В третьем наборе тестовых данных из примера в массиве \(a\) нет подпоследовательностей длины хотя бы \(3\), которые являются палиндромами. В четвертом наборе тестовых данных из примера массив \(a\) содержит одну последовательность длины \(4\), которая является палиндромом: \([1, 2, 2, 1]\) (и содержит две подпоследовательности длины \(3\), которые являются палиндромами: обе равны \([1, 2, 1]\)). В пятом наборе тестовых данных из примера в массиве \(a\) нет подпоследовательностей длины хотя бы \(3\), которые являются палиндромами. | |
![]()
|
|
D1. Префиксно-суффиксный палиндром (упрощенная версия)
Строки
строковые суфф. структуры
хэши
*1500
Это упрощенная версия этой задачи. Различие в ограничениях на сумму длин строк и на количество тестовых случаев. Вы можете делать взломы, только если обе версии этой задачи решены. Вам дана строка \(s\), состоящая из строчных букв латинского алфавита. Вы должны найти строку \(t\) максимальной длины, которая удовлетворяет следующим условиям: - Длина строки \(t\) не превосходит длину строки \(s\).
- \(t\) является палиндромом, то есть она равна себе перевернутой.
- Существует две строки \(a\) и \(b\) (возможно пустые), такие что \(t = a + b\) (здесь операция «\(+\)» это конкатенация строк) и \(a\) является префиксом строки \(s\) и \(b\) является суффиксом строки \(s\).
Выходные данные Для каждого тестового случая выведите строку максимальной длины, которая удовлетворяет описанным условиям. Если существует несколько решений, вы можете вывести любое. Примечание В первом тестовом случае, вся строка \(s = \)«a» удовлетворяет всем условиям. Во втором тестовом случае, строка «abcdfdcba» удовлетворяет всем условиям, потому что: - ее длина равна \(9\), что не превосходит длину строки \(s\), которая равна \(11\);
- она палиндром;
- «abcdfdcba» \(=\) «abcdfdc» \(+\) «ba», где строка «abcdfdc» является префиксом строки \(s\) и строка «ba» является суффиксом строки \(s\).
Можно доказать, что невозможно найти более длинную такую строку. В четвертом тестовом случае, строка «c» это правильный ответ, потому что «c» \(=\) «c» \(+\) «» и это допустимо, потому что по условию строки \(a\) и \(b\) могут быть пустыми. Другой возможный ответ на этот тест это строка «s». | |
![]()
|
|
D2. Префиксно-суффиксный палиндром (усложненная версия)
Бинарный поиск
жадные алгоритмы
Строки
строковые суфф. структуры
хэши
*1800
Это усложненная версия этой задачи. Различия в ограничениях на сумму длин строк и на количество тестовых случаев. Вы можете делать взломы, только если обе версии этой задачи решены. Вам дана строка \(s\), состоящая из строчных букв латинского алфавита. Вы должны найти строку \(t\) максимальной длины, которая удовлетворяет следующим условиям: - Длина строки \(t\) не превосходит длину строки \(s\).
- \(t\) является палиндромом, то есть она равна себе перевернутой.
- Существует две строки \(a\) и \(b\) (возможно пустые), такие что \(t = a + b\) (здесь операция «\(+\)» это конкатенация строк) и \(a\) является префиксом строки \(s\) и \(b\) является суффиксом строки \(s\).
Выходные данные Для каждого тестового случая выведите строку максимальной длины, которая удовлетворяет описанным условиям. Если существует несколько решений, вы можете вывести любое. Примечание В первом тестовом случае, вся строка \(s = \)«a» удовлетворяет всем условиям. Во втором тестовом случае, строка «abcdfdcba» удовлетворяет всем условиям, потому что: - ее длина равна \(9\), что не превосходит длину строки \(s\), которая равна \(11\);
- она палиндром;
- «abcdfdcba» \(=\) «abcdfdc» \(+\) «ba», где строка «abcdfdc» является префиксом строки \(s\) и строка «ba» является суффиксом строки \(s\).
Можно доказать, что невозможно найти более длинную такую строку. В четвертом тестовом случае, строка «c» это правильный ответ, потому что «c» \(=\) «c» \(+\) «» и это допустимо, потому что по условию строки \(a\) и \(b\) могут быть пустыми. Другой возможный ответ на этот тест это строка «s». | |
![]()
|
|
F. Элементарно!
*особая задача
дп
Перебор
Строки
Выходные данные Выведите «YES» или «NO». | |
![]()
|
|
C. K-полное слово
жадные алгоритмы
поиск в глубину и подобное
реализация
снм
Строки
*1500
Слово \(s\) длины \(n\) называется \(k\)-полным, если - \(s\) — палиндром, то есть \(s_i=s_{n+1-i}\) для всех \(1 \le i \le n\);
- \(s\) имеет период \(k\), то есть \(s_i=s_{k+i}\) для всех \(1 \le i \le n-k\).
Например, «abaaba» — это \(3\)-полное слово, а «abccba» нет. Бобу вручили слово \(s\) длины \(n\), состоящее только из строчных букв латинского алфавита, и целое число \(k\) такое, что \(n\) делится на \(k\). Он хочет превратить слово \(s\) в любое \(k\)-полное слово. Для этого Боб может выбирать некоторую позицию \(i\) (\(1 \le i \le n\)) и заменять букву на позиции \(i\) на любую другую строчную букву латинского алфавита. Поэтому теперь Боба интересует минимальное количество позиций, буквы на которых ему необходимо заменить, чтобы превратить \(s\) в любое \(k\)-полное слово. Обратите внимание, что Боб может сделать ноль изменений, если слово \(s\) уже \(k\)-полное. Требуется ответить на \(t\) независимых наборов входных данных. Выходные данные Для каждого набора входных данных выведите одно целое число, обозначающее минимальное количество позиций, буквы на которых ему придется заменить, чтобы превратить \(s\) в любое \(k\)-полное слово. Примечание В первом наборе входных данных одно из оптимальных решений — это «aaaaaa». Во втором наборе входных данных слово уже \(k\)-полное. | |
![]()
|
|
C. Kaavi и магическое заклинание
дп
Строки
*2200
Kaavi, таинственная гадалка, глубоко верит в то, что судьба человека неизбежна и неотвратима. Конечно, она зарабатывает себе на жизнь предсказывая будущее других людей. Занимаясь гаданием, Kaavi верит, что магические заклинания могут дать ей огромную силу видеть будущее.  У Kaavi есть строка \(T\) длины \(m\) и все строки, имеющие префикс \(T\) это магические заклинания. У Kaavi также есть строка \(S\) длины \(n\) и пустая строка \(A\). Во время гадания, Kaavi нужно применить некоторую последовательность операций. Есть две различные операции: - Удалить первый символ строки \(S\) и добавить его в начало строки \(A\).
- Удалить первый символ строки \(S\) и добавить его в конец строки \(A\).
Kaavi может сделать не более, чем \(n\) операций. Для того, чтобы завершить гадание, она хочет узнать количество различных последовательностей операций, для того, чтобы сделать \(A\) магическим заклинанием (то есть эта строка имеет префикс \(T\)). Как ее ассистент, можете ли вы помочь ей? Поскольку ответ может быть очень большим, Kaavi хочет знать его остаток при делении на \(998\,244\,353\). Две последовательности операций считаются различными, если они различаются по длине или существует такое \(i\), что их \(i\)-е операции различаются. Подстрокой называется некоторая последовательность последовательных символов строки. Префиксом строки \(S\) называется подстрока \(S\), которая начинается в начале строки \(S\). Выходные данные Выведите единственное целое число — ответ на задачу по модулю \(998\,244\,353\). Примечание В первом тесте: 
Красные строки это магические заклинания. В первой операции, Kaavi может добавить символ «a» в начало или в конец \(A\). Хотя в обоих случаях результат будет одинаковым, это две разные операции. Поэтому ответ \(6\times2=12\). | |
![]()
|
|
B. Двоичный период
Конструктив
Строки
*1100
Скажем, что строка \(s\) имеет период \(k\), если \(s_i = s_{i + k}\) для всех \(i\) от \(1\) по \(|s| - k\) (\(|s|\) — это длина строки \(s\)), и \(k\) — минимальное положительное целое число с этим свойством. Несколько примеров вычисления периода: для \(s\)=«0101» период равен \(k=2\), для \(s\)=«0000» период равен \(k=1\), для \(s\)=«010» период равен \(k=2\), для \(s\)=«0011» период равен \(k=4\). Вам задана строка \(t\), состоящая только из 0 и 1, и вам нужно найти такую строку \(s\), что: - Строка \(s\) состоит только из 0 и 1;
- Длина \(s\) не превосходит \(2 \cdot |t|\);
- Строка \(t\) является подпоследовательностью строки \(s\);
- Строка \(s\) имеет минимальный возможный период среди всех строк, удовлетворяющих условиям 1—3.
Напомним, что \(t\) является подпоследовательностью \(s\), если \(t\) можно получить из \(s\) путем удаления нуля или более элементов (любых) и не меняя порядок оставшихся элементов. Например, \(t\)=«011» — это подпоследовательность строки \(s\)=«10101». Выходные данные Выведите по одной строке на каждый набор входных данных — строку \(s\), которую вам надо найти. Если существует несколько решений — выведите любое из них. Примечание В первом и втором наборе \(s = t\), так как это уже одни из оптимальных решений. Периоды ответов равны \(1\) и \(2\), соответственно. В третьем наборе, есть и другие более короткие ответы, но все в порядке, потому что не требуется минимизировать ответ \(s\). Строка \(s\) имеет период \(1\). | |
![]()
|
|
C. Феникс и распределение
жадные алгоритмы
Конструктив
сортировки
Строки
*1600
У Феникса есть строка \(s\), состоящая из строчных букв латинского алфавита. Он хочет распределить все буквы своей строки по \(k\) непустым строкам \(a_1, a_2, \dots, a_k\) так, что каждая буква из \(s\) попадет ровно в одну из строк \(a_i\). Строки \(a_i\) не обязаны быть подстроками \(s\). Феникс может распределить буквы \(s\) и переупорядочить их внутри каждой строки \(a_i\) так как захочет. Например, если \(s = \) baba и \(k=2\), Феникс может распределить буквы своей строки множеством способов, в том числе: - ba и ba
- a и abb
- ab и ab
- bb и aa
Однако получить такие варианты он не может: - baa и ba
- b и ba
- baba и пустая строка (\(a_i\) должны быть непустыми)
Феникс хочет разделить свою строку \(s\) на \(k\) строк \(a_1, a_2, \dots, a_k\) так, чтобы минимизировать лексикографически максимальную строку среди них, т. е. минимизировать \(max(a_1, a_2, \dots, a_k)\). Помогите ему найти оптимальное распределение и выведите минимально возможное значение \(max(a_1, a_2, \dots, a_k)\). Строка \(x\) лексикографически меньше, чем строка \(y\), если либо \(x\) является префиксом \(y\) (и \(x \ne y\)), либо существует такой индекс \(i\) (\(1 \le i \le min(|x|, |y|))\), что \(x_i\) < \(y_i\) и для всех \(j\) \((1 \le j < i)\) \(x_j = y_j\). Здесь \(|x|\) обозначает длину строки \(x\). Выходные данные Выведите \(t\) ответов — по одному на набор входных данных; \(i\)-й ответ — минимально возможный \(max(a_1, a_2, \dots, a_k)\) в \(i\)-м наборе. Примечание В первом наборе входных данных, одно из оптимальных решений — разбить baba на ab и ab. Во втором наборе входных данных, одно из оптимальных решений — разбить baacb на abbc и a. В третьем наборе, одно из оптимальных решений — разбить baacb на ac, ab и b. В четвертом наборе, одно из оптимальных решений — разбить aaaaa на aa, aa и a. В пятом наборе, одно из оптимальных решений — разбить aaxxzz на az, az, x и x. В шестом наборе, одно из оптимальных решений — разбить phoenix на ehinopx. | |
![]()
|
|
F. Строка-шпион
битмаски
дп
Конструктив
Перебор
Строки
хэши
*1700
Вам даны \(n\) строк \(a_1, a_2, \ldots, a_n\), все они имеют одинаковую длину \(m\). Строки состоят из строчных букв латинского алфавита. Найдите любую такую строку \(s\) длины \(m\), что каждая из заданных \(n\) строк отличается от \(s\) не более чем в одной позиции. Формально, для каждой заданной строки \(a_i\) должно существовать не более одной позиции \(j\), в которой \(a_i[j] \ne s[j]\). Заметим, что искомая строка \(s\) может как совпадать с одной из заданных строк \(a_i\), так и отличаться от всех заданных строк. Например, если вам даны строки abac и zbab, тогда ответом на задачу может быть строка abab, которая отличается от первой только последним символом, а от второй только первым. Выходные данные Выведите \(t\) ответов на наборы тестовых данных. Каждый ответ (если он существует) — это строка длины \(m\), состоящая из строчных латинских букв. Если существует несколько ответов, то выведите любой из них. Если ответа не существует, выведите «-1» («минус один», без кавычек). Примечание Первый набор тестовых данных примера разобран в условии. Во втором наборе ответа не существует. | |
![]()
|
|
B. Ненависть к подпоследовальностям
реализация
Строки
*1400
У Shubham есть бинарная строка \(s\). Бинарная строка — это строка, содержащая только символы «0» и «1». Он может выполнить следующую операцию над строкой любое количество раз: - Выбрать индекс строки, и поменять символ с этим индексом. Это означает, что если символ был «0», он становится «1», и наоборот.
Строка называется хорошей, если она не содержит строк «010» или «101» в качестве подпоследовательностей — например, «1001» содержит «101» как подпоследовательность, следовательно, это не хорошая строка, а «1000» не содержит ни «010» ни «101» как подпоследовательностей, поэтому это хорошая строка. Какое минимальное количество операций ему придется выполнить, чтобы строка стала хорошей? Можно показать, что с помощью данных операций можно сделать любую строку хорошей. Строка \(a\) является подпоследовательностью строки \(b\), если \(a\) может быть получена из \(b\) удалением нескольких (возможно, ни одного или всех) символов. Выходные данные Для каждой строки выведите минимальное количество операций необходимых для того, чтобы сделать ее хорошей. Примечание В наборах входных данных \(1\), \(2\), \(5\), \(6\) строки уже являются хорошими — поэтому никаких операций не требуется. Для набора \(3\): «001» можно получить, поменяв первый символ, и это один из возможных способов получить хорошую строку. Для набора \(4\): «000» можно получить, поменяв второй символ, и это один из возможных способов получить хорошую строку. Для набора \(7\): «000000» можно получить, поменяв третий и четвертый символы, и это один из возможных способов получить хорошую строку. | |
![]()
|
|
F. Вращение подстрок
дп
Строки
*2600
Вам даны две строки \(s\) и \(t\), каждая из которых имеет длину \(n\) и состоит из строчных букв латинского алфавита. Вы хотите сделать \(s\) равной \(t\). Вы можете выполнить следующую операцию над \(s\) любое количество раз, чтобы достичь этого — Строка \(a\) является подстрокой \(b\), если \(a\) может быть получена из \(b\) удалением нескольких (возможно, ни одного или всех) символов из начала и нескольких (возможно, ни одного или всех) символов из конца. Найдите минимальное количество операций, необходимых для преобразования \(s\) в \(t\), или определите, что это невозможно. Выходные данные Для каждого набора входных данных выведите минимальное количество операций для преобразования \(s\) в \(t\). Если невозможно преобразовать \(s\) в \(t\), вместо этого выведите \(-1\). Примечание Для первого набора входных данных, поскольку \(s\) и \(t\) равны, вам не нужно применять какие-либо операции. Для второго набора входных данных вам нужно применить только одну операцию ко всей строке ab, чтобы преобразовать ее в ba. Для третьего набора входных данных вам нужно только применить одну операцию ко всей строке abc, чтобы преобразовать ее в cab. Для четвертого набора входных данных вам нужно применить операцию дважды: сначала для всей строки abc, чтобы преобразовать ее в cab, а затем для подстроки длины \(2\), начинающейся со второго символа для преобразования ее в cba. Для пятого набора входных данных вам нужно применить только одну операцию ко всей строке abab, чтобы преобразовать ее в baba. Для шестого набора входных данных превратить строку \(s\) в строку \(t\) не является возможным. | |
![]()
|
|
G. Построй строку
дп
Строки
Структуры данных
*2700
Определим функцию \(f(s)\), которая принимает строку \(s\), состоящую из строчных латинских букв и точек, и возвращает строку, состоящую из строчных латинских букв следующим образом: - пусть \(r\) пустая строка;
- будем обрабатывать символы \(s\) слева направо. Для каждого символа \(c\) выполним следующее: если \(c\) является строчной латинской буквой, то добавим \(c\) в конец строки \(r\); в противном случае удалим последний символ из \(r\) (если \(r\) пустая — функция аварийно завершает работу);
- вернуть \(r\) как результат функции.
Вам заданы две строки \(s\) и \(t\). Вы должны удалить минимально возможное количество символов из \(s\), чтобы \(f(s) = t\) (и функция не завершалась аварийно). Обратите внимание, что вам не разрешается вставлять новые символы в \(s\) или менять порядок существующих. Выходные данные Выведите одно целое число — минимально возможное количество символов, которое необходимо удалить из \(s\), чтобы \(f(s)\) не завершалась аварийно и вернула \(t\) в качестве результата выполнения. | |
![]()
|
|
A. Короткие подстроки
реализация
Строки
*800
Алиса отгадывает строки, которые загадал ей Боб. Сначала Боб придумал придумал секретную строку \(a\), состоящую из строчных букв латинского алфавита. Строка \(a\) имеет длину \(2\) или более символов. Затем по строке \(a\) он строит новую строку \(b\) и даёт Алисе строку \(b\), чтобы она могла угадать строку \(a\). Боб строит \(b\) по \(a\) следующим образом: он выписывает все подстроки длины \(2\) строки \(a\) в порядке слева направо, а потом соединяет их в том же порядке в строку \(b\). Например, если Боб загадал строку \(a\)=«abac», то все подстроки длины \(2\) строки \(a\) таковы: «ab», «ba», «ac». Следовательно, строка \(b\)=«abbaac». Вам задана строка \(b\). Помогите Алисе определить строку \(a\), которую загадал Боб. Гарантируется, что \(b\) была построена по алгоритму, приведенному выше. Можно доказать, что ответ на задачу единственный. Выходные данные Выведите \(t\) ответов на наборы тестовых данных. Каждый ответ — это строка \(a\), состоящая из строчных букв латинского алфавита, которую загадал Боб. Примечание Первый набор тестовых данных разобран в условии. Во втором наборе тестовых данных Боб загадал строку \(a\)=«ac», строка \(a\) имеет длину \(2\), поэтому строка \(b\) совпадает со строкой \(a\). В третьем наборе тестовых данных Боб загадал строку \(a\)=«bcdaf», подстроки длины \(2\) строки \(a\) таковы: «bc», «cd», «da», «af», поэтому строка \(b\)=«bccddaaf». | |
![]()
|
|
B. Подпоследовательности Codeforces
жадные алгоритмы
Конструктив
математика
Перебор
Строки
*1500
Карл любит Codeforces и подпоследовательности. Он хочет составить строку из маленьких английских букв, которая содержит как минимум \(k\) подпоследовательностей codeforces. Из всех таких строк Карл хочет выбрать самую короткую. Формально, подпоследовательность codeforces строки \(s\) — это подмножество из десяти символов \(s\), которые образуют codeforces, если читать их в строке слева направо. Например, строка codeforces содержит одну подпоследовательность codeforces, а codeforcesisawesome содержит четыре подпоследовательности codeforces: codeforcesisawesome, codeforcesisawesome, codeforcesisawesome, codeforcesisawesome. Помогите Карлу найти любую кратчайшую строку, которая содержит как минимум \(k\) подпоследовательностей codeforces. Выходные данные Выведите кратчайшую строку из маленьких английских букв, которая содержит не менее \(k\) подпоследовательностей codeforces. Если таких строк несколько, выведите любую из них. | |
![]()
|
|
B. ОчиститеЛи
жадные алгоритмы
реализация
Строки
*1200
Ли убирался у себя в дома перед вечеринкой, когда нашел под ковром «грязную» строку. Теперь он хочет очистить строку, но сделать это стильно... Строка \(s\), которую нашел Ли, является двоичной строкой длины \(n\) (т. е. строка состоит только из символов 0 и 1). За один шаг, он может выбрать два последовательных символа \(s_i\) и \(s_{i+1}\) и, если символ \(s_i\) равен 1 и \(s_{i + 1}\) равен 0, он может удалить ровно один из символов (Ли может выбрать какой удалить, но не может удалить оба символа одновременно). После удаления строка сжимается. Ли может сделать произвольное количество шагов (возможно, ни одного шага) и он хочет сделать строку \(s\) как можно более чистой. Он считает, что из двух различных строк \(x\) и \(y\) более короткая строка чище, а если они равны по длине, то чище та, что лексикографически меньше. Сейчас же вам необходимо ответить на \(t\) наборов входных данных: для \(i\)-го набора, выведите самую чистую строку, которую может получить Ли за произвольное количество шагов. Небольшое напоминание: если у нас есть две строки \(x\) и \(y\) равной длины, то \(x\) лексикографически меньше чем \(y\), если существует такая позиция \(i\), что \(x_1 = y_1\), \(x_2 = y_2\),..., \(x_{i - 1} = y_{i - 1}\) и \(x_i < y_i\). Выходные данные Выведите \(t\) ответов — по одному на набор входных данных. Ответом на \(i\)-й набор является самая чистая строка, которую может получить Ли за произвольное (возможно, нулевое) количество шагов. Примечание В первом наборе входных данных, Ли не может сделать ни одного шага. Во втором наборе, Ли должен удалить \(s_2\). В третьем наборе, Ли может, например, выполнить следующие шаги: 11001101 \(\rightarrow\) 1100101 \(\rightarrow\) 110101 \(\rightarrow\) 10101 \(\rightarrow\) 1101 \(\rightarrow\) 101 \(\rightarrow\) 01. | |
![]()
|
|
D. Палиндромы
дп
Строки
*1900
Пятница — любимый день недели Поликарпа. Не потому, что за пятницей идут выходные, а потому что в пятницу по расписанию 2 урока информатики, 2 математики и 2 литературы. Поликарп, конечно, подготовился ко всем урокам, чего не скажешь о его хорошем друге Иннокентие. Иннокентий не успел подготовиться к уроку литературы, поскольку весь вечер четверга провел за игрой в любимую игру Fur2. Чтобы не получить двойку Иннокентий решил выполнить домашнее задание по литературе и прочитать книгу «Буря и затишье» во время уроков информатики и математики (с этими предметами у Иннокентия никогда не было проблем). Увидев это, учитель информатики Валерий Петрович решил дать Иннокентию задание (чтобы тот не скучал и не занимался посторонними вещами). Валерий Петрович сказал, что палиндромом называется строка, одинаково читающаяся как слева направо, так и справа налево. А конкатенацией строк a, b называется строка ab, получающаяся последовательным приписыванием строки b к строке a. Это все Иннокентий, конечно, знал, но задание было намного сложнее, чем он мог себе представить. Валерий Петрович попросил изменить в книге «Буря и затишье» наименьшее число символов, чтобы текст книги оказался конкатенацией не более k палиндромов. С такой задачей Иннокентий не в силах справиться, поэтому попросил вас помочь ему. Выходные данные В первой строке выведите наименьшее число изменений, которые придётся сделать Иннокентию. Во второй строке выведите строку, состоящую из не более чем k палиндромов. Каждый палиндром должен быть непустым и состоять из строчных и заглавных латинских букв. Для разделения палиндромов используйте знак «+» (ASCII-код 43). Если существует несколько решений выведите любое. Регистр букв имеет значения, то есть большая буква считается не эквивалентной соответствующей маленькой букве. | |
![]()
|
|
E. Последний шанс
реализация
Строки
Структуры данных
*2000
Прочитав половину книги «Буря и затишье» на уроках информатики, Иннокентий был полон решимости дочитать книгу на математике. И все было хорошо, пока учительница математики Елена Олеговна не увидела, что Иннокентий вместо решения уравнений пятой степени занят литературой. Поскольку Иннокентий на прошлом уроке предложил алгоритм решения уравнений пятой степени в общем случае, у Елены Олеговны не оставалось другого выбора, как дать ему новое задание. Учительница попросила записать подряд без пробелов все слова из книги «Буря и затишье» в одну длинную строку s. По ее мнению строка является хорошей, если количество гласных букв в строке не более чем вдвое больше количества согласных. Другими словами, строка, в которой v гласных и c согласных, является хорошей тогда и только тогда, когда v ≤ 2c. Задача, которую должен решить Иннокентий, оказалась достаточно простой: необходимо найти количество наибольших по длине хороших подстрок строки s. Выходные данные Выведите в одну строку через пробел два числа: максимальную длину хорошей подстроки, а также количество максимальных по длине хороших подстрок. Если не существует ни одной хорошей подстроки, выведите «No solution» без кавычек. Две подстроки считаются различными, если их позиции вхождения различны. Значит, если какая-то строка встречается несколько раз, то она должна быть учтена такое же количество раз. Примечание В первом примере есть только одна наидлиннейшая хорошая подстрока: сама «Abo». Остальные хорошие подстроки имеют меньшую длину: «b», «Ab», «bo». Во втором примере есть только одна наидлиннейшая хорошая подстрока: «EIS». Остальные хорошие подстроки: «S», «IS». | |
![]()
|
|
C. Перемещай скобки
жадные алгоритмы
Строки
*1000
Вам задана скобочная последовательность \(s\) длины \(n\), где \(n\) четное (без остатка делится на 2). Строка \(s\) состоит из \(\frac{n}{2}\) открывающих скобок '(' и \(\frac{n}{2}\) закрывающих скобок ')'. За один ход вы можете выбрать ровно одну скобку и передвинуть ее в начало или в конец строки (т.е. вы можете выбрать некоторый индекс \(i\), удалить \(i\)-й символ из \(s\) и вставить его перед или после всех остальных символов в \(s\)). Ваша задача — найти минимальное количество ходов, необходимое, чтобы получить правильную скобочную последовательность из \(s\). Можно доказать, что ответ всегда существует при данных ограничениях. Напомним, что такое правильная скобочная последовательность: - «()» — правильная скобочная последовательность;
- если \(s\) — правильная скобочная последовательность, то «(» + \(s\) + «)» — правильная скобочная последовательность;
- если \(s\) и \(t\) — правильные скобочные последовательности, то \(s\) + \(t\) — правильная скобочная последовательность.
Например, «()()», «(())()», «(())» и «()» являются правильными скобочными последовательностями, а «)(», «()(» и «)))» — нет. Вам нужно ответить на \(t\) независимых наборов тестовых данных. Выходные данные Для каждого набора тестовых данных выведите ответ на него — минимальное количество ходов, необходимое, чтобы получить правильную скобочную последовательность из \(s\). Можно доказать, что ответ всегда существует при данных ограничениях. Примечание В первом наборе тестовых данных примера достаточно передвинуть первую скобку в конец строки. В третьем наборе тестовых данных примера достаточно передвинуть последнюю скобку в начало строки. В четвертом наборе тестовых данных примера мы можем выбрать три последние открывающие скобки, переместить их в начало строки и получить «((()))(())». | |
![]()
|
|
A. Акакий и строка
Перебор
реализация
Строки
*1500
Акакий Владиславович изучает строки. Сегодня он столкнулся со следующей задачей. Дана строка \(s\) длины \(n\), состоящая из строчных букв английского алфавита и знаков вопроса. Можно ли заменить знаки вопроса на строчные буквы английского алфавита так, чтобы в полученную строку строка «abacaba» входила как подстрока ровно один раз? Каждый знак вопроса должен быть заменён ровно на одну букву. Например, строка «a?b?c» может быть преобразована в строки «aabbc» или «azbzc», но не может быть преобразована в строки «aabc», «a?bbc» или «babbc». Вхождением строки \(t\) длины \(m\) в строку \(s\) длины \(n\) называется такой индекс \(i\) (\(1 \leq i \leq n - m + 1\)), что строка \(s[i..i+m-1]\), образованная последовательными \(m\) символами строки \(s\), начиная с \(i\)-го, совпадает со строкой \(t\). Например, в строке «ababa» есть два вхождения строки «aba» как подстроки: \(i = 1\) и \(i = 3\), а в строке «acba» вхождения строки «aba» как подстроки нет. Помогите Акакию Владиславовичу проверить можно ли заменить все знаки вопроса на строчные буквы английского алфавита так, чтобы в полученную строку строка «abacaba» входила как подстрока ровно один раз. Выходные данные Для каждого набора входных данных выведите ответ на него. В случае, если невозможно заменить знаки вопроса в строке \(s\) на строчные буквы английского алфавита так, чтобы в получившейся строке было ровно одно вхождение строки «abacaba» как подстроки, выведите «No». В противном случае, выведите «Yes», а во второй строке выведите строку, состоящую из \(n\) строчный букв английского алфавита, — полученную строку. Если существует несколько подходящий строк, выведите любую. Вы можете выводить «Yes» и «No» в любом регистре (например, строки yEs, yes, Yes и YES будут распознаны как положительный ответ). Примечание В первом примере в строке «abacaba» есть ровно одно вхождение строки «abacaba» как подстроки, совпадающее со всей строкой. Во втором примере строка из семи знаков вопроса может быть преобразована в любую строку из семи строчных букв английского алфавита, в том числе и в «abacaba». В шестом примере в строке есть два вхождения строки «abacaba» как подстроки. | |
![]()
|
|
A. Акакий и строка
Перебор
реализация
Строки
*1500
Акакий Владиславович изучает строки. Сегодня он столкнулся со следующей задачей. Дана строка \(s\) длины \(n\), состоящая из строчных букв английского алфавита и знаков вопроса. Можно ли заменить знаки вопроса на строчные буквы английского алфавита так, чтобы в полученную строку строка «abacaba» входила как подстрока ровно один раз? Каждый знак вопроса должен быть заменён ровно на одну букву. Например, строка «a?b?c» может быть преобразована в строки «aabbc» или «azbzc», но не может быть преобразована в строки «aabc», «a?bbc» или «babbc». Вхождением строки \(t\) длины \(m\) в строку \(s\) длины \(n\) называется такой индекс \(i\) (\(1 \leq i \leq n - m + 1\)), что строка \(s[i..i+m-1]\), образованная последовательными \(m\) символами строки \(s\), начиная с \(i\)-го, совпадает со строкой \(t\). Например, в строке «ababa» есть два вхождения строки «aba» как подстроки: \(i = 1\) и \(i = 3\), а в строке «acba» вхождения строки «aba» как подстроки нет. Помогите Акакию Владиславовичу проверить можно ли заменить все знаки вопроса на строчные буквы английского алфавита так, чтобы в полученную строку строка «abacaba» входила как подстрока ровно один раз. Выходные данные Для каждого набора входных данных выведите ответ на него. В случае, если невозможно заменить знаки вопроса в строке \(s\) на строчные буквы английского алфавита так, чтобы в получившейся строке было ровно одно вхождение строки «abacaba» как подстроки, выведите «No». В противном случае, выведите «Yes», а во второй строке выведите строку, состоящую из \(n\) строчный букв английского алфавита, — полученную строку. Если существует несколько подходящий строк, выведите любую. Вы можете выводить «Yes» и «No» в любом регистре (например, строки yEs, yes, Yes и YES будут распознаны как положительный ответ). Примечание В первом примере в строке «abacaba» есть ровно одно вхождение строки «abacaba» как подстроки, совпадающее со всей строкой. Во втором примере строка из семи знаков вопроса может быть преобразована в любую строку из семи строчных букв английского алфавита, в том числе и в «abacaba». В шестом примере в строке есть два вхождения строки «abacaba» как подстроки. | |
![]()
|
|
A. Акакий и строка
Перебор
реализация
Строки
*1500
Акакий Владиславович изучает строки. Сегодня он столкнулся со следующей задачей. Дана строка \(s\) длины \(n\), состоящая из строчных букв английского алфавита и знаков вопроса. Можно ли заменить знаки вопроса на строчные буквы английского алфавита так, чтобы в полученную строку строка «abacaba» входила как подстрока ровно один раз? Каждый знак вопроса должен быть заменён ровно на одну букву. Например, строка «a?b?c» может быть преобразована в строки «aabbc» или «azbzc», но не может быть преобразована в строки «aabc», «a?bbc» или «babbc». Вхождением строки \(t\) длины \(m\) в строку \(s\) длины \(n\) называется такой индекс \(i\) (\(1 \leq i \leq n - m + 1\)), что строка \(s[i..i+m-1]\), образованная последовательными \(m\) символами строки \(s\), начиная с \(i\)-го, совпадает со строкой \(t\). Например, в строке «ababa» есть два вхождения строки «aba» как подстроки: \(i = 1\) и \(i = 3\), а в строке «acba» вхождения строки «aba» как подстроки нет. Помогите Акакию Владиславовичу проверить можно ли заменить все знаки вопроса на строчные буквы английского алфавита так, чтобы в полученную строку строка «abacaba» входила как подстрока ровно один раз. Выходные данные Для каждого набора входных данных выведите ответ на него. В случае, если невозможно заменить знаки вопроса в строке \(s\) на строчные буквы английского алфавита так, чтобы в получившейся строке было ровно одно вхождение строки «abacaba» как подстроки, выведите «No». В противном случае, выведите «Yes», а во второй строке выведите строку, состоящую из \(n\) строчный букв английского алфавита, — полученную строку. Если существует несколько подходящий строк, выведите любую. Вы можете выводить «Yes» и «No» в любом регистре (например, строки yEs, yes, Yes и YES будут распознаны как положительный ответ). Примечание В первом примере в строке «abacaba» есть ровно одно вхождение строки «abacaba» как подстроки, совпадающее со всей строкой. Во втором примере строка из семи знаков вопроса может быть преобразована в любую строку из семи строчных букв английского алфавита, в том числе и в «abacaba». В шестом примере в строке есть два вхождения строки «abacaba» как подстроки. | |
![]()
|
|
A. Акакий и строка
Перебор
реализация
Строки
*1500
Акакий Владиславович изучает строки. Сегодня он столкнулся со следующей задачей. Дана строка \(s\) длины \(n\), состоящая из строчных букв английского алфавита и знаков вопроса. Можно ли заменить знаки вопроса на строчные буквы английского алфавита так, чтобы в полученную строку строка «abacaba» входила как подстрока ровно один раз? Каждый знак вопроса должен быть заменён ровно на одну букву. Например, строка «a?b?c» может быть преобразована в строки «aabbc» или «azbzc», но не может быть преобразована в строки «aabc», «a?bbc» или «babbc». Вхождением строки \(t\) длины \(m\) в строку \(s\) длины \(n\) называется такой индекс \(i\) (\(1 \leq i \leq n - m + 1\)), что строка \(s[i..i+m-1]\), образованная последовательными \(m\) символами строки \(s\), начиная с \(i\)-го, совпадает со строкой \(t\). Например, в строке «ababa» есть два вхождения строки «aba» как подстроки: \(i = 1\) и \(i = 3\), а в строке «acba» вхождения строки «aba» как подстроки нет. Помогите Акакию Владиславовичу проверить можно ли заменить все знаки вопроса на строчные буквы английского алфавита так, чтобы в полученную строку строка «abacaba» входила как подстрока ровно один раз. Выходные данные Для каждого набора входных данных выведите ответ на него. В случае, если невозможно заменить знаки вопроса в строке \(s\) на строчные буквы английского алфавита так, чтобы в получившейся строке было ровно одно вхождение строки «abacaba» как подстроки, выведите «No». В противном случае, выведите «Yes», а во второй строке выведите строку, состоящую из \(n\) строчный букв английского алфавита, — полученную строку. Если существует несколько подходящий строк, выведите любую. Вы можете выводить «Yes» и «No» в любом регистре (например, строки yEs, yes, Yes и YES будут распознаны как положительный ответ). Примечание В первом примере в строке «abacaba» есть ровно одно вхождение строки «abacaba» как подстроки, совпадающее со всей строкой. Во втором примере строка из семи знаков вопроса может быть преобразована в любую строку из семи строчных букв английского алфавита, в том числе и в «abacaba». В шестом примере в строке есть два вхождения строки «abacaba» как подстроки. | |
![]()
|
|
A1. Префиксные перевороты (простая версия)
Конструктив
Строки
Структуры данных
*1300
Это простая версия задачи. Различия между версиями заключаются в ограничениях на \(n\) и необходимое количество операций. Вы можете делать взломы только если обе версии задачи сданы. Есть две бинарные строки \(a\) и \(b\) длины \(n\) (бинарная строка это строка, состоящая из символов \(0\) и \(1\)). За одну операцию вы выбираете префикс строки \(a\), меняете все биты этого префикса на другие (\(0\) меняется на \(1\), \(1\) меняется на \(0\)) и переворачиваете этот префикс. За одну операцию вы выполняете оба этих действия. Например, если \(a=001011\) и вы выбираете префикс длины \(3\), строка становится равной \(011011\). Затем, если вы вы выберете всю строку как префикс для операции, она станет равной \(001001\). Ваша задача превратить строку \(a\) в строку \(b\) за не больше, чем \(3n\) операций. Можно доказать, что это всегда возможно. Выходные данные Для каждого набора входных данных выведите целое число \(k\) (\(0\le k\le 3n\)), затем \(k\) целых чисел \(p_1,\ldots,p_k\) (\(1\le p_i\le n\)). Здесь \(k\) равно количеству операций, которое вы использовали и \(p_i\) равно длине префикса в \(i\)-й операции. Примечание В первом наборе входных данных процесс превращения выглядит так: \(01\to 11\to 00\to 10\). Во втором наборе входных данных процесс превращения выглядит так: \(01011\to 00101\to 11101\to 01000\to 10100\to 00100\to 11100\). В третьем наборе входных данных данные строки уже совпадают. Другим решением будет, например, сделать операцию с префиксом длины \(2\), от чего строка \(a\) не поменяется. | |
![]()
|
|
A2. Префиксные перевороты (сложная версия)
Конструктив
реализация
Строки
Структуры данных
*1700
Это сложная версия задачи. Различия между версиями заключаются в ограничениях на \(n\) и необходимое количество операций. Вы можете делать взломы только если обе версии задачи сданы. Есть две бинарные строки \(a\) и \(b\) длины \(n\) (бинарная строка это строка, состоящая из символов \(0\) и \(1\)). За одну операцию вы выбираете префикс строки \(a\), меняете все биты этого префикса на другие (\(0\) меняется на \(1\), \(1\) меняется на \(0\)) и переворачиваете этот префикс. За одну операцию вы выполняете оба этих действия. Например, если \(a=001011\) и вы выбираете префикс длины \(3\), строка становится равной \(011011\). Затем, если вы вы выберете всю строку как префикс для операции, она станет равной \(001001\). Ваша задача превратить строку \(a\) в строку \(b\) за не больше, чем \(2n\) операций. Можно доказать, что это всегда возможно. Выходные данные Для каждого набора входных данных выведите целое число \(k\) (\(0\le k\le 2n\)), затем \(k\) целых чисел \(p_1,\ldots,p_k\) (\(1\le p_i\le n\)). Здесь \(k\) равно количеству операций, которое вы использовали и \(p_i\) равно длине префикса в \(i\)-й операции. Примечание В первом наборе входных данных процесс превращения выглядит так: \(01\to 11\to 00\to 10\). Во втором наборе входных данных процесс превращения выглядит так: \(01011\to 00101\to 11101\to 01000\to 10100\to 00100\to 11100\). В третьем наборе входных данных данные строки уже совпадают. Другим решением будет, например, сделать операцию с префиксом длины \(2\), от чего строка \(a\) не поменяется. | |
![]()
|
|
A. Трансформация строки 1
графы
Деревья
жадные алгоритмы
снм
сортировки
Строки
*1700
Обратите внимание, что единственная разница между Трансформация строки 1 и Трансформация строки 2 заключается в операции, которую делает Коа. В этой версии буква \(y\), которую выбирает Koa, должна быть строго больше по алфавиту, чем \(x\) (для лучшего понимания прочитайте условие). Вы можете делать взломы по этим задачам независимо. У Коалы Коа есть две строки \(A\) и \(B\) одинаковой длины \(n\) (\(|A|=|B|=n\)), состоящие из первых \(20\) строчных букв английского алфавита (то есть от a до t). В один ход Коа: - выбирает некоторое подмножество позиций \(p_1, p_2, \ldots, p_k\) (\(k \ge 1; 1 \le p_i \le n; p_i \neq p_j\) если \(i \neq j\)) из \(A\), такое что \(A_{p_1} = A_{p_2} = \ldots = A_{p_k} = x\) (т. е. все буквы на этой позиции равны некоторой букве \(x\)).
- выбирает букву \(y\) (из первых \(20\) строчных букв английского алфавита) такую, что \(y>x\) (т. е. буква \(y\) в алфавитном порядке строго больше, чем \(x\)).
- делает все буквы в позициях \(p_1, p_2, \ldots, p_k\) равными \(y\). Более формально: для каждого \(i\) (\(1 \le i \le k\)) Коа устанавливает \(A_{p_i} = y\).
Обратите внимание, что вы можете изменять только буквы в строке \(A\).
Коа хочет знать наименьшее число ходов, которые она должна сделать, чтобы сделать строки равными друг другу (\(A = B\)) или определить, что нет никакого способа сделать их равными. Помогите ей! Выходные данные Для каждого набора входных данных: Выведите в единственной строке минимальное количество ходов, которое Koa должна сделать, чтобы строки стали равны друг другу (\(A = B\)) или \(-1\), если нет никакого способа сделать их равными. Примечание - В \(1\)-м наборе входных данных Коа:
- выбирает позиции \(1\) и \(2\) и устанавливает \(A_1 = A_2 = \) b (\(\color{red}{aa}b \rightarrow \color{blue}{bb}b\)).
- выбирает позиции \(2\) b \(3\) и устанавливает \(A_2 = A_3 = \) c (\(b\color{red}{bb} \rightarrow b\color{blue}{cc}\)).
- Во \(2\)-м наборе входных данных Коа не может сделать строку \(A\) равной строке \(B\).
- В \(3\)-м наборе входных данных Коа:
- выбирает позицию \(1\) и устанавливает \(A_1 = \) t (\(\color{red}{a}bc \rightarrow \color{blue}{t}bc\)).
- выбирает позицию \(2\) и устанавливает \(A_2 = \) s (\(t\color{red}{b}c \rightarrow t\color{blue}{s}c\)).
- выбирает позицию \(3\) и устанавливает \(A_3 = \) r (\(ts\color{red}{c} \rightarrow ts\color{blue}{r}\)).
| |
![]()
|
|
A. Общие префиксы
жадные алгоритмы
Конструктив
Строки
*1200
Длина самого длинного общего префикса двух строк \(s = s_1 s_2 \ldots s_n\) и \(t = t_1 t_2 \ldots t_m\) определяется как наибольшее целое число \(k\) (\(0 \le k \le min(n,m)\)) такое, что \(s_1 s_2 \ldots s_k\) равняется \(t_1 t_2 \ldots t_k\). У Коалы Коа изначально есть \(n+1\) строка \(s_1, s_2, \dots, s_{n+1}\). Для каждого \(i\) (\(1 \le i \le n\)) она вычислила \(a_i\) — длину самого длинного общего префикса \(s_i\) и \(s_{i+1}\). Несколько дней спустя Коа нашла эти числа, но не могла вспомнить строки. Поэтому Коа хотела бы найти какие-нибудь строки \(s_1, s_2, \dots, s_{n+1}\), которые дали бы числа \(a_1, a_2, \dots, a_n\). Можете ли вы ей помочь? Если ответов несколько, выведите любой. Можно показать, что для данных ограничений ответ всегда существует. Выходные данные Для каждого набора входных данных: Выведите \(n+1\) строку. В \(i\)-й строке выведите строку \(s_i\) (\(1 \le |s_i| \le 200\)), , состоящую из строчных латинских букв. Длина самого длинного общего префикса строк \(s_i\) и \(s_{i+1}\) должна быть равна \(a_i\). Если ответов несколько, выведите любой. Можно показать, что для данных ограничений ответ всегда существует. Примечание В \(1\)-м наборе входных данных один из возможных ответов это \(s = [aeren, ari, arousal, around, ari]\). Длины самых длинных общих префиксов равны: - Между \(\color{red}{a}eren\) и \(\color{red}{a}ri\) \(\rightarrow 1\)
- Между \(\color{red}{ar}i\) и \(\color{red}{ar}ousal\) \(\rightarrow 2\)
- Между \(\color{red}{arou}sal\) и \(\color{red}{arou}nd\) \(\rightarrow 4\)
- Между \(\color{red}{ar}ound\) и \(\color{red}{ar}i\) \(\rightarrow 2\)
| |
![]()
|
|
E1. Искорка и древний свиток (упрощенная версия)
дп
реализация
Строки
строковые суфф. структуры
хэши
*2800
Это более простая версия задачи E с меньшими ограничениями. Сумеречная Искорка получила новое задание от принцессы Селестии. В этот раз Искорке нужно расшифровать древний свиток, содержащий важные знания о происхождении пони. Чтобы скрыть важнейшую информацию от злых глаз, старейшины пони заколдовали свиток. Заклинание вставляет ровно одну букву в любое место каждого словa, к которому оно применено. Чтобы сделать путь к знанию более запутанным, старейшины выбрали некоторые из слов свитка и применили к ним заклинание. Сумеречная Искорка знает, что старейшины во всем почитали порядок, поэтому изначально свиток содержал слова в лексикографически неубывающем порядке. Искорке нужно удалить по одной букве из некоторых слов в свитке (чтобы отменить заклинание), для того чтобы получить какую-то версию изначального свитка. К сожалению, Искорка не всегда может однозначно восстановить древний свиток. Чтобы не упустить важные знания, ей придется перебрать все варианты изначального свитка и найти нужный. Чтобы оценить максимальное время, которое Искорка потратит на работу, ей нужно знать количество вариантов, которые ей нужно перебрать. Она просит вас найти это количество! Так как это количество может быть слишком большим, Искорке достаточно лишь знать его по модулю \(10^9+7\), остальную часть она сможет оценить сама. Могло случиться так, что принцесса Селестия отправила неверный свиток, и Искорка не сможет получить никакую версию изначального свитка. Строка \(a\) лексикографически меньше строки \(b\), если и только если выполняется один из следующих пунктов: - \(a\) — префикс \(b\), но \(a \ne b\);
- в первой позиции, где \(a\) и \(b\) различны, в строке \(a\) находится буква, которая встречается в алфавите раньше, чем соответствующая буква в \(b\).
Выходные данные Выведите одно целое число — количество вариантов получить версию оригинала из свитка по модулю \(10^9+7\). Примечание Заметьте, что старейшины могли написать пустое слово (но тогда они точно применили к нему заклинание, и таким образом это слово теперь имеет длину \(1\)). | |
![]()
|
|
E2. Искорка и древний свиток (усложненная версия)
дп
реализация
Строки
строковые суфф. структуры
хэши
*3200
Это более сложная версия задачи E с большими ограничениями. Сумеречная Искорка получила новое задание от принцессы Селестии. В этот раз Искорке нужно расшифровать древний свиток, содержащий важные знания о происхождении пони. Чтобы скрыть важнейшую информацию от злых глаз, старейшины пони заколдовали свиток. Заклинание вставляет ровно одну букву в любое место каждого словa, к которому оно применено. Чтобы сделать путь к знанию более запутанным, старейшины выбрали некоторые из слов свитка и применили к ним заклинание. Сумеречная Искорка знает, что старейшины во всем почитали порядок, поэтому изначально свиток содержал слова в лексикографически неубывающем порядке. Искорке нужно удалить по одной букве из некоторых слов в свитке (чтобы отменить заклинание), для того чтобы получить какую-то версию изначального свитка. К сожалению, Искорка не всегда может однозначно восстановить древний свиток. Чтобы не упустить важные знания, ей придется перебрать все варианты изначального свитка и найти нужный. Чтобы оценить максимальное время, которое Искорка потратит на работу, ей нужно знать количество вариантов, которые ей нужно перебрать. Она просит вас найти это количество! Так как это количество может быть слишком большим, Искорке достаточно лишь знать его по модулю \(10^9+7\), остальную часть она сможет оценить сама. Могло случиться так, что принцесса Селестия отправила неверный свиток, и Искорка не сможет получить никакую версию изначального свитка. Строка \(a\) лексикографически меньше строки \(b\), если и только если выполняется один из следующих пунктов: - \(a\) — префикс \(b\), но \(a \ne b\);
- в первой позиции, где \(a\) и \(b\) различны, в строке \(a\) находится буква, которая встречается в алфавите раньше, чем соответствующая буква в \(b\).
Выходные данные Выведите одно целое число — количество вариантов получить версию оригинала из свитка по модулю \(10^9+7\). Примечание Заметьте, что старейшины могли написать пустое слово (но тогда они точно применили к нему заклинание, и таким образом это слово теперь имеет длину \(1\)). | |
![]()
|
|
E. Boboniu и коллекция банкнот
Строки
*3500
No matter what trouble you're in, don't be afraid, but face it with a smile. I've made another billion dollars! — Boboniu Boboniu выпустил свои валюты, под названием Bobo Yuan. Bobo Yuan (BBY) это серия валют. Boboniu присвоил каждой из них положительные целочисленные номера, такие как BBY-1, BBY-2, и так далее. У Boboniu есть коллекция BBY. Его коллекция выглядит как последовательность. Например:  Мы можем использовать последовательность \(a=[1,2,3,3,2,1,4,4,1]\) длины \(n=9\) чтобы описать ее. Теперь Boboniu хочет сложить его коллекцию. Вы можете представить, что Boboniu приклеил свою последовательность на длинный лист бумаги и сгибает его между валютами:  Boboniu будет складывать вместе только валюты с одинаковым номером. Иначе говоря, если \(a_i\) после сгиба находится над \(a_j\) (\(1\le i,j\le n\)), то должно выполняться условие \(a_i=a_j\). Boboniu не волнует, выполнялось ли это условие во время сгиба. Но когда сгиб совершен, это условие должно соблюдаться. Формально определение сгиба описано в примечании. Согласно картинке выше, вы можете согнуть \(a\) два раза. На самом деле, вы можете согнуть \(a=[1,2,3,3,2,1,4,4,1]\) не более двух раз. Поэтому максимальное число сгибов равно \(2\). Как международного фаната Boboniu, вас просят найти наибольшее число сгибов. Вам дана последовательность \(a\) длины \(n\), для каждого \(i\) (\(1\le i\le n\)), вам нужно найти наибольшее возможное число сгибов последовательности \([a_1,a_2,\ldots,a_i]\). Выходные данные Выведите \(n\) целых чисел. \(i\)-е из них должно быть равно максимальному числу сгибов последовательности \([a_1,a_2,\ldots,a_i]\). Примечание Формально, для последовательности \(a\) длины \(n\), определим последовательность сгибов как такую последовательность \(b\) длины \(n\), что: - \(b_i\) (\(1\le i\le n\)) равно \(1\) или \(-1\).
- Определим \(p(i)=[b_i=1]+\sum_{j=1}^{i-1}b_j\). Для всех \(1\le i<j\le n\), если \(p(i)=p(j)\), то \(a_i\) должно быть равно \(a_j\).
(\([A]\) это значение логического выражения \(A\). т.е. \([A]=1\) если \(A\) истинно, иначе \([A]=0\)). Определим количество сгибов \(b\) как \(f(b)=\sum_{i=1}^{n-1}[b_i\ne b_{i+1}]\). Максимальное количество сгибов \(a\) это \(F(a)=\max\{ f(b)\mid b \text{ является последовательностью сгибов }a \}\). | |
![]()
|
|
A. Жонглирование буквами
жадные алгоритмы
Строки
*800
Вам дано \(n\) строк \(s_1, s_2, \ldots, s_n\) состоящих из строчных букв латинского алфавита. За одну операцию вы можете удалить один символ из строки \(s_i\) и вставить его в любую позицию строки \(s_j\) (\(j\) может быть равно \(i\)). Вы можете совершать эту операцию сколько угодно раз. Возможно ли сделать все \(n\) строк равными? Выходные данные Если возможно сделать все строки равными, выведите «YES» (без кавычек). Иначе, выведите «NO» (без кавычек). Вы можете выводить каждый символ как в нижнем, так и в верхнем регистре. Примечание В первом наборе входных данных, вы можете сделать следующее: - Удалить третий символ первой строки и вставить его после второго символа второй строки, превратив две строки в «ca» и «cbab», соотвестственно.
- Удалить второй символ второй строки и вставить его после второго символа первой строки, сделав обе строки равными «cab».
Во втором наборе входных данных невозможно сделать все \(n\) строк равными. | |
![]()
|
|
A. Похожие строки
Конструктив
Строки
*800
Двоичная строка — это такая строка, каждый символ которой — либо 0, либо 1. Назовем две двоичные строки \(a\) и \(b\) одинаковой длины похожими, если хотя бы в одной позиции их символы совпадают (существует такое число \(i\), что \(a_i = b_i\)). Например: - 10010 и 01111 похожи (у них один и тот же символ в позиции \(4\));
- 10010 и 11111 похожи;
- 111 и 111 похожи;
- 0110 и 1001 не являются похожими.
Вам дано целое число \(n\) и двоичная строка \(s\), состоящая из \(2n-1\) символов. Обозначим за \(s[l..r]\) непрерывную подстроку \(s\), начиная с \(l\)-го символа и заканчивая \(r\)-м символом (иными словами, \(s[l..r] = s_l s_{l + 1} s_{l + 2} \dots s_r\)). Постройте двоичную строку \(w\) длины \(n\), похожую на все строки из этого списка: \(s[1..n]\), \(s[2..n+1]\), \(s[3..n+2]\), ..., \(s[n..2n-1]\). Выходные данные Для каждого набора входных данных выведите удовлетворяющую условию двоичную строку \(w\) длины \(n\). Если существует несколько таких строк — выведите любую из них. Можно показать, что хотя бы одна такая строка \(w\) всегда существует. Примечание Объяснение примера из условия (совпадающие символы в одинаковых позициях выделены жирным): Первый набор входных данных: - \(\mathbf{1}\) похожа на \(s[1..1] = \mathbf{1}\).
Второй набор входных данных: - \(\mathbf{000}\) похожа на \(s[1..3] = \mathbf{000}\);
- \(\mathbf{000}\) похожа на \(s[2..4] = \mathbf{000}\);
- \(\mathbf{000}\) похожа на \(s[3..5] = \mathbf{000}\).
Третий набор входных данных: - \(\mathbf{1}0\mathbf{10}\) похожа на \(s[1..4] = \mathbf{1}1\mathbf{10}\);
- \(\mathbf{1}01\mathbf{0}\) похожа на \(s[2..5] = \mathbf{1}10\mathbf{0}\);
- \(\mathbf{10}1\mathbf{0}\) похожа на \(s[3..6] = \mathbf{10}0\mathbf{0}\);
- \(1\mathbf{0}1\mathbf{0}\) похожа на \(s[4..7] = 0\mathbf{0}0\mathbf{0}\).
Четвертый набор входных данных: - \(0\mathbf{0}\) похожа на \(s[1..2] = 1\mathbf{0}\);
- \(\mathbf{0}0\) похожа на \(s[2..3] = \mathbf{0}1\).
| |
![]()
|
|
F. x-простые подстроки
дп
Перебор
поиск в глубину и подобное
Строки
строковые суфф. структуры
*2800
Дано целое число \(x\) и строка \(s\), состоящая из цифр от \(1\) до \(9\) включительно. Подстрокой строки называется последовательная подпоследовательность этой строки. Пусть \(f(l, r)\) будет равно сумме цифр в подстроке \(s[l..r]\). Назовем подстроку \(s[l_1..r_1]\) \(x\)-простой, если - \(f(l_1, r_1) = x\);
- не существует таких значений \(l_2, r_2\), что
- \(l_1 \le l_2 \le r_2 \le r_1\);
- \(f(l_2, r_2) \neq x\);
- \(x\) делится на \(f(l_2, r_2)\).
Разрешено удалять любые символы из строки. Если вы удаляете символ, то две полученные части строки склеиваются, не меняя порядок. Какое минимальное количество символов надо удалить из строки, чтобы она не содержала \(x\)-простых подстрок? Если \(x\)-простых подстрок нет в данной строке \(s\), то выведите \(0\). Выходные данные Выведите одно целое число — минимальное количество символов, которые надо удалить из строки, чтобы она не содержала \(x\)-простых подстрок? Если \(x\)-простых подстрок нет в данной строке \(s\), то выведите \(0\). Примечание В первом примере в строке две \(8\)-простых подстроки «8» и «53». Можно удалить данные символы, чтобы избавиться от обеих: «116285317». Полученная строка «1162317» не содержит \(8\)-простых подстрок. Также можно удалить такие символы: «116285317». Во втором примере необходимо просто удалить обе единицы. В третьем примере нет \(13\)-простых подстрок. В нем вообще нет подстрок с суммой цифр равной \(13\). В четвертом примере в строке не должно быть ни «34», ни «43». Поэтому необходимо удалить либо все тройки, либо все четверки. Их по \(5\) штук, поэтому можно удалить любые из них. | |
![]()
|
|
A. Сбалансированная бинарная строка
реализация
Строки
*1500
Бинарная строка это строка, состоящая только из символов 0 и 1. Бинарная строка называется \(k\)-сбалансированной, если каждая подстрока длины \(k\) этой бинарной строки содержит равное количество символов 0 и 1 (\(\frac{k}{2}\) каждого). Вам дается целое число \(k\) и строка \(s\), состоящая только из символов 0, 1 и ?. Вам необходимо определить, можно ли получить \(k\)-сбалансированную бинарную строку, заменив каждый символ ? в \(s\) либо на 0, либо на 1. Строка \(a\) является подстрокой \(b\), если \(a\) может быть получена из \(b\) удалением нескольких (возможно, ни одного или всех) символов из начала и нескольких (возможно, ни одного или всех) символов из конца. Выходные данные Для каждого набора входных данных выведите YES, если мы можем заменить каждый ? в \(s\) на 0 или 1 так, чтобы получившаяся бинарная строка была \(k\)-сбалансированной, или NO если это невозможно. Примечание В первом наборе входных данных строка уже является \(4\)-сбалансированной бинарной строкой. Во втором наборе входных данных строка может быть преобразована в 101. В третьем наборе входных данных строку можно преобразовать в 0110. В четвертом наборе входных данных строку можно преобразовать в 1100110. | |
![]()
|
|
F. Подпоследовательности длины два
дп
Строки
*2100
Вам задано две строки \(s\) и \(t\), состоящие из строчных букв латинского алфавита. Длина \(t\) равна \(2\) (то есть эта строка состоит ровно из двух символов). За один ход вы можете выбрать любой символ \(s\) и заменить его на любую строчную букву латинского алфавита. Более формально, вы выбираете какое-то \(i\) и заменяете \(s_i\) (символ на позиции \(i\)) на какой-то символ от 'a' до 'z'. Вы хотите сделать не более \(k\) замен таким образом, чтобы максимизировать количество вхождений \(t\) в \(s\) в качестве подпоследовательности. Напомним, что подпоследовательность — это последовательность, которая может быть получена из заданной последовательности путем удаления нуля или более элементов без изменения порядка остальных элементов. Выходные данные Выведите одно целое число — максимально возможное количество вхождений \(t\) в \(s\) в качестве подпоследовательности при оптимальной замене не более \(k\) символов в \(s\). Примечание В первом примере можно получить строку «abab», заменив \(s_1\) на 'a' и \(s_4\) на 'b'. Тогда ответ будет равен \(3\). Во втором примере можно получить строку «ssddsdd» и получить ответ \(10\). В четвертом примере можно получить строку «aaacaaa» и получить ответ \(15\). | |
![]()
|
|
A. Веселая шутка
реализация
сортировки
Строки
*800
Вот и прошли новогодние праздники. Для Деда Мороза и его коллег пришло время отдыха и приема гостей. Когда встречаются два «Новогодних Деда», то их помощники в честь такого знаменательного события вырезают из картона буквы имен гостя и хозяина, и вывешивают над парадным входом. Однажды ночью, когда все легли спать, кто-то снял все буквы имен наших персонажей. Затем он, возможно, перемешал эти буквы, и положил в одну кучку перед дверью. Наутро так и не удалось найти виновника беспорядка, но всех заинтересовал еще один вопрос: можно ли из букв, сложенных перед дверью, заново составить имена гостя и хозяина? То есть нужно проверить, что не останется лишних, и не придется вырезать дополнительные буквы. Помогите «Новогодним Дедам» и их друзьям разобраться с этой проблемой, если вам даны обе надписи, висевшие над парадной дверью вечером, и буквы в кучке, найденной перед парадной дверью утром. Выходные данные Выведите «YES» без кавычек, если из букв в кучке можно составить имена «Новогодних Дедов», и «NO» без кавычек в противном случае. Примечание В первом примере: из букв, записанных в последней строке можно составить имена, записанные в первых двух, и не останется лишних букв. Во втором примере: в кучке не хватает буквы «P» и лишняя буква «L». В третьем примере: лишняя буква «L». | |
![]()
|
|
D. Грайм Зоопарк
жадные алгоритмы
Перебор
реализация
Строки
*2100
Сейчас рэп ХХОСа представляет из себя строку из нулей, единиц и знаков вопроса. К сожалению, хейтеры не дремлют. За каждое вхождение подпоследовательности 01 в рэп ХХОСа хейтеры напишут \(x\) гневных комментариев, а за каждое вхождение подпоследовательности 10 будет написано \(y\) гневных комментариев. Вы должны заменить каждый знак вопроса на 0 либо 1, чтобы минимизировать число гневных комментариев, которые получит ХХОС. Подпоследовательностью строки \(a\) называется строка \(b\), которая может получиться в результате удаления нескольких символов из строки \(a\). Два вхождения подпоследовательности считаются разными, если различаются множества позиций оставленных символов. Выходные данные В единственной строке выведите минимальное число гневных комментариев, которые может получить ХХОС. Примечание В первом примере одним из оптимальных вариантов замены является 001. Тогда в строке будет \(2\) подпоследовательности 01 и \(0\) подпоследовательностей 10. Суммарное количество гневных комментариев равно \(2 \cdot 2 + 0 \cdot 3 = 4\). Во втором примере одним из оптимальных вариантов замены является 11111. Тогда в строке будет \(0\) подпоследовательностей 01 и \(0\) подпоследовательностей 10. Суммарное количество гневных комментариев равно \(0 \cdot 13 + 0 \cdot 37 = 0\). В третьем примере одним из оптимальных вариантов замены является 1100. Тогда в строке будет \(0\) подпоследовательностей 01 и \(4\) подпоследовательности 10. Суммарное количество гневных комментариев равно \(0 \cdot 239 + 4 \cdot 7 = 28\). В четвёртом примере одним из оптимальных вариантов замены является 01101001. Тогда в строке будет \(8\) подпоследовательностей 01 и \(8\) подпоследовательностей 10. Суммарное количество гневных комментариев равно \(8 \cdot 5 + 8 \cdot 7 = 96\). | |
![]()
|
|
E. Ромские цифры
битмаски
жадные алгоритмы
математика
Строки
*2300
Ваш друг прислал вам строку \(S\), состоящую из \(n\) строчных английских букв. Оказывается, это число, записанное в ромской системе счисления. Знания о ромских числах давно утрачены, но сохранился алгоритм перевода ромских чисел в привычные нам. Пронумеруем символы \(S\) от \(1\) до \(n\) слева направо. Значение числа \(S\) обозначим как \(f(S)\), оно определяется следующим образом: - Если \(|S| > 1\), то выбирается произвольное значение \(m\) (\(1 \le m < |S|\)) и считается, что \(f(S) = -f(S[1, m]) + f(S[m + 1, |S|])\), где \(S[l, r]\) — это подстрока \(S\) с \(l\)-й позиции до \(r\)-й включительно.
- Иначе \(S = c\), где \(c\) — какая-то буква. В таком случае \(f(S) = 2^{pos(c)}\), где \(pos(c)\) — это позиция буквы \(c\) в английском алфавите (\(pos(\)a\() = 0\), \(pos(\)z\() = 25\)).
Обратите внимание, что \(m\) выбирается независимо на каждом шаге. Друг уверен, что правильно выбирая \(m\) на каждом шаге, можно получить \(f(S) = T\). Прав ли он? Выходные данные Выведите «Yes», если можно получить требуемое значение, иначе выведите «No». Вы можете выводить каждую букву в любом регистре (строчную или заглавную). Примечание Во втором примере нельзя получить \(-7\). Но можно получить, например, \(1\) следующим образом: - Сперва выбираем \(m = 1\), тогда \(f(\)abc\() = -f(\)a\() + f(\)bc\()\)
- \(f(\)a\() = 2^0 = 1\)
- \(f(\)bc\() = -f(\)b\() + f(\)c\() = -2^1 + 2^2 = 2\)
- Итого \(f(\)abc\() = -1 + 2 = 1\)
| |
![]()
|
|
C. XOR-инверсии
битмаски
Деревья
дп
жадные алгоритмы
математика
разделяй и властвуй
сортировки
Строки
Структуры данных
*2000
Вам задан массив \(a\), состоящий из \(n\) неотрицательных целых чисел. Вы должны выбрать неотрицательное целое число \(x\) и сформировать массив \(b\) из \(n\) элементов по следующему правилу: для всех \(i\) от \(1\) до \(n\), \(b_i = a_i \oplus x\) (\(\oplus\) обозначает операцию побитового исключающего ИЛИ). Назовем инверсией в массиве \(b\) такую пару целых чисел \(i\) и \(j\), что \(1 \le i < j \le n\) и \(b_i > b_j\). Вы должны выбрать \(x\) таким образом, чтобы количество инверсий в массиве \(b\) было минимально возможным. Если таких \(x\) несколько — выведите минимальное из них. Выходные данные Выведите два целых числа: минимально возможное количество инверсией в массиве \(b\), и минимальное значение \(x\), при котором достигается такое количество инверсий. Примечание В первом примере из условия оптимально оставить массив без изменений, выбрав \(x = 0\). Во втором примере из условия при выборе \(x = 14\) получается следующий массив \(b\): \([4, 9, 7, 4, 9, 11, 11, 13, 11]\). В нем \(4\) инверсии: - \(i = 2\), \(j = 3\);
- \(i = 2\), \(j = 4\);
- \(i = 3\), \(j = 4\);
- \(i = 8\), \(j = 9\).
В третьем примере из условия при выборе \(x = 8\) получается следующий массив \(b\): \([0, 2, 11]\). В нем нет ни одной инверсии. | |
![]()
|
|
C. Палиндромайзер
Конструктив
Строки
*1400
Ринго нашел строку \(s\) длиной \(n\) в своей желтой субмарине. Строка содержит только строчные буквы английского алфавита. Поскольку Ринго и его друзья любят палиндромы, он хотел бы превратить строку \(s\) в палиндром, применяя к ней два типа операций. Первая операция позволяет ему выбрать \(i\) (\(2 \le i \le n-1\)) и приписать перевернутую подстроку \(s_2s_3 \ldots s_i\) (всего \(i - 1\) символ) в начало строки \(s\). Вторая операция позволяет выбрать \(i\) (\(2 \le i \le n-1\)) и приписать перевернутую подстроку \(s_i s_{i + 1}\ldots s_{n - 1}\) (всего \(n - i\) символов) в конец \(s\). Обратите внимание, что символы строки в этой нумеруются с \(1\). Например, предположим, что \(s=\)abcdef. Если он выполнит первую операцию с \(i=3\), то добавит cb в начало \(s\), и результат будет cbabcdef. Выполнение второй операции над полученной строкой с \(i=5\) даст cbabcdefedc. Ваша задача — помочь Ринго сделать строку палиндромом, применяя любые из двух операций (в сумме) не более \(30\) раз. Также, длина полученного палиндрома должна не превышать \(10^6\). Гарантируется, что для данных ограничений решение существует. Также обратите внимание, что не нужно минимизировать ни количество применяемых операций, ни длину результирующей строки, но они должны вписываться в ограничения. Выходные данные Первая строка должна содержать \(k\) (\(0\le k \le 30\)) — количество выполненных операций. Каждая из следующих \(k\) строк должна описывать операцию в виде L i или R i. \(L\) обозначает первую операцию, \(R\) — вторую, \(i\) — выбранный индекс. Длина полученного палиндрома должна не превышать \(10^6\). Примечание Для первого примера выполняются следующие операции: abac \(\to\) abacab \(\to\) abacaba Для второго примера выполняются следующие операции: acccc \(\to\) cccacccc \(\to\) ccccacccc. Третий пример уже является палиндромом, поэтому никаких операций не требуется. | |
![]()
|
|
E. Минлексы
дп
жадные алгоритмы
реализация
Строки
*2700
Недавно в поле зрения Лёши попала одна занимательная строка \(s\), состоящая из маленьких латинских букв. Лёша сразу же разработал уникальный алгоритм с этой строкой и поспешил поделиться им с вами. Суть алгоритма заключалась в следующем. Лёша выбирал любое количество пар символов на позициях \((i, i + 1)\) так, чтобы выполнялись следующие условия: - для любой пары \((i, i + 1)\) выполняется \(0 \le i < |s| - 1\);
- для любой пары \((i, i + 1)\) выполняется \(s_i = s_{i + 1}\);
- не существует индекса, который находится в нескольких парах одновременно.
Далее Лёша удалял все символы строки по индексам, содержащимся в выбранных парах, и завершал алгоритм. Теперь Лёшу интересует, какую лексикографически минимальную строку можно получить после выполнения алгоритма на каждом суффиксе заданной строки. Выходные данные В \(|s|\) строках выведите длины искомых строк и сами искомые строки для всех суффиксов, начиная с наибольшего по длине. Вывод может получится слишком большим, и поэтому, если длина ответа больше \(10\) символов, то вместо самого ответа выведите только первые \(5\) символов, далее «...», и далее последние \(2\) символа ответа. Примечание Рассмотрим первый пример. - Наибольший по длине суффикс — вся строка «abcdd». Выбирая одну пару \((4, 5)\), Лёша может получить строку «abc».
- Следующий по длине суффикс — строка «bcdd». Выбирая одну пару \((3, 4)\), получаем «bc».
- Следующий по длине суффикс — строка «cdd». Выбирая одну пару \((2, 3)\), получаем «c».
- Следующий по длине суффикс — строка «dd». Выбирая одну пару \((1, 2)\), получаем «» (пустую строку).
- Последний суффикс — строка «d». Нельзя выбрать ни одну пару, поэтому ответ «d».
Во втором примере для наибольшего по длине суффикса «abbcdddeaaffdfouurtytwoo» выбираем три пары \((11, 12)\), \((16, 17)\), \((23, 24)\) и получаем «abbcdddeaadfortytw» | |
![]()
|
|
F. Количество подпоследовательностей
дп
Комбинаторика
Строки
*2000
Вам задана строка \(s\), состоящая из строчных букв «a», «b» и «c», а также из знаков вопроса «?». Пусть количество знаков вопроса в строке \(s\) равно \(k\). Заменим каждый знак вопроса на одну из букв «a», «b» и «c». Таким образом, мы получим \(3^{k}\) всевозможных строк, состоящих только из букв «a», «b» и «c». Например, если \(s = \)«ac?b?c» после замены знаков вопроса мы получим строки \([\)«acabac», «acabbc», «acabcc», «acbbac», «acbbbc», «acbbcc», «accbac», «accbbc», «accbcc»\(]\). Перед вами стоит задача определить количество подпоследовательностей «abc» во всех получившихся строках. Так как ответ может быть достаточно большим, выведите его по модулю числа \(10^{9} + 7\). Подпоследовательность строки \(t\) — это такая последовательность, которую можно получить из строки \(t\) путем удаления некоторого (возможно нулевого) количества букв, при этом порядок оставшихся букв должен быть неизменным. Например, в строке «baacbc» есть две подпоследовательности «abc». Это подпоследовательность, состоящая из букв в позициях \((2, 5, 6)\), и подпоследовательность, состоящая из букв в позициях \((3, 5, 6)\). Выходные данные Выведите суммарное количество подпоследовательностей вида «abc» во всех строках, которые можно получить путем замены знаков вопроса на буквы «a», «b» и «c», по модулю \(10^{9} + 7\). Примечание В первом примере после замены знаков вопроса получим \(9\) строк: - «acabac» — в этой строке \(2\) подпоследовательности «abc»,
- «acabbc» — в этой строке \(4\) подпоследовательности «abc»,
- «acabcc» — в этой строке \(4\) подпоследовательности «abc»,
- «acbbac» — в этой строке \(2\) подпоследовательности «abc»,
- «acbbbc» — в этой строке \(3\) подпоследовательности «abc»,
- «acbbcc» — в этой строке \(4\) подпоследовательности «abc»,
- «accbac» — в этой строке \(1\) подпоследовательность «abc»,
- «accbbc» — в этой строке \(2\) подпоследовательности «abc»,
- «accbcc» — в этой строке \(2\) подпоследовательности «abc».
Таким образом, во всех строках содержатся \(2 + 4 + 4 + 2 + 3 + 4 + 1 + 2 + 2 = 24\) подпоследовательности «abc». | |
![]()
|
|
C. ABBB
жадные алгоритмы
Перебор
Строки
Структуры данных
*1100
Смотритель зоопарка играет в игру. В этой игре он должен использовать бомбы, чтобы взрывать строку, состоящую из символов «A» и «B». Он может использовать бомбы, чтобы взорвать подстроку, которая равна либо «AB», либо «BB». Когда он взрывает такую подстроку, она удаляется из строки, а оставшиеся части строки объединяются вместе в новую строку. Например, смотритель зоопарка может сделать следующие две операции: AABABBA \(\to\) AABBA \(\to\) AAA. Смотритель зоопарка интересуется, какую наименьшую длину строки он может получить после нескольких взрывов. Можете ли вы ему помочь найти эту наименьшую длину строки? Выходные данные Для каждого набора входных данных выведите единственное целое число: наименьшую длину строки, которую смотритель зоопарка может получить. Примечание В первом наборе входных данных вы не можете сделать ни одну операцию, поэтому ответ \(3\). Во втором наборе входных данных одна из оптимальных последовательностей операций BABA \(\to\) BA. Поэтому ответ \(2\). В третьем наборе входных данных одна из оптимальных последовательностей операций AABBBABBBB \(\to\) AABBBABB \(\to\) AABBBB \(\to\) ABBB \(\to\) AB \(\to\) (пустая строка). Поэтому ответ \(0\). | |
![]()
|
|
B. Помогите Тридевятому царству 2
реализация
Строки
*1200
Некоторое время программа для округления чисел, разработанная участниками Codeforces во время одного из предыдущих раундов, помогала жителям Тридевятого царства переводить числа в более удобочитаемый формат. Однако время шло, экономика Тридевятого царства развивалась, росли масштабы операций, царским указом был основан Тридевятый банк, и очень скоро даже округление не помогало быстро определить хотя бы порядок чисел, с которыми проводились операции. Да и округление до целого было не очень удобно — ведь банку нужно представлять все числа с точностью до 0.01, а не до целого. Царь издал новый указ — ввести для представления чисел, обозначающих денежные суммы, финансовый формат. Формально, правила записи числа в финансовом формате следующие: - Число содержит целую и дробную части, разделенные символом «.» (десятичная точка).
- Цифры целой части числа разбиваются для удобочитаемости на группы по три разряда, начиная с младших разрядов, группы разделяются символом «,» (запятая). Например, если целая часть числа равна 12345678, то она запишется в финансовом формате как 12,345,678
- Дробная часть числа в финансовом формате должна содержать ровно 2 цифры. Соответственно, если исходное число (которое переводится в финансовый формат) содержит менее двух цифр в дробной части (или не содержит их вовсе) — она дополняется нулями до длины 2. Если дробная часть числа содержит более двух цифр — лишние цифры просто отбрасываются (округление не производится — см. примеры тестов).
- Знак минус при записи числа в финансовом формате не пишется. Вместо этого, если исходное число имело знак минус, результат записывается в круглых скобках.
- Не стоит забывать, что Тридевятый банк работает в заморской валюте — змейках ($), поэтому непосредственно перед числом в финансовом формате (внутри скобок, если они необходимы в записи числа) необходимо ставить знак «$».
Например, по вышеизложенным правилам число 2012 запишется в финансовом формате как «$2,012.00», а число -12345678.9 — как «($12,345,678.90)». Купцы Тридевятого царства снова пришли к вам с поклоном и надеждой, что вы обеспечите их программой для перевода произвольных чисел в финансовый формат. Поможете? Выходные данные Выведите число, заданное на входе, в финансовом формате, как описано в условии задачи. Примечание Обратите внимание на второй и третий тесты из примеров, демонстрирующие, что знак числа в финансовом формате (и, соответственно, наличие скобок) определяется знаком округляемого числа, а не знаком числа, полученного после округления. | |
![]()
|
|
E. Переворот строки
жадные алгоритмы
Строки
Структуры данных
*1900
Вам задана строка \(s\). Вам необходимо перевернуть эту строку. То есть последняя буква строки должна стать первой, предпоследняя буква строки должна стать второй, и так далее. Например, перевернутая строка «abddea» равна «aeddba». Для достижения цели (то есть для переворота заданной строки) вы можете менять местами соседние элементы строки. Перед вами стоит задача определить минимальное количество обменов соседних элементов строки, необходимых для того, чтобы перевернуть строку. Выходные данные Выведите минимальное количество обменов соседних элементов строки, необходимых для того, чтобы перевернуть строку. Примечание В первом примере нужно сначала поменять местами третью и четвертую буквы, тогда строка станет равна «aazaa». Затем нужно поменять вторую и третью буквы, тогда строка станет равна «azaaa». Таким образом, за два обмена соседних букв мы сможем перевернуть заданную строку. Во втором примере заданная строка является палиндромом, то есть перевернутая строка равна исходной строке, поэтому никаких обменов делать не нужно. | |
![]()
|
|
I. Циклические сдвиги
*особая задача
Строки
*2900
Вам задана матрица, состоящая из \(n\) строк и \(m\) столбцов. Матрица содержит строчные буквы латинского алфавита. Вы можете выполнить следующую операцию любое количество раз: выбрать два целых числа \(i\) (\(1 \le i \le m\)) и \(k\) (\(0 < k < n\)), циклически сдвинуть все столбцы \(j\), такие, что \(i \le j \le m\), на \(k\). Сдвиг осуществляется вверх. Например, если у вас есть матрица \(\left( \begin{array} \\ a & b & c \\ d & e & f \\ g & h & i \end{array}\right) \) и вы выполните операцию с \(i = 2\), \(k = 1\), тогда матрица станет равна: \(\left( \begin{array} \\ a & e & f \\ d & h & i \\ g & b & c \end{array}\right) \) Вам необходимо обработать \(q\) запросов. Каждый из запросов — строка длины \(m\), состоящая из строчных букв латинского алфавита. Для каждого запроса необходимо определить минимальное количество вышеописанных операций, которые необходимо выполнить, чтобы одна строк матрицы была равна строке из запроса. Обратите внимание, что все запросы независимы, то есть операции, выполняемые в запросе, не влияют на исходную матрицу в других запросах. Выходные данные Выведите \(q\) целых чисел. \(i\)-е число должно быть равно минимальному количеству операций, которые необходимо выполнить, чтобы матрица содержала строку из \(i\)-го запроса или \(-1\), если заданную строку невозможно получить. | |
![]()
|
|
G. СУБД смерти
Деревья
Строки
строковые суфф. структуры
Структуры данных
*2600
Для простоты скажем, что «Тетрадь смерти» — это блокнот, который убивает того, чье имя в него вписывается. С помощью него легко убивать, но довольно сложно поддерживать актуальную информацию о тех людях, кого вы еще не убили, но планируете. Поэтому вы решили создать «Систему управления базой данных смерти» — компьютерную программу, которая предоставляет удобный доступ к базе данных возможных жертв. Позвольте мне описать ее особенности. Определим объект жертвы: у жертвы есть имя (необязательно уникальное), которое состоит только из строчных латинских букв, и целое значение подозрительности. В начале программы пользователь вводит список из \(n\) жертв в базу данных, значение подозрительности каждого устанавливается равным \(0\). Затем пользователь делает запросы двух типов: - \(1~i~x\) — выставить значение подозрительности \(i\)-й жертвы равным \(x\);
- \(2~q\) — по заданной строке \(q\) найти максимальное значение подозрительности жертвы, чье имя входит в \(q\) как подстрока (символы на подряд идущих позициях).
Просто напоминаю, что программа не убивает людей, она только помогает искать их имена для записи в настоящую тетрадь. Поэтому список жертв в базе данных не меняется на протяжении всех запросов. Ну и чего вы ждете? Напишите эту программу! Выходные данные На каждый запрос второго типа выведите одно целое число. Если нет такой жертвы, чье имя является подстрокой \(q\), то выведите \(-1\). Иначе выведите максимальное значение подозрительности жертвы, чье имя входит в \(q\) как подстрока. | |
![]()
|
|
C. Поиск анаграмм
реализация
Строки
*1500
Строка t называется анаграммой строки s, если в строке t можно переставить буквы местами так, чтобы получилась строка s. Например, строка «aab» является анаграммой строки «aba», а строка «aaa» — нет. Строка t называется подстрокой строки s, если ее можно прочитать начиная с некоторой позиции в строке s. Например, у строки «aba» есть шесть подстрок: «a», «b», «a», «ab», «ba», «aba». Дана строка s, состоящая из строчных латинских букв и символов «?», и строка p, состоящая только из строчных латинских букв. Назовем строку хорошей, если из нее можно получить анаграмму строки p заменой символов «?» на символы латинского алфавита (каждый символ «?» заменяется на ровно один символ латинского алфавита). Например, если строка p = «aba», то строка «a??» хорошая, а строка «?bc» нет. Ваша задача найти количество хороших подстрок строки s (одинаковые подстроки нужно учесть в ответе несколько раз). Выходные данные Выведите единственное число — количество хороших подстрок строки s. Две подстроки считаются различными, если их позиции вхождения различны. Значит, если какая-то строка встречается несколько раз, то она должна быть учтена такое же количество раз. Примечание Рассмотрим первый тест из условия. Здесь у строки s две хорошие подстроки: «b??» (после замены вопросов получится «baa»), «???» (после замены вопросов получится «baa»). Рассмотрим второй тест из условия. Здесь у строки s две хорошие подстроки: «ab?» (можно заменить «?» на «c»), «b?c» (можно заменить «?» на «a»). | |
![]()
|
|
B. Ловя мошенников
дп
Строки
*1800
Вам даны две строки \(A\) и \(B\), представляющие эссе двух учеников, которые подозреваются в мошенничестве. Для любых двух строк \(C\), \(D\) мы определяем оценку их сходства \(S(C,D)\) как \(4\cdot LCS(C,D) - |C| - |D|\), где \(LCS(C,D)\) обозначает длину наибольшей общей подпоследовательности строк \(C\) и \(D\). Вы считаете, что могла быть скопирована только часть эссе, поэтому вас интересуют их подстроки. Вычислите максимальную оценку сходства по всем парам подстрок. Более формально, выведите максимальное значение \(S(C, D)\), по всем парам \((C, D)\), где \(C\) — некоторая подстрока \(A\), а \(D\) — некоторая подстрока \(B\). Если \(X\) — строка, то \(|X|\) обозначает ее длину. Строка \(a\) является подстрокой строки \(b\), если \(a\) может быть получена из \(b\) удалением нескольких (возможно, ни одного или всех) символов из начала и нескольких (возможно, ни одного или всех) символов из конца. Строка \(a\) является подпоследовательностью строки \(b\), если \(a\) можно получить из \(b\) путем удаления нескольких (возможно, нуля или всех) символов. Обратите внимание на разницу между подстрокой и подпоследовательностью, так как оба термина встречаются в условии задачи. Возможно, вам будет интересно прочитать страницу Википедии о наибольшей общей подпоследовательности. Выходные данные Выведите максимальное значение \(S(C, D)\), по всем парам \((C, D)\), где \(C\) — некоторая подстрока \(A\), а \(D\) — некоторая подстрока \(B\). Примечание В первом примере: abb из первой строки и abab из второй строки имеют LCS равный abb. Результат равен \(S(abb, abab) = (4 \cdot |abb|\)) - \(|abb|\) - \(|abab|\) = \(4 \cdot 3 - 3 - 4 = 5\). | |
![]()
|
|
B. Неподстрочные подпоследовательности
дп
жадные алгоритмы
реализация
Строки
*900
У Hr0d1y есть \(q\) запросов на бинарной строке \(s\) длины \(n\). Бинарная строка это строка, содержащая только символы «0» и «1». Запрос задается парой целых чисел \(l_i\), \(r_i\) \((1 \leq l_i \lt r_i \leq n)\). Для каждого запроса ему необходимо определить, есть ли хорошая подпоследовательность в строке \(s\), которая равна подстроке \(s[l_i\ldots r_i]\). - Подстрока \(s[i\ldots j]\) строки \(s\) — это строка из символов \(s_i s_{i+1} \ldots s_j\).
- Строка \(a\) называются подпоследовательностью строки \(b\), если \(a\) может быть получена из \(b\) удалением некоторых символов, не меняя порядка оставшихся.
- Подпоследовательность называется хорошей, если она не последовательная и имеет длину \(\ge 2\). Например, если \(s\) равна «1100110», то подпоследовательности \(s_1s_2s_4\) («1100110») и \(s_1s_5s_7\) («1100110») являются хорошими, а \(s_1s_2s_3\) («1100110») не является.
Можете ли вы помочь Hr0d1y ответить на каждый запрос? Выходные данные Для каждого набора входных данных выведите \(q\) строк. В \(i\)-й строке ответа на каждый набор входных данных должно быть записано «YES», если есть хорошая подпоследовательность, равная подстроке \(s[l_i...r_i]\), и «NO» иначе. Вы можете выводить каждый символ в любом регистре (верхнем или нижнем). Примечание В первом наборе входных данных: - \(s[2\ldots 4] = \) «010». В этом случае \(s_1s_3s_5\) («001000») и \(s_2s_3s_6\) («001000») являются подходящими хорошими подпоследовательностями, а \(s_2s_3s_4\) («001000») — нет.
- \(s[1\ldots 3] = \) «001». Нет подходящей хорошей подпоследовательности.
- \(s[3\ldots 5] = \) «100». В этом случае \(s_3s_5s_6\) («001000») — это подходящая хорошая подпоследовательность.
| |
![]()
|
|
C. Равенство строк
дп
жадные алгоритмы
реализация
Строки
хэши
*1400
У Ashish есть две строки \(a\) и \(b\) длины \(n\) и целое число \(k\). Строки содержат только строчные буквы латинского алфавита. Он хочет превратить строку \(a\) в строку \(b\), исполнив несколько (возможно, ноль) операций над \(a\). За одну операцию он может сделать одно из двух возможных действий: - выбрать индекс \(i\) (\(1 \leq i\leq n-1\)) и поменять местами \(a_i\) и \(a_{i+1}\), или
- выбрать индекс \(i\) (\(1 \leq i \leq n-k+1\)) и, если все символы среди \(a_i, a_{i+1}, \ldots, a_{i+k-1}\) равны какому-то символу \(c\) (\(c \neq\) «z»), заменить каждый из них на символ \((c+1)\), таким образом, «a» заменяется на «b», «b» заменяется на «c» и так далее.
Обратите внимание, что он может исполнить любое число операций, и операции можно выполнять только на строке \(a\). Помогите Ashish определить, возможно ли превратить \(a\) в \(b\), сделав несколько (возможно, ноль) операций на ней. Выходные данные Для каждого набора входных данных выведите «Yes», если Ashish может превратить \(a\) в \(b\) после некоторого числа операций, иначе выведите «No». Вы можете выводить каждый символ в любом регистре (верхнем или нижнем). Примечание В первом наборе входных данных можно доказать, что невозможно превратить \(a\) в \(b\). Во втором наборе входных данных «abba» \(\xrightarrow{\text{inc}}\) «acca» \(\xrightarrow{\text{inc}}\) \(\ldots\) \(\xrightarrow{\text{inc}}\) «azza». Здесь «swap» обозначает операцию первого типа, а «inc» обозначает операцию второго типа. В третьем наборе входных данных «aaabba» \(\xrightarrow{\text{swap}}\) «aaabab» \(\xrightarrow{\text{swap}}\) «aaaabb» \(\xrightarrow{\text{inc}}\) \(\ldots\) \(\xrightarrow{\text{inc}}\) «ddaabb» \(\xrightarrow{\text{inc}}\) \(\ldots\) \(\xrightarrow{\text{inc}}\) «ddddbb» \(\xrightarrow{\text{inc}}\) \(\ldots\) \(\xrightarrow{\text{inc}}\) «ddddcc». | |
![]()
|
|
B. Прошлогодняя подстрока
дп
реализация
Строки
*800
У Поликарпа есть строка \(s[1 \dots n]\) длины \(n\), состоящая из десятичных цифр. Поликарп делает следующую операцию со строкой \(s\) не более одного раза (то есть делает операцию \(0\) или \(1\) раз): - Поликарп выбирает два числа \(i\) и \(j\) (\(1 \leq i \leq j \leq n\)) и удаляет из строки \(s\) символы на позициях \(i, i+1, i+2, \ldots, j\) (то есть удаляет подстроку \(s[i \dots j]\)). Более формально, Поликарп превращает строку \(s\) в строку \(s_1 s_2 \ldots s_{i-1} s_{j+1} s_{j+2} \ldots s_{n}\).
Например, строку \(s = \)«20192020» Поликарп может превратить в строки: - «2020» (в таком случае \((i, j)=(3, 6)\) или \((i, j)=(1, 4)\));
- «2019220» (в таком случае \((i, j)=(6, 6)\));
- «020» (в таком случае \((i, j)=(1, 5)\));
- возможны и другие ходы, выше перечислены лишь только некоторые из них.
Поликарпу очень нравится строка «2020», поэтому ему интересно, можно ли превратить строку \(s\) в строку «2020» не более чем за одну операцию? Заметьте, что проводить ноль операций допустимо. Выходные данные Для каждого набора входных данных в отдельной строке выведите: - «YES», если Поликарп может превратить строку \(s\) в строку «2020» не более чем за одну операцию (то есть за \(0\) или \(1\) операцию);
- «NO» в противном случае.
Вы можете выводить «YES» и «NO» в любом регистре (например, строки yEs, yes, Yes и YES будут распознаны как положительный ответ). Примечание В первом наборе входных данных Поликарп мог выбрать \(i=3\) и \(j=6\). Во втором наборе входных данных Поликарп мог выбрать \(i=2\) и \(j=5\). В третьем наборе входных данных Поликарп не делал ни одну операцию со строкой. | |
![]()
|
|
C. Псиная поэзия
дп
жадные алгоритмы
Строки
*1300
После трагической смерти его жены, Эвридики, Орфей решил спуститься в царство мертвых, чтобы увидеть её. Достичь врат царства было непросто, однако пройти через них будет еще сложнее. В основном, из-за Цербера — трёхглавого пса Аида. Орфей, известный поэт и музыкант, планирует усыпить Цербера своей поэзией и спокойно пройти мимо него. Он создал очень своеобразную поэму специально для Цербера. Она состоит только из строчных английских букв. Подстрока поэмы является палиндромом, если она читается одинаково слева направо и справа налево. Строка \(a\) является подстрокой строки \(b\), если \(a\) может быть получена из \(b\) удалением нескольких (возможно, нуля или всех) символов из начала и нескольких (возможно, нуля или всех) символов из конца. К сожалению, Цербер не любит палиндромы длины больше \(1\). Например, в поэме abaa псу Аида не понравились бы подстроки aba и aa. Орфей сможет успокоить Цербера только если псу понравится его поэзия. Поэтому, он хочет изменить свою поэму так, чтобы она не содержала ни одной подстроки палиндрома с длиной строго больше \(1\). Орфей может изменять поэму, заменяя букву на любой позиции любой строчной английской буквой. Он может применять эту операцию произвольное количество раз (возможно, ноль). Так как в его поэме могут быть палиндромы, ему придется сделать несколько изменений. Но сколько именно? Вам дана поэма, определите минимальное количество букв, которые нужно изменить, чтобы поэма перестала содержать подстроки палиндромы длины больше \(1\). Выходные данные Вы должны вывести \(t\) строк, \(i\)-я из них должна содержать одно целое число — ответ на \(i\)-й набор входных данных. Примечание В первом наборе входных данных можно заменить третий символ на c и получить поэму bacba, не содержащую палиндромных подстрок. Во втором наборе входных данных можно заменить третий символ на d и получить поэму abdac, не содержащую палиндромных подстрок. В третьем наборе входных данных исходная поэма уже не содержит палиндромных подстрок, поэтому Орфею не нужно больше ничего делать. | |
![]()
|
|
G. Песни сирен
Комбинаторика
математика
разделяй и властвуй
Строки
строковые суфф. структуры
хэши
*2600
Кто по незнанию приближается к ним и слышит голос сирен, тот больше не возвращается.Гомер, Одиссея Во времена Ясона и Аргонавтов, было хорошо известно, что сирены используют свои песни, чтобы заманивать моряков к себе на погибель. Но немногие знали, что каждый раз сирены, когда зовут моряков по имени, те становятся слабее и более уязвимыми. Для целей этой задачи, и песни сирен, и имена моряков будем представлять строками, состоящими из строчных английских букв. Чем больше раз имя моряка появляется как непрерывная подстрока в песне, тем моряк в большей опасности. Ясон обнаружил, что сирены могут петь одну из \(n+1\) песен, которые имеют следующую структуру: пусть \(s_i\) (\(0 \leq i \leq n\)) будет \(i\)-й песней, а \(t\) — некоторой строкой длины \(n\), тогда для всех \(i < n\): \(s_{i+1} = s_i t_i s_i\). другими словами, \(i+1\)-я песня это конкатенация \(i\)-й песни, \(i\)-й буквы (в \(0\) индексации) строки \(t\), и \(i\)-й песни. К счастью, он также знает \(s_0\) и \(t\). Ясон интересуется, сколько раз имя моряка встречается в конкретной песне. Ответьте на \(q\) вопросов: дано имя моряка (\(w\)) и номер песни (\(i\)), выведите количество вхождений \(w\) в \(s_i\) как подстроки. Так как это число может быть довольно большим, выведите его по модулю \(10^9+7\). Выходные данные Выведите \(q\) строк, \(i\)-я из них должна содержать остаток по модулю \(10^9+7\) от числа вхождений \(w\) в \(s_k\). Примечание В первом примере песни сирен выглядят так: - Песня \(0\): aa
- Песня \(1\): aabaa
- Песня \(2\): aabaacaabaa
- Песня \(3\): aabaacaabaadaabaacaabaa
| |
![]()
|
|
E. Немного похожи
битмаски
Перебор
Строки
строковые суфф. структуры
хэши
*2400
Назовем две строки \(a\) и \(b\) (обе длиной \(k\)) немного похожими, если они имеют один и тот же символ в некоторой позиции, то есть существует по крайней мере одно \(i \in [1, k]\) такое, что \(a_i = b_i\). Задана двоичная строка \(s\) длины \(n\) (строка из \(n\) символов 0 и/или 1) и целое число \(k\). Обозначим строку \(s[i..j]\) как подстроку \(s\), начинающуюся с \(i\)-го символа и заканчивающуюся \(j\)-м символом (то есть \(s[i..j] = s_i s_{i + 1} s_{i + 2} \dots s_{j - 1} s_j\)). Назовем двоичную строку \(t\) длины \(k\) красивой, если она немного похожа на все подстроки \(s\), имеющие длину ровно \(k\); то есть она немного похожа на \(s[1..k], s[2..k+1], \dots, s[n-k+1..n]\). Ваша задача — найти лексикографически наименьшую строку \(t\), которая является красивой, или сообщить, что такой строки не существует. Строка \(x\) лексикографически меньше строки \(y\), если \(x\) является префиксом \(y\) (и \(x \ne y\)), либо существует такое \(i\) (\(1 \le i \le \min(|x|, |y|)\)), что \(x_i < y_i\), и для любого \(j\) (\(1 \le j < i\)) \(x_j = y_j\). Выходные данные Для каждого набора входных данных выведите ответ следующим образом: - если невозможно построить красивую строку, выведите одну строку, содержащую слово NO (Примечание: именно в верхнем регистре, например, нельзя выводить No);
- в противном случае выведите две строки. Первая строка должна содержать слово YES (именно в верхнем регистре); вторая строка — лексикографически наименьшая красивая строка, состоящая из \(k\) символов 0 и/или 1.
| |
![]()
|
|
A. Пунктуация
реализация
Строки
*1300
Дан текст, состоящий из маленьких латинских букв, пробелов и знаков препинания (точка, запятая, восклицательный и вопросительный знаки). Слово — это последовательность подряд идущих латинских букв. Ваша задача — расставить пробелы по следующим правилам: - если между двумя словами нет знака препинания, тогда они должны разделяться ровно одним пробелом
- перед каждым знаком препинания не должно быть пробелов
- после каждого знака препинания должен быть ровно один пробел
Гарантируется, что между двумя знаками препинания содержится хотя бы одно слово. Текст начинается и заканчивается латинской буквой. Выходные данные Выведите отформатированный в соответствии с правилами текст. В этой задаче необходимо крайне точно следовать правилам вывода, например, наличие лишнего пробела в конце строки вывода является ошибкой. Обратите внимание, что заключительный перевод строки при проверке правильности ответа значения не имеет. Можете выводить его, а можете не выводить. | |
![]()
|
|
B. LCM строк
математика
Перебор
Строки
теория чисел
*1000
Давайте определим операцию умножения между строкой \(a\) и положительным целым числом \(x\): \(a \cdot x\) — это строка, которая является результатом записи \(x\) копий \(a\) одна за другой. Например, «abc» \(\cdot~2~=\) «abcabc», «a» \(\cdot~5~=\) «aaaaa». Строка \(a\) делится на другую строку \(b\), если существует целое число \(x\) такое, что \(b \cdot x = a\). Например, «abababab» делится на «ab», но не делится на «ababab» или «aa». LCM из двух строк \(s\) и \(t\) (определяется как \(LCM(s, t)\)) — это самая короткая непустая строка, которая делится как на \(s\), так и на \(t\). Вам даны две строки \(s\) и \(t\). Найдите \(LCM(s, t)\) или сообщите, что он не существует. Можно показать, что если \(LCM(s, t)\) существует, то он единственный. Выходные данные Для каждого набора входных данных выведите \(LCM(s, t)\), если он существует; в противном случае выведите -1. Можно показать, что если \(LCM(s, t)\) существует, то он единственный. Примечание В первом примере «baba» = «baba» \(\cdot~1~=\) «ba» \(\cdot~2\). Во втором примере, «aaaaaa» = «aa» \(\cdot~3~=\) «aaa» \(\cdot~2\). | |
![]()
|
|
D. Программа
дп
реализация
Строки
Структуры данных
*1700
Задана программа, состоящая из \(n\) инструкций. Изначально единственная переменная \(x\) присваивается \(0\). После этого следуют инструкции двух типов: - увеличить \(x\) на \(1\);
- уменьшить \(x\) на \(1\).
Даны \(m\) запросов следующего типа: - запрос \(l\) \(r\) — сколько различных значений принимает переменная \(x\), если все инструкции между \(l\)-й и \(r\)-й включительно пропускаются, а остальные исполняются без изменения порядка?
Выходные данные На каждый набор входных данных выведите \(m\) целых чисел — для каждого запроса \(l\), \(r\) выведите количество различных значений, которые принимает переменная \(x\), если все инструкции между \(l\)-й и \(r\)-й включительно пропускаются, а остальные исполняются без изменения порядка. Примечание Инструкции, которые остаются в каждом запросе первого набора входных данных: - пустая программа — \(x\) был равен только \(0\);
- «-» — \(x\) принимал значения \(0\) и \(-1\);
- «---+» — \(x\) принимал значения \(0\), \(-1\), \(-2\), \(-3\), \(-2\) — среди них \(4\) различных значения;
- «+--+--+» — различные значения — это \(1\), \(0\), \(-1\), \(-2\).
| |
![]()
|
|
E. Сопоставление шаблонов
битмаски
графы
поиск в глубину и подобное
сортировки
Строки
Структуры данных
хэши
*2300
Вам даны \(n\) шаблонов \(p_1, p_2, \dots, p_n\) и \(m\) строк \(s_1, s_2, \dots, s_m\). Каждый шаблон \(p_i\) состоит из \(k\) символов, каждый из которых — это либо строчная латинская буква или символ подчеркивания. Все шаблоны попарно различны. Каждая строка \(s_j\) состоит из \(k\) строчных латинских букв. Строка \(a\) подходит под шаблон \(b\), если для каждого \(i\) от \(1\) до \(k\) либо \(b_i\) — это подчеркивание, либо \(b_i=a_i\). Вам требуется переупорядочить шаблоны таким образом, что первый шаблон, под который подходит \(j\)-я строка, — это \(p[mt_j]\). Разрешается не изменять порядок шаблонов. Можно ли осуществить такое переупорядочивание? Если можно, то выведите любой корректный порядок. Выходные данные Выведите «NO», если невозможно переупорядочить шаблоны так, чтобы первый шаблон, под который подходит \(j\)-я строка, был \(p[mt_j]\). В противном случае выведите «YES» в первой строке. Во второй строке выведите \(n\) различных целых чисел от \(1\) до \(n\) — порядок шаблонов. Если существует несколько ответов, выведите любой из них. Примечание Порядок шаблонов в первом примере после переупорядочивания: Тогда первая строка подходит под шаблоны ab__, _bcd, _b_d в таком порядке, первый из них равен ab__, который действительно \(p[4]\). Вторая строка подходит под шаблоны __b_ и ab__, первый из них __b_, который равен \(p[2]\). Последняя строка подходит под шаблоны _bcd и _b_d, первый из них _bcd, который равен \(p[5]\). Ответ на этот тест не единственный, другие корректные порядки существуют. Во втором примере cba не подходит под шаблон __c, а значит, корректного порядка не существует. В третьем примере в порядке (a_, _b) получается, что первый шаблон под который подходят обе строки — это \(1\), а в порядке (_b, a_) получается, что первый шаблон под который подходят обе строки — это \(2\). Значит, не существует такого порядка, что ответ равен \(1\) и \(2\). | |
![]()
|
|
A. Еще одна игра со строкой
жадные алгоритмы
игры
Строки
*800
У Гомера есть два друга — Алиса и Боб. Оба они фанаты строк. Однажды Алиса и Боб решили сыграть в игру на строке \(s = s_1 s_2 \dots s_n\) длиной \(n\), состоящей из строчных английских букв. Они ходят по очереди, Алиса начинает. В свой ход игрок должен выбрать индекс \(i\) (\(1 \leq i \leq n\)), который не был выбран ранее, и поменять \(s_i\) на любую другую строчную английскую букву \(c\), удовлетворяющую \(c \neq s_i\). Когда все индексы уже были выбраны по одному разу, игра заканчивается. Цель Алисы — сделать финальную строку лексикографически как можно меньше, в то время как цель Боба — сделать финальную строку лексикографически как можно больше. Оба они являются профессиональными игроками, поэтому всегда играют оптимально. Гомер не является профессиональным игроком, поэтому ему интересно, какой будет финальная строка. Строка \(a\) лексикографически меньше строки \(b\), если и только если выполняется один из следующих пунктов: - \(a\) — префикс \(b\), но \(a \ne b\);
- в первой позиции, где \(a\) и \(b\) различны, в строке \(a\) находится буква, которая встречается в алфавите раньше, чем соответствующая буква в \(b\).
Выходные данные Для каждого набора входных данных выведите финальную строку в отдельной строке. Примечание В первом наборе входных данных: Алиса делает первый ход и должна поменять единственную букву на другую, поэтому она меняет ее на «b». Во втором наборе входных данных: Алиса меняет первую букву на «a», затем Боб меняет вторую букву на «z», Алиса меняет третью букву на «a», а затем Боб меняет четвертую букву на «z». В третьем наборе входных данных: Алиса меняет первую букву на «b», а затем Боб меняет вторую букву на «y». | |
![]()
|
|
A. Космическая навигация
жадные алгоритмы
Строки
*800
Однажды вам приснилось, будто вы отправились на планету Planetforces на своем собственном космическом корабле. Однако его система пилотирования была повреждена, а потому, чтобы отправиться на Planetforces, вам нужно ее починить.  Представим космическое пространство как плоскость \(XY\). Вы начинаете в точке \((0, 0)\), а Planetforces расположена в точке \((p_x, p_y)\). Система пилотирования вашего корабля следует списку команд, который можно представить как строку \(s\). Система считывает \(s\) слева направо. Предположим, в данный момент вы находитесь в позиции \((x, y)\) и текущая команда — \(s_i\): - если \(s_i = \text{U}\), вы перемещаетесь в \((x, y + 1)\);
- если \(s_i = \text{D}\), вы перемещаетесь в \((x, y - 1)\);
- если \(s_i = \text{R}\), вы перемещаетесь в \((x + 1, y)\);
- если \(s_i = \text{L}\), вы перемещаетесь в \((x - 1, y)\).
Так как строка \(s\) могла быть повреждена, то существует вероятность, что в результате вы так и не достигнете Planetforces. К счастью, вы можете удалить некоторые команды из \(s\), но вы не можете менять их порядок. Можете ли вы удалить несколько (возможно, ни одной) команд из \(s\) так, чтобы вы достигли Planetforces после того, как система обработает все команды? Выходные данные Для каждого набора входных данных выведите «YES», если вы можете удалить несколько (возможно, ни одной) команд \(s\) так, что вы достигнете Planetforces. В противном случае выведите «NO». Вы можете выводить какую букву в любом регистре. Примечание В первом наборе входных данных вам не нужно никак изменять \(s\), так как заданная \(s\) доставит вас на Planetforces. Во втором наборе вы можете удалить команды \(s_2\), \(s_3\), \(s_4\), \(s_6\), \(s_7\) и \(s_8\), и \(s\) станет равна «UR». В третьем наборе вы должны удалить команду \(s_9\), в противном случае вы не закончите полет в позиции планеты Planetforces. | |
![]()
|
|
E. Марсианские строки
Строки
строковые суфф. структуры
*2300
За время своего изучения марсиан Петя хорошо понял, что марсиане крайне ленивые. Они любят спать и совсем не любят просыпаться. Представьте себе марсианина имеющего ровно n глаз расположенных в ряд, и пронумерованных слева направо от 1 до n. Когда марсианин спит, он одевает на каждый свой глаз по повязке (чтобы утром марсианский свет не заставил его проснуться). С внутренней стороны каждой повязки написана одна прописная буква латинского алфавита, поэтому, когда марсианин утром просыпается и открывает все свои глаза, он видит строку s из прописных букв латинского алфавита длины n. «Динь-дилинь!» — звонит будильник. Марсианин уже проснулся, но еще не открыл ни одного своего глаза. Он догадывается, что день сегодня будет трудным, поэтому ему хочется открыть глаза и увидеть что-нибудь хорошее. Марсианин считает, что только m слов марсианского языка красивые. Также с утра ему очень сложно открыть все глаза сразу, поэтому он открывает два не накладывающихся отрезка последовательных глаз. Более формально, марсианин выбирает четыре числа a, b, c, d (1 ≤ a ≤ b < c ≤ d ≤ n) и открывает все глаза с номерами i такими, что a ≤ i ≤ b или c ≤ i ≤ d. После того как марсианин открыл нужные ему глаза, он читает все видимые символы слева направо, получая тем самым какое-то слово. Рассмотрим все различные слова, которые может увидеть с утра марсианин. Вам требуется узнать, сколько среди этих слов красивых. Выходные данные Выведите одно целое число — количество различных красивых слов, которые может увидеть сегодня утром марсианин. Примечание Рассмотрим тестовый пример. В нем можно получить только вторую красивую строку, если открыть отрезки глаз a = 1, b = 2 и c = 4, d = 5 или отрезки глаз a = 1, b = 2 и c = 6, d = 7. Первую красивую строку получить никак нельзя. | |
![]()
|
|
C. K-красивые строки
Бинарный поиск
жадные алгоритмы
Конструктив
Перебор
Строки
*2000
Дана строка \(s\) из строчных букв английского алфавита и число \(k\). Назовем строку из строчных букв английского алфавита красивой, если количество вхождений каждой буквы в эту строку кратно числу \(k\). Требуется найти лексикографически минимальную красивую строку длины \(n\), которая лексикографически больше или равна строке \(s\). Если такой строки не существует, выведите \(-1\). Строка \(a\) лексикографически меньше строки \(b\), если и только если выполняется один из следующих пунктов: - \(a\) — префикс \(b\), но \(a \ne b\);
- в первой позиции, где \(a\) и \(b\) различны, в строке \(a\) находится буква, которая встречается в алфавите раньше, чем соответствующая буква в \(b\).
Выходные данные Для каждого тестового случая в отдельной строке выведите лексикографически минимальную красивую строку длины \(n\), которая больше или равна строке \(s\), или \(-1\), если такой строки не существует. Примечание В первом наборе входных данных «acac» лексикографически больше или равна \(s\), а каждая буква в ней встречается \(2\) или \(0\) раз, поэтому она красивая. Во втором наборе входных данных каждая буква в \(s\) встречается \(0\) или \(1\) раз, поэтому сама \(s\) является ответом. Можно показать, что в третьем наборе подходящей строки нет. В четвертом примере каждая буква встречается \(0\), \(3\) или \(6\) раз в «abaabaaab». Все эти числа делятся на \(3\). | |
![]()
|
|
E. Огромный XOR
битмаски
жадные алгоритмы
Конструктив
математика
Строки
*2600
Даны два целых числа \(l\) и \(r\) в двоичном представлении. Пусть \(g(x, y)\) равняется побитовому исключающему ИЛИ всех целых чисел от \(x\) до \(y\) включительно (т. е. \(x \oplus (x+1) \oplus \dots \oplus (y-1) \oplus y\)). Определим \(f(l, r)\) как максимум по всем значениям \(g(x, y)\) при \(l \le x \le y \le r\). Выведите \(f(l, r)\). Выходные данные В единственной строке выведите значение \(f(l, r)\) в двоичном представлении без лишних ведущих нулей для данных \(l\) и \(r\). Примечание В примере из условия \(l=19\), \(r=122\). \(f(x,y)\) максимально и равно \(127\), например, при \(x=27\), \(y=100\). | |
![]()
|
|
A. Раздели!
жадные алгоритмы
Конструктив
Перебор
Строки
*900
Каваширо Нитори — девочка, любящая спортивное программирование. Однажды она нашла строку и целое число. Будучи опытным составителем задач, она сразу подумала о следующей задаче. Дана строка \(s\) и параметр \(k\), проверьте, существует ли последовательность из \(k+1\) непустой строки \(a_1,a_2...,a_{k+1}\) такая, что \(\)s=a_1+a_2+\ldots +a_k+a_{k+1}+R(a_k)+R(a_{k-1})+\ldots+R(a_{1}).\(\) Здесь \(+\) обозначает конкатенацию (соединение) строк. \(R(x)\) — разворот строки \(x\), например, \(R(abcd) = dcba\). Обратите внимание, что в выражении выше специально пропущено слагаемое вида \(R(a_{k+1})\). Выходные данные Для каждого набора входных данных выведите «YES» (без кавычек), если можно найти \(a_1,a_2,\ldots,a_{k+1}\), и «NO» (без кавычек) иначе. Вы можете выводить каждую букву в любом регистре (строчную или заглавную). Примечание В первом наборе входных данных одно из решений \(a_1=qw\) и \(a_2=q\). Во втором наборе входных данных одно из решений \(a_1=i\) и \(a_2=o\). В пятом наборе входных данных одно из решений — это \(a_1=dokidokiliteratureclub\). | |
![]()
|
|
E. Хаотичное слияние
дп
Комбинаторика
математика
Строки
*2400
Заданы две строки \(x\) и \(y\), обе состоят из строчных латинских букв. Пусть \(|s|\) будет длиной строки \(s\). Назовем последовательность \(a\) последовательностью слияния, если она состоит из ровно \(|x|\) нулей и ровно \(|y|\) единиц в некотором порядке. Слияние \(z\) получается из последовательности \(a\) по следующим правилам: - если \(a_i=0\), то удалить букву из начала \(x\) и приписать ее в конец \(z\);
- если \(a_i=1\), то удалить букву из начала \(y\) и приписать ее в конец \(z\).
Две последовательности слияния \(a\) и \(b\) считаются различными, если существует такая позиция \(i\), что \(a_i \neq b_i\). Назовем строку \(z\) хаотичной, если для всех \(i\) от \(2\) до \(|z|\) \(z_{i-1} \neq z_i\). Пусть \(s[l,r]\) для некоторых \(1 \le l \le r \le |s|\) будет подстрокой последовательных букв \(s\), начинающейся с позиции \(l\) и заканчивающейся в позиции \(r\) включительно. Пусть \(f(l_1, r_1, l_2, r_2)\) будет количеством различных последовательностей слияния \(x[l_1,r_1]\) и \(y[l_2,r_2]\), которые производят хаотичные слияния. Обратите внимание, что рассматриваются только непустые подстроки \(x\) и \(y\). Посчитайте \(\sum \limits_{1 \le l_1 \le r_1 \le |x| \\ 1 \le l_2 \le r_2 \le |y|} f(l_1, r_1, l_2, r_2)\). Выведите ответ по модулю \(998\,244\,353\). Выходные данные Выведите одно число — сумму \(f(l_1, r_1, l_2, r_2)\) по \(1 \le l_1 \le r_1 \le |x|\) и \(1 \le l_2 \le r_2 \le |y|\) по модулю \(998\,244\,353\). Примечание В первом примере: - \(6\) пар подстрок «a» and «b», каждая с корректными последовательностями слияния «01» and «10»;
- \(3\) пары подстрок «a» and «bb», каждая с корректной последовательностью слияния «101»;
- \(4\) пары подстрок «aa» and «b», каждая с корректной последовательностью слияния «010»;
- \(2\) пары подстрок «aa» and «bb», каждая с корректными последовательностями слияния «0101» and «1010»;
- \(2\) пары подстрок «aaa» and «b», каждая без корректных последовательностей слияния;
- \(1\) пара подстрок «aaa» and «bb» с корректной последовательностью слияния «01010».
Поэтому ответ равен \(6 \cdot 2 + 3 \cdot 1 + 4 \cdot 1 + 2 \cdot 2 + 2 \cdot 0 + 1 \cdot 1 = 24\). | |
![]()
|
|
D. Миссия непроходима
дп
Строки
*2600
На прилавках магазинов появилась долгожданная игра The Colder Scrools V: XXXvodsk. Игра оказалась дьявольски сложна, и большинство студентов не могут пройти последнюю миссию («Мы не ходим в XXXводск...»), в связи с чем зимняя сессия оказалась под угрозой. Ректор уже подумывал о переносе сессии на апрель (ему и самому хотелось пройти эту миссию), когда на пороге его кабинета возник незнакомец. «Здравствуйте. Меня зовут Петрович, и я решаю любые проблемы», — сказал он. Теперь они уже сидят вместе и все равно не могут пройти эту миссию. Ведь чтобы одолеть финального босса, требуется показать все свое мастерство в искусстве управления буквами. Нужно быть настоящими волшебниками, а уж что говорить, когда волшебники начинают соревноваться... Но, давайте более формально: дана строка и набор целых чисел ai. Разрешается выбрать любую подстроку, являющуюся палиндромом, и удалить ее. При этом мы получаем количество очков равное ak, где k — длина удаляемого палиндрома. Для некоторых k ak = -1, что означает, что удалять подстроки-палиндромы такой длины запрещено. После удаления подстроки оставшаяся часть «сдвигается», то есть строка ни в какой момент времени не содержит пропусков. Этот процесс повторяется, пока строка содержит хотя бы одну подстроку-палиндром, которую можно удалить. Все полученные очки суммируются. Определите, какое максимальное количество очков можно получить. «Эх», — сказал, вставая из-за стола, Петрович, — «когда-то я тоже любил удалять палиндромы, как и вы, но потом мне прострелили колено». Выходные данные Выведите одно целое число — максимальное количество очков, которое можно получить, играя на данной строке. Примечание В первом примере у нас нет возможности удалить ни одной подстроки, поэтому лучший результат 0. Во втором примере нам разрешено удалять палиндромы длины только 1, таким образом, удалив всю строку, мы получим 7 очков. В третьем примере следующая оптимальная стратегия: сначала удаляем символ c, затем строку aa, затем bb, и последнюю aa. При этом получаем 1 + 3 * 5 = 16 очков. | |
![]()
|
|
A. Дежавю
Конструктив
Строки
*800
Палиндром — это строка, которая читается одинаково в обоих направлениях. Например, строки «z», «aa», «aba» и «abccba» — палиндромы, а «codeforces» и «ab» — нет. Вы ненавидите палиндромы, потому что они вызывают у вас дежавю. Дана строка \(s\). Вы должны вставить ровно один символ 'a' в \(s\). Если таким образом можно получить строку, которая не является палиндромом, вам нужно найти одну из них. В противном случае следует сообщить, что это невозможно. Например, предположим, что \(s=\) «cbabc». Вставив 'a', можно получить «acbabc», «cababc», «cbaabc», «cbabac», или «cbabca». Строка «cbaabc» — палиндром, и не подходит, поэтому вы должны вывести другую из вышеперечисленных строк. Выходные данные Для каждого набора входных данных, если нет решения, выведите «NO». В противном случае выведите «YES», а в следующей строке выведите строку длиной \(|s|+1\). Если есть несколько решений, можно вывести любое из них. Вы можете выводить каждый символ «YES» и «NO» в любом регистре. Примечание Первый набор входных данных описан в условии. Во втором наборе входных данных можно получить либо «aab», либо «aba». Но «aba» — это палиндром, поэтому «aab» — единственный правильный ответ. В третьем наборе входных данных «zaza» и «zzaa» — правильные ответы, а «azza» — нет. В четвертом наборе входных данных «baa» — единственный правильный ответ. В пятом наборе входных данных мы можем получить только «aa», что является палиндромом. Следовательно, ответ «NO». В шестом наборе входных данных «anutforajaroftuna» — палиндром, но вставка 'a' в любом другом месте подходит. | |
![]()
|
|
C. Двусторонние строки
Перебор
реализация
Строки
*1000
Вам заданы строки \(a\) и \(b\), состоящие из строчных букв латинского алфавита. Вы можете сделать произвольное число следующих операций в произвольном порядке: - если \(|a| > 0\) (длина строки \(a\) больше нуля), удалить первый символ строки \(a\), то есть заменить \(a\) на \(a_2 a_3 \ldots a_n\);
- если \(|a| > 0\), удалить последний символ строки \(a\), то есть заменить \(a\) на \(a_1 a_2 \ldots a_{n-1}\);
- если \(|b| > 0\) (длина строки \(b\) больше нуля), удалить первый символ строки \(b\), то есть заменить \(b\) на \(b_2 b_3 \ldots b_n\);
- если \(|b| > 0\), удалить последний символ строки \(b\), то есть заменить \(b\) на \(b_1 b_2 \ldots b_{n-1}\).
Заметьте, что после каждой из операций строка \(a\) или \(b\) могут стать пустыми. Например, если \(a=\)«hello» и \(b=\)«icpc», то вы можете применить следующую последовательность операций: - удалить первый символ строки \(a\) \(\Rightarrow\) \(a=\)«ello» и \(b=\)«icpc»;
- удалить первый символ строки \(b\) \(\Rightarrow\) \(a=\)«ello» и \(b=\)«cpc»;
- удалить первый символ строки \(b\) \(\Rightarrow\) \(a=\)«ello» и \(b=\)«pc»;
- удалить последний символ строки \(a\) \(\Rightarrow\) \(a=\)«ell» и \(b=\)«pc»;
- удалить последний символ строки \(b\) \(\Rightarrow\) \(a=\)«ell» и \(b=\)«p».
По заданным строкам \(a\) и \(b\) найдите минимальное количество операций, за которые можно сделать строки \(a\) и \(b\) равными. Обратите внимание, что пустые строки также являются равными. Выходные данные Для каждого набора входных данных выведите одно число — минимальное количество операций, за которые можно сделать строки \(a\) и \(b\) равными. | |
![]()
|
|
G. Максимизируй оставшуюся строку
дп
жадные алгоритмы
Перебор
Строки
Структуры данных
*2000
Вам задана строка \(s\), состоящая из строчных букв латинского алфавита. Пока в строке \(s\) есть хотя бы один символ, повторяющийся хотя бы дважды, вы выполняете следующую операцию: - вы выбираете индекс \(i\) (\(1 \le i \le |s|\)), такой что символ на позиции \(i\) встречается хотя бы два раза в строке \(s\), и удаляете символ на позиции \(i\), то есть заменяете \(s\) на \(s_1 s_2 \ldots s_{i-1} s_{i+1} s_{i+2} \ldots s_n\).
Например, если \(s=\)«codeforces», то вы можете применить следующую последовательность операций: - \(i=6 \Rightarrow s=\)«codefrces»;
- \(i=1 \Rightarrow s=\)«odefrces»;
- \(i=7 \Rightarrow s=\)«odefrcs»;
По заданной строке \(s\) найдите лексикографически максимальную строку, которая может быть получена после применения некоторой последовательности операций, оставляющей в строке только уникальные символы. Строка \(a\) длины \(n\) лексикографически меньше строки \(b\) длины \(m\), если: - существует индекс \(i\) (\(1 \le i \le \min(n, m)\)), такой что первые \(i-1\) символов у строк \(a\) и \(b\) совпадают, а \(i\)-й символ строки \(a\) меньше, чем \(i\)-й символ строки \(b\);
- или первые \(\min(n, m)\) символов у строк \(a\) и \(b\) совпадают и \(n < m\).
Например строка \(a=\)«aezakmi» лексикографически меньше строки \(b=\)«aezus». Выходные данные Для каждого набора входных данных выведите лексикографически максимальную строку, которая может быть получена после применения некоторой последовательности операций, оставляющей в строке только уникальные символы. | |
![]()
|
|
A. Бинарная литература
жадные алгоритмы
Конструктив
реализация
Строки
*1900
Бинарная строка — это строка, содержащая только символы 0 и 1. Koyomi Kanou усердно работает над своей мечтой стать писательницей. Чтобы попрактиковаться, она решила принять участие в Конкурсе по Написанию Бинарных Романов. Указание к конкурсу состоит из трёх бинарных строк длины \(2n\). Корректным романом для конкурса является бинарная строка длины не более \(3n\), содержащая в качестве подпоследовательностей не менее двух из трёх данных строк. Koyomi только что получила три строки — указание от организаторов конкурса. Помогите ей написать корректный роман для конкурса. Строка \(a\) является подпоследовательностью строки \(b\), если \(a\) можно получить из \(b\), удалив несколько (возможно, ноль) символов. Выходные данные Для каждого набора входных данных выведите одну строку, содержащую бинарную строку длины не более \(3n\), которая в качестве подпоследовательностей содержит как минимум две из заданных бинарных строк. Можно доказать, что при данных ограничениях такая бинарная строка существует всегда. Если есть несколько возможных ответов, вы можете вывести любой из них. Примечание В первом наборе входных данных бинарные строки 00 и 01 являются подпоследовательностями выходной строки: 010 и 010. Обратите внимание, что 11 не является подпоследовательностью выходной строки, но это не требуется. Во втором наборе входных данных все три входных строки являются подпоследовательностями выходной строки: 011001010, 011001010 и 011001010. | |
![]()
|
|
B. Телефонные номера
реализация
Строки
*1200
В городе XXXводске просто чертовски холодно этой зимой! Поэтому компания из n друзей предпочитает ездить на такси, заказывать пиццу в гостиницу и звонить знакомым девушкам домой. Телефонные номера в этом городе состоят из трех пар цифр (например, 12-34-56). У каждого из друзей есть своя записная книжка размера si (количество номеров). Известно, что номера такси состоят из шести одинаковых цифр (например, 22-22-22), номера заказа пиццы обязательно являются убывающей последовательностью из шести различных цифр (например, 98-73-21), остальные номера являются номерами знакомых девушек. Вам даны записные книжки ваших друзей, посчитайте к кому из них лучше всего обращаться по каждому из этих вопросов (у кого больше номеров каждого типа). Если в записной книжке одного человека какой-то номер встречается дважды, его следует считать дважды. То есть каждый номер нужно учесть столько же раз, сколько он встречается в записной книжке. Выходные данные В первой строке выведите фразу «If you want to call a taxi, you should call: ». Далее выведите имена всех друзей, имеющих в своих записных книжках максимальное количество номеров такси. Во второй строке выведите фразу «If you want to order a pizza, you should call: ». Далее выведите имена всех друзей с максимальным количеством номеров доставки пиццы. В третьей строке выведите фразу «If you want to go to a cafe with a wonderful girl, you should call: ». Далее выведите имена всех друзей с максимальным количеством номеров девушек. Имена выводите в том же порядке, в котором они даны во входных данных. Два последовательных имени разделяйте запятой и пробелом. Каждая строка должна заканчиваться ровно одной точкой. Для уточнения формата вывода смотрите примеры. Необходимо строго следовать формату вывода. Лишние пробелы не допускаются. Примечание В первом примере дано четыре друга. В записной книжке Fedorov находится один номер такси и один номер доставки пиццы, у Melnikov есть только 3 номера девушек, Rogulenko — 6 номеров такси и один номер доставки пиццы, Kaluzhin — 2 номера такси и один номер доставки пиццы. Таким образом, если требуется заказать такси очевидно звонить нужно Rogulenko, чтобы заказать пиццу нужно позвонить любому из Rogulenko, Fedorov, Kaluzhin (у каждого по одному номеру), по количеству номеров девушек первое место единолично занимает Melnikov. | |
![]()
|
|
D. Строка минимальной стоимости
графы
жадные алгоритмы
Конструктив
Перебор
Строки
*1600
Определим стоимость строки \(s\) как количество пар индексов \(i\) и \(j\) (\(1 \le i < j < |s|\)) таких, что \(s_i = s_j\) и \(s_{i+1} = s_{j+1}\). Заданы два положительных целых числа \(n\) и \(k\). Среди всех строк длины \(n\), содержащих только первые \(k\) букв латинского алфавита, найдите строку с минимально возможной стоимостью. Если таких строк несколько — найдите любую из них. Выходные данные Выведите строку \(s\) такую, что она состоит из \(n\) символов, каждый из которых является одной из первых \(k\) латинских букв, и она имеет минимально возможную стоимость среди всех таких строк. Если таких строк несколько — выведите любую из них. | |
![]()
|
|
F. Чайнворд
дп
матрицы
Перебор
Строки
строковые суфф. структуры
Структуры данных
*2700
Чайнворд — это особый тип кроссворда. Как и в большинстве кроссвордов, в нем есть клетки, в которые надо вписать буквы, и некоторые подсказки, которые указывают на то, какие буквы должны быть. В чайнворде клетки для букв расположены в одну строку. В этой задаче мы будем рассматривать чайнворды длины \(m\). Подсказка к чайнворду — это последовательность отрезков такая, что отрезки не пересекаются между собой и покрывают все \(m\) клеток. Каждый отрезок содержит описание слова в соответствующих клетках. Особенность в том, что подсказки на самом деле две: одна последовательность находится в строке над клетками для букв, а другая — под ней. Когда эти последовательности разные, они помогают разрешить неоднозначность в ответах. Дан словарь из \(n\) слов, каждое слово состоит из строчных латинских букв. Все слова попарно различны. Экземпляр чайнворда — это следующая тройка: - строка из \(m\) строчных латинских букв;
- первая подсказка: последовательность отрезков такая, что буквы, соответствующие каждому отрезку, составляют некоторое слово из словаря;
- вторая подсказка: еще одна последовательность отрезков такая, что буквы, соответствующие каждому отрезку, составляют некоторое слово из словаря.
Обратите внимание, что последовательности отрезков не обязаны различаться. Два экземпляра чайнвордов считаются различными, если различаются их строки, первые подсказки или вторые подсказки. Посчитайте количество различных экземпляров чайнвордов. Так как их число может быть достаточно велико, выведите его остаток от деления на \(998\,244\,353\). Выходные данные Выведите одно целое число — количество различных экземпляров чайнвордов длины \(m\) для данного словаря по модулю \(998\,244\,353\). Примечание Здесь приведены все примеры различных чайнвордов для первого примера:  Красные полоски над буквами означают отрезки первой подсказки, синие полоски под буквами означают отрезки второй подсказки. Во втором примере возможные строки: «abab», «abcd», «cdab» и «cdcd». Все подсказки — это отрезки, которые покрывают первые две буквы и последние две буквы. | |
![]()
|
|
C. A-B палиндром
Конструктив
реализация
Строки
*1200
Вам дана строка \(s\), состоящая из символов '0', '1' и '?'. Вам необходимо заменить все символы '?' в строке \(s\) на '0' или '1' так, чтобы строка стала палиндромом и чтобы в ней было ровно \(a\) символов '0' и ровно \(b\) символов '1'. Обратите внимание, что каждый из символов '?' вы заменяете независимо от других. Строка \(t\) длины \(n\) называется палиндромом, если для всех \(i\) (\(1 \le i \le n\)) верно равенство \(t[i] = t[n-i+1]\). Например, если \(s=\)«01?????0», \(a=4\) и \(b=4\), то можно заменить символы '?' следующими способами: Для заданной строки \(s\) и чисел \(a\) и \(b\) замените все символы '?' в строке \(s\) на '0' или '1' так, чтобы строка стала палиндромом и чтобы в ней было ровно \(a\) символов '0' и ровно \(b\) символов '1'. Выходные данные Для каждого набора входных данных выведите: - «-1», если нельзя заменить все символы '?' в строке \(s\) на '0' или '1' так, чтобы строка стала палиндромом и чтобы в ней было ровно \(a\) символов '0' и ровно \(b\) символов '1';
- строку, которая получается в результате замены, в противном случае.
Если существует несколько подходящий способов замены символов, то можете выводить любой. | |
![]()
|
|
D. Убить Антона
Конструктив
математика
Перебор
Строки
Структуры данных
*2200
После того, как Антон отклонил \(10^{100}\) задач на структуры данных, Errorgorn очень зол на него и решил его убить. ДНК Антона можно представить в виде строки \(a\), которая содержит только символы из строки «ANTON» (всего \(4\) различных символов). Errorgorn может заменить ДНК Антона на строку \(b\), которая должна быть перестановкой \(a\). Однако тело Антона может защититься от этой атаки. За \(1\) секунду его тело может поменять местами \(2\) соседних символа его ДНК, чтобы превратить ее обратно в \(a\). Тело Антона умно и будет использовать минимальное количество ходов. Чтобы максимизировать вероятность смерти Антона, Errorgorn хочет изменить ДНК Антона на строку, которая максимизирует время, необходимое телу Антона для возвращения к его исходному ДНК. Но поскольку Errorgorn занят решением новых задач на структуры данных, ему нужна ваша помощь, чтобы найти лучшую строку \(B\). Сможете ли вы ему помочь? Выходные данные Для каждого набора входных данных выведите единственную строку \(b\). Если ответов несколько, вы можете вывести любой из них. \(b\) должна быть перестановкой строки \(a\). Примечание Для первого набора входных данных, телу Антона требуется \(7\) секунд, чтобы превратить NNOTA в ANTON: NNOTA \(\to\) NNOAT \(\to\) NNAOT \(\to\) NANOT \(\to\) NANTO \(\to\) ANNTO \(\to\) ANTNO \(\to\) ANTON. Обратите внимание, что нельзя вывести такие строки, как AANTON, ANTONTRYGUB, AAA и anton, так как они не являются перестановкой ANTON. Для первого тестового случая телу Антона требуется \(2\) секунды, чтобы преобразовать AANN в NAAN. Обратите внимание, что другие строки, такие как NNAA и ANNA также будут приняты. | |
![]()
|
|
E. Минимакс
жадные алгоритмы
Конструктив
Строки
*2100
Префикс-функция от строки \(t = t_1 t_2 \ldots t_n\) и позиции \(i\) в ней — это длина \(k\) наибольшего собственного (не равного всей подстроке) префикса подстроки \(t_1 t_2 \ldots t_i\), который одновременно является суффиксом этой подстроки. Например, для строки \(t = \) abacaba значения префикс-функции от позиций \(1, 2, \ldots, 7\) равны \([0, 0, 1, 0, 1, 2, 3]\). Введём функцию \(f(t)\), равную максимальному значению префикс-функции строки \(t\) по всем её позициям. Например, \(f(\)abacaba\() = 3\). Вам дана строка \(s\). Переставьте её символы произвольным образом, чтобы получить строку \(t\) (количество вхождений любого символа в строки \(s\) и \(t\) должно совпадать). Значение \(f(t)\) должно быть минимальным возможным. Среди всех вариантов минимизировать \(f(t)\) выберите тот, где строка \(t\) лексикографически минимальна. Выходные данные Для каждого набора входных данных выведите одну строку \(t\). Мультимножество букв в строках \(s\) и \(t\) должно совпадать. Значение \(f(t)\), максимума префикс-функции в строке \(t\), должно быть минимальным возможным. Строка \(t\) должна быть лексикографически минимальной среди всех строк, удовлетворяющих предыдущим условиям. Примечание Строка \(a\) лексикографически меньше строки \(b\), если и только если выполняется один из следующих пунктов: - \(a\) — префикс \(b\), но \(a \ne b\);
- в первой позиции, где \(a\) и \(b\) различны, в строке \(a\) находится буква, которая встречается в алфавите раньше, чем соответствующая буква в \(b\).
В первом наборе входных данных \(f(t) = 0\) и значения префикс-функции равны \([0, 0, 0, 0, 0]\) для любой перестановки букв. Строка ckpuv является лексикографически минимальной перестановкой букв строки vkcup. Во втором наборе входных данных \(f(t) = 1\), значения префикс-функции равны \([0, 1, 0, 1, 0, 1, 0]\). В третьем наборе входных данных \(f(t) = 5\), значения префикс-функции равны \([0, 1, 2, 3, 4, 5]\). | |
![]()
|
|
C. Нестабильная строка
Бинарный поиск
дп
жадные алгоритмы
реализация
Строки
*1400
Вам задана строка \(s\), состоящая из символов 0, 1 и ?. Назовем строку нестабильной, если она состоит из символов 0 и 1 и любые два соседних символа различаются (т. е. имеет вид 010101... или 101010...). Назовем строку красивой, если она состоит из символов 0, 1 и ?, и в ней можно заменить символы ? на 0 или 1 (для каждого символа выбор происходит независимо), чтобы строка стала нестабильной. Например, строки 0??10, 0 и ??? являются красивыми, а строки 00 и ?1??1 — нет. Посчитайте количество красивых непрерывных подстрок строки \(s\). Выходные данные Для каждого набора выходных данных выведите одно целое число — количество красивых подстрок строки \(s\). | |
![]()
|
|
F. Расстояние между строками
Бинарный поиск
Перебор
реализация
Строки
Структуры данных
хэши
*3000
Предположим, вам даны две строки \(a\) и \(b\). Вы можете применить следующую операцию любое количество раз: выбрать любую непрерывную подстроку \(a\) или \(b\) и отсортировать символы в ней в порядке неубывания. Пусть \(f(a, b)\) — минимальное количество операций, которое необходимо применить, чтобы сделать строки равными (или \(f(a, b) = 1337\), если невозможно сделать \(a\) и \(b\) равными с помощью этих операций). Например: - \(f(\text{ab}, \text{ab}) = 0\);
- \(f(\text{ba}, \text{ab}) = 1\) (за одну операцию мы можем отсортировать всю первую строку);
- \(f(\text{ebcda}, \text{ecdba}) = 1\) (за одну операцию мы можем отсортировать подстроку со \(2\)-го по \(4\)-й символ второй строки);
- \(f(\text{a}, \text{b}) = 1337\).
Вам задано \(n\) строк \(s_1, s_2, \dots, s_k\) одинаковой длины. Вычислите \(\sum \limits_{i = 1}^{n} \sum\limits_{j = i + 1}^{n} f(s_i, s_j)\). Выходные данные Выведите одно целое число: \(\sum \limits_{i = 1}^{n} \sum\limits_{j = i + 1}^{n} f(s_i, s_j)\). | |
![]()
|
|
B. Принцесса Веруртейлунга
Конструктив
Перебор
Строки
*1200
Я, Фишль, принцесса Веруртейлунга, спустилась на эту землю по зову судьбы — О, ты тоже путешественница из другого мира? Очень хорошо, я разрешаю вам путешествовать со мной. Нет ничего удивительного в том, что Фишль говорит, так странно выбирая выражения. Однако на этот раз даже Оз, ее друг-ворон, не может истолковать их! Может быть, вы поможете нам понять, что говорит эта юная принцесса? Вам дана строка из \(n\) строчных латинских букв — слово, которое только что произнесла Фишль. Вы думаете, что MEX строки может помочь вам найти смысл этого сообщения. MEX строки определяется как самая короткая строка, которая не встречается как непрерывная подстрока во входных данных. Если существует несколько таких строк, то за MEX считается лексикографически наименьшая из них. Обратите внимание, что пустая подстрока НЕ считается MEX. Строка \(a\) лексикографически меньше строки \(b\), если и только если выполняется один из следующих пунктов: - \(a\) — префикс \(b\), но \(a \ne b\);
- в первой позиции, где \(a\) и \(b\) различны, в строке \(a\) находится буква, которая встречается в алфавите раньше, чем соответствующая буква в \(b\).
Строка \(a\) является подстрокой \(b\), если \(a\) может быть получена из \(b\) удалением нескольких (возможно, ни одного или всех) символов из начала и нескольких (возможно, ни одного или всех) символов из конца. Узнайте, что представляет собой строка MEX! Выходные данные Для каждого набора входных данных выведите MEX строки в отдельной строке. | |
![]()
|
|
E1. Удаляй и удлиняй (простая версия)
Бинарный поиск
дп
жадные алгоритмы
Перебор
реализация
Строки
строковые суфф. структуры
хэши
*1600
Это простая версия задачи. Единственное отличие — это ограничения на \(n\) и \(k\). Вы можете делать взломы, только если все версии задачи решены. У вас есть строка \(s\), и вы можете выполнять над ней два типа операций: - Удалить последний символ строки.
- Дублировать строку: \(s:=s+s\), где \(+\) обозначает конкатенацию.
Вы можете использовать каждую операцию любое количество раз (возможно, ни одного). Ваша задача — найти лексикографически наименьшую строку длины ровно \(k\), которую можно получить, выполнив эти операции над строкой \(s\). Строка \(a\) лексикографически меньше строки \(b\) тогда и только тогда, когда выполняется одно из следующих условий: - \(a\) является префиксом \(b\), но \(a\ne b\);
- В первой позиции, где \(a\) и \(b\) отличаются, строка \(a\) имеет букву, которая появляется раньше в алфавите, чем соответствующая буква в \(b\).
Выходные данные Выведите лексикографически наименьшую строку длины \(k\), которая может быть получена путем выполнения операций над строкой \(s\). Примечание В первом тесте оптимально сделать одно дублирование: «dbcadabc» \(\to\) «dbcadabcdbcadabc». Во втором тесте оптимально удалить последние \(3\) символа, затем продублировать строку \(3\) раза, затем удалить последние \(3\) символов, чтобы строка имела длину \(k\). «abcd» \(\to\) «abc» \(\to\) «ab» \(\to\) «a» \(\to\) «aa» \(\to\) «aaaa» \(\to\) «aaaa» \(\to\) «aaaa» \(\to\) «aaaa» \(\to\) «aaaa». | |
![]()
|
|
E2. Удаляй и удлиняй (сложная версия)
Бинарный поиск
жадные алгоритмы
Строки
строковые суфф. структуры
Структуры данных
хэши
*2200
Это сложная версия задачи. Единственное отличие — это ограничения на \(n\) и \(k\). Вы можете делать взломы, только если все версии задачи решены. У вас есть строка \(s\), и вы можете выполнять над ней два типа операций: - Удалить последний символ строки.
- Дублировать строку: \(s:=s+s\), где \(+\) обозначает конкатенацию.
Вы можете использовать каждую операцию любое количество раз (возможно, ни одного). Ваша задача — найти лексикографически наименьшую строку длины ровно \(k\), которую можно получить, выполнив эти операции над строкой \(s\). Строка \(a\) лексикографически меньше строки \(b\) тогда и только тогда, когда выполняется одно из следующих условий: - \(a\) является префиксом \(b\), но \(a\ne b\);
- В первой позиции, где \(a\) и \(b\) отличаются, строка \(a\) имеет букву, которая появляется раньше в алфавите, чем соответствующая буква в \(b\).
Выходные данные Выведите лексикографически наименьшую строку длины \(k\), которая может быть получена путем выполнения операций над строкой \(s\). Примечание В первом тесте оптимально сделать одно дублирование: «dbcadabc» \(\to\) «dbcadabcdbcadabc». Во втором тесте оптимально удалить последние \(3\) символа, затем продублировать строку \(3\) раза, затем удалить последние \(3\) символов, чтобы строка имела длину \(k\). «abcd» \(\to\) «abc» \(\to\) «ab» \(\to\) «a» \(\to\) «aa» \(\to\) «aaaa» \(\to\) «aaaa» \(\to\) «aaaa» \(\to\) «aaaa» \(\to\) «aaaa». | |
![]()
|
|
E. Смешные подстроки
матрицы
реализация
Строки
Структуры данных
хэши
*2100
Поликарп придумал новый язык программирования. В нем есть только два типа команд: - «x := s» — назначить переменной с именем x значение s (где s - строка). Например, команда var := hello присваивает переменной с именем var значение hello. Обратите внимание, что s - это значение строки, а не имя переменной. Между названием переменной, оператором := и строкой находится ровно по одному пробелу.
- «x = a + b» — назначить переменной с именем x конкатенацию двух переменных a и b. Например, если программа состоит из трех команд a := hello, b := world, c = a + b, то переменная c будет содержать строку helloworld. Гарантируется, что программа корректна и переменные a и b были определены ранее. Между названиями переменных и операторами = и + находится ровно по одному пробелу.
Все имена переменных и строки состоят только из строчных букв английского алфавита и состоят не больше, чем из \(5\) символов. Результатом работы программы является количество вхождений строки haha в строке, которая была записана в переменную в последней команде. Поликарп очень устал, изобретая этот язык. Он просит вас реализовать его. Ваша задача состоит в том, чтобы — для заданных программных операторов вычислить количество вхождений строки haha в последней назначенной переменной. Выходные данные Для каждого набора входных данных выведите количество вхождений подстроки haha в строку, которая была записана в переменную в последней команде. Примечание В первом наборе входных данных результат — значение переменной d=hhahahaha. | |
![]()
|
|
B. Песня о любви
дп
реализация
Строки
*800
Однажды Петя в очередной раз написал грустную песню про любовь и поспешил показать ее Васе. Песня представляет собой строку из маленьких букв английского алфавита. У Васи сразу возникло \(q\) вопросов про эту песню. Каждый вопрос представляет собой некоторый отрезок песни с позиции \(l\) до позиции \(r\). Вася рассматривает подстроку, образованную символами на этом отрезке, а затем повторяет каждую букву в этой подстроке \(k\) раз, где \(k\) — порядковый номер буквы в алфавите. Например, если Вася выбрал подстроку «abbcb», то он повторит букву «a» один раз, каждую из букв «b» — по два раза, букву «c» — три раза, и полученная строка будет равна «abbbbcccbb», ее длина равна \(10\). Вася интересуется именно длиной полученной строки. Помогите Пете ответить Васе на его вопросы, а именно, для каждого из заданных вопросов определите длину строки, которую выпишет Вася. Выходные данные Выведите \(q\) строк — для каждого вопроса выведите длину строки, которую выпишет Вася. Примечание В первом примере Васю интересуют три вопроса. В первом вопросе Вася рассматривает подстроку «aba», которая превратится в «abba», а значит, ответ на этот вопрос равен \(4\). Во втором вопросе Вася рассматривает подстроку «baca», которая превратится в «bbaccca», а значит, ответ на этот вопрос будет равен \(7\). В третьем вопросе Вася рассматривает всю строку «abacaba», которая превратится в «abbacccabba» — строку длины \(11\). | |
![]()
|
|
B. Алфавитные строки
жадные алгоритмы
реализация
Строки
*800
Строка \(s\) длины \(n\) (\(1 \le n \le 26\)) называется алфавитной, если она может быть получена с помощью следующего алгоритма: - вначале записываем в \(s\) пустую строку (то есть выполняем присваивание \(s\) := "");
- далее выполним следующий шаг \(n\) раз;
- при \(i\)-м выполнении шага берем \(i\)-ю строчную букву латинского алфавита и приписываем её либо слева к строке \(s\), либо справа к строке \(s\) (то есть осуществляем присвоение \(s\) := \(c+s\) или \(s\) := \(s+c\), где \(c\) — \(i\)-я буква латинского алфавита).
Иными словами, переберем \(n\) первых букв латинского алфавита от 'a' и далее. Каждый раз к строке \(s\) будем приписывать букву либо слева, либо справа. Строки, которые можно получить таким образом — алфавитные. Например, следующие строки являются алфавитными: «a», «ba», «ab», «bac» и «ihfcbadeg». Следующие строки не являются алфавитными: «z», «aa», «ca», «acb», «xyz» и «ddcba». По заданной строке определите, является ли она алфавитной. Выходные данные Выведите \(t\) строк, каждая из строк должна содержать ответ на соответствующий набор входных данных. Выведите YES, если заданная строка \(s\) является алфавитной и NO в противном случае. Вы можете выводить YES и NO в любом регистре (например, строки yEs, yes, Yes и YES будут распознаны как положительный ответ). Примечание Пример содержит наборы входных данных из основной части условия. | |
![]()
|
|
E. Stringforces
Бинарный поиск
битмаски
дп
Перебор
Строки
*2500
Задана строка \(s\) длины \(n\). Каждый символ — это либо одна из первых \(k\) строчных латинских букв, либо знак вопроса. Требуется заменить каждый знак вопрос на одну из первых \(k\) строчных латинских букв таким образом, чтобы максимизировать следующее значение. Пусть \(f_i\) будет максимальной длиной подстроки строки \(s\), которая состоит целиком из \(i\)-й латинской буквы. Подстрока строки — это некоторый ее непрерывный подотрезок. Если \(i\)-я буква не встречается в строке, то \(f_i\) равно \(0\). Значение строки \(s\) — это минимальное значение среди \(f_i\) для всех \(i\) от \(1\) до \(k\). Какое наибольшее значение может иметь строка? Выходные данные Выведите одно целое число — наибольшее значение, которое может иметь строка, если заменить каждый знак вопроса на одну из первых \(k\) строчных латинских букв. Примечание В первом примере знаки вопроса можно заменить следующим образом: «aaaababbbb». \(f_1 = 4\), \(f_2 = 4\), поэтому ответ равен \(4\). Можно заменить и таким образом: «aaaabbbbbb». Тогда \(f_1 = 4\), \(f_2 = 6\), однако, минимум из них все еще равен \(4\). Во втором примере одна из возможных строк такая: «aabbccdda». В третьем примере хотя бы одна буква не встретится в строке, поэтому минимум из значений \(f_i\) всегда равен \(0\). | |
![]()
|
|
B1. Чудесная раскраска - 1
жадные алгоритмы
Строки
*800
Это упрощенная версия задачи B2. Возможно, вы захотите сначала ознакомиться с B2 до того как приступить к решению B1. У Паши и Маши есть любимая строка \(s\), состоящая из строчных букв латинского алфавита. Они захотели её раскрасить с помощью мелков двух цветов: красного и зелёного. Раскраска строки называется чудесной, если выполняются следующие условия: - каждый символ строки либо закрашивается ровно в один цвет (красный или зелёный), либо не закрашивается вовсе;
- любые два символа, покрашенные в один цвет, различны;
- количество символов, покрашенных в красный цвет, совпадает с количеством символов, покрашенных в зелёный цвет;
- количество покрашенных символов при соблюдении первых трёх условий максимально возможно.
Например, пусть строка \(s\) имеет вид «kzaaa». Одна из её возможных чудесных раскрасок изображена на рисунке.  Пример возможной чудесной раскраски для строки «kzaaa». Пример возможной чудесной раскраски для строки «kzaaa». Паша и Маша хотят сами научиться делать чудесную раскраску строки. Поскольку они очень маленькие, им нужна помощь в виде подсказки. Помогите им найти \(k\) — количество красных (или зелёных, эти числа равны) букв в чудесной раскраске строки. Выходные данные Для каждого набора входных данных в отдельной строке выведите одно целое неотрицательное число \(k\) — количество символов, которые будут покрашены в красный цвет. Примечание В первом наборе входных данных содержится строка из условия. Одна из чудесных раскрасок представлена на рисунке. Чудесная раскраска, содержащая \(3\) и более красных букв, не существует, поскольку в таком случае общее количество раскрашенных символов превысит количество символов в строке. Строку из второго набора входных данных можно раскрасить следующим образом. Первые вхождения букв «c», «o», «e» покрасим в красный цвет, вторые — в зелёный. Буквы «d» и «f» покрасим в красный цвет, «r», «s» — в зелёный. Таким образом, каждый символ будет покрашен либо в красный цвет, либо в зелёный, следовательно, ответа лучше \(5\) не существует. В третьем наборе входных данных все буквы различны, поэтому в красный цвет можно покрасить любой набор символов, количество которых не превышает половину длины строки и является максимально возможным. В четвёртом наборе входных данных всего один символ, поэтому, если покрасить его в красный, мы не сможем покрасить какой-либо другой символ в зелёный цвет. В пятом наборе входных данных все буквы одинаковы, поэтому нельзя покрасить более одного символа в красный цвет. | |
![]()
|
|
C. Интересный рассказ
жадные алгоритмы
сортировки
Строки
*1500
Стивен Квин хочет написать новый рассказ. Вы знаете, он очень необычный писатель — Стивен использует только буквы 'a', 'b', 'c', 'd' и 'e'! Чтобы написать рассказ, Стивен выписал \(n\) слов, состоящих из первых \(5\) строчных букв латинского алфавита. Из них он хочет выбрать максимальное количество слов таким образом, чтобы получился интересный рассказ. Рассказ представляет собой список слов, необязательно различных. Рассказ называется интересным, если существует буква, которая встречается во всех входящих в него словах большее количество раз, чем все остальные буквы латинского алфавита вместе взятые. Например, рассказ, состоящий из слов «bac», «aaada», «e», является интересным (буква «a» встречается в словах рассказа всего \(5\) раз, остальные — \(4\)), а рассказ, состоящий из слов «aba», «abcde» — нет (не существует буквы, встречающейся во всех словах рассказа большее число раз, чем все остальные вместе взятые). Вам дан список из \(n\) слов. Выберите из этого списка максимальное количество слов так, чтобы они образовывали интересный рассказ. Если невозможно составить непустой интересный рассказ, выведите \(0\). Выходные данные Для каждого набора входных данных выведите максимальное количество слов из заданного списка, которые могут образовать интересный рассказ. Если невозможно составить непустой интересный рассказ, выведите 0. Примечание В первом наборе входных данных примера все \(3\) слова могут быть использованы одновременно, чтобы составить интересный рассказ. Рассказ будет иметь вид «bac aaada e». Во втором наборе входных данных примера \(1\)-е и \(3\)-е слова могут быть использованы для составления интересного рассказа. Рассказ будет иметь вид «aba aba». Заметим, что все три слова одновременно использовать нельзя. В третьем наборе входных данных примера автор не может составить непустой интересный рассказ. Поэтому ответ равен \(0\). В четвертом наборе входных данных примера \(3\)-е и \(4\)-е слова могут быть использованы для составления интересного рассказа. Рассказ будет иметь вид «c bc». | |
![]()
|
|
A. Перестановка подпоследовательности
сортировки
Строки
*800
Дана строка \(s\) длины \(n\), состоящая из строчных букв английского алфавита. Вы должны выбрать некоторое число \(k\) между \(0\) и \(n\). Затем вы выбираете некоторые \(k\) символов \(s\) и переставляете их как угодно. При этом позиции остальных символов \(n-k\) остаются неизменными. Эту операцию нужно выполнить ровно один раз. Например, если \(s=\texttt{"andrea"}\), то можно выбрать \(k=4\) символов \(\texttt{"a_d_ea"}\) и переставить их в порядке \(\texttt{"d_e_aa"}\) так, чтобы после операции строка стала \(\texttt{"dneraa"}\). Определите минимально возможное значение \(k\), выбрав которое можно отсортировать \(s\) в алфавитном порядке (то есть, чтобы после операции ее символы располагались в алфавитном порядке). Выходные данные Для каждого набора входных данных выведите минимальное значение \(k\), которое позволяет получить строку, отсортированную по алфавиту, с помощью операции, описанной выше. Примечание В первом наборе входных данных мы можем выбрать \(k=2\) символа \(\texttt{"_ol"}\) и переставить их как \(\texttt{"_lo"}\) (так что результирующая строка будет \(\texttt{"llo"}\)). Невозможно отсортировать строку, выбирая строго менее \(2\) символов. Во втором наборе входных данных одним из возможных способов сортировки \(s\) является рассмотрение \(k=6\) символов \(\texttt{"_o__force_"}\) и перестановка их как \(\texttt{"_c__efoor_"}\) (так что результирующая строка будет \(\texttt{"ccdeefoors"}\)). Можно показать, что невозможно отсортировать строку, выбирая строго меньше \(6\) символов. В третьем наборе входных данных, строка \(s\) уже отсортирована (поэтому мы можем выбрать \(k=0\) символов). В четвертом наборе входных данных мы можем выбрать все \(k=4\) символов \(\texttt{"dcba"}\) и перевернуть всю строку (так что результирующая строка будет \(\texttt{"abcd"}\)). | |
![]()
|
|
B. Переворот строки
дп
Перебор
реализация
Строки
хэши
*1300
У вас есть строка \(s\) и фишка, которую вы можете поставить на любой символ этой строки. После того, как вы поставите фишку, вы можете подвинуть ее вправо несколько (возможно, ноль) раз, то есть сделать следующее действие несколько раз: если текущая позиция фишки обозначена как \(i\), фишка перемещается в позицию \(i + 1\). Конечно же, это действие невозможно, если фишка находится в последней позиции строки. После того, как вы закончите двигать фишку вправо, вы можете подвинуть ее влево несколько (возможно, ноль) раз, то есть сделать следующее действие несколько раз: если текущая позиция фишки обозначена как \(i\), фишка перемещается в позицию \(i - 1\). Конечно же, это действие невозможно, если фишка находится в первой позиции строки. Когда вы ставите фишку или перемещаете ее, вы выписываете символ, на котором оказалась фишка. Например, если строка \(s\) — abcdef, вы ставите фишку на \(3\)-й символ, двигаете ее вправо \(2\) раза, а затем двигаете ее влево \(3\) раза, вы выпишете строку cdedcb. Вам даны две строки \(s\) и \(t\). Ваше задание — определить, можно ли так выполнить описанные операции со строкой \(s\), что в результате вы выпишете строку \(t\). Выходные данные Для каждого набора выходных данных выведите «YES», если можно выписать строку \(t\), проводя описанные в условии действия со строкой \(s\), или «NO» в противном случае. Каждую букву можно выводить в любом регистре (YES, yes, Yes будут распознаны как положительный ответ, NO, no и nO будут распознаны как отрицательный ответ). Примечание Рассмотрим примеры из условия. Первый набор входных данных разобран в условии. Во втором наборе входных данных можно поместить фишку на \(1\)-ю позицию, подвинуть ее дважды вправо, а затем дважды влево. В четвертом наборе входных данных можно поместить фишку на \(2\)-ю позицию, а потом не двигать ее вообще. В пятом наборе входных данных можно поставить фишку на \(1\)-ю позицию, подвинуть ее \(5\) раз вправо и завершить процесс. | |
![]()
|
|
D. Backspace
дп
жадные алгоритмы
Строки
*1500
Вам заданы две строки \(s\) и \(t\), каждая из которых состоит из строчных букв латинского алфавита. Вы собираетесь посимвольно напечатать строку \(s\), начиная с первого символа и заканчивая последним. Когда вы собираетесь напечатать какой-то символ, вместо того, чтобы нажать на кнопку, печатающую этот символ, вы можете нажать кнопку «Backspace». Нажатие на эту кнопку удаляет последний напечатанный символ, который еще не был удален (или ничего не делает, если все напечатанные символы уже удалены или вы еще не напечатали ни одного символа). Например, если строка \(s\) — «abcbd», и вы нажимаете на кнопку Backspace вместо печати первого и четвертого символа, в результате получится строка «bd» (первое нажатие Backspace не удалит ни одного символа, а второе нажатие этой кнопки удалит символ «c»). Другой пример: если \(s\) равна «abcaa», и вы нажимаете Backspace вместо двух последних букв, получается «a». Вы должны определить, можно ли получить строку \(t\), если вы попробуете набрать строку \(s\), нажимая Backspace вместо нажатия кнопок, соответствующих некоторым (возможно, ни одному) буквам строки \(s\). Выходные данные Для каждого набора выходных данных выведите «YES», если можно получить строку \(t\), набирая строку \(s\) и заменяя некоторые символы нажатиями клавиши Backspace, или «NO» в противном случае. Каждую букву можно выводить в любом регистре (YES, yes, Yes будут распознаны как положительный ответ, NO, no и nO будут распознаны как отрицательный ответ). Примечание Рассмотрим пример из условия. Чтобы получить «ba» из «ababa», можно нажать Backspace вместо первого и четвертого символа. Нет способа получить «bb» при попытке напечатать «ababa». Нет способа получить «aaaa» при попытке напечатать «aaa». Чтобы получить «ababa» при попытке напечатать «aababa», можно нажать Backspace вместо печати первого символа, а затем напечатать все оставшиеся символы. | |
![]()
|
|
D. Диана
жадные алгоритмы
Конструктив
Строки
*1800
Вам дано целое число \(n\). Найдите любую строку \(s\) длины \(n\), состоящую только из латинских строчных букв, такую, что каждая непустая подстрока \(s\) встречается в \(s\) нечетное количество раз. Если таких строк несколько, выведите любую. Можно показать, что такая строка всегда существует при заданных ограничениях. Строка \(a\) является подстрокой \(b\), если \(a\) может быть получена из \(b\) удалением нескольких (возможно, ни одного или всех) символов из начала и нескольких (возможно, ни одного или всех) символов из конца. Выходные данные Для каждого наборам входных данных выведите одну строку, содержащую строку \(s\). Если таких строк несколько, выведите любую. Можно показать, что такая строка всегда существует при заданных ограничениях. Примечание В первом наборе входных данных каждая подстрока «abc» встречается ровно один раз. В третьем наборе входных данных каждая подстрока «bbcaabbba» встречается нечетное число раз. В частности, «b» встречается \(5\) раз, «a» и «bb» встречаются по \(3\) раза, а каждая из оставшихся подстрок встречается ровно один раз. | |
![]()
|
|
D. Скажите палиндромам - нет!
дп
Конструктив
Перебор
Строки
*1600
Назовем строку красивой, если в ней нет подстроки длины хотя бы \(2\), которая является палиндромом. Напомним, что палиндром — это строка, читающаяся одинаково от первого символа к последнему и от последнего символа к первому. Например, строки a, bab, acca, bcabcbacb являются палиндромами, а строки ab, abbbaa, cccb — нет. Определим стоимость строки, как минимальное количество операций, чтобы строка стала красивой, если за одну операцию разрешено изменить любой символ строки на одну из первых \(3\) букв латинского алфавита (в нижнем регистре). Вам задана строка \(s\) длины \(n\), каждый символ строки — одна из первых \(3\) букв латинского алфавита (в нижнем регистре). Вам предстоит ответить на \(m\) запросов — вычислите стоимость подстроки строки \(s\) с \(l_i\)-й по \(r_i\)-ю позицию включительно. Выходные данные Для каждого запроса выведите одно целое число — стоимость подстроки строки \(s\) с \(l_i\)-й по \(r_i\)-ю позицию включительно. Примечание Рассмотрим запросы в примере из условия. - в первом запросе интересующая нас подстрока — baa, ее можно превратить в bac за одну операцию;
- во втором запросе интересующая нас подстрока — baacb, ее можно превратить в cbacb за две операции;
- в третьем запросе интересующая нас подстрока — cb, ее можно оставить без изменений;
- в четвертом запросе интересующая нас подстрока — aa, ее можно превратить в ba за одну операцию.
| |
![]()
|
|
D. Сделай степень двойки
жадные алгоритмы
математика
Строки
*1300
Дано число \(n\). За \(1\) ход можно сделать одно из следующих действий: - стереть любую цифру этого числа (допустимо, чтобы число состояло из одной цифры и после этой операции стало «пустым»);
- дописать справа любую цифру.
Действия можно производить в любом порядке произвольное количество раз. Обратите внимание, что если после удаления некоторой цифры из числа оно будет содержать ведущие нули, то они не будут удаляться автоматически. Например, если из числа \(301\) удалить \(3\), то останется \(01\), а не \(1\). Необходимо совершить минимальное количество действий, так чтобы число стало степенью \(2\) (т. е. чтобы нашлось целое число \(k\) (\(k \ge 0\)) такое, что полученное число равно \(2^k\)). Полученное число не должно содержать ведущих нулей. Например, если \(n=1052\), то ответ равен \(2\). Сначала можно дописать справа цифру \(4\) (получится \(10524\)). Затем стереть цифру \(5\), в результате получится \(1024\), что является степенью числа \(2\). Например, если \(n=8888\), то ответ равен \(3\). Три раза сотрём любую из цифр \(8\). В результате получится \(8\), что является степенью числа \(2\). Выходные данные Для каждого набора входных данных в отдельной строке выведите целое число \(m\) — минимальное количество ходов, которые нужно совершить, чтобы число стало степенью \(2\). Примечание Ответ на первый набор входных данных разобран выше. Ответ на второй набор входных данных разобран выше. В третьем наборе входных данных достаточно приписать справа цифру \(4\) — число \(6\) превратится в \(64\). В четвёртом наборе входных данных можно сначала приписать справа \(8\), затем удалить \(7\) и \(5\) — получится число \(8\). В пятом и шестом наборах входных данных числа уже являются степенями двойки, поэтому ни одного хода делать не нужно. В седьмом наборе данных можно сначала удалить цифру \(3\) (останется \(01\)), затем удалить цифру \(0\) (получится \(1\)). | |
![]()
|
|
E. Поликарп и преобразование строки
Бинарный поиск
реализация
сортировки
Строки
*1800
У Поликарп есть строка \(s\). Поликарп делает следующие действия до тех пор, пока строка \(s\) не станет пустой (изначально \(t\) — пустая строка): - дописывает справа к \(t\) строку \(s\), то есть совершает присвоение \(t = t + s\), где \(t + s\) обозначает конкатенацию (соединение) строк \(t\) и \(s\);
- выбирает произвольным образом какую-то одну букву из \(s\) и удаляет из \(s\) все её вхождения (выбранная буква обязательно должна встречаться в \(s\) на момент выполнения этого действия).
Поликарп выполняет данную последовательность действий строго в заданном порядке. Отметим, что в конце концов строка \(s\) станет пустой, а строка \(t\) будет равна некоторому значению (и это значение определяется неоднозначно, оно зависит от порядка удаления). Например, если изначально \(s\)=«abacaba», то события могли разворачиваться следующим образом: - \(t\)=«abacaba», выбрана буква 'b', теперь \(s\)=«aacaa»;
- \(t\)=«abacabaaacaa», выбрана буква 'a', теперь \(s\)=«c»;
- \(t\)=«abacabaaacaac», выбрана буква 'c', теперь \(s\)=«» (пустая строка).
Вам необходимо восстановить исходное значение строки \(s\) по итоговому значению \(t\) и найти порядок, в котором удалялись буквы из \(s\). Выходные данные Для каждого набора входных данных выведите в отдельной строке: - \(-1\), если ответа не существует;
- две строки через пробел. Первая строка должна содержать начальное возможное значение \(s\). Вторая строка должна содержать последовательность букв — в каком порядке надо удалять буквы из \(s\), чтобы получилась строка \(t\). Например, если выведена строка «bac», то сначала удалялись все вхождения буквы 'b', потом — все вхождения буквы 'a', затем — все вхождения буквы 'c'. Если существует несколько решений, выведите любое из них.
Примечание Первый набор входных данных разобран в условии. | |
![]()
|
|
E. Спасти Нивен!
дп
жадные алгоритмы
Строки
строковые суфф. структуры
*2500
Morning desert sun horizonRise above the sands of time... Fates Warning, «Exodus» Преодолев, наконец, Подветренные Пустоши, Ори добрался до Развалин Ветров, дабы отыскать Сердце Леса! Однако древнее хранилище, содержащее этот бесценный свет Ивы, не желало открываться! Ори очень этому удивился, но огонек объяснил ему: хитрые Горлеки решили наложить дополнительную защиту на хранилище. Горлеки очень любили операцию «разворачивания строки». А еще они очень любили возрастающие подпоследовательности. Пусть дана строка \(s_1s_2s_3 \ldots s_n\). Тогда «разворачиванием» этой строки назовем последовательность строк \(s_1\), \(s_1 s_2\), ..., \(s_1 s_2 \ldots s_n\), \(s_2\), \(s_2 s_3\), ..., \(s_2 s_3 \ldots s_n\), \(s_3\), \(s_3 s_4\), ..., \(s_{n-1} s_n\), \(s_n\). Например, «разворачиванием» строки 'abcd' будет последовательность строк 'a', 'ab', 'abc', 'abcd', 'b', 'bc', 'bcd', 'c', 'cd', 'd'. Чтобы открыть древнее хранилище, Ори должен найти длину наибольшей возрастающей подпоследовательности «разворачивания» строки \(s\). Здесь строки сравниваются лексикографически. Помогите Ори справиться с этой задачей! Строка \(a\) лексикографически меньше строки \(b\), если и только если выполняется один из следующих пунктов: - \(a\) — префикс \(b\), но \(a \ne b\);
- в первой позиции, где \(a\) и \(b\) различны, в строке \(a\) находится буква, которая встречается в алфавите раньше, чем соответствующая буква в \(b\).
Выходные данные Для каждого набора входных данных выведите в отдельной строке одно целое число — ответ на задачу. Примечание В первом наборе входных данных «разворачивание» строки выглядит так: 'a', 'ac', 'acb', 'acba', 'acbac', 'c', 'cb', 'cba', 'cbac', 'b', 'ba', 'bac', 'a', 'ac', 'c'. В качестве наибольшей возрастающей подпоследовательности можно выбрать, например, 'a', 'ac', 'acb', 'acba', 'acbac', 'b', 'ba', 'bac', 'c'. | |
![]()
|
|
A. Доска с домино
реализация
Строки
*800
У Алисы есть клеточная доска из \(2\) рядов и \(n\) столбцов. Она полностью покрыла доску с помощью \(n\) доминошек размера \(1 \times 2\) — Алиса могла класть их как вертикально, так и горизонтально, и каждая клетка доски была покрыта ровно одной доминошкой. Теперь Алиса решила показать одну из строк Бобу. Помогите Бобу и определите, как может выглядеть другая строка доски! Выходные данные Для каждого набора входных данных выведите одну строку — возможную другую строку доски, используя такой же формат строки, как и во входных данных. Если существует несколько ответов, выведите любой из них. Примечание В первом наборе входных данных Алиса показывает Бобу верхнюю строку. Вся доска может выглядеть следующим образом:  Во втором наборе Алиса показывает Бобу нижнюю строку. Вся доска может выглядеть следующим образом:  В третьем наборе Алиса показывает Бобу нижнюю строку. Вся доска может выглядеть следующим образом:  В четвертом наборе входных данных Алиса показывает Бобу верхнюю строку. Вся доска может выглядеть следующим образом:  | |
![]()
|
|
A. Another Sorting Problem
сортировки
Строки
Структуры данных
*1100
Andi and Budi were given an assignment to tidy up their bookshelf of \(n\) books. Each book is represented by the book title — a string \(s_i\) numbered from \(1\) to \(n\), each with length \(m\). Andi really wants to sort the book lexicographically ascending, while Budi wants to sort it lexicographically descending. Settling their fight, they decided to combine their idea and sort it asc-desc-endingly, where the odd-indexed characters will be compared ascendingly, and the even-indexed characters will be compared descendingly. A string \(a\) occurs before a string \(b\) in asc-desc-ending order if and only if in the first position where \(a\) and \(b\) differ, the following holds: - if it is an odd position, the string \(a\) has a letter that appears earlier in the alphabet than the corresponding letter in \(b\);
- if it is an even position, the string \(a\) has a letter that appears later in the alphabet than the corresponding letter in \(b\).
Output Output \(n\) integers — the indices of the strings after they are sorted asc-desc-endingly. Note The following illustrates the first example.  | |
![]()
|
|
H. Holiday Wall Ornaments
дп
Строки
*2200
The Winter holiday will be here soon. Mr. Chanek wants to decorate his house's wall with ornaments. The wall can be represented as a binary string \(a\) of length \(n\). His favorite nephew has another binary string \(b\) of length \(m\) (\(m \leq n\)). Mr. Chanek's nephew loves the non-negative integer \(k\). His nephew wants exactly \(k\) occurrences of \(b\) as substrings in \(a\). However, Mr. Chanek does not know the value of \(k\). So, for each \(k\) (\(0 \leq k \leq n - m + 1\)), find the minimum number of elements in \(a\) that have to be changed such that there are exactly \(k\) occurrences of \(b\) in \(a\). A string \(s\) occurs exactly \(k\) times in \(t\) if there are exactly \(k\) different pairs \((p,q)\) such that we can obtain \(s\) by deleting \(p\) characters from the beginning and \(q\) characters from the end of \(t\). Output Output \(n - m + 2\) integers — the \((k+1)\)-th integer denotes the minimal number of elements in \(a\) that have to be changed so there are exactly \(k\) occurrences of \(b\) as a substring in \(a\). Note For \(k = 0\), to make the string \(a\) have no occurrence of 101, you can do one character change as follows. 100101011 \(\rightarrow\) 100100011 For \(k = 1\), you can also change a single character. 100101011 \(\rightarrow\) 100001011 For \(k = 2\), no changes are needed. | |
![]()
|
|
H. Higher Order Functions
реализация
Строки
*1700
Helen studies functional programming and she is fascinated with a concept of higher order functions — functions that are taking other functions as parameters. She decides to generalize the concept of the function order and to test it on some examples. For her study, she defines a simple grammar of types. In her grammar, a type non-terminal \(T\) is defined as one of the following grammar productions, together with \(\textrm{order}(T)\), defining an order of the corresponding type: - "()" is a unit type, \(\textrm{order}(\textrm{"}\texttt{()}\textrm{"}) = 0\).
- "(" \(T\) ")" is a parenthesized type, \(\textrm{order}(\textrm{"}\texttt{(}\textrm{"}\,T\,\textrm{"}\texttt{)}\textrm{"}) = \textrm{order}(T)\).
- \(T_1\) "->" \(T_2\) is a functional type, \(\textrm{order}(T_1\,\textrm{"}\texttt{->}\textrm{"}\,T_2) = max(\textrm{order}(T_1) + 1, \textrm{order}(T_2))\). The function constructor \(T_1\) "->" \(T_2\) is right-to-left associative, so the type "()->()->()" is the same as the type "()->(()->())" of a function returning a function, and it has an order of \(1\). While "(()->())->()" is a function that has an order-1 type "(()->())" as a parameter, and it has an order of \(2\).
Helen asks for your help in writing a program that computes an order of the given type. Output Print a single integer — the order of the given type. | |
![]()
|
|
A. Строковый пасьянс Казимира
математика
Строки
*800
У Казимира есть строка \(s\), которая состоит исключительно из прописных латинских букв 'A', 'B' и 'C'. За один ход он может сделать одно из двух действий: - либо он удаляет ровно одну букву 'A' и ровно одну букву 'B' из произвольных мест строки (эти буквы могут не быть соседними);
- либо он удаляет ровно одну букву 'B' и ровно одну букву 'C' из произвольных мест строки (эти буквы могут не быть соседними).
Таким образом, за один ход длина строки уменьшается ровно на \(2\). Ходы не зависят друг от друга, и каждый ход Казимир может выбрать любое из двух возможных действий. Например, если \(s\) \(=\) «ABCABC», то за один ход он может получить строку \(s\) \(=\) «ACBC» (удалил первое вхождение 'B' и второе вхождение 'A'). Это лишь один пример исхода среди большого количества других возможностей сделать ход. Для заданной строки \(s\) определите, существует ли последовательность ходов, приводящая к пустой строке. Иными словами, цель Казимира — удалить все буквы из строки. Существует ли способ это сделать? Выходные данные Выведите \(t\) строк, каждая из которых содержит ответ на соответствующий набор входных данных. В качестве ответа выведите YES, если соответствующую строку можно удалить полностью, и NO в противном случае. Вы можете выводить ответ в любом регистре (например, строки yEs, yes, Yes и YES будут распознаны как положительный ответ). | |
![]()
|
|
C. Баба Капа вяжет шарф
жадные алгоритмы
Перебор
Строки
Структуры данных
*1200
Баба Капа решила связать шарф и попросила Деда Шера сделать для него шаблон, представляющий собой строку из строчных букв латинского алфавита. Деда Шер написал строку \(s\) длины \(n\). Баба Капа хочет связать красивый шарф, а по ее мнению красивый шарф можно связать только из строки, являющейся палиндромом. Она хочет изменить шаблон, написанный Дедой Шером, но, чтобы его сильно не обидеть, она выберет одну любую строчную букву латинского алфавита и уберет какие-то (на свой выбор, возможно никакие или все) вхождения этой буквы в строку \(s\). При этом она хочет, чтобы количество удаленных из шаблона символов было как можно меньше. Помогите ей и скажите, какое минимальное количество символов она может удалить, чтобы строка \(s\) стала палиндромом, или скажите, что это невозможно. Заметьте, что она может удалять только символы, равные одной букве, которую она выбрала. Строка называется палиндромом, если она одинаково читается слева направо и справа налево. Например, строки 'kek', 'abacaba', 'r' и 'papicipap' — палиндромы, а строки 'abb' и 'iq' — нет. Выходные данные Для каждого набора входных данных выведите минимальное количество символов, которое потребуется удалить Бабе Капе, чтобы строка стала палиндромом, если это возможно, а если невозможно, выведите \(-1\). Примечание В первом наборе входных данных можно выбрать букву 'a' и удалить ее первое и последнее вхождение, получится строка 'bcaacb', являющаяся палиндромом. Также можно выбрать букву 'b' и удалить все ее вхождения, получится строка 'acaaca', также являющаяся палиндромом. Во втором наборе входных данных можно показать, что нельзя выбрать букву и удалить какие-то ее вхождения так, чтобы получилась строка-палиндром. В третьем наборе входных данных можно ничего не удалять, строка и так является палиндромом. | |
![]()
|
|
F. Странная НОП
битмаски
графы
дп
жадные алгоритмы
Строки
*2600
Вам даны \(n\) строк \(s_1, s_2, \ldots, s_n\), состоящих из строчных и заглавных латинских букв. Более того, каждый символ в каждой строке встречается не более двух раз. Найдите самую длинную общую подпоследовательность этих строк. Строка \(t\) является подпоследовательностью строки \(s\), если \(t\) может быть получена из \(s\) удалением нескольких (возможно, ни одного или всех) символов. Выходные данные Для каждого набора входных данных выведите ответ в двух строках. В первой строке выведите длину самой длинной общей подпоследовательности. Во второй — саму подпоследовательность. Если существует несколько самых длинных общих подпоследовательностей, выведите любую из них. Примечание В первом наборе входных данных одна из самых длинных общих подпоследовательностей это «A». Нет ни одной общей подпоследовательности длины \(2\). Во втором наборе входных данных множества символов строк не пересекаются, поэтому никакая непустая строка не может быть общей подпоследовательностью. | |
![]()
|
|
C. String Manipulation 1.0
*особая задача
Бинарный поиск
Перебор
Строки
Структуры данных
*1400
На одном популярном интернет-ресурсе разработали необычный механизм редактирования имени пользователя. Менять имя пользователя можно только удалением из него некоторых символов: чтобы изменить текущее имя s, пользователь может выбрать число p и символ c и удалить p-е вхождение символа c из имени. После того как пользователь изменил своё имя, отменить это изменение он не может. Например, имя «arca» можно изменить, удалив второе вхождение символа «a», и получится «arc». Поликарп узнал, что изначально некий пользователь зарегистрировался под именем t, где t представляет собой строку s, записанную k раз подряд. Также Поликарпу известна последовательность изменений имени этого пользователя. Помогите Поликарпу выяснить итоговое имя пользователя. Выходные данные Выведите единственную строку — итоговое имя пользователя после применения всех операций изменения. Примечание Рассмотрим первый пример. Изначально у нас будет имя «bacbac»; после первой операции оно превратится в «bacbc», после второй — в «acbc», и, наконец, после третьей — в «acb». | |
![]()
|
|
D. Палиндромные пары
*особая задача
дп
Перебор
Строки
*1500
Дана непустая строка s, состоящая из строчных латинских букв. Найдите количество пар непересекающихся подстрок-палиндромов этой строки. Более формально: найдите количество четверок (a, b, x, y) таких, что 1 ≤ a ≤ b < x ≤ y ≤ |s| и подстроки s[a... b], s[x... y] являются палиндромами. Палиндромом называется строка, которая одинаково читается слева направо и справа налево. Например, строки «abacaba», «z», «abba» — палиндромы. Подстрокой s[i... j] (1 ≤ i ≤ j ≤ |s|) строки s = s1s2... s|s| называется строка, равная sisi + 1... sj. Например, подстрока s[2...4] строки s = «abacaba» равна «bac». Выходные данные Выведите единственное число — количество пар непересекающихся подстрок-палиндромов заданной строки. Пожалуйста, не используйте спецификатор %lld для чтения или записи 64-х битовых чисел на С++. Рекомендуется использовать потоки cin, cout или спецификатор %I64d. | |
![]()
|
|
C. Сделай их равными
жадные алгоритмы
математика
Перебор
Строки
*1200
У Теофаниса есть строка \(s_1 s_2 \dots s_n\) и символ \(c\). Он хочет сделать все символы своей строки равными \(c\), используя наименьшее количество операций. За одну операцию, он может выбрать число \(x\) (\(1 \le x \le n\)) и для каждой позиции \(i\), где \(i\) не делится на \(x\), заменить \(s_i\) на \(c\). Определите наименьшее количество операций, для того чтобы сделать все символы строки равными \(c\) и соответствующие \(x\)-ы, которые нужно выбрать. Выходные данные Для каждого набора входных данных, сначала выведите одно целое число \(m\) — наименьшее количество операций для того, чтобы сделать все символы равными \(c\). Далее выведите \(m\) целых чисел \(x_1, x_2, \dots, x_m\) (\(1 \le x_j \le n\)) — \(x\)-ы, которые нужно использовать в заданном порядке. Можно доказать, что при заданных ограничениях ответ всегда существует. Если существует несколько ответов, выведите любой. Примечание Опишем, что происходит в третьем наборе входных данных: - \(x_1 = 2\): выбираем все позиции, которые не делятся на \(2\), и заменяем их, т. е. bzyx \(\rightarrow\) bzbx;
- \(x_2 = 3\): выбираем все позиции, которые не делятся на \(3\), и заменяем их, т. е. bzbx \(\rightarrow\) bbbb.
| |
![]()
|
|
G. Сумма хороших чисел
математика
Строки
строковые суфф. структуры
хэши
*3200
Назовем целое положительное число хорошим, если в его десятичной записи нет цифры 0. Для массива хороших чисел \(a\) обнаружили, что сумма некоторых двух соседних элементов равна \(x\) (т.е. \(x = a_i + a_{i + 1}\) для некоторого \(i\)). Оказалось, что \(x\) также является хорошим числом. Затем элементы массива \(a\) выписали последовательно без разделителей в одну строку \(s\). Например, если \(a = [12, 5, 6, 133]\), то \(s = 1256133\). Ваша задача — по заданной строке \(s\) и числу \(x\) определить, где в строке находятся соседние элементы массива, которые в сумме дают число \(x\). Если существует несколько возможных ответов, вы можете вывести любой. Выходные данные В первой строке выведите два целых числа \(l_1\), \(r_1\), означающих, что первое слагаемое (\(a_i\)) находится в строке \(s\) с позиции \(l_1\) до позиции \(r_1\). Во второй строке выведите два целых числа \(l_2\), \(r_2\), означающих, что второе слагаемое (\(a_{i + 1}\)) находится в строке \(s\) с позиции \(l_2\) до позиции \(r_2\). Примечание В первом примере из условия \(s[1;2] = 12\) и \(s[3;3] = 5\), \(12+5=17\). Во втором примере из условия \(s[2;3] = 54\) и \(s[4;6] = 471\), \(54+471=525\). В третьем примере из условия \(s[1;1] = 2\) и \(s[2;2] = 3\), \(2+3=5\). В четвертом примере из условия \(s[2;7] = 218633\) и \(s[8;13] = 757639\), \(218633+757639=976272\). | |
![]()
|
|
D. Журналирование
реализация
Строки
*1900
На главный сервер компании Гомбл недавно пришёл лог одного сверхсекретного процесса даже название которого не разрешено разглашать. Лог был записан в формате «[дата:время]: сообщение», где для каждого значения «[дата:время]» существовало не более 10 строк. Все файлы были зашифрованы сверхсложным способом и расшифровать их мог только программист Леша. Шифр был настолько сложен, что Леше понадобилось четыре недели на их расшифровку. Сразу после расшифровки все файлы были уничтожены. И только после удаления файлов Леша заметил, что он сохранял записи в формате «[время]: сообщение». Таким образом, информация о датах была утеряна. Однако так как строки добавлялись в лог в хронологическом порядке, то, например, несложно сделать вывод о том, могли ли все записи появиться в течение одних суток. Также можно определить минимальное количество суток, в которые лог мог быть записан. Теперь чтобы хоть как-то оправдать себя перед начальством Леша должен узнать какое минимальное число суток затрагивают логи. Заметим, что Леше требуется найти не количество суток между началом и концом журналирования, а количество суток, в которые производились записи (см. пример 2). Напомним, что за минуту процесс производил не более 10 записей. Считайте, что полночь принадлежит наступающим суткам. Выходные данные Выведите одно число — минимальное количество суток, затрагиваемых записями. Примечание Формально 12-часовой формат времени описан: - http://ru.wikipedia.org/wiki/12-часовой_формат_времени,
- http://en.wikipedia.org/wiki/12-hour_clock.
Авторы рекомендуют ознакомиться с формальными описаниями до решения задачи. | |
![]()
|
|
C. Доминантный характер
жадные алгоритмы
Перебор
реализация
Строки
*1400
У Ashish есть строка \(s\) длины \(n\), содержащая только символы 'a', 'b' и 'c'. Он хочет найти длину наименьшей подстроки, которая удовлетворяет следующим условиям: - Длина подстроки не меньше чем \(2\)
- 'a' встречается строго больше раз в этой подстроке, чем 'b'
- 'a' встречается строго больше раз в этой подстроке, чем 'c'
Ashish занят планированием следующего раунда Codeforces. Помогите ему решить задачу. Строка \(a\) является подстрокой строки \(b\), если \(a\) можно получить из \(b\), удалив несколько (возможно, ноль или все) символов из начала и несколько (возможно, ноль или все) символов из конца. Выходные данные Для каждого набора входных данных выведите длину наименьшей подстроки, удовлетворяющей заданным условиям, или выведите \(-1\), если такой подстроки нет. Примечание Рассмотрим первый набор входных данных. В подстроке «aa», 'a' встречается дважды, а 'b' и 'c' встречаются ноль раз. Поскольку 'a' встречается строго больше раз, чем 'b' и 'c', подстрока «aa» удовлетворяет условию, и ответ равен \(2\). Подстрока «a» также удовлетворяет этому условию, однако ее длина меньше \(2\). Во втором наборе входных данных можно показать, что ни в одной из подстрок «cbabb» 'a' не встречается строго больше раз, чем 'b' и 'c'. В третьем наборе входных данных, «cacabccc», длина наименьшей подстроки, удовлетворяющей условиям, равна \(3\). | |
![]()
|
|
A. Баланс AB
Строки
*900
Вам задана строка \(s\) длины \(n\), состоящая из букв a и/или b. Пусть \(\operatorname{AB}(s)\) — это количество вхождений строки ab в \(s\) как подстроки. Аналогично, \(\operatorname{BA}(s)\) — это количество вхождений ba в \(s\) как подстроки. За один шаг, вы можете выбрать индекс \(i\) и заменить \(s_i\) на букву a или b. Какое наименьшее количество шагов нужно сделать, что бы достигнуть строки в которой \(\operatorname{AB}(s) = \operatorname{BA}(s)\)? Напоминание: Количество вхождений строки \(d\) в \(s\) как подстроки — это количество индексов \(i\) (\(1 \le i \le |s| - |d| + 1\)) таких, что подстрока \(s_i s_{i + 1} \dots s_{i + |d| - 1}\) равна \(d\). Например, \(\operatorname{AB}(\)aabbbabaa\() = 2\) так как есть ровно два индекса \(i\): \(i = 2\) с aabbbabaa и \(i = 6\) с aabbbabaa. Выходные данные Для каждого набора входных данных, выведите результирующую строку \(s\), в которой \(\operatorname{AB}(s) = \operatorname{BA}(s)\), и которую вы получите, сделав наименьшее возможное количество ходов. Если существует несколько ответов, выведите любой из них. Примечание В первом наборе входных данных, и \(\operatorname{AB}(s) = 0\), и \(\operatorname{BA}(s) = 0\) (строка ab (ba) ни разу не входит в строку b). А потому мы можем оставить \(s\) нетронутой. Во втором наборе, \(\operatorname{AB}(s) = 2\) и \(\operatorname{BA}(s) = 2\). Строку \(s\) можно оставить нетронутой. В третьем наборе, \(\operatorname{AB}(s) = 1\) и \(\operatorname{BA}(s) = 0\). Можно, например, заменить \(s_1\) на b, сделав оба значения равными нулю. В четвертом наборе, \(\operatorname{AB}(s) = 2\) и \(\operatorname{BA}(s) = 1\). Можно, например, заменить \(s_6\) на a, сделав оба значения равными \(1\). | |
![]()
|
|
A. Линейная клавиатура
реализация
Строки
*800
Перед вами клавиатура, которая состоит из \(26\) клавиш. Клавиши расположены в один ряд друг за другом в некотором порядке. Каждой клавише соответствует своя строчная латинская буква. Требуется напечатать на этой клавиатуре слово \(s\). Оно тоже состоит только из строчных латинских букв. Чтобы напечатать слово, требуется последовательно напечатать все его буквы. Чтобы напечатать очередную букву, необходимо расположить руку в точности над соответствующей клавишей и нажать эту клавишу. Перемещение руки между клавишами занимает время, которое равно модулю (абсолютной величине) разности позиций этих клавиш (клавиши пронумерованы слева направо). На нажатия и размещение руки над первой буквой слова время не тратится. Например, рассмотрим клавиатуру, на которой буквы от 'a' до 'z' расположены подряд в алфавитном порядке. Буквы 'h', 'e', 'l' и 'o' в таком случае расположены на позициях \(8\), \(5\), \(12\) и \(15\), соответственно. Поэтому, чтобы напечатать слово «hello», потребуется \(|5 - 8| + |12 - 5| + |12 - 12| + |15 - 12| = 13\) единиц времени. Определите, сколько времени понадобится, чтобы напечатать слово \(s\). Выходные данные Выведите \(t\) строк, каждая из которых содержит ответ на соответствующий набор входных данных. В качестве ответа выведите минимальное время, которое надо потратить, чтобы напечатать слово \(s\) на заданной клавиатуре. | |
![]()
|
|
G. Алфавитное дерево
Бинарный поиск
Деревья
поиск в глубину и подобное
Строки
строковые суфф. структуры
Структуры данных
хэши
*3500
Вам даны \(m\) строк и дерево на \(n\) вершинах. На каждом ребре написана какая-то буква. Вы должны ответить на \(q\) запросов. Каждый запрос описывается \(4\) целыми числами \(u\), \(v\), \(l\) и \(r\). Ответом на запрос является общее количество вхождений \(str(u,v)\) в строки с индексами от \(l\) до \(r\). \(str(u,v)\) определяется как строка, составленная путем конкатенации букв, записанных на ребрах кратчайшего пути от \(u\) до \(v\) (в порядке их прохождения). Выходные данные Для каждого запроса выведите одно целое число — ответ на запрос. | |
![]()
|
|
B. Внимательный Василий
реализация
Строки
*1100
 Перед тем как стать успешным трейдером, Василий закончил университет. Во время его обучения произошел один случай, после которого Василий стал намного внимательнее слушать условия заданий для домашней работы. Далее приведено правильное формальное условие домашнего задания. Дана строка \(s\) длины \(n\), состоящая только из символов «a», «b» и «c». Есть \(q\) запросов вида (\(pos, c\)), который обозначает замену элемента строки \(s\) на позиции \(pos\) на символ \(c\). После каждого запроса требуется вывести минимальное количество символов в строке, которые нужно заменить, чтобы строка не содержала строку «abc» в качестве подстроки. Правильной заменой символа является его изменение на символ «a», «b» или «c». Строка \(x\) является подстрокой \(y\), если \(x\) может быть получена из \(y\) удалением нескольких (возможно, ни одного или всех) символов из начала и нескольких (возможно, ни одного или всех) символов из конца. Выходные данные Для каждого запроса выведите минимальное количество символов, которые необходимо заменить, чтобы строка не содержала «abc» как подстроку. Примечание Рассмотрим состояния строки после каждого запроса: - \(s =\) «abcabcabc». В этом случае можно сделать \(3\) замены и получить, например, строку \(s =\) «bbcaccabb». Эта строка не содержит «abc» как подотрезок.
- \(s =\) «bbcabcabc». В этом случае можно сделать \(2\) замены и получить, например, строку \(s =\) «bbcbbcbbc». Эта строка не содержит «abc» как подотрезок.
- \(s =\) «bccabcabc». В этом случае можно сделать \(2\) замены и получить, например, строку \(s =\) «bccbbcbbc». Эта строка не содержит «abc» как подотрезок.
- \(s =\) «bcaabcabc». В этом случае можно сделать \(2\) замены и получить, например, строку \(s =\) «bcabbcbbc». Эта строка не содержит «abc» как подотрезок.
- \(s =\) «bcabbcabc». В этом случае можно сделать \(1\) замену и получить, например, строку \(s =\) «bcabbcabb». Эта строка не содержит «abc» как подотрезок.
- \(s =\) «bcabccabc». В этом случае можно сделать \(2\) замены и получить, например, строку \(s =\) «bcabbcabb». Эта строка не содержит «abc» как подотрезок.
- \(s =\) «bcabccaac». В этом случае можно сделать \(1\) замену и получить, например, строку \(s =\) «bcabbcaac». Эта строка не содержит «abc» как подотрезок.
- \(s =\) «bcabccaab». В этом случае можно сделать \(1\) замену и получить, например, строку \(s =\) «bcabbcaab». Эта строка не содержит «abc» как подотрезок.
- \(s =\) «ccabccaab». В этом случае можно сделать \(1\) замену и получить, например, строку \(s =\) «ccabbcaab». Эта строка не содержит «abc» как подотрезок.
- \(s =\) «ccaaccaab». В этом случае строка не содержит «abc» как подотрезок, поэтому замен делать не требуется.
| |
![]()
|
|
B. Зеркало в строке
жадные алгоритмы
Строки
*1100
У вас есть строка \(s_1 s_2 \ldots s_n\), вы стоите слева от нее и смотрите направо. Вы хотите выбрать индекс \(k\) (\(1 \le k \le n\)) и поставить зеркало после \(k\)-го символа строки, таким образом, вы будете видеть строку \(s_1 s_2 \ldots s_k s_k s_{k - 1} \ldots s_1\). Какую лексикографически минимальную строку вы можете увидеть? Строка \(a\) лексикографически меньше строки \(b\), если и только если выполняется один из следующих пунктов: - \(a\) — префикс \(b\), но \(a \ne b\);
- в первой позиции, где \(a\) и \(b\) различны, в строке \(a\) находится буква, которая встречается в алфавите раньше, чем соответствующая буква в \(b\).
Выходные данные Для каждого набора входных данных выведите лексикографически минимальную строку, которую вы можете увидеть. Примечание В первом примере выберем \(k = 1\), чтобы получить «cc». Во втором примере выберем \(k = 3\), чтобы получить «cbaabc». В третьем примере выберем \(k = 1\), чтобы получить «aa». В четвертом примере выберем \(k = 1\), чтобы получить «bb». | |
![]()
|
|
E. Лексикографически достаточно малая
жадные алгоритмы
Перебор
Строки
Структуры данных
*2200
Вам даны две строки \(s\) и \(t\) равной длины \(n\). За одну операцию вы можете поменять местами любые два соседних символа в строке \(s\). Вам нужно сказать, какое наименьшее количество операций вам потребуется, чтобы строка \(s\) стала лексикографически меньше строки \(t\). Строка \(a\) лексикографически меньше строки \(b\), если и только если выполняется один из следующих пунктов: - \(a\) — префикс \(b\), но \(a \ne b\);
- в первой позиции, где \(a\) и \(b\) различны, в строке \(a\) находится буква, которая встречается в алфавите раньше, чем соответствующая буква в \(b\).
Выходные данные Для каждого тестового случая в отдельной строке выведите наименьшее количество операций, которое вам потребуется, чтобы строка \(s\) стала лексикографически меньше строки \(t\), или \(-1\), если это невозможно сделать. | |
![]()
|
|
A. Запрещённая подпоследовательность
жадные алгоритмы
Конструктив
сортировки
Строки
*800
Вам даны строки \(S\) и \(T\), состоящие из строчных символов латинского алфавита. Гарантируется, что \(T\) является перестановкой строки abc. Найдите строку \(S'\), которая является лексикографически минимальной перестановкой \(S\), и при этом \(T\) не является подпоследовательностью \(S'\). Строка \(a\) является перестановкой строки \(b\), если количество вхождений для всех различных символов одинаковое в обеих строках. Строка \(a\) является подпоследовательностью строки \(b\), если \(a\) может быть получена из \(b\) удалением нескольких (возможно нуля или всех) символов. Строка \(a\) лексикографически меньше строки \(b\), если и только если выполняется один из следующих пунктов: - \(a\) — префикс \(b\), но \(a \ne b\);
- в первой позиции, где \(a\) и \(b\) различны, в строке \(a\) находится буква, которая встречается в алфавите раньше, чем соответствующая буква в \(b\).
Выходные данные Для каждого набора входных данных выведите единственную строку \(S'\), которая является лексикографически минимальной перестановкой \(S\), и при этом \(T\) не является подпоследовательностью \(S'\). Примечание В первом наборе входных данных и aaaabbc, и aaaabcb лексикографически меньше, чем aaaacbb, но они содержат abc как подпоследовательность. Во втором наборе входных данных abccc является лексикографически минимальной перестановкой cccba и не содержит acb как подпоследовательность. В третьем наборе входных данных bcdis является лексикографически минимальной перестановкой dbsic и не содержит bac как подпоследовательность. | |
![]()
|
|
F. Развороты
битмаски
Конструктив
математика
поиск в глубину и подобное
реализация
Строки
*2000
Вам даны два целых положительных числа \(x\) и \(y\). Вы можете совершать с числом \(x\) следующую операцию: записать его в двоичном виде без ведущих нулей, приписать справа \(0\) или \(1\), затем развернуть двоичную запись и превратить ее в десятичное число, которое окажется новым значением \(x\). Например: - \(34\) можно одной операцией превратить в \(81\): двоичная запись \(34\) — это \(100010\), если приписать справа \(1\), развернуть и убрать ведущие нули, можно получить \(1010001\), что является двоичной записью числа \(81\);
- \(34\) можно одной операцией превратить в \(17\): двоичная запись \(34\) — это \(100010\), если приписать справа \(0\), развернуть и убрать ведущие нули, можно получить \(10001\), что является двоичной записью числа \(17\);
- \(81\) можно одной операцией превратить в \(69\): двоичная запись \(81\) — это \(1010001\), если приписать справа \(0\), развернуть и убрать ведущие нули, можно получить \(1000101\), что является двоичной записью числа \(69\);
- \(34\) можно превратить в \(69\) за две операции: сначала превратить \(34\) в \(81\), а потом превратить \(81\) в \(69\).
Ваша задача — выяснить, можно ли превратить \(x\) в \(y\) за какое-то (возможно, нулевое) число операций. Выходные данные Выведите YES, если вы можете сделать \(x\) равным \(y\), или NO, если это невозможно. Примечание В первом примере не надо совершать никаких действий. Четвертый пример разобран в условии задачи. | |
![]()
|
|
A. Квадратная строка?
реализация
Строки
*800
Строка называется квадратной, если она состоит из двух одинаковых половин, записанных дважды подряд. Например, строки «aa», «abcabc», «abab» и «baabaa» — квадратные. Строки «aaa», «abaaab» и «abcdabc» квадратными не являются. Для заданной строки \(s\) определите, является ли она квадратной. Выходные данные Для каждого набора входных данных в отдельной строке выведите: - YES, если строка во наборе входных данных является квадратной,
- NO в противном случае.
Вы можете выводить YES и NO в любом регистре (например, строки yEs, yes, Yes и YES будут распознаны как положительный ответ). | |
![]()
|
|
E. Дублирование среднего
Деревья
жадные алгоритмы
поиск в глубину и подобное
Строки
Структуры данных
*2500
Дано бинарное дерево из \(n\) вершин. Вершины дерева пронумерованы от \(1\) до \(n\), корень дерева имеет номер \(1\). Каждая вершина может не иметь детей, иметь только правого или только левого ребенка, или иметь двух детей. Для удобства обозначим за \(l_u\) и \(r_u\) левого и правого ребенка вершины \(u\) соответственно, при этом \(l_u = 0\), если у \(u\) нет левого ребенка, и \(r_u = 0\), если у \(u\) нет правого ребенка. В каждой вершине дерева записана некоторая строка, изначально состоящая из одного символа \(c_u\). Определим строковое представление дерева как конкатенацию всех строк, записанных в вершинах, в порядке центрированного обхода. Формально, пусть \(f(u)\) — строковое представление поддерева с корнем в вершине \(u\). \(f(u)\) определена так: \(\) f(u) = \begin{cases} \texttt{<пустая строка>,} & \text{если }u = 0; \\ f(l_u) + c_u + f(r_u) & \text{иначе}, \end{cases} \(\) где \(+\) обозначает строковую конкатенацию. Представление всего дерева это \(f(1)\). Для каждой вершины мы можем продублировать строку, записанную в ней, не более одного раза, а именно, заменить \(c_u\) на \(c_u + c_u\). Эта операция возможна только если \(u\) — корень дерева, или строка, записанная в родителе этой вершины уже продублирована. Вам дано дерево и целое число \(k\). Какое лексикографически минимальное строковое представление дерево может иметь, если мы можем продублировать строку в не более чем \(k\) вершинах? Строка \(a\) лексикографически меньше строки \(b\), если и только если выполняется один из следующих пунктов: - \(a\) — префикс \(b\), но \(a \ne b\);
- в первой позиции, где \(a\) и \(b\) различны, в строке \(a\) находится буква, которая встречается в алфавите раньше, чем соответствующая буква в \(b\).
Выходные данные Выведите одну строку, содержащую лексикографически минимальное строковое представление, которое может иметь дерево после не более чем в \(k\) вершинах строка будет продублирована. Примечание Рисунке ниже иллюстрируют примеры. Число в вершине обозначает номер вершины, а строка в нижнем индексе — строку, написанную в вершине. Справа находится строковое представление дерева, где каждая буква имеет цвет соответствующей вершине дерева. Ниже находится дерево для первого примера. Мы продублировали строки в вершинах \(1\) и \(3\). Строку в вершине \(2\) не нужно дублировать, так как в таком случае представление будет «bbaaab», что лексикографически больше, чем «baaaab».  Во втором примере можно продублировать строки в вершинах \(1\) и \(2\). Обратите внимание, что если продублировать только строку в корне, то представление будет хуже, чем у изначального дерева.  В третьем примере не нужно ничего дублировать. Даже если мы продублируем строку в вершине \(3\), мы будем обязаны также продублировать строку в вершине \(2\), что сделает результат хуже.  Нет способа получить строку «darkkcyan» из дерева с начальным представлением «darkcyan» :(. | |
![]()
|
|
D. Раскраска палиндромов
Бинарный поиск
жадные алгоритмы
сортировки
Строки
*1400
У вас есть строка \(s\), состоящая из строчных букв латинского алфавита. Вы можете покрасить некоторые буквы в цвета от \(1\) до \(k\). Необязательно красить все буквы. Для каждого цвета должна быть буква, покрашенная в этот цвет. Затем вы можете сколько угодно раз менять местами любые два символа, покрашенные в один цвет. После этого будет создано \(k\) строк, \(i\)-я из них будет содержать все символы, покрашенные в цвет \(i\), записанные в порядке их следования в строке \(s\). Ваша задача покрасить символы строки так, чтобы все полученные \(k\) строк были палиндромами, а длина самой короткой из этих \(k\) строк была как можно больше. Прочтите пояснение к первому набору входных данных примера, если вам требуется пояснение к условию задачи. Напомним, что строка является палиндромом, если она читается одинаково как слева направо, так и справа налево. Например, строки abacaba, cccc, z и dxd являются палиндромами, а строки abab и aaabaa — нет. Выходные данные Для каждого набора входных данных выведите единственное целое число — максимальную длину самой короткой строки-палиндрома, которую возможно получить. Примечание - В первом наборе входных данных \(s\)=«bxyaxzay», \(k=2\). Далее будем использовать индексы в строке от \(1\) до \(8\). Подойдет следующая раскраска: \(\mathtt{\mathbf{\color{red}{b}\color{blue}{xy}\color{red}{a}\color{blue}{x}z\color{red}{a}\color{blue}{y}}}\) (буква z осталась непокрашенной). После покраски:
- поменяем местами два красных символа (с индексами \(1\) и \(4\)) местами, получим \(\mathtt{\mathbf{\color{red}{a}\color{blue}{xy}\color{red}{b}\color{blue}{x}z\color{red}{a}\color{blue}{y}}}\);
- поменяем местами два синих символа (с индексами \(5\) и \(8\)) местами, получим \(\mathtt{\mathbf{\color{red}{a}\color{blue}{xy}\color{red}{b}\color{blue}{y}z\color{red}{a}\color{blue}{x}}}\).
Теперь, если для каждого из двух цветов выписать соответствующие буквы слева направо, то получим две строки \(\mathtt{\mathbf{\color{red}{aba}}}\) и \(\mathtt{\mathbf{\color{blue}{xyyx}}}\). Обе они являются палиндромами, длина наименьшей равна \(3\). Можно показать, что большую длину наименее длинного палиндрома достичь нельзя. - Во втором наборе входных данных подойдёт такая раскраска: \([1, 1, 2, 2, 3, 3]\). Менять символы местами не нужно. Обе полученные строки равны aa, они являются палиндромами и их длина равна \(2\).
- В третьем наборе входных данных можно покрасить любой символ и взять его в строку.
- В четвёртом наборе входных данных можно покрасить \(i\)-й символ в цвет \(i\).
- В пятом наборе входных данных можно покрасить в каждый из цветов по одному символу.
- В шестом наборе входных данных подойдёт такая раскраска: \([1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 0]\). Переставим символы так, чтобы получить палиндромы abcba и acbca.
| |
![]()
|
|
E. Маша-забываша
дп
Конструктив
Перебор
реализация
Строки
хэши
*2000
Маша познакомилась с новым другом и узнала его номер телефона — \(s\). Она хочет как можно скорее запомнить его. Номер телефона — это строка длины \(m\), которая состоит из цифр от \(0\) до \(9\). Допустимо, что телефон начинается с 0. Маша уже знает \(n\) номеров телефонов (все номера имеют одинаковую длину \(m\)). Ей будет проще запомнить новый номер, если строку \(s\) представить как отрезки уже известных ей номеров. Каждый такой отрезок должен быть длины не менее \(2\), иначе отрезков будет слишком много, и Маша запутается. Например, Маше нужно запомнить номер: \(s = \) «12345678» и она уже знает \(n = 4\) номера: «12340219», «20215601», «56782022», «12300678». Можно представить \(s\) как \(3\) отрезка: «1234» из первого номера, «56» из второго номера и «78» из третьего номера. Есть и другие способы представления \(s\). Маша обратилась к вам за помощью, она просит вас разбить строку \(s\) на отрезки длины \(2\) или более из уже известных ей номеров. Если существует несколько возможных ответов, выведите любой из них. Выходные данные Вам нужно вывести ответы на \(t\) запросов. В первой строке ответа должно содержаться одно число \(k\), соответствующее количеству отрезков, на которые вы разбили номер телефона \(s\). Выведите -1, если такого разбиения получить нельзя. В случае положительного ответа далее должны следовать \(k\) строк, содержащие тройки чисел \(l, r, i\). Такая тройка обозначает, что очередные \(r-l+1\) цифр номера \(s\) равны отрезку (подстроке) с границами \([l, r]\) телефона под номером \(i\). И телефоны и цифры в них нумеруются от \(1\). Обратите внимание, что \(r-l+1 \ge 2\) для всех \(k\) строк. Примечание Первый тестовый случай соответствует примеру из условия. Во втором случае невозможно представить отрезками известных номеров длины 2 или более. В третьем случае можно получить отрезки «12» и «21» из первого номера телефона. | |
![]()
|
|
B. Небольшое сжатие
жадные алгоритмы
Строки
*1100
Дана десятичная запись целого числа \(x\) без лидирующих нулей. Требуется проделать над ним следующую операцию, называемую сжатием, ровно один раз: взять две соседние цифры в \(x\) и заменить на их сумму без лидирующих нулей (если сумма равна \(0\), то она представляется как один \(0\)). Например, если \(x = 10057\), то возможные сжатия следующие: - выбрать первую и вторую цифры \(1\) и \(0\), заменить на \(1+0=1\); результат \(1057\);
- выбрать вторую и третью цифры \(0\) и \(0\), заменить на \(0+0=0\); результат тоже \(1057\);
- выбрать третью и четвертую цифры \(0\) и \(5\), заменить на with \(0+5=5\); результат все еще \(1057\);
- выбрать четвертую и пятую цифры \(5\) и \(7\), заменить на \(5+7=12\); результат \(10012\).
Какое наибольшее число можно получить? Выходные данные На каждый набор входных данных выведите одно целое число — наибольшее число, которое можно получить после применения сжатия ровно один раз. Число не должно содержать лидирующих нулей. Примечание Первый набор входных данных уже объяснен в условии. Во втором наборе входных данных есть только одно возможное сжатие: первая и вторая цифры. | |
![]()
|
|
B. Особые предпочтения в фильмах
жадные алгоритмы
Строки
*1700
Mihai планирует посмотреть фильм. Ему нравятся только фильмы-палиндромы, поэтому он хочет пропустить некоторые (возможно, ноль) сцен, чтобы оставшиеся части фильма образовали палиндром. Вам дан список \(s\) из \(n\) непустых строк длины не более \(3\), представляющих сцены из фильма Mihai. Подпоследовательность \(s\) называется классной, если она не пуста и конкатенация строк подпоследовательности по порядку является палиндромом. Можете ли вы помочь Mihai проверить, есть ли хотя бы одна классная подпоследовательность \(s\)? Палиндром — это строка, которая читается одинаково в обоих направлениях. Например, строки «z», «aaa», «aba», «abccba» являются палиндромами, а строки «codeforces», «reality», «ab» таковыми не являются. Последовательность \(a\) называется непустой подпоследовательностью последовательности \(b\), если \(a\) получается из \(b\) удалением нескольких (возможно, нуля, но не всех) элементов. Выходные данные Для каждого набора входных данных выведите «YES», если есть классная подпоследовательность \(s\), или «NO» в противном случае (без учета регистра). Примечание В первом наборе входных данных из \(s\) можно выбрать классную подпоследовательность \([ab, cc, ba]\). | |
![]()
|
|
E. Электронное правительство
Деревья
дп
поиск в глубину и подобное
Строки
Структуры данных
*2800
В рамках проекта «Электронное правительство» лучшим программистам страны Распиляндии поручили создание системы автоматизации сбора статистики и анализа прессы. Известно, что членами правительства Распиляндии может стать любой из k граждан. Их фамилии — a1, a2, ..., ak. Все фамилии различны. Изначально в правительство входят все k граждан из этого списка. Система должна поддерживать следующие возможности: - Включить гражданина ai в состав правительства.
- Исключить гражданина ai из состава правительства.
- По заданному тексту статьи определить, насколько она политизирована. Для этого, для каждого действующего члена правительства, вычисляется количество раз, которое его фамилия встречается в тексте как подстрока. Считаются все вхождения, в том числе и пересекающиеся. Степень политизированности текста определяется как сумма этих количеств по всем действующим членам правительства.
Реализуйте эту систему. Выходные данные Для каждой операции «подсчитать политизированность» выведите на отдельной строке степень политизированности заданного в ней текста. Для остальных операций ничего выводить не нужно. | |
![]()
|
|
A. Разворачивай и конкатенируй
жадные алгоритмы
Строки
*800
Real stupidity beats artificial intelligence every time. — Terry Pratchett, Hogfather, Discworld Вам дана строка \(s\) длины \(n\) и число \(k\). Обозначим за \(rev(s)\) развёрнутую строку \(s\) (т.е. \(rev(s) = s_n s_{n-1} ... s_1\)). Вы можете выполнять два типа операций: - заменить строку \(s\) на \(s + rev(s)\)
- заменить строку \(s\) на \(rev(s) + s\)
После выполнения ровно \(k\) операций (возможно, различных) над строкой, какое количество различных строк вы можете получить из начальной строки \(s\)? Мы обозначили конкатенацию строк \(s\) и \(t\) как \(s + t\). Другими словами, \(s + t = s_1 s_2 ... s_n t_1 t_2 ... t_m\), где \(n\) и \(m\) - длины строк \(s\) и \(t\) соответственно. Выходные данные Для каждого набора входных данных в отдельной строке выведите количество различных строк, которые вы можете получить после применения ровно \(k\) операций. Можно показать, что при данных ограничениях ответ не превосходит \(10^9\). Примечание Рассмотрим первый набор входных данных: После первой операции строка \(s\) может стать либо aabbaa, либо baaaab. После второй операции \(s\) может принимать только такие 2 значения: aabbaaaabbaa и baaaabbaaaab. | |
![]()
|
|
D. Бесконечный набор
битмаски
дп
математика
матрицы
Строки
теория чисел
*1800
Вам дан массив \(a\), состоящий из \(n\) различных целых положительных чисел. Рассмотрим бесконечное множество целых чисел \(S\), содержащее все целые числа \(x\), удовлетворяющие хотя бы одному из следующих условий: - \(x = a_i\) для некоторого \(1 \leq i \leq n\).
- \(x = 2y + 1\) и \(y\) находится в \(S\).
- \(x = 4y\) и \(y\) находится в \(S\).
Например, если \(a = [1,2]\), то \(10\) наименьших элементов в \(S\) будут равны \(\{1,2,3,4,5,7,8,9,11,12\}\) . Найдите количество элементов в \(S\), строго меньших, чем \(2^p\). Так как это число может быть слишком большим, выведите его по модулю \(10^9 + 7\). Выходные данные Выведите единственное целое число — количество элементов в \(S\), строго меньших \(2^p\). Не забудьте вывести его по модулю \(10^9 + 7\). Примечание В первом примере элементы меньше \(2^4\) равны \(\{1, 3, 4, 6, 7, 9, 12, 13, 15\}\). Во втором примере элементы меньше \(2^7\) равны \(\{5,11,20,23,39,41,44,47,79,80,83,89,92,95\}\). | |
![]()
|
|
C. Еще одна строковая задача
Бинарный поиск
дп
математика
Перебор
Строки
*1600
Строка называется бинарной, если она состоит только из символов «0» и «1». Строка v называется подстрокой строки w, если она имеет ненулевую длину, и ее можно прочитать, начиная с некоторой позиции, в строке w. Например, у строки «010» есть шесть подстрок: «0», «1», «0», «01», «10», «010». Две подстроки считаются различными, если их позиции вхождения различны. Другими словами, каждую подстроку нужно учитывать столько раз, сколько она встречается. Дана бинарная строка s. Ваша задача — найти количество ее подстрок, содержащих ровно k единиц. Выходные данные Выведите одно целое число — количество подстрок данной строки, содержащих ровно k символов «1». Пожалуйста, не используйте спецификатор %lld для чтения или записи 64-х битовых чисел на С++, вместо него рекомендуется использовать потоки cin, cout, а также спецификатор %I64d. Примечание В первом примере искомые подстроки: «1», «1», «10», «01», «10», «010». Во втором примере искомые подстроки: «101», «0101», «1010», «01010». | |
![]()
|
|
A. Удаления двух соседних букв
реализация
Строки
*800
Задана строка \(s\), длина строки — нечётное число. Строка состоит из строчных букв латинского алфавита. Пока длина строки строго больше \(1\), над ней можно производить следующую операцию: выбрать любые две соседние в строке \(s\) буквы и удалить их из строки. Например, из строки «lemma» за одну операцию можно получить любую из четырёх строк: «mma», «lma», «lea» или «lem». В частности, за одну операцию длина строки уменьшается на \(2\). Формально, пусть строка \(s\) имеет вид \(s=s_1s_2 \dots s_n\) (\(n>1\)). Во время одного хода вы выбираете произвольный индекс \(i\) (\(1 \le i < n\)) и делаете замену \(s=s_1s_2 \dots s_{i-1}s_{i+2} \dots s_n\). Для заданных строки \(s\) и буквы \(c\) определите, можно ли совершить такую последовательность ходов, что в итоге будет верно равенство \(s=c\)? Иными словами, существует ли такая последовательность действий, что процесс завершится строкой длины \(1\), которая состоит из буквы \(c\)? Выходные данные Для каждого набора входных данных в отдельной строке выведите: - YES, если строка \(s\) может быть преобразована так, что будет верно \(s=c\);
- NO в противном случае.
Вы можете выводить YES и NO в любом регистре (например, строки yEs, yes, Yes и YES будут распознаны как положительный ответ). Примечание В первом наборе входных данных примера \(s\)=«abcde». Требуется получить \(s\)=«c». За первый ход удалим первые две буквы, получим \(s\)=«cde». За второй ход удалим последние две буквы, получим ожидаемое значение \(s\)=«c». В третьем наборе входных данных примера \(s\)=«x», требуется получить \(s\)=«y». Очевидно, что это невозможно сделать. | |
![]()
|
|
B. Обращение битов
битмаски
жадные алгоритмы
Конструктив
Строки
*1300
Вам дана битовая строка длины \(n\). Вы должны сделать ровно \(k\) ходов. На каждом ходу вы должны выбрать один бит строки. Состояние всех битов кроме выбранного изменятся на противоположное (\(0\) станет \(1\), \(1\) станет \(0\)). Вам нужно вывести лексикографически максимальную строку, которую вы можете получить, используя все \(k\) ходов. Кроме того, для каждого бита выведите, сколько раз вы его выбираете для получения такой строки. Если есть несколько возможных решений, выведите любое из них. Битовая строка \(a\) лексикографически больше битовой строки \(b\) такой же длины, если и только если выполняется следующее: - в первой позиции, где \(a\) и \(b\) различны, в строке \(a\) находится \(1\), а в строке \(b\) — \(0\).
Выходные данные Для каждого набора входных данных выведите две строки. Первая строка должна содержать лексикографически максимальную строку, которую вы можете получить. Вторая строка должна содержать \(n\) целых чисел \(f_1, f_2, \ldots, f_n\), где \(f_i\) — количество раз, которое вы выбираете \(i\)-й бит. Сумма всех чисел должна быть равна \(k\). Примечание Рассмотрим первый пример. Ниже пошагово показано, как изменяется строка после каждого хода. - Выбирается бит \(1\): \(\color{red}{\underline{1}00001} \rightarrow \color{red}{\underline{1}}\color{blue}{11110}\).
- Выбирается бит \(4\): \(\color{red}{111\underline{1}10} \rightarrow \color{blue}{000}\color{red}{\underline{1}}\color{blue}{01}\).
- Выбирается бит \(4\): \(\color{red}{000\underline{1}01} \rightarrow \color{blue}{111}\color{red}{\underline{1}}\color{blue}{10}\).
Итоговая строка равна \(111110\), это лексикографически максимальная строка, которую можно получить. | |
![]()
|
|
C. Получи четную строку
дп
жадные алгоритмы
Строки
*1300
Строка \(a=a_1a_2\dots a_n\) называется чётной, если она состоит из конкатенации (соединения) строк длины \(2\), состоящих из одинаковых символов. Иными словами, строка \(a\) четная, если одновременно выполняются два условия: - чётна её длина \(n\);
- для всех нечётных \(i\) (\(1 \le i \le n - 1\)) выполнено \(a_i = a_{i+1}\).
Например, следующие строки являются чётными: «» (пустая строка), «tt», «aabb», «oooo» и «ttrrrroouuuuuuuukk». Следующие строки чётными не являются: «aaa», «abab» и «abba». Задана строка \(s\), состоящая из строчных латинских букв. Необходимо найти, какое минимальное количество символов нужно удалить из строки \(s\), чтобы она стала четной. Удалённые символы не обязаны идти подряд. Выходные данные Для каждого набора входных данных выведите единственное число — минимальное количество символов, которые необходимо удалить, чтобы строка \(s\) стала четной. Примечание В первом наборе входных данных можно удалить символы под номерами \(6\), \(7\) и \(9\), получив четную строку «aabbddcc». Во втором наборе входных данных каждый символ встречается ровно один раз, поэтому для того, чтобы получить четную строку, необходимо удалить все символы из строки. В третьем наборе входных данных можно получить четную строку «aaaabb», удалив, например, \(4\)-й и \(6\)-й символы, или строку «aabbbb», удалив \(5\)-й символ и любой из первых трех. | |
![]()
|
|
F1. Перспективные подстроки (простая версия)
математика
Перебор
реализация
Строки
*1700
Это простая версия задачи F. Единственное различие между простой и сложной версиями заключается в ограничениях. Будем называть непустую строку сбалансированной, если она содержит одинаковое количество знаков плюс и минус. Например: строки «+--+» и «++-+--» являются сбалансированными, а строки «+--», «--» и «» не являются сбалансированными. Будем называть строку перспективной, если строку можно сделать сбалансированной при помощи нескольких(возможно нуля) применений следующей операции: - заменим два соседних знака минуса на один знак плюс.
В частности, всякая сбалансированная строка является перспективной. Однако обратное неверно: не всякая перспективная строка — сбалансирована. Например: строка «-+---» является перспективной, так как можно заменить два соседних минуса на плюс и получить сбалансированную строку «-++-», либо получить другую сбалансированную строку «-+-+». Сколько непустых подстрок данной строки \(s\) являются перспективными? Каждая непустая перспективная подстрока должна быть учтена в ответе столько раз, сколько раз она встречается в строке \(s\). Напомним, что подстрока — это последовательность подряд идущих символов строки. Например, для строки «+-+» её подстроками являются строки «+-», «-+», «+», «+-+» (строка является подстрокой самой себя) и некоторые другие. Но следующие строки её подстроками не являются: «--», «++», «-++». Выходные данные Для каждого набора входных данных выведите единственное число — количество непустых перспективных подстрок строки \(s\). Каждая непустая перспективная подстрока должна быть учтена в ответе столько раз, сколько раз она встречается в строке \(s\). Примечание Ниже перечислены перспективные подстроки для первых трёх наборов входных данных примера: - \(s[1 \dots 2]\)=«+-», \(s[2 \dots 3]\)=«-+»;
- \(s[1 \dots 2]\)=«-+», \(s[2 \dots 3]\)=«+-», \(s[1 \dots 5]\)=«-+---», \(s[3 \dots 5]\)=«---»;
- \(s[1 \dots 3]\)=«---», \(s[2 \dots 4]\)=«---».
| |
![]()
|
|
F2. Перспективные подстроки (сложная версия)
математика
реализация
Строки
Структуры данных
*2100
Это сложная версия задачи F. Единственное различие между простой и сложной версиями заключается в ограничениях. Будем называть непустую строку сбалансированной, если она содержит одинаковое количество знаков плюс и минус. Например: строки «+--+» и «++-+--» являются сбалансированными, а строки «+--», «--» и «» не являются сбалансированными. Будем называть строку перспективной, если строку можно сделать сбалансированной при помощи нескольких(возможно нуля) применений следующей операции: - заменим два соседних знака минуса на один знак плюс.
В частности, всякая сбалансированная строка является перспективной. Однако обратное неверно: не всякая перспективная строка — сбалансирована. Например: строка «-+---» является перспективной, так как можно заменить два соседних минуса на плюс и получить сбалансированную строку «-++-», либо получить другую сбалансированную строку «-+-+». Сколько непустых подстрок данной строки \(s\) являются перспективными? Каждая непустая перспективная подстрока должна быть учтена в ответе столько раз, сколько раз она встречается в строке \(s\). Напомним, что подстрока — это последовательность подряд идущих символов строки. Например, для строки «+-+» её подстроками являются строки «+-», «-+», «+», «+-+» (строка является подстрокой самой себя) и некоторые другие. Но следующие строки её подстроками не являются: «--», «++», «-++». Выходные данные Для каждого набора входных данных выведите единственное число — количество непустых перспективных подстрок строки \(s\). Каждая непустая перспективная подстрока должна быть учтена в ответе столько раз, сколько раз она встречается в строке \(s\). Примечание Ниже перечислены перспективные подстроки для первых трёх наборов входных данных примера: - \(s[1 \dots 2]\)=«+-», \(s[2 \dots 3]\)=«-+»;
- \(s[1 \dots 2]\)=«-+», \(s[2 \dots 3]\)=«+-», \(s[1 \dots 5]\)=«-+---», \(s[3 \dots 5]\)=«---»;
- \(s[1 \dots 3]\)=«---», \(s[2 \dots 4]\)=«---».
| |
![]()
|
|
B. Toys
жадные алгоритмы
Строки
Vittorio has three favorite toys: a teddy bear, an owl, and a raccoon. Each of them has a name. Vittorio takes several sheets of paper and writes a letter on each side of every sheet so that it is possible to spell any of the three names by arranging some of the sheets in a row (sheets can be reordered and flipped as needed). The three names do not have to be spelled at the same time, it is sufficient that it is possible to spell each of them using all the available sheets (and the same sheet can be used to spell different names). Find the minimum number of sheets required. In addition, produce a list of sheets with minimum cardinality which can be used to spell the three names (if there are multiple answers, print any). Output The first line of the output contains a single integer \(m\) — the minimum number of sheets required. Then \(m\) lines follow: the \(j\)-th of these lines contains a string of two uppercase letters of the English alphabet — the letters appearing on the two sides of the \(j\)-th sheet. Note that you can print the sheets and the two letters of each sheet in any order. Note In the first sample, the solution uses two sheets: the first sheet has A on one side and G on the other side; the second sheet has A on one side and M on the other side. The name AA can be spelled using the A side of both sheets. The name GA can be spelled using the G side of the first sheet and the A side of the second sheet. Finally, the name MA can be spelled using the M side of the second sheet and the A side of the first sheet. | |
![]()
|
|
D. Evolution of Weasels
жадные алгоритмы
реализация
Строки
A wild basilisk just appeared at your doorstep. You are not entirely sure what a basilisk is and you wonder whether it evolved from your favorite animal, the weasel. How can you find out whether basilisks evolved from weasels? Certainly, a good first step is to sequence both of their DNAs. Then you can try to check whether there is a sequence of possible mutations from the DNA of the weasel to the DNA of the basilisk. Your friend Ron is a talented alchemist and has studied DNA sequences in many of his experiments. He has found out that DNA strings consist of the letters A, B and C and that single mutations can only remove or add substrings at any position in the string (a substring is a contiguous sequence of characters). The substrings that can be removed or added by a mutation are AA, BB, CC, ABAB or BCBC. During a sequence of mutations a DNA string may even become empty. Ron has agreed to sequence the DNA of the weasel and the basilisk for you, but finding out whether there is a sequence of possible mutations that leads from one to the other is too difficult for him, so you have to do it on your own. Output For each test case, print YES if there is a sequence of mutations to get from \(u\) to \(v\) and NO otherwise. | |
![]()
|
|
F. In Every Generation...
*особая задача
Строки
In every generation there is a Chosen One. She alone will stand against the vampires, the demons, and the forces of darkness. She is the Slayer. — Joss Whedon Output A single string. If there is no answer, print "none" (without the quotes). | |
![]()
|
|
G. Six Characters
*особая задача
Конструктив
Строки
Aenar should go to the string's home. Output A string consisting of only \(6\) characters. Note If many answers are possible, the jury will still only accept one! | |
![]()
|
|
E. Двухбуквенные строки
математика
Строки
Структуры данных
*1200
Даны \(n\) строк, каждая имеет длину \(2\) и состоит из строчных латинских букв от 'a' до 'k'. Выведите количество пар индексов \((i, j)\) таких, что \(i < j\) и \(i\)-я строка с \(j\)-й строкой различаются ровно в одной позиции. Другими словами найдите количество пар \((i, j)\) (\(i < j\)) таких, что \(i\)-я строка с \(j\)-й строкой различаются ровно в одной позиции \(p\) (\(1 \leq p \leq 2\)), то есть \({s_{i}}_{p} \neq {s_{j}}_{p}\). Ответ может не влезать в 32-разрядный целочисленный тип, поэтому вам следует использовать 64-разрядные целые числа, такие как long long в C++, чтобы избежать переполнения целочисленного типа. Выходные данные Для каждого набора выведите единственное число — количество пар \((i, j)\) (\(i < j\)) таких, что \(i\)-я строка с \(j\)-й строкой различаются ровно в одной позиции \(p\) (\(1 \leq p \leq 2\)), то есть \({s_{i}}_{p} \neq {s_{j}}_{p}\). Пожалуйста, обратите внимание, что ответ для некоторых тестовых примеров не будет помещаться в 32-разрядный целочисленный тип, поэтому вы должны использовать по крайней мере 64-разрядный целочисленный тип в вашем языке программирования (например, long long для C++). Примечание В первом примере ровно в одной позиции различаются следующие пары: («ab», «cb»), («ab», «db»), («ab», «aa»), («cb», «db») and («cb», «cc»). Во втором примере ровно в одной позиции различаются следующие пары: («aa», «ac»), («aa», «ca»), («cc», «ac»), («cc», «ca»), («ac», «aa») and («ca», «aa»). В третьем примере нет пар, удовлетворяющих условиям. | |
![]()
|
|
B. Общажные войны
Перебор
реализация
Строки
*1100
Хоссам решил проникнуть в комнату Хемоса, пока он спит, и сменить пароль на его ноутбуке. Он уже знает исходный пароль, равный строке \(s\) длины \(n\). Он также знает, что существуют \(k\) особых букв в алфавите: \(c_1,c_2,\ldots, c_k\). Хоссам написал программу, которая делает следующее. - Программа рассматривает текущий пароль \(s\) некоторой длины \(m\).
- Затем она находит все такие позиции \(i\) (\(1\le i<m\)), что \(s_{i+1}\) — одна из \(k\) особых букв.
- После этого она удаляет все символы на таких позициях из пароля \(s\) даже если \(s_{i}\) — особая буква. Если таких позиций нет, программа выдает ошибку с очень громким звуком.
Например, пусть строка \(s\) равна «abcdef», а особые буквы — «b» и «d». Если Хоссам запустит программу один раз, символы на позициях \(1\) и \(3\) будут удалены, так как они находятся перед особыми символами, и пароль станет равным «bdef». Если он запустит программу еще раз, она удалит символ на позиции \(1\), и пароль станет «def». Хоссам поступит разумно, если не будет запускать программу в третий раз. Хоссам хочет узнать, сколько максимум раз он может запустить программу на ноутбуке Хемоса, не разбудив его сигналом ошибки. Можете помочь ему? Выходные данные Для каждого набора входных данных выведите максимальное количество раз, которое Хоссам может запустить программу, не вызвав ошибку. Примечание В первом наборе входных данных программу можно запустить \(5\) раз: \(\text{iloveslim} \to \text{ilovslim} \to \text{iloslim} \to \text{ilslim} \to \text{islim} \to \text{slim}\) Во втором наборе входных данных программу можно запустить \(2\) раза: \(\text{joobeel} \to \text{oel} \to \text{el}\) В третьем наборе входных данных программу можно запустить \(3\) раза: \(\text{basiozi} \to \text{bioi} \to \text{ii} \to \text{i}\). В четвертом наборе входных данных программу можно запустить \(5\) раз: \(\text{khater} \to \text{khatr} \to \text{khar} \to \text{khr} \to \text{kr} \to \text{r}\) В пятом наборе входных данных программу можно запустить только раз: \(\text{abobeih} \to \text{h}\) В шестом наборе программу нельзя запустить ни разу, так как пароль не содержит особых символов. | |
![]()
|
|
A. Хитрое удаление подстроки
жадные алгоритмы
игры
Строки
*800
Алиса и Боб играют в игру со строками. Всего в игре будет \(t\) раундов. В каждом раунде будет строка \(s\), состоящая из строчных латинских букв. Оба игрока делают ходы по очереди, Алиса ходит первой. Алиса может удалить любую подстроку чётной длины (возможно пустую) и Боб может удалить любую подстроку нечётной длины из \(s\). Более формально, если была строка \(s = s_1s_2 \ldots s_k\) игрок может выбрать подстроку \(s_ls_{l+1} \ldots s_{r-1}s_r\) длины соответствующей чётности и удалить её. После этого строка станет \(s = s_1 \ldots s_{l-1}s_{r+1} \ldots s_k\). Когда строка становится пустой, раунд заканчиваются и каждый игрок считает его/её очки за этот раунд. Количество очков игрока равно сумме стоимостей символов, удалённых им/ей. Стоимость \(\texttt{a}\) равна \(1\), стоимость \(\texttt{b}\) равна \(2\), стоимость \(\texttt{c}\) равна \(3\), \(\ldots\), и стоимость \(\texttt{z}\) равна \(26\). Игрок с большим количеством очков побеждает в раунде. Для каждого раунда определите победителя и разницу очков победителя и проигравшего. Считайте, что оба игрока играют оптимально с целью максимизировать свои очки. Можно доказать, что ничья невозможна. Выходные данные Для каждого раунда выведите единственную строку, содержащую строку и число. Если Алиса выиграет в раунде, строка должна быть «Alice». Если Боб выигрывает в раунде, строка должна быть «Bob». Число должно быть равно разности очков, если оба игрока играют оптимально. Примечание В первом раунде \(\texttt{"aba"}\xrightarrow{\texttt{Alice}}\texttt{"}{\color{red}{\texttt{ab}}}\texttt{a"}\xrightarrow{} \texttt{"a"}\xrightarrow{\texttt{Bob}}\texttt{"}{\color{red}{\texttt{a}}}\texttt{"}\xrightarrow{}\texttt{""}\). Общее количество очков Алисы равно \(1+2=3\). Общее количество очков Боба равно \(1\). Во втором раунде \(\texttt{"abc"}\xrightarrow{\texttt{Alice}}\texttt{"a}{\color{red}{\texttt{bc}}}\texttt{"}\xrightarrow{} \texttt{"a"}\xrightarrow{\texttt{Bob}}\texttt{"}{\color{red}{\texttt{a}}}\texttt{"}\xrightarrow{}\texttt{""}\). Общее количество очков Алисы равно \(2+3=5\). Общее количество очков Боба равно \(1\). В третьем раунде \(\texttt{"cba"}\xrightarrow{\texttt{Alice}}\texttt{"}{\color{red}{\texttt{cb}}}\texttt{a"}\xrightarrow{} \texttt{"a"}\xrightarrow{\texttt{Bob}}\texttt{"}{\color{red}{\texttt{a}}}\texttt{"}\xrightarrow{}\texttt{""}\). Общее количество очков Алисы равно \(3+2=5\). Общее количество очков Боба равно \(1\). В четвёртом раунде \(\texttt{"n"}\xrightarrow{\texttt{Alice}}\texttt{"n"}\xrightarrow{} \texttt{"n"}\xrightarrow{\texttt{Bob}}\texttt{"}{\color{red}{\texttt{n}}}\texttt{"}\xrightarrow{}\texttt{""}\). Общее количество очков Алисы равно \(0\). Общее количество очков Боба равно \(14\). В пятом раунде \(\texttt{"codeforces"}\xrightarrow{\texttt{Alice}}\texttt{"}{\color{red}{\texttt{codeforces}}}\texttt{"}\xrightarrow{} \texttt{""}\). Общее количество очков Алисы равно \(3+15+4+5+6+15+18+3+5+19=93\). Общее количество очков Боба равно \(0\). | |
![]()
|
|
B. Идеально сбалансированная строка?
жадные алгоритмы
Перебор
Строки
*1100
Назовём строку \(s\) идеально сбалансированной, если для всех возможных троек \((t,u,v)\) таких, что \(t\) является непустой подстрокой \(s\), а \(u\) и \(v\) являются символами, присутствующими в \(s\), разница в количествах вхождений \(u\) и \(v\) в \(t\) отличается не более, чем на \(1\). Например, строки «aba» и «abc» являются идеально сбалансированными, а «abb» нет, потому что для тройки («bb»,'a','b') условие не выполняется. Вам дана строка \(s\), состоящая только из строчных латинских букв. Ваша задача состоит в том, чтобы определить, является ли \(s\) идеально сбалансированной или нет. Строка \(b\) называется подстрокой строки \(a\), если \(b\) может быть получена удалением нескольких (возможно \(0\)) символов из начала и нескольких (возможно \(0\)) символов из конца \(a\). Выходные данные Для каждого набора входных данных выведите «YES», если \(s\) является идеально сбалансированной, и «NO» иначе. Вы можете выводить каждую букву в любом регистре (например, «YES», «Yes», «yes», «yEs» будут распознаны как положительный ответ). Примечание Пусть \(f_t(c)\) обозначает количество вхождений символа \(c\) в строку \(t\). Для первого набора входных данных получается: | \(t\) | \(f_t(a)\) | \(f_t(b)\) | | \(a\) | \(1\) | \(0\) | | \(ab\) | \(1\) | \(1\) | | \(aba\) | \(2\) | \(1\) | | \(b\) | \(0\) | \(1\) | | \(ba\) | \(1\) | \(1\) |
Можно увидеть, что для любой подстроки \(t\) в \(s\), разница между \(f_t(a)\) и \(f_t(b)\) не превышает \(1\). Значит, строка \(s\) идеально сбалансирована. Для второго набора входных данных получается: | \(t\) | \(f_t(a)\) | \(f_t(b)\) | | \(a\) | \(1\) | \(0\) | | \(ab\) | \(1\) | \(1\) | | \(abb\) | \(1\) | \(2\) | | \(b\) | \(0\) | \(1\) | | \(bb\) | \(0\) | \(2\) |
Можно увидеть, что для подстроки \(t=bb\), разница в количествах вхождений \(f_t(a)\) и \(f_t(b)\) равна \(2\), что больше \(1\). Значит, строка \(s\) не идеально сбалансирована. Для третьего набора входных данных получается: | \(t\) | \(f_t(a)\) | \(f_t(b)\) | \(f_t(c)\) | | \(a\) | \(1\) | \(0\) | \(0\) | | \(ab\) | \(1\) | \(1\) | \(0\) | | \(abc\) | \(1\) | \(1\) | \(1\) | | \(b\) | \(0\) | \(1\) | \(0\) | | \(bc\) | \(0\) | \(1\) | \(1\) | | \(c\) | \(0\) | \(0\) | \(1\) |
Можно увидеть, что для любой подстроки \(t\) в \(s\) и любых двух символов \(u,v\in\{a,b,c\}\), разница между \(f_t(u)\) и \(f_t(v)\) не превышает \(1\). Значит, строка \(s\) идеально сбалансирована. | |
![]()
|
|
C. Бесконечная замена
Комбинаторика
реализация
Строки
*1000
Дана строка \(s\), состоящая только из латинских букв 'a', и строка \(t\), состоящая из строчных латинских букв. За один ход вы можете заменить любую букву 'a' в строке \(s\) на строку \(t\). Обратите внимание, что после замены в строке \(s\) могут оказаться буквы, отличные от 'a'. Можно проделать произвольное количество ходов (включая ноль). Сколько различных строк можно получить? Выведите это число или скажите, что оно бесконечно большое. Две строки считаются различными, если у них различается длина, или они различаются в какой-либо позиции. Выходные данные На каждый набор входных данных выведите количество различных строк \(s\), которые можно получить после применения произвольного количества ходов (включая ноль). Если это число бесконечно большое, то выведите -1. Иначе выведите это число. Примечание В первом примере можно заменить любую букву 'a' на строку «a», но это не изменит строку. Так что вне зависимости от того, сколько ходов вы проделаете, вы не сможете получить строку отличную от начальной. Во втором примере можно заменить вторую букву 'a' на «abc». Строка \(s\) становится равна «aabc». Затем снова вторую букву 'a'. Строка \(s\) становится равна «aabcbc». И так далее, производя бесконечно много различных строк. В третьем примере можно либо оставить строку \(s\) как есть, проделав ноль ходов, либо заменить единственную 'a' на «b». Строка \(s\) становится равна «b», так что над ней больше нельзя проделать ходы. | |
![]()
|
|
E. Замени на предыдущий, минимизируй
жадные алгоритмы
снм
Строки
*1500
Дана строка \(s\), состоящая из строчных латинских букв. Можно применять следующую операцию: - выбрать один символ (от 'a' до 'z'), который хотя бы один раз встречается в строке. И все такие символы в строке заменить на предыдущий в алфавитном порядке по циклу. Например, все 'c' заменить на 'b' или все 'a' заменить на 'z'.
Задано число \(k\) — максимальное количество операций, которое можно совершить. Найдите минимальную лексикографически строку, которую можно получить, совершив не более \(k\) операций. Строка \(a=a_1a_2 \dots a_n\) лексикографически меньше строки \(b = b_1b_2 \dots b_n\), если существует такой индекс \(k\) (\(1 \le k \le n\)), что \(a_1=b_1\), \(a_2=b_2\), ..., \(a_{k-1}=b_{k-1}\), но \(a_k < b_k\). Выходные данные Для каждого набора входных данных выведите лексикографически минимальную строку, которую можно получить из строки \(s\), применив не более чем \(k\) операций. | |
![]()
|
|
C. Самые похожие слова
жадные алгоритмы
математика
Перебор
реализация
реализация
Строки
*800
Вам даны \(n\) слов одинаковой длины \(m\), состоящие из строчных букв латинского алфавита, \(i\)-е слово обозначается \(s_i\). За один ход вы можете выбрать любую позицию в любом отдельном слове и заменить букву в этой позиции на предыдущую или следующую букву в алфавитном порядке. Например: - вы можете заменить 'e' на 'd' или на 'f';
- 'a' может быть заменена только на 'b';
- 'z' может быть заменена только на 'y'.
Разница между двумя словами — это минимальное число ходов, необходимое для того, чтобы сделать их равными. Например, разница между «best» и «cost» составляет \(1 + 10 + 0 + 0 = 11\). Найдите минимальную разницу между \(s_i\) и \(s_j\) такую, что \((i < j)\). Другими словами, найдите минимальную разницу по всем возможным парам из \(n\) слов. Выходные данные Для каждого набора входных данных выведите одно целое число — минимальную разница среди всех возможных пар заданных строк. Примечание Для второго набора входных данных можно показать, что наилучшей парой является («abb», «bef»), которая имеет разницу, равную \(8\), что можно получить следующим образом: заменить первый символ первой строки на 'b' за один ход, заменить второй символ второй строки на 'b' за \(3\) хода и заменить третий символ второй строки на 'b' за \(4\) хода, что в сумме дает \(1 + 3 + 4 = 8\) ходов. В третьем наборе существует только одна возможная пара, и можно показать, что минимальное количество ходов, необходимое для того, чтобы строки стали равными, равно \(35\). В четвертом наборе есть пара строк, которые уже равны, поэтому ответ равен \(0\). | |
![]()
|
|
E. Типичная вечеринка в общаге
битмаски
дп
Комбинаторика
Строки
*2400
Сегодня в общаге праздник — приехал Олег, в честь чего девочки подарили ему строку. Олегу очень понравился подарок, поэтому он тут же придумал и предложил вам, лучшему его другу, следующую задачу. Вам дана строка \(s\) длины \(n\), которая состоит из первых \(17\) строчных букв латинского алфавита {\(a\), \(b\), \(c\), \(\ldots\), \(p\), \(q\)} и знаков вопроса. А также \(q\) запросов. Каждый запрос характеризуется набором попарно различных строчных первых \(17\) букв латинского алфавита, которые можно использовать чтобы заменить знаки вопроса в строке \(s\). Ответом на запрос является сумма количества различных подстрок, которые являются палиндромами, по всем строкам, которые можно получить из изначальной строки \(s\) путем замены знаков вопроса на разрешенные символы. Ответ необходимо посчитать по модулю \(998\,244\,353\). Обратите внимание! Две подстроки являются различными, когда отличаются их позиции начала и окончания в строке. Т. е. количество различных подстрок, которые являются палиндромами, для строки aba будет \(4\): a, b, a, aba. Рассмотрим примеры замены знаков вопроса на буквы. Например, из строки aba??ee при запросе {\(a\), \(b\)} можно получить строки ababaee или abaaaee но нельзя получить строки pizza, abaee, abacaba, aba?fee, aba47ee, или abatree. Напомним, что палиндромом называется строка, которая одинаково читается как слева направо, так и справа налево. Выходные данные На каждый запрос выведите одно число — суммарное количество подстрок-палиндромов во всех возможных строках, которые можно получить из строки \(s\), по модулю \(998\,244\,353\). Примечание Рассмотрим первый пример и первый запрос в нём. У нас может получится только одна строка по итогам замены знаков вопроса — abaaaba. В ней есть такие подстроки-палиндромы: - a — подстрока [\(1\); \(1\)].
- b — подстрока [\(2\); \(2\)].
- a — подстрока [\(3\); \(3\)].
- a — подстрока [\(4\); \(4\)].
- a — подстрока [\(5\); \(5\)].
- b — подстрока [\(6\); \(6\)].
- a — подстрока [\(7\); \(7\)].
- aa — подстрока [\(3\); \(4\)].
- aa — подстрока [\(4\); \(5\)].
- aba — подстрока [\(1\); \(3\)].
- aaa — подстрока [\(3\); \(5\)].
- aba — подстрока [\(5\); \(7\)].
- baaab — подстрока [\(2\); \(6\)].
- abaaaba — подстрока [\(1\); \(7\)].
В третьем запросе у нас может получится 4 строки: abaaaba, abababa, abbaaba, abbbaba. | |
![]()
|
|
B. Волшебники и минимальное заклинание
реализация
Строки
*1700
Давайте немного окунемся в одну из самых интересных областей магии — написание заклинаний. Обучение этой интересной, но сложной науке — дело крайне хлопотное, поэтому сегодня Вы не будете учить магические слова, а лишь познакомитесь с основными правилами написания заклинаний. Каждое заклинание состоит из нескольких строк. Строка, первым непробельным символом которой является символ «#», называется усиливающей строкой и отвечает за мощь заклинания. Остальные строки являются обычными и определяют действие заклинания. Вам на глаза попался текст некоторого заклинания. Заклинание оказалось слишком длинным, чтобы вы смогли понять его смысл. Поэтому Вы хотите сделать его как можно короче, не меняя смысла. Единственный способ сократить заклинание, известный вам, — это удаление некоторых пробелов и переводов строк. Известно, что в тексте любого заклинания пробелы несут какую-то смысловую нагрузку только в усиливающих строках, поэтому все пробелы в остальных строках необходимо удалить. Переводы строк также не важны, если ни одна из двух разделяемых строк не является усиливающей. Таким образом, если две подряд идущие строки не являются усиливающими, то их необходимо соединить в одну (то есть к первой строке приписать вторую). Удалять пробелы в усиливающих строках и объединять их с чем-либо запрещено. Обратите внимание, что пустые строки должны обрабатываться так же, как и все остальные: они должны быть объединены с соседними строками, не являющимися усиливающими, или сохранены в выходных данных, если они окружены с обеих сторон усиливающими (то есть строчка выше, если такая есть, является усиливающей, и строчка ниже, если такая есть, тоже является усиливающей). Пока это все удаления лишних символов, которые надо сделать (да-да, перевод строки тоже символ). На вход вам дан текст заклинания, который необходимо уменьшить. Удалите из него лишние символы и выведите результат. Выходные данные Выведите заклинание, из которого удалены все лишние символы. Обращаем ваше внимание, что после каждой строки вывода также должен идти перевод строки. Осторожно, в задаче в качестве проверки ответа на правильность используется побайтовое сравнение ответа с ответом жюри. Поэтому все пробелы и переводы строк имеют значение. Примечание В первом примере усиливающими строками являются 1 и 7. Поэтому строки со 2 по 6 объединены, из них удалены все пробелы. Во втором примере усиливающими являются 1 и 3 строки. Поэтому не объединено ничего. | |
![]()
|
|
C. Двоичная строка
Бинарный поиск
жадные алгоритмы
Строки
*1600
Дана строка \(s\), состоящая из символов 0 и/или 1. Вы должны удалить несколько (возможно, ноль) символов из начала строки и несколько (возможно, ноль) символов с конца. Получившаяся строка может оказаться пустой. Стоимость удаления — это максимум из двух величин: - количество символов 0, оставшихся в строке;
- количество символов 1, удаленных из строки.
Чему равна минимальная стоимость удаления, которую можно достигнуть? Выходные данные Для каждого набора входных данных выведите одно целое число — минимальную возможную стоимость удаления. Примечание Рассмотрим наборы входных данных из примера: - в первом наборе можно удалить два символа из начала и один символ с конца. Только один 1 был удален, только один 0 остался, поэтому стоимость равна \(1\);
- во втором наборе можно удалить три символа из начала и шесть символов с конца. Два символа 0 останутся, будут удалены три символа 1, поэтому стоимость равна \(3\);
- в третьем наборе входных данных оптимально удалить четыре символа из начала строки;
- в четвертом наборе входных данных оптимально удалить всю строку;
- в пятом наборе входных данных оптимально не удалять ни один символ.
| |
![]()
|
|
A. Палиндромные индексы
жадные алгоритмы
Строки
*800
Вам дана строка \(s\) длины \(n\), которая является палиндромом. Вы должны посчитать количество индексов \(i\) \((1 \le i \le n)\) таких, что строка после удаления \(s_i\) из \(s\) остается палиндромом. Например, рассмотрим \(s\) = «aba» - Если мы удалим \(s_1\) из \(s\), то строка станет «ba», что не является палиндромом.
- Если мы удалим \(s_2\) из \(s\), строка станет «aa», что является палиндромом.
- Если мы удалим \(s_3\) из \(s\), строка станет «ab», что не является палиндромом.
Палиндром — это строка, которая слева направо читается так же, как справа налево. Например, «abba», «a», «fef» являются палиндромами, а «codeforces», «acd», «xy» — нет. Выходные данные Для каждого набора входных данных выведите одно целое число — количество индексов \(i\) \((1 \le i \le n)\) таких, что строка после удаления \(s_i\) из \(s\) остается палиндромом. Примечание Первый набора входных данных описан в условии. Во втором наборе входных данных индексы \(i\), которые приводят к палиндрому после удаления \(s_i\), это \(3, 4, 5, 6\). Следовательно, ответ — \(4\). В третьем наборе входных данных удаление любого из индексов приводит к «d», что является палиндромом. Следовательно, ответ равен \(2\). | |
![]()
|
|
A. Много цифр
игры
Конструктив
математика
Строки
*800
У самых истоков CrowdForces, ещё совсем давно, стояла именно Тётя Люсине. За это время она заработала много денег, даже забыла все цифры и теперь просто платит. Но совершенно неожиданно ей на ревью попалась задача как раз на цифры! Тётя Люсине не может решить даже on-ramp задачу. Помогите ей, ведь судьба вашего аккаунта в её руках! Дано целое число \(n\) без нулей в десятичной записи. Алиса и Боб играют в игру с этим числом. Алиса начинает первой. Они делают ходы по очереди. В своем ходу Алиса должна поменять местами любые две цифры в числе, стоящие на разных позициях. Боб в свой ход всегда удаляет последнюю цифру числа. Игра заканчивается, когда остаётся ровно одна цифра. Вам необходимо найти минимальное число, которое Алиса может получить в результате игры. Выходные данные Для каждого набора входных данных выведите одно целое число — минимальное число, которое Алиса может получить в результате игры. Примечание В первом наборе входных данных Алиса должна поменять местами \(1\) и \(2\). После этого Боб удаляет последнюю цифру, т. е. \(1\), поэтому ответ \(2\). Во втором наборе входных данных Алиса может поменять местами \(3\) и \(1\): \(312\). После этого Боб удаляет последнюю цифру: \(31\). Потом Алиса меняет местами \(3\) и \(1\): \(13\) и Боб удаляет \(3\), поэтому ответ \(1\). | |
![]()
|
|
B. Лингвистика
жадные алгоритмы
реализация
сортировки
Строки
*2000
Алина обнаружила странный язык, который содержит всего \(4\) слова: \(\texttt{A}\), \(\texttt{B}\), \(\texttt{AB}\), \(\texttt{BA}\). Оказалось, что в этом языке нет пробелов: предложение записывается путем объединения (конкатенации) его слов в одну строку. Алина нашла одно такое предложение \(s\) и ей интересно: возможно ли, что оно состоит ровно из \(a\) слов \(\texttt{A}\), \(b\) слов \(\texttt{B}\), \(c\) слов \(\texttt{AB}\) и \(d\) слов \(\texttt{BA}\)? Другими словами, определите, можно ли объединить (конкатенировать) эти слова \(a+b+c+d\) в некотором порядке так, чтобы получилась строка \(s\). Каждое из слов \(a+b+c+d\) должно быть использовано в конкатенации ровно один раз, но вы можете выбрать порядок, в котором они будут конкатенироваться. Выходные данные Для каждого набора входных данных выведите \(\texttt{YES}\), если возможно, что предложение \(s\) состоит ровно из \(a\) слов \(\texttt{A}\), \(b\) слов \(\texttt{B}\), \(c\) слов \(\texttt{AB}\) и \(d\) слов \(\texttt{BA}\), и \(\texttt{NO}\) в противном случае. Вы можете выводить каждую букву в любом регистре. Примечание В первом наборе входных данных предложение \(s\) — это \(\texttt{B}\). Очевидно, что оно не может состоять из одного слова \(\texttt{A}\), поэтому ответ — \(\texttt{NO}\). Во втором наборе входных данных предложение \(s\) — \(\texttt{AB}\), и возможно, что оно состоит из одного слова \(\texttt{AB}\), поэтому ответ — \(\texttt{YES}\). В третьем наборе входных данных предложение \(s\) — \(\texttt{ABAB}\), и возможно, что оно состоит из одного слова \(\texttt{A}\), одного слова \(\texttt{B}\) и одного слова \(\texttt{BA}\), так как \(\texttt{A} + \texttt{BA} + \texttt{B} = \texttt{ABAB}\). В четвертом наборе входных данных предложение \(s\) — \(\texttt{ABAAB}\), и возможно, что оно состоит из одного слова \(\texttt{A}\), одного слова \(\texttt{AB}\) и одного слова \(\texttt{BA}\), так как \(\texttt{A} + \texttt{BA} + \texttt{AB} = \texttt{ABAAB}\). В пятом наборе входных данных предложение \(s\) — \(\texttt{BAABBABBAA}\), и возможно, что оно состоит из одного слова \(\texttt{A}\), одного слова \(\texttt{B}\), двух слов \(\texttt{AB}\) и двух слов \(\texttt{BA}\), так как \(\texttt{BA} + \texttt{AB} + \texttt{B} + \texttt{AB} + \texttt{BA} + \texttt{A}= \texttt{BAABBABBAA}\). | |
![]()
|
|
C. Управление историей
жадные алгоритмы
Конструктив
Строки
*1700
Keine обладает способностью управлять историей. История Gensokyo представляет собой строку \(s\) начальной длины \(1\). Чтобы исправить хаос, вызванный Yukari, ей нужно выполнить следующие операции \(n\) раз, в \(i\)-й раз: - Она выбирает непустую подстроку \(t_{2i-1}\) из \(s\).
- Она заменяет \(t_{2i-1}\) на непустую строку, \(t_{2i}\). Обратите внимание, что длины строк \(t_{2i-1}\) и \(t_{2i}\) могут различаться.
Обратите внимание, что если \(t_{2i-1}\) встречается более одного раза в \(s\), ровно одно из них будет заменено. Например, пусть \(s=\)«marisa», \(t_{2i-1}=\)«a» и \(t_{2i}=\)«z». После операции \(s\) становится «mzrisa» или «marisz». После \(n\) операций Keine получил окончательную строку и последовательность операций \(t\) длины \(2n\). Keine думал, что уже решил задачу, но появился Yukari и перемешал порядок \(t\). Что еще хуже, Keine забыл изначальную историю. Помогите Keine найти изначальную историю Gensokyo! Напомним, что подстрока — это последовательность последовательных символов строки. Например, для строки «abc» ее подстроки: «ab», «c», «bc» и некоторые другие . Но следующие строки не являются его подстрокой: «ac», «cba», «acb». Взломы Вы не можете делать взломы в этой задаче. Выходные данные Для каждого теста выведите исходную строку в одной строке. Примечание В первом наборе входных данных изначально \(s\) равно «a». - В первой операции Keine выбирает «a» и заменяет его на «ab». \(s\) становится «ab».
- Во второй операции Keine выбирает «b» и заменяет его на «cd». \(s\) становится «acd».
Таким образом, последняя строка будет «acd», а \(t=[\)«a», «ab», «b» , «cd»\(]\) перед перемешиванием. Во втором наборе входных данных изначально \(s\) равно «z». - В первой операции Keine выбирает «z» и заменяет его на «aa». \(s\) становится «aa».
- Во второй операции Keine выбирает «a» и заменяет его на «ran». \(s\) становится «aran».
- В третьей операции Keine выбирает «a» и заменяет его на «yakumo». \(s\) становится «yakumoran».
Таким образом, последняя строка будет «yakumoran», а \(t=[\)«z», «aa», «a» , «ran», «a», «yakumo»\(]\) перед перемешиванием. | |
![]()
|
|
F. Движущаяся строка
графы
математика
Строки
теория чисел
*1700
Поликарп нашёл строку \(s\) и перестановку \(p\). Их длины оказались одинаковы и равны \(n\). Перестановка из \(n\) элементов — это массив длины \(n\), в котором каждое целое число от \(1\) до \(n\) встречается ровно по одному разу. Например, \([1, 2, 3]\) и \([4, 3, 5, 1, 2]\) — это перестановки, но \([1, 2, 4]\), \([4, 3, 2, 1, 2]\) и \([0, 1, 2]\) — это не перестановки. За одну операцию он может умножить \(s\) на \(p\), то есть заменить строку \(s\) на строку \(new\), в которой для каждого \(i\) от \(1\) до \(n\) верно, что \(new_i = s_{p_i}\). Например, при \(s=wmbe\) и \(p = [3, 1, 4, 2]\), после применения операции строка превратится в \(s=s_3 s_1 s_4 s_2=bwem\). Поликарпу стало интересно, через сколько операций строка впервые вернётся к своему первоначальному виду. Так как это может занять слишком много времени, он просит вашей помощи в этом вопросе. Можно доказать, что искомое количество операций всегда существует. Оно может оказаться очень большим, используйте 64-битный целочисленный тип. Выходные данные Выведите \(t\) строк, каждая из которых содержит ответ на соответствующий набор входных данных. В качестве ответа выведите единственное число — минимальное количество операций, после которого строка \(s\) станет такой же, какой была до их применения. Примечание В первом наборе входных данных применение операции не изменяет строку, поэтому она станет равной самой себе после \(1\) операции. Во втором наборе входных данных строка будет меняться следующим образом: - \(s\) = babaa
- \(s\) = abaab
- \(s\) = baaba
- \(s\) = abbaa
- \(s\) = baaab
- \(s\) = ababa
| |
![]()
|
|
C. Сумма подстрок
жадные алгоритмы
Конструктив
математика
Перебор
Строки
*1400
Вам дана бинарная строка \(s\) длины \(n\). Пусть \(d_i\) — число, в десятичной системе счисления записываемое как \(s_i s_{i+1}\) (возможно, с ведущим нулем). Определим \(f(s)\) как сумму всех корректных значений \(d_i\). Иными словами, \(f(s) = \sum\limits_{i=1}^{n-1} d_i\). Например, для строки \(s = 1011\): - \(d_1 = 10\) (десять);
- \(d_2 = 01\) (один);
- \(d_3 = 11\) (одиннадцать);
- \(f(s) = 10 + 01 + 11 = 22\).
За одну операцию вы можете поменять местами любые два соседних символа строки. Найдите минимально возможное значение \(f(s)\), которое может быть получено после не более чем \(k\) операций. Выходные данные Для каждого набора входных данных выведите минимально возможное значение \(f(s)\) после не более чем \(k\) операций. Примечание - В первом примере делать операции нельзя, поэтому оптимальный ответ — сама строка \(s\). \(f(s) = f(1010) = 10 + 01 + 10 = 21\).
- Во втором примере одно из оптимальных решений — строка «0011000». Для данной строки значение \(f\) равно \(22\).
- В третьем примере одно из оптимальных решений — строка «00011». Для данной строки значение \(f\) равно \(12\).
| |
![]()
|
|
C. Любимая задача awoo
Бинарный поиск
жадные алгоритмы
Конструктив
реализация
Строки
Структуры данных
*1400
Заданы две строки \(s\) и \(t\), обе длины \(n\). Каждый символ в обеих строках — 'a', 'b' или 'c'. За один ход разрешается совершить одно из следующих действий: - выбрать вхождение «ab» в \(s\) и заменить его на «ba»;
- выбрать вхождение «bc» в \(s\) и заменить его на «cb».
Разрешается совершить произвольное количество ходов (включая ноль). Можно ли сделать строку \(s\) равной строке \(t\)? Выходные данные На каждый набор входных данных выведите «YES», если возможно сделать строку \(s\) равной строке \(t\), совершив произвольное количество ходов (возможно, ноль). В противном случае выведите «NO». | |
![]()
|
|
E. Палисечение
Строки
*2900
На уроке английского языка Никите совсем нечем было заняться, и он вспомнил о замечательных строках под названием палиндромы. Напомним, что строка называется палиндромом, если она читается одинаково слева направо и справа налево. Примеры таких строк: «eye», «pop», «level», «aba», «deed», «racecar», «rotor», «madam». Никита стал старательно искать все палиндромы в тексте, который они читали в тот момент на уроке. Для каждого вхождения каждого палиндрома он выписывал пару — позицию начала и позицию конца этого вхождения палиндрома в текст. Каждое вхождение каждого палиндрома Никита называет подпалиндромом. Когда Никита нашел все подпалиндромы, ему стало интересно, сколько различных пар из них пересекается. Два подпалиндрома пересекаются, если они содержат общую позицию в тексте, причем считается, что никакой палиндром не пересекается сам с собой. Рассмотрим на примере текста «babb» все действия, которые делал Никита. Сначала он выписал все подпалиндромы: • «b» — 1..1 • «bab» — 1..3 • «a» — 2..2 • «b» — 3..3 • «bb» — 3..4 • «b» — 4..4 Далее Никита посчитал количество различных пар подпалиндромов, которые пересекаются. Таких пар оказалось шесть: 1. 1..1 пересекается с 1..3 2. 1..3 пересекается с 2..2 3. 1..3 пересекается с 3..3 4. 1..3 пересекается с 3..4 5. 3..3 пересекается с 3..4 6. 3..4 пересекается с 4..4 Так как это всё изнурительно тяжело делать вручную, Никита попросил вас помочь ему и разработать программу, которая по заданному тексту будет определять количество различных пар пересекающихся подпалиндромов. Две пары подпалиндромов называются различными, если есть подпалиндром, который входит в одну из них и не входит в другую. Выходные данные В единственной строке выходных данных должно содержаться количество различных неупорядоченных пар пересекающихся подпалиндромов. Ответ нужно выводить по модулю 51123987. | |
![]()
|
|
E. Текстовый редактор
дп
жадные алгоритмы
Перебор
Строки
*2500
Вы хотели написать текст \(t\), состоящий из \(m\) строчных букв латинского алфавита. Но вместо этого вы написали текст \(s\), состоящий из \(n\) строчных букв латинского алфавита, и теперь вы хотите исправить это, получив текст \(t\) из текста \(s\). Изначально курсор вашего текстового редактора находится в конце текста \(s\) (после последнего символа текста). За один ход вы можете совершить одно из следующих действий: - нажать кнопку «влево», таким образом, курсор переместится на одну позицию влево (или не сделает ничего, если он уже указывает на начало текста, то есть стоит перед первым символом текста);
- нажать кнопку «вправо», таким образом, курсор переместится на одну позицию вправо (или не сделает ничего, если он уже указывает на конец текста, то есть стоит после последнего символа текста);
- нажать кнопку «home», таким образом, курсор переместится в начало текста (на позицию перед первым символом текста);
- нажать кнопку «end», таким образом, курсор переместится в конец текста (на позицию после последнего символа текста);
- нажать кнопку «backspace», таким образом, символ слева от курсора удалится из текста (если такого символа нет, ничего не произойдет).
Ваша задача — посчитать минимальное количество ходов, необходимое для того, чтобы получить текст \(t\) из текста \(s\) при помощи заданного набора действий, или же определить, что невозможно получить текст \(t\) из текста \(s\). Вам необходимо ответить на \(T\) независимых наборов тестовых данных. Выходные данные Для каждого набора выведите одно целое число — минимальное количество ходов, необходимое для того, чтобы получить текст \(t\) из текста \(s\) при помощи заданного набора действий, или же -1, если невозможно получить текст \(t\) из текста \(s\) в данном наборе тестовых данных. | |
![]()
|
|
A. YES или YES?
Перебор
реализация
Строки
*800
Дана строка \(s\) длины \(3\), состоящая из строчных и заглавных букв латинского алфавита. Ваша задача состоит в том, чтобы определить, равняется ли она строке «YES» (без кавычек), где каждая буква может быть как заглавной, так и строчной. Например, «yES», «Yes» и «yes» все являются допустимыми. Выходные данные Для каждого набора входных данных выведите «YES» (без кавычек) если \(s\) удовлетворяет условию, и «NO» в противном случае. Вы можете выводить «Yes» и «No» в любом регистре (например, строки «yES», «yes» и «Yes» будут распознаны как правильный ответ). Примечание Первые пять наборов входных данных содержат строки «YES», «yES», «yes», «Yes», «YeS». Все они равны строке «YES», где каждый символ либо заглавный, либо строчный. | |
![]()
|
|
C. Шифр
Перебор
реализация
Строки
*800
Лука имеет шифр, представляющий собой последовательность из \(n\) колёсиков, каждое с написанной на нём цифрой \(a_i\). Известно, что он прокрутил \(i\)-е колёсико \(b_i\) раз. Каждое колёсико может крутиться: - вверх (обозначено символом \(\texttt{U}\)): прокрутка вверх увеличивает значение на \(i\)-м колёсике на \(1\). После прокрутки \(9\) вверх, значение становится равным \(0\).
- вниз (обозначено символом \(\texttt{D}\)): прокрутка вниз уменьшает значение на \(i\)-м колёсике на \(1\). После прокрутки \(0\) вниз, значение становится равным \(9\).
 Пример для \(n=4\). Текущая последовательность цифр: 0 0 0 0. Пример для \(n=4\). Текущая последовательность цифр: 0 0 0 0. Лука знает конечные значения колёсиков и последовательность совершённых прокруток для каждого из них. Помогите ему восстановить изначальную последовательность цифр, чтобы взломать шифр! Выходные данные Для каждого набора выведите \(n\) разделённых пробелом цифр — изначальные значения на колёсиках шифра. Примечание В первом наборе можно показать, что изначальным шифром являлось \([2,1,1]\). В таком случае колёсики были прокручены следующим образом: - Первое колёсико: \(2 \xrightarrow[\texttt{D}]{} 1 \xrightarrow[\texttt{D}]{} 0 \xrightarrow[\texttt{D}]{} 9\).
- Второе колёсико: \(1 \xrightarrow[\texttt{U}]{} 2 \xrightarrow[\texttt{D}]{} 1 \xrightarrow[\texttt{U}]{} 2 \xrightarrow[\texttt{U}]{} 3\).
- Третье колёсико: \(1 \xrightarrow[\texttt{D}]{} 0 \xrightarrow[\texttt{U}]{} 1\).
Получившаяся последовательность \([9,3,1]\) совпадает с заданной во входных данных. | |
![]()
|
|
D. Двойные строки
Перебор
Строки
Структуры данных
*1100
Вам даны \(n\) строк \(s_1, s_2, \dots, s_n\) длины не более \(\mathbf{8}\). Для каждой строки \(s_i\), проверьте, существуют ли такие \(s_j\) и \(s_k\), что \(s_i = s_j + s_k\). То есть определите, является ли \(s_i\) конкатенацией \(s_j\) и \(s_k\). Обратите внимание, что \(j\) может быть равным \(k\). Напомним, что конкатенацией строк \(s\) и \(t\) называется строка \(s + t = s_1 s_2 \dots s_p t_1 t_2 \dots t_q\), где \(p\) и \(q\) длины строк \(s\) и \(t\) соответственно. Например, конкатенация строк «code» и «forces» равна «codeforces». Выходные данные Для каждого набора выведите бинарную строку длины \(n\). \(i\)-й бит строки должен равняться \(\texttt{1}\) если существуют две строки \(s_j\) и \(s_k\) таких, чтобы \(s_i = s_j + s_k\), или же \(\texttt{0}\) в противном случае. Обратите внимание, что \(j\) может совпадать с \(k\). Примечание В первом наборе мы имеем следующее: - \(s_1 = s_2 + s_2\), так как \(\texttt{abab} = \texttt{ab} + \texttt{ab}\). Помните, что \(j\) может совпадать с \(k\).
- \(s_2\) не может быть представлена как конкатенация никаких двух строк.
- \(s_3 = s_2 + s_5\), так как \(\texttt{abc} = \texttt{ab} + \texttt{c}\).
- \(s_4\) не может быть представлена как конкатенация никаких двух строк.
- \(s_5\) не может быть представлена как конкатенация никаких двух строк.
Так как только \(s_1\) и \(s_3\) удовлетворяют условиям, то только первый и третий биты в ответе будут равняться \(\texttt{1}\), поэтому ответ — \(\texttt{10100}\). | |
![]()
|
|
G. Mio и счастливый массив
бпф
Конструктив
математика
Строки
*3500
У Mio есть массив \(a\), состоящий из \(n\) целых чисел, и массив \(b\), состоящий из \(m\) целых чисел. Mio может выполнить следующую операцию над \(a\): - Выберите целое число \(i\) (\(1 \leq i \leq n\)), которое не было выбрано ранее, затем прибавьте \(1\) к \(a_i\), вычтите \(2\) из \(a_{i+1}\) , добавьте \(3\) к \(a_{i+2}\) и так далее. Формально операция состоит в добавлении \((-1)^{j-i} \cdot (j-i+1) \) к \(a_j\) для \(i \leq j \leq n\).
Mio хочет преобразовать \(a\) так, чтобы он содержал \(b\) как подмассив. Не могли бы вы ответить на ее вопрос и указать последовательность операций для этого, если это возможно? Массив \(b\) является подмассивом массива \(a\), если \(b\) получается из \(a\) удалением нескольких (возможно, нуля или всех) элементов с начала и нескольких (возможно, нуля или всех) элементов с конца. Выходные данные Если невозможно преобразовать \(a\) так, чтобы он содержал \(b\) в качестве подмассива, выведите \(-1\). В противном случае первая строка вывода должна содержать целое число \(k\) (\(0 \leq k \leq n\)), количество операций, которые необходимо выполнить. Вторая строка должна содержать \(k\) различных целых чисел, представляющих операции, выполняемые по порядку. Если решений несколько, можно вывести любое. Обратите внимание, что вам не нужно минимизировать количество операций. Примечание В первом наборе входных данных последовательность \(a\) = \([1,2,3,4,5]\). Одним из возможных решений является выполнение одной операции при \(i = 1\) (прибавьте \(1\) к \(a_1\), вычтите \(2\) из \(a_2\), прибавьте \(3\) к \(a_3\), вычтите \(4\) из \(a_4\), прибавьте \(5\) до \(a_5\)). Затем массив \(a\) преобразуется в \(a\) = \([2,0,6,0,10]\), который содержит \(b\) = \([2, 0, 6, 0, 10]\) в качестве подмассива. Во втором наборе входных данных последовательность \(a\) = \([1,2,3,4,5]\). Одно из возможных решений — сделать одну операцию при \(i = 4\) (прибавить \(1\) к \(a_4\), вычесть \(2\) из \(a_5\)). Затем массив \(a\) преобразуется в \(a\) = \([1,2,3,5,3]\), который содержит \(b\) = \([3,5,3]\) в качестве подмассива. В третьем наборе входных данных последовательность \(a\) = \([-3, 2, -3, -4, 4, 0, 1, -2]\). Одним из возможных решений является следующее. - Выберите целое число \(i=8\) для выполнения операции. Затем массив \(a\) преобразуется в \(a\) = \([-3, 2, -3, -4, 4, 0, 1, -1]\).
- Выберите целое число \(i=6\), чтобы выполнить операцию. Затем массив \(a\) преобразуется в \(a\) = \([-3, 2, -3, -4, 4, 1, -1, 2]\).
- Выберите целое число \(i=4\) для выполнения операции. Затем массив \(a\) преобразуется в \(a\) = \([-3, 2, -3, -3, 2, 4, -5, 7]\).
- Выберите целое число \(i=3\) для выполнения операции. Затем массив \(a\) преобразуется в \(a\) = \([-3, 2, -2, -5, 5, 0, 0, 1]\).
- Выберите целое число \(i=1\) для выполнения операции. Затем массив \(a\) преобразуется в \(a\) = \([-2, 0, 1, -9, 10, -6, 7, -7]\).
В результате \(a\) равно \([-2, 0, 1, -9, 10, -6, 7, -7]\), что содержит \(b\) = \([10, -6, 7, -7]\) в качестве подмассива. В четвертом наборе входных данных невозможно преобразовать \(a\) так, чтобы он содержал \(b\) в качестве подмассива. В пятом наборе входных данных невозможно преобразовать \(a\) так, чтобы он содержал \(b\) в качестве подмассива. | |
![]()
|
|
A. Очередная задача на минимизацию строки
2-sat
жадные алгоритмы
Конструктив
Строки
строковые суфф. структуры
*800
У вас есть последовательность \(a_1, a_2, \ldots, a_n\) длины \(n\), состоящая из целых чисел от \(1\) до \(m\). Также у вас есть строка \(s\), состоящая из \(m\) латинских букв «B». Вы примените \(n\) операций к этой строке. - На \(i\)-й (\(1 \le i \le n\)) операции вы можете заменить \(a_i\)-й либо \((m + 1 - a_i)\)-й символ строки \(s\) на «A». Можно заменять символ на одной и той же позиции несколько раз.
Найдите лексикографически минимальную строку, которую Вы можете получить после выполнения всех операций. Строка \(x\) лексикографически меньше строки \(y\) такой же длины, если и только если в первой позиции, где \(x\) и \(y\) различны, в строке \(x\) находится буква, которая встречается в алфавите раньше, чем соответствующая буква в \(y\). Выходные данные Для каждого набора входных данных выведите строку длины \(m\) — лексикографически минимальную строку, которую можно получить. Каждый символ строки должен быть заглавной латинской буквой «A» или заглавной латинской буквой «B». Примечание В первом наборе входных данных последовательность \(a = [1, 1, 3, 1]\). Одно из возможных решений следующее. - На \(1\)-й операции вы можете заменить \(1\)-й символ строки \(s\) на A. После этого \(s\) становится равной ABBBB.
- На \(2\)-й операции вы можете заменить \(5\)-й символ строки \(s\) на A (так как \(m+1-a_2=5\)). После этого \(s\) становится равной ABBBA.
- На \(3\)-й операции вы можете заменить \(3\)-й символ строки \(s\) на A. После этого \(s\) становится равной ABABA.
- На \(4\)-й операции вы можете заменить \(1\)-й символ строки \(s\) на A. После этого \(s\) остаётся равной ABABA.
Вы получите строку ABABA. Можно показать, что нельзя получить лексикографически меньшую строку. Во втором наборе входных данных вы сделаете только одну операцию. Вы можете заменить \(2\)-й либо \(4\)-й символ строки \(s\) на A. Вы можете получить строки BABBB и BBBAB после операции. Строка BABBB является лексикографически наименьшей из этих строк. В третьем наборе входных данных вы можете получить только строку A. В четвёртом наборе входных данных вы можете заменить \(1\)-й и \(2\)-й символы строки \(s\) на A, чтобы получить строку AABB. В пятом наборе входных данных вы можете заменить \(1\)-й и \(3\)-й символы строки \(s\) на A, чтобы получить строку ABABBBB. | |
![]()
|
|
C. Восстанови ПСП
жадные алгоритмы
Конструктив
реализация
Строки
*1800
Скобочная последовательность — это строка, содержащая только символы «(» и «)». Правильная скобочная последовательность (или, коротко говоря, ПСП) — это скобочная последовательность, которая может быть преобразована в правильное арифметическое выражение путем вставки символов «1» и «+» между исходными символами последовательности. Например: - скобочные последовательности «()()» и «(())» являются правильными (возможные выражения: «(1)+(1)» и «((1+1)+1)»);
- скобочные последовательности «)(», «(» и «)» не являются правильными.
В начале была некоторая ПСП. Некоторые скобки заменили на знаки вопроса. Верно ли, что существует единственный способ заменить знаки вопроса на скобки так, чтобы получилась ПСП? Выходные данные На каждый набор входных данных выведите «YES», если способ заменить знаки вопроса на скобки так, чтобы получилась ПСП, единственный. Если существует больше одного способа, то выведите «NO». Примечание В первом наборе входных данных единственная возможная оригинальная ПСП — это «(())». Во втором наборе существует несколько способов восстановить ПСП. В третьем и четвертом наборах единственная возможная ПСП — это «()». В пятом наборе оригинальная ПСП может быть «((()()))» или «(())()()». | |
![]()
|
|
D. Покрась вхождениями
дп
жадные алгоритмы
Перебор
Строки
Структуры данных
*1600
Вам задан некоторый текст \(t\) и набор из \(n\) строк \(s_1, s_2, \dots, s_n\). За один ход вы можете выбрать любое вхождение любой строки \(s_i\) в текст \(t\) и покрасить соответствующие символы текста в красный цвет. Например, если \(t=\texttt{bababa}\) и \(s_1=\texttt{ba}\), \(s_2=\texttt{aba}\), то за один ход можно получить \(t=\color{red}{\texttt{ba}}\texttt{baba}\), \(t=\texttt{b}\color{red}{\texttt{aba}}\texttt{ba}\) или \(t=\texttt{bab}\color{red}{\texttt{aba}}\). Вы хотите сделать все буквы текста \(t\) красными. При повторной покраске буквы в красный цвет, она остаётся красной. В примере выше достаточно три хода: - Перекрасим в красный цвет \(t[2 \dots 4]=s_2=\texttt{aba}\), получим \(t=\texttt{b}\color{red}{\texttt{aba}}\texttt{ba}\);
- Перекрасим в красный цвет \(t[1 \dots 2]=s_1=\texttt{ba}\), получим \(t=\color{red}{\texttt{baba}}\texttt{ba}\);
- Перекрасим в красный цвет \(t[4 \dots 6]=s_2=\texttt{aba}\), получим \(t=\color{red}{\texttt{bababa}}\).
Каждая строка \(s_i\) может применяться произвольное количество раз (или не применяться вообще). Вхождения для покраски могут пересекаться произвольным образом. Определите, какое минимальное количество ходов надо сделать, чтобы покрасить все буквы \(t\) в красный цвет и как для этого надо совершать ходы. Если сделать все буквы текста \(t\) красными невозможно, то выведите -1. Выходные данные Для каждого набора входных данных выведите ответ на отдельной строке. Если невозможно сделать все буквы текста красными, то выведите единственную строку, содержащую число -1. Иначе, на первой строке выведите число \(m\) — минимальное количество ходов, которые потребуются, чтобы сделать все буквы \(t\) красными. Затем в последующих \(m\) строках выведите пары чисел: \(w_j\) и \(p_j\) (\(1 \le j \le m\)), которые обозначают, что строка с индексом \(w_j\) была использована как подстрока для покрытия вхождения, начинающегося в тексте \(t\) с позиции \(p_j\). Пары можно выводить в любом порядке. Если вариантов ответа несколько, выведите любой из них. Примечание Первый набор входных данных разобран в условии задачи. Во втором наборе входных данных невозможно сделать все буквы текста красными. | |
![]()
|
|
D1. Xor-подпоследовательность (простая версия)
битмаски
Деревья
дп
Перебор
Строки
*1800
Это простая версия задачи. Единственное различие состоит в том, что в этой версии \(a_i \le 200\). Дан массив из \(n\) целых чисел \(a_0, a_1, a_2, \ldots a_{n - 1}\). Бряп захотел найти в данном массиве самую длинную хорошую подпоследовательность. Массив \(b = [b_0, b_1, \ldots, b_{m-1}]\), где \(0 \le b_0 < b_1 < \ldots < b_{m - 1} < n\), будем называть подпоследовательностью длины \(m\) массива \(a\). Подпоследовательность \(b = [b_0, b_1, \ldots, b_{m-1}]\) длины \(m\) называется хорошей, если выполняется следующее условие: - Для любого целого числа \(p\) (\(0 \le p < m - 1\)) выполняется условие: \(a_{b_p} \oplus b_{p+1} < a_{b_{p+1}} \oplus b_p\).
Здесь \(a \oplus b\) обозначает побитовое исключающее ИЛИ чисел \(a\) и \(b\). Например, \(2 \oplus 4 = 6\), а \(3 \oplus 1=2\). Так как Бряп не очень любознательная персона, он хочет знать лишь длину такой подпоследовательности. Помогите ему найти ответ на данную задачу. Выходные данные Для каждого набора входных данных единственное число — максимальную длину хорошей подпоследовательности. Примечание В первом наборе входных данных в качестве подпоследовательности мы можем выбрать оба элемента массива, так как \(1 \oplus 1 < 2 \oplus 0\). Во втором наборе входных данных мы можем взять элементы с индексами \(1\), \(2\) и \(4\) (в \(0\)-нумерации). Для них выполняется: \(2 \oplus 2 < 4 \oplus 1\) и \(4 \oplus 4 < 1 \oplus 2\). | |
![]()
|
|
D2. Xor-подпоследовательность (сложная версия)
битмаски
Деревья
дп
Строки
Структуры данных
*2400
Это сложная версия задачи. Единственное различие состоит в том, что в этой версии \(a_i \le 10^9\). Дан массив из \(n\) целых чисел \(a_0, a_1, a_2, \ldots a_{n - 1}\). Бряп захотел найти в данном массиве самую длинную хорошую подпоследовательность. Массив \(b = [b_0, b_1, \ldots, b_{m-1}]\), где \(0 \le b_0 < b_1 < \ldots < b_{m - 1} < n\), будем называть подпоследовательностью длины \(m\) массива \(a\). Подпоследовательность \(b = [b_0, b_1, \ldots, b_{m-1}]\) длины \(m\) называется хорошей, если выполняется следующее условие: - Для любого целого числа \(p\) (\(0 \le p < m - 1\)) выполняется условие: \(a_{b_p} \oplus b_{p+1} < a_{b_{p+1}} \oplus b_p\).
Здесь \(a \oplus b\) обозначает побитовое исключающее ИЛИ чисел \(a\) и \(b\). Например, \(2 \oplus 4 = 6\), а \(3 \oplus 1=2\). Так как Бряп не очень любознательная персона, он хочет знать лишь длину такой подпоследовательности. Помогите ему найти ответ на данную задачу. Выходные данные Для каждого набора входных данных единственное число — максимальную длину хорошей подпоследовательности. Примечание В первом наборе входных данных в качестве подпоследовательности мы можем выбрать оба элемента массива, так как \(1 \oplus 1 < 2 \oplus 0\). Во втором наборе входных данных мы можем взять элементы с индексами \(1\), \(2\) и \(4\) (в \(0\) нумерации). Для них выполняется: \(2 \oplus 2 < 4 \oplus 1\) и \(4 \oplus 4 < 1 \oplus 2\). | |
![]()
|
|
E. Запросы про префикс функцию
Деревья
дп
поиск в глубину и подобное
Строки
строковые суфф. структуры
хэши
*2200
Задана строка \(s\), состоящая из строчных латинских букв. К ней приходят \(q\) запросов: дана другая строка \(t\), состоящая из строчных латинских букв; проделайте следующие шаги: - склеить \(s\) и \(t\);
- посчитать префикс-функцию полученной строки \(s+t\);
- выведите значения префикс-функции на позициях \(|s|+1, |s|+2, \dots, |s|+|t|\) (\(|s|\) и \(|t|\) — это длины строк \(s\) и \(t\), соответственно);
- вернуть строку обратно к \(s\).
Префикс-функция строки \(a\) — это последовательность \(p_1, p_2, \dots, p_{|a|}\), где \(p_i\) — это наибольшее значение \(k\) такое, что \(k < i\) и \(a[1..k]=a[i-k+1..i]\) (\(a[l..r]\) обозначает непрерывную подстроку строку \(a\) с позиции \(l\) до позиции \(r\) включительно). Другими словами, это наибольший собственный префикс строки \(a[1..i]\), который равен ее суффиксу такой же длины. Выходные данные На каждый запрос выведите значения префикс-функции строки \(s+t\) на позициях \(|s|+1, |s|+2, \dots, |s|+|t|\). | |
![]()
|
|
B. Расшифруй строку
жадные алгоритмы
Строки
*800
У Поликарпа есть строка \(s\), состоящая из строчных латинских букв. Он кодирует её, используя следующий алгоритм. Он идёт по буквам строки \(s\) слева направо и для каждой буквы Поликарп рассматривает её номер в алфавите: - если номер буквы — однозначное число (меньше \(10\)), то он просто выписывает его;
- если номер буквы — двузначное число (больше или равен \(10\)), то он выписывает его и дополнительно приписывает справа цифру 0.
Например, если строка \(s\) равна code, то Поликарп будет кодировать её следующим образом: - 'c' — это \(3\)-я буква алфавита. Следовательно, Поликарп дописывает к коду 3 (код становится равен 3);
- 'o' — это \(15\)-я буква алфавита. Следовательно, Поликарп дописывает к коду 15 и ещё 0 (код становится равен 3150);
- 'd' — это \(4\)-я буква алфавита. Следовательно, Поликарп дописывает к коду 4 (код становится равен 31504);
- 'e' — это \(5\)-я буква алфавита. Следовательно, Поликарп дописывает к коду 5 (код становится равен 315045).
Таким образом, Поликарп код строки code равен 315045. Вам дана строка \(t\), полученная в результате кодирования строки \(s\). Ваша задача — декодировать её (получить по \(t\) исходную строку \(s\)). Выходные данные Для каждого набора входных данных выведите искомую строку \(s\) — строку, в результате кодирования которой будет получена строка \(t\). Гарантируется, что такая строка всегда существует. Можно показать, что такая строка всегда уникальна. Примечание Первый набор входных данных примера разобран в условии. Во втором наборе примера ответ равен aj. В самом деле, номер буквы a равен \(1\), следовательно к коду будет дописано 1. Номер буквы j равен \(10\), следовательно к коду будет дописано 100. В результате код равен 1100. Во третьем наборе входных данных нет нулей, а значит номера всех букв меньше \(10\) и кодируются одной цифрой. Исходная строка равна abacaba. В четвёртом наборе входных данных строка \(s\) равна ll. Буква l имеет номер \(12\) и кодируется как 120. Таким образом, код ll в самом деле равен 120120. | |
![]()
|
|
C. Прыжки по плиткам
Конструктив
Строки
*1100
Поликарпу дали ряд из плиток. На каждой плитке находится по одной строчной букве латинского алфавита. Вся последовательность из плиток образует строку \(s\). Иными словами, вам задана строка \(s\), состоящая из строчных букв латинского алфавита. Изначально Поликарп находится на первой плитке ряда и хочет попасть на последнюю, прыгая по плиткам. Прыжок от плитки \(i\) к плитке \(j\) имеет стоимость равную \(|index(s_i) - index(s_j)|\), где \(index(c)\) означает индекс буквы \(c\) в алфавите (например, \(index(\)'a'\()=1\), \(index(\)'b'\()=2\), ..., \(index(\)'z'\()=26\)). Поликарп хочет добраться до \(n\)-й плитки за минимальную суммарную стоимость, но при этом сделать максимальное количество прыжков. Иными словами, среди всех возможных способов добраться до последней плитки за минимальную суммарную стоимость, он выберет такой, в котором количество прыжков максимально. Поликарп может посетить каждую плитку не более одного раза. Поликарп просит вас помочь — выведите последовательность индексов строки \(s\), по которым он должен прыгать. Выходные данные Ответ на каждый набор входных данных состоит из двух строк. В первой строке выведите два целых числа \(cost\), \(m\), где \(cost\) — минимальная суммарная стоимость пути, а \(m\) — максимальное количество плиток, которые Поликарп может посетить, чтобы добраться до \(n\)-й плитки за минимальную суммарную стоимость \(cost\) (т.е. количество прыжков равно \(m-1\)). В следующей строке выведите \(m\) различных чисел \(j_1, j_2, \dots, j_m\) (\(1 \le j_i \le |s|\)) — последовательность индексов плиток по которым будет прыгать Поликарп. Первым числом последовательности должна быть \(1\) (то есть \(j_1=1\)), а последним числом должно быть значение \(|s|\) (то есть \(j_m=|s|\)). Если вариантов ответа несколько, выведите любой из них. Примечание В первом наборе входных данных примера искомый путь соответствует картинке:  В данном случае достигается минимальная возможная суммарная стоимость пути. Так как \(index(\)'l'\()=12\), \(index(\)'o'\()=15\), \(index(\)'g'\()=7\), \(index(\)'i'\()=9\), \(index(\)'c'\()=3\), то суммарная стоимость пути равна \(|12-9|+|9-7|+|7-3|=3+2+4=9\). | |
![]()
|
|
G. Вырежи подстроки
дп
Комбинаторика
Строки
хэши
*2100
Вам даны две непустые строки \(s\) и \(t\), состоящие из латинских букв. За один ход вы можете выбрать вхождение строки \(t\) в строку \(s\) и заменить его на точки. Ваша задача — за минимальное количество ходов убрать все вхождения строки \(t\) в строке \(s\), а также посчитать, сколько существует различных последовательностей ходов минимальной длины. Две последовательности ходов считаются различными, если множества индексов, в которых начинаются убираемые вхождения строки \(t\) в \(s\), различаются. Например, множества \(\{1, 2, 3\}\) и \(\{1, 2, 4\}\) считаются различными, множества \(\{2, 4, 6\}\) и \(\{2, 6\}\) — тоже, а множества \(\{3, 5\}\) и \(\{5, 3\}\) — нет. Например, пусть строка \(s =\) «abababacababa», а строка \(t =\) «aba». Мы можем убрать все вхождения строки \(t\) за \(2\) хода, заменив вхождения строки \(t\) на \(3\)-й и \(9\)-й позициях на точки. В этом случае строка \(s\) пример вид «ab...bac...ba». Также можно вырезать вхождения строки \(t\) на \(3\)-й и \(11\)-й позициях. Всего есть две различные последовательности ходов минимальной длины. Так как ответ может быть большим, выведите его по модулю \(10^9 + 7\). Выходные данные Для каждого набора входных данных выведите два целых числа — минимальное количество ходов и количество различных оптимальных последовательностей, взятое по модулю \(10^9 + 7\). Примечание Первый набор входных данных разобран в условии. Во втором наборе достаточно заменить любое из четырёх вхождений. В третьем наборе строка \(s\) является конкатенацией двух строк \(t =\) «xyz», поэтому существует единственная оптимальная последовательность из \(2\) ходов. В четвёртом и шестом наборах строка \(s\) изначально не содержит вхождений строки \(t\). В пятом наборе строка \(s\) содержит ровно одно вхождение строки \(t\). | |
![]()
|
|
D. Префиксы и суффиксы
Конструктив
Строки
*2200
У вас есть две строки \(s_1\) и \(s_2\) длины \(n\), состоящие из строчных латинских букв. Вы можете выполнить следующую операцию любое (возможно, нулевое) количество раз: - Выберите положительное целое число \(1 \leq k \leq n\).
- Поменяйте местами префикс строки \(s_1\) и суффикс строки \(s_2\) длины \(k\).
Можно ли вы сделать эти две строки равными с помощью описанных операций? Выходные данные Для каждого набора входных данных выведите «YES» (без кавычек), если можно сделать строки равными, и «NO» (без кавычек), иначе. Примечание В первом наборе входных данных: - Изначально \(s_1 = \mathtt{cbc}\), \(s_2 = \mathtt{aba}\).
- Сделаем операцию с \(k = 1\), в результате получим строки \(s_1 = \mathtt{abc}\), \(s_2 = \mathtt{abc}\).
Во втором наборе входных данных: - \(s_1 = \mathtt{abcaa}\), \(s_2 = \mathtt{cbabb}\).
- Сделаем операцию с \(k = 2\), в результате получим строки \(s_1 = \mathtt{bbcaa}\), \(s_2 = \mathtt{cbaab}\).
- Сделаем операцию с \(k = 3\), в результате получим строки \(s_1 = \mathtt{aabaa}\), \(s_2 = \mathtt{cbbbc}\).
- Сделаем операцию с \(k = 1\), в результате получим строки \(s_1 = \mathtt{cabaa}\), \(s_2 = \mathtt{cbbba}\).
- Сделаем операцию с \(k = 2\), в результате получим строки \(s_1 = \mathtt{babaa}\), \(s_2 = \mathtt{cbbca}\).
- Сделаем операцию с \(k = 1\), в результате получим строки \(s_1 = \mathtt{aabaa}\), \(s_2 = \mathtt{cbbcb}\).
- Сделаем операцию с \(k = 2\), в результате получим строки \(s_1 = \mathtt{cbbaa}\), \(s_2 = \mathtt{cbbaa}\).
В третьем наборе входных данных невозможно сделать строки равными. | |
![]()
|
|
C. Сдвиг по фазе
графы
жадные алгоритмы
поиск в глубину и подобное
реализация
снм
Строки
*1400
Была строка \(s\), которую захотели зашифровать. Для этого взяли все \(26\) строчных латинских букв, расположили их в некотором порядке по кругу, после чего заменили каждую букву в \(s\) на ту, что является следующей по часовой стрелке, получив таким образом строку \(t\). Вам дали строку \(t\). Определите лексикографически минимальную строку \(s\), из которой могла быть получена данная строка \(t\). Строка \(a\) лексикографически меньше строки \(b\) такой же длины, если и только если: - в первой позиции, где \(a\) и \(b\) различны, в строке \(a\) находится буква, которая встречается в алфавите раньше, чем соответствующая буква в \(b\).
Выходные данные Для каждого набора входных данных выведите одну строку — лексикографически минимальную строку \(s\), из которой могла получиться \(t\). Примечание В первом наборе входных данных мы не могли иметь строку «a», поскольку тогда буква a переходила бы сама в себя, что невозможно. В качестве ответа нам подходит лексикографически вторая строка «b». Во втором наборе нам не подходит «aa», поскольку a переходила бы в себя, и не подходит «ab», поскольку круг переходов замкнулся бы на \(2\) буквах, а он должен состоять из всех \(26\). Следующая строка «ac» нам подходит. Ниже приведены схемы для первых трех наборов входных данных. В круге пропущены неучаствующие буквы, их можно расставить произвольно в пропуски.  | |
![]()
|
|
D. Одинаковые бинарные подпоследовательности
геометрия
жадные алгоритмы
Конструктив
реализация
Строки
*2200
У Эврула есть бинарная строка \(s\) длины \(2n\). Бинарная строка — это строка, состоящая только из символов \(0\) и \(1\). Он хочет разбить \(s\) на две непересекающиеся одинаковые подпоследовательности. Для этого ему нужна ваша помощь. Вы можете выполнить следующую операцию один раз. - Выберите любую подпоследовательность (возможно пустую) символов \(s\) и циклически сдвиньте ее направо на одну позицию.
Другими словами, выберите последовательность индексов \(b_1, b_2, \ldots, b_m\), где \(1 \le b_1 < b_2 < \ldots < b_m \le 2n\). После этого одновременно присвойте \(\)s_{b_1} := s_{b_m},\(\) \(\)s_{b_2} := s_{b_1},\(\) \(\)\ldots,\(\) \(\)s_{b_m} := s_{b_{m-1}}.\(\) Можете ли вы разбить \(s\) на две непересекающиеся одинаковые подпоследовательности после того, как выполните указанную операцию ровно один раз? Разбиением \(s\) на две непересекающиеся одинаковые подпоследовательности \(s^p\) и \(s^q\) называются два возрастающих массива индексов \(p_1, p_2, \ldots, p_n\) и \(q_1, q_2, \ldots, q_n\) такие, что каждое целое число от \(1\) до \(2n\) встречается \(p\) и \(q\) ровно один раз, при этом \(s^p = s_{p_1} s_{p_2} \ldots s_{p_n}\), \(s^q = s_{q_1} s_{q_2} \ldots s_{q_n}\), и \(s^p = s^q\). Если невозможно выполнить операцию и разбиение, выведите \(-1\). Если можно выполнить операцию и разбить \(s\) на две непересекающиеся подпоследовательности \(s^p\) и \(s^q\) так, чтобы \(s^p = s^q\), выведите индексы подпоследовательности \(b\) и индексы \(s^p\), т. е. значения \(p_1, p_2, \ldots, p_n\). Выходные данные Для каждого набора входных данных следуйте следующему формату. Если решения не существует, выведите \(-1\). Иначе: - В первой строке выведите целое число \(m\) (\(0 \leq m \leq 2n\)) и затем \(m\) различных индексов в возрастающем порядке \(b_1\), \(b_2\), ..., \(b_m\).
- Во второй строке выведите \(n\) различных индексов в возрастающем порядке \(p_1\), \(p_2\), ..., \(p_n\).
Если существуют несколько решений, выведите любое из них. Примечание В первом примере \(b\) пустая, поэтому строка \(s\) не меняется. Выберем \(s^p = s_1 s_2 = \mathtt{10}\), тогда \(s^q = s_3s_4 = \mathtt{10}\). Во втором примере \(b=[3,5]\). Изначально \(s_3=\mathtt{0}\), и \(s_5=\mathtt{1}\). После выполнения операции мы одновременно присваиваем \(s_3=\mathtt{1}\) и \(s_5=\mathtt{0}\). Поэтому \(s\) становится 101000 после выполнения операции. Возьмем символы на позициях \([1,2,5]\) в \(s^p\), получим \(s_1=\mathtt{100}\). Символы на позициях \([3,4,6]\) будут в \(s^q\), получим \(s^q=100\). Это решение, потому что \(s^p=s^q\). В четвертом примере можно показать, что невозможно выполнить разбиение строки после любой операции. | |
![]()
|
|
A. Эла распределяет книги
жадные алгоритмы
реализация
Строки
*900
 | Эла очень любит читать, как и ее новые коллеги по DTL! В первый же день её работы в DTL коллега попросил её распределить книги по отсекам на книжной полке. |
\(n\) книг должны быть распределены по \(k\) отсекам на книжной полке (\(n\) нацело делится на \(k\)). Каждой книге можно сопоставить одну строчную латинскую букву от 'a' до 'y' включительно, которая является начальной буквой в названии книги. Эла должна положить ровно \(\frac{n}{k}\) книг в каждый отсек. Отсеки пронумерованы от \(1\) до \(k\). Положив книги, для каждого отсека она возьмет ровно одну букву — MEX мультимножества букв, соответствующих книгам в этом отсеке, и затем объединит полученные буквы в одну строку. Первая буква итоговой строки — это буква MEX мультимножества букв в первом отсеке, вторая буква итоговой строки — это буква MEX мультимножества букв во втором отсеке, и так далее. Обратите внимание, что в ограничениях этой задачи MEX всегда может быть определен для любого мультимножества букв, соответствующих книгам, потому что 'z' не может являться начальной буквой в названиях книг. Какую лексикографически наибольшую результирующую строку может получить Эла? Строка \(a\) лексикографически больше строки \(b\) тогда и только тогда, когда выполняется одно из следующих условий: - \(b\) является префиксом \(a\), но \(b \ne a\);
- в первой позиции, где \(a\) и \(b\) различаются, в строке \(a\) стоит буква, которая представлена в алфавите позже, чем соответствующая буква в \(b\).
MEX мультимножества букв – это первая в алфавите буква, которая не входит в это мультимножество. Например, если мультимножество букв содержит \(7\) букв 'b', 'a', 'b', 'c', 'e', 'c', 'f', то MEX этого мультимножества будет 'd', поскольку 'd' не содержится в мультимножестве, и все буквы, предшествующие 'd' в алфавите, а именно 'a', 'b' и 'c', содержатся в мультимножестве. Выходные данные Для каждого набора входных данных выведите строку длины \(k\), которая является лексикографически наибольшей строкой, которую может получить Эла. Примечание В первом наборе входных данных книги можно распределить по \(3\) отсекам как показано ниже: - в первом отсеке находятся книги с индексами \(1, 2, 3, 7\): \(multiset_1 = \{\)'c', 'a', 'b', 'd'\(\}\) \(\rightarrow\) \(MEX(multiset_1) =\) 'e'
- во втором отсеке находятся книги с индексами \(4, 5, 6, 9\) : \(multiset_2 = \{\)'c', 'c', 'a', 'b'\(\}\) \(\rightarrow\) \(MEX(multiset_2) =\) 'd'
- в третьем отсеке находятся книги с индексами \(8, 10, 11, 12\): \(multiset_3 = \{\)'a', 'a' , 'a', 'c'\(\}\) \(\rightarrow\) \(MEX(multiset_3) =\) 'b'
Следовательно, ответ 'edb'. Можно доказать, что Эла никак не может расположить книги так, чтобы в результате получилась лексикографически большая строка.  | |
![]()
|
|
H. Упоротые палиндромы
Строки
Структуры данных
*3300
Ваша задача состоит в том, чтобы поддерживать очередь содержащую строчные буквы Латинского алфавита со следующими операциями: - «push \(c\)»: вставить букву \(c\) в конец очереди;
- «pop»: удалить букву из начала очереди.
Изначально очередь пустая. После каждой операции, вы должны посчитать число различных подстрок палиндромов в строке, которая получается соединением букв от начала к концу очереди. Число различных подстрок палиндромов пустой строки равняется \(0\). Строка \(s[1..n]\) длины \(n\) является палиндромом, если \(s[i] = s[n-i+1]\) для любого \(1 \leq i \leq n\). Строка \(s[l..r]\) является подстрокой строки \(s[1..n]\) для любого \(1 \leq l \leq r \leq n\). Две строки \(s[1..n]\) и \(t[1..m]\) различные, если выполняется как минимум одно из условий. - \(n \neq m\);
- \(s[i] \neq t[i]\) для некоторого \(1 \leq i \leq \min\{n,m\}\).
Выходные данные После каждой операции, выведите количество различных подстрок палиндромов в строке, представленной в очереди. Примечание Пусть \(s_k\) это строка находящаяся в очереди после \(k\)-й операции, и пусть \(c_k\) будет число различных подстрок палиндромов строки \(s_k\). Следующая таблица иллюстрирует пример. | \(k\) | \(s_k\) | \(c_k\) | | \(1\) | \(a\) | \(1\) | | \(2\) | \(\textsf{empty}\) | \(0\) | | \(3\) | \(a\) | \(1\) | | \(4\) | \(aa\) | \(2\) | | \(5\) | \(aab\) | \(3\) | | \(6\) | \(aabb\) | \(4\) | | \(7\) | \(aabba\) | \(5\) | | \(8\) | \(aabbaa\) | \(6\) | | \(9\) | \(abbaa\) | \(5\) | | \(10\) | \(bbaa\) | \(4\) | | \(11\) | \(baa\) | \(3\) | | \(12\) | \(baab\) | \(4\) |
Стоит заметить, что - После \(2\)-й операции, строка пустая и у нее нет подстрок. Значит ответ \(0\);
- После \(8\)-й операции, строка «\(aabbaa\)». У нее \(6\) различных подстрок палиндромов «\(a\)», «\(aa\)», «\(aabbaa\)», «\(abba\)», «\(b\)», and «\(bb\)».
| |
![]()
|
|
F. Дизайн клавиатуры
битмаски
дп
Строки
строковые суфф. структуры
Структуры данных
*2600
У Монокарпа есть словарь из \(n\) слов, состоящих из первых \(12\) букв латинского алфавита. Слова пронумерованы от \(1\) до \(n\). Во всех парах соседних букв в слове буквы различны. Каждому слову \(i\) Монокарп сопоставил целое число \(c_i\) — как часто он использует это слово. Монокарп хочет выбрать такой дизайн клавиатуры, чтобы он помог ему проще печатать некоторые слова. Клавиатуру можно описать, как последовательность из \(12\) первых букв латинского алфавита, где каждая буква от a до l встречается ровно один раз. Слово можно легко напечатать на клавиатуре, если для каждой пары соседних символов в слове эти символы на клавиатуре тоже соседние. Оптимальность клавиатуры — это сумма \(c_i\) по всем словам \(i\), которые могут быть легко на ней напечатаны. Помогите Монокарпу создать дизайн клавиатуры с максимальной оптимальностью. Выходные данные Выведите последовательность из \(12\) первых букв латинского алфавита, где каждая буква от a до l встречается ровно один раз, определяющую оптимальную клавиатуру. Если ответов несколько, выведите любой из них. | |
![]()
|
|
A. Сравни размеры футболок
реализация
реализация
Строки
*800
Даны размеры двух футболок: \(a\) и \(b\). Размер футболки — это либо строка M, либо строка, состоящая из нескольких (возможно нуля) символов X и одного из символов: S или L. Например, строки M, XXL, S, XXXXXXXS могут быть размерами некоторых футболок. А строки XM, LL, SX — не являются размерами. Буква M обозначает средний размер (от англ. medium), S — маленький (small), L — большой (large). Буква X — степень величины размера (от англ. eXtra). Например, XXL — это экстра-экстра-большой (от больше чем XL, и меньше чем XXXL). Вам нужно сравнить два заданных размера футболок \(a\) и \(b\). Футболки сравниваются следующим образом: - любой маленький размер (не зависимо от количества букв X) меньше среднего и любого большого;
- любой большой размер (не зависимо от количества букв X) больше среднего и любого маленького;
- чем больше букв X перед S, тем меньше размер;
- чем больше букв X перед L, тем больше размер.
Например: - XXXS < XS
- XXXL > XL
- XL > M
- XXL = XXL
- XXXXXS < M
- XL > XXXS
Выходные данные Для каждого набора входных данных выведите в отдельной строке результат сравнения футболок \(a\) и \(b\) (строки «<», «>» либо «=» без кавычек). | |
![]()
|
|
F. Меньше
жадные алгоритмы
Конструктив
Строки
*1500
У Альперена есть две строки, \(s\) и \(t\), которые обе изначально равны «a». Он выполнит \(q\) операций двух видов над данными строками: - \(1 \;\; k \;\; x\) — Добавить строку \(x\) ровно \(k\) раз в конец строки \(s\). Другими словами, \(s := s + \underbrace{x + \dots + x}_{k \text{ times}}\).
- \(2 \;\; k \;\; x\) — Добавить строку \(x\) ровно \(k\) раз в конец строки \(t\). Другими словами, \(t := t + \underbrace{x + \dots + x}_{k \text{ times}}\).
После каждой операции определите, можно ли переставить символы \(s\) и \(t\) так, чтобы \(s\) была лексикографически меньше \(^{\dagger}\), чем \(t\). Обратите внимание, что строки изменяются после выполнения каждой операции и не возвращаются в исходное состояние. \(^{\dagger}\) Проще говоря, лексикографический порядок - это порядок, в котором слова перечислены в словаре. Формальное определение таково: строка \(p\) лексикографически меньше строки \(q\), если существует позиция \(i\) такая, что \(p_i < q_i\), и для всех \(j < i\), \(p_j = q_j\). Если такой позиции \(i\) не существует, то \(p\) лексикографически меньше \(q\), если длина \(p\) меньше длины \(q\). Например, \(\texttt{abdc} < \texttt{abe}\) и \(\texttt{abc} < \texttt{abcd}\), где мы пишем \(p < q\), если \(p\) лексикографически меньше \(q\). Выходные данные Для каждой операции выведите «YES», если возможно расположить элементы в обеих строках таким образом, что \(s\) будет лексикографически меньше \(t\) и «NO» в противном случае. Примечание В первом примере строки изначально являются \(s = \) «a» и \(t = \) «a». После первой операции строка \(t\) становится «aaa». Поскольку «a» уже лексикографически меньше, чем «aaa», ответом на эту операцию должно быть «YES». После второй операции строка \(s\) становится «aaa», а поскольку \(t\) также равна «aaa», мы не можем переставить символы \(s\) так, чтобы она была лексикографически меньше \(t\), поэтому ответ «NO». После третьей операции строка \(t\) становится «aaaaaa», а \(s\) уже лексикографически меньше нее, поэтому ответом будет «YES». После четвертой операции \(s\) становится «aaabb» и нет способа сделать ее лексикографически меньше, чем «aaaaaa», поэтому ответ «NO». После пятой операции строка \(t\) становится «aaaaaaabcaabcaabca», и мы можем переставить символы в строках так: «bbaaa» и «caaaaaabcaabcaabaa», так что \(s\) будет лексикографически меньше \(t\), поэтому мы должны ответить «YES». | |
![]()
|
|
B. Разнообразные подстроки
Перебор
реализация
Строки
*1400
Непустая строка из цифр является разнообразной, если количество вхождений каждого символа в неё не превосходит количество различных символов в ней. Например, - строка «7» разнообразная, так как 7 встречается в ней \(1\) раз, и количество различных символов в ней равно \(1\);
- строка «77» не является разнообразной, так как 7 встречается в ней \(2\) раза, а количество различных символов в ней равно \(1\);
- строка «1010» разнообразная, так как 0 и 1 встречаются в ней по \(2\) раза, и количество различных символов в ней равно \(2\);
- строка «6668» не является разнообразной, так как 6 встречается в ней \(3\) раза, а количество различных символов в ней равно \(2\).
Вам дана строка \(s\) длины \(n\), состоящая из цифр от \(0\) до \(9\). Найдите, сколько из ее \(\frac{n(n+1)}{2}\) подстрок являются разнообразными. Строка \(a\) является подстрокой \(b\), если \(a\) может быть получена из \(b\) удалением нескольких (возможно, ни одного или всех) символов из начала и нескольких (возможно, ни одного или всех) символов из конца. Обратите внимание, что если некоторая разнообразная строка встречается в \(s\) несколько раз, то каждое её вхождение должно быть подсчитано независимо. Например, в строке «77» есть две разнообразных подстроки, равных «7», поэтому ответ для строки «77» равен \(2\). Выходные данные Для каждого набора входных данных выведите одно число: количество разнообразных подстрок строки \(s\). Примечание В первом наборе входных данных подстрока «7» разнообразная. Во втором наборе входных данных подстрока «7» разнообразная. Так как она встречается дважды, ответ равен \(2\). В третьем наборе входных данных следующие подстроки являются разнообразными: «0» (\(2\) вхождения), «01», «010», «1» (\(2\) вхождения), «10» (\(2\) вхождения), «101» и «1010». В четвёртом наборе входных данных следующие подстроки являются разнообразными: «0» (\(3\) вхождения), «01», «011», «0110», «1» (\(2\) вхождения), «10», «100», «110» и «1100». В пятом наборе входных данных следующие подстроки являются разнообразными: «3», «39», «399», «6», «9» (\(4\) вхождения), «96» и «996». В шестом наборе входных данных все \(15\) непустых подстрок строки «23456» являются разнообразными. | |
![]()
|
|
E. Скобочная стоимость
Бинарный поиск
дп
жадные алгоритмы
разделяй и властвуй
Строки
Структуры данных
*2400
Деймон Таргариен решил перестать быть похожим на персонажа Metin2. Он превратил себя в прекраснейшую вещь — скобочную последовательность. Для последовательности скобок мы можем выполнять два вида операций: - Выберите одну из её подстрок\(^\dagger\) и циклически сдвиньте её вправо. Например, после циклического сдвига вправо «(())» станет «)(()»;
- Вставьте любую скобку, открывающую «(» или закрывающую «)», в любом месте последовательности.
Мы определяем стоимость скобочной последовательности как минимальное количество таких операций, чтобы сделать её правильной\(^\ddagger\). Для заданной скобочной последовательности \(s\) длины \(n\) найдите сумму стоимостей всех \(\frac{n(n+1)}{2}\) её непустых подстрок. Обратите внимание, что для каждой подстроки мы вычисляем стоимость независимо. \(^\dagger\) Строка \(a\) является подстрокой \(b\), если \(a\) может быть получена из \(b\) удалением нескольких (возможно, ни одного или всех) символов из начала и нескольких (возможно, ни одного или всех) символов из конца. \(^\ddagger\) Последовательность скобок называется правильной, если её можно превратить в правильное математическое выражение, добавив символы \(+\) и \(1\). Например, последовательности «(())()», «()» и «(()(()))» правильные, в то время как «)(», «(()» и «(()))(» не являются правильными. Выходные данные Для каждого набора входных данных выведите единственное целое число — сумму стоимостей всех подстрок \(s\). Примечание В первом наборе входных данных есть единственная подстрока «)». Её стоимость \(1\), потому что мы можем вставить «(» в начало этой подстроки и получить строку «()», то есть сбалансированную строку. Во втором наборе входных данных стоимость каждой подстроки длины один равна \(1\). Стоимость подстроки «)(» равна \(1\), потому что мы можем циклически сдвинуть ее вправо и получить строку «()». Стоимость строк « )()» и «()(» равна \(1\), потому что достаточно вставить по одной скобке в каждую из них. Стоимость подстроки «)()(» равна \(1\), потому что мы можем циклически сдвинуть её вправо и получить строку «()()». Таким образом, есть \(4 + 2 + 2 + 1 = 9\) подстрока стоимостью \(1\) и \(1\) подстрока из стоимостью \(0\). Таким образом, сумма стоимостей равна \(9\). В третьем наборе входных данных: - «(», стоимость равна \(1\);
- «()», стоимость равна \(0\);
- «())», стоимость равна \(1\);
- «)», стоимость равна \(1\);
- «))», стоимость равна \(2\);
- «)», стоимость равна \(1\).
Таким образом, сумма стоимостей равна \(6\). | |
![]()
|
|
F. Большинство
дп
Комбинаторика
математика
Строки
*2700
Ибти пытался придумать историю, которая придала бы смысл этой задаче. Он решил вставить грустную историю. Все были счастливы программировать, пока внезапно не случился перебой в электроснабжении, и лучший сайт спортивного программирования не вышел из строя. К счастью, системный администратор недавно купил новое оборудование, в том числе несколько ИБП. Таким образом, есть несколько серверов, которые всё ещё находятся в сети, но нам нужно, чтобы они все работали, чтобы раунд остался рейтинговым. Представьте, что серверы представляют собой бинарную строку \(s\) длины \(n\). Если \(i\)-й сервер находится онлайн, то \(s_i = 1\), иначе \(s_i = 0\). Системный администратор может выполнить следующую операцию под названием распределение электроэнергии, которая состоит из следующих этапов: - Выберите два сервера в позициях \(1 \le i < j \le n\) так, чтобы оба были подключены к сети (т. е. \(s_i=s_j=1\)). Распределение начинается только с онлайн-серверов.
- Проверьте, достаточно ли мощности для распространения. Мы считаем, что мощности достаточно, если количество включенных серверов в диапазоне \([i, j]\) не меньше количества выключенных серверов в диапазоне \([i, j]\). Более формально, проверьте, что \(2 \cdot (s_i + s_{i+1} + \ldots + s_j) \ge j - i + 1\).
- Если условие выше выполнено, включите все серверы в оффлайне в диапазоне \([i, j]\). Более формально, присвоить \(s_k := 1\) для всех \(k\) от \(i\) до \(j\).
Мы называем бинарную строку \(s\) длины \(n\) рейтинговой, если мы можем включить все серверы (т.е. сделать \(s_i = 1\) для \(1 \le i \le n\)) с помощью операции распределения электроэнергии произвольное количество раз (возможно, \(0\)). Ваша задача — найти количество рейтинговых строк длины \(n\) по модулю \(m\). Выходные данные Выведите единственное целое число — количество рейтинговых бинарных строк длины \(n\). Так как это число может быть большим, выведите его по модулю \(m\). Примечание В первом примере единственной рейтинговой строкой является 11. Таким образом, ответ \(1\). Во втором примере рейтинговыми строками являются: - 111;
- 101, потому что мы можем выполнить операцию с \(i = 1\) и \(j = 3\).
Таким образом, ответ равен \(2\). В третьем примере рейтинговые строки: Таким образом, ответ \(4\). | |
![]()
|
|
A. Ддввооииттссяя вв ггллааззаахх
Конструктив
Строки
*800
Палиндромом называется строка, которая читается одинаково слева направо и справа налево. Например, строки \(\texttt{z}\), \(\texttt{aaa}\), \(\texttt{aba}\) и \(\texttt{abccba}\) — палиндромы, а \(\texttt{codeforces}\) и \(\texttt{ab}\) — нет. Удвоением строки \(s\) называется строка, полученная записыванием каждой буквы два раза. Например, удвоение \(\texttt{seeing}\) — это \(\texttt{sseeeeiinngg}\). Вам дана строка \(s\). Переставьте буквы в ее удвоении так, чтобы получился палиндром. Выведите полученную строку. Можно показать, что это всегда можно сделать. Выходные данные Для каждого набора входных данных выведите палиндром длины \(2 \cdot |s|\), являющийся перестановкой удвоения \(s\). Примечание В первом примере удвоением \(\texttt{a}\) является \(\texttt{aa}\), что уже палиндром. Во втором примере удвоением \(\texttt{sururu}\) является \(\texttt{ssuurruurruu}\). Если передвинуть первую \(\texttt{s}\) в конец, получится \(\texttt{suurruurruus}\), что палиндром. В третьем примере удвоением \(\texttt{errorgorn}\) является \(\texttt{eerrrroorrggoorrnn}\). Можно переупорядочить буквы так, чтобы получился \(\texttt{rgnororerrerorongr}\), что является палиндромом. | |
![]()
|
|
A. Ддввооииттссяя вв ггллааззаахх
Конструктив
Строки
*800
Палиндромом называется строка, которая читается одинаково слева направо и справа налево. Например, строки \(\texttt{z}\), \(\texttt{aaa}\), \(\texttt{aba}\) и \(\texttt{abccba}\) — палиндромы, а \(\texttt{codeforces}\) и \(\texttt{ab}\) — нет. Удвоением строки \(s\) называется строка, полученная записыванием каждой буквы два раза. Например, удвоение \(\texttt{seeing}\) — это \(\texttt{sseeeeiinngg}\). Вам дана строка \(s\). Переставьте буквы в ее удвоении так, чтобы получился палиндром. Выведите полученную строку. Можно показать, что это всегда можно сделать. Выходные данные Для каждого набора входных данных выведите палиндром длины \(2 \cdot |s|\), являющийся перестановкой удвоения \(s\). Примечание В первом примере удвоением \(\texttt{a}\) является \(\texttt{aa}\), что уже палиндром. Во втором примере удвоением \(\texttt{sururu}\) является \(\texttt{ssuurruurruu}\). Если передвинуть первую \(\texttt{s}\) в конец, получится \(\texttt{suurruurruus}\), что палиндром. В третьем примере удвоением \(\texttt{errorgorn}\) является \(\texttt{eerrrroorrggoorrnn}\). Можно переупорядочить буквы так, чтобы получился \(\texttt{rgnororerrerorongr}\), что является палиндромом. | |
![]()
|
|
A. Да-да?
реализация
Строки
*800
Вы разговаривали с Поликарпом и задали ему вопрос. Вы знаете, что когда он хочет ответить «да», он повторяет Yes много раз подряд. Из-за шума вы услышали только часть ответа — некоторую его подстроку. То есть, если он ответил YesYes, то вы могли услышать esY, YesYes, sYes, e, но не могли Yess, YES или se. Определите, правда ли, что заданная строка \(s\) является подстрокой YesYesYes... (Yes, повторенного много раз подряд). Выходные данные Выведите \(t\) строк, каждая из которых является ответом на соответствующий набор входных данных. В качестве ответа выведите «YES», если заданная строка \(s\) является подстрокой строки YesYesYes...Yes (кол-во слов Yes произвольное), и «NO» в противном случае. Вы можете выводить ответ в любом регистре (например, строки «yEs», «yes», «Yes» и «YES» будут распознаны как положительный ответ). | |
![]()
|
|
B. Любимая задача Atilla
жадные алгоритмы
реализация
Строки
*800
Для того чтобы написать строку, Atilla должен сначала выучить все буквы, которые содержатся в строке. Он хочет написать сообщение \(s\). Он просит вас узнать минимальный размер алфавита, который ему предстоит выучить, чтобы он смог написать эту всю эту строку. Алфавит размером \(x\) (\(1 \leq x \leq 26\)) содержит только первые \(x\) латинских букв. Например, алфавит размера \(4\) содержит только символы \(\texttt{a}\), \(\texttt{b}\), \(\texttt{c}\) и \(\texttt{d}\). Выходные данные Для каждого набора выведите одно целое число — минимальный размер алфавита, необходимого для того, чтобы Atilla смог написать строку \(s\). Примечание Для первого набора нужен только символ \(\texttt{a}\), поэтому достаточно алфавита размером \(1\), который содержит только \(\texttt{a}\). Для второго набора нужны символы \(\texttt{d}\), \(\texttt{o}\), \(\texttt{w}\), \(\texttt{n}\). Минимальный размер алфавита, который содержит их все, равен \(23\) (такой алфавит можно представить в виде строки \(\texttt{abcdefghijklmnopqrstuvw}\)). | |
![]()
|
|
G1. Строки Фибоначчи
Строки
*2400
Строки Фибоначчи определяются следующим образом: - f1 = «a»
- f2 = «b»
- fn = fn - 1 fn - 2, n > 2
Таким образом, первые пять строк Фибоначчи: «a», «b», «ba», «bab», «babba». Вам дана строка Фибоначчи и m строк si. Для каждой строки si найдите, сколько раз она встречается в данной строке Фибоначчи в качестве подстроки. Выходные данные Для каждой строки si выведите, сколько раз она встречается в заданной строке Фибоначчи в качестве подстроки. Так как числа могут оказаться достаточно большими, выводите их остатки от деления на 1000000007 (109 + 7). Ответы для строк выводите в том порядке, в котором строки записаны во входных данных. | |
![]()
|
|
D. Хоссам и дерево (под-)палиндромов
Деревья
дп
Перебор
поиск в глубину и подобное
Строки
Структуры данных
*2100
У Хоссама есть невзвешенное дерево \(G\), в вершинах которого записаны буквы. Через \(s(v, \, u)\) Хоссам обозначает строку, которая получается при написании всех букв на единственном простом пути из вершины \(v\) в вершину \(u\) в дереве \(G\). Строка \(a\) является подпоследовательностью строки \(s\), если \(a\) может быть получена из \(s\) путем удаления нескольких символов (возможно, ни одного). Например, «dores», «cf» и «for» являются подпоследовательностями «codeforces», а «decor» и «fork» не являются. Палиндромом называется строка, читающаяся одинаково слева направо и справа налево. Например, «abacaba» — палиндром, а «abac» — нет. Под-палиндромом строки \(s\) Хоссам называет подпоследовательность \(s\), являющуюся палиндромом. Например, «k», «abba» и «abhba» являются под-палиндромом строки «abhbka», а «abka» и «cat» — нет. Максимальным под-палиндромом строки \(s\) Хоссам называет под-палиндром \(s\), имеющий максимальную длину среди всех под-палиндромов \(s\). Например, у строки «abhbka» есть только один максимальный под-палиндром — «abhba». Но может быть и так, что у строки несколько максимальных под-палиндромов: у строки «abcd» целых \(4\) максимальных под-палиндрома. Хоссам просит вас найти длину самого длинного максимального под-палиндрома среди всех \(s(v, \, u)\) в заданном дереве \(G\). Еще раз обращаем Ваше внимание на то, что под-палиндром — это подпоследовательность, а не подстрока. Выходные данные Для каждого набора входных данных выведите одно число — длину самого длинного максимального под-палиндрома среди всех \(s(v, \, u)\). Примечание В первом примере искомым подпалиндромом может быть «aaa», символы которого расположены в вершинах \(1, \, 3, \, 5\) или «aca», символы которого расположены в вершинах \(1, \, 4, \, 5\).  Дерево из первого примера. Дерево из первого примера. Во втором примере единственным искомым палиндромом является «bacab», символы которого расположены в вершинах \(4, \, 2, \, 1, \, 5, \, 9\).  Дерево из второго примера. Дерево из второго примера. | |
![]()
|
|
F. Хоссам и минимум на отрезке
Бинарный поиск
битмаски
Деревья
Строки
Структуры данных
Теория вероятностей
хэши
*2500
Хоссам дал вам последовательность целых чисел \(a_1, \, a_2, \, \dots, \, a_n\) длины \(n\). Кроме того, он последовательно дает вам \(q\) запросов вида \((l, \, r)\). Для каждого запроса он хочет знать среди чисел \(a_l, \, a_{l + 1}, \, \dots, \, a_r\) такое минимальное число, что оно встречается в заданном отрезке последовательности нечетное количество раз. Вы должны посчитать ответ на каждый запрос, прежде чем отвечать на следующий. Выходные данные Для каждого запроса выведите минимальное число, которое встречается на заданном отрезке последовательности нечетное количество раз. Если такого числа не существует, выведите \(0\). Примечание В данном примере \(\)l_1 = 1, \, r_1 = 2,\(\) \(\)l_2 = 1, \, r_2 = 3,\(\) \(\)l_3 = 2, \, r_3 = 4,\(\) \(\)l_4 = 1, \, r_4 = 4,\(\) \(\)l_5 = 2, \, r_5 = 2,\(\) \(\)l_6 = 1, \, r_6 = 5.\(\) | |
![]()
|
|
G. Another Wine Tasting Event
Комбинаторика
Конструктив
математика
Строки
*2100
After the first successful edition, Gabriella has been asked to organize a second wine tasting event. There will be \(2n - 1\) bottles of wine arranged in a row, each of which is either red wine or white wine. This time, Gabriella has already chosen the type and order of all the bottles. The types of the wines are represented by a string \(s\) of length \(2n - 1\). For each \(1 \le i \le 2n - 1\), it holds that \(s_i = \texttt{R}\) if the \(i\)-th bottle is red wine, and \(s_i = \texttt{W}\) if the \(i\)-th bottle is white wine. Exactly \(n\) critics have been invited to attend. The critics are numbered from \(1\) to \(n\). Just like last year, each critic \(j\) wants to taste an interval of wines, that is, the bottles at positions \(a_j, \, a_j + 1, \, \dots, \, b_j\) for some \(1 \le a_j \le b_j \le 2n - 1\). Moreover, they have the following additional requirements: - each of them wants to taste at least \(n\) wines, that is, it must hold that \(b_j - a_j + 1 \ge n\);
- no two critics must taste exactly the same wines, that is, if \(j \ne k\) it must hold that \(a_j \ne a_k\) or \(b_j \ne b_k\).
Gabriella knows that, since the event is held in a coastal region of Italy, critics are especially interested in the white wines, and don't care much about the red ones. (Indeed, white wine is perfect to accompany seafood.) Thus, to ensure fairness, she would like that all critics taste the same number of white wines. Help Gabriella find an integer \(x\) (with \(0 \le x \le 2n - 1\)) such that there exists a valid assignment of intervals to critics where each critic tastes exactly \(x\) white wines. It can be proved that at least one such \(x\) always exists. Output Print an integer \(x\) — the number of white wines that each critic will taste. It can be proved that at least one solution exists. If multiple solutions exist, any of them will be accepted. Note In the first sample, there are \(5\) critics and \(2 \cdot 5 - 1 = 9\) bottles of wine. A possible set of intervals that makes each critic taste \(2\) white wines is the following: \([2, 6],\) \([1, 6],\) \([4, 8],\) \([1, 5],\) \([3, 7]\). Note that all intervals contain at least \(5\) bottles. In the second sample, there is \(1\) critic and \(2 \cdot 1 - 1 = 1\) bottle of wine. The only possible interval is \([1, 1]\), which gives \(x = 0\). | |
![]()
|
|
F. Немота массива
битмаски
Деревья
разделяй и властвуй
Строки
Структуры данных
*2400
Дан массив \(a\), состоящий из \(n\) неотрицательных целых чисел. Немотой подмассива \(a_l, a_{l+1}, \ldots, a_r\) (для произвольных \(l \leq r\)) назовем величину \(\)\max(a_l, a_{l+1}, \ldots, a_r) \oplus (a_l \oplus a_{l+1} \oplus \ldots \oplus a_r),\(\) где \(\oplus\) обозначает операцию побитового исключающего ИЛИ. Найдите максимальную немоту среди всех подмассивов. Выходные данные Для каждого набора входных данных выведите одно число — максимальную немоту среди всех подмассивов данного массива. Примечание В первом наборе входных данных рассмотрим подмассив \([3, 4, 5]\). В нем максимальное значение равно \(5\). Значит, его немота равна \(3 \oplus 4 \oplus 5 \oplus 5\) = \(7\). Это максимально возможное значение немоты по всем подмассивам. Во втором наборе входных данных подмассив \([47, 52]\) обеспечивает наибольшее значение немоты. | |
![]()
|
|
C. Гибкая строка
битмаски
Перебор
Строки
*1600
У вас есть строка \(a\) и строка \(b\). Обе строки имеют длину \(n\). В строке \(a\) содержится не более \(10\) различных символов. У вас также есть множество \(Q\). Изначально множество \(Q\) пусто. Вы можете применить следующую операцию к строке \(a\) любое количество раз: - Выберите индекс \(i\) (\(1\leq i \leq n\)) и строчный латинскую букву \(c\). Добавьте \(a_i\) в множество \(Q\) и замените \(a_i\) на \(c\).
Например, пусть строка \(a\) — это «\(\tt{abecca}\)». Мы можем выполнить следующие операции: - В первой операции, если выбрать \(i = 3\) и \(c = \tt{x}\), символ \(a_3 = \tt{e}\) будет добавлен к множеству \(Q\). Таким образом, множество \(Q\) будет равняться \(\{\tt{e}\}\), а строка \(a\) станет «\(\tt{ab\underline{x}cca}\)».
- Во второй операции, если выбрать \(i = 6\) и \(c = \tt{s}\), то символ \(a_6 = \tt{a}\) будет добавлен к множеству \(Q\). Таким образом, множество \(Q\) будет равняться \(\{\tt{e}, \tt{a}\}\), а строка \(a\) будет «\(\tt{abxcc\underline{s}}\)».
Со строкой \(a\) можно выполнить любое количество операций, но в конце множество \(Q\) должно содержать не более \(k\) различных символов. Учитывая это ограничение, вам нужно максимизировать количество пар целых чисел \((l, r)\) (\(1\leq l\leq r \leq n\)) таких, что \(a[l,r] = b[l,r]\). Здесь \(s[l,r]\) означает подстроку строки \(s\), начинающуюся с индекса \(l\) (включительно) и заканчивающуюся индексом \(r\) (включительно). Выходные данные Для каждого набора входных данных выведите в строке одно целое число — максимальное количество пар \((l, r)\), удовлетворяющих ограничениям. Примечание В первом наборе входных данных мы можем выбрать индекс \(i = 3\) и заменить его символом \(c = \tt{d}\). Все возможные пары \((l,r)\) будут удовлетворять условию. Во втором наборе мы не можем выполнить ни одну операцию. \(3\) удовлетворяющие условию пары \((l,r)\): - \(a[1,1] = b[1,1] =\) «\(\tt{a}\)»,
- \(a[1,2] = b[1,2] =\) «\(\tt{ab}\)»,
- \(a[2,2] = b[2,2] =\) «\(\tt{b}\)».
В третьем наборе мы можем выбрать индекс \(2\) и индекс \(3\) и заменить их символами \(\tt{c}\) и \(\tt{d}\) соответственно. Множество \(Q\) в конце будет равняться \(\{\tt{b}\}\) (размер равен \(1\), не превышает \(k\)). Все возможные пары \((l,r)\) будут подходить под условие. | |
![]()
|
|
A. Зал славы
жадные алгоритмы
Конструктив
Строки
*800
Талия — легендарный гроссмейстер в шахматах. У нее есть \(n\) кубков, расположеных в ряд, кубки пронумерованы от \(1\) до \(n\) (слева направо), и по одной лампе рядом с каждым из кубков (лампы пронумерованы так же, как и кубки). Каждая лампа направлена либо налево, либо направо; лампа освещает все кубки в заданном направлении (но не освещает кубок, рядом с которым стоит). Формально, у Талии есть строка \(s\) из символов «L» и «R», описывающая направления ламп. Лампа номер \(i\) освещает: - кубки \(1,2,\ldots, i-1\), если \(s_i\) это «L»;
- кубки \(i+1,i+2,\ldots, n\), если \(s_i\) это «R».
Талия может выполнить следующую операцию не более одного раза: - Выбрать индекс \(i\) (\(1 \leq i < n\));
- Поменять местами лампы \(i\) и \(i+1\) (не меняя их направление). Другими словами, поменять \(s_i\) и \(s_{i+1}\).
Талия попросила вас осветить все кубки (то есть сделать так, чтобы каждый кубок был освещен хотя бы одной лампой), или сообщить, что это невозможно сделать. Если это можно сделать, вы можете выполнить одну операцию или ничего не делать. Обратите внимание, что нельзя менять направления освещения ламп, можно только поменять местами соседние лампы. Выходные данные Для каждого набора входных данных выведите \(-1\), если невозможно осветить все кубки, выполнив одну операцию или ничего не делая. Иначе выведите \(0\), если операцию выполнять не надо (т. е. все кубки освещены при изначальном положении ламп), или индекс \(i\) (\(1 \leq i < n\)), если нужно поменять местами лампы \(i\) и \(i+1\). Если существует несколько решений, выведите любое из них. Примечание В первом примере можно поменять местами лампы \(1\) и \(2\) или ничего не делать. В любом случае мы получим строку «LL». Не все кубки будут освещены, так как кубок \(2\) не освещен ни одной лампой: лампа \(1\) ничего не освещает, а лампа \(2\) освещает только кубок \(1\). Во втором примере необходимо поменять местами лампы \(1\) и \(2\). Строка станет равной «RL«. Кубок \(1\) освещен лампой \(2\), а кубок \(2\) освещен лампой \(1\), поэтому можно подсветить все кубки. В третьем примере все кубки изначально освещены, поэтому не выполнять операцию является корректным решением. В последних двух примерах не обязательно менять местами лампы, так как все кубки изначально освещены. Однако представленные решения тоже верные. | |
![]()
|
|
C. Равные частоты
жадные алгоритмы
Конструктив
Перебор
реализация
сортировки
Строки
*1600
Назовём строку сбалансированной, если все символы, которые в ней присутствуют, входят в неё одинаковое число раз. Например, «coder», «appall» и «ttttttt» — сбалансированные строки, а «wowwow» и «codeforces» — нет. Вам дана строка \(s\) длины \(n\), состоящая из строчных латинских букв. Найдите сбалансированную строку \(t\) той же длины \(n\), состоящую из строчных латинских букв и отличающуюся от строки \(s\) в как можно меньшем числе позиций. Другими словами, число индексов \(i\) таких, что \(s_i \ne t_i\), должно быть минимальным возможным. Выходные данные Для каждого набора входных данных выведите наименьшее число позиций, в которых строка \(s\) и сбалансированная строка \(t\) могут отличаться, и далее выведите саму такую строку \(t\). Если существует несколько решений, выведите любое из них. Можно показать, что хотя бы одна сбалансированная строка всегда существует. Примечание В первом наборе входных данных заданная строка «hello» не является сбалансированной: буквы «h», «e» и «o» встречаются в ней по одному разу, а буква «l» — два раза. С другой стороны, строка «helno» сбалансирована: в ней присутствуют пять разных букв, и каждая из них встречается ровно один раз. Строки «hello» и «helno» отличаются всего в одной позиции — в четвёртом символе. Возможны и другие решения. Во втором наборе входных данных строка «codefofced» сбалансирована, так как в ней присутствуют только буквы «c», «o», «d», «e» и «f», и каждая из них встречается ровно два раза. В третьем наборе входных данных строка «eeeee» сбалансирована, так как в ней присутствует только буква «e». В четвёртом наборе входных данных заданная строка «appall» уже сбалансирована. | |
![]()
|
|
B. Serval и Инверсионная магия
Перебор
реализация
Строки
*800
У Serval есть бинарная строка \(s\), которая может состоять только из символов 0 и 1, длины \(n\). \(i\)-й символ \(s\) обозначается как \(s_i\), где \(1\leq i\leq n\). Serval может применять следующую операцию, названную Инверсионной магией, к строке \(s\): - Выбрать отрезок \([l, r]\) (\(1\leq l\leq r\leq n\)). Для \(l\leq i\leq r\), заменить \(s_i\) на 1, если \(s_i\) является 0, и заменить \(s_i\) на 0, если \(s_i\) является 1.
Например, пусть \(s\) равна 010100 и выбран отрезок \([2,5]\). Строка \(s\) будет равна 001010 после применения Инверсионной магии. Serval хочет сделать \(s\) палиндромом после применения Инверсионной магии ровно один раз. Помогите ему определить, возможно ли это. Строка является палиндромом тогда и только тогда, когда она одинаково читается слева направо и справа налево. Например, 010010 является палиндромом, но 10111 не является. Выходные данные Для каждого набора входых данных выведите Yes, если \(s\) может стать палиндромом, после применения Инверсионной магии один раз, и No, если нет. Вы можете вывести Yes и No в любом регистре (например, строки yEs, yes, Yes и YES будут распознаны как положительный ответ). Примечание В первом наборе входных данных Serval может применить Инверсионную магию на отрезке \([1,4]\). Строка \(s\) станет равной 0110 после магии. Во втором наборе входных данных Serval может применить Инверсионную магию на отрезке \([1,3]\). Строка \(s\) станет равной 01110 после магии. В третьем наборе входных данных Serval не может сделать \(s\) палиндромом после применения Инверсионной магии ровно один раз. | |
![]()
|
|
F. Serval и Brain Power
битмаски
дп
жадные алгоритмы
Перебор
реализация
Строки
*2700
Serval любит Brain Power и свою интеллектуальную задачу. Serval называет строку \(T\) мощной тогда и только тогда, когда \(T\) можно получить конкатенацией некоторой строки \(T'\) несколько раз. Формально говоря, \(T\) является мощной тогда и только тогда, когда существует строка \(T'\) и целое число \(k\geq 2\) такие, что \(\)T=\underbrace{T'+T'+\dots+T'}_{k\text{ раз}}\(\) Например, gogogo является мощной, потому что её можно получить конкатенацией go три раза, но power не является мощной. У Serval есть строка \(S\), состоящая из строчных латинских букв. Ему любопытно узнать о самой длинной мощной подпоследовательности \(S\), и ему достаточно, чтобы вы узнали её длину. Если все непустые подпоследовательности \(S\) не являются мощными, ответ считается равным \(0\). Строка \(a\) является подпоследовательностью строки \(b\), если \(a\) может быть получена из \(b\) удалением нескольких (возможно, ни одного или всех) символов. Выходные данные Выведите единственное целое число — длину самой длинной мощной подпоследовательности \(S\). Если все непустые подпоследовательности \(S\) не являются мощными, выведите \(0\). Примечание В первом примере все непустые подпоследовательности buaa перечислены ниже: - b
- u
- a (встречается дважды, buaa и buaa)
- bu
- ba (встречается дважды, buaa и buaa)
- ua (встречается дважды, buaa и buaa)
- aa
- bua (встречается дважды, buaa и buaa )
- baa
- uaa
- buaa
Так как aa \(=\) a \(+\) a, aa является мощной подпоследовательностью. Можно доказать, что aa является единственной мощной подпоследовательностью среди них. Поэтому ответ равен \(2\). Во втором примере самой длинной мощной подпоследовательностью является codcod из codeforcesround. Поэтому ответ равен \(6\). | |
![]()
|
|
A. Поликарп и День числа Пи
математика
реализация
Строки
*800
14 марта во всем мире отмечается день числа \(\pi\). Это очень важная математическая константа, равная отношению длины окружности к её диаметру. Поликарпу рассказали в школе, что число \(\pi\) иррациональное, следовательно, имеет бесконечное число цифр в десятичной записи. Он захотел подготовиться ко Дню числа \(\pi\), запомнив это число как можно точнее. Поликарп выписал все цифры, которые ему удалось запомнить. Например, если Поликарп запомнил \(\pi\) как \(3.1415\), он выписал 31415. Поликарп очень торопился и мог ошибиться, поэтому вы решили проверить, сколько первых цифр числа \(\pi\) Поликарп помнит правильно на самом деле. Выходные данные Выведите \(t\) чисел, каждое из которых является ответом на соответствующий набор входных данных. В качестве ответа выведите, сколько первых цифр числа \(\pi\) Поликарп помнит правильно. | |
![]()
|
|
A. Проверка Codeforces
реализация
Строки
*800
Дана строчная буква из латинского алфавита, проверьте, встречается ли она в строке \(\texttt{codeforces}\). Выходные данные Для каждого набора входных данных выведите «YES» (без кавычек), если \(c\) удовлетворяет условию, иначе выведите «NO» (без кавычек). Вы можете выводить строки в любом регистре (например, строки «yEs», «yes», «Yes» и «YES» будут распознаны как положительный ответ). | |
![]()
|
|
D. Непересекающееся разделение
жадные алгоритмы
Перебор
Строки
*1000
Обозначим за \(f(x)\) функцию от строки \(x\), равную числу различных символов, содержащихся в строке. Например, \(f(\texttt{abc}) = 3\), \(f(\texttt{bbbbb}) = 1\), а \(f(\texttt{babacaba}) = 3\). Дана строка \(s\), разделите её на две непустых строки \(a\) и \(b\) таких, что \(f(a) + f(b)\) максимально возможно. Другими словами, найдите наибольшее возможное значение \(f(a) + f(b)\) такое, что \(a + b = s\) (конкатенация строк \(a\) и \(b\) равна строке \(s\)). Выходные данные Для каждого набора входных данных выведите единственное целое число — максимально возможное значение \(f(a) + f(b)\) такое, что \(a + b = s\). Примечание В первом наборе входных данных существует только один корректный способ разделить \(\texttt{aa}\) на две непустых строки: \(\texttt{a}\) и \(\texttt{a}\). \(f(\texttt{a}) + f(\texttt{a}) = 1 + 1 = 2\). Во втором наборе, разделив \(\texttt{abcabcd}\) на \(\texttt{abc}\) и \(\texttt{abcd}\) мы можем получить наибольший возможный ответ \(f(\texttt{abc}) + f(\texttt{abcd}) = 3 + 4 = 7\) В третьем наборе не важно как мы разделим строку, ответ будет равен \(2\) при любом разделении. | |
![]()
|
|
A. Массив префиксов и суффиксов
Строки
*800
Маркос очень любит строки, поэтому у него есть любимая строка \(s\), состоящая из строчных латинских букв. Для этой строки он записал все ее непустые префиксы и суффиксы (кроме \(s\)) на листе бумаги в произвольном порядке. Вы увидели все эти строки и задумались, является ли любимая строка Маркоса палиндромом или нет? Ваша задача — выяснить, является ли \(s\) палиндромом. Строка \(a\) является префиксом строки \(b\), если \(a\) получается из \(b\) удалением нескольких (возможно, нуля или всех) символов с конца. Строка \(a\) является суффиксом строки \(b\), если \(a\) получается из \(b\) удалением нескольких (возможно, нуля или всех) символов с начала. Палиндром — это строка, которая читается одинаково как в прямом, так и в обратном направлении, например строки «gg», «ioi», «abba», «icpci» являются палиндромами, а строки «codeforces», «abcd», «alt» — нет. Выходные данные Для каждого набора входных данных выведите «YES», если \(s\) является палиндромом, и «NO» в противном случае. Вы можете выводить каждую букву в любом регистре (строчную или заглавную). Например, строки «yEs», «yes», «Yes» и «YES» будут приняты как положительный ответ. Примечание В первом наборе входных данных \(s\) равна «abcd». Ее префиксы «a», «ab» и «abc», а ее суффиксы «d», «cd» и «bcd». Поскольку строка «abcd» не является палиндромом, ответ будет «NO». Во втором наборе входных данных \(s\) равна «ioi». Ее префиксы «i» и «io», а ее суффиксы «i» и «oi». Поскольку строка «ioi» является палиндромом, ответ будет «YES». В третьем наборе входных данных \(s\) равна «gg», что является палиндромом. В четвертом наборе входных данных \(s\) равна «alt», что не является палиндромом. | |
![]()
|
|
A. Две башни
Перебор
реализация
Строки
*800
Даны две башни, состоящие из кубиков двух цветов: красные и синие. Обе башни описываются строками, состоящими из символов B и/или R, задающими порядок кубиков в них снизу вверх, где B соответствует синему кубику, а R соответствует красному кубику.  Эти две башни задаются строками BRBB и RBR. Эти две башни задаются строками BRBB и RBR. Можно выполнять следующую операцию произвольное количество раз: выбрать башню с хотя бы двумя кубиками и переместить ее верхний кубик на вершину другой башни.   Пара башен называется красивой, если все пары соседних кубиков различных цветов; т. е. никакой красный кубик не лежит на другом красном кубике и никакой синий кубик не лежит на другом синем кубике. Ваша задача — проверить, можно ли совершить несколько (возможно, ноль) операций так, чтобы пара башен стала красивой. Выходные данные На каждый набор входных данных выведите YES, если возможно совершить несколько (возможно, ноль) операций так, чтобы пара башен стала красивой; иначе выведите NO. Каждую букву можно выводить в любом регистре (YES, yes, Yes будут распознаны как положительный ответ, NO, no и nO будут распознаны как отрицательный ответ). Примечание В первом наборе входных данных можно переместить верхний кубик с первой башни на вторую башню (смотрите третью картинку). Во втором наборе входных данных можно переместить верхний кубик со второй башни на первую башню \(6\) раз. В третьем наборе входных данных пара башен уже красивая. | |
![]()
|
|
A. Типичная задача с интервью
Перебор
реализация
Строки
*800
FB-строка формируется следующим образом. Изначально она пустая. Рассмотрим все положительные целые числа, начиная с \(1\), в возрастающем порядке, и для каждого из них сделаем следующее: - если текущее число делится на \(3\), допишем F в конец FB-строки;
- если текущее число делится на \(5\), допишем B в конец FB-строки.
Обратите внимание, что если число делится и на \(3\), и на \(5\), мы сначала приписываем F, потом B, не в обратном порядке. Первые \(10\) символов FB-строки — это FBFFBFFBFB: первый символ F соответствует числу \(3\), следующий за ним символ (B) соответствует числу \(5\), следующий F соответствует числу \(6\), и так далее. Легко заметить, что эта строка бесконечна. Обозначим за \(f_i\) \(i\)-й символ FB-строки; например, \(f_1\) — это F, \(f_2\) — это B, \(f_3\) —- это F, \(f_4\) — это F, и так далее. Нам дана строка \(s\), состоящая из символов F и/или B. Вы должны определить, является ли она подстрокой (непрерывной подпоследовательностью) FB-строки. Другими словами, проверьте, можно ли выбрать два целых числа \(l\) и \(r\) (\(1 \le l \le r\)) так, чтобы строка \(f_l f_{l+1} f_{l+2} \dots f_r\) была в точности равна \(s\). Например: - FFB — подстрока FB-строки: можно выбрать \(l = 3\) и \(r = 5\), строка \(f_3 f_4 f_5\) — это в точности FFB;
- BFFBFFBF — подстрока FB-строки: можно выбрать \(l = 2\) и \(r = 9\), строка \(f_2 f_3 f_4 \dots f_9\)— это в точности BFFBFFBF;
- BBB — не подстрока FB-строки.
Выходные данные Для каждого набора входных данных выведите YES, если \(s\) — подстрока FB-строки, или NO, если это не так. Каждую букву можно выводить в любом регистре (например, YES, yes, Yes будут распознаны как положительный ответ, NO, no и nO будут распознаны как отрицательный ответ). | |
![]()
|
|
B. Хитрый шаблон
реализация
Строки
*1000
Заданы две строки \(a\) и \(b\), состоящие из строчных латинских букв. Шаблон \(t\) — это строка, состоящая из строчных латинских букв и звездочек (символ '*'). Шаблон называется хитрым, если количество звездочек в нем меньше или равно количеству букв в нем. Говорят, что строка \(s\) подходит под шаблон \(t\), если можно заменить каждую звездочку в \(t\) на строку из строчных лантинских букв (возможно, пустую) так, чтобы он стал равен \(s\). Найдите такой хитрый шаблон, что и \(a\), и \(b\) подходят под него или скажите, что такого шаблона не существует. Если существуют несколько ответов, то выведите любой из них. Выходные данные На каждый набор входных данных выведите «NO», если не существует хитрого шаблона, под который подходят и \(a\), и \(b\). Иначе в первой строке выведите «YES», а во второй строке выведите шаблон. Если существуют несколько ответов, то выведите любой из них. Шаблон должен состоять только из строчных латинских букв и звездочек (символ '*'). Количество звездочек должно быть меньше или равно количеству букв. Примечание В первом наборе входных данных в шаблоне «*b» можно заменить единственную звездочку на «aaa» и получить «aaab» (что равно \(a\)) или на «zzz» и получить «zzzb» (что равно \(b\)). В третьем наборе входных данных шаблон «*o*» не хитрый, так как в нем больше звездочек, чем букв. Не существует хитрых шаблонов, под которые подходят и \(a\), и \(b\). В четвертом наборе входных данных в шаблоне «a*a*a*a» можно заменить все звездочки на пустые строки и получить «aaaa» (что равно \(a\)) или два из них на «a» и два на пустые строки и получить «aaaaaa» (что равно \(b\)). В пятом наборе входных данных в шаблоне «abcd» нет звездочек, поэтому только «abcd» может подходить под него (что по счастливой случайности равно и \(a\), и \(b\)). | |
![]()
|
|
C. Двойной лексикографический минимум
жадные алгоритмы
Строки
*1700
Вам дана строка \(s\). Вы можете поменять порядок символов и получить строку \(t\). Определим \(t_{\mathrm{max}}\) как лексикографический максимум строки \(t\) и перевернутой строки \(t\). По данной строке \(s\) определите лексикографически минимальное значение \(t_{\mathrm{max}}\) по всем перестановкам \(t\) строки \(s\). Строка \(a\) лексикографически меньше строки \(b\) тогда и только тогда, когда одно из двух условий выполнено: - \(a\) является префиксом \(b\), но \(a \ne b\);
- в первой позиции, в которой \(a\) и \(b\) отличаются, в строке \(a\) стоит символ, который встречается в алфавите раньше, чем соответствующий символ в строке \(b\).
Выходные данные Для каждого набора входных данных выведите лексикографически минимальное значение строки \(t_{\mathrm{max}}\) по всем перестановкам \(t\) строки \(s\). Примечание В первом наборе входных данных есть одна перестановка символов строки \(s\), это «a». Во втором наборе входных данных есть три возможных перестановки символов \(s\): - \(t = \mathtt{aab}\): \(t_{\mathrm{max}} = \max(\mathtt{aab}, \mathtt{baa}) = \mathtt{baa}\)
- \(t = \mathtt{aba}\): \(t_{\mathrm{max}} = \max(\mathtt{aba}, \mathtt{aba}) = \mathtt{aba}\)
- \(t = \mathtt{baa}\): \(t_{\mathrm{max}} = \max(\mathtt{baa}, \mathtt{aab}) = \mathtt{baa}\)
Лексикографически минимальное значение \(t_{\mathrm{max}}\) по всем случаям это «aba». | |
![]()
|
|
D. Имя
жадные алгоритмы
Строки
*1900
В далеком созвездии Тау Кита все стало для нас непонятно. В частности, таукитяне очень хитро выбирают имена своим детям. Молодые родители abac и bbad думают как назвать своего первенца. Решено, что имя будет перестановкой букв строки s. Чтобы не отставать от соседей, они решили назвать ребеночка так, чтобы имя оказалось лексикографически строго больше имени t соседского сына. С другой стороны, они подозревают о скором введении налога на имена. В соответствии с ним таукитяне с лексикографически большими именами будут платить большие суммы. По этой причине abac и bbad хотят назвать первенца так, чтобы имя было лексикографически строго больше имени t и при этом лексикографически наименьшим. Лексикографический порядок строк — это привычный нам порядок «как в словаре». Такое сравнение используется во всех современных языках программирования для сравнения строк. Формально, строка p длины n лексикографически меньше строки q длины m, если верно одно из двух утверждений: - n < m, а p является началом (префиксом) строки q (например, «aba» меньше строки «abaa»),
- p1 = q1, p2 = q2, ..., pk - 1 = qk - 1, pk < qk для некоторого k (1 ≤ k ≤ min(n, m)), здесь символы в строках нумеруются от 1.
Напишите программу, которая по заданной строке s и имени соседского ребенка t определяет такую строку, которая получается перестановкой букв s, лексикографически строго больше t и при этом лексикографически как можно меньше. Выходные данные Выведите искомое имя или -1, если такового не существует. Примечание В первом примере данная строка s является искомой, следовательно, порядок букв в ней менять не надо. | |
![]()
|
|
A. Это кошка?
реализация
Строки
*800
Вы шли по улице и услышали некоторый звук. Звук описывается строкой \(s\), состоящей из строчных и заглавных латинских символов. Теперь вы хотите понять, являлся ли этот звук мяуканьем кошки. Звук является мяуканьем, если описывающая его строка состоит только из символов 'm', 'e', 'o', 'w', записанных в любом регистре. При этом: - строка должна начинаться с последовательности, состоящей только из символов 'm' или 'M';
- сразу за ней должна следовать последовательность, состоящая только из символов 'e' или 'E';
- сразу за ней должна следовать последовательность, состоящая только из символов 'o' или 'O';
- сразу за ней должна следовать последовательность, состоящая только из символов 'w' и 'W', эта последовательность завершает строку, после этой последовательности сразу наступает конец строки.
Например, строки «meow», «mMmmEeOWwW», «MeOooOw» описывают мяуканье, а строки «Mweo», «MeO», «moew», «MmEW», «meowmeow» — нет. Определите, услышали вы мяуканье кошки или какой-то другой звук? Выходные данные Для каждого набора входных данных в отдельной строке выведите: - YES, если звук является мяуканьем кошки;
- NO в противном случае.
Вы можете выводить YES и NO в любом регистре (например, строки yEs, yes, Yes и YES будут распознаны как положительный ответ). Примечание В первом наборе входных данных строка состоит из последовательно идущих символов 'm', 'e', 'O', 'w', что удовлетворяет определению мяуканья. Во втором наборе входных данных строка состоит из последовательности из \(3\)-х символов 'm' и 'M', одного символа 'e', последовательности из \(3\)-х символов 'o' и 'O' и последовательности из \(7\)-ми символов 'w' и 'W', что удовлетворяет определению мяуканья. В третьем наборе строка не описывает мяуканье, так как в ней отсутствует последовательность из символов 'o' или 'O' между символами 'e' и 'w'. В четвертом наборе входных данных в строке присутствует символ 'U', поэтому она не описывает мяуканье. | |
![]()
|
|
B. Посчитай количество пар
жадные алгоритмы
Строки
*1000
У Кристины есть строка \(s\) длины \(n\), состоящая только из строчных и заглавных латинских букв. За каждую пару из строчной буквы и соответствующей ей заглавной Кристина может получить \(1\) бурль. При этом, пары из символов не могут пересекаться, то есть каждый символ может быть только в одной паре. Например, если у нее есть строка \(s\) = «aAaaBACacbE», то она может получить бурль за следующие пары символов: - \(s_1\) = «a» и \(s_2\) = «A»
- \(s_4\) = «a» и \(s_6\) = «A»
- \(s_5\) = «B» и \(s_{10}\) = «b»
- \(s_7\)= «C» и \(s_9\) = «c»
Кристина хочет получить больше бурлей за свою строку, поэтому она собирается совершить над ней не более \(k\) операций. За одну операцию она может: - либо выбрать строчный символ \(s_i\) (\(1 \le i \le n\)) и сделать его заглавным.
- либо выбрать заглавный символ \(s_i\) (\(1 \le i \le n\)) и сделать его строчным.
Например, при \(k\) = 2 и \(s\) = «aAaaBACacbE» она может совершить одну операцию: выбрать \(s_3\) = «a» и сделать его заглавным. Тогда она получит еще одну пару из \(s_3\) = «A» и \(s_8\) = «a». Найдите максимальное количество бурлей, которое Кристина может получить за свою строку. Выходные данные Для каждого набора входных данных на отдельной строке выведите ровно одно целое число: максимальное количество бурлей, которое Кристина может получить за строку \(s\). Примечание Первый набор входных данных разобран в условии. Во втором наборе входных данных невозможно получить ни одну пару выполнив любое количество операций. | |
![]()
|
|
D. Удали два символа
жадные алгоритмы
Строки
Структуры данных
хэши
*1200
У Дмитрия есть строка \(s\), состоящая из строчных латинских букв. Дмитрий решил удалить два подряд идущих символа из строки \(s\) и вам интересно, какое количество различных строк может получиться после такой операции. Например, у Дмитрия есть строка «aaabcc». Вы можете получить следующие различные строки: «abcc»(при удалении первых двух или второго и третьего символов), «aacc»(при удалении третьего и четвёртого символов),«aaac»(при удалении четвертого и пятого символов) и «aaab»(при удалении последних двух). Выходные данные Для каждого набора входных данных выведите одно целое число — количество различных строк, которые можно получить, удалив две подряд идущие буквы. Примечание Первый пример разобран в условии. В третьем примере получатся следующие строки: «cdef», «adef», «abef», «abcf», «abcd». В седьмом примере при любом удалении получится строка «aba». | |
![]()
|
|
E1. Непростительное заклятие (простая версия)
графы
жадные алгоритмы
Конструктив
Перебор
снм
Строки
*1400
Это простая версия задачи. В этой версии \(k\) всегда равно \(3\). Верховный чародей Визенгамота однажды поймал злого волшебника Drahyrt, но злой волшебник вернулся и хочет отомстить верховному чародею. Поэтому он украл у его ученика Гарри заклинание \(s\). Заклинание — это строка длины \(n\), состоящая из строчных латинских букв. Drahyrt хочет заменить заклинание на непростительное заклятие — строку \(t\). Drahyrt с помощью древней магии может менять местами буквы на расстоянии \(k\) или \(k+1\) в заклинании сколько угодно раз. В этой версии задачи можно менять буквы на расстоянии \(3\) или \(4\). Другими словами, Drahyrt может поменять буквы на позициях \(i\) и \(j\) в заклинании \(s\) если \(|i-j|=3\) или \(|i-j|=4\). Например, если \(s = \) «talant» и \(t = \) «atltna», то Drahyrt может действовать следующим образом: - поменять местами буквы на позициях \(1\) и \(4\), получив заклинание «aaltnt».
- поменять местами буквы на позициях \(2\) и \(6\), получив заклинание «atltna».
Вам даны заклинания \(s\) и \(t\). Может ли Drahyrt изменить заклинание \(s\) на \(t\)? Выходные данные Для каждого набора входных данных выведите в отдельной строке «YES» если Drahyrt может изменить заклинание \(s\) на \(t\) и «NO» иначе. Вы можете выводить ответ в любом регистре (например, строки «yEs», «yes», «Yes» и «YES» будут распознаны как положительный ответ). Примечание Первый пример разобран в условии. Во втором примере можно действовать следующим образом: - Поменять местами буквы на позициях \(2\) и \(5\) (расстояние \(3\)), тогда получим заклинание «aaacbba».
- Поменять местами буквы на позициях \(4\) и \(7\) (расстояние \(3\)), тогда получим заклинание «aaaabbc».
Во третьем примере можно показать, что из строки \(s\) невозможно получить строку \(t\) меняя местами буквы на расстоянии \(3\) или \(4\). В четвертом примере подходит например следующая последовательность преобразований: - «accio» \(\rightarrow\) «aocic» \(\rightarrow\) «cocia» \(\rightarrow\) «iocca» \(\rightarrow\) «aocci» \(\rightarrow\) «aicco» \(\rightarrow\) «cicao».
В пятом примере можно показать, что невозможно получить из строки \(s\) строку \(t\). В шестом примере достаточно поменять местами две крайние буквы. | |
![]()
|
|
E2. Непростительное заклятие (сложная версия)
графы
жадные алгоритмы
Конструктив
Перебор
поиск в глубину и подобное
снм
Строки
*1500
Это сложная версия задачи. В этой версии нет дополнительных ограничений на число \(k\). Верховный чародей Визенгамота однажды поймал злого волшебника Drahyrt, но злой волшебник вернулся и хочет отомстить верховному чародею. Поэтому он украл у его ученика Гарри заклинание \(s\). Заклинание — это строка длины \(n\), состоящая из строчных латинских букв. Drahyrt хочет заменить заклинание на непростительное заклятие — строку \(t\). Drahyrt с помощью древней магии может менять местами буквы на расстоянии \(k\) или \(k+1\) в заклинании сколько угодно раз. Другими словами, Drahyrt может поменять буквы на позициях \(i\) и \(j\) в заклинании \(s\) если \(|i-j|=k\) или \(|i-j|=k+1\). Например, если \(k = 3, s = \) «talant» и \(t = \) «atltna», то Drahyrt может действовать следующим образом: - поменять местами буквы на позициях \(1\) и \(4\), получив заклинание «aaltnt».
- поменять местами буквы на позициях \(2\) и \(6\), получив заклинание «atltna».
Вам даны заклинания \(s\) и \(t\). Может ли Drahyrt изменить заклинание \(s\) на \(t\)? Выходные данные Для каждого набора входных данных выведите в отдельной строке «YES» если Drahyrt может изменить заклинание \(s\) на \(t\) и «NO» иначе. Вы можете выводить ответ в любом регистре (например, строки «yEs», «yes», «Yes» и «YES» будут распознаны как положительный ответ). Примечание Первый пример разобран в условии. Во втором примере можно менять соседние буквы местами, так что можем отсортировать строку например с помощью сортировки пузырьком. Во третьем примере можно показать, что из строки \(s\) невозможно получить строку \(t\) меняя местами буквы на расстоянии \(6\) или \(7\). В четвертом примере подходит например следующая последовательность преобразований: - «accio» \(\rightarrow\) «aocic» \(\rightarrow\) «cocia» \(\rightarrow\) «iocca» \(\rightarrow\) «aocci» \(\rightarrow\) «aicco» \(\rightarrow\) «cicao».
В пятом примере можно показать, что невозможно получить из строки \(s\) строку \(t\). В шестом примере достаточно поменять местами две крайние буквы. | |
![]()
|
|
F. Даша и кошмары
meet-in-the-middle
битмаски
Строки
хэши
*1900
Отличница Даша учится в лучшем математическом лицее страны. Недавно таинственный незнакомец принёс в лицей \(n\) слов из маленьких латинских букв \(s_1, s_2, \ldots, s_n\). С того дня Дашу начали мучить кошмары. Рассмотрим некоторую пару целых чисел \(\langle i, j \rangle\) (\(1 \le i \le j \le n\)). Кошмаром называется строка, для которой верно: - Она получена склеиванием \(s_{i}s_{j}\);
- Её длина нечётна;
- Количество различных букв, входящих в неё, ровно \(25\);
- Количество каждой отдельной буквы, входящей в неё, нечётно.
Например, если \(s_i=\) «abcdefg» и \(s_j=\) «ijklmnopqrstuvwxyz», пара \(\langle i, j \rangle\) образует кошмар. Даша знает, что кошмары исчезнут, если их посчитать. Кошмаров слишком много, поэтому Даше нужна ваша помощь. Посчитайте количество различных кошмаров. Кошмары считаются различными, если различны соответствующие им пары \(\langle i, j \rangle\). Пары \(\langle i_1, j_1 \rangle\) и \(\langle i_2, j_2 \rangle\) считаются различными, если \(i_1 \neq i_2\) или \(j_1 \neq j_2\). Выходные данные Выведите единственное целое число — количество различных кошмаров. Примечание В первом тесте кошмары образуются парами \(\langle 1, 3 \rangle\), \(\langle 2, 5 \rangle\), \(\langle 3, 4 \rangle\), \(\langle 6, 7 \rangle\), \(\langle 9, 10 \rangle\). | |
![]()
|
|
G. Задачечка на подстрочечки
Строки
строковые суфф. структуры
Структуры данных
*3400
Филипп очень любит задачечки на строчечки. Он уже решил все известные ему задачечки, но этого ему было мало. Поэтому Филипп решил придумать свою собственную задачечку. Для этого он взял строку \(t\) и набор из \(n\) строк \(s_1\), \(s_2\), \(s_3\), ..., \(s_n\). У Филиппа есть \(m\) запросов, в \(i\)-м из них Филипп хочет взять подстроку строки \(t\) с \(l_i\)-го по \(r_i\)-й символ, и посчитать число её подстрок, которые совпадают с какой-то строкой из набора. Более формально, Филипп хочет посчитать число пар позиций \(a\), \(b\), таких что \(l_i \le a \le b \le r_i\), и подстрока строки \(t\) с \(a\)-го по \(b\)-й символ совпадает с некоторой строкой \(s_j\) из набора. Подстрокой строки \(t\) с \(a\)-го по \(b\)-й символ называется строка, полученная из \(t\) путём удаления \(a - 1\) символа из начала и \(|t| - b\) символами из конца, где \(|t|\) обозначает длину строки \(t\). Филипп уже решил эту задачу, а сможете ли вы? Выходные данные В единственной строке выведите \(m\) целых чисел, \(i\)-е из них должно быть равно ответу на \(i\)-й запрос. Примечание В первом примере в первом запросе требуется у всей строки посчитать число подстрок, которые входят в набор. Со строкой «aba» совпадают подстроки \([1, 3]\) и \([4, 6]\). Со строкой «a» совпадают подстроки \([1, 1]\), \([3, 3]\), \([5, 5]\), \([7, 7]\). Со строкой «ac» совпадает подстрока \([3, 4]\). Всего получается, что 7 подстрок строки «abacaba» совпадают со строками из набора. Во втором запросе от исходной строки берется подстрока с 1 по 3 позицию, это строка «aba». В неё строка «aba» входит 1 раз, строка «a» входит 2 раза и строка «ac» не входит ни одного раза как подстрока. В третьем запросе от исходной строки берется подстрока с 2 по 7 позицию, это строка «bacaba». В неё строка «aba» входит 1 раз, строка «a» входит 3 раза и строка «ac» входит 1 раз как подстрока. | |
![]()
|
|
B. У строки есть цель
жадные алгоритмы
Строки
*800
Дана строка \(s\). Можно ровно один раз применить к строке такую операцию: выбрать индекс \(i\) и переставить символ \(s_i\) в начало строки (удалив его на старой позиции). Например, если к строке «abaacd» применить операцию с индексом \(i=4\) в нумерации с \(1\), то получится строка «aabacd». Какую лексикографически минимальную\(^{\dagger}\) строку можно получить одной такой операцией? \(^{\dagger}\)Строка \(a\) лексикографически меньше строки \(b\) такой же длины, если и только если выполняется следующее: - в первой позиции, где \(a\) и \(b\) различны, в строке \(a\) находится буква, которая встречается в алфавите раньше, чем соответствующая буква в \(b\).
Выходные данные Для каждого набора входных данных в отдельной строке выведите лексикографически минимальную строку, которую можно получить после применения одной операции из условия к исходной строке ровно один раз. Примечание В первом наборе нужно переместить последний символ в начало. Во втором наборе входных данных нужно перенести в начало вторую букву «a». В третьем наборе нужно применить операцию с \(i=1\), тогда строка не изменится. | |
![]()
|
|
C. Найти и заменить
жадные алгоритмы
реализация
Строки
*800
Вам дана строка \(s\), состоящая из строчных латинских букв. За одну операцию можно выбрать символ и заменить все вхождения этого символа на \(\texttt{0}\), или заменить все вхождения этого символа на \(\texttt{1}\). Можно ли выполнить некоторое количество ходов так, чтобы в результате получилась чередующаяся бинарная строка\(^{\dagger}\)? Например, рассмотрим строку \(\texttt{abacaba}\). Вы можете сделать следующие ходы: - Заменить \(\texttt{a}\) на \(\texttt{0}\). Тогда строка будет иметь вид \(\color{red}{\texttt{0}}\texttt{b}\color{red}{\texttt{0}}\texttt{c}\color{red}{\texttt{0}}\texttt{b}\color{red}{\texttt{0}}\).
- Заменить \(\texttt{b}\) на \(\texttt{1}\). Тогда строка будет иметь вид \({\texttt{0}}\color{red}{\texttt{1}}{\texttt{0}}\texttt{c}{\texttt{0}}\color{red}{\texttt{1}}{\texttt{0}}\).
- Заменить \(\texttt{c}\) на \(\texttt{1}\). Теперь строка имеет вид \({\texttt{0}}{\texttt{1}}{\texttt{0}}\color{red}{\texttt{1}}{\texttt{0}}{\texttt{1}}{\texttt{0}}\). Это чередующаяся бинарная строка.
\(^{\dagger}\)Чередующаяся бинарная строка — это такая строка из \(\texttt{0}\) и \(\texttt{1}\), что никакие два соседних символа не равны. Например, \(\texttt{01010101}\), \(\texttt{101}\), \(\texttt{1}\) являются чередующимися бинарными строками, а \(\texttt{0110}\), \(\texttt{0a0a0}\), \(\texttt{10100}\) — нет. Выходные данные Для каждого набора входных данных выведите «YES» (без кавычек), если вы можете превратить строку в чередующуюся бинарную строку, и «NO» (без кавычек) в противном случае. Вы можете выводить каждую букву в любом регистре (строчную или заглавную). Например, строки «yEs», «yes», «Yes» и «YES» будут приняты как положительный ответ. Примечание Первый набор входных данных объясняется в условии. Во втором наборе входных данных единственными возможными бинарными строками, которые вы можете получить, являются \(\texttt{00}\) и \(\texttt{11}\). Но они обе не являются чередующимися. В третьем наборе входных данных можно получить \(\texttt{1}\), что является чередующейся бинарной строкой. | |
![]()
|
|
A. Вставь цифру
жадные алгоритмы
математика
Строки
*800
У вас есть положительное число длины \(n\) и одна дополнительная цифра. Вы можете вставить эту цифру в любое место в числе, в том числе в начало или в конец. Ваша задача — сделать результат как можно больше. Например, у вас есть число \(76543\), а дополнительная цифра равна \(4\). Тогда максимальное число, которое вы можете получить, равно \(765443\), и оно может быть получено двумя способами — вставкой цифры после \(3\)-й или после \(4\)-й цифры числа. Выходные данные Для каждого набора входных данных выведите строку, состоящую из \(n + 1\) цифры — максимально возможное число, которое можно получить. | |
![]()
|
|
J. Не-загадочный язык
*особая задача
Конструктив
Строки
Существует не-загадочный язык. Вам следует отправить свое решение на этом языке, и судья прочитает вашу работу, чтобы определить, будет ли она принята. Вы можете отправлять только на таинственном языке, который мы предоставили. Вы можете просмотреть ответ на вердикт на странице «Мои посылки». | |
![]()
|
|
E. Bosco and частица
дп
математика
Строки
теория чисел
*3100
Bosco изучает поведение частиц. Он решил исследовать особенности поведения так называемой частицы «четыре-один-два». Он поступает следующим образом: Имеется прямая длиной \(n+1\), где самая верхняя точка — позиция \(0\), а самая нижняя — позиция \(n+1\). Частица первоначально (в момент времени \(t=0\)) находится в позиции \(0\) и движется вниз. Частица движется со скоростью \(1\) единица в секунду. В позициях \(1,2,\ldots,n\) находятся \(n\) излучателей. Каждый излучатель может быть описан бинарной строкой. Начальное состояние каждого излучателя — это первый символ его бинарной строки. Когда частица сталкивается с излучателем, она меняет направление своего движения, если текущее состояние излучателя равно \(\texttt{1}\), и продолжает двигаться в том же направлении, если его текущее состояние равно \(\texttt{0}\), и этот излучатель переходит в следующее состояние (следующее состояние для последнего состояния определяется как первое состояние). Кроме того, частица всегда меняет свое направление, если она находится в положении \(0\) или \(n+1\) в момент времени \(t > 0\). Bosco хотел бы узнать длину цикла движения частицы. Длина цикла определяется как минимальное значение \(c\), такое, что для любого времени \(t \ge 0\) положение частицы в момент времени \(t\) совпадает с положением частицы в момент времени \(t+c\). Можно доказать, что такое значение \(c\) существует всегда. Поскольку он понимает, что ответ может быть слишком большим, он просит вас вывести ответ по модулю \(998244353\). Выходные данные Выведите единственное целое число — длину цикла движения частицы, взятую по модулю \(998244353\). Примечание В первом примере единственный излучатель на позиции \(1\) всегда имеет состояние \(\texttt{0}\). В моменты времени \(0,1,2,3\) позиции частицы равны \(0,1,2,1\) соответственно. Затем те же позиции будут повторяться, поэтому \(c=4\). Анимация для второго примера: здесь или более плавная анимация. | |
![]()
|
|
F. Запутанные строки
Строки
строковые суфф. структуры
*3500
Квантовое запутывание происходит, когда две частицы связываются определенным образом независимо от того, насколько далеко они находятся друг от друга в пространстве. Дана строка \(s\). Две непустые подстроки \((a, b)\) называются запутанными, если существует (возможно, пустая) связующая строка \(c\) такая, что: - Каждое вхождение \(a\) в \(s\) непосредственно следует за вхождением \(cb\);
- Каждое вхождение \(b\) в \(s\) непосредственно предшествует вхождению \(ac\).
Иными словами, \(a\) и \(b\) встречаются в \(s\) только как подстроки \(acb\). Вычислите общее количество запутанных пар подстрок строки \(s\). Строка \(a\) является подстрокой \(b\), если \(a\) может быть получена из \(b\) удалением нескольких (возможно, ни одного или всех) символов из начала и нескольких (возможно, ни одного или всех) символов из конца. Выходные данные Выведите одно целое число, количество запутанных пар подстрок строки \(s\). Примечание В первом примере единственная запутанная пара — (ab,ba). Для этой пары соответствующая связующая строка \(c\) пуста, так как они встречаются только как подстроки всей строки abba, которая не имеет никаких символов между ab и ba. Во втором примере запутанных пар нет. В третьем примере запутанные пары: (a,b), (b,c), (a,c), (a,bc) и (ab,c). Для большинства пар соответствующая связующая строка \(c\) пуста, за исключением пары (a,c), для которой связующая строка \(c\) равна b, так как a и c встречаются только как подстроки строки abc. | |
![]()
|
|
D. Общие делители
математика
Перебор
реализация
Строки
хэши
*1400
Недавно Вася узнал в школе, что такое делитель числа, и решил определить делитель строки. Вот что он придумал. Строка a является делителем строки b тогда и только тогда, когда существует целое положительное число x такое, что если строку a выписать x раз подряд получится строка b. Например, у строки «abab» два делителя — «ab» и «abab». Теперь Вася захотел написать программу, которая вычисляет количество общих делителей двух строк. Помогите ему, пожалуйста. Выходные данные Выведите количество общих делителей строк s1 и s2. Примечание В первом примере общими делителями являются строки «abcd» и «abcdabcd». В втором примере общим делителем является единственная строка «a». Строка «aa» не входит в ответ, так как не является делителем строки «aaa». | |
![]()
|
|
A. Новое имя Юры
реализация
Строки
*800
После проведения «ЛКОШПа» мальчик Юра очень устал и захотел изменить свою жизнь и переехать в Японию. В честь такой перемены Юра сменить имя на что-то милое. Загоревшись этой идеей он уже придумал себе имя \(s\), состоящее только из символов «_» и «^». Но вот незадача Юра очень любит смайлики «^_^» и «^^». Поэтому любой символ имени должен быть частью хотя бы одного такого смайлика. Обратите внимание, что смайликом могут являться только подряд идущие символы имени. Более формально, рассмотрим все вхождения строк «^_^» и «^^» в строку \(s\). Тогда все такие вхождения должны покрывать всю строку \(s\), возможно, с пересечениями. Например, в строке «^^__^_^^__^» символы на позициях \(3,4,9,10\) и \(11\) не содержатся внутри ни одного смайлика, а остальные символы на позициях \(1,2,5,6,7\) и \(8\) содержатся внутри смайликов. За одну операцию Юра может вставить один из символов «_» и «^» в своё имя \(s\) (вставлять можно на любую позицию в строке). Он просит вас сказать минимальное количество операций, которые нужно сделать, чтобы имя подходило под критерий Юры. Выходные данные Для каждого набора входных данных выведите ровно одно целое число — минимальное количество символов, которое нужно добавить в имя, чтобы оно подходило для Юры. Если ничего в имени менять не нужно, то выведите \(0\). Примечание В первом наборе входных данных можно получить следующее имя, добавив \(5\) символов: ^_^_^_^_^_^_^ В третьем наборе входных данных мы можем добавить один символ «^» в конец имени, тогда получится имя: ^_^ В четвёртом наборе входных данных мы можем добавить один символ «^» в конец имени, тогда получится имя: ^^ В пятом наборе входных данных все символы уже содержатся в смайликах, поэтому ответ равен \(0\). В седьмом наборе входных данных можно добавить один символ «^» в начало имени и один символ «^» в конец имени, тогда получится имя: ^_^ | |
![]()
|
|
B. Невероятные приключения ДжоДжо
математика
Строки
*1100
Ты думал, что тут будет легенда про ДжоДжо? Но нет, это был я, Дио! Дана бинарная строка \(s\) длины \(n\), состоящая из символов 0 и 1. Построим квадратную таблицу размера \(n \times n\), состоящую из символов 0 и 1 следующим образом. В первую строку таблицы запишем исходную строку \(s\). Во вторую строку таблицы запишем циклический сдвиг строки \(s\) на один вправо. В третью строку таблицы запишем циклический сдвиг строки \(s\) на два вправо. И так далее. Таким образом, в строке с номером \(k\) будет записан циклический сдвиг строки \(s\) на \(k\) вправо. Строки таблицы пронумерованы от \(0\) до \(n - 1\) сверху вниз. В получившейся таблице требуется найти прямоугольник, состоящий только из единиц, имеющий наибольшую площадь. Прямоугольником мы называем множество всех клеток таблицы \((i, j)\) таких, что \(x_1 \le i \le x_2\) и \(y_1 \le j \le y_2\) для некоторых целых чисел \(0 \le x_1 \le x_2 < n\) и \(0 \le y_1 \le y_2 < n\). Напомним, что циклическим сдвигом строки \(s\) на \(k\) вправо называется строка \(s_{n-k+1} \ldots s_n s_1 s_2 \ldots s_{n-k}\). Например, циклическим сдвигом строки «01011» на \(0\) вправо является сама строка «01011», её циклическим сдвигом на \(3\) вправо является строка «01101». Выходные данные Для каждого набора входных данных выведите одно целое число — максимальную площадь прямоугольника, состоящего только из единиц. Если такого прямоугольника не существует, выведите \(0\). Примечание В первом наборе входных данных получается таблица \(1 \times 1\), состоящая из единственного символа 0, таким образом нет прямоугольников, состоящих из единиц, и ответ \(0\). Во втором наборе входных данных получается таблица \(1 \times 1\), состоящая из единственного символа 1, поэтому ответ равен \(1\). В третьем наборе входных данных получается таблица: В четвёртом наборе входных данных получается таблица: | 0 | 1 | 1 | 1 | 1 | 0 | | 0 | 0 | 1 | 1 | 1 | 1 | | 1 | 0 | 0 | 1 | 1 | 1 | | 1 | 1 | 0 | 0 | 1 | 1 | | 1 | 1 | 1 | 0 | 0 | 1 | | 1 | 1 | 1 | 1 | 0 | 0 |
В пятом наборе входных данных получается таблица: | 1 | 0 | 1 | 0 | 1 | 0 | | 0 | 1 | 0 | 1 | 0 | 1 | | 1 | 0 | 1 | 0 | 1 | 0 | | 0 | 1 | 0 | 1 | 0 | 1 | | 1 | 0 | 1 | 0 | 1 | 0 | | 0 | 1 | 0 | 1 | 0 | 1 |
Прямоугольники с максимальной площадью выделены жирным шрифтом. | |
![]()
|
|
C. Разорвать на части
математика
Перебор
реализация
Строки
*1300
Дана строка \(s\), состоящая из строчных латинских букв. За одно действие вы можете выбрать несколько (одну или больше) позиций в ней так, что никакие две выбранные позиции не соседние друг другу. Затем вы удаляете все буквы на выбранных позициях из строки. Полученные части строки затем склеиваются без изменения порядка. Какое наименьшее количество действий необходимо совершить, чтобы все буквы в строке \(s\) стали одинаковые? Выходные данные На каждый набор входных данных выведите одно целое число — наименьшее количество действий, которые необходимо совершить, чтобы все буквы в строке \(s\) стали одинаковые. Примечание В первом наборе входных данных вы можете выбрать позиции \(2, 4\) и \(6\), и удалить соответствующие буквы 'b', 'c' и 'b'. В третьем примере все буквы в строке уже одинаковые, поэтому не нужно совершать никаких действий. В четвертом примере одно из возможных решений за \(2\) действия следующее. Сначала выбираете позиции \(1, 4, 6\). Строка становится «bce». Затем выбираете позиции \(1\) и \(3\). Строка становится «c». Все буквы в ней одинаковые, так как это просто одна буква. | |
![]()
|
|
E. Переставь скобки
дп
жадные алгоритмы
Перебор
сортировки
Строки
*2100
Правильная скобочная последовательность — это скобочная последовательность, которую можно превратить в корректное арифметическое выражение, вставив символы «1» и «+» между исходными символами. Например: - скобочные последовательности «()()» и «(())» — правильные (из них можно получить выражения «(1)+(1)» и «((1+1)+1)»);
- скобочные последовательности «)(», «(» и «)» — неправильные.
Дана правильная скобочная последовательность. За один ход вы можете удалить пару соседних скобок такую, что левая скобка открывающая, а правая — закрывающая. Затем склеить полученные части, не изменяя порядка. Стоимость такого хода равна количеству скобок справа от правой скобки из этой пары. Стоимость правильной скобочной последовательности равна наименьшей суммарной стоимости ходов, необходимых, чтобы сделать последовательность пустой. На самом деле, никаких скобок вы не удаляете. Вместо этого вам дана правильная скобочная последовательность и целое число \(k\). Вы можете проделать следующее действие не больше \(k\) раз: - вытащить скобку из последовательности и вставить ее в любую позицию (между двух скобок, в начало или в конец; возможно, туда же, где она и была).
После всех действий скобочная последовательность должна быть правильной. Какая наименьшая стоимость полученной правильной скобочной последовательности? Выходные данные На каждый набор входных данных выведите одно целое число — наименьшая стоимость правильной скобочной последовательности после того, как вы проделаете над ней не более \(k\) действий. | |
![]()
|
|
E. Делаем антипалиндромы
жадные алгоритмы
математика
Строки
*1600
Вам дана строка \(s\), состоящая из строчных букв латинского алфавита. За одну операцию вы можете поменять местами любые два символа в строке \(s\). Строка \(s\) длины \(n\) называется антипалиндромом, если \(s[i] \ne s[n - i + 1]\) для каждого \(i\) (\(1 \le i \le n\)). Например, строки «codeforces», «string» являются антипалиндромами, а строки «abacaba», «abc», «test» — не являются. Определите минимальное число операций, необходимое, чтобы сделать из строки \(s\) антипалиндром, или выведите \(-1\), если это невозможно. Выходные данные Для каждого набора входных данных выведите одно целое число — минимальное количество операций, необходимое, чтобы сделать из строки \(s\) антипалиндром, или \(-1\), если это невозможно. Примечание В первом примере строка «codeforces» изначально является антипалиндромом, поэтому ответом является \(0\). Во втором примере можно показать, что строку «abc» нельзя сделать антипалиндромом с помощью таких операций, поэтому ответом является \(-1\). В третьем примере в строке «taarrrataa» достаточно переставить местами второй и пятый символы, и новая строка «trararataa» будет антипалиндромом, поэтому ответом является \(1\). | |
![]()
|
|
D. Уникальные палиндромы
Конструктив
математика
Строки
*1900
Палиндром — это строка, которая читается одинаково с обеих сторон. Например, строка abcba — палиндром, а строка abca — нет. Пусть \(p(t)\) — это количество уникальных палиндромных подстрок строки \(t\), т.е. количество подстрок \(t[l \dots r]\), которые сами являются палиндромами. Даже если некоторые подстроки присутствуют в \(t\) несколько раз, они учитываются ровно один раз. (Вся строка \(t\) также является подстрокой \(t\)). Например, строка \(t\) \(=\) abcbbcabcb имеет \(p(t) = 6\) уникальных палиндромных подстрок: a, b, c, bb, bcb и cbbc. Теперь определим \(p(s, m) = p(t)\) где \(t = s[1 \dots m]\). Другими словами, \(p(s, m)\) это количество палиндромных подстрок префикса строки \(s\) длины \(m\). Например, \(p(\)abcbbcabcb\(, 5)\) \(=\) \(p(\)abcbb\() = 5\). Вам даны целое число \(n\) и \(k\) «условий» (\(k \le 20\)). Назовем строку \(s\), состоящую из \(n\) строчных латинских букв, хорошей если все \(k\) условий удовлетворены одновременно. Условие — это пара \((x_i, c_i)\), обозначающая что: - \(p(s, x_i) = c_i\), то есть префикс строки \(s\) длины \(x_i\) содержит ровно \(c_i\) уникальных палидромных подстрок.
Найдите хорошую строку \(s\) или сообщите, что такой \(s\) нет. Изучите примечание, если вам нужны дополнительные пояснения. Выходные данные Для каждого набора входных данных если нет хорошей строки \(s\) длины \(n\), которая удовлетворяет всем запросам, выведите NO. Иначе, выведите YES и строку \(s\) длины \(n\), состоящую из строчных латинских букв, которая удовлетворяет всем запросам. Если есть несколько ответов, выведите любой из них. Примечание В первом наборе строка \(s\) \(=\) abcbbcabcb удовлетворяет \(k = 2\) условиям: - \(p(s, x_1) = p(s, 5) =\) \(p(\)abcbb\() = 5 = s_1\). Палиндромные подстроки здесь: a, b, c, bb и bcb.
- \(p(s, x_2) = p(s, 10) =\) \(p(\)abcbbcabcb\() = 6 = s_2\). Палиндромные подстроки здесь те же, что выше, и дополнительно подстрока cbbc.
Во втором наборе строка foo удовлетворяет \(k = 1\) условию: - \(p(\)foo\() = 3\). Палиндромные подстроки здесь f, o и oo.
Есть другие возможные ответы. В третьем наборе строка ayda удовлетворяет \(k = 2\) условиям: - \(p(\)ayd\() = 3\). Палиндромные подстроки здесь a, y и d.
- \(p(\)ayda\() = 3\). Палиндромные подстроки здесь те же.
В четвертом наборе строка wada удовлетворяет \(k = 2\) условиям: - \(p(\)wad\() = 3\). Палиндромные подстроки здесь w, a и d.
- \(p(\)wada\() = 4\). Палиндромные подстроки здесь те же, и одна дополнительная подстрока ada.
В пятом наборе можно доказать, что нет строки длины \(4\) которая имеет \(5\) палиндромных подстрок. В шестом наборе строке abcbcacbab удовлетворяет \(k = 3\) условиям: - \(p(\)abcb\() = 4\). Палиндромные подстроки здесь a, b, c и bcb.
- \(p(\)abcbca\() = 5\). Палиндромные подстроки здесь те же, и одна дополнительная подстрока cbc.
- \(p(\)abcbcacbab\() = 8\). Палиндромные подстроки здесь те же, и три дополнительные подстроки cac, bab и bcacb.
| |
![]()
|
|
A. LuoTianyi и строка-палиндром
жадные алгоритмы
Строки
*800
LuoTianyi дала вам палиндром\(^{\dagger}\) \(s\), и она хочет, чтобы вы нашли длину самой большой непустой подпоследовательности\(^{\ddagger}\) \(s\), которая не является палиндромом. Если таких подпоследовательностей нет, выведите \(-1\). \(^{\dagger}\) Палиндромом называется строка, которая читается одинаково как слева направо, так и справа налево. Например, строки «z», «aaa», «aba», «abccba» являются палиндромами, а строки «codeforces», «reality», «ab» не являются. \(^{\ddagger}\) Строка \(a\) является подпоследовательностью строки \(b\), если \(a\) может быть получена из \(b\) удалением нескольких (возможно, ни одного или всех) символов из \(b\). Например, строки «a», «aaa», «bab» являются подпоследовательностями строки «abaab», но строки «codeforces», «bbb», «h» не являются. Выходные данные Для каждого набора входных данных выведите одно целое число — длину самой длинной непустой подпоследовательности, не являющейся строкой-палиндромом. Если такой подпоследовательности нет, выведите \(-1\). Примечание В первом наборе входных данных «abcaba» является подпоследовательностью «abacaba», так как мы можем удалить третью букву «abacaba», чтобы получить «abcaba», а «abcaba» не является строкой-палиндромом. Мы можем доказать, что «abcaba» является примером самой длинной подпоследовательности «abacaba», не являющейся палиндромом, так что ответ равен \(6\). Во втором наборе входных данных мы можем получить только «a» и «aa», но все они являются строками-палиндромами, поэтому ответ равен \(-1\). | |
![]()
|
|
C. Разбиение на палиндромы
Бинарный поиск
дп
Перебор
Строки
Структуры данных
хэши
*2600
Подстрокой называется непрерывный и непустой подотрезок букв из данной строки, без изменения порядка. Чётным палиндромом называется строка, которая читается одинаково как слева направо, так и справа налево, и имеет чётную длину. Например, строки «zz», «abba», «abccba» являются чётными палиндромами, а строки «codeforces», «reality», «aba», «c» не являются. Красивой строкой называется чётный палиндром или строка, которую можно разбить на несколько меньших чётных палиндромов. Дана строка \(s\), состоящая из \(n\) строчных латинских букв. Подсчитайте количество красивых подстрок в \(s\). Выходные данные Для каждого набора входных данных выведите количество красивых подстрок. Примечание В первом наборе входных данных красивыми подстроками являются «abaaba», «baab», «aa». В последнем наборе входных данных красивыми подстроками являются «aa» (подсчитано дважды), «abba», «bb», «bbaa», «abbaaa». | |
![]()
|
|
A. История любви
реализация
Строки
*800
Тимур любит Codeforces. Поэтому у него есть строка \(s\) длиной \(10\) символов, состоящая только из строчных латинских букв. Тимур хочет знать, на скольких позициях строка \(s\) отличается от строки «codeforces». Например, строка \(s =\) «coolforsez» отличается от «codeforces» в \(4\) позициях, выделенных жирным шрифтом. Помогите Тимуру, найдя количество позиций, на которых строка \(s\) отличается от «codeforces». Обратите внимание, что вы не можете менять порядок символов в строке \(s\). Выходные данные Для каждого набора выведите одно целое число — количество позиций, на которых строка \(s\) отличается от «codeforces». | |
![]()
|
|
A. Новый палиндром
Строки
*800
Палиндром — это строка, которая читается одинаково как слева направо, так и справа налево. Например, строки abacaba, aaaa, abba, racecar — палиндромы. Дана строка \(s\), состоящая из строчных латинских букв. Строка \(s\) является палиндромом. Ваша задача — проверить, можно ли переставить буквы в строке так, чтобы получить другой палиндром (отличный от заданной строки \(s\)). Выходные данные Для каждого набора входных данных выведите YES, если можно переставить буквы в заданной строке так, чтобы получить другой палиндром; в противном случае выведите NO. Вы можете выводить каждую букву в любом регистре (YES, yes, Yes будут распознаны как положительный ответ, NO, no и nO будут распознаны как отрицательный ответ). Примечание В первом наборе входных данных можно переставить буквы в палиндроме codedoc, чтобы получить строку ocdedco, которая отличается от заданной строки, но также является палиндромом. | |
![]()
|
|
A. Музыкальный паззл
реализация
Строки
*800
Влад решил записать мелодию на своей гитаре. Представим мелодию как последовательность нот, которым соответствуют символы 'a', 'b', 'c', 'd', 'e', 'f' и 'g'. Однако, он не очень опытен в игре на гитаре и может записать ровно две ноты за раз. Влад хочет получить мелодию \(s\) и для этого он может сводить записанные мелодии вместе. При этом, последний звук в первой мелодии должен совпадать с первым звуком второй мелодии. Например, если Влад записал мелодии «ab» и «ba», он может свести их вместе и получить мелодию «aba», а потом свести результат с «ab» и получить «abab». Помогите Владу определить, какое минимальное количество мелодий из двух нот ему нужно записать, чтобы получить мелодию \(s\). Выходные данные Выведите \(t\) целых чисел, каждое из которых является ответом на соответствующий набор входных данных. В качестве ответа выведите минимальное количество мелодий из двух нот, которое нужно записать Владу. Примечание В первом примере нужно записать мелодии «ab» и «ba», как и было описано в условии. Во втором примере нужно записать мелодии «ab», «ba», «aс» и «сa». В третьем примере единственная необходимая мелодия это «aa». | |
![]()
|
|
C. Игра с переворотом
жадные алгоритмы
игры
математика
Строки
*1200
Алиса и Боб играют в игру. У них есть две строки \(S\) и \(T\) одинаковой длины \(n\), состоящие из строчных латинских букв. Игроки ходят по очереди, первой ходит Алиса. В свой ход Алиса выбирает число \(i\) от \(1\) до \(n\), одну из строк \(S\) или \(T\), а также любую строчную латинскую букву \(c\), и заменяет \(i\)-й символ в выбранной строке на символ \(c\). Боб же в свой ход выбирает одну из строк \(S\) или \(T\), и переворачивает её. Более формально, Боб делает замену \(S := \operatorname{rev}(S)\) или \(T := \operatorname{rev}(T)\), где \(\operatorname{rev}(P) = P_n P_{n-1} \ldots P_1\). Игра длится до тех пор, пока строки \(S\) и \(T\) не равны. Как только строки становятся равны, игра моментально заканчивается. Определим длительность игры как суммарное количество ходов, сделанных обоими игроками в процессе игры. Например, если всего Алиса сделала \(2\) хода, а Боб — \(1\) ход, то длительность такой игры равна \(3\). Цель Алисы — минимизировать длительность игры, а цель Боба — максимизировать длительность игры. Чему будет равна длительность игры, при оптимальной игре обоих игроков? Можно показать, что игра завершится за конечное число ходов. Выходные данные Для каждого набора входных данных в отдельной строке выведите единственное целое число — длительность описанной игры, при оптимальной игре обоих игроков. Примечание В первом наборе входных данных Алиса в свой ход может заменить третий символ строки \(S\) на x. После чего обе строки станут равны «abxde» и игра завершится после одного хода. Так как цель Алисы закончить игру за минимальное число ходов, этот ход будет одним из оптимальных первых ходов для неё, и итоговый ответ равен \(1\). Во втором наборе входных данных Алиса в свой ход может заменить пятый символ строки \(T\) на h. После этого хода \(S =\) «hello», \(T =\) «olleh». Далее ходит Боб. В свой ход он обязан перевернуть одну из строк. Если Боб выберет строку \(S\), то после его хода обе строки будут равны «olleh», а если он выберет строку \(T\), то после его хода обе строки будут равны «hello». Таким образом, после представленного первого хода Алисы игра гарантированно завершится через \(2\) хода. Несложно показать, что стратегии, гарантирующей завершение игры менее чем за \(2\) хода, у Алисы не существует. Итоговый ответ равен \(2\). В третьем наборе входных данных Алиса в свой первый ход может заменить второй символ строки \(S\) на c. После этого хода \(S =\) «ac», \(T =\) «cd». Далее ходит Боб. Если Боб перевернёт строку \(S\), то после его хода \(S =\) «ca», \(T =\) «cd». Тогда несложно видеть, что в этом случае Алиса может гарантированно закончить игру на \(3\)-м ходу, заменив второй символ строки \(T\) на a, после чего обе строки станут равны «ca». Если же Боб перевернёт строку \(T\), то после его хода \(S =\) «ac», \(T =\) «dc». В этом случае Алиса также может гарантированно закончить игру на \(3\)-м ходу, заменив первый символ строки \(S\) на d, после чего обе строки станут равны «dc». Таким образом Алиса может гарантированно закончить игру за \(3\) хода вне зависимости от ходов Боба. Можно показать, что меньше чем за \(3\) хода, при оптимальной игре Боба, игра завершиться не может. В пятом наборе входных данных строки \(S\) и \(T\) равны, а значит игра завершится, не начавшись, за \(0\) ходов. | |
![]()
|
|
D. Прогулка по скобкам
жадные алгоритмы
Строки
Структуры данных
*2100
Дана строка \(s\) длины \(n\), состоящая из символов '(' и ')'. Вы идете по этой строке. Вы начинаете с первого символа \(s\) и хотите сделать последовательность шагов так, чтобы закончить на \(n\)-м символе. За один шаг вы можете переместиться на один символ влево (если вы стоите не на первом символе) или на один символ вправо (если вы стоите не на последнем символе). Вы не можете оставаться на одном и том же месте, однако вы можете посетить любой символ, включая первый и последний, любое количество раз. В каждый момент времени вы записываете символ, на котором вы сейчас стоите. Мы говорим, что строка проходима, если существует некоторая последовательность ходов, начинающаяся в первом символе и заканчивающаяся в последнем, такая, что записанная вами строка является правильной скобочной последовательностью. Правильная скобочная последовательность — это последовательность скобок, которая может быть преобразована в правильное арифметическое выражение путем добавления символов '1' и '+' между исходными символами последовательности. Например, последовательности скобок «()()», «(())» являются правильными ( итоговыми выражениями являются: «(1)+(1)», «((1+1)+1)»), а последовательности «)(» и «(» не являются правильными.  Один возможный корректный путь по \(s=\mathtt{(())()))}\). Красная точка указывает на ваше текущее положение, а красная строка — на записанную вами строку. Обратите внимание, что итоговая красная строка — это правильная скобочная последовательность. Один возможный корректный путь по \(s=\mathtt{(())()))}\). Красная точка указывает на ваше текущее положение, а красная строка — на записанную вами строку. Обратите внимание, что итоговая красная строка — это правильная скобочная последовательность. Вам даны \(q\) запросов. Каждый запрос меняет значение символа с '(' на ')' или наоборот. После каждого изменения определите, является ли данная строка проходимой. Запросы сохраняются, то есть эффект от каждого запроса распространяется на последующие запросы. Выходные данные Для каждого запроса выведите «YES», если строка проходима после этого запроса, и «NO» в противном случае. Вы можете выводить ответ в любом регистре (верхнем или нижнем). Например, строки «YEs», «Yes», «Yes» и «YES» будут распознаны как положительные ответы. Примечание В первом примере: - После первого запроса строка имеет вид (())()()(). Эта строка является правильной скобочной последовательностью, поэтому ее можно пройти, просто перемещаясь вправо.
- После второго запроса строка имеет вид (())()))(). Если вы сдвинетесь один раз вправо, затем влево, затем пройдете вправо до конца строки, вы получите строку (((()(())())(), которая является правильной скобочной последовательностью.
- После третьего запроса строка имеет вид ()))())())(). Мы можем показать, что эта строка не является проходимой.
Во втором примере, строки после запросов равны ()) и ()(, ни одна из которых не является проходимой. | |
![]()
|
|
A. Шифр шифер
реализация
Строки
*800
Есть строка \(a\) (она вам неизвестна), состоящая из латинских строчных букв, зашифрованная по следующему правилу в строку \(s\): - после каждого символа строки \(a\) дописывается произвольное (возможно, нулевое) количество любых латинских строчных букв, отличных от самого символа;
- после каждого такого дописывания ставится тот символ, который мы дополняли.
Вам дана строка \(s\), выведите изначальную строку \(a\). Другими словами, вам нужно расшифровать строку \(s\). Обратите внимание, что каждая зашифрованная таким образом строка расшифровывается единственным образом. Выходные данные Для каждого запроса выведите в отдельной строке строку \(a\) — расшифрованное сообщение. Примечание В первом зашифрованном сообщении буква \(a\) зашифрована в виде \(aba\), и буква \(c\) зашифрована в виде \(cabac\). Во втором зашифрованном сообщении всего одна буква \(q\) зашифрована в виде \(qzxcq\). В третьем зашифрованном сообщении к каждой букве дописано нулевое количество символов. | |
![]()
|
|
C. Мирские числа
дп
жадные алгоритмы
математика
Перебор
Строки
*1800
Мирские цифры обозначаются заглавными латинскими буквами от A до E. Кроме того, значение буквы A равно \(1\), B равно \(10\), C равно \(100\), D равно \(1000\), E равно \(10000\). Мирское число — это последовательность мирских цифр. Значение мирского числа вычисляется следующим образом: суммируются значения всех цифр, но некоторые цифры берутся со знаком минус; цифра берется со знаком минус, если справа от нее есть цифра со значением строго больше (не обязательно сразу после нее); в противном случае цифра берется со знаком плюс. Например, значение мирского числа DAAABDCA равно \(1000 - 1 - 1 - 1 - 10 + 1000 + 100 + 1 = 2088\). Вам дано мирское число. Вы можете изменить не более одной цифры в нем. Вычислите максимально возможное значение полученного числа. Выходные данные Для каждого набора входных данных выведите одно целое число — максимально возможное значение числа, если вы можете изменить в нем не более одной цифры. Примечание В первом примере можно получить EAAABDCA со значением \(10000-1-1-1-10+1000+100+1=11088\). Во втором примере можно получить EB со значением \(10000+10=10010\). | |
![]()
|
|
D. Построчная склейка
жадные алгоритмы
Конструктив
математика
Строки
теория чисел
*1400
Пусть дана таблица символов \(A\), которая имеет размеры \(r \times c\). Её построчной склейкой назовём строку, получаемую конкатенацией всех её строк, т. е. \(\) A_{11}A_{12} \dots A_{1c}A_{21}A_{22} \dots A_{2c} \dots A_{r1}A_{r2} \dots A_{rc}. \(\) Таблицу символов \(A\) назовём плохой, если в каких-то двух её соседних клетках (в клетках, имеющих общую сторону) записаны одинаковые символы. Вам дано целое положительное число \(n\). Рассмотрим все строки \(s\), состоящие только из маленьких латинских букв, которые при это не являются построчной склейкой никакой плохой таблицы. Найдите произвольную такую строку, в которой число различных символов минимально среди всех таких строк длины \(n\). Можно доказать, что строка, удовлетворяющая всем условиям задачи, всегда существует. Выходные данные Для каждого набора входных данных выведите строку с минимальным числом различных символов среди всех подходящих строк длины \(n\). Если существует несколько решений, выведите любое из них. Примечание В первом наборе входных данных есть \(3\) способа, как можно построчно вписать строку \(s\) в матрицу, причём все они не являются плохими: Можно доказать, что меньше чем \(3\) различными символами обойтись нельзя. Во втором наборе входных данных есть \(2\) способа, как можно построчно вписать строку \(s\) в матрицу, причём все они не являются плохими: Можно доказать, что меньше чем \(2\) различными символами обойтись нельзя. В третьем наборе входных данных есть всего \(1\) способ, как можно построчно вписать строку \(s\) в матрицу, причём он не является плохим. В четвёртом наборе входных данных есть \(4\) способа, как можно построчно вписать строку \(s\) в матрицу, причём все они не являются плохими: Можно доказать, что меньше чем \(4\) различными символами обойтись нельзя. Обратите внимание, что, например, строка « orange» не является корректным ответом, поскольку в ней \(6 > 4\) различных символов, строка же « banana» не является корректным ответом, потому что она является построчной склейкой следующей плохой таблицы: | |
![]()
|
|
C. Сильный пароль
Бинарный поиск
дп
жадные алгоритмы
Строки
*1400
Монокарп наконец-то набрался смелости зарегистрироваться на ForceCoders. Он придумал ник, но все еще думает насчет пароля. Он хочет, чтобы пароль был как можно сильнее, поэтому придумал следующие критерии: - длина пароля должна быть ровно \(m\);
- пароль должен состоять только из цифр от \(0\) до \(9\);
- пароль не должен встречаться в базе данных паролей (заданной строкой \(s\)) как подпоследовательность (не обязательно подряд идущих цифр).
Монокарп также придумал две строки длины \(m\): \(l\) и \(r\), обе состоящие только из цифр от \(0\) до \(9\). Он хочет, чтобы \(i\)-я цифра его пароля была от \(l_i\) до \(r_i\) включительно. Существует ли пароль, который подходит под все условия? Выходные данные На каждый набор входных данных выведите «YES», если существует пароль, который подходит под все условия. Иначе выведите «NO». Примечание В первом наборе входных данных Монокарп может выбрать пароль «50». Он не встречается в \(s\) как подпоследовательность. Во втором наборе все наборы из трех цифр, каждая из которых от \(1\) до \(4\), подходит под условия на \(l\) и \(r\). Однако, все они встречаются в \(s\) как подпоследовательности. Например, «314» встречается на позициях \([3, 5, 12]\), а «222» встречается на позициях \([2, 6, 10]\). В третьем наборе Монокарп может выбрать пароль «4321». На самом деле это единственный пароль, который подходит под условия на \(l\) и \(r\). К счастью, он не встречается в \(s\) как подпоследовательность. В четвертом наборе только «49» и «59» подходят под условия на \(l\) и \(r\). Оба они встречаются в \(s\) как подпоследовательности. В пятом набор Монокарп может выбрать пароль «11». | |
![]()
|
|
B. Рудольф и крестики-нолики-плюсики
Перебор
реализация
Строки
*800
Рудольф изобрел игру крестики-нолики на троих. Она имеет классические правила, не считая третьего игрока, играющего плюсиками. У Рудольфа есть поле \(3 \times 3\) — результат завершенной игры. Каждая ячейка поля содержит либо крестик, либо нолик, либо плюсик, либо ничего. В игре побеждает игрок, сделавший горизонтальный, вертикальный или диагональный ряд из \(3\)-х своих символов. Рудольф хочет узнать результат игры. Либо ровно один из трех игроков выиграл, либо игра закончилась вничью. Гарантируется, что несколько игроков не могут победить одновременно. Выходные данные Для каждого набора входных данных выведите строку «X», если победили крестики, «O», если победили нолики, «+», если победили плюсики, «DRAW», если была ничья. | |
![]()
|
|
D. Профессор Хигасиката
жадные алгоритмы
реализация
снм
Строки
Структуры данных
*1900
Джосуке устал от спокойной жизни в Мориохе. Пойдя по стопам своего племянника Дзётаро, он решает упорно учиться и стать профессором информатики. Просматривая в Интернете задачи по программированию, он наткнулся на следующую. Пусть \(s\) — бинарная строка длины \(n\). Операция над \(s\) определяется как выбор двух различных целых чисел \(i\) и \(j\) (\(1 \leq i < j \leq n\)), и обмен местами символов \(s_i, s_j\). Рассмотрим \(m\) строк \(t_1, t_2, \ldots, t_m\), где \(t_i\) — подстрока\(^\dagger\) из \(s\) от \(l_i\) до \(r_i\). Определим \(t(s) = t_1+t_2+\ldots+t_m\) как конкатенацию строк \(t_i\) в таком порядке. Существует \(q\) обновлений строки. В \(i\)-м обновлении \(s_{x_i}\) инвертируется. То есть, если \(s_{x_i}=1\), то \(s_{x_i}\) становится \(0\) и наоборот. После каждого обновления найдите минимальное количество операций, которые нужно выполнить над \(s\), чтобы сделать \(t(s)\) лексикографически как можно большим\(^\ddagger\). Обратите внимание, что на самом деле ни одна операция не применяется. Нужно найти только количество операций. Помогите Йосуке в его мечте, решив за него эту задачу. —————————————————————— \(\dagger\) Строка \(a\) является подстрокой строки \(b\), если \(a\) может быть получена из \(b\) удалением нескольких (возможно, нуля или всех) символов из начала и нескольких (возможно, нуля или всех) символов из конца. \(\ddagger\) Строка \(a\) лексикографически больше строки \(b\) такой же длины тогда и только тогда, когда выполняется следующее условие: - в первой позиции, где \(a\) и \(b\) отличаются, в строка \(a\) стоит \(1\), а в строке \(b\) стоит \(0\).
Выходные данные Выведите \(q\) целых чисел. В строке \(i\) выведите минимальное количество операций, которое необходимо выполнить над \(s\), чтобы получить лексикографически наибольшую возможную строку \(t(s)\) после \(i\)-го обновления. Примечание В первом примере: Изначально \(t(s) = s(1,2) + s(1,2) = 0101\). После \(1\)-го запроса, \(s\) становится \(11\) и, соответственно, \(t\) становится \(1111\). Никаких операций выполнять не нужно, так как \(t(s)\) уже является лексикографически наибольшей строкой из возможных. После \(2\)-го запроса \(s\) становится \(01\) и, следовательно, \(t\) становится \(0101\). Необходимо выполнить операцию \(1\), поменяв местами \(s_1\) и \(s_2\). Следовательно, \(t(s)\) становится \(1010\), что является лексикографически наибольшей строкой, которую можно получить. | |
![]()
|
|
C. Копирование бинарной строки
Бинарный поиск
Перебор
Строки
Структуры данных
хэши
*1600
Вам задана строка \(s\), состоящая из \(n\) символов 0 и/или 1. Вы делаете \(m\) копий этой строки. Пусть \(i\)-я копия — это строка \(t_i\). Затем вы выполняете ровно одну операцию над каждой из копий: в \(i\)-й копии вы сортируете подстроку \([l_i; r_i]\) (подстроку, начинающуюся с \(l_i\)-го символа и заканчивающуюся \(r_i\)-м символом, обе границы включаются). Заметьте, что каждая операция затрагивает только одну копию, и каждая копия затрагивается только одной операцией. Ваша задача — посчитать количество различных строк среди \(t_1, t_2, \ldots, t_m\). Заметьте, что изначальная строка \(s\) должна считаться только тогда, когда хотя бы одна копия остается неизменной после операции. Выходные данные Выведите одно целое число — количество различных строк среди \(t_1, t_2, \ldots, t_m\). Примечание Рассмотрим первый тестовый пример. Копии ниже представлены в порядке операций из входных данных. Сортируемые подстроки подчеркнуты: - 101100 \(\rightarrow\) 011100;
- 101100 \(\rightarrow\) 011100;
- 101100 \(\rightarrow\) 101100;
- 101100 \(\rightarrow\) 101100;
- 101100 \(\rightarrow\) 000111.
Среди \(t_1, t_2, t_3, t_4, t_5\) всего три различные строки: 000111, 011100 и 101100. Рассмотрим второй тестовый пример: - 100111 \(\rightarrow\) 100111;
- 100111 \(\rightarrow\) 001111;
- 100111 \(\rightarrow\) 001111;
- 100111 \(\rightarrow\) 010111.
Среди \(t_1, t_2, t_3, t_4\) всего три различные строки: 001111, 010111 и 100111. | |
![]()
|
|
C. Слово на бумаге
реализация
Строки
*800
На сетке из точек размером \(8 \times 8\) вертикально в одном столбце написали слово, состоящее из строчных латинских букв, сверху вниз. Что это за слово? Выходные данные Для каждого тестового случая выведите одну строку, содержащую слово, состоящее из строчных латинских букв (\(\texttt{a}\)–\(\texttt{z}\)), которое написано вертикально в одном столбце сверху вниз. | |
![]()
|
|
F. Лиза и марсиане
битмаски
Деревья
жадные алгоритмы
математика
Строки
*1800
Девочку Лизу похитили марсиане! Не беда, ведь она смотрела много телепередач про инопланетян, поэтому знает, что её ждёт. Назовём число марсианским, если оно является целым неотрицательным и строго меньше \(2^k\), например, при \(k = 12\), числа \(51\), \(1960\), \(0\) — марсианские, а числа \(\pi\), \(-1\), \(\frac{21}{8}\), \(4096\) — нет. Инопланетяне выдадут Лизе \(n\) марсианских чисел \(a_1, a_2, \ldots, a_n\). Затем они попросят её назвать любое марсианское число \(x\). После чего Лиза выберет в выданной последовательности пару чисел \(a_i, a_j\) (\(i \neq j\)) и посчитает \((a_i \oplus x) \& (a_j \oplus x)\). Операция \(\oplus\) означает Побитовое исключающее ИЛИ, операция \(\&\) означает Побитовое И. Например, \((5 \oplus 17) \& (23 \oplus 17) = (00101_2 \oplus 10001_2) \& (10111_2 \oplus 10001_2) = 10100_2 \& 00110_2 = 00100_2 = 4\). Лиза уверена, что чем больше окажется посчитанное значение, тем выше её шансы вернуться домой. Помогите девочке выбрать такие \(i, j, x\), чтобы максимизировать посчитанное значение. Выходные данные Для каждого набора входных данных выведите три целых числа \(i, j, x\) (\(1 \le i, j \le n\), \(i \neq j\), \(0 \le x < 2^k\)). Значение \((a_i \oplus x) \& (a_j \oplus x)\) должно быть максимально возможным. Если решений несколько, вы можете вывести любое. Примечание Первый набор входных данных: \((3 \oplus 14) \& (1 \oplus 14) = (0011_2 \oplus 1110_2) \& (0001_2 \oplus 1110_2) = 1101_2 = 1101_2 \& 1111_2 = 1101_2 = 13\). Второй набор входных данных: \((1 \oplus 0) \& (1 \oplus 0) = 1\). Третий набор входных данных: \((9 \oplus 4082) \& (13 \oplus 4082) = 4091\). Четвёртый набор входных данных: \((3 \oplus 7) \& (0 \oplus 7) = 4\). | |
![]()
|
|
A. Строкосравнитель
реализация
Строки
*1100
Некоторым гномам, которые заканчивают бакалавриат ГоГну (Государственный Гномий университет), сказали — «Нет генома, нет диплома». Что означало, что всем гномам надо защищать диплом на тему генома. Геном у гномов совсем не простой. Он представляет собой строку, состоящую из строчных букв латинского алфавита. Гном Миша уже выбрал тему диплома: определить по двум геномам гномов, принадлежат ли они одной и той же расе. Два гнома принадлежат одной и той же расе, если в геноме первого гнома, можно поменять два символа местами так, чтобы получился геном второго гнома. Помогите гному Мише, определите принадлежат два гнома одной расе или нет. Выходные данные Выведите «YES», если гномы принадлежат одной расе, иначе выведите «NO». Примечание - Первый пример: в строчке «ab» нужно просто поменять две буквы местами, тогда мы получим «ba».
- Второй пример: строчку «aa» нельзя перевести в строчку «ab», так как в первой строке нет символа «b».
| |
![]()
|
|
A. Не подстрока
Конструктив
Строки
*900
Скобочная последовательность — это строка из символов «(» и/или «)». Правильная скобочная последовательность — это скобочная последовательность, которую можно превратить в корректное арифметическое выражение, вставив символы «1» и «+» между исходными символами. Например: - скобочные последовательности «()()» и «(())» — правильные (из них можно получить выражения «(1)+(1)» и «((1+1)+1)», соответственно);
- скобочные последовательности «)(», ( и ) — неправильные.
Вам задана скобочная последовательность \(s\); обозначим ее длину за \(n\). Вы должны найти такую правильную скобочную последовательность \(t\) длины \(2n\), что \(s\) не входит в \(t\) как непрерывная подстрока, или сказать, что это невозможно. Выходные данные Для каждого набора входных данных выведите ответ на него. Если требуемой правильной скобочной последовательности не существует, выведите NO в отдельной строке. В противном случае выведите YES в первой строке, а во второй строке выведите требуемую правильную скобочную последовательность \(t\). Если ответов несколько — выведите любой из них. | |
![]()
|
|
C. Запросы к массиву
Деревья
поиск в глубину и подобное
реализация
Строки
Структуры данных
*1600
У Монокарпа был массив \(a\), состоящий из целых чисел. Изначально массив был пустым. Монокарп выполнял три типа запросов к этому массиву: - выбрать число и добавить его в конец массива. Каждый раз, когда Монокарп выполнял этот запрос, он выписывал символ +;
- удалить последний элемент из массива. Каждый раз, когда Монокарп выполнял этот запрос, он выписывал символ -. Монокарп не выполнял этот запрос, если массив был пуст;
- проверить, отсортирован ли массив в порядке неубывания, т. е. выполняется ли \(a_1 \le a_2 \le \dots \le a_k\), где \(k\) — количество элементов в массиве на данный момент. Любой массив, содержащий меньше \(2\) элементов, считается отсортированным. Если массив отсортирован в момент запроса, Монокарп выписывал символ 1. Иначе он выписывал символ 0.
Вам задана строка \(s\), состоящая из \(q\) символов 0, 1, + и/или -. Это символы, выписанные Монокарпом, строго в том порядке, в каком он их выписывал. Вам нужно выяснить, является ли эта строка непротиворечивой, т. е. мог ли Монокарп выполнять такие запросы, что выписанная после них строка равна строке \(s\). Выходные данные Для каждого набора входных данных выведите YES, если Монокарп мог выполнить такие запросы, в результате которых будет выписана строка \(s\). Иначе выведите NO. Вы можете выводить символы в ответе в любом регистре. Примечание В первом наборе входных данных Монокарп мог выполнить следующие запросы: - добавить число \(13\);
- добавить число \(37\);
- проверить, что массив \([13, 37]\) отсортирован в порядке неубывания (и он действительно отсортирован).
В пятом наборе входных данных Монокарп мог выполнить следующие запросы: - добавить число \(3\);
- добавить число \(2\);
- проверить, что массив \([3, 2]\) отсортирован (он не отсортирован);
- удалить последний элемент;
- добавить число \(3\);
- проверить, что массив \([3, 3]\) отсортирован (он отсортирован);
- удалить последний элемент;
- добавить число \(-5\);
- проверить, что массив \([3, -5]\) отсортирован (он не отсортирован);
В остальных наборах входных данных Монокарп не мог выписать строку \(s\), выполняя свои запросы. | |
![]()
|
|
A. Ковёр в подарок
дп
жадные алгоритмы
реализация
Строки
*800
Недавно Тёма и Вика праздновали день семьи. Их подруга Арина подарила им ковёр, который может быть представлен в виде таблицы \(n \cdot m\) из строчных латинских букв. Вика ещё не видела подарок, но Тёма знает, какие ковры она любит. Вике понравится ковёр, если она сможет прочитать на нём своё имя слева направо. Формально, ковёр понравится девушке, если можно выбрать четыре различных столбца в порядке слева направо так, что первый содержит «v», второй — «i», третий — «k» и четвёртый — «a». Помогите Тёме заранее понять, понравится ли Вике подарок Арины. Выходные данные Для каждого набора входных данных выведите «YES», если ковёр понравится Вике, в противном случае выведите «NO». Вы можете выводить каждую букву в любом регистре (строчную или заглавную). Например, строки «yEs», «yes», «Yes» и «YES» будут приняты как положительный ответ. Примечание В первом примере Вика может прочитать своё имя слева направо. Во втором примере Вика не сможет прочитать символ «v», поэтому ковёр ей не понравится. | |
![]()
|
|
B. Обмен и разворот
жадные алгоритмы
Конструктив
сортировки
Строки
*1100
Дана строка \(s\) длины \(n\), состоящая из строчных латинских букв, а также целое число \(k\). За один шаг вы можете выполнить одну любую операцию из следующих двух: - Выбрать индекс \(i\) (\(1 \le i \le n - 2\)), затем поменять местами \(s_{i}\) и \(s_{i+2}\).
- Выбрать индекс \(i\) (\(1 \le i \le n-k+1\)), затем развернуть порядок следования букв на отрезке \([i,i+k-1]\) строки. Формально, если строка в текущий момент равна \(s_1\ldots s_{i-1}s_is_{i+1}\ldots s_{i+k-2}s_{i+k-1}s_{i+k}\ldots s_{n-1}s_n\), то она заменяется на \(s_1\ldots s_{i-1}s_{i+k-1}s_{i+k-2}\ldots s_{i+1}s_is_{i+k}\ldots s_{n-1}s_n\).
Вы можете сделать произвольное (возможно, нулевое) число шагов. Найдите лексикографически наименьшую строку, которую можно получить после какого-либо числа шагов. Строка \(a\) лексикографически меньше строки \(b\) такой же длины, если выполняется следующее: - в первой позиции, где \(a\) и \(b\) различны, в строке \(a\) находится буква, которая встречается в алфавите раньше, чем соответствующая буква в \(b\).
Выходные данные Для каждого набора входных данных выведите лексикографически наименьшую строку, которую можно получить после какого-либо (возможно, нулевого) числа шагов. Примечание В первом наборе входных данных можно получить строку «aimn», выполняя следующие операции: - Развернуть отрезок \([3,4]\). Строка превратится в «niam».
- Поменять местами \(s_1\) и \(s_3\). Строка превратится в «ainm».
- Развернуть отрезок \([3,4]\). Строка превратится в «aimn».
Можно доказать, что невозможно получить строку, лексикографически меньшую, чем «aimn». Значит, «aimn» и является ответом. Во втором наборе входных данных можно получить строку «aandp», выполняя следующие операции: - Поменять местами \(s_3\) и \(s_5\). Строка превратится в «paadn».
- Поменять местами \(s_1\) и \(s_3\). Строка превратится в «aapdn».
- Поменять местами \(s_3\) и \(s_5\). Строка превратится в «aandp».
Можно доказать, что невозможно получить строку, лексикографически меньшую, чем «aandp». Значит, «aandp» и является ответом. | |
![]()
|
|
E. Угадайка
битмаски
Деревья
игры
математика
сортировки
Строки
Структуры данных
Теория вероятностей
*2100
У Кэрол есть последовательность \(s\) из \(n\) неотрицательных целых чисел. Она хочет сыграть с Алисой и Бобом в «Угадайку». Игра устроена следующим образом. Сначала Кэрол случайно выберет два целых индекса \(i_a\) и \(i_b\) из диапазона \([1, n]\) и обозначит \(a=s_{i_a}\), \(b=s_{i_b}\). Обратите внимание: \(i_a\) и \(i_b\) могут совпасть. Затем Кэрол сообщит: - значение \(a\) — Алисе;
- значение \(b\) — Бобу;
- значение \(a \mid b\) и Алису и Бобу, где \(|\) обозначает операцию побитового ИЛИ.
Обратите внимание: Кэрол не сообщит никакой информации об \(s\) ни Алисе, ни Бобу. Затем начинается процесс угадывания. Алиса и Боб ходят по очереди, причём первой ходит Алиса. Цель обоих игроков — выяснить, какое из утверждений верно: \(a < b\), \(a > b\), или \(a = b\). На своём ходу игрок может сделать одно из двух: - сказать «Я не знаю» и передать ход другому игроку;
- сказать «Я знаю», а затем сообщить ответ: «\(a<b\)», «\(a>b\)», или же «\(a=b\)»; после этого игра заканчивается.
Алиса и Боб слышат фразы друг друга и могут использовать их в своих рассуждениях. Оба игрока достаточно умны. Сказать «Я знаю» они могут только в том случае, если точно уверены в ответе. Найдите математическое ожидание числа шагов в такой игре. Выведите ответ по модулю \(998\,244\,353\). Формально, пусть \(M = 998\,244\,353\). Можно показать, что ответ может быть представлен в виде несократимой дроби \(\frac{p}{q}\), где \(p\) и \(q\) — целые числа, и \(q \not \equiv 0 \pmod{M}\). Выведите целое число, равное \(p \cdot q^{-1} \bmod M\). Другими словами, выведите такое целое число \(x\), что \(0 \le x < M\) и \(x \cdot q \equiv p \pmod{M}\). Выходные данные Для каждого набора входных данных выведите одно число — ответ на задачу по модулю \(998\,244\,353\). Примечание В первом наборе входных данных есть всего \(4\) возможные ситуации: - \(i_a=1\), \(i_b=1\), \(a=2\), \(b=2\), число шагов равно \(2\);
- \(i_a=1\), \(i_b=2\), \(a=2\), \(b=3\), число шагов равно \(3\);
- \(i_a=2\), \(i_b=1\), \(a=3\), \(b=2\), число шагов равно \(2\);
- \(i_a=2\), \(i_b=2\), \(a=3\), \(b=3\), число шагов равно \(3\).
Математическое ожидание числа шагов равно \(\frac{2+3+2+3}{4}=\frac{5}{2}=499122179\pmod{998244353}\). Рассмотрим первый случай, когда \(a=2\), \(b=2\). Процесс угадывания происходит следующим образом. На первом ходу Алиса думает так: «Я знаю, что \(a=2, a\mid b=2\). Можно сделать вывод, что \(b=0\) или \(b=2\), но какой из этих двух случаев имеет место — пока неясно». Поэтому она говорит: «Я не знаю». На втором ходу Боб думает так: «Я знаю, что \(b=2, a\mid b=2\). Можно сделать вывод, что \(a=0\) или \(a=2\). Однако если \(a=0\), то Алиса на своём ходу уже бы сказала, что \(a<b\). Но она этого не сказала. Значит, \(a=2\)». Поэтому он говорит: «Я знаю, \(a=b\)». Игра завершается. Во втором наборе входных данных, при \(a=0\), \(b=0\), Алиса сразу заключает, что \(a=b\). Ожидаемое число ходов равно \(1\). | |
![]()
|
|
B. Палиндромный XOR
битмаски
Конструктив
Строки
*1100
Вам дана бинарная строка \(s\) длины \(n\) (строка - состоящая только из \(0\) и \(1\)). Число \(x\) является хорошим, если существует такая бинарная строка \(l\) длины \(n\), содержащая \(x\) единиц, что если каждый символ \(s_i\) заменить на \(s_i \oplus l_i\) (где \(\oplus\) обозначает операцию Побитового исключающего ИЛИ) то строка \(s\) станет палиндромом. Нужно вывести бинарную строку \(t\) длины \(n+1\), где \(t_i\) (\(0 \leq i \leq n\)) равно \(1\) если число \(i\) хорошее, и \(0\) иначе. Палиндром — это строка, которая читается одинаково как слева направо, так и справа налево. Например, строки 01010, 1111, 0110 — палиндромы. Выходные данные Для каждого набора входных данных выведите одну строку \(t\) длины \(n+1\) - ответ на задачу. Примечание Рассмотрим первый пример. - \(t_2 = 1\) так как можно выбрать \(l = \) 010100 тогда строка \(s\) станет равна 111111, что является палиндромом.
- \(t_4 = 1\) так как можно выбрать \(l = \) 101011.
- Можно показать, что для всех остальных \(i\) ответа не существует, поэтому остальные символы равны \(0\).
| |
![]()
|
|
A. Не пытайтесь посчитать
Перебор
Строки
*800
Даны строка \(x\) длины \(n\) и строка \(s\) длины \(m\) (\(n \cdot m \le 25\)), состоящие из строчных латинских букв. Вы можете применить любое количество операций к строке \(x\). За одну операцию вы приписываете текущее значение строки \(x\) к концу \(x\). Обратите внимание, что значение \(x\) после этого изменится. Например, если \(x =\)«aba», то при применении операций \(x\) будет меняться следующим образом: «aba» \(\rightarrow\) «abaaba» \(\rightarrow\) «abaabaabaaba». После какого минимального количества операций \(s\) встретится в \(x\) в качестве подстроки? Подстрокой строки называется любой её непрерывный отрезок. Выходные данные Для каждого набора входных данных выведите одно число — минимальное количество операций, после которых \(s\) встретится в \(x\) в качестве подстроки. Если это невозможно, выведите \(-1\). Примечание В первом наборе входных данных примера, после \(2\) применений операции строка станет равна «aaaa», а после \(3\) «aaaaaaaa», так что ответ \(3\). Во втором наборе входных данных примера после применения \(1\) операции строка станет равна «\(\text{e}\color{red}{\text{force}}\text{forc}\)», вхождение подстроки выделено красным. В четвёртом наборе входных данных примера можно показать, что получить нужную строку как подстроку невозможно. | |
![]()
|
|
B. Химия
Строки
*900
Вам дана строка \(s\) длины \(n\), состоящая из строчных латинских букв, и число \(k\). Вам нужно проверить, можно ли из строки \(s\) удалить ровно \(k\) символов, чтобы из оставшихся символов строки можно было сделать палиндром. Обратите внимание, что вы можете переупорядочить оставшиеся символы как угодно. Палиндромом называется строка, которая читается одинаково как слева направо, так и справа налево. Например, строки «z», «aaa», «aba», «abccba» являются палиндромами, а строки «codeforces», «reality», «ab» не являются. Выходные данные Для каждого набора входных данных выведите «YES», если можно удалить из строки \(s\) ровно \(k\) символов, чтобы из оставшихся символов можно было собрать палиндром, и «NO» иначе. Вы можете вывести ответ в любом регистре (верхнем или нижнем). Например, строки «yEs», «yes», «Yes» и «YES» будут распознаны как положительные ответы. Примечание В первом наборе входных данных ничего удалять нельзя, а строка «a» является палиндромом. Во втором наборе входных данных ничего удалять нельзя, но строки «ab» и «ba» палиндромами не являются. В третьем наборе входных данных можно удалить любой символ и получившаяся строка будет палиндромом. В четвертом наборе входных данных можно удалить одно вхождение символа «a» и получится строка «bb», которая является палиндромом. В шестом наборе входных данных можно удалить по одному вхождению символов «b» и «d», получится строка «acac», которую можно переупорядочить в строку «acca». В девятом наборе входных данных можно удалить по одному вхождению символов «t» и «k» и получится строка «aagaa», которая является палиндромом. | |
![]()
|
|
C. Уменьшающаяся строка
реализация
Строки
*1600
Напомним, что строка \(a\) лексикографически меньше строки \(b\), если \(a\) является префиксом \(b\) (и \(a \ne b\)), либо существует такое \(i\) (\(1 \le i \le \min(|a|, |b|)\)), что \(a_i < b_i\), и для любого \(j\) (\(1 \le j < i\)) \(a_j = b_j\). Рассмотрим последовательность строк \(s_1, s_2, \dots, s_n\), каждая из которых состоит из строчных букв латинского алфавита. Строка \(s_1\) задана явно, все остальные строки создаются по следующему правилу: для получения строки \(s_i\) берется строка \(s_{i-1}\) и из нее удаляется символ так, чтобы строка \(s_i\) была лексикографически минимальной. Например, если \(s_1 = \mathrm{dacb}\), то строка \(s_2 = \mathrm{acb}\), строка \(s_3 = \mathrm{ab}\), строка \(s_4 = \mathrm{a}\). После этого мы получаем строку \(S = s_1 + s_2 + \dots + s_n\) (\(S\) — это конкатенация всех строк \(s_1, s_2, \dots, s_n\)). Вам нужно вывести символ, который стоит в строке \(S\) на позиции \(pos\) (то есть символ \(S_{pos}\)). Выходные данные Для каждого набора входных данных выведите ответ — символ, стоящий в строке \(S\) на позиции \(pos\). Обратите внимание, что ответы между разными наборами входных данных не разделяются ни пробелом, ни переводом строки. | |
![]()
|
|
A. Секретный спорт
реализация
Строки
*800
Рассмотрим игру, в которую играют два человека: A и B. Эта игра характеризуется двумя целыми положительными числами: \(X\) и \(Y\). Игра состоит из сетов, каждый сет состоит из розыгрышей. В каждом розыгрыше побеждает ровно один из игроков — либо A, либо B. Сет заканчивается ровно тогда, когда один из игроков набирает \(X\) побед в розыгрышах в течении этого сета. Этот игрок объявляется победителем сета. Игроки разыгрывают сеты до тех пор, пока один из них не наберёт \(Y\) побед в сетах. После этого игра заканчивается, и этот игрок объявляется победителем всей игры. Вы только что посмотрели игру, но не заметили, кого объявили победителем. Вы запомнили, что в течение игры было сыграно \(n\) розыгрышей, а также кто из игроков победил в каждом из розыгрышей. Однако, вам неизвестны значения \(X\) и \(Y\). По имеющейся информации определите, кто из игроков победил во всей игре — A или B. Если информации недостаточно, чтобы определить победителя, вы также должны сообщить об этом. Выходные данные Для каждого набора входных данных в отдельной строке выведите: - \(\texttt{A}\) — если победителем игры гарантированно является игрок A.
- \(\texttt{B}\) — если победителем игры гарантированно является игрок B.
- \(\texttt{?}\) — если невозможно однозначно определить победителя игры.
Примечание В первом наборе входных данных игра могла проходить с параметрами \(X = 3\), \(Y = 1\). Игра состояла из \(1\) сета, в котором победил игрок A, так как он первым выиграл \(3\) розыгрыша. При таком сценарии победителем является игрок A. Также игра могла проходить с параметрами \(X = 1\), \(Y = 3\). Можно показать, что не существует таких \(X\) и \(Y\), при которых победителем будет игрок B. Во втором наборе входных данных все розыгрыши выиграл игрок B. Несложно показать, что тогда игрок B гарантированно является победителем игры. В четвёртом наборе входных данных игра могла проходить с параметрами \(X = 3\), \(Y = 3\): - В первом сете было сыграно \(3\) розыгрыша: AAA. Победителем сета считается игрок A.
- Во втором сете было сыграно \(3\) розыгрыша: AAA. Победителем сета считается игрок A.
- В третьем сете было сыграно \(5\) розыгрышей: AABBB. Победителем сета считается игрок B.
- В четвёртом сете было сыграно \(5\) розыгрышей: AABBB. Победителем сета считается игрок B.
- В пятом сете было сыграно \(4\) розыгрыша: BBAB. Победителем сета считается игрок B.
В итоге первым игроком, выигравшим \(3\) сета, был игрок B. Он и считается победителем игры. | |
![]()
|
|
B. AB-обмен
жадные алгоритмы
Строки
*900
Дана строка \(s\) длины \(n\), состоящая из символов \(\texttt{A}\) и \(\texttt{B}\). Вам разрешено выполнять следующую операцию: - Выбрать индекс \(1 \le i \le n - 1\) такой, что \(s_i = \texttt{A}\) и \(s_{i + 1} = \texttt{B}\), и поменять местами \(s_i\) и \(s_{i+1}\).
Для каждого индекса \(1 \le i \le n - 1\) вам разрешается выполнить данную операцию не более одного раза. Однако вы можете делать это в любом порядке. Найдите максимальное количество операций, которое вы можете выполнить. Выходные данные Для каждого набора входных данных выведите одно целое число — максимальное количество операций, которое можно выполнить. Примечание В первом наборе входных данных можно выполнить операцию ровно один раз для \(i=1\), так как \(s_1=\texttt{A}\) и \(s_2=\texttt{B}\). Во втором наборе входных данных можно показать, что для любого индекса выполнить операцию невозможно. В третьем наборе входных данных можно выполнить операцию с \(i=2\) и получить \(\texttt{ABAB}\). Затем еще одну операцию с \(i=3\), чтобы получить \(\texttt{ABBA}\). И, наконец, еще одну операцию с \(i=1\), чтобы получить \(\texttt{BABA}\). Заметим, что хотя в конце \(s_2 = \texttt{A}\) и \(s_3 = \texttt{B}\), мы не можем повторно выполнить операцию с \(i=2\), так как для каждого индекса операция может быть выполнена не более одного раза. | |
![]()
|
|
A. Мария и строка
Перебор
реализация
Строки
*800
У Марии есть строка \(s\) длины \(n\), состоящая из букв «A» и «B». Она хочет сделать так, чтобы строка \(s\) содержала ровно \(k\) символов «B». Для этого она может использовать следующую операцию. - Выбрать целое число \(i\) (\(1 \leq i \leq n\)) и букву \(c\) (\(c\) должна быть равна «A» или «B»).
- После этого заменить каждую из первых \(i\) букв строки \(s\) (то есть, буквы \(s_1, s_2, \ldots, s_i\)) на \(c\).
Мария просит вас найти минимальное количество операций, которое необходимо выполнить для того, чтобы строка \(s\) содержала ровно \(k\) символов «B». Также она просит вас найти сами эти операции (то есть, число \(i\) и букву \(c\) в каждой операции). Выходные данные Для каждого набора входных данных в первой строке выведите число \(m\) — минимальное количество операций, которое нужно выполнить Марии. В \(j\)-й из следующих \(m\) строк выведите число \(i\) (\(1 \le i \le n\)) и букву \(c\) (\(c\) должна быть равна «A» или «B») — параметры \(j\)-й операции. Если существует несколько решений с минимальным возможным количеством операций, вы можете вывести любое из них. Примечание В первом наборе входных данных в строке \(s\) уже \(2\) символа «B», поэтому Марии не нужно выполнять ни одной операции. Во втором наборе входных данных единственный способ добиться того, чтобы строка \(s\) содержала \(3\) символа «B» после одной операции — заменить первый символ строки \(s\) на «B»: «AABAB» \(\rightarrow\) «BABAB». В третьем наборе входных данных единственный способ добиться того, чтобы строка \(s\) содержала \(0\) символов «B» после одной операции — заменить первые \(5\) символов строки \(s\) на «A»: «BBBBB» \(\rightarrow\) «AAAAA». В четвёртом наборе входных один из способов добиться того, чтобы строка \(s\) содержала \(0\) символов «B» после одной операции — заменить первые \(2\) символа строки \(s\) на «A»: «BAA» \(\rightarrow\) «AAA». Обратите внимание, что «1 A» и «3 A» тоже являются правильными решениями в одну операцию. | |
![]()
|
|
E. София и строки
жадные алгоритмы
сортировки
Строки
Структуры данных
*2200
У Софии есть строка \(s\) длины \(n\), состоящая из строчных латинских букв. Она может выполнять следующие операции с этой строкой. - Выбрать позицию \(1 \le i \le |s|\) и удалить \(s_i\) из строки.
- Выбрать пару позиций \((l, r)\) (\(1 \le l \le r \le |s|\)) и отсортировать подстроку \(s_{l} s_{l+1} \ldots s_r\) в алфавитном порядке.
Здесь \(|s|\) обозначает текущую длину строки \(s\). В частности, \(|s| = n\) перед первой операцией. Например, если \(s = \mathtt{sofia}\), то, применив операцию первого типа с \(i=4\), мы сделаем строку \(s\) равной \(\mathtt{sofa}\). Применив после этого операцию второго типа с \((l, r) = (2, 4)\), получим строку \(s\), равную \(\mathtt{safo}\). София хочет получить строку \(t\) длины \(m\) из строки \(s\), используя операции, описанные выше, несколько раз (возможно, ноль). Определите, возможно ли это. Выходные данные Для каждого набора входных данных выведите «YES», если София может получить строку \(t\) из строки \(s\), используя операции из условия. Иначе, выведите «NO». Вы можете выводить каждую букву в любом регистре (строчную или заглавную). Например, строки «yEs», «yes», «Yes» и «YES» будут приняты как положительный ответ. Примечание В первом наборе входных данных София может сделать следующую операцию: - операция второго типа с \(l=1\) и \(r=5\): строка \(s\) станет равной \(\mathtt{afios}\) после операции.
Во втором наборе входных данных София может сделать следующие операции: - операция второго типа с \(l=1\) и \(r=2\): строка \(s\) станет равной \(\mathtt{bca}\) после операции;
- операция первого типа с \(i=3\): строка \(s\) станет равной \(\mathtt{bc}\) после операции.
В третьем наборе входных данных можно показать, что невозможно получить строку \(t\) из строки \(s\) используя операции из условия. | |
![]()
|
|
A. Заполните водой
жадные алгоритмы
Конструктив
реализация
Строки
*800
У Филиппа есть ряд клеток, некоторые из которых заблокированы, а остальные — пусты. Он хочет, чтобы во всех пустых клетках оказалась вода. Для этого он может применять 2 типа операций: - \(1\) — поместить воду в пустую клетку.
- \(2\) — переместить воду из клетки с водой в любую другую пустую клетку. Обратите внимание, что при перемещении воды из одной клетки в другую Филипп удаляет воду из начальной клетки.
Если клетка \(i\) (\(2 \le i \le n-1\)) пустая, а клетки \(i-1\) и \(i+1\) содержат воду, то она заполняется водой. Найдите минимальное количество раз, которое ему нужно выполнить операцию \(1\) типа, чтобы заполнить все пустые клетки водой. Заметим, что минимизировать использование операций \(2\) типа не нужно. Также заметим, что заблокированные клетки не содержат воду, и Филипп не может поместить в них воду. Выходные данные Для каждого набора входных данных выведите единственное число — минимальное количество операций \(1\) типа, необходимое для заполнения всех пустых клеток водой. Примечание Набор входных данных 1 В первом наборе входных данных Филипп может поместить воду в клетки \(1\) и \(3\). Поскольку клетка \(2\) находится между \(2\) клетками с водой, она тоже заполняется водой. Набор входных данных 2 Во втором наборе он может поместить источники воды в клетки \(3\) и \(5\). В результате клетка \(4\) заполнится водой. Затем он удалит воду из клетки \(5\) и поместит ее в клетку \(6\). Поскольку соседи клетки \(5\) — клетки \(4\) и \(6\) — имеют воду, клетка \(5\) также заполняется водой. Иллюстрация этого процесса приведена ниже.  Операции во втором наборе входных данных. Белые клетки — пустые, серые — заблокированные, синие — вода. Операции во втором наборе входных данных. Белые клетки — пустые, серые — заблокированные, синие — вода. Набор входных данных 3 В третьем наборе входных данных он может поместить воду во все пустые клетки. Для этого требуется \(5\) операций \(1\) типа. Набор входных данных 4 В четвертом наборе пустых клеток нет. Следовательно, ни одной операции применять не нужно. Набор входных данных 5 В пятом наборе входных данных существует последовательность операций, которая требует только \(2\) операции типа \(1\). | |
![]()
|
|
E. Коллапс строк
Деревья
Строки
Структуры данных
*1900
Заданы \(n\) строк \(s_1, s_2, \dots, s_n\), состоящие из строчных латинских букв. Пусть \(|x|\) означает длину строки \(x\). Определим операцию коллапса \(C(a, b)\) двух строк \(a\) и \(b\) следующим образом: - если \(a\) пуста, \(C(a, b) = b\);
- если \(b\) пуста, \(C(a, b) = a\);
- если последняя буква \(a\) совпадает с первой буквой \(b\), то \(C(a, b) = C(a_{1,|a|-1}, b_{2,|b|})\), где \(s_{l,r}\) — подстрока \(s\) с \(l\)-й по \(r\)-ю букву;
- в противном случае, \(C(a, b) = a + b\), то есть, конкатенация двух строк.
Вычислите \(\sum\limits_{i=1}^n \sum\limits_{j=1}^n |C(s_i, s_j)|\). Выходные данные Выведите одно целое число — \(\sum\limits_{i=1}^n \sum\limits_{j=1}^n |C(s_i, s_j)|\). | |
![]()
|
|
C. Наибольшая подпоследовательность
жадные алгоритмы
Строки
*1400
Дана строка \(s\) длины \(n\). За одну операцию можно выбрать лексикографически наибольшую\(^\dagger\) подпоследовательность строки \(s\) и циклически сдвинуть её вправо\(^\ddagger\). Ваша задача — вычислить минимальное количество операций, необходимых для того, чтобы \(s\) стала отсортированной, или сообщить, что она никогда не достигнет отсортированного состояния. \(^\dagger\)Строка \(a\) лексикографически меньше строки \(b\) тогда и только тогда, когда выполняется одно из следующих условий: - \(a\) является префиксом \(b\), но \(a \ne b\);
- В первой позиции, где \(a\) и \(b\) отличаются, строка \(a\) имеет букву, которая встречается раньше в алфавите, чем соответствующая буква в \(b\).
\(^\ddagger\)Циклическим сдвигом строки \(t_1t_2\ldots t_m\) вправо называется строка \(t_mt_1\ldots t_{m-1}\). Выходные данные Для каждого набора входных данных выведите единственное целое число — минимальное количество операций, необходимых для того, чтобы сделать \(s\) отсортированной, или \(-1\), если это невозможно. Примечание В первом наборе входных данных строка \(s\) уже отсортирована, поэтому нам не нужны операции. Во втором наборе входных данных, сделав одну операцию, мы выберем cb и циклически сдвинем её. Теперь строка \(s\) становится равной abc, которая отсортирована. В третьем наборе входных данных \(s\) не может быть отсортирована. В четвертом наборе входных данных мы сделаем следующие операции: - Лексикографически наибольшая подпоследовательность равна zca. Тогда \(s\) становится равной abzc.
- Лексикографически наибольшая подпоследовательность равна zc. Тогда \(s\) становится равной abcz. Строка становится отсортированной.
Таким образом, нам нужно \(2\) операции. | |
![]()
|
|
B. YetnotherrokenKeoard
реализация
Строки
Структуры данных
*1000
У Поликарпа беда — сломалась клавиатура на его ноутбуке. Теперь, когда он нажимает клавишу 'b', она отрабатывает подобно необычному backspace: происходит удаление последней (самой правой) строчной буквы в набранной строке. Если в набранной строке нет ни одной строчной буквы, то нажатие полностью игнорируется. Аналогично, когда он нажимает клавишу 'B', то происходит удаление последней (самой правой) прописной буквы в набранной строке. Если в набранной строке нет ни одной прописной буквы, то нажатие полностью игнорируется. В обоих случаях буквы 'b' и/или 'B' при нажатии на эти клавиши не добавляются в набранную строку. Рассмотрим пример. Пусть последовательность нажатий имела вид «ARaBbbitBaby». В этом случае набранная строка будет изменяться следующим образом: «» \(\xrightarrow{\texttt{A}}\) «A» \(\xrightarrow{\texttt{R}}\) «AR» \(\xrightarrow{\texttt{a}}\) «ARa» \(\xrightarrow{\texttt{B}}\) «Aa» \(\xrightarrow{\texttt{b}}\) «A» \(\xrightarrow{\texttt{b}}\) «A» \(\xrightarrow{\texttt{i}}\) «Ai» \(\xrightarrow{\texttt{t}}\) «Ait» \(\xrightarrow{\texttt{B}}\) «it» \(\xrightarrow{\texttt{a}}\) «ita» \(\xrightarrow{\texttt{b}}\) «it» \(\xrightarrow{\texttt{y}}\) «ity». По заданной последовательности нажатых клавиш выведите набранную строку после обработки всех нажатий. Выходные данные Для каждого набора входных данных выведите результат обработки нажатий в отдельной строке. Если набранная строка пустая, то выведите пустую строку. | |
![]()
|
|
C. Удаление некрасивых пар
жадные алгоритмы
Конструктив
математика
Строки
*1200
Влад нашёл строку \(s\) из \(n\) строчных латинских букв, и он хочет сделать её как можно короче. Для этого он может любое число раз удалять из \(s\) любые два соседних символа, если они различны. Например, если \(s\)=racoon, то удалив одну пару символов, он может получить строку coon, roon, raon и raco, но не может получить racn (потому что удалённые буквы были одинаковы) или rcon (потому что удалённые буквы не были соседними). Какой минимальной длины может добиться Влад, применив любое число удалений? Выходные данные Для каждого набора выведите единственное число — минимальную длину строки \(s\), после удаления пар соседних символов, значения которых различны. Примечание В первом наборе выходных данных примера нужно действовать следующим образом «aabc» \(\rightarrow\) «ac» \(\rightarrow\) «». Обратите внимание, что при другом порядке удалений строка не станет пустой. | |
![]()
|
|
G. Лемма о накачке
Строки
хэши
*3000
Вам даны две строки \(s\), \(t\) длины \(n\), \(m\), соответственно. Обе строки состоят из строчных букв латинского алфавита. Подсчитайте тройки \((x, y, z)\) строк, для которых справедливы следующие условия: - \(s = x+y+z\) (символ \(+\) обозначает конкатенацию);
- \(t = x+\underbrace{ y+\dots+y }_{k \text{ раз}} + z\) для некоторого целого числа \(k\).
Выходные данные Выведите одно целое число: количество допустимых троек \((x, y, z)\). Примечание В первом наборе входных данных единственной подходящей тройкой является \((x, y, z) = (\texttt{"a"}, \texttt{"bc"}, \texttt{"d"})\). Действительно, - \(\texttt{"abcd"} = \texttt{"a"} + \texttt{"bc"} + \texttt{"d"}\);
- \(\texttt{"abcbcbcd"} = \texttt{"a"} + \texttt{"bc"} + \texttt{"bc"} + \texttt{"bc"} + \texttt{"d"}\).
Во втором наборе входных данных существует \(5\) подходящих троек: - \((x, y, z) = (\texttt{""}, \texttt{"a"}, \texttt{"aa"})\);
- \((x, y, z) = (\texttt{""}, \texttt{"aa"}, \texttt{"a"})\);
- \((x, y, z) = (\texttt{"a"}, \texttt{"a"}, \texttt{"a"})\);
- \((x, y, z) = (\texttt{"a"}, \texttt{"aa"}, \texttt{""})\);
- \((x, y, z) = (\texttt{"aa"}, \texttt{"a"}, \texttt{""})\).
В третьем наборе входных данных существует \(8\) подходящих троек: - \((x, y, z) = (\texttt{"ab"}, \texttt{"ba"}, \texttt{"babacaab"})\);
- \((x, y, z) = (\texttt{"abb"}, \texttt{"ab"}, \texttt{"abacaab"})\);
- \((x, y, z) = (\texttt{"abba"}, \texttt{"ba"}, \texttt{"bacaab"})\);
- \((x, y, z) = (\texttt{"ab"}, \texttt{"baba"}, \texttt{"bacaab"})\);
- \((x, y, z) = (\texttt{"abbab"}, \texttt{"ab"}, \texttt{"acaab"})\);
- \((x, y, z) = (\texttt{"abb"}, \texttt{"abab"}, \texttt{"acaab"})\);
- \((x, y, z) = (\texttt{"abbaba"}, \texttt{"ba"}, \texttt{"caab"})\);
- \((x, y, z) = (\texttt{"abba"}, \texttt{"baba"}, \texttt{"caab"})\).
| |
![]()
|
|
B. Обмен и удаление
Строки
*1000
Вам задана бинарная строка \(s\) (строка, состоящая только из символов 0 и/или 1). Вы можете выполнять операции двух типов над \(s\): - удалить один символ из \(s\). Эта операция стоит \(1\) монету;
- поменять местами любую пару символов в \(s\). Эта операция бесплатна (стоит \(0\) монет).
Вы можете выполнять эти операции в любом порядке любое количество раз. Давайте обозначим строку, которую вы получили после выполнения вышеуказанных операций, как \(t\). Строка \(t\) является хорошей, если для каждого \(i\) от \(1\) до \(|t|\) \(t_i \neq s_i\) (\(|t|\) — длина строки \(t\)). Пустая строка — всегда хорошая. Обратите внимание, что вы сравниваете результирующую строку \(t\) с исходной строкой \(s\). Какова минимальная суммарная стоимость сделать строку \(t\) хорошей? Выходные данные Для каждого набора входных данных выведите минимальную суммарную стоимость сделать строку \(t\) хорошей. Примечание В первом наборе вам нужно удалить символ из \(s\), чтобы получить пустую строку \(t\). Только после этого \(t\) станет хорошей. Одно удаление стоит \(1\). Во втором тесте вы, например, можете удалить второй символ из \(s\), чтобы получить строку 01, а затем поменять местами первый и второй символы, чтобы получить строку \(t\) \(=\) 10. Строка \(t\) — хорошая, так как \(t_1 \neq s_1\) и \(t_2 \neq s_2\). Общая стоимость составляет \(1\). В третьем тесте вы, например, можете поменять местами \(s_1\) с \(s_2\), \(s_3\) с \(s_4\), \(s_5\) с \(s_7\), \(s_6\) с \(s_8\) и \(s_9\) с \(s_{10}\). Вы получите строку \(t\) \(=\) 1010001110. Все операции обмена бесплатны, поэтому общая стоимость составляет \(0\). | |
![]()
|
|
F. Палиндромы и изменения
Бинарный поиск
Строки
строковые суфф. структуры
Структуры данных
хэши
*2800
Вам дана строка \(s\) длины \(n\), состоящая из строчных латинских букв. Вам разрешено заменить не более одного символа строки на произвольную строчную латинскую букву. Выведите лексикографически минимальную строку, которая получается из исходной и содержит максимальное количество палиндромов в качестве подстрок. Если какой-то палиндром входит как подстрока несколько раз, он учитывается столько же раз, сколько встречается в строке. Строка \(a\) лексикографически меньше строки \(b\), если и только если выполняется один из следующих пунктов: - \(a\) — префикс \(b\), но \(a \ne b\);
- в первой позиции, где \(a\) и \(b\) различаются, в строке \(a\) находится буква, которая встречается в алфавите раньше, чем соответствующая буква в \(b\).
Выходные данные В первой строке выведите одно целое число — максимальное количество подстрок-палиндромов, которое может быть у строки, которую можно получить, применив операцию не более одного раза. Во второй строке выведите строку, которую можно получить из \(s\) и которая содержит максимальное количество подстрок-палиндромов. Если таких строк несколько, выведите лексикографически минимальную. | |
![]()
|
|
A. Журнал решения задач
реализация
Строки
*800
Монокарп участвует в соревновании по программированию, в котором \(26\) задач, обозначенных от 'A' до 'Z'. Задачи отсортированы по сложности. Более того, известно, что Монокарп может решить задачу 'A', потратив на нее \(1\) минуту, задачу 'B', потратив на нее \(2\) минуты, ..., задачу 'Z', потратив на нее \(26\) минут. После соревнования вы нашли его журнал соревнования — строку, состоящую из заглавных латинских букв, такую, что \(i\)-я буква означает, какую задачу Монокарп решал в \(i\)-ю минуту соревнования. Если Монокарп потратил суммарно достаточно времени на решение задачи, он ее решил. Обратите внимание, что Монокарп мог думать о задаче после ее решения. По журналу соревнования Монокарпа, вычислите количество задач, которые он решил во время соревнования. Выходные данные На каждый набор входных данных выведите одно целое число — количество задач, которые Монокарп решил во время соревнования. | |
![]()
|
|
D. Нестандартная обработка языка
жадные алгоритмы
реализация
Строки
*900
Лура скучала и решила создать простой язык, используя пять букв \(\texttt{a}\), \(\texttt{b}\), \(\texttt{c}\), \(\texttt{d}\), \(\texttt{e}\). Существуют два типа букв: - гласные — буквы \(\texttt{a}\) и \(\texttt{e}\). Они обозначаются как \(\textsf{V}\).
- согласные — буквы \(\texttt{b}\), \(\texttt{c}\), \(\texttt{d}\). Они обозначаются как \(\textsf{C}\).
В языке существуют два типа слогов: \(\textsf{CV}\) (согласная, за которой следует гласная) или \(\textsf{CVC}\) (гласная с согласной до и после). Например, \(\texttt{ba}\), \(\texttt{ced}\), \(\texttt{bab}\) являются слогами, но \(\texttt{aa}\), \(\texttt{eda}\), \(\texttt{baba}\) — нет. Слово в языке — это последовательность слогов. Лура написала слово на этом языке, но не знает, как разбить его на слоги. Помогите ей разбить слово на слоги. Например, для слова \(\texttt{bacedbab}\) оно будет разбито на слоги как \(\texttt{ba.ced.bab}\) (точка \(\texttt{.}\) обозначает границу слога). Выходные данные Для каждого набора входных данных выведите строку, обозначающую слово, разбитое на слоги, вставив точку \(\texttt{.}\) между каждой парой смежных слогов. Если существует несколько возможных разбиений, выведите любое из них. Ввод предоставлен таким образом, что по крайней мере одно возможное разбиение существует. | |
![]()
|
|
B. Удалить первый или второй символ
дп
Комбинаторика
Перебор
Строки
Структуры данных
*1100
Вам дана строка \(s\) длины \(n\). Определим две операции, которые можно применить к строке: - удалить первый символ строки;
- удалить второй символ строки.
Ваша задача — найти количество различных непустых строк, которые можно получить, применяя заданные операции над исходной строкой любое количество раз (возможно, нулевое), в любом порядке. Выходные данные Для каждого набора входных данных выведите одно целое число: количество различных непустых строк, которые вы можете получить. Примечание В первом наборе входных данных мы можем получить следующие строки: \(a\), \(aa\), \(aaa\), \(aaaa\), \(aaaaa\). В третьем наборе входных данных, например, слово \(ba\) можно получить следующим образом: - удалить первый символ текущей строки \(ababa\), получив \(baba\);
- удалить второй символ текущей строки \(baba\), получив \(bba\);
- удалить второй символ текущей строки \(bba\), получив \(ba\).
| |
![]()
|
|
A. Необычный шаблон
Конструктив
реализация
Строки
*800
Задано целое число \(n\) и три строки \(a, b, c\), каждая из которых состоит из \(n\) строчных латинских букв. Назовем шаблоном строку \(t\), состоящую из \(n\) строчных и/или заглавных латинских букв. Строка \(s\) подходит под шаблон \(t\), если для всех \(i\) от \(1\) до \(n\) выполняются следующие условия: - если \(i\)-я буква шаблона строчная, то буква \(s_i\) должна совпадать с \(t_i\);
- если \(i\)-я буква шаблона заглавная, то буква \(s_i\) должна отличаться от строчной версии буквы \(t_i\). Например, если в шаблоне в какой-то позиции находится символ 'A', то в этой позиции в строке не должно быть буквы 'a'.
Соответственно, строка не подходит под шаблон, если хотя бы для одного \(i\) условие не выполняется. Определите, существует ли шаблон \(t\) такой, что строки \(a\) и \(b\) подходят под него, а строка \(c\) не подходит. Выходные данные На каждый набор входных данных выведите «YES», если существует такой шаблон \(t\), под который подходят строки \(a\) и \(b\), но не подходит строка \(c\). В противном случае выведите «NO». Примечание В первом наборе входных данных можно использовать шаблон «C». У строк \(a\) и \(b\) первая буква отличается от 'c', поэтому они подходят под шаблон. У строки \(c\) первая буква совпадает с 'c', поэтому она не подходит. В третьем наборе можно использовать шаблон «CODEforces». | |
![]()
|
|
F. Shrink-Reverse
Бинарный поиск
жадные алгоритмы
Перебор
реализация
Строки
строковые суфф. структуры
хэши
*2800
Вам задана бинарная строка \(s\) длины \(n\) (строка, состоящая из \(n\) символов, и каждый символ — либо 0, либо 1). Посмотрим на строку \(s\) как на двоичное представление некоторого числа, и назовем это число значением строки \(s\). Например, значение строки 000 равно \(0\), значение 01101 равно \(13\), значение 100000 — это \(32\), и так далее. Вы можете применить не более \(k\) операций к \(s\). Каждая операция должна иметь один из следующих двух типов: - SWAP: выбрать два индекса \(i < j\) в \(s\) и поменять местами \(s_i\) и \(s_j\);
- SHRINK-REVERSE: удалить все лидирующие нули из \(s\) и перевернуть строку \(s\).
Например, после применения SHRINK-REVERSE к строке 000101100 вы получите строку 001101. Какое минимальное значение строки \(s\) вы можете получить, применив не более \(k\) операций к \(s\)? Выходные данные Выведите одно целое число — наименьшее возможное значение строки \(s\), которое вы можете получить, применив не более \(k\) операций. Так как ответ может быть слишком большим, выведите его по модулю \(10^{9} + 7\). Заметим, что вы должны минимизировать само значение, а не его остаток. Примечание В первом примере, одна из оптимальных стратегий — следующая: - 10010010 \(\xrightarrow{\texttt{SWAP}}\) 00010110;
- 00010110 \(\xrightarrow{\texttt{SWAP}}\) 00000111.
Значение строки 00000111 равно \(7\). Во втором примере, одна из оптимальных стратегий — следующая: - 01101000 \(\xrightarrow{\texttt{SHRINK}}\) 1101000 \(\xrightarrow{\texttt{REVERSE}}\) 0001011;
- 0001011 \(\xrightarrow{\texttt{SWAP}}\) 0000111.
Значение строки 0000111 равно \(7\). | |
![]()
|
|
A. Покрыли ли мы всё?
дп
жадные алгоритмы
Конструктив
кратчайшие пути
Строки
*1500
Вам дано два целых числа \(n\) и \(k\) вместе со строкой \(s\). Ваша задача состоит в том, чтобы проверить, входят ли все возможные строки длины \(n\), которые могут быть получены из первых \(k\) прописных букв латинского алфавита, как подпоследовательности в \(s\). Если ответ NO, вам необходимо также найти строку длины \(n\) из первых \(k\) прописных букв латинского алфавита такую, что она не входит как подпоследовательность в \(s\). Если существует несколько ответов — выведите любой. Примечание: Строка \(a\) называется подпоследовательностью другой строки \(b\), если \(a\) может быть получена удалением нескольких (возможно нуля) символов из \(b\) без изменения порядка оставшихся символов. Выходные данные Для каждого набора входных данных выведите YES если все возможные строки длины \(n\) состоящие только из первых \(k\) прописных букв латинского алфавита присутствуют как подпоследовательность в \(s\), а иначе выведите NO. Если ваш ответ NO, дополнительно выведите строку длины \(n\), которая состоит только из первых \(k\) прописных букв латинского алфавита, и не входит как подпоследовательность \(s\), в следующей строке. Вы можете писать каждую букву YES и NO в любом регистре (например, YES, yES, YeS будут распознаны как положительный ответ). Примечание В первом наборе входных данных все возможные строки (aa, ab, ba, bb) длины \(2\), которые могут быть получены из первых \(2\) прописных букв латинского алфавита, присутствуют как подпоследовательности в строке abba. Во втором наборе входных данных строка aa не является подпоследовательностью abb. | |
![]()
|
|
A. Покрыть всё!
жадные алгоритмы
Конструктив
Строки
*800
Вам дано два положительных целых числа \(n\) и \(k\). Ваша задача найти строку \(s\) такую, что все возможные строки длины \(n\), которые состоят из первых \(k\) прописных букв латинского алфавита, присутствуют в \(s\) как подпоследовательность. Если существует несколько ответов, выведите ответ минимальной длины. Если таких ответов существует несколько — можно вывести любой. Примечание: Строка \(a\) называется подпоследовательностью другой строки \(b\), если \(a\) может быть получена удалением нескольких (возможно нуля) символов из \(b\) без изменения порядка оставшихся символов. Выходные данные Для каждого набора входных данных выведите одну строку \(s\) которая удовлетворяет условиям. Если существует несколько ответов, выведите ответ минимальной длины. Если таких ответов существует несколько — можно вывести любой. Примечание В первом наборе входных данных существует две строки длины \(1\) которые могут быть получены используя первые \(2\) прописные буквы латинского алфавита, и они входят в \(s\) как подпоследовательности: - \(\texttt{a}: {\color{red}{\texttt{a}}}\texttt{b}\)
- \(\texttt{b}: \texttt{a}{\color{red}{\texttt{b}}}\)
Во втором наборе входных данных существует только одна строка длины \(2\) которая может быть получена используя лишь первую прописную букву латинского алфавита, и она входит в \(s\) как подпоследовательность: - \(\texttt{aa}: {\color{red}{\texttt{aa}}}\)
В третьем наборе входных данных существует \(4\) строки длины \(2\) которые могут быть получены с использованием первых \(2\) прописных букв латинского алфавита, и они входят в \(s\) как подпоследовательности: - \(\texttt{aa}: \texttt{b}{\color{red}{\texttt{aa}}}\texttt{b}\)
- \(\texttt{ab}: \texttt{ba}{\color{red}{\texttt{ab}}}\)
- \(\texttt{ba}: {\color{red}{\texttt{ba}}}\texttt{ab}\)
- \(\texttt{bb}: {\color{red}{\texttt{b}}}\texttt{aa}{\color{red}{\texttt{b}}}\)
В четвертом наборе входных данных существует \(9\) строк длины \(2\) которые могут быть получены с использованием первых \(3\) прописных букв латинского алфавита, и они входят в \(s\) как подпоследовательности: - \(\texttt{aa}: {\color{red}{\texttt{a}}}\texttt{bcb}{\color{red}{\texttt{a}}}\texttt{c}\)
- \(\texttt{ab}: {\color{red}{\texttt{ab}}}\texttt{cbac}\)
- \(\texttt{ac}: \texttt{abcb}{\color{red}{\texttt{ac}}}\)
- \(\texttt{ba}: \texttt{abc}{\color{red}{\texttt{ba}}}\texttt{c}\)
- \(\texttt{bb}: \texttt{a}{\color{red}{\texttt{b}}}\texttt{c}{\color{red}{\texttt{b}}}\texttt{ac}\)
- \(\texttt{bc}: \texttt{a}{\color{red}{\texttt{bc}}}\texttt{bac}\)
- \(\texttt{ca}: \texttt{ab}{\color{red}{\texttt{c}}}\texttt{b}{\color{red}{\texttt{a}}}\texttt{c}\)
- \(\texttt{cb}: \texttt{ab}{\color{red}{\texttt{cb}}}\texttt{ac}\)
- \(\texttt{cc}: \texttt{ab}{\color{red}{\texttt{c}}}\texttt{ba}{\color{red}{\texttt{c}}}\)
| |
![]()
|
|
A. Сделайте белой
жадные алгоритмы
Строки
*800
У вас есть полоска из \(n\) клеток. Каждая клетка либо белая, либо чёрная. Вы можете один раз выбрать непрерывный отрезок клеток и покрасить их все в белый цвет. После этого действия все чёрные клетки этого отрезка станут белыми, а белые останутся белыми. Какое минимальное количество подряд идущих клеток нужно покрасить в белый цвет, чтобы все \(n\) клеток стали белыми. Выходные данные Для каждого набора входных данных выведите единственное число — минимальную длину непрерывного отрезка клеток, который нужно покрасить в белый цвет, чтобы вся полоска стала белой. Примечание В первом наборе входных данных для полоски «WBBWBW» минимальная длина отрезка для перекрашивания в белый цвет равна \(4\). Необходимо перекрасить отрезок от \(2\)-й до \(5\)-й клетки в белый цвет (клетки нумеруются от \(1\) слева направо). | |
![]()
|
|
B. По следам строки
жадные алгоритмы
Конструктив
Строки
*900
Поликарп потерял строку \(s\) из \(n\) строчных латинских букв, но у него остался её след. Следом строки \(s\) называется массив \(a\) из \(n\) целых чисел, в котором \(a_i\) равен количеству таких \(j\) (\(j < i\)), что \(s_i=s_j\). Например, следом строки abracadabra является массив [\(0, 0, 0, 1, 0, 2, 0, 3, 1, 1, 4\)]. По заданному следу строки найдите любую строку \(s\), из которой он мог быть получен. Строка \(s\) должна состоять только из строчных латинских букв a-z. Выходные данные Для каждого набора входных данных выведите строку \(s\), которой соответствует данный след. Если таких строк \(s\) несколько, то выведите любую из них. Строка \(s\) должна состоять из строчных латинских букв a-z. Гарантируется, что для каждого набора входных данных ответ существует. | |
![]()
|
|
D1. Сумма по всем подстрокам (простая версия)
дп
жадные алгоритмы
Перебор
Строки
*1800
Это простая версия задачи. Единственное отличие между версиями заключается в ограничениях на \(t\) и \(n\). Вы можете делать взломы только тогда, когда обе версии задачи решены. Для бинарного\(^\dagger\) шаблона \(p\) и бинарной строки \(q\) одинаковой длины \(m\), скажем, что строка \(q\) называется \(p\)-хорошей, если для каждого \(i\) (\(1 \leq i \leq m\)) существуют индексы \(l\) и \(r\) такие, что: - \(1 \leq l \leq i \leq r \leq m\), и
- \(p_i\) является модой\(^\ddagger\) строки \(q_l q_{l+1} \ldots q_{r}\).
Для шаблона \(p\) определим \(f(p)\) как минимально возможное количество \(\mathtt{1}\) в \(p\)-хорошей бинарной строке (такой же длины, как и шаблон). Вам дана бинарная строка \(s\) длины \(n\). Найдите \(\)\sum_{i=1}^{n} \sum_{j=i}^{n} f(s_i s_{i+1} \ldots s_j).\(\) Другими словами, вам нужно просуммировать значения \(f\) по всем \(\frac{n(n+1)}{2}\) подстрокам \(s\). \(^\dagger\) Бинарный шаблон — это строка, состоящая только из символов \(\mathtt{0}\) и \(\mathtt{1}\). \(^\ddagger\) Символ \(c\) является модой строки \(t\) длины \(m\), если число вхождений \(c\) в \(t\) не меньше \(\lceil \frac{m}{2} \rceil\). Например, \(\mathtt{0}\) является модой \(\mathtt{010}\), \(\mathtt{1}\) не является модой \(\mathtt{010}\), и оба символа \(\mathtt{0}\) и \(\mathtt{1}\) являются модами \(\mathtt{011010}\). Выходные данные Для каждого набора входных данных выведите сумму значений \(f\) по всем подстрокам \(s\). Примечание В первом наборе входных данных единственной \(\mathtt{1}\)-хорошей строкой является \(\mathtt{1}\). Таким образом, \(f(\mathtt{1})=1\). Во втором наборе входных данных \(f(\mathtt{10})=1\), так как \(\mathtt{01}\) является \(\mathtt{10}\)-хорошей, а \(\mathtt{00}\) не является \(\mathtt{10}\)-хорошей. Таким образом, ответ равен \(f(\mathtt{1})+f(\mathtt{10})+f(\mathtt{0}) = 1 + 1 + 0 = 2\). В третьем наборе входных данных \(f\) равна \(0\) для всех \(1 \leq i \leq j \leq 5\). Таким образом, ответ равен \(0\). | |
![]()
|
|
D2. Сумма по всем подстрокам (сложная версия)
битмаски
дп
жадные алгоритмы
разделяй и властвуй
реализация
снм
Строки
*2100
Это простая версия задачи. Единственное отличие между версиями заключается в ограничениях на \(t\) и \(n\). Вы можете делать взломы только тогда, когда обе версии задачи решены. Для бинарного\(^\dagger\) шаблона \(p\) и бинарной строки \(q\) одинаковой длины \(m\), скажем, что строка \(q\) называется \(p\)-хорошей, если для каждого \(i\) (\(1 \leq i \leq m\)) существуют индексы \(l\) и \(r\) такие, что: - \(1 \leq l \leq i \leq r \leq m\), и
- \(p_i\) является модой\(^\ddagger\) строки \(q_l q_{l+1} \ldots q_{r}\).
Для шаблона \(p\) определим \(f(p)\) как минимально возможное количество \(\mathtt{1}\) в \(p\)-хорошей бинарной строке (такой же длины, как и шаблон). Вам дана бинарная строка \(s\) длины \(n\). Найдите \(\)\sum_{i=1}^{n} \sum_{j=i}^{n} f(s_i s_{i+1} \ldots s_j).\(\) Другими словами, вам нужно просуммировать значения \(f\) по всем \(\frac{n(n+1)}{2}\) подстрокам \(s\). \(^\dagger\) Бинарный шаблон — это строка, состоящая только из символов \(\mathtt{0}\) и \(\mathtt{1}\). \(^\ddagger\) Символ \(c\) является модой строки \(t\) длины \(m\), если число вхождений \(c\) в \(t\) не меньше \(\lceil \frac{m}{2} \rceil\). Например, \(\mathtt{0}\) является модой \(\mathtt{010}\), \(\mathtt{1}\) не является модой \(\mathtt{010}\), и оба символа \(\mathtt{0}\) и \(\mathtt{1}\) являются модами \(\mathtt{011010}\). Выходные данные Для каждого набора входных данных выведите сумму значений \(f\) по всем подстрокам \(s\). Примечание В первом наборе входных данных единственной \(\mathtt{1}\)-хорошей строкой является \(\mathtt{1}\). Таким образом, \(f(\mathtt{1})=1\). Во втором наборе входных данных \(f(\mathtt{10})=1\), так как \(\mathtt{01}\) является \(\mathtt{10}\)-хорошей, а \(\mathtt{00}\) не является \(\mathtt{10}\)-хорошей. Таким образом, ответ равен \(f(\mathtt{1})+f(\mathtt{10})+f(\mathtt{0}) = 1 + 1 + 0 = 2\). В третьем наборе входных данных \(f\) равна \(0\) для всех \(1 \leq i \leq j \leq 5\). Таким образом, ответ равен \(0\). | |
![]()
|
|
A. Восстановление маленькой строки
Перебор
Строки
*800
У Никиты было слово, состоящее ровно из \(3\)-х строчных латинских букв. Буквы в латинском алфавите пронумерованы от \(1\) до \(26\), где буква «a» имеет номер \(1\), буква «z» — номер \(26\). Он закодировал это слово, сложив позиции всех символов в алфавите. Например, слово «cat» он бы закодировал числом \(3 + 1 + 20 = 24\), так как буква «c» имеет номер \(3\) в алфавите, буква «a» имеет номер \(1\), а буква «t» — номер \(20\). Однако, такая кодировка оказалась не однозначной! Так, при кодировании слова «ava» также получается число \(1 + 22 + 1 = 24\). Определите лексикографически минимальное слово из \(3\)-х букв, которое могло быть закодировано. Строка \(a\) лексикографически меньше строки \(b\), если и только если выполняется один из следующих пунктов: - \(a\) — префикс \(b\), но \(a \ne b\);
- в первой позиции, где \(a\) и \(b\) различны, в строке \(a\) находится буква, которая встречается в алфавите раньше, чем соответствующая буква в \(b\).
Выходные данные Для каждого набора входных данных в отдельной строке выведите лексикографически минимальное трехсимвольное слово, которое могло быть закодировано. | |
![]()
|
|
A. Развлечение в ЦПМ
Конструктив
Строки
*800
Поздравляю, вы поступили в Центр Помощи Магистрам! Однако, на уроках вам было безумно скучно и вам надоело ничего не делать, поэтому вы придумали себе развлечение. Вам дана строка \(s\) и чётное число \(n\). Есть два типа операций, которые вы можете к ней применять: - Добавить в конец строки \(s\) перевёрнутую строку \(s\) (например, если \(s = \) cpm, то после применения операции \(s = \) cpmmpc).
- Перевернуть текущую строку \(s\) (например, если \(s = \) cpm, то после применения операции \(s = \) mpc).
Требуется определить лексикографически минимальную\(^{\dagger}\) строку, которую можно получить после применения ровно \(n\) операций. Обратите внимание, что вы можете применять операции разных типов в произвольном порядке, но суммарно вы должны применить ровно \(n\) операций. \(^{\dagger}\)Строка \(a\) лексикографически меньше строки \(b\), если и только если выполняется один из следующих пунктов: - \(a\) является префиксом \(b\), но \(a \ne b\);
- в первой позиции, где \(a\) и \(b\) различны, в строке \(a\) находится буква, которая встречается в алфавите раньше, чем соответствующая буква в \(b\).
Выходные данные Для каждого набора входных данных выведите одну строку — лексикографически минимальную строку, которую можно получить после применения ровно \(n\) операций. Примечание В первом наборе входных данных можно применить операцию второго типа (то есть перевернуть строку \(s\)) \(4\) раза. Тогда строка \(s\) останется равной cpm. Во втором наборе входных данных можно сделать следующее: - Применить операцию второго типа, после чего \(s\) станет равной birg.
- Применить операцию первого типа (то есть добавить в конец строки \(s\) перевёрнутую строку \(s\)), после чего \(s\) станет равной birggrib.
| |
![]()
|
|
C. Рудольф и некрасивая строка
дп
жадные алгоритмы
Строки
*900
У Рудольфа есть строка \(s\) длины \(n\). Рудольф считает, что строка \(s\) является некрасивой, если содержит в качестве подстроки\(^\dagger\) хотя бы одну строку «pie» или хотя бы одну строку «map», в противном случае строка \(s\) будет красивой. Например, «ppiee», «mmap», «dfpiefghmap» — некрасивые строки, а «mathp», «ppiiee» — красивые строки. Рудольф хочет сократить строку \(s\), удалив некоторые символы, чтобы она стала красивой. Главный герой не любит напрягаться, поэтому просит вас сделать строку красивой, удалив при этом минимальное количество символов. Он может удалять символы из любых позиций в строке (а не только с начала/конца строки). \(^\dagger\) Строка \(a\) является подстрокой \(b\), если в строке \(b\) существует последовательный отрезок символов равный \(a\). Выходные данные Для каждого набора входных данных выведите единственное целое число — минимальное количество символов, которые нужно удалить, чтобы строка \(s\) стала красивой. Если строка изначально красивая, то выведите \(0\). Примечание В первом наборе можно удалить, например, \(4\)-й и \(9\)-й символы, чтобы строка стала красивой. Во втором наборе строка уже является красивой. | |
![]()
|
|
B. Непалиндромная подстрока
математика
реализация
Строки
хэши
*2000
Строка \(t\) считается \(k\)-хорошей, если существует хотя бы одна подстрока\(^\dagger\) длины \(k\), которая не является палиндромом\(^\ddagger\). Пусть \(f(t)\) обозначает сумму всех значений \(k\), при которых строка \(t\) является \(k\)-хорошей. Вам дана строка \(s\) длины \(n\). Вы должны ответить на \(q\) следующих запросов: - Для данных \(l\) и \(r\) (\(l < r\)), найдите значение \(f(s_ls_{l + 1}\ldots s_r)\).
\(^\dagger\) Подстрока строки \(z\) — это последовательность подряд идущих символов строки \(z\). Например, «\(\mathtt{defor}\)», «\(\mathtt{code}\)» и «\(\mathtt{o}\)» являются подстроками «\(\mathtt{codeforces}\)», а «\(\mathtt{codes}\)» и «\(\mathtt{aaa}\)» не являются. \(^\ddagger\) Палиндром — это строка, которая одинаково читается как слева направо, так и справа налево. Например, строки «\(\texttt{z}\)», «\(\texttt{aa}\)» и «\(\texttt{tacocat}\)» являются палиндромами, а «\(\texttt{codeforces}\)» и «\(\texttt{ab}\)» — нет. Выходные данные Для каждого запроса выведите \(f(s_ls_{l + 1}\ldots s_r)\). Примечание В первом запросе первого набора входных данных строка равняется \(\mathtt{aaab}\). Подстроки \(\mathtt{aaab}\), \(\mathtt{aab}\) и \(\mathtt{ab}\) не являются палиндромами и имеют длины \(4\), \(3\) и \(2\) соответственно. Таким образом, строка является \(2\)-хорошей, \(3\)-хорошей и \(4\)-хорошей. Следовательно, \(f(\mathtt{aaab}) = 2 + 3 + 4 = 9\). Во втором запросе первого набора строка имеет вид \(\mathtt{aaa}\). В ней нет непалиндромных подстрок. Следовательно, \(f(\mathtt{aaa}) = 0\). В первом запросе второго набора входных данных строка имеет вид \(\mathtt{abc}\). Подстроки \(\mathtt{ab}\), \(\mathtt{bc}\) и \(\mathtt{abc}\) не являются палиндромами и имеют длины \(2\), \(2\) и \(3\) соответственно. Таким образом, строка является \(2\)-хорошей и \(3\)-хорошей. Следовательно, \(f(\mathtt{abc}) = 2 + 3 = 5\). Заметим, что даже если существует \(2\) непалиндромных подстроки длины \(2\), мы считаем их только один раз. | |
![]()
|
|
D. Тандемные повторы?
Перебор
Строки
*1700
Вам дана строка \(s\), состоящая из строчных латинских букв и/или знаков вопроса. Тандемный повтор — это строка четной длины, такая, что ее первая половина равна второй половине. Строка \(a\) является подстрокой \(b\), если \(a\) может быть получена из \(b\) удалением нескольких (возможно, ни одного или всех) символов из начала и нескольких (возможно, ни одного или всех) символов из конца. Ваша цель — заменить каждый знак вопроса некоторой строчной латинской буквой таким образом, чтобы длина самой длинной подстроки, являющейся тандемным повтором, была максимально возможной. Выходные данные Для каждого набора входных данных выведите одно целое число — максимальную длину самой длинной подстроки, являющейся тандемным повтором после замены каждого знака вопроса в строке некоторой строчной латинской буквой. Если невозможно создать подстроки, являющиеся тандемными повторами в строке, выведите \(0\). | |
![]()
|
|
E. Почти самая короткая повторяющаяся подстрока
Перебор
реализация
Строки
теория чисел
*1500
Вам дана строка \(s\) длиной \(n\), состоящая из строчных латинских символов. Найдите длину самой короткой строки \(k\), такой что несколько (возможно одна) копий \(k\) могут быть сконкатенированы вместе, чтобы образовать строку той же длины, что и \(s\), и при этом имеется не более одного отличающегося символа. Формально, найдите длину самой короткой строки \(k\), такой что \(c = \underbrace{k + \cdots + k}_{x\rm\ \text{раз}}\) для некоторого положительного целого \(x\), строки \(s\) и \(c\) имеют одинаковую длину и \(c_i \neq s_i\) для не более чем одного \(i\) (т.е. существует \(0\) или \(1\) такая позиция). Выходные данные Для каждого теста выведите длину самой короткой строки \(k\), удовлетворяющей условиям в условии. Примечание В первом примере вы можете выбрать \(k = \texttt{a}\) и \(k+k+k+k = \texttt{aaaa}\), которая отличается от \(s\) только во второй позиции. Во втором примере вы не можете выбрать \(k\) длиной один или два. Мы можем взять \(k = \texttt{abba}\), которая равна \(s\). | |
![]()
|
|
G. Перемешивание песен
битмаски
графы
дп
поиск в глубину и подобное
реализация
Строки
хэши
*1900
У Владислава есть плейлист, состоящий из \(n\) песен, пронумерованных от \(1\) до \(n\). Песня \(i\) имеет жанр \(g_i\) и автора \(w_i\). Он хочет составить плейлист таким образом, чтобы каждая пара соседних песен либо имела одного и того же автора, либо была из того же жанра (или и то, и другое). Он называет такой плейлист захватывающим. И \(g_i\), и \(w_i\) являются строками, длины не более \(10^4\). Не всегда возможно составить захватывающий плейлист, используя все песни, поэтому процесс перемешивания происходит в два этапа. Сначала удаляются некоторое количество (возможно, нулевое) песен, а затем оставшиеся песни в плейлисте переставляются, чтобы сделать его захватывающим. Поскольку Владислав не любит, когда песни удаляются из его плейлиста, он хочет, чтобы составление плейлиста выполнялось с минимальным количеством удалений. Помогите ему найти минимальное количество удалений, которые необходимо выполнить, чтобы можно было переставить оставшиеся песни, чтобы сделать плейлист захватывающим. Выходные данные Для каждого теста выведите одно целое число — минимальное количество удалений, необходимых для того, чтобы получившийся плейлист можно было сделать захватывающим. Примечание В первом тесте плейлист уже захватывающий. Во втором тесте, если у вас есть песни в порядке \(4, 3, 1, 2\), это захватывающий плейлист, поэтому вам не нужно удалять никакие песни. В третьем тесте вы можете удалить песни \(4, 5, 6, 7\). Тогда плейлист с песнями в порядке \(1, 2, 3\) будет захватывающим. | |
![]()
|
|
E. Без палиндромов
жадные алгоритмы
Конструктив
математика
Перебор
разделяй и властвуй
реализация
Строки
хэши
*2000
Вам дана строка \(s\), состоящая из строчных латинских букв. Вам нужно разбить\(^\dagger\) эту строку на некоторое количество подстрок так, чтобы каждая подстрока не была палиндромом\(^\ddagger\). \(^\dagger\) Разбиение строки \(s\) — это упорядоченная последовательность некоторых \(k\) строк \(t_1, t_2, \ldots, t_k\), таких, что \(t_1 + t_2 + \ldots + t_k = s\), где \(+\) обозначает операцию конкатенации. \(^\ddagger\) Строка \(s\) называется палиндромом, если она читается одинаково как слева направо, так и справа налево. Например, \(\mathtt{racecar}\), \(\mathtt{abccba}\) и \(\mathtt{a}\) являются палиндромами, а \(\mathtt{ab}\), \(\mathtt{dokibird}\) и \(\mathtt{kurosanji}\) — нет. Выходные данные Для каждого набора входных данных выведите в отдельной строке «YES», если существует разбиение \(s\), части которого не являются палиндромами, или «NO», если такого разбиения не существует. Если ответ «YES», то во второй строке выведите целое число \(k\) — количество частей, на которое нужно разбить \(s\), чтобы каждая часть не была палиндромом. В третьей строке выведите \(k\) строк \(t_1, t_2, \ldots, t_k\), представляющих такое разбиение. Если таких разбиений несколько, выведите любое из них. Примечание В первом наборе входных данных, поскольку \(\mathtt{sinktheyacht}\) уже не является палиндромом, разбиение \([\mathtt{sinktheyacht}]\) является допустимым. Во втором наборе входных данных, поскольку любая подстрока строки \(s\) является палиндромом, не существует допустимых разбиений. В третьем наборе входных данных еще одно допустимое разбиение — \([\mathtt{uw},\mathtt{uo}, \mathtt{wou}, \mathtt{wu}]\). | |
![]()
|
|
B. Is it stated?
*особая задача
Строки
Выходные данные Для каждого набора входных данных выведите «YES» или «NO» в качестве ответа. | |
![]()
|
|
H. Палиндром
*особая задача
реализация
Строки
Палиндром — это строка, которая читается одинаково в обоих направлениях, например z, uwu или moom. Выходные данные Для каждого набора входных данных выведите «YES» или «NO» в качестве ответа. | |
![]()
|
|
A. Лексикографически максимальная подпоследовательность
жадные алгоритмы
Строки
*1100
Дана строка s, состоящая только из строчных латинских букв. Найдите ее лексикографически максимальную подпоследовательность. Непустую строку s[p1p2... pk] = sp1sp2... spk(1 ≤ p1 < p2 < ... < pk ≤ |s|) будем называть подпоследовательностью строки s = s1s2... s|s|. Строка x = x1x2... x|x| лексикографически больше строки y = y1y2... y|y|, если либо |x| > |y| и x1 = y1, x2 = y2, ... , x|y| = y|y|, либо существует такое число r (r < |x|, r < |y|), что x1 = y1, x2 = y2, ... , xr = yr и xr + 1 > yr + 1. Символы в строках сравниваются как их ASCII-коды. Выходные данные Выведите лексикографически максимальную подпоследовательность строки s. Примечание Рассмотрим примеры и покажем, как именно выглядят искомые подпоследовательности (они выделены прописными буквами полужирным шрифтом). Первый пример: aBaBBA Второй пример: abbCbCCaCbbCBaaBA | |
![]()
|
|
D. Следующая хорошая строка
жадные алгоритмы
Строки
Структуры данных
хэши
*2800
В задачах на строки часто требуется найти строку, обладающую какими-то особыми свойствами. В очередной раз авторам задачи было лень придумывать название для такой строки, поэтому они назвали ее хорошей. Строка называется хорошей, если в ней нет подстрок-палиндромов длины большей или равной d. Дана строка s, состоящая только из строчных латинских букв. Найдите хорошую строку t длины |s|, состоящую из строчных латинских букв, и лексикографически большую, чем s. Из всех таких строк строка t должна быть лексикографически минимальной. Непустую строку s[a ... b] = sasa + 1... sb (1 ≤ a ≤ b ≤ |s|) будем называть подстрокой строки s = s1s2... s|s|. Непустая строка s = s1s2... sn называется палиндромом, если для всех i от 1 до n выполняется si = sn - i + 1. Другими словами, палиндромы читаются одинаково в обоих направлениях. Строка x = x1x2... x|x| лексикографически больше строки y = y1y2... y|y|, если либо |x| > |y| и x1 = y1, x2 = y2, ... , x|y| = y|y|, либо существует такое число r (r < |x|, r < |y|), что x1 = y1, x2 = y2, ... , xr = yr и xr + 1 > yr + 1. Символы в строках сравниваются как их ASCII-коды. Выходные данные Выведите следующую после s в лексикографическом порядке хорошую строку той же длины, состоящую только из строчных латинских букв. Если такой строки не существует, выведите «Impossible» (без кавычек). | |
![]()
|
|
C. Складывание полоски
жадные алгоритмы
Конструктив
Строки
*2300
У вас есть полоска бумаги с бинарной строкой \(s\) длины \(n\). Вы можете сложить бумагу между любой парой соседних цифр. Последовательность складок считается допустимой, если после складок все символы, находящиеся друг над другом или под другим, совпадают. Обратите внимание, что все складки делаются одновременно, поэтому символы не обязательно должны совпадать между складками. Например, вот допустимые складки для \(s = \mathtt{110110110011}\) и \(s = \mathtt{01110}\):  Длина сложенной полоски — это длина, видимая сверху после всех складок. Таким образом, для двух приведенных выше примеров после указанных выше складок длины будут равны \(7\) и \(3\) соответственно. Обратите внимание, что для приведенной выше складки для \(s = \mathtt{01110}\), если бы мы сделали любую из двух складок по отдельности, это была бы недопустимая последовательность складок. Однако, поскольку мы не проверяем допустимость до тех пор, пока все складки не будут сделаны, эта последовательность складок допустима. После выполнения последовательности допустимых складок, какова минимальная длина полоски, которую вы можете получить? Выходные данные Для каждого теста выведите одно целое число — минимально возможную длину полоски после допустимой последовательности складок. Примечание Для первого примера одной из оптимальных последовательностей складок является складывание полоски посередине, что приводит к полоске длиной 3. Третий и четвертый примеры соответствуют изображениям выше. Обратите внимание, что складка, показанная выше для \(s = \mathtt{110110110011}\), не является минимальной по длине. | |
![]()
|
|
G1. Деление + LCP (простая версия)
Бинарный поиск
дп
Строки
строковые суфф. структуры
Структуры данных
хэши
*1900
Это простая версия задачи. В этой версии \(l=r\). Дана строка \(s\). Для фиксированного \(k\) рассмотрим деление \(s\) на ровно \(k\) непрерывных подстрок \(w_1,\dots,w_k\). Пусть \(f_k\) — максимально возможное \(LCP(w_1,\dots,w_k)\) среди всех делений. \(LCP(w_1,\dots,w_m)\) — это длина самого длинного общего префикса строк \(w_1,\dots,w_m\). Например, если \(s=abababcab\) и \(k=4\), то возможное деление \(\color{red}{ab}\color{blue}{ab}\color{orange}{abc}\color{green}{ab}\). \(LCP(\color{red}{ab},\color{blue}{ab},\color{orange}{abc},\color{green}{ab})\) равно \(2\), так как \(ab\) — самый длинный общий префикс этих четырех строк. Обратите внимание, что каждая подстрока состоит из непрерывного сегмента символов, и каждый символ принадлежит ровно одной подстроке. Ваша задача — найти \(f_l,f_{l+1},\dots,f_r\). В этой версии \(l=r\). Выходные данные Для каждого набора входных данных выведите \(r-l+1\) значений: \(f_l,\dots,f_r\). Примечание В первом примере \(n=k\), поэтому единственное деление \(aba\) — \(\color{red}a\color{blue}b\color{orange}a\). Ответ — ноль, потому что у этих строк нет общего префикса. Во втором примере единственное деление — \(\color{red}a\color{blue}a\color{orange}a\). Их самый длинный общий префикс равен одному. | |
![]()
|
|
G2. Деление + LCP (сложная версия)
Бинарный поиск
дп
математика
Перебор
Строки
строковые суфф. структуры
Структуры данных
хэши
*2200
Это cложная версия задачи. В этой версии \(l\le r\). Дана строка \(s\). Для фиксированного \(k\) рассмотрим деление \(s\) на ровно \(k\) непрерывных подстрок \(w_1,\dots,w_k\). Пусть \(f_k\) — максимально возможное \(LCP(w_1,\dots,w_k)\) среди всех делений. \(LCP(w_1,\dots,w_m)\) — это длина самого длинного общего префикса строк \(w_1,\dots,w_m\). Например, если \(s=abababcab\) и \(k=4\), то возможное деление \(\color{red}{ab}\color{blue}{ab}\color{orange}{abc}\color{green}{ab}\). \(LCP(\color{red}{ab},\color{blue}{ab},\color{orange}{abc},\color{green}{ab})\) равно \(2\), так как \(ab\) — самый длинный общий префикс этих четырех строк. Обратите внимание, что каждая подстрока состоит из непрерывного сегмента символов, и каждый символ принадлежит ровно одной подстроке. Ваша задача — найти \(f_l,f_{l+1},\dots,f_r\). Выходные данные Для каждого набора входных данных выведите \(r-l+1\) значений: \(f_l,\dots,f_r\). | |
![]()
|
|
D1. Arithmancy (Easy)
интерактив
Конструктив
Перебор
Строки
*2100
Professor Vector is preparing to teach her Arithmancy class. She needs to prepare \(n\) distinct magic words for the class. Each magic word is a string consisting of characters X and O. A spell is a string created by concatenating two magic words together. The power of a spell is equal to the number of its different non-empty substrings. For example, the power of the spell XOXO is equal to 7, because it has 7 different substrings: X, O, XO, OX, XOX, OXO and XOXO. Each student will create their own spell by concatenating two magic words. Since the students are not very good at magic yet, they will choose each of the two words independently and uniformly at random from the \(n\) words provided by Professor Vector. It is therefore also possible that the two words a student chooses are the same. Each student will then compute the power of their spell, and tell it to Professor Vector. In order to check their work, and of course to impress the students, Professor Vector needs to find out which two magic words and in which order were concatenated by each student. Your program needs to perform the role of Professor Vector: first, create \(n\) distinct magic words, and then handle multiple requests where it is given the spell power and needs to determine the indices of the two magic words, in the correct order, that were used to create the corresponding spell. Interaction This is an interactive problem. First, your program should read a single integer \(n\) (\(1 \le n \le 3\)), the number of magic words to prepare. Then, it should print \(n\) magic words it has created, one per line. The magic words must be distinct, each magic word must have at least 1 and at most \(30\cdot n\) characters, and each character must be either X or O. We will denote the \(i\)-th magic word you printed as \(w_i\) (\(1 \le i \le n\)). Then, your program should read a single integer \(q\) (\(1 \le q \le 1000\)), the number of students in the class. Then, it should repeat the following process \(q\) times, one per student. For the \(j\)-th student, it should first read a single integer \(p_j\), the power of their spell. It is guaranteed that this number is computed by choosing two indices \(u_j\) and \(v_j\) independently and uniformly at random between 1 and \(n\) inclusive, concatenating \(w_{u_j}\) and \(w_{v_j}\), and finding the number of different non-empty substrings of the resulting string. Then, your program must print the numbers \(u_j\) and \(v_j\), in this order (\(1 \le u_j, v_j \le n\)). Note that it is not enough to find any two magic words that concatenate into a spell with the given power. You must find the exact words used by the student in the exact order. Remember to flush the output stream after printing all magic words and after printing \(u_j\) and \(v_j\) for each student. | |
![]()
|
|
D2. Arithmancy (Medium)
интерактив
Конструктив
Строки
Теория вероятностей
*2600
The only difference between the versions of this problem is the maximum value of \(n\). Professor Vector is preparing to teach her Arithmancy class. She needs to prepare \(n\) distinct magic words for the class. Each magic word is a string consisting of characters X and O. A spell is a string created by concatenating two magic words together. The power of a spell is equal to the number of its different non-empty substrings. For example, the power of the spell XOXO is equal to 7, because it has 7 different substrings: X, O, XO, OX, XOX, OXO and XOXO. Each student will create their own spell by concatenating two magic words. Since the students are not very good at magic yet, they will choose each of the two words independently and uniformly at random from the \(n\) words provided by Professor Vector. It is therefore also possible that the two words a student chooses are the same. Each student will then compute the power of their spell, and tell it to Professor Vector. In order to check their work, and of course to impress the students, Professor Vector needs to find out which two magic words and in which order were concatenated by each student. Your program needs to perform the role of Professor Vector: first, create \(n\) distinct magic words, and then handle multiple requests where it is given the spell power and needs to determine the indices of the two magic words, in the correct order, that were used to create the corresponding spell. Interaction This is an interactive problem. First, your program should read a single integer \(n\) (\(1 \le n \le 30\)), the number of magic words to prepare. Then, it should print \(n\) magic words it has created, one per line. The magic words must be distinct, each magic word must have at least 1 and at most \(30\cdot n\) characters, and each character must be either X or O. We will denote the \(i\)-th magic word you printed as \(w_i\) (\(1 \le i \le n\)). Then, your program should read a single integer \(q\) (\(1 \le q \le 1000\)), the number of students in the class. Then, it should repeat the following process \(q\) times, one per student. For the \(j\)-th student, it should first read a single integer \(p_j\), the power of their spell. It is guaranteed that this number is computed by choosing two indices \(u_j\) and \(v_j\) independently and uniformly at random between 1 and \(n\) inclusive, concatenating \(w_{u_j}\) and \(w_{v_j}\), and finding the number of different non-empty substrings of the resulting string. Then, your program must print the numbers \(u_j\) and \(v_j\), in this order (\(1 \le u_j, v_j \le n\)). Note that it is not enough to find any two magic words that concatenate into a spell with the given power. You must find the exact words used by the student in the exact order. Remember to flush the output stream after printing all magic words and after printing \(u_j\) and \(v_j\) for each student. | |
![]()
|
|
B. Различные строки
реализация
Строки
*800
Вам дана строка \(s\), состоящая из строчных латинских букв. Переставьте символы \(s\), чтобы получить новую строку \(r\), которая не равна \(s\), или сообщите, что это невозможно. Выходные данные Для каждого набора входных данных, если такая строка \(r\) не существует в соответствии с условием, выведите «NO» (без кавычек). В противном случае выведите «YES» (без кавычек). Затем выведите одну строку — строку \(r\), состоящую из символов строки \(s\). Вы можете выводить «YES» и «NO» в любом регистре (например, строки «yEs», «yes», и «Yes» будут распознаны как положительный ответ). Если существует несколько ответов, вы можете вывести любой из них. Примечание В первом примере другой возможный ответ — \(\texttt{forcescode}\). Во втором примере все перестановки \(\texttt{aaaaa}\) равны \(\texttt{aaaaa}\). | |
![]()
|
|
D. Бинарное разбиение
дп
жадные алгоритмы
реализация
сортировки
Строки
*1100
Вам дана бинарная строка\(^{\dagger}\). Пожалуйста, найдите минимальное количество частей, которые вам нужно отрезать, чтобы полученные части можно было переставить в отсортированную бинарную строку.  Обратите внимание, что: - каждый символ должен принадлежать ровно одной из частей;
- части должны быть непрерывными подстроками исходной строки;
- вам нужно использовать все части при перестановке.
\(^{\dagger}\) Бинарная строка — это строка, состоящая из символов \(\texttt{0}\) и \(\texttt{1}\). Отсортированная бинарная строка — это бинарная строка, в которой все символы \(\texttt{0}\) идут перед всеми символами \(\texttt{1}\). Выходные данные Для каждого набора входных данных выведите одно целое число — минимальное количество частей, необходимое для того, чтобы можно было переставить строку в отсортированную бинарную строку. Примечание Первый пример изображен в условии. Можно доказать, что вам понадобится не менее \(3\) частей. Во втором и третьем примерах случаях бинарная строка уже отсортирована, поэтому нужна только \(1\) часть. В четвертом примере вам нужно сделать один разрез между двумя символами и переставить их, чтобы получить строку \(\texttt{01}\). | |
![]()
|
|
B. Симметричное кодирование
реализация
сортировки
Строки
*800
У Поликарпа есть строка \(s\), которая состоит из строчных латинских букв. Он кодирует эту строку по следующему алгоритму: - сначала он строит новую вспомогательную строку \(r\), которая состоит из всех различных букв строки \(s\), записанных в алфавитном порядке;
- далее кодирование происходит так: каждый символ в строке \(s\) заменяется на симметричный ему символ из строки \(r\) (первый символ строки \(r\) будет заменён на последний, второй на предпоследний и так далее).
Например, кодирование строки \(s\)=«codeforces» происходит так: - строка \(r\) получается равной «cdefors»;
- первый символ \(s_1\)='c' заменяется на 's';
- второй символ \(s_2\)='o' заменяется на 'e';
- третий символ \(s_3\)='d' заменяется на 'r';
- ...
- последний символ \(s_{10}\)='s' заменяется на 'c'.
 Строка \(r\) и замены для \(s\)="codeforces". Строка \(r\) и замены для \(s\)="codeforces". Таким образом, результатом кодирования строки \(s\)=«codeforces» является строка «serofedsoc». Напишите программу, которая осуществляет декодирование — то есть по результату кодирования восстанавливает исходную строку \(s\). Выходные данные Для каждого набора входных данных выведите строку \(s\) из которой был получен результат кодирования \(b\). | |
![]()
|
|
G. Фан-клуб Zimpha
бпф
жадные алгоритмы
математика
Строки
*3000
Однажды Zimpha придумал задачу. Как член фан-клуба Zimpha, вы решили её решить. Вам даны две строки \(s\) и \(t\) длины \(n\) и \(m\) соответственно. Обе строки состоят только из строчных латинских букв, а также символов - и *. Вам нужно заменить все вхождения - и *, соблюдая следующие правила: - Для каждого символа - вы должны заменить его на любую строчную латинскую букву.
- Для каждого символа * вы должны заменить его любой строкой (возможно, пустой), состоящей только из строчных латинских букв.
Обратите внимание, что вы можете заменить два разных символа - разными символами. Вы также можете заменить два разных символа * разными строками. Предположим, что \(s\) и \(t\) были преобразованы в \(s'\) и \(t'\). Теперь вы задаетесь вопросом, существуют ли замены, в результате которых получается \(s'=t'\). Выходные данные Для каждого набора входных данных выведите «Yes», если существует замена, в результате которой получается \(s'=t'\), и «No» в противном случае. Вы можете выводить каждую букву в любом регистре (строчную или заглавную). Например, строки «yEs», «yes», «Yes» и «YES» будут приняты как положительный ответ. Примечание Во втором наборе входных данных мы можем преобразовать обе строки в ttklwxx. В \(s\) - будет заменено на l. В \(t\) * будет заменена пустой строкой, а первая и вторая - будут заменены на k и w соответственно. В пятом наборе входных данных мы можем преобразовать обе строки в bulijiojioxdibuliduo. | |
![]()
|
|
H. 378QAQ и ядро
жадные алгоритмы
Строки
*3500
У 378QAQ есть строка \(s\) длины \(n\). Определим ядро строки как подстроку\(^\dagger\) с максимальным лексикографическим\(^\ddagger\) порядком. Например, ядром «\(\mathtt{bazoka}\)» является «\(\mathtt{zoka}\)», а ядром «\(\mathtt{aaa}\)» является «\(\mathtt{aaa}\)». 378QAQ хочет переставить символы в строке \(s\) так, чтобы ядро было лексикографически минимальным. Найдите лексикографически минимальное возможное ядро среди всех перестановок \(s\). \(^\dagger\) Подстрока строки \(s\) — это непрерывный отрезок букв из \(s\). Например, «\(\mathtt{defor}\)», «\(\mathtt{code}\)» и «\(\mathtt{o}\)» являются подстроками «\(\mathtt{codeforces}\)», а «\(\mathtt{codes}\)» и «\(\mathtt{aaa}\)» не являются. \(^\ddagger\) Строка \(p\) лексикографически меньше строки \(q\) тогда и только тогда, когда выполняется одно из следующих условий: - \(p\) является префиксом \(q\), но \(p \ne q\); или
- в первой позиции, где \(p\) и \(q\) отличаются, строка \(p\) имеет меньший символ, чем символ на соответствующей поозиции в \(q\) (при сравнении по их ASCII-коду).
Например, «\(\mathtt{code}\)» и «\(\mathtt{coda}\)» лексикографически меньше, чем «\(\mathtt{codeforces}\)», а «\(\mathtt{codeforceston}\)» и «\(\mathtt{z}\)» — нет. Выходные данные Для каждого набора входных данных выведите лексикографически минимальное возможное ядро среди всех перестановок \(s\). Примечание В первом наборе входных данных все возможные перестановки и соответствующие им ядра выглядят следующим образом: - «\(\mathtt{qaq}\)», его ядро — «\(\mathtt{qaq}\)».
- «\(\mathtt{aqq}\)», его ядро — «\(\mathtt{qq}\)».
- «\(\mathtt{qqa}\)», его ядро — «\(\mathtt{qqa}\)».
Таким образом, ядро с минимальным лексикографическим порядком среди всех перестановок — это «\(\mathtt{qaq}\)». | |
![]()
|
|
A. Проверка пароля
реализация
сортировки
Строки
*800
Монокарп работает над своим новым сайтом, и сейчас он пытается заставить пользователей выбирать надежные пароли. Монокарп решил, что надежные пароли должны удовлетворять следующим условиям: - пароль должен состоять только из строчных латинских букв и цифр;
- не должно быть цифр, идущих после буквы (то есть, после каждой буквы следует либо другая буква, либо конец строки);
- все цифры должны быть отсортированы в неубывающем порядке;
- все буквы должны быть отсортированы в неубывающем порядке.
Обратите внимание, что разрешено, чтобы пароль состоял только из букв или только из цифр. Монокарпу удалось реализовать первое условие, но он не справляется с оставшимися. Можете ли вы помочь ему проверить пароли? Выходные данные Для каждого набора входных данных выведите «YES», если данный пароль является надежным, и «NO» в противном случае. Примечание Во втором наборе входных данных буквы не отсортированы в неубывающем порядке. В четвертом наборе есть цифра, идущая после буквы — цифра '1' после буквы 'c'. | |
![]()
|
|
D. Исправление бинарной строки
битмаски
дп
жадные алгоритмы
Конструктив
Перебор
Строки
хэши
*1800
Вам дана бинарная строка \(s\) длины \(n\), состоящая из нулей и единиц. Вы можете сделать следующую операцию ровно один раз: - Выбрать целое число \(p\) (\(1 \le p \le n\)).
- Перевернуть подстроку \(s_1 s_2 \ldots s_p\). После выполнения этого шага строка \(s_1 s_2 \ldots s_n\) превратится в строку \(s_p s_{p-1} \ldots s_1 s_{p+1} s_{p+2} \ldots s_n\).
- После этого сделать циклический сдвиг строки \(s\) влево \(p\) раз. После выполнения этого шага изначальная строка \(s_1s_2 \ldots s_n\) превратится в строку \(s_{p+1}s_{p+2} \ldots s_n s_p s_{p-1} \ldots s_1\).
Например, если применить операцию к строке 110001100110 при \(p=3\), то после второго шага получится строка 011001100110, а после третьего шага 001100110011. Строка \(s\) называется \(k\)-правильной, если выполняются два условия: - \(s_1=s_2=\ldots=s_k\);
- \(s_{i+k} \neq s_i\) для любого \(i\) (\(1 \le i \le n - k\)).
Например, при \(k=3\) строки 000, 111000111 и 111000 являются \(k\)-правильными, а строки 000000, 001100 и 1110000 нет. Дано целое число \(k\), которое является делителем \(n\). Найдите целое число \(p\) (\(1 \le p \le n\)), после выполнения операции с которым строка \(s\) станет \(k\)-правильной или определите, что это невозможно. Обратите внимание, что если строка изначально является \(k\)-правильной, то к ней всё равно нужно применить ровно одну операцию. Выходные данные Для каждого набора входных данных выведите одно целое число — значение \(p\), чтобы сделать строку \(k\)-правильной, или \(-1\), если это невозможно. Если существует несколько решений, выведите любое из них. Примечание В первом наборе входных данных, если применить операцию при \(p=3\), то после второго шага операции строка станет равна 11100001, а после третьего 00001111. Эта строка является \(4\)-правильной. Во втором наборе входных данных можно показать, что не существует операции, после которой строка становится \(2\)-правильной. В третьем наборе входных данных, если применить операцию при \(p=7\), то после второго шага операции строка станет равна 100011100011, а после третьего 000111000111. Эта строка является \(3\)-правильной. В четвертом наборе входных данных после операции c любым \(p\) строка является \(5\)-правильной. | |
![]()
|
|
G. Яся и таинственное дерево
битмаски
графы
Деревья
жадные алгоритмы
поиск в глубину и подобное
Строки
Структуры данных
*2300
Яся гуляла по лесу и совершенно случайно нашла дерево на \(n\) вершинах. Дерево — это связный неориентированный граф, в котором отсутствуют циклы. Рядом с деревом девочка нашла древний манускрипт, на котором записаны \(m\) запросов. Запросы бывают двух видов. Первый вид запросов описывается числом \(y\). Вес каждого ребра в дереве заменяется на побитовое исключающее «ИЛИ» веса этого ребра и числа \(y\). Второй вид описывается вершиной \(v\) и числом \(x\). Яся выбирает вершину \(u\) (\(1 \le u \le n\), \(u \neq v\)) и мысленно проводит в дереве двунаправленное ребро веса \(x\) из \(v\) в \(u\). Затем Яся находит простой цикл в получившемся графе и считает побитовое исключающее «ИЛИ» от всех рёбер на нём. Она хочет выбрать такую вершину \(u\), чтобы посчитанное значение было максимально. Это посчитанное значение и будет ответом на запрос. Можно показать существование и единственность такого цикла в указанных ограничениях (независимо от выбора \(u\)). Если ребро между \(v\) и \(u\) уже существовало, простым циклом будет путь \(v \to u \to v\). Обратите внимание, что запрос второго типа выполняется мысленно, то есть дерево после него никак не меняется. Помогите Ясе ответить на все запросы. Выходные данные Для каждого набора входных данных выведите ответы на запросы второго типа. | |
![]()
|
|
D. Задача про строку "a"
математика
Перебор
реализация
Строки
строковые суфф. структуры
хэши
*2000
Вам дана строка \(s\), состоящая из строчных латинских букв. Подсчитайте количество непустых строк \(t \neq\) «\(\texttt{a}\)», таких, что можно разбить\(^{\dagger}\) \(s\) на некоторые подстроки, удовлетворяющие следующим условиям: - каждая подстрока равна либо \(t\), либо «\(\texttt{a}\)», и
- хотя бы одна подстрока равна \(t\).
\(^{\dagger}\) Разбиение строки \(s\) — это упорядоченная последовательность некоторых \(k\) строк \(t_1, t_2, \ldots, t_k\) (называемых подстроками), таких, что \(t_1 + t_2 + \ldots + t_k = s\), где \(+\) обозначает операцию конкатенации строк. Выходные данные Для каждого набора входных данных выведите одно целое число — количество непустых строк \(t \neq\) «\(\texttt{a}\)», удовлетворяющих всем ограничениям. Примечание В первом наборе входных данных \(t\) может быть «\(\texttt{aa}\)», «\(\texttt{aaa}\)», «\(\texttt{aaaa}\)» или всей строкой. Во втором наборе входных данных \(t\) может быть «\(\texttt{b}\)», «\(\texttt{bab}\)», «\(\texttt{ba}\)» или всей строкой. В третьем наборе входных данных единственной подходящей \(t\) является вся строка. | |
![]()
|
|
A. Создание слов
реализация
Строки
*800
Мэттью получил две строки \(a\) и \(b\), обе длиной \(3\). Ему кажется особенно забавным создать два новых слова, поменяв местами первый символ \(a\) с первым символом \(b\). Он хочет, чтобы вы вывели \(a\) и \(b\) после обмена. Обратите внимание, что новые слова не обязательно будут разными. Выходные данные Для каждого набора входных данных после обмена выведите \(a\) и \(b\), разделенные пробелом. | |
![]()
|
|
B. Подстрока и подпоследовательность
жадные алгоритмы
Перебор
Строки
*1200
Задано две строки \(a\) и \(b\), состоящие из строчных латинских букв. Подпоследовательность строки — это строка, которую можно получить из исходной строки удалением любого количества символов (возможно, ни одного). Подстрока строки — это ее непрерывная подпоследовательность. Например, рассмотрим строку abac: - a, b, c, ab, aa, ac, ba, bc, aba, abc, aac, bac и abac — подпоследовательности этой строки;
- a, b, c, ab, ba, ac, aba, bac и abac — подстроки этой строки.
Ваша задача — вычислить минимально возможную длину строки, которая содержит \(a\) в качестве подстроки и \(b\) в качестве подпоследовательности. Выходные данные Для каждого набора выведите одно целое число — минимально возможную длину строки, которая содержит \(a\) в качестве подстроки и \(b\) в качестве подпоследовательности. Примечание В приведенных ниже примерах подпоследовательность символов, соответствующая строке \(b\), выделена жирным шрифтом. В первом примере один из возможных ответов — caba. Во втором примере один из возможных ответов — ercf. В третьем примере один из возможных ответов — mmm. В четвертом примере один из возможных ответов — contest. В пятом примере один из возможных ответов — abcdefg. | |
![]()
|
|
E. Ошибка новичка
Конструктив
математика
Перебор
реализация
Строки
*1700
Одна из первых задач K1o0n по программированию выглядела так: «У Noobish_Monk есть \(n\) \((1 \le n \le 100)\) друзей. На день рождения каждый из них подарил \(a\) \((1 \le a \le 10000)\) яблок. Обрадовавшись такому подарку, Noobish_Monk вернул \(b\) \((1 \le b \le \min(10000, a \cdot n))\) яблок друзьям. Сколько яблок осталось у Noobish_Monk?» K1o0n написал решение, но случайно считал значение \(n\) как строку, поэтому значение \(n \cdot a - b\) было посчитано по-другому. Конкретно: - при умножении строки \(n\) на число \(a\) он получит строку \(s=\underbrace{n + n + \dots + n + n}_{a\ \text{раз}}\)
- при вычитании из строки \(s\) числа \(b\), из неё удалятся последние \(b\) символов, если \(b\) больше или равно длине строки \(s\), то она станет пустой.
Узнав об этом, ErnKor стало интересно, сколько для данного \(n\) существует пар \((a, b)\), удовлетворяющих ограничениям задачи, на которых решение K1o0n выдаёт правильный ответ. «Решение выдаёт правильный ответ» означает, что оно выводит непустую строку, и эта строка при переводе в целое число равна правильному ответу, то есть значению \(n \cdot a - b\). Выходные данные Для каждого набора входных данных выведите ответ в следующем формате: В первой строке выведите число \(x\) — количество плохих тестов для заданного \(n\). В следующих \(x\) строках выведите по два числа \(a_i\) и \(b_i\) — такие числа, что решение K1o0n выдает на тест «\(n\) \(a_i\) \(b_i\)» выдаёт правильный ответ. Примечание В первом примере \(a = 20\), \(b = 18\) подходят, так как «\(\text{2}\)» \(\cdot 20 - 18 =\) «\(\text{22222222222222222222}\)» \(- 18 = 22 = 2 \cdot 20 - 18\) | |
![]()
|
|
H. Fortnite
жадные алгоритмы
игры
интерактив
Комбинаторика
Конструктив
математика
Строки
теория чисел
хэши
*3500
Это интерактивная задача! Тимофей пишет соревнование, которое называется Capture the flag (или сокращённо CTF). Ему осталась одна задача, в которой нужно взломать систему безопасности. Вся система основана на полиномиальных хеш-функциях\(^{\text{∗}}\). Тимофей может ввести в систему строку, состоящую из строчных латинских букв, и система выдаст её полиномиальный хеш. Чтобы взломать систему, Тимофею нужно узнать параметры полиномиального хеша, которые использует система (\(p\) и \(m\)). У Тимофея осталось очень мало времени, поэтому он успеет сделать только \(3\) запроса. Помогите ему решить задачу. Протокол взаимодействия Чтобы сделать запрос в систему выведите ? \(s\), где \(s\) — строка, длины не более \(50\), хеш которой вы хотите узнать. В ответ на этот запрос вы получите полиномиальный хеш строки \(s\). Чтобы вывести ответ, выведите ! \(p\) \(m\), где — \(p\) основание хеша, а \(m\) — модуль. После этого сразу же переходите к следующему набору входных данных. Вы должны сделать не более \(3\) запросов ?, в противном случае вы получите вердикт Wrong Answer. После вывода запроса не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте: - fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Примечание Ответом на первый запрос будет \((ord(a) \cdot 31^0 + ord(a) \cdot 31^1) \mod 59 = (1 + 1 \cdot 31) \mod 59 = 32\). Ответом на второй запрос является \((ord(y) \cdot 31^0 + ord(b) \cdot 31^1) \mod 59 = (25 + 2 \cdot 31) \mod 59 = 28\). | |
![]()
|
|
D. Падежи
битмаски
дп
Перебор
Строки
*2300
Вы лингвист, изучающий загадочный древний язык. Вы знаете, что - Его слова состоят только из первых \(c\) букв латинского алфавита.
- Каждое слово имеет падеж, который можно однозначно определить по его последней букве (разные буквы соответствуют разным падежам). Например, слова "ABACABA" и "ABA" (если они существуют) имеют одинаковый падеж в этом языке, потому что у них обоих одинаковое окончание 'A', в то время как "ALICE" и "BOB" принадлежат разным падежам. Если в языке нет падежа, соответствующего какой-либо букве, это означает, что слово не может заканчиваться на эту букву.
- Длина каждого слова составляет \(k\) или меньше.
У вас есть один текст, написанный на этом языке. К сожалению, поскольку язык действительно древний, пробелы между словами отсутствуют, и все буквы заглавные. Вам интересно, каково минимальное количество падежей может быть в этом языке. Можете ли вы это выяснить? Выходные данные Для каждого набора входных данных выведите одну строку, состоящую из одного целого числа, — минимальное количество падежей в языке. Примечание В первом наборе входных данных в языке должно быть пять падежей (для каждой из букв 'A', 'B', 'C', 'D', и 'E' должен быть падеж, который имеет соответствующее окончание). В четвертом наборе входных данных достаточно одного падежа с окончанием 'B'. | |
![]()
|
|
C. Сортировка
дп
жадные алгоритмы
сортировки
Строки
*1200
Вам даны две строки \(a\) и \(b\) длиной \(n\). Затем вам (против вашей воли) придется ответить на \(q\) запросов. Для каждого запроса вам дан отрезок, ограниченный позициями \(l\) и \(r\). За одну операцию вы можете выбрать целое число \(i\) (\(l \leq i \leq r\)) и установить \(a_i = x\), где \(x\) — любой символ, который вы захотите. Выведите минимальное количество операций, которые вам нужно выполнить, чтобы \(\texttt{sorted(a[l..r])} = \texttt{sorted(b[l..r])}\). Операции, которые вы выполняете в одном запросе, не влияют на другие запросы. Для произвольной строки \(c\), \(\texttt{sorted(c[l..r])}\) обозначает подстроку, состоящую из символов \(c_l, c_{l+1}, ... , c_r\), отсортированных в лексикографическом порядке. Выходные данные Для каждого запроса выведите целое число, минимальное количество операций, которые вам нужно выполнить, на новой строке. Примечание Для первого запроса \(\texttt{sorted(a[1..5])} =\) abcde и \(\texttt{sorted(b[1..5])} =\) abcde, поэтому операции не требуются. Для второго запроса вам нужно установить \(a_1 = \) e. Тогда \(\texttt{sorted(a[1..4])} = \texttt{sorted(b[1..4])} = \) bcde. | |
![]()
|
|
A. Сильный пароль
Перебор
реализация
Строки
*800
Текущий пароль Монокарпа на Codeforces — это строка \(s\), состоящая из строчных латинских букв. Монокарп считает, что его текущий пароль слишком слабый, поэтому он хочет вставить ровно одну строчную латинскую букву в пароль, чтобы сделать его сильнее. Монокарп может выбрать любую букву и вставить ее в любое место, даже перед первым символом или после последнего символа. Монокарп считает, что сила пароля пропорциональна времени, которое ему требуется для его ввода. Время, необходимое для ввода пароля, рассчитывается следующим образом: - время для ввода первого символа составляет \(2\) секунды;
- для каждого символа, кроме первого, время ввода составляет \(1\) секунда, если он такой же, как предыдущий символ, или \(2\) секунды в противном случае.
Например, время, необходимое для ввода пароля abacaba, составляет \(14\); время, необходимое для ввода пароля a, составляет \(2\); время, необходимое для ввода пароля aaabacc, составляет \(11\). Вам нужно помочь Монокарпу — вставить строчную латинскую букву в его пароль так, чтобы получившийся пароль требовал максимально возможное время для ввода. Выходные данные Для каждого набора входных данных выведите новый пароль — строку, которую можно получить из \(s\), вставив одну строчную латинскую букву. Строка, которую вы выводите, должна занимать максимальное возможное время для ввода. Если есть несколько ответов, выведите любой из них. | |
![]()
|
|
D. Экзамен Славика
жадные алгоритмы
реализация
Строки
*1100
У Славика очень сложный экзамен, и ему нужна ваша помощь, чтобы его сдать. Вот задача, с которой он столкнулся: Дана строка \(s\), которая состоит из строчных английских букв и, возможно, нуля или более «?». Славик должен заменить каждый «?» на строчную английскую букву так, чтобы строка \(t\) стала подпоследовательностью (необязательно непрерывной) строки \(s\). Выведите любую подходящую строку или скажите, что это невозможно, если не существует строки, которая соответствует условиям. Выходные данные Для каждого набора входных данных, если такой строки не существует, как описано в условии, выведите «NO» (без кавычек). В противном случае выведите «YES» (без кавычек). Затем выведите одну строку — строку, которая соответствует всем условиям. Вы можете выводить «YES» и «NO» в любом регистре (например, строки «yEs», «yes», и «Yes» будут признаны положительным ответом). Если возможно несколько ответов, вы можете вывести любой из них. | |
![]()
|
|
A. Первостепенная задача
математика
реализация
Строки
*800
Дмитрий записал на доске \(t\) чисел, и это хорошо. Он уверен, что потерял среди них важное число \(n\), и это плохо. Число \(n\) имело вид \(\text{10^x}\) (\(x \ge 2\)), где символ '\(\text{^}\)' обозначает возведение в степень. Что-то пошло не так, и Дмитрий при записи важного числа пропустил символ '\(\text{^}\)'. Например, вместо числа \(10^5\) он бы записал \(105\), а вместо \(10^{19}\) он бы записал \(1019\). Дмитрий хочет понять, какие из чисел на доске могли быть важным числом, а какие нет. Выходные данные Для каждого числа с доски выведите «YES», если оно могло быть важным числом и «NO» иначе. Вы можете выводить каждую букву в любом регистре (строчную или заглавную). Например, строки «yEs», «yes», «Yes» и «YES» будут приняты как положительный ответ. | |
![]()
|
|
C. Числовой шаблон строки
Строки
Структуры данных
*1000
У Кристины есть массив \(a\), называемый шаблоном, и состоящий из \(n\) целых чисел. Также у нее есть \(m\) строк, каждая из которых состоит только из строчных латинских букв. Строки пронумерованы от \(1\) до \(m\). Она хочет проверить, какие из них соответствуют шаблону. Считается, что некоторая строка \(s\) соответствует шаблону, если одновременно верны все следующие условия: - Длина строки \(s\) равна количеству элементов в массиве \(a\).
- Одинаковым числам из \(a\) соответствуют одинаковые символы из \(s\). То есть, если \(a_i = a_j\), то \(s_i = s_j\) для (\(1 \le i, j \le n\)).
- Одинаковым символам из \(s\) соответствуют одинаковые числа из \(a\). То есть, если \(s_i = s_j\), то \(a_i = a_j\) для (\(1 \le i, j \le n\)).
Другими словами, между символами строки и элементами массива должно существовать взаимно-однозначное соответствие. Например, если \(a\) = [\(3, 5, 2, 1, 3\)], то строка «abfda» соответствует шаблону, а строка «afbfa» — нет, так как символу «f» одновременно соответствуют числа \(1\) и \(5\). Выходные данные Для каждого набора входных данных выведите \(m\) строк. На \(i\)-й строке (\(1 \le i \le m\)) выведите: - «YES», если строка с индексом \(i\) соответствует шаблону;
- «NO» иначе.
Вы можете выводить ответ в любом регистре (например, строки «yEs», «yes», «Yes» и «YES» будут распознаны как положительный ответ). Примечание Первый набор входных данных разобран в условии задачи. | |
![]()
|
|
A. Черепаха и хорошие строки
жадные алгоритмы
Строки
*800
Черепаха считает строку \(s\) хорошей строкой, если существует последовательность строк \(t_1, t_2, \ldots, t_k\) (\(k\) — произвольное целое число) такая, что: - \(k \ge 2\).
- \(s = t_1 + t_2 + \ldots + t_k\), где \(+\) обозначает операцию конкатенации. Например, \(\texttt{abc} = \texttt{a} + \texttt{bc}\).
- Для всех \(1 \le i < j \le k\) первый символ \(t_i\) не равен последнему символу \(t_j\).
Черепахе дана строка \(s\), состоящая из строчных латинских букв. Пожалуйста, скажите ей, является ли строка \(s\) хорошей строкой! Выходные данные Для каждого набора входных данных выведите «YES», если строка \(s\) является хорошей строкой, и «NO» в противном случае. Вы можете выводить ответ в любом регистре (верхнем или нижнем). Например, строки «yEs», «yes», «Yes» и «YES» будут распознаны как положительные ответы. Примечание В первом наборе входных данных последовательность строк \(\texttt{a}, \texttt{a}\) удовлетворяет условию \(s = t_1 + t_2 + \ldots + t_k\), но первый символ \(t_1\) равен последнему символу \(t_2\). Можно увидеть, что не существует никакой последовательности строк, которая удовлетворяет всем условиям, поэтому ответ «NO». В третьем наборе входных данных последовательность строк \(\texttt{ab}, \texttt{cb}\) удовлетворяет всем условиям. В четвертом наборе входных данных последовательность строк \(\texttt{abca}, \texttt{bcab}, \texttt{cabc}\) удовлетворяет всем условиям. | |
![]()
|
|
C. Черепаха и хорошие пары
жадные алгоритмы
Конструктив
сортировки
Строки
*1200
Черепаха дает вам строку \(s\), состоящую из строчных латинских букв. Черепаха считает пару целых чисел \((i, j)\) (\(1 \le i < j \le n\)) приятной парой, если и только если существует целое число \(k\), такое что \(i \le k < j\) и выполняются оба из следующих двух условий: - \(s_k \ne s_{k + 1}\);
- \(s_k \ne s_i\) или \(s_{k + 1} \ne s_j\).
Кроме того, Черепаха считает пару целых чисел \((i, j)\) (\(1 \le i < j \le n\)) хорошей парой, если и только если \(s_i = s_j\) или \((i, j)\) является приятной парой. Черепаха хочет переставить буквы в строке \(s\) так, чтобы количество хороших пар было максимизировано. Пожалуйста, помогите ей! Выходные данные Для каждого набора выведите строку \(s\) после перестановки букв, которая максимизирует количество хороших пар. Если есть несколько ответов, выведите любой из них. Примечание В первом наборе \((1, 3)\) является хорошей парой в строке из переставленных букв. Можно заметить, что мы не можем переставить буквы так, чтобы количество хороших пар было больше \(1\). bac и cab также могут быть ответом. Во втором наборе \((1, 2)\), \((1, 4)\), \((1, 5)\), \((2, 4)\), \((2, 5)\), \((3, 5)\) являются хорошими парами в строке из переставленных букв. efddd также может быть ответом. | |
![]()
|
|
C. Лентяй Нарек
дп
реализация
Строки
*1800
Нареку лень придумывать третью задачу этого контеста, поэтому его друг Артур предложил использовать ChatGPT. ChatGPT сгенерировал \(n\) задач, каждая из которых состоит из \(m\) букв, и Нарек рассматривает их как \(n\) строк. Чтобы усложнить задачу, он комбинирует задачи, выбирая некоторые из \(n\) строк (возможно, ни одной) и располагая их без изменения порядка. Его шанс решить задачу определяется как \(score_n - score_c\), где \(score_n\) — счёт Нарека, а \(score_c\) — счёт ChatGPT. Нарек вычисляет \(score_n\), изучая выбранную строку (он двигается слева направо). Изначально он ищет букву \(\texttt{«n»}\), после неё буквы \(\texttt{«a»}\), \(\texttt{«r»}\), \(\texttt{«e»}\) и \(\texttt{«k»}\). Найдя все вхождения этих букв, он увеличивает \(score_n\) на \(5\) и возобновляет поиск \(\texttt{«n»}\) (он не возвращается назад, а просто продолжает с того места, на котором остановился). После того как Нарек закончит, ChatGPT просматривает строку и увеличивает \(score_c\) на \(1\) для каждой буквы \(\texttt{«n»}\), \(\texttt{«a»}\), \(\texttt{«r»}\), \(\texttt{«e»}\), или \(\texttt{«k»}\), которые Нарек не смог использовать. Обратите внимание, что если Нарек не смог завершить последнее вхождение, найдя все \(5\) букв, то использованные им буквы учитываются в счёте ChatGPT \(score_c\), а Нарек не получает никаких очков, если он не закончил поиск всех 5 букв. Помогите Нареку максимизировать значение \(score_n - score_c\), выбрав наиболее оптимальное подмножество начальных строк. Выходные данные Для каждого набора входных данных выведите одно целое число: максимально возможное значение \(score_n - score_c\). Примечание В первом наборе входных данных один из оптимальных ответов — когда Нарек не выбирает ни одну из строк, поэтому ответ равен \(0\). В качестве альтернативы он может выбрать все строки. В этом случае полная строка становится «nnaarreekk». Нарек может выбрать первые появления всех букв и добавить к счету \(5\). Его соперник добавит по \(1\) за все вторые появления, что в сумме составит \(5\). Поэтому ответ будет \(5 - 5 = 0\). В третьем наборе входных данных единственный оптимальный ответ — когда Нарек не выбирает строку. Обратите внимание, что если бы он выбрал строку, то не смог бы найти последнюю букву «k», поэтому его счёт остался бы на уровне \(0\), а не стал бы \(5\). Затем ChatGPT добавил бы \(4\) за \(4\) буквы, и разница счётов стала бы \(0 - 4 = -4\). В последнем наборе входных данных Нареку нужно выбрать первую и последнюю строки. Поместив эти две строки рядом друг с другом, он получает «\({\color{red}{n}}rr{\color{red}{a}}{\color{red}{r}}{\color{red}{e}}{\color{red}{k}}{\color{red}{n}}k{\color{red}{a}}{\color{red}{r}}{\color{red}{e}}{\color{red}{k}}{\color{blue}{z}}\)». Нарек может выбрать буквы, отмеченные красным цветом, и добавить к своему счету \(10\). Так как буквы чёрного цвета, которые оставил Нарек, может забрать соперник (они используются в слове «Нарек»), то он прибавляет к счету все остальные буквы и получает счет \(3\). Таким образом, ответ составляет \(10 - 3 = 7\). | |
![]()
|
|
B. Квадрат или нет
математика
Перебор
Строки
*800
Красивая двоичная матрица — это матрица, по краям которой стоят единицы, а внутри нули.  Примеры четырёх красивых двоичных матриц. Примеры четырёх красивых двоичных матриц. Сегодня Сакурако играла с красивой двоичной матрицей размера \(r \times c\) и сделала из неё двоичную строку \(s\), выписав все строки матрицы, начиная с первой и заканчивая \(r\)-й. Более формально, элемент из матрицы в \(i\)-й строке и \(j\)-м столбце совпадает с \(((i-1)*c+j)\)-м элементом строки. Необходимо проверить, могла ли красивая матрица, из которой получена строка \(s\), быть квадратной. Иными словами, вам надо проверить, могла ли строка \(s\) быть получена из квадратной красивой бинарной матрицы (то есть такой, что \(r=c\)). Выходные данные Выведите «Yes», если исходная матрица могла быть квадратной, и «No» иначе. Примечание Во втором примере из матрицы можно получить строку 1111: В третьем примере строка 111101111 может быть получена из матрицы: | \(1\) | \(1\) | \(1\) | | \(1\) | \(0\) | \(1\) | | \(1\) | \(1\) | \(1\) |
В четвёртом примере не существует квадратной матрицы, из которой можно получить строку. | |
![]()
|
|
E. Чередующаяся строка
дп
жадные алгоритмы
Перебор
реализация
Строки
Структуры данных
*1500
Сакурако очень любит чередующиеся строки. Она называет строку \(s\) из строчных латинских букв чередующейся строкой, если символы на четных позициях одинаковы, если символы на нечетных позициях одинаковы и длина строки четная. Например, строки 'abab' и 'gg' являются чередующимися, а строки 'aba' и 'ggwp' — нет. Как хороший друг, вы решили подарить такую строку, но не смогли её найти. К счастью, вы можете выполнить два типа операций над строкой: - Выберите индекс \(i\) и удалите из строки \(i\)-й символ, что уменьшит длину строки на \(1\). Такую операцию можно выполнить не более \(1\) раза;
- Выберите индекс \(i\) и замените \(s_i\) на любую другую букву.
Поскольку вы торопитесь, вам нужно определить минимальное количество операций, необходимых для превращения строки в чередующуюся. Выходные данные Для каждого тестового случая выведите одно целое число — минимальное количество операций, необходимых для превращения строки \(s\) в чередующуюся. Примечание Для строки ababa можно удалить первый символ, чтобы получить baba, что является чередующейся строкой. Для строки acdada можно изменить первые два символа, чтобы получить dadada, что является чередующейся строкой. | |
![]()
|
|
C1. Ошибка передачи сообщения (простая версия)
Перебор
Строки
*1400
Это упрощенная версия задачи. Она отличается от сложной только ограничениями. В Берляндском государственном университете локальная сеть между серверами не всегда работает без ошибок. При передаче двух одинаковых сообщений подряд возможна ошибка, в результате которой эти два сообщения сливаются в одно. При таком слиянии конец первого сообщения совмещается с началом второго. Конечно, совмещение может происходить только по одинаковым символам. Длина совмещения должна быть положительным числом, меньшим длины текста сообщения. Например, при передаче двух сообщений «abrakadabra» подряд возможно, что оно будет передано с ошибкой описанного вида, и тогда будет получено сообщение вида «abrakadabrabrakadabra» или «abrakadabrakadabra» (в первом случае совмещение произошло по одному символу, а во втором — по четырем). По полученному сообщению t определите, возможно ли, что это результат ошибки описанного вида работы локальной сети, и если возможно, определите возможное значение s. Не следует считать ошибкой ситуацию полного наложения друга на друга двух сообщений. К примеру, если получено сообщение «abcd», следует считать, что в нём ошибки нет. Аналогично, простое дописывание одного сообщения вслед за другим не является признаком ошибки. Например, если получено сообщение «abcabc», следует считать, что в нём ошибки нет. Выходные данные Если сообщение t не может содержать ошибки, выведите «NO» (без кавычек) в единственную строку выходных данных. В противном случае в первой строке выведите «YES» (без кавычек), а в следующей строке выведите строку s — возможное сообщение, которое могло привести к ошибке. Если возможных ответов несколько, разрешается вывести любой из них. Примечание Во втором примере подходящим ответом также является строка acacaca. | |
![]()
|
|
C2. Ошибка передачи сообщения (сложная версия)
Строки
строковые суфф. структуры
хэши
*1700
Это усложнённая версия задачи. Она отличается от простой только ограничениями. В Берляндском государственном университете локальная сеть между серверами не всегда работает без ошибок. При передаче двух одинаковых сообщений подряд возможна ошибка, в результате которой эти два сообщения сливаются в одно. При таком слиянии конец первого сообщения совмещается с началом второго. Конечно, совмещение может происходить только по одинаковым символам. Длина совмещения должна быть положительным числом, меньшим длины текста сообщения. Например, при передаче двух сообщений «abrakadabra» подряд возможно, что оно будет передано с ошибкой описанного вида, и тогда будет получено сообщение вида «abrakadabrabrakadabra» или «abrakadabrakadabra» (в первом случае совмещение произошло по одному символу, а во втором — по четырем). По полученному сообщению t определите, возможно ли, что это результат ошибки описанного вида работы локальной сети, и если возможно, определите возможное значение s. Не следует считать ошибкой ситуацию полного наложения друга на друга двух сообщений. К примеру, если получено сообщение «abcd», следует считать, что в нём ошибки нет. Аналогично, простое дописывание одного сообщения вслед за другим не является признаком ошибки. Например, если получено сообщение «abcabc», следует считать, что в нём ошибки нет. Выходные данные Если сообщение t не может содержать ошибки, выведите «NO» (без кавычек) в единственную строку выходных данных. В противном случае в первой строке выведите «YES» (без кавычек), а в следующей строке выведите строку s — возможное сообщение, которое могло привести к ошибке. Если возможных ответов несколько, разрешается вывести любой из них. Примечание Во втором примере подходящим ответом также является строка acacaca. | |
![]()
|
|
E. Бот для игры: Камень-ножницы-бумага
*особая задача
жадные алгоритмы
Строки
«Камень-ножницы-бумага» — это игра для двух игроков. Игра состоит из раундов. В каждом раунде каждый игрок выбирает один из трех ходов: камень, бумага или ножницы. В зависимости от выбранных ходов происходит следующее: - если один игрок выбрал камень, а другой игрок выбрал бумагу, выигрывает игрок, выбравший бумагу, и получает одно очко;
- если один игрок выбрал ножницы, а другой игрок выбрал бумагу, выигрывает игрок, выбравший ножницы, и получает одно очко;
- если один игрок выбрал ножницы, а другой игрок выбрал камень, выигрывает игрок, выбравший камень, и получает одно очко;
- если оба игрока выбрали один и тот же ход, никто не выигрывает и никто не получает очко.
Монокарп решил сыграть против бота. В ходе игры Монокарп заметил, что поведение бота очень предсказуемо, а именно: - в первом раунде он выбирает камень;
- в каждом раунде, кроме первого, он выбирает тот ход, который выигрывает у хода оппонента в предыдущем раунде (например, если в предыдущем раунде его оппонент сыграл ножницы, то сейчас бот выберет камень).
У Монокарпа есть любимая строка \(s\), состоящая из символов R, P и/или S. Монокарп решил сыграть серию раундов против бота. Однако он хочет, чтобы выполнялись оба следующих условия: - итоговый счет был в пользу Монокарпа (то есть количество раундов, которые он выиграл, было строго больше, чем количество раундов, которые выиграл бот);
- в последовательности ходов бота (где R обозначает камень, P обозначает бумагу, а S — ножницы) строка \(s\) встречалась как непрерывная подстрока.
Помогите Монокарпу и посчитайте минимальное количество раундов, которое ему необходимо сыграть против бота, чтобы удовлетворить оба вышеописанных условия. Выходные данные Для каждого набора входных данных выведите одно целое число — минимальное количество раундов, которое необходимо сыграть Монокарпу против бота, чтобы удовлетворить оба вышеописанных условия. Примечание В первом примере Монокарп может сыграть PPR, тогда ходы бота будут RSS, и счет будет \(2:1\) в пользу Монокарпа. Во втором примере Монокарп может сыграть P, тогда ход бота будет R, и счет будет \(1:0\) в пользу Монокарпа. В третьем примере Монокарп может сыграть RPR, тогда ходы бота будут RPS, и счет будет \(1:0\) в пользу Монокарпа. В четвертом примере Монокарп может сыграть RRRSPR, тогда ходы бота будут RPPPRS, и счет будет \(3:2\) в пользу Монокарпа. В пятом примере Монокарп может сыграть PRRSPRS, тогда ходы бота будут RSPPRSP, и счет будет \(6:1\) в пользу Монокарпа. В шестом примере Монокарп может сыграть PRRRS, тогда ходы бота будут RSPPP, и счет будет \(3:2\) в пользу Монокарпа. В седьмом примере Монокарп может сыграть RSR, тогда ходы бота будут RPR, и счет будет \(1:0\) в пользу Монокарпа. | |
![]()
|
|
C. Взлом пароля
интерактив
Конструктив
Строки
*1400
Димаш узнал, что Мансур написал про него что-то очень нехорошее своему знакомому, поэтому он решил во что бы ни стало узнать его пароль и узнать, что же именно он написал. Поверив в силу своего пароля, Мансур сообщил, что его пароль — это бинарная строка размера \(n\). А также он готов отвечать на вопросы Димаша следующего вида: Димаш говорит бинарную строку \(t\), и Мансур отвечает, правда ли, что \(t\) является подстрокой его пароля. Помогите Димашу узнать пароль не более чем за \(2n\) операций, иначе Мансур поймет подвох и перестанет с ним общаться. Протокол взаимодействия В начале каждого набора входных данных вначале прочитайте \(n\) (\(1 \le n \le 100\)) — размер бинарной строки. Затем приступайте к ее угадыванию. Для угадывания каждой строки \(s\) вы можете сделать не более \(2n\) запросов следующего вида: - «? t», где \(t\) — бинарная строка, где (\(1 \le |t| \le n\)).
В ответ на этот запрос вы получите \(1\), если \(t\) является подстрокой \(s\), и \(0\) в противном случае. Когда вы узнаете ответ, выведите одну строку следующего формата: - «! s», где \(s\) — бинарная строка размера \(n\).
После этого переходите к решению следующего набора входных данных. Если вы сделаете некорректную попытку или превысите лимит в \(2n\) попыток, вы считаете \(-1\) вместо ответа и получите вердикт Неправильный ответ. В таком случае ваша программа должна немедленно завершиться, чтобы избежать неопределенных вердиктов. После вывода запросов не забудьте выводить символ перевода строки и сбрасывать буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте: - fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Взломы: Для взломов используйте следующий формат: Первая строка должна содержать одно целое число \(t\) (\(1\le t\le 100\)) — количество наборов входных данных. Первая строка каждого набора должна содержать одно число \(n\) (\(1 \le n \le 100\)) — длину строки. А вторая строка должна содержать бинарную строку размера \(n\). Примечание В первом примере задана строка \(010\). Поэтому ответы на запросы следующие: «? 00» \(00\) не является подстрокой \(010\), поэтому ответ \(0\). «? 000» \(000\) не является подстрокой, поэтому ответ \(0\). «? 010» \(010\) является подстрокой, поэтому ответ \(1\). Во втором примере задана строка \(1100\), в третьем \(0110\), а в четвертом \(10\). | |
![]()
|
|
A. ЛНПП
Бинарный поиск
битмаски
жадные алгоритмы
Перебор
реализация
Строки
*800
Настоящее название этой задачи — «Лексикографически наибольшая подпоследовательность-палиндром» — слишком длинное, чтобы уместиться в заголовке страницы. Дана строка s, состоящая только из строчных латинских букв. Найдите ее лексикографически наибольшую подпоследовательность, являющуюся палиндромом. Непустую строку s[p1p2... pk] = sp1sp2... spk (1 ≤ p1 < p2 < ... < pk ≤ |s|) будем называть подпоследовательностью строки s = s1s2... s|s|, где |s| — длина строки s. Например, строки «abcb», «b» и «abacaba» являются подпоследовательностями строки «abacaba». Строка x = x1x2... x|x| лексикографически больше строки y = y1y2... y|y|, если либо |x| > |y| и x1 = y1, x2 = y2, ..., x|y| = y|y|, либо существует такое число r (r < |x|, r < |y|), что x1 = y1, x2 = y2, ..., xr = yr и xr + 1 > yr + 1. Символы в строках сравниваются как их ASCII-коды. Например, строка «ranger» лексикографически больше строки «racecar», а строка «poster» лексикографически больше строки «post». Строка s = s1s2... s|s| называется палиндромом, если она в точности совпадает со строкой rev(s) = s|s|s|s| - 1... s1. Иными словами, строка называется палиндромом, если она читается одинаково как слева направо, так и справа налево. Например, строками-палиндромами являются «racecar», «refer» и «z». Выходные данные Выведите лексикографически наибольшую подпоследовательность строки s, являющуюся палиндромом. Примечание Из всех различных подпоследовательностей строки «radar» палиндромами являются «a», «d», «r», «aa», «rr», «ada», «rar», «rdr», «raar» и «radar». Лексикографически наибольшей из них является «rr». | |
![]()
|
|
C. Ч+К+С
графы
жадные алгоритмы
Конструктив
поиск в глубину и подобное
реализация
Строки
хэши
*2400
Вам даны два сильно связных\(^{\dagger}\) ориентированных графа, в каждом из которых ровно \(n\) вершин, но может быть разное количество рёбер. Посмотрев на них внимательно, вы заметили важную особенность — длина любого цикла в этих графах делится на \(k\). Каждая из \(2n\) вершин относится ровно к одному из двух типов: входящая или исходящая. Для каждой вершины вам известен её тип. Вам нужно определить, можно ли провести ровно \(n\) ориентированных рёбер между исходными графами так, чтобы выполнялись следующие четыре условия: - Концы любого добавленного ребра лежат в разных графах.
- Из каждой исходящей вершины исходит ровно одно добавленное ребро.
- В каждую входящую вершину входит ровно одно добавленное ребро.
- В получившемся графе длина любого цикла делится на \(k\).
\(^{\dagger}\)Сильно связный граф — это граф, в котором из каждой вершины существует путь до любой другой вершины. Входные данные Каждый тест состоит из нескольких наборов входных данных. Первая строка содержит единственное целое число \(t\) (\(1 \le t \le 10^4\)) — количество наборов входных данных. Далее следует описание наборов входных данных. Первая строка каждого набора входных данных содержит два целых числа \(n\) и \(k\) (\(2 \le k \le n \le 2 \cdot 10^5\)) — количество вершин в каждом из графов и значение, на которое делится длина каждого цикла. Вторая строка каждого набора входных данных содержит \(n\) целых чисел \(a_1, a_2, \ldots, a_n\) (\(a_i \in \{0, 1\}\)). Если \(a_i = 0\), то вершина \(i\) первого графа является входящей. Если \(a_i = 1\), то вершина \(i\) первого графа является исходящей. Третья строка каждого набора входных данных содержит одно целое число \(m_1\) (\(1 \le m_1 \le 5 \cdot 10^5\)) — количество рёбер в первом графе. Следующие \(m_1\) строк содержат описания рёбер первого графа. \(i\)-я из них содержит два целых числа \(v_i\) и \(u_i\) (\(1 \le v_i, u_i \le n\)) — ребро в первом графе, ведущее из вершины \(v_i\) в вершину \(u_i\). Далее в таком же формате следует описание второго графа. Следующая строка содержит \(n\) целых чисел \(b_1, b_2, \ldots, b_n\) (\(b_i \in \{0, 1\}\)). Если \(b_i = 0\), то вершина \(i\) второго графа является входящей. Если \(b_i = 1\), то вершина \(i\) второго графа является исходящей. Следующая строка содержит одно целое число \(m_2\) (\(1 \le m_2 \le 5 \cdot 10^5\)) — количество рёбер во втором графе. Следующие \(m_2\) строк содержат описания рёбер второго графа. \(i\)-я из них содержит два целых числа \(v_i\) и \(u_i\) (\(1 \le v_i, u_i \le n\)) — ребро во втором графе, ведущее из вершины \(v_i\) в вершину \(u_i\). Гарантируется, что оба графа являются сильно связными, а также длины всех циклов кратны \(k\). Гарантируется, что сумма \(n\) по всем наборам входных данных не превосходит \(2 \cdot 10^5\). Гарантируется, что сумма \(m_1\) и сумма \(m_2\) по всем наборам входных данных не превосходят \(5 \cdot 10^5\). Выходные данные Для каждого набора входных данных выведите «YES» (без кавычек), если можно провести \(n\) новых рёбер так, чтобы выполнялись все условия, и «NO» (без кавычек) иначе. Вы можете выводить ответ в любом регистре (например, строки «yEs», «yes», «Yes» и «YES» будут распознаны как положительный ответ). Примечание В первом наборе входных данных можно провести из первого графа во второй граф рёбра \((1, 3)\) и \((4, 2)\) (первое число в паре — номер вершины в первом графе, второе число в паре — номер вершины во втором графе), а из второго графа в первый граф провести рёбра \((1, 2)\), \((4, 3)\) (первое число в паре — номер вершины во втором графе, второе число в паре — номер вершины в первом графе). Во втором наборе входных данных всего есть \(4\) входящих вершины и \(2\) исходящих, поэтому нельзя провести \(3\) рёбер. | |
![]()
|
|
A. Два экрана
Бинарный поиск
жадные алгоритмы
Строки
*800
Рассмотрим два экрана, которые могут отображать последовательности заглавных латинских букв. Изначально оба экрана ничего не отображают. За одну секунду вы можете выполнить одно из следующих двух действий: - выбрать экран и заглавную латинскую букву, и добавить эту букву в конец последовательности, отображаемой на этом экране;
- выбрать экран и скопировать последовательность с него на другой экран, перезаписывая последовательность, которая была отображена на другом экране.
Вам нужно вычислить минимальное количество секунд, которое вам нужно потратить, чтобы первый экран отображал последовательность \(s\), а второй экран отображал последовательность \(t\). Выходные данные Для каждого набора входных данных выведите одно целое число — минимально возможное количество секунд, которое вам нужно потратить, чтобы первый экран отображал последовательность \(s\), а второй экран отображал последовательность \(t\). Примечание В первом наборе входных данных возможна следующая последовательность действий: - потратить \(6\) секунд, чтобы написать последовательность GARAGE на первом экране;
- скопировать последовательность с первого экрана на второй экран;
- потратить \(7\) секунд, чтобы завершить последовательность на втором экране, написав FORSALE.
Во втором наборе входных данных возможна следующая последовательность действий: - потратить \(1\) секунду, чтобы написать последовательность A на втором экране;
- скопировать последовательность со второго экрана на первый экран;
- потратить \(4\) секунды, чтобы завершить последовательность на первом экране, написав BCDE;
- потратить \(4\) секунды, чтобы завершить последовательность на втором экране, написав ABCD.
В третьем наборе входных данных самый быстрый способ — это набрать оба сообщения по одному символу, что займет \(16\) секунд. | |
![]()
|
|
B. Замена
игры
Конструктив
Строки
*1100
У вас есть бинарная строка\(^{\text{∗}}\) \(s\) длины \(n\), и Айрис дал вам другую бинарную строку \(r\) длины \(n-1\). Айрис собирается сыграть с вами в игру. В ходе игры вы выполните \(n-1\) операций над \(s\). В \(i\)-й операции (\(1 \le i \le n-1\)): - Сначала вы выбираете индекс \(k\) такой, что \(1\le k\le |s| - 1\) и \(s_{k} \neq s_{k+1}\). Если выбрать такой индекс невозможно, вы проигрываете;
- Затем вы заменяете \(s_ks_{k+1}\) на \(r_i\). Обратите внимание, что это уменьшает длину \(s\) на \(1\).
Если все \(n-1\) операций выполнены успешно, вы выигрываете. Определите, возможно ли вам выиграть в этой игре. Выходные данные Для каждого набора входных данных выведите «YES» (без кавычек), если вы можете выиграть, и «NO» (без кавычек) в противном случае. Вы можете выводить каждую букву в любом регистре (строчную или заглавную). Например, строки «yEs», «yes», «Yes» и «YES» будут приняты как положительный ответ. Примечание В первом наборе входных данных вы не можете выполнить первую операцию. Таким образом, вы проигрываете. Во втором наборе входных данных вы можете выбрать \(k=1\) в единственной операции, и после этого \(s\) станет равным \(\mathtt{1}\). Таким образом, вы выигрываете. В третьем наборе входных данных вы можете выполнить следующие операции: \(\mathtt{1}\underline{\mathtt{10}}\mathtt{1}\xrightarrow{r_1=\mathtt{0}} \mathtt{1}\underline{\mathtt{01}} \xrightarrow{r_2=\mathtt{0}} \underline{\mathtt{10}} \xrightarrow{r_3=\mathtt{1}} \mathtt{1}\). | |
![]()
|
|
I. Polyathlon
Бинарный поиск
Строки
строковые суфф. структуры
Структуры данных
хэши
*2500
Berland is this year's host country of the International Collegiate Polyathlon Competition! Similar to biathlon being a competition of two sports, polyathlon is a competition of many sports. This year, there are \(m\) sports. Also, there are \(n\) participants in the event. The sports are numbered from \(1\) to \(m\), and the participants are numbered from \(1\) to \(n\). Some participants are skilled in multiple sports. You are given a binary matrix \(n \times m\) such that the \(j\)-th character of the \(i\)-th row is 1 if the \(i\)-th participant is skilled in the \(j\)-th sport, and 0, otherwise. It's also known that, for each pair of participants, there exists at least one sport such that one of them is skilled in that sport and the other one isn't. The order of sports in the competition is determined at the opening ceremony. Historically, it's done by the almighty Random Number Generator. A random number \(x\) from \(1\) to \(m\) is rolled. The competition then starts with the sport \(x\), then the sport \((x \bmod m + 1)\) is played, then the sport \(((x + 1) \bmod m + 1)\), and so on. Each sport is played as follows. If all remaining participants (all participants which are not eliminated yet) are not skilled in that sport, everyone goes through to the next sport. Otherwise, all skilled participants go through to the next sport, and all unskilled participants are eliminated from the competition. Once there is a single participant remaining in the competition, the competition ends, and that participant is declared the winner. As an organizer of the competition, you are curious of the possible outcomes of the competition beforehand (not that you are going to rig the random roll, how could you possibly think that...). For each sport \(x\), print the index of the winner if the competition starts with the sport \(x\). Output Print \(m\) integers. For each \(x\) from \(1\) to \(m\), print the index of the winner if the competition starts with the sport \(x\). | |
![]()
|
|
B. Shohag любит строки
жадные алгоритмы
Конструктив
реализация
Строки
*1000
Для строки \(p\) определим \(f(p)\) — количество уникальных непустых подстрок\(^{\text{∗}}\) строки \(p\). У Shohag есть строка \(s\). Помогите ему найти непустую строку \(p\), такую, что \(p\) является подстрокой \(s\), а \(f(p)\) чётно, или скажите, что такой строки не существует. Выходные данные Для каждого набора входных данных выведите непустую строку, удовлетворяющую условиям, или \(-1\), если такой строки не существует. Если существует несколько решений, выведите любое из них. Примечание В первом наборе входных данных мы можем выбрать \(p = \) abaa, потому что это подстрока \(s\), а уникальными подстроками \(p\) являются a, b, aa, ab, ba, aba, baa и abaa — всего \(8\) уникальных подстрок, что является чётным числом. Во втором наборе входных данных мы можем выбрать только \(p = \) a, но у этой строки есть одна уникальная подстрока, что является нечётным числом, поэтому эта строка не подходит. В третьем наборе входных данных вся строка содержит \(52\) уникальных подстроки, поэтому сама строка является корректным ответом. | |
![]()
|
|
I. Auto Complete
Бинарный поиск
Деревья
реализация
сортировки
Строки
Структуры данных
хэши
*2300
 You are designing a snazzy new text editor, and you want to add a nifty auto-complete feature to help users save time. Here is how it will work: if a user types "App", your editor will magically suggest the word "Application"! Even better, users can personalize the words that auto-complete in your editor. Your editor will support 4 kinds of operations (Let's say the current text in your editor is \(t\)): - Add an auto complete pattern \(p_i\).
- Delete an auto complete pattern \(p_i\).
- Append a string \(s\) to the end of \(t\).
- Delete \(c\) characters from the end of \(t\). Note that if \(c\) is larger then the length of \(t\), delete all the characters from \(t\).
After each action, your editor should suggest an auto-complete candidate \(i\) that matches the following criteria: - The string \(p_i\) has a prefix equal to \(t\).
- If there are multiple \(p_i\), pick the longest one.
- If there are still multiple \(p_i\), pick the one with the smallest lexicographic order.
- If there are still multiple \(p_i\), pick the one with the smallest ID.
To simplify the question, for each action, print the suggested auto complete pattern ID. If there's no match, print -1. For example, let us say we have three candidates: "alice", "bob", and "charlie", with ID 1, 2, and 3. At first, there is nothing on the screen, so "charlie" (3) should be suggested because it is the longest. Then, let us say the user types "b". You should suggest "bob" (2) because it is the only one that starts with "b". Finally, let us say the user type "body". You should print -1 because there is no matched pattern. Output The program should output \(n\) lines. For each action, output an integer \(i\), which means that after the action, \(p_i\) is the suggested auto complete candidate. If there is no \(p_i\) that matches the requirement, output -1. | |
![]()
|
|
B. Обычная задача
реализация
Строки
*800
На стеклянной витрине магазина написана строка, состоящая только из символов 'p', 'q' и 'w'. Ship проходит мимо магазина, стоя прямо перед стеклянной витриной, и наблюдает строку \(a\). Затем Ship заходит внутрь магазина, смотрит прямо на ту же стеклянную витрину и наблюдает строку \(b\). Ship дает вам строку \(a\). Ваша задача — найти и вывести строку \(b\). Выходные данные Для каждого набора входных данных выведите строку \(b\), строку, которую Ship наблюдает изнутри магазина, на новой строке. | |
![]()
|
|
C. Saraga
жадные алгоритмы
Строки
*1400
The word saraga is an abbreviation of sarana olahraga, an Indonesian term for a sports facility. It is created by taking the prefix sara of the word sarana and the suffix ga of the word olahraga. Interestingly, it can also be created by the prefix sa of the word sarana and the suffix raga of the word olahraga. An abbreviation of two strings \(S\) and \(T\) is interesting if there are at least two different ways to split the abbreviation into two non-empty substrings such that the first substring is a prefix of \(S\) and the second substring is a suffix of \(T\). You are given two strings \(S\) and \(T\). You want to create an interesting abbreviation of strings \(S\) and \(T\) with minimum length, or determine if it is impossible to create an interesting abbreviation. Output If it is impossible to create an interesting abbreviation, output -1. Otherwise, output a string in a single line representing an interesting abbreviation of strings \(S\) and \(T\) with minimum length. If there are multiple solutions, output any of them. Note Explanation for the sample input/output #1 You can split saga into s and aga, or sa and ga. The abbreviation saraga is interesting, but saga has a smaller length. Explanation for the sample input/output #2 The abbreviation belhijau is also interesting with minimum length, so it is another valid solution. | |
![]()
|
|
H. Missing Separators
дп
сортировки
Строки
строковые суфф. структуры
*2200
You have a dictionary, which is a list of distinct words sorted in alphabetical order. Each word consists of uppercase English letters. You want to print this dictionary. However, there is a bug with the printing system, and all words in the list are printed next to each other without any separators between words. Now, you ended up with a string \(S\) that is a concatenation of all the words in the dictionary in the listed order. Your task is to reconstruct the dictionary by splitting \(S\) into one or more words. Note that the reconstructed dictionary must consist of distinct words sorted in alphabetical order. Furthermore, you want to maximize the number of words in the dictionary. If there are several possible dictionaries with the maximum number of words, you can choose any of them. Output First, output an integer in a single line representing the maximum number of the words in the reconstructed dictionary. Denote this number as \(n\). Then, output \(n\) lines, each containing a single string representing the word. The words must be distinct, and the list must be sorted alphabetically. The concatenation of the words in the listed order must equal \(S\). If there are several possible dictionaries with the maximum number of words, output any of them. | |
![]()
|
|
B. Замените символ
жадные алгоритмы
Комбинаторика
Перебор
Строки
*900
Вам дана строка \(s\) длиной \(n\), состоящая только из строчных латинских букв. Вы должны сделать ровно одну операцию следующего вида: - Выбрать любые два индекса \(i\) и \(j\) (\(1 \le i, j \le n\)). Вы можете выбрать \(i = j\).
- Установить \(s_i := s_j\).
Вам нужно минимизировать количество различных перестановок\(^\dagger\) строки \(s\). Выведите любую строку с наименьшим количеством различных перестановок после выполнения ровно одной операции. \(^\dagger\) Перестановка строки — это расположение её символов в любом порядке. Например, «bac» является перестановкой «abc», но «bcc» — нет. Выходные данные Для каждого набора входных данных выведите требуемую строку \(s\) после выполнения ровно одной операции. Если есть несколько решений, выведите любое из них. Примечание В первом наборе входных данных мы можем получить следующие строки за одну операцию: «abc», «bbc», «cbc», «aac», «acc», «aba» и «abb». Строка «abc» имеет \(6\) различных перестановок: «abc», «acb», «bac», «bca», «cab», и «cba». Строка «cbc» имеет \(3\) различных перестановки: «bcc», «cbc», и «ccb», что является наименьшим из всех получаемых строк. На самом деле, все получаемые строки, кроме «abc», имеют \(3\) перестановки, так что любая из них будет принята. | |
![]()
|
|
C. Кевин и бинарные строки
битмаски
жадные алгоритмы
Перебор
реализация
Строки
*1200
Кевин обнаружил бинарную строку \(s\), которая начинается с 1 и передал её вам. Ваша задача — выбрать две непустые подстроки\(^{\text{∗}}\) строки \(s\) (которые могут пересекаться), чтобы максимизировать значение XOR этих двух подстрок. XOR двух бинарных строк \(a\) и \(b\) определяется как результат операции \(\oplus\), примененной к двум числам, полученным путем представления \(a\) и \(b\) как бинарных чисел, где самый левый бит является старшим. Здесь \(\oplus\) обозначает операцию побитового исключающего ИЛИ (XOR). Выбранные вами строки могут содержать ведущие нули. Выходные данные Для каждого тестового случая выведите четыре целых числа \(l_1, r_1, l_2, r_2\) (\(1 \le l_1 \le r_1 \le |s|\), \(1 \le l_2 \le r_2 \le |s|\)) — в случае если две подстроки, которые вы выбрали, это \(s_{l_1} s_{l_1 + 1} \ldots s_{r_1}\) и \(s_{l_2} s_{l_2 + 1} \ldots s_{r_2}\). Если есть несколько решений, выведите любое из них. Примечание В первом наборе мы можем выбрать \( s_2=\texttt{1} \) и \( s_1 s_2 s_3=\texttt{111} \), и \( \texttt{1}\oplus\texttt{111}=\texttt{110} \). Можно доказать, что невозможно получить больший результат. Кроме того, \( l_1=3\), \(r_1=3\), \(l_2=1\), \(r_2=3 \) также является допустимым решением. Во втором наборе, \( s_1 s_2 s_3=\texttt{100} \), \( s_1 s_2 s_3 s_4=\texttt{1000} \), результат \( \texttt{100}\oplus\texttt{1000}=\texttt{1100} \), что является максимумом. | |
![]()
|
|
D. Максимизация цифровой строки
жадные алгоритмы
математика
Перебор
Строки
*1300
Дана строка \(s\), состоящая из цифр от \(0\) до \(9\). За одно действие можно выбрать любую цифру, кроме \(0\) или самой левой цифры, уменьшить её на \(1\) и поменять с цифрой слева от неё местами. Например, за одну операцию из строки \(1023\) можно получить строки \(1103\), \(1022\). Найдите, какую лексикографически максимальную строку можно получить с помощью этой операции. Выходные данные Для каждого набора входных данных выведите ответ в единственной строке. Примечание В первом примере подойдёт следующая последовательность операций: \(19 \rightarrow 81\). Во втором примере подойдёт следующая последовательность операций: \(1709 \rightarrow 1780 \rightarrow 6180 \rightarrow 6710\). В четвёртом примере подойдёт следующая последовательность операций: \(51476 \rightarrow 53176 \rightarrow 53616 \rightarrow 53651 \rightarrow 55351 \rightarrow 55431\). | |
![]()
|
|
E. Три строки
дп
реализация
Строки
*1500
Даны три строки: \(a\), \(b\) и \(c\), состоящие из строчных латинских букв. Строка \(c\) была получена следующим образом: - На каждом шаге случайно выбиралась строка \(a\) или строка \(b\), и первый символ выбранной строки удалялся из неё и приписывался в конец строки \(c\), пока одна из строк не заканчивалась. После этого оставшиеся символы непустой строки добавлялись в конец \(c\).
- Затем в строке \(c\) было произвольно изменено некоторое количество символов.
Например, из строк \(a=\color{red}{\text{abra}}\) и \(b=\color{blue}{\text{cada}}\) без замен символов могли получиться строки \(\color{blue}{\text{ca}}\color{red}{\text{ab}}\color{blue}{\text{d}}\color{red}{\text{ra}}\color{blue}{\text{a}}\), \(\color{red}{\text{abra}}\color{blue}{\text{cada}}\), \(\color{red}{\text{a}}\color{blue}{\text{cada}}\color{red}{\text{bra}}\). Найдите минимальное количество символов, которые могли быть изменены в строке \(c\). Выходные данные Для каждого набора входных данных выведите одно целое число — минимальное количество символов, которые могли быть изменены в строке \(c\). | |
![]()
|
|
G. Наивные разбиения строк
Бинарный поиск
жадные алгоритмы
математика
Перебор
Строки
теория чисел
хэши
*3400
And I will: love the world that you've adored; wish the smile that you've longed for. Your hand in mine as we explore, please take me to tomorrow's shore. У Коколи есть строка \(t\) длины \(m\), состоящая из строчных латинских букв, и он хотел бы разделить её на части. Он называет пару строк \((x, y)\) прекрасной тогда и только тогда, когда существует последовательность строк \(a_1, a_2, \ldots, a_k\), такая, что: - \(t = a_1 + a_2 + \ldots + a_k\), где \(+\) обозначает конкатенацию строк.
- Для каждого \(1 \leq i \leq k\) выполняется по крайней мере одно из следующих условий: \(a_i = x\), или \(a_i = y\).
У Коколи есть другая строка \(s\) длины \(n\), состоящая из строчных латинских букв. Теперь, для каждого \(1 \leq i < n\), Коколи хочет, чтобы вы определили, является ли пара строк \((s_1s_2 \ldots s_i, \, s_{i+1}s_{i+2} \ldots s_n)\) прекрасной. Обратите внимание: поскольку входные и выходные данные большие, вам, возможно, потребуется оптимизировать их для решения этой задачи. Например, в C++ достаточно использовать следующие строки в начале функции main(): int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr); std::cout.tie(nullptr);
}
Выходные данные Для каждого набора входных данных выведите бинарную строку \(r\) длины \(n - 1\): для каждого \(1 \leq i < n\), если \(i\)-я пара красива, \(r_i=\texttt{1}\); в противном случае, \(r_i=\texttt{0}\). Не выводите пробелы. Примечание В первом наборе входных данных, \(s = \tt aba\), \(t = \tt ababa\). - Для \(i = 1\): Коколи может разделить так: \(t = \texttt{a} + \texttt{ba} + \texttt{ba}\), поэтому пара строк \((\texttt{a}, \texttt{ba})\) прекрасна.
- Для \(i = 2\): Коколи может разделить так: \(t = \texttt{ab} + \texttt{ab} + \texttt{a}\), поэтому пара строк \((\texttt{ab}, \texttt{a})\) прекрасна.
Во втором наборе входных данных, \(s = \tt czzz\), \(t = \tt czzzzzczzz\). - Для \(i = 1\): Можно доказать, что не существует разбиения \(t\) с использованием строк \(\texttt{c}\) и \(\texttt{zzz}\).
- Для \(i = 2\): Коколи может разделить \(t\) на \(\texttt{cz} + \texttt{zz} + \texttt{zz} + \texttt{cz} + \texttt{zz}\).
- Для \(i = 3\): Коколи может разделить \(t\) на \(\texttt{czz} + \texttt{z} + \texttt{z} + \texttt{z} + \texttt{czz} + \texttt{z}\).
| |
![]()
|
|
F. Космическое разбиение
геометрия
математика
Перебор
Строки
хэши
*3200
| Когда артефакт находится у тебя в руках, ткань реальности уступает место своему истинному хозяину — мужчине из Флориды. |
Полимино является связной\(^{\text{∗}}\) фигурой, построенной путем присоединения одного или нескольких равных квадратов \(1 \times 1\) сторона к стороне. Полимино является выпуклым, если для любых двух квадратов в полимино, которые находятся в одной строке или одном столбце, все квадраты между ними также являются частью полимино. Ниже приведены четыре полимино, только первое и второе из которых выпуклые.  Вам дано выпуклое полимино с \(n\) строками и четной площадью. Для каждой строки \(i\) от \(1\) до \(n\) единичные квадраты от столбца \(l_i\) до столбца \(r_i\) являются частью полимино. Другими словами, в \(i\)-й строке находится \(r_i - l_i + 1\) единичных квадратов, которые являются частью полимино: \((i, l_i), (i, l_i + 1), \ldots, (i, r_i-1), (i, r_i)\). Два полимино являются конгруэнтными тогда и только тогда, когда вы можете точно совместить их друг с другом в результате перемещений. Обратите внимание, что вам не разрешается поворачивать или отражать полимино. Определите, возможно ли разбить данное выпуклое полимино на два непересекающихся связных полимино, конгруэнтных друг другу. Следующие примеры иллюстрируют допустимое разбиение каждого из двух выпуклых полимино, показанных выше:  Полученные части полимино не обязательно должны быть выпуклыми. Каждый единичный квадрат должен принадлежать ровно одной из двух частей разбиения. Выходные данные Для каждого набора входных данных выведите одну строку, содержащую либо «YES» или «NO» — может ли полимино быть разбито на части, как описано в задаче. Вы можете выводить каждую букву в любом регистре (строчную или заглавную). Например, строки «yEs», «yes», «Yes», и «YES» будут приняты как положительный ответ. Примечание Первый и второй наборы входных данных являются полимино, показанными в условиях задачи, и могут быть разбиты, как показано на рисунке из условия. Можно показать, что полимино в третьем наборе входных данных, показанное ниже, невозможно разбить. Ни одно из следующих разбиений не является корректным:  В разбиении слева полимино нельзя совместить только перемещениями, а в разбиении справа полимино не являются связными. Можно показать, что полимино в четвертом наборе входных данных, показанное ниже, не поддается разбиению.  Обратите внимание, что хотя вы можете разбить его на два прямоугольника размера \(1 \times 2\), эти прямоугольники нельзя совместить перемещениями. | |
![]()
|
|
E1. Хватит гамать (простая версия)
жадные алгоритмы
Конструктив
Перебор
Строки
хэши
*2500
Это простая версия задачи. Отличие между версиями заключается в том, что в этой версии вам нужно найти только минимальное количество операций. Вы можете делать взломы только в том случае, если решили все версии этой задачи. Вам даны \(n\) массивов, каждый из которых имеет длину \(m\). Обозначим \(j\)-й элемент \(i\)-го массива как \(a_{i, j}\). Гарантируется, что все \(a_{i, j}\) попарно различны. За одну операцию вы можете сделать следующее: - Выбрать какое-то целое число \(i\) (\(1 \le i \le n\)) и целое число \(x\) (\(1 \le x \le 2 \cdot n \cdot m\)).
- Для всех целых чисел \(k\) от \(i\) до \(n\) в порядке возрастания сделать следующее:
- Добавить элемент \(x\) в начало \(k\)-го массива.
- Присвоить \(x\) значение, равное последнему элементу в \(k\)-м массиве.
- Удалить последний элемент из \(k\)-го массива.
Другими словами, вы можете вставить элемент в начало любого массива, после чего все элементы в этом и всех следующих массивах сдвигаются на один вправо. При этом последний элемент последнего массива удаляется. Также вам дано описание массивов, которые необходимо получить после всех операций. То есть после выполнения операций \(j\)-й элемент в \(i\)-м массиве должен быть равен \(b_{i, j}\). Гарантируется, что все \(b_{i, j}\) попарно различны. Определите минимальное количество операций, которое необходимо выполнить, чтобы получить нужные массивы. Выходные данные Для каждого набора входных данных выведите единственное целое число — минимальное количество операций, которые необходимо выполнить. Примечание В первом наборе входных данных подходит следующая последовательность из \(3\) операций: - Применим операцию к первому массиву с \(x = 1\). Тогда в начало первого массива добавится элемент \(1\), а значение \(x\) станет равным \(6\). Последний элемент удалится, и первый массив будет иметь вид \([1, 2]\). Далее, элемент \(x\) добавляется в начало второго массива, и значение \(x\) становится равным \(4\). Последний элемент второго массива удаляется, и оба массива имеют вид \([1, 2]\) и \([6, 3]\) соответственно после первой операции.
- Применим операцию ко второму массиву с \(x = 8\). Тогда первый массив не изменится, и оба массива будут иметь вид \([1, 2]\) и \([8, 6]\) соответственно.
- Применим операцию ко второму массиву при \(x = 7\), тогда оба массива будут иметь необходимый вид \([1, 2]\) и \([7, 8]\) соответственно.
Во втором наборе входных данных получить нужный массив можно только за \(5\) операций. В третьем наборе входных данных подходит следующая последовательность из \(3\) операций: - Применим операцию с \(x = 11\) к первому массиву.
- Применим операцию с \(x = 12\) ко второму массиву.
- Применим операцию с \(x = 13\) к третьему массиву.
| |
![]()
|
|
E2. Хватит гамать (сложная версия)
Конструктив
Перебор
Строки
Структуры данных
хэши
*2900
Это сложная версия задачи. Отличие между версиями заключается в том, что в этой версии вам нужно вывести все операции, которые нужно сделать. Вы можете делать взломы только в том случае, если решили все версии этой задачи. Вам даны \(n\) массивов, каждый из которых имеет длину \(m\). Обозначим \(j\)-й элемент \(i\)-го массива как \(a_{i, j}\). Гарантируется, что все \(a_{i, j}\) попарно различны. За одну операцию вы можете сделать следующее: - Выбрать какое-то целое число \(i\) (\(1 \le i \le n\)) и целое число \(x\) (\(1 \le x \le 2 \cdot n \cdot m\)).
- Для всех целых чисел \(k\) от \(i\) до \(n\) в порядке возрастания сделать следующее:
- Добавить элемент \(x\) в начало \(k\)-го массива.
- Присвоить \(x\) значение, равное последнему элементу в \(k\)-м массиве.
- Удалить последний элемент из \(k\)-го массива.
Другими словами, вы можете вставить элемент в начало любого массива, после чего все элементы в этом и всех следующих массивах сдвигаются на один вправо. При этом последний элемент последнего массива удаляется. Также вам дано описание массивов, которые необходимо получить после всех операций. То есть после выполнения операций \(j\)-й элемент в \(i\)-м массиве должен быть равен \(b_{i, j}\). Гарантируется, что все \(b_{i, j}\) попарно различны. Определите минимальное количество операций, которое необходимо выполнить, чтобы получить нужные массивы, а также выведите саму последовательность всех операций. Выходные данные Для каждого набора входных данных выведите в первой строке единственное целое число — минимальное количество операций, которые необходимо выполнить. Далее, для каждой операции выведите два целых числа \(i\) и \(x\) (\(1 \le i \le n\), \(1 \le x \le 2 \cdot n \cdot m\)) — номер массива, куда вставляется элемент, и значение элемента, соответственно. Если существует несколько возможных последовательностей с минимальным количеством операций, выведите любую из них. Примечание В первом наборе входных данных подходит следующая последовательность из \(3\) операций: - Применим операцию к первому массиву с \(x = 1\). Тогда в начало первого массива добавится элемент \(1\), а значение \(x\) станет равным \(6\). Последний элемент удалится, и первый массив будет иметь вид \([1, 2]\). Далее, элемент \(x\) добавляется в начало второго массива, и значение \(x\) становится равным \(4\). Последний элемент второго массива удаляется, и оба массива имеют вид \([1, 2]\) и \([6, 3]\) соответственно после первой операции.
- Применим операцию ко второму массиву с \(x = 8\). Тогда первый массив не изменится, и оба массива будут иметь вид \([1, 2]\) и \([8, 6]\) соответственно.
- Применим операцию ко второму массиву при \(x = 7\), тогда оба массива будут иметь необходимый вид \([1, 2]\) и \([7, 8]\) соответственно.
Во втором наборе входных данных получить нужный массив можно только за \(5\) операций. В третьем наборе входных данных подходит следующая последовательность из \(3\) операций: - Применим операцию с \(x = 11\) к первому массиву.
- Применим операцию с \(x = 12\) ко второму массиву.
- Применим операцию с \(x = 13\) к третьему массиву.
| |
![]()
|
|
A. Строка
жадные алгоритмы
Конструктив
математика
Строки
*800
Вам дана строка \(s\) длины \(n\), состоящая из символов \(\mathtt{0}\) и \(\mathtt{1}\). За одну операцию вы можете выбрать непустую подпоследовательность \(t\) из \(s\), такую, что любые два соседних символа \(t\) различны. Затем вы инвертируете каждый символ в \(t\) (\(\mathtt{0}\) становится \(\mathtt{1}\), а \(\mathtt{1}\) становится \(\mathtt{0}\)). Например, если \(s=\mathtt{\underline{0}0\underline{101}}\) и \(t=s_1s_3s_4s_5=\mathtt{0101}\), то после операции \(s\) станет \(\mathtt{\underline{1}0\underline{010}}\). Вычислите минимальное количество операций, необходимых для того, чтобы сделать все символы \(s\) равными \(\mathtt{0}\). Напомним, что для строки \(s = s_1s_2\ldots s_n\), любая строка \(t=s_{i_1}s_{i_2}\ldots s_{i_k}\) (\(k\ge 1\)), где \(1\leq i_1 < i_2 < \ldots <i_k\leq n\), является подпоследовательностью \(s\). Выходные данные Для каждого набора входных данных выведите минимальное количество операций, необходимых для изменения всех символов в \(s\) на \(\mathtt{0}\). Примечание В первом наборе входных данных вы можете инвертировать \(s_1\). Строка \(s\) станет \(\mathtt{0}\), поэтому ответ равен \(1\). В четвертом наборе входных данных вы можете выполнить следующие три операции по порядку: - Инвертируйте \(s_1s_2s_3s_4s_5\). Тогда \(s\) станет \(\mathtt{\underline{01010}}\).
- Инвертируйте \(s_2s_3s_4\). Тогда \(s\) станет \(\mathtt{0\underline{010}0}\).
- Инвертируйте \(s_3\). Тогда \(s\) станет \(\mathtt{00\underline{0}00}\).
Можно показать, что вы не можете изменить все символы в \(s\) на \(\mathtt{0}\) менее чем за три операции, поэтому ответ равен \(3\). | |
![]()
|
|
A. Скибидус и Амог'у
жадные алгоритмы
Конструктив
Перебор
реализация
Строки
*800
Скибидус приземляется на чужой планете, где местное племя Амог говорит на языке Амог'у. В Амог'у существуют две формы существительных: единственное и множественное. Учитывая, что корень существительного записывается как \(S\), две формы записываются следующим образом: - Единственное: \(S\) \(+\) «us»
- Множественное: \(S\) \(+\) «i»
Здесь \(+\) обозначает конкатенацию строк. Например, abc \(+\) def \(=\) abcdef. Например, когда \(S\) записывается как «amog», то форма единственного числа записывается как «amogus», а форма множественного числа записывается как «amogi». Обратите внимание, что существительные Амог'у могут иметь пустой корень — в частности, «us» является формой единственного числа для «i». Дано существительное Амог'у в форме единственного числа, пожалуйста, преобразуйте его в соответствующее существительное во множественном числе. Выходные данные Для каждого набора входных данных выведите соответствующее существительное во множественном числе на отдельной строке. | |
![]()
|
|
B. Скибидус и Огайо
Строки
*800
Скибидусу дана строка \(s\), состоящая из строчных латинских букв. Пока \(s\) содержит более чем \(1\) букву, он может: - Выбрать индекс \(i\) (\(1 \leq i \leq |s| - 1\), \(|s|\) обозначает текущую длину \(s\)), такой что \(s_i = s_{i+1}\). Заменить \(s_i\) на любую строчную латинскую букву по своему выбору. Удалить \(s_{i+1}\) из строки.
Скибидус должен определить минимально возможную длину, которую он может достичь за любое количество операций. Выходные данные Для каждого набора входных данных выведите целое число на новой строке — минимально достижимую длину \(s\). Примечание В первом наборе входных данных Скибидус может: - Выполнить операцию на \(i = 2\). Он заменяет \(s_2\) на b и удаляет \(s_3\) из строки. Затем \(s\) становится bb.
- Выполнить операцию на \(i = 1\). Он заменяет \(s_1\) на b и удаляет \(s_2\) из строки. Затем \(s\) становится b.
- Поскольку \(s\) содержит только \(1\) букву, Скибидус не может выполнить больше операций.
Таким образом, ответ равен \(1\) для первого набора входных данных. Во втором наборе входных данных он не может выполнить операцию ни на одном индексе. Поэтому ответ по-прежнему равен длине начальной строки, \(8\). | |
![]()
|
|
E. Скибидус и rizz
жадные алгоритмы
Конструктив
Строки
*1600
С приближением Дня Святого Валентина Скибидус отчаянно нуждается в способе привлечь внимание своей возлюбленной! К счастью, он знает, как это сделать: создать идеальную двоичную строку! Дана двоичная строка\(^{\text{∗}}\) \(t\), пусть \(x\) представляет количество \(\texttt{0}\) в \(t\), а \(y\) представляет количество \(\texttt{1}\) в \(t\). Тогда её баланс определяется как значение \(\max(x-y, y-x)\). Скибидус дает вам три целых числа \(n\), \(m\) и \(k\). Он просит вас помочь ему построить двоичную строку \(s\) длиной \(n+m\) из ровно \(n\) символов \(\texttt{0}\) и \(m\) символов \(\texttt{1}\), так что максимальный баланс среди всех её подстрок\(^{\text{†}}\) равен ровно \(k\). Если это невозможно, выведите -1. Выходные данные Для каждого набора входных данных, если возможно построить строку \(s\), выведите её на новой строке. Если существует несколько возможных строк \(s\), выведите любую. В противном случае выведите -1 на новой строке. Примечание В первом примере мы должны построить \(s\) так, чтобы он содержал одну \(\texttt{0}\), две \(\texttt{1}\) и максимальный баланс \(1\) среди всех её подстрок. Одним из возможных корректных \(s\) является \(\texttt{101}\), потому что: - Рассмотрим подстроку, ограниченную индексами \([1, 1]\). Её баланс равен \(\max(0 - 1, 1 - 0) = 1\).
- Рассмотрим подстроку, ограниченную индексами \([1, 2]\). Её баланс равен \(\max(1 - 1, 1 - 1) = 0\).
- Рассмотрим подстроку, ограниченную индексами \([1, 3]\). Её баланс равен \(\max(1 - 2, 2 - 1) = 1\).
- Рассмотрим подстроку, ограниченную индексами \([2, 2]\). Её баланс равен \(\max(1 - 0, 0 - 1) = 1\).
- Рассмотрим подстроку, ограниченную индексами \([2, 3]\). Её баланс равен \(\max(1 - 1, 1 - 1) = 0\).
- Рассмотрим подстроку, ограниченную индексами \([3, 3]\). Её баланс равен \(\max(0 - 1, 1 - 0) = 1\).
Среди всех возможных подстрок максимальный баланс равен \(1\). Во втором примере подстрока с максимальным балансом — это \(0100\), которая имеет баланс \(max(3-1, 1-3)=2\). | |
![]()
|
|
A. Дабстеп
Строки
*900
Вася работает диджеем в самом лучшем ночном клубе Берляндии, и часто в своих выступлениях он использует музыку в стиле «дабстеп». Недавно он решил взять несколько старых песен и сделать из них дабстеп-ремиксы. Пусть песня состоит из некоторого количества слов. Для того, чтобы сделать дабстеп-ремикс этой песни, Вася вставляет некоторое количество слов «WUB» до первого слова песни (возможно нулевое количество), после последнего слова (возможно нулевое количество) и между словами (между любой парой соседних слов песни хотя бы одно слово «WUB»), а затем склеивает все слова, включая «WUB», в одну строку и проигрывает в клубе. Например, из песни со словами «I AM X» может получиться дабстеп-ремикс «WUBWUBIWUBAMWUBWUBX» и не может получиться дабстеп-ремикс «WUBWUBIAMWUBX». Недавно Петя услышал новую дабстеп-композицию Васи, но так как он не очень любит современную музыку, то решил понять, из какой же песни Вася сделал свой ремикс. Помогите Пете восстановить оригинал. Выходные данные Выведите слова песни, которую Вася использовал для создания дабстеп-ремикса. Слова при выводе разделяйте пробелом. Примечание В первом примере: «WUBWUBABCWUB» = «WUB» + «WUB» + «ABC» + «WUB». Значит, в оригинале песня состоит из одного слова «ABC», так как все слова «WUB» добавил Вася. Во втором примере между всеми соседними словами, а также в начало и в конец, Вася добавил по одному слову «WUB», кроме как между словами «ARE» и «THE» — между ними Вася добавил два «WUB». | |
![]()
|
|
A. Jabber ID
реализация
Строки
*1900
Jabber ID на национальном берляндском сервисе «Babber» должен иметь вид <username>@<hostname>[/resource], где - <username> — это последовательность латинских букв любого регистра, цифр и символа подчеркивания «_», длина <username> от 1 до 16 символов.
- <hostname> — это последовательность слов, разделенных точками (символами «.»), где каждое слово может содержать допустимые символы для <username>, длина каждого слова от 1 до 16. Длина <hostname> — от 1 до 32.
- <resource> — это последовательность латинских букв любого регистра, цифр и символа подчеркивания «_», длина <resource> от 1 до 16 символов.
Квадратные скобки указывают на опциональность заключенного в них — содержимое квадратных скобок может присутствовать или нет. Вот примеры корректных Jabber ID: [email protected], [email protected]/contest. Ваша задача написать программу, которая проверяет заданную строку на соответствие описанным правилам. Выходные данные Выведите YES или NO. | |
![]()
|
|
E. Две перестановки
Строки
Структуры данных
хэши
*2700
Рубик очень увлекается перестановками чисел. Перестановкой a длины n назовем последовательность, состоящую из n различных чисел от 1 до n. Элемент номер i (1 ≤ i ≤ n) перестановки будем обозначать ai. Фурик решил сделать Рубику подарок и придумал для него новую задачу про перестановки. Фурик говорит Рубику две перестановки чисел: перестановку a длиной n и перестановку b длиной m. Рубик должен дать ответ на задачу: сколько существует различных целых чисел d таких, что последовательность c (c1 = a1 + d, c2 = a2 + d, ..., cn = an + d) длины n является подпоследовательностью b. Последовательность a называется подпоследовательностью последовательности b, если найдутся такие индексы i1, i2, ..., in (1 ≤ i1 < i2 < ... < in ≤ m), что a1 = bi1, a2 = bi2, ..., an = bin, где n — длина последовательности a, а m — длина последовательности b. Вам заданы перестановки a и b, помогите Рубику решить описанную задачу. Выходные данные В единственной строке выведите ответ на задачу. | |
![]()
|
|
A. k-Строка
реализация
Строки
*1000
Строка называется k-строкой, если она может быть представлена в виде k копий некоторой строки, записанных подряд. Например, строка aabaabaabaab является одновременно 1-строкой, 2-строкой и 4-строкой, но не является 3-строкой, 5-строкой, 6-строкой и так далее. Очевидно, любая строка является 1-строкой. Вам задана строка s из строчных букв латинского алфавита и целое положительное число k. Требуется переставить буквы в строке s таким образом, чтобы результат являлся k-строкой. Выходные данные Переупорядочите буквы в строке s так, чтобы результат являлся k-строкой. В единственную строку выходных данных выведите результат. Если решений несколько, выведите любое из них. Если решения не существует, выведите «-1» (без кавычек). | |
![]()
|
|
B. Две строки
дп
Строки
Структуры данных
*1900
Подпоследовательностью длины |x| строки s = s1s2... s|s| (где |s| — длина строки s) называется строка x = sk1sk2... sk|x| (1 ≤ k1 < k2 < ... < k|x| ≤ |s|). Вам даны две строки — s и t. Рассмотрим все подпоследовательности строки s, совпадающие со строкой t. Верно ли, что каждый символ строки s находится хотя бы в одной из этих подпоследовательностей? Другими словами, верно ли, что для всех i (1 ≤ i ≤ |s|), существует такая подпоследовательность x = sk1sk2... sk|x| строки s, что x = t и для некоторого j (1 ≤ j ≤ |x|) kj = i. Выходные данные Выведите «Yes» (без кавычек), если каждый символ строки s находится хотя бы в одной из описанных подпоследовательностей, или «No» (без кавычек) в противном случае. Примечание В первом примере строка t может входить в строку s как подпоследовательность тремя способами: abab, abab и abab. При этом каждый символ строки s попадает хотя бы в одно вхождение. Во втором примере 4-й символ строки s не попадает ни в одно вхождение строки t. В третьем примере нет ни одного вхождения строки t в строку s. | |
![]()
|
|
C. Циклическая Задача
Строки
строковые суфф. структуры
Структуры данных
*2700
Несколько дней назад WJMZBMR научился быстро отвечать на запрос «сколько раз строка x встречается в строке s», путем предварительной обработки строки s. Но сейчас он хочет немного усложнить этот запрос. Итак, его новый запрос: «сколько последовательных подстрок s циклически изоморфны данной строке x». Вам дана строка s и n строк xi, для каждой строки xi найдите количество последовательных подстрок s, циклически изоморфных строке xi. Две строки называются циклически изоморфными, если одну из них можно получить из другой путем вращения. Здесь под вращением имеется в виду перемещение некоторого количества подряд идущих символов (возможно, это количество равняется нулю) из начала строки в конец строки в том же порядке. Например, строку «abcde» можно вращением превратить в строку «deabc». Мы можем взять символы «abc» из начала строки и поставить их в конец после «de». Выходные данные Для каждого запроса xi выведите единственное целое число — количество последовательных подстрок в s, которые циклически изоморфны xi. Выводите ответы на запросы в том порядке, в котором запросы заданы во входных данных. | |
![]()
|
|
A. Девушка или Юноша
Перебор
реализация
Строки
*800
В наши дни очень много парней ставят себе фотографии красивых девушек на аватарки на форумах. Из-за этого очень часто сложно определить пол пользователя на форуме. В прошлом году наш герой пообщался в чате на форуме с одной красоткой (как он думал). После этого наш герой и предполагаемая красотка стали общаться еще чаще и в конце концов стали парой в сети. Но вчера наш герой захотел увидеть свою красотку в реальной жизни и, каково же было его удивление, когда красоткой оказался здоровенный мужчина! Наш герой очень расстроился и теперь он, наверное, никогда больше не сможет полюбить. Сейчас к нему пришла в голову идея, как по имени пользователя определить его пол. Вот его метод: если количество различных символов в имени пользователя нечетное, тогда пользователь мужского пола, иначе — женского. Вам дана строка, обозначающая имя пользователя, помогите нашему герою определить по ней пол пользователя по описанному методу. Выходные данные Если пользователь оказался женского пола по методу нашего героя, выведите «CHAT WITH HER!» (без кавычек), иначе, выведите «IGNORE HIM!» (без кавычек). Примечание Рассмотрим первый тестовый пример. В этом примере в имени пользователя «wjmzbmr» 6 различных символов. Это символы: «w», «j», «m», «z», «b», «r». Таким образом по методу нашего героя «wjmzbmr» женского пола, то есть надо вывести «CHAT WITH HER!». | |
![]()
|
|
B. Интернет-адрес
реализация
Строки
*1100
Вася — активный пользователь сети Интернет. Однажды ему очень понравился интернет-ресурс, поэтому он записал его адрес к себе в блокнот. Известно, что адрес записанного ресурса имеет формат: <протокол>://<домен>.ru[/<контекст>] Где: - <протокол> — может быть равен либо «http» (без кавычек) либо «ftp» (без кавычек),
- <домен> — непустая строка, состоящая из строчных букв латинского алфавита,
- часть /<контекст> — может отсутствовать, если она присутствует, то <контекст> — это непустая строка, состоящая из строчных букв латинского алфавита.
Если строка <контекст> отсутствует в адресе, то дополнительный символ «/» не ставится. Таким образом, в адресе либо два символа «/» (те, что идут перед доменом), либо три (один дополнительный перед контекстом). Когда мальчик пришел домой, он обнаружил, что записанный адрес в блокноте не содержит никаких знаков препинания. Наверное, Вася сильно торопился и не стал записывать символы «:», «/», «.». Помогите Васе восстановить возможный адрес записанного интернет ресурса. Выходные данные Выведите единственную строку — адрес интернет-ресурса, который понравился Васе. Если существует несколько адресов, подходящих под ограничения задачи, разрешается вывести любой. Примечание Во втором тестовом примере также возможны ответы: «ftp://httpruru.ru» и «ftp://httpru.ru/ru». | |
![]()
|
|
F. Анализ потока логов
Бинарный поиск
Перебор
реализация
Строки
*2000
Вам задан поток логов о предупреждениях в программе. Каждая запись потока логов представляет собой строку в формате: «2012-MM-DD HH:MM:SS:MESSAGE» (без кавычек). Строка «MESSAGE» состоит из пробелов, заглавных и строчных букв латинского алфавита, а также символов «!», «.», «,», «?». Строка «2012-MM-DD» определяет корректную дату в 2012 году. Строка «HH:MM:SS» определяет корректное время в 24 часовом формате. Описанная запись потока логов обозначает, что в определенное в записи время произошло некоторое предупреждение в программе (описание предупреждения содержит строка «MESSAGE»). Ваша задача вывести первый момент времени, когда количество предупреждений за последние n секунд стало не менее m. Выходные данные Если не существует искомого момента времени выведите -1. Иначе выведите строку в формате «2012-MM-DD HH:MM:SS» (без кавычек) — первый момент времени, когда количество предупреждений за последние n секунд стало не менее m. | |
![]()
|
|
H. Запросы на количество палиндромов
дп
Строки
хэши
*1800
Задана строка s = s1s2... s|s| длины |s|, состоящая из строчных букв латинского алфавита. А также q запросов, каждый запрос описывается двумя целыми числами li, ri (1 ≤ li ≤ ri ≤ |s|). Ответ на запрос — количество подстрок строки s[li... ri], которые являются палиндромами. Строка s[l... r] = slsl + 1... sr (1 ≤ l ≤ r ≤ |s|) называется подстрокой строки s = s1s2... s|s|. Строка t называется палиндромом, если она одинаково читается как слева направо, так и справа налево. Формально, если t = t1t2... t|t| = t|t|t|t| - 1... t1. Выходные данные Выведите q целых чисел — ответы на запросы. Ответы на запросы выводите в том порядке, в котором запросы заданы во входных данных. Выведенные числа разделяйте пробельными символами. Примечание Рассмотрим четвертый запрос в первом тестовом примере. Строка s[4... 6] = «aba». Ее подстроки, являющиеся палиндромами: «a», «b», «a», «aba». | |
![]()
|
|
E. Тест
Строки
хэши
*2200
Иногда делать тесты к задачам трудно. Сейчас Вася делает тесты к новой задаче на строки — входными данными к его задаче является одна строка. У Васи есть 3 неправильных решения этой задачи. Первое выдает неправильный ответ, если входные данные содержат подстроку s1, второе входит в бесконечный цикл, если входные данные содержат подстроку s2, а третье требует слишком много памяти, если входные данные содержат подстроку s3. Вася хочет завалить эти решения одним тестом. Какую наименьшую длину может иметь тест, который не проходят все три Васиных решения? Выходные данные Выведите одно число — наименьшую возможную длину строки, содержащей s1, s2 и s3 как подстроки. | |
![]()
|
|
C. Анаграмма
жадные алгоритмы
Строки
*1800
Строка x называется анаграммой строки y, если можно переставить буквы в строке x, чтобы получилась в точности строка y. Например, строки «DOG» и «GOD» являются анаграммами, строки «BABA» и «AABB» — тоже, а вот строки «ABBAC» и «CAABA» — нет. Вам задано две строки s и t одинаковой длины, состоящие из заглавных букв латинского алфавита. Вам необходимо получить из строки s анаграмму строки t. Вам разрешается выполнять операции замены: каждая операция состоит в замене какого-то символа строки s на любой другой. Получите анаграмму строки t за наименьшее количество операций замены. Если можно получить несколько анаграмм строки t за наименьшее количество операций, получите лексикографически наименьшую строку. Лексикографический порядок строк — это привычный нам порядок «как в словаре». Формально, строка p длины n лексикографически меньше строки q такой же длины, если p1 = q1, p2 = q2, ..., pk - 1 = qk - 1, pk < qk для некоторого k (1 ≤ k ≤ n). Здесь символы в строках нумеруются от 1. Символы строк сравниваются по алфавитному порядку. Выходные данные В первой строке выведите z — наименьшее количество операций замены, требуемых для того, чтобы получить анаграмму строки t из строки s. Во второй строке выведите лексикографически минимальную анаграмму, которую можно получить за z операций. Примечание Во втором примере существует восемь анаграмм строки t, которые можно получить из строки s заменой ровно двух букв: «ADBADC», «ADDABC», «CDAABD», «CDBAAD», «CDBADA», «CDDABA», «DDAABC», «DDBAAC». Эти анаграммы перечислены в лексикографическом порядке. Лексикографически минимальная анаграмма — это «ADBADC». | |
![]()
|
|
A. Маленький Слоник и шахматы
Перебор
Строки
*1000
Маленький Слоник очень любит шахматы. Однажды, Маленький Слоник и его друг захотели сыграть в шахматы. Фигуры у них есть, а вот с доской проблематично. У них есть клетчатая доска размером 8 × 8, каждая клетка которой покрашена либо в черный, либо в белый цвет. Маленький Слоник и его друг знают, что в правильной шахматной доске нету соседних по сторонам клеток с одинаковым цветом, а левая верхняя клетка — белого цвета. Чтобы поиграть в шахматы, они хотят превратить имеющуюся у них доску в правильную шахматную доску. Для этого друзья могут выбрать любую строку имеющейся доски и циклически сдвинуть клетки выбранной строки, то есть последнюю клетку (самую правую) поставить на первое место в строке, а остальные сдвинуть на одну позицию вправо. Описанную операцию можно выполнять несколько раз (можно вообще не выполнять). Например, если первая строка доски имела вид «BBBBBBWW» (белые клетки строки обозначены символом «W», черные символом — «B»), то после одного циклического сдвига она будет иметь вид «WBBBBBBW». Помогите Маленькому Слонику и его другу выяснить, смогут ли они с помощью любого количества описанных операций превратить имеющуюся доску в правильную шахматную доску. Выходные данные В единственной строке выведите «YES» (без кавычек), если доску можно превратить в правильную шахматную и «NO» (без кавычек) иначе. Примечание В первом примере нужно сдвинуть на одну позицию следующие строки — 3-ю, 6-ю, 7-ю и 8-ю. Во втором примере достичь цели никак не получится. | |
![]()
|
|
B. Древнее пророчество
Перебор
реализация
Строки
*1600
Древнее Пророчество, найденное недавно, по мнению ученых содержит в себе точную дату Конца Света. Пророчество представляет собой строку, состоящую только из цифр и символов «-». Будем говорить, что какая-либо дата упоминается в Пророчестве, если существует подстрока Пророчества, представляющая собой запись этой даты в формате «dd-mm-yyyy». Количеством упоминаний даты будем называть количество таких подстрок в Пророчестве. Например, в Пророчестве «0012-10-2012-10-2012» дата 12-10-2012 упоминается два раза (первый раз — «0012-10-2012-10-2012», второй — «0012-10-2012-10-2012»). Дата Конца Света — это такая корректная дата, что количество ее упоминаний в Пророчестве строго больше, чем у любой другой корректной даты. Дата называется корректной, если год лежит в диапазоне от 2013 до 2015, месяц — от 1 до 12, а номер дня строго больше нуля и не превышает количество дней в текущем месяце. Обратите внимание, что дата записывается в формате «dd-mm-yyyy», это значит, что, при необходимости, к числу месяцев или дней дописываются лидирующие нули. Другими словами дата «1-1-2013» не записана в формате «dd-mm-yyyy», а дата «01-01-2013» — записана в нем. Обратите внимание, что между 2013 и 2015 годами нет ни одного високосного года. Выходные данные В единственной строке выведите дату Конца Света. Гарантируется, что такая дата существует и единственна. | |
![]()
|
|
E. Теория струн
геометрия
математика
Строки
*3100
Эмускальд — музыкант-новатор, он всегда пытается выйти за рамки творения музыки. Теперь он придумал революционный музыкальный инструмент — прямоугольную арфу. Прямоугольная арфа является прямоугольником n × m единиц, она состоит из n рядов и m столбцов. Ряды пронумерованы от 1 до n сверху вниз. Аналогично, столбцы пронумерованы от 1 до m слева направо. Крепления для струн расположены равномерно по каждой стороне, по одному креплению на единице длины. Таким образом, существует по n креплений на левой и правой сторонах арфы и по m креплений на верхней и нижней сторонах. Арфа имеет ровно n + m различных струн, каждая струна соединяет два разных крепления, расположенных на разных сторонах арфы. Эмускальд приказал своему ученику изготовить первую в мире прямоугольную арфу. Однако, он не упомянул, что никакие две струны не могут пересекаться (если струны пересекаются, то играть на арфе невозможно). Две струны пересекаются, если отрезки, соединяющие их крепления, пересекаются. Чтобы исправить арфу, Эмускальд может выполнять операции двух типов: - выбрать два различных столбца и поменять их крепления на каждой стороне арфы, не меняя сцепления каждой струны;
- выбрать два различных ряда и поменять их крепления на каждой стороне арфы, не меняя сцепления каждой струны.
В следующем примере он может починить арфу, поменяв местами два столбца:  Помогите Эмускальду завершить свое детище и найдите перестановки, показывающие, как надо расположить ряды и колонки арфы. В противном случае сообщите, что сделать это невозможно. Юноша может снимать и натягивать струны на крепления, так что физическое расположение струн не имеет значения. Выходные данные Если можно переставить ряды и столбцы так, чтобы исправить арфу, в первой строке выведите n целых чисел — старые номера рядов, теперь размещенные сверху вниз в исправленной арфе. Во второй строке выведите m целых чисел, разделенных пробелом — старые номера столбцов, теперь расположенные слева направо в исправленной арфе. Если же невозможно переставить ряды и столбцы так, чтобы исправить арфу, выведите «No solution» (без кавычек). | |
![]()
|
|
D. Хорошие подстрочки
Строки
Структуры данных
*1800
Вам дана строка s, состоящая из строчных латинских букв. Некоторые из латинских букв являются хорошими, остальные — плохими. Подстрокой s[l...r] (1 ≤ l ≤ r ≤ |s|) строки s = s1s2...s|s| (где |s| — длина строки s) называется строка slsl + 1...sr. Подстроку s[l...r] назовем хорошей, если среди букв sl, sl + 1, ..., sr не более k являются плохими (смотрите пояснения к примерам для лучшего понимания). Ваша задача — найти количество различных хороших подстрок данной строки s. Две подстроки s[x...y] и s[p...q] различны, если различно их содержимое, то есть s[x...y] ≠ s[p...q]. Выходные данные Выведите единственное целое число — количество различных хороших подстрок строки s. Примечание В первом примере хорошими подстроками являются: «a», «ab», «b», «ba», «bab». Во втором примере хорошими подстроками являются: «a», «aa», «ac», «b», «ba», «c», «ca», «cb». | |
![]()
|
|
B. Новая задача
Перебор
Строки
*1500
Придумать новую задачу не так просто, как многие думают. Иногда даже придумать название задачи бывает трудно. Будем считать название оригинальным, если оно не встречается в качестве подстроки ни в одном из названий недавних задач на Codeforces. Вам даны названия n последних задач — строки, состоящие из строчных букв латинского алфавита. Ваша задача — найти кратчайшее оригинальное название для новой задачи. Если таких несколько, требуется выбрать лексикографически минимальное. Обратите внимание, название задачи не может быть пустой строкой. Подстрокой s[l... r] (1 ≤ l ≤ r ≤ |s|) строки s = s1s2... s|s| (где |s| — длина строки s) называется строка slsl + 1... sr. Строка x = x1x2... xp лексикографически меньше строки y = y1y2... yq, если либо p < q и x1 = y1, x2 = y2, ... , xp = yp, либо существует такое число r (r < p, r < q), что x1 = y1, x2 = y2, ... , xr = yr и xr + 1 < yr + 1. Символы строк сравниваются как их ASCII коды. Выходные данные Выведите строку, состоящую из строчных букв латинского алфавита — лексикографически минимальное кратчайшее оригинальное название. Примечание В первом примере первые 9 букв латинского алфавита (a, b, c, d, e, f, g, h, i) встречаются в названиях задач, поэтому ответ — буква j. Во втором примере в названиях содержатся все 26 букв латинского алфавита, поэтому кратчайшее оригинальное название не может иметь длину 1. Название aa содержится в качестве подстроки в первом названии. | |
![]()
|
|
A. Капитализация слова
реализация
Строки
*800
Капитализация — это запись слова, в которой первая буква слова записывается как прописная буква. Ваша задача, вывести капитализацию заданного слова. Обратите внимание, что в капитализации все буквы слова кроме первой остаются не измененными. Выходные данные Выведите капитализацию слова. | |
![]()
|
|
B. Аргументы командной строки
*особая задача
реализация
Строки
*1300
В данной задаче используется описание свойств командной строки, близкое к тому, что вы привыкли видеть в настоящих операционных системах. Однако, в деталях существуют отличия в поведении. Внимательно прочтите условие, используйте его как формальный документ при разработке решения. В операционной системе Pindows лексемами командной строки являются строки — первая из них трактуется как имя запускаемой программы, а последующие как ее аргументы. Например, выполняя команду « run.exe one, two . », мы передаем командной строке Pindows четыре лексемы: «run.exe», «one,», «two», «.». Более формально, если мы выполняем команду, которая представима строкой s (и не содержит кавычек), то лексемами командной строки являются максимальные по включению подстроки строки s, которые не содержат пробелов. Для того, чтобы передать в качестве лексемы командной строки строку с пробелами или пустую строку, используются двойные кавычки. Блок символов, который должен рассматриваться как одна лексема, берется в кавычки. При этом вложенные кавычки запрещаются — то есть про каждое вхождение символа «"» можно однозначно сказать — что это, открывающие кавычки или закрывающие. Например, выполняя команду «"run.exe o" "" " ne, " two . " " », мы передаем командной строке Pindows шесть лексем: «run.exe o», «» (пустая строка), « ne, », «two», «.», « » (единичный пробел). Гарантируется, что каждая из лексем командной строки окружена с обеих сторон пробелами или упирается в соответствующий край командной строки. Из этого, например, следует, что открывающие кавычки либо являются первым символом строки, либо слева от них находится пробел. Вам задана строка, состоящая из прописных, строчных букв латинского алфавита, цифр, символов «.,?!"» и пробелов. Гарантируется, что эта строка — корректная командная строка OS Pindows. Выведите все лексемы этой командной строки. Считайте, что символ «"» используется в команде только для выделения единого блока символов в одну лексему командной строки, в частности, из этого следует, что таких символов в заданной строке четное количество. Выходные данные В первой строке выведите первую лексему, во второй строке — вторую, и так далее. Для наглядности слева от каждой лексемы выведите символ «<» (меньше), а справа — символ «>» (больше). Выводите лексемы в том порядке, в котором они встречаются в команде. Строго следуйте описанному формату вывода. Для лучшего понимания формата вывода посмотрите тестовые примеры. | |
![]()
|
|
E. Древесно-строковая задача
*особая задача
поиск в глубину и подобное
Строки
хэши
*2000
Корневым деревом называется неориентированный связный граф без циклов с выделенной вершиной, которая называется корнем дерева. Будем считать, что вершины корневого дерева из n вершин пронумерованы от 1 до n. В этой задаче корнем дерева будет вершина с номером 1. Обозначим через d(v, u) длину кратчайшего по количеству ребер пути в дереве между вершинами v и u. Родителем вершины v в корневом дереве с корнем в вершине r (v ≠ r) называется вершина pv, такая, что d(r, pv) + 1 = d(r, v) и d(pv, v) = 1. Например, на рисунке родителем вершины v = 5 является вершина p5 = 2. Как-то раз Поликарп раздобыл корневое дерево из n вершин. Дерево было не совсем обычное — на его ребрах были написаны строки. Поликарп расположил дерево на плоскости так, что все ребра ведут сверху вниз при прохождении от родителя вершины к вершине (см. рисунок). Для каждого ребра, ведущего из вершины pv в вершину v (1 < v ≤ n), известна строка sv, которая на нем написана. Все строки записаны на ребрах сверху вниз. Например, на рисунке s7=«ba». Символы в строках пронумерованы от 0.  Пример дерева Поликарпа (соответствует примеру из условия) Пример дерева Поликарпа (соответствует примеру из условия) Позицией в этом дереве Поликарп называет конкретную букву конкретной строки. Позиция записывается как пара целых чисел (v, x), которая обозначает, что позицией является x-ая буква строки sv (1 < v ≤ n, 0 ≤ x < |sv|), где |sv| — длина строки sv. Например, выделенные буквы — это позиции (2, 1) и (3, 1). Рассмотрим пару позиций (v, x) и (u, y) в дереве Поликарпа, такую, что путь от первой позиции ко второй идет сверху вниз в дереве Поликарпа, нарисованном на плоскости. Будем считать, что пара этих позиций определяет строку z. Строка z состоит из всех букв на пути от (v, x) к (u, y), записанных в порядке прохождения этого пути. Например, на рисунке выделенные позиции определяют строку «bacaba». У Поликарпа есть строка t, он хочет узнать, сколько существует пар позиций, которые определяют строку t. Обратите внимание, что путь от первой позиции ко второй в паре должен всюду вести вниз. Помогите ему с этой нелегкой древесно-строковой задачей! Выходные данные Выведите единственное целое число — искомое количество. Пожалуйста, не используйте спецификатор %lld для чтения или записи 64-х битовых чисел на С++. Рекомендуется использовать потоки cin, cout или спецификатор %I64d Примечание В первом тестовом примере строку «aba» определяют пары позиций: (2, 0) и (5, 0); (5, 2) и (6, 1); (5, 2) и (3, 1); (4, 0) и (4, 2); (4, 4) и (4, 6); (3, 3) и (3, 5). Обратите внимание, что эту строку не определяет пара позиций (7, 1) и (5, 0), потому как путь между ними не всегда идет вниз. | |
![]()
|
|
E. Хитрый и умный пароль
Бинарный поиск
жадные алгоритмы
Конструктив
Строки
Структуры данных
хэши
*2800
В эпоху своей молодости герой нашего рассказа Царь Цопа решил, что все его личные данные не очень хорошо скрыты от посторонних глаз, а для монарха это недопустимо. Поэтому он придумал хитрый и умный пароль (лишь спустя много лет Цопа узнал, что его пароль — это палиндром нечетной длины), а затем зашифровал все свои данные. Как известно, монархи в душе такие же люди, как и все остальные смертные, и поэтому чтобы не забыть свой хитрый и умный пароль, Цопа решил записать его на бумажку. Зная, что опасно хранить пароль в таком виде, он решил его зашифровать следующим образом: с конца и с начала своего пароля-палиндрома он отрезал по x символов (x может быть равно 0, и 2x строго меньше, чем длина пароля). У него получились 3 части пароля. Назовем их prefix, middle и suffix соответственно, причем prefix и suffix имеют одинаковую, возможно нулевую, длину, а middle — всегда нечётной длины. Из этих трех частей он сделал строку A + prefix + B + middle + C + suffix, где A, B и C — некоторые придуманные Цопой строки (возможно нулевой длины), а « + » означает операцию конкатенации («склеивания» строк). Прошло много лет, и буквально вчера Царь Цопа нашел бумажку, где был записан его пароль, зашифрованный описанным выше способом. Сам пароль, а также строки A, B и C давно уже забыты, и поэтому Цопа просит вас найти пароль максимальной длины, который мог бы быть придуман, зашифрован и записан Цопой. Выходные данные В первую строку выведите одно целое число k — количество непустых частей пароля в получившемся у вас ответе ( ). Далее выведите k строк по два целых числа xi и li — позицию начала и длину соответствующей части пароля. Пары выводите в порядке возрастания xi. Числа в паре при выводе разделяйте одним пробелом. ). Далее выведите k строк по два целых числа xi и li — позицию начала и длину соответствующей части пароля. Пары выводите в порядке возрастания xi. Числа в паре при выводе разделяйте одним пробелом. Позиция начала xi — целое число от 1 до длины входной строки. Никакая длина li не может быть равна 0, так как части пароля нулевой длины выводить не нужно. Среднее из чисел li обязательно должно быть нечётным. Если решений несколько, выведите любое. Учтите, что ваша задача — максимизировать не k, а сумму li. | |
![]()
|
|
B. Сисадмин Вася
жадные алгоритмы
реализация
Строки
*1500
Адрес электронной почты в Берляндии — это строка вида A@B, где A и B — любые непустые строки из маленьких латинских букв. Вася работает сисадмином в компании «Берсофт». Он хранит список адресов электронной почты всех сотрудников компании в виде одной большой строки, где все адреса записаны через запятую в произвольном порядке. Один и тот же адрес может быть записан более одного раза. Однажды по непонятной причине все запятые в Васином списке исчезли, и все адреса «склеились». У Васи осталась одна большая строка, в которой адреса электронной почты записаны подряд без каких-либо разделителей, и невозможно определить, где заканчивается один адрес и начинается другой. К несчастью, именно в этот же день Васино начальство потребовало от Васи исходный список всех адресов. Теперь Вася хочет расцепить адреса произвольным образов (вряд ли начальство будет разбираться). Помогите ему это сделать. Выходные данные Если не существует такого списка корректных (по берляндским правилам) адресов электронной почты, что после удаления запятых список совпадает с заданной строкой, выведите No solution. Иначе выведите сам список. Один и тот же адрес может быть записан в этом списке более одного раза. Если решений несколько, выведите любое. | |
![]()
|
|
A. Чье это предложение?
реализация
Строки
*1100
Однажды liouzhou_101 получил логи чата между Фредой и Рейнбоу. Из любопытства он хотел узнать, какое предложение сказала Фреда, а какое сказал Рейнбоу. Исходя из своего опыта, он знал, что Фреда всегда говорит в конце предложений «lala.», а Рейнбоу всегда говорит в начале предложения «miao.» Помогите liouzhou_101, для каждого предложения из записей чата определите, чье это предложение? Выходные данные Для каждого предложения выведите «Freda's», если предложения сказала Фреда, «Rainbow's», если предложение было сказано Рейнбоу, или «OMG>.< I don't know!», если liouzhou_101 не может определить, чье это предложение. Он не может распознать, чье это предложение, если оно содержит и «miao.» в начале, и «lala.» в конце, либо не содержит ни одного из них. | |
![]()
|
|
B. Сережа и периоды
Бинарный поиск
поиск в глубину и подобное
Строки
*2000
Введем обозначение,  , где x — строка, n — целое положительное число, а операция « + » обозначает конкатенацию строк. Например, [abc, 2] = abcabc. , где x — строка, n — целое положительное число, а операция « + » обозначает конкатенацию строк. Например, [abc, 2] = abcabc. Будем говорить, что строку s можно получить из строки t, если можно удалить некоторые символы строки t и получить строку s. Например, строки ab и aсba можно получить из строки xacbac, а строки bx и aaa — нет. У Сережи есть две строки w = [a, b] и q = [c, d]. Он хочет найти такое максимальное целое число p (p > 0), что [q, p] можно получить из строки w. Выходные данные В единственную строку выведите целое число — наибольшее число p. Если не существует искомого значения p, выведите 0. | |
![]()
|
|
G1. Хорошие подстроки
Строки
хэши
*1700
Умный Бобер недавно увлекся новой игрой в слова. Ее суть состоит в следующем: подсчитать количество различных хороших подстрок некоторой строки s. Для определения того, является ли строка хорошей, в игре используются правила. Их всего n штук. Каждое правило описывается тройкой (p, l, r), где p — строка, а l и r (l ≤ r) — целые числа. Будем говорить, что строка t удовлетворяет правилу (p, l, r), если количество вхождений строки t в строку p лежит в пределах от l до r включительно. Например, строка «ab», удовлетворяет правилам («ab», 1, 2) и («aab», 0, 1), но не удовлетворяет правилам («cd», 1, 2) и («abab», 0, 1). Подстрокой s[l... r] (1 ≤ l ≤ r ≤ |s|) строки s = s1s2... s|s| (где |s| — длина строки s) называется строка slsl + 1... sr. Будем считать, что количество вхождений строки t в строку p — это количество пар целых чисел l, r (1 ≤ l ≤ r ≤ |p|) таких, что p[l... r] = t. Будем говорить, что строка t является хорошей, если она удовлетворяет всем n правилам. Умный Бобер просит вас помочь ему в написании программы, которая будет вычислять количество различных хороших подстрок строки s. Две подстроки s[x... y] и s[z... w] считаются различными, если s[x... y] ≠ s[z... w]. Выходные данные Выведите ровно одно целое число — количество различных хороших подстрок строки s. Примечание В первом тестовом примере подходят подстроки «aab», «ab» и «b». Во втором тестовом примере «e» и «t». | |
![]()
|
|
B. Энергетические строчки
реализация
Строки
*1300
Володя любит слушать хэви-метал и иногда — читать. Особый интерес для Володи представляют тексты про его любимый музыкальный стиль. Володя называет строчку энергетической, если она начинается на «heavy» и заканчивается на «metal». Когда Володя читает текст, он отмечает в нем все энергетические подстрочки и становится ужасно довольным (подстрокой Володя называет последовательность подряд идущих символов в тексте). Совсем недавно он, прочитав особенно впечатляющий текст, испытал небывалый прилив сил и решил похвастаться перед друзьями, назвав им точное количество энергетических подстрок в этом тексте. Помогите Володе посчитать, сколько было энергетических подстрок в прочитанном им тексте. Две подстроки считаются различными, если они встречаются в разных местах в тексте. Для простоты будем считать, что текст Володи задается единственной строкой. Выходные данные Выведите единственное число — количество энергетических подстрок в данной строке. Пожалуйста, не используйте спецификатор %lld для чтения или записи 64-х битных чисел на С++. Рекомендуется использовать потоки cin, cout или спецификатор %I64d). Примечание В первом примере в строке «heavymetalisheavymetal» дважды встречается энергетическая подстрока «heavymetal», кроме того, вся строка «heavymetalisheavymetal» является энергетической. Во втором примере в строке «heavymetalismetal» есть две энергетические подстрочки: «heavymetal» и «heavymetalismetal». | |
![]()
|
|
D. Вам знакомо это слово?
жадные алгоритмы
Строки
строковые суфф. структуры
хэши
*2800
Подстрока строки — это непрерывная подпоследовательность символов данной строки. Таким образом, строка bca является подстрокой строки abcabc, а строка cc — нет. Повторяющийся блок — это строка, полученная конкатенацией некоторой строки с собой же. Таким образом, строка abcabc — это повторяющийся блок, а строки abcabd, ababab — нет. Вам дана последовательность символов латинского алфавита (строка). За один ход Вы находите наикратчайшую подстроку, которая является повторяющимся блоком. Если таких подстрок несколько, выбираете ближайшую к левому краю строки. Пусть найденная подстрока имеет вид XX (X — некоторая строка), тогда Вы заменяете ее строкой X, иными словами, Вы удаляете одну из подстрок X в этой подстроке. Вы повторяете процесс до тех пор, пока в строке не остается повторяющихся блоков. Как будет выглядеть результирующая строка? Посмотрите пояснения к тестовым примерам, чтобы лучше понять условие. Выходные данные Выведите итоговую строку после применения операций. Примечание В первом примере строка превращается так: abccabc → abcabc → abc. Во втором примере строка превращается так: aaaabaaab → aaabaaab → aabaaab → abaaab → abaab → abab → ab. | |
![]()
|
|
A. Математика спешит на помощь
жадные алгоритмы
реализация
сортировки
Строки
*800
Начинающий математик Ксения учится в третьем классе. Сейчас в школе она проходит операцию сложения. Учитель записал на доске сумму нескольких чисел, которую требуется посчитать. Чтобы было проще считать, в сумме используются только числа 1, 2 и 3. Но и этого Ксении мало. Ксения только учится считать, и поэтому она может посчитать сумму, только если слагаемые в сумме идут в порядке неубывания. Например, сумму 1+3+2+1 она посчитать не может, а суммы 1+1+2 и 3+3 может. Вам задана сумма, которая записана на доске. Переставьте слагаемые и выведите ее в виде, в котором Ксения сможет посчитать сумму. Выходные данные Выведите новую сумму, которую сможет посчитать Ксения. | |
![]()
|
|
C. Список
Разбор выражений
реализация
сортировки
Строки
*1300
Компания «Bersoft» работает над новой версией своего самого известного текстового редактора, Bord 2010. В Bord, как и во многих других текстовых редакторах, должна быть реализована возможность печати многостраничных документов. Пользователь перечисляет через запятую (без пробелов) номера страниц документа, которые он хочет распечатать. Вам поручено написать часть программы, выполняющую «нормализацию» списка. На вход вашей программе подается список, который ввел пользователь. Ваша программа должна вывести этот список в формате l1-r1,l2-r2,...,lk-rk, где ri + 1 < li + 1 для всех i от 1 до k - 1, и li ≤ ri. Новый список должен содержать все страницы которые ввел пользователь и ничего больше. Повторные появлений одной и той же страницы в списке пользователя следует игнорировать. В случае, если для некоторого элемента i нового списка li = ri, этот элемент необходимо выводить как li, а не «li - li». Например, список 1,2,3,1,1,2,6,6,2 нужно вывести в виде 1-3,6. Выходные данные Выведите список в требуемом формате. | |
![]()
|
|
G. Суффиксный поднабор
*особая задача
Строки
*2200
Вам задан набор s1, s2, ..., sn, состоящий из n строк. Требуется найти такой поднабор этого набора si1, si2, ..., sik (1 ≤ i1 < i2 < ... < ik ≤ n), что выполняются два условия: - существует строка t, такая, что все строки поднабора являются ее суффиксами;
- количество строк в поднаборе максимально.
Ваша задача, вывести количество строк в таком поднаборе. Выходные данные Выведите единственное целое число — количество строк в описанном поднаборе. Примечание В первом тестовом примере искомый поднабор состоит из трех строк: s1, s2, s3. | |
![]()
|
|
B. Счастливая общая подпоследовательность
дп
Строки
*2000
В математике подпоследовательность — это последовательность, которую можно получить из другой последовательности путем удаления некоторых элементов, не меняя порядок оставшихся элементов. Например, последовательность BDF — это подпоследовательность последовательности ABCDEF. Подстрока строки — это непрерывная подпоследовательность данной строки. Например, BCD — это подстрока ABCDEF. Вам даны две строки s1, s2 и еще одна строка под названием virus. Ваша задача — найти наидлиннейшую общую подпоследовательность s1 и s2, такую, что она не содержит подстроку virus. Выходные данные Выведите наидлиннейшую общую подпоследовательность s1, s2, не содержащую подстроку virus. Если имеется несколько решений, любое из них будет засчитано. Если требуемой общей подпоследовательности нет, выведите 0. | |
![]()
|
|
E. Ксюша и строковая задача
дп
реализация
Строки
строковые суфф. структуры
хэши
*3000
На олимпиаде по информатике программисту Ксюше попалась задача на строки. К сожалению, Ксюша не сильна в строковых алгоритмах. Помогите ей решить задачу. Строкой s назовем последовательность символов s1s2... s|s|, где записью |s| будем обозначать длину строки. Подстрокой s[i... j] строки s будем называть строку sisi + 1... sj. Строка s является строкой Грея, если она удовлетворяет условиям: - длина строки |s| нечетная;
- символ
 встречается в строке ровно один раз; встречается в строке ровно один раз; - либо |s| = 1, либо подстроки
 и и  равны между собой и являются строками Грея. равны между собой и являются строками Грея. Например, строки «abacaba», «xzx», «g» являются строками Грея, а строки «aaa», «xz», «abaxcbc» — нет. Красотой строки p называется сумма квадратов длин всех подстрок строки p, которые являются строками Грея. Другими словами, рассмотрим все пары значений i, j (1 ≤ i ≤ j ≤ |p|). Если подстрока p[i... j] является строкой Грея, к красоте нужно прибавить (j - i + 1)2. В задаче Ксюше задана строка t, состоящая из символов латинского алфавита. Ей разрешается изменить не более одного символа этой строки на любой другой символ латинского алфавита. Задача состоит в том, чтобы получить строку как можно большей красоты. Выходные данные Выведите искомое максимальное значение красоты, которое удастся получить Ксюше. Пожалуйста, не используйте спецификатор %lld для чтения или записи 64-битных чисел на С++. Рекомендуется использовать потоки cin, cout или спецификатор %I64d. Примечание В первом тестовом примере из заданной строки можно получить строку p = «zbz». В такой строке строками Грея являются подстроки p[1... 1], p[2... 2], p[3... 3] и p[1... 3]. Итого, красота строки p получается равна 12 + 12 + 12 + 32 = 12. Более красивую строку получить нельзя. Во втором тестовом примере можно не применять никаких операций. Изначальная строка имеет наибольшую возможную красоту. | |
![]()
|
|
B. Дима и СМС
Перебор
Строки
*1500
Сережа крайне не постоянен, на этот раз он не уступил место Диме и его девушке (кстати, ее зовут Инна). Но ребята всегда найдут способ пообщаться, сегодня они переписываются по смс. Дима и Инна используют тайный шифр в своих смсках. Когда Дима хочет отправить Инне какую-то фразу, он выписывает все слова, ставя перед каждым словом и после последнего сердечку. Сердечка — это последовательность из двух символов: знака меньше (<) и цифры тройки (3). После этого этапа шифрования смс выглядит следующим образом: <3word1<3word2<3 ... wordn<3. На этом шифрование не заканчивается. Далее Дима вставляет произвольное количество маленьких латинских символов, цифр, знаков больше и меньше (<, >) в любые места сообщения. Инна знает Диму как облупленного, так что наперед знает, какую фразу Дима собирается ей отправить. Инне только что пришла смс, помогите ей определить, правильно ли ее зашифровал Дима. Другими словами определите, могла ли смс быть получена методом шифрования описанным выше. Выходные данные В единственной строке выведите «yes» (без кавычек), если Дима правильно зашифровал смс, и «no» (без кавычек) в противном случае. Примечание Прошу заметить, что за второй пример из условия Дима еще и по шапке получил потом. | |
![]()
|
|
F. Умный мальчик
дп
игры
Строки
*2100
Однажды Вася и Петя придумали новую игру и назвали ее «Умный мальчик». Для игры они зафиксировали некоторый набор слов — словарь. Допускается, что словарь содержит одинаковые слова. Правила игры таковы: сначала первый игрок выбирает любую букву (слово длины 1) из любого слова из словаря и записывает ее на лист бумаги. Второй игрок приписывает к этой букве некоторую другую в начало или в конец, таким образом получая уже слово длины 2, затем опять ходит первый игрок, и он опять приписывает некоторую букву в начало или в конец, получая слово длины 3. И так далее. Но игрок не имеет права нарушать условие: новое записанное слово должно являться подстрокой некоторого слова из словаря. Проигрывает тот, кто не может увеличить текущую строку так, чтобы не нарушалось условие. Также если после хода на бумаге записана некоторая строка s, то игрок, сделавший этот ход, получает количество очков по формуле:  где: -
 — порядковый номер символа c в латинском алфавите, пронумерованном с 1. Например, — порядковый номер символа c в латинском алфавите, пронумерованном с 1. Например,  , а , а  . . -
 — количество слов из словаря, где встречается строка s как подстрока хотя бы один раз. — количество слов из словаря, где встречается строка s как подстрока хотя бы один раз. Ваша задача — узнать, кто выиграет в этой игре, и итоговый счет. Каждый игрок играет оптимально, и в первую очередь стремится выиграть, во вторую — максимизировать свои очки, в третью — минимизировать очки соперника. Выходные данные В первую строку выходных данных выведите строку «First» или «Second» — кто выиграет в игре. Во вторую строку выведите количество очков у первого игрока и количество очков у второго игрока после завершения игры. Числа разделите одним пробелом. | |
![]()
|
|
B. Медведь и строки
жадные алгоритмы
математика
Перебор
реализация
Строки
*1200
У медведя есть строка s = s1s2... s|s| (записью |s| обозначается длина строки), состоящая из строчных букв латинского алфавита. Медведь хочет посчитать количество таких пар индексов i, j (1 ≤ i ≤ j ≤ |s|), что строка x(i, j) = sisi + 1... sj содержит в себе хотя бы одну строку «bear» в качестве подстроки. Строка x(i, j) содержит в себе строку «bear», если существует такой индекс k (i ≤ k ≤ j - 3), что sk = b, sk + 1 = e, sk + 2 = a, sk + 3 = r. Помогите медведю справиться с поставленной задачей. Выходные данные Выведите одно целое число — ответ на задачу. Примечание В первом примере подходят следующие пары (i, j): (1, 4), (1, 5), (1, 6), (1, 7), (1, 8), (1, 9). Во втором примере подходят следующие пары (i, j): (1, 4), (1, 5), (1, 6), (1, 7), (1, 8), (1, 9), (1, 10), (1, 11), (2, 10), (2, 11), (3, 10), (3, 11), (4, 10), (4, 11), (5, 10), (5, 11), (6, 10), (6, 11), (7, 10), (7, 11). | |
![]()
|
|
C. Разнообразные подстроки
дп
Строки
*2000
Разнообразностью строки назовем количество различных символов, которые в ней встречаются хотя бы один раз. Разнообразность строки s будем обозначать как d(s). К примеру, d('aaa') = 1, d('abacaba') = 3. Пусть задана строка s, состоящая из строчных символов латинского алфавита. Рассмотрим все ее подстроки. Очевидно, что разнообразность любой подстроки — это число от 1 до d(s). Выдайте статистику разнообразности подстрок, посчитав для каждого k от 1 до d(s), сколько подстрок строки s имеет разнообразность ровно k. Выходные данные В первой строке выведите d(s) — разнообразность строки s. Далее выведите d(s) строк. В k-й из этих строк выведите количество подстрок строки s, имеющих разнообразность k. Примечание Рассмотрим первый пример. Обозначим через s(i, j) подстроку строки 'abca' с символа номер i по символ номер j. - s(1, 1) = 'a', d('a') = 1
- s(2, 2) = 'b', d('b') = 1
- s(3, 3) = 'c', d('c') = 1
- s(4, 4) = 'a', d('a') = 1
- s(1, 2) = 'ab', d('ab') = 2
- s(2, 3) = 'bc', d('bc') = 2
- s(3, 4) = 'ca', d('ca') = 2
- s(1, 3) = 'abc', d('abc') = 3
- s(2, 4) = 'bca', d('bca') = 3
- s(1, 4) = 'abca', d('abca') = 3
Всего количество подстрок с разнообразностью 1 равно 4, с разнообразностью 2 равно 3, с разнообразностью 3 равно 3. | |
![]()
|
|
J. Проверка правописания
реализация
Строки
хэши
*1500
Петя заметил, что когда он набирает текст на клавиатуре, у него часто нажимаются лишние клавиши и в словах возникают лишние буквы. Конечно же, система проверки правописания подчеркивает ему эти слова, ему приходится кликать на слово и выбирать правильный вариант. Пете надоело исправлять свои ошибки вручную, поэтому он решил реализовать функцию, которая сама будет вносить исправления. Петя начал с разбора наиболее часто встречающегося у него случая, когда из слова достаточно удалить одну букву, чтобы оно совпало с некоторым словом из словаря. Итак, Петя столкнулся с такой подзадачей: дано введенное слово и слово из словаря, нужно удалить из первого слова одну букву, чтобы получилось второе. И тогда перед Петей встал весьма нетривиальный вопрос: какую букву удалять? Выходные данные В первой строке выведите количество позиций символов в первой строке, при удалении каждого из которых получается вторая строка. Во второй строке через пробел выведите сами позиции в порядке возрастания. Позиции нумеруются с 1. Если из первой строки невозможно получить вторую путем удаления одного символа, выведите одно число 0. | |
![]()
|
|
A. Перевод
реализация
Строки
*800
Перевод с берляндского языка на бирляндский — задача не из легких. Эти языки очень похожи: слово на бирляндском языке отличается от такого же по смыслу слова на берляндском только тем, что оно пишется (и произносится) наоборот. Например, слову code в берляндском языке соответствует слово edoc в бирляндском. Несмотря на это, при «переводе» легко ошибиться. Вася перевел слово s с берляндского на бирляндский как t. Помогите ему: определите, правильно ли он выполнил перевод? Выходные данные Если слово t является словом s, записанным наоборот, выведите YES, иначе выведите NO. | |
![]()
|
|
C. Строка-шаблон
реализация
Строки
*1200
Разработчики часто сталкиваются с понятием шаблона регулярных выражений. Под шаблоном обычно понимают строку-образец, состоящую из символов и метасимволов и задающую правило поиска. Такие шаблоны чаще всего используют для того, чтобы проверить, соответствует ли некоторая строка определенным правилам. В этой задаче шаблоном будет называться строка, состоящая из маленьких латинских букв и знаков вопроса («?»). Знак вопроса в шаблоне — метасимвол, который обозначает произвольную маленькую букву латинского алфавита. Будем считать, что строка удовлетворяет шаблону, если из шаблона можно получить эту строку, заменив знаки вопроса на соответствующие символы. Например, строка aba удовлетворяет шаблонам: ???, ??a, a?a, aba. Программисты компании R1 любят озадачить друг друга (и сами себя) головоломками. Одна из них выглядит следующим образом: заданы n строк-шаблонов одинаковой длины, нужно найти шаблон, содержащий как можно меньше знаков вопроса, который пересекается с каждым из заданных. Два шаблона пересекаются, если существует строка, которая удовлетворяет и первому и второму шаблону. Сможете ли вы решить эту задачку? Выходные данные В единственной строке выведите ответ на задачу — шаблон с минимальным количеством знаков «?», который пересекается с каждым из заданных. Если существует несколько правильных ответов, разрешается вывести любой из них. Примечание Рассмотрим первый тестовый пример. Шаблон xab пересекается с каждым из заданных. Шаблон ??? также пересекается с каждым из заданных, но он содержит больше знаков вопроса, поэтому не является оптимальным ответом. Очевидно, xab является оптимальным ответом, так как он совсем не содержит знаков вопроса. Есть и другие оптимальные ответы на этот тест, например: aab, bab, cab, dab и так далее. | |
![]()
|
|
D. Расшифровка сигнала
дп
Строки
строковые суфф. структуры
*2200
Штаб-квартира полиции отслеживает сигналы на разных частотах. Недавно они записали две подозрительные строки, s1 и s2, на двух частотах. Полиция подозревает, что эти две строки принадлежат двум преступникам, планирующим сделать какое-то злое деяние. Поэтому полиция пытается найти общую подстроку этих двух строк. Искомая подстрока должна быть уникальной в первой строке и во второй строке. Другими словами, она должна встречаться ровно один раз в первой строке и ровно один раз во второй строке. Среди всех таких строк, полицию интересует строка с минимальной длиной. Вам даны две строки, s1 и s2, состоящие из строчных букв латинского алфавита. Чему равна длина минимальной по длине общей уникальной подстроки строк s1 и s2? Формальное определение подстроки и уникальности смотрите в примечании. Выходные данные Выведите длину наименьшей общей уникальной подстроки s1 и s2. Если общих уникальных подстрок у s1 и s2 нет, выведите -1. Примечание Представьте, что у нас есть строка a = a1a2a3...a|a|, где |a| — это длина строки a, а ai — i-я буква строки. Строку alal + 1al + 2...ar (1 ≤ l ≤ r ≤ |a|) будем называть подстрокой [l, r] строки a. Подстрока [l, r] уникальная в a тогда и только тогда, когда нет пары l1, r1, такой, что l1 ≠ l и подстрока [l1, r1] равняется подстроке [l, r] в a. | |
![]()
|
|
A. Футбол
Строки
*1000
Однажды Вася решил посмотреть результаты финала чемпионата Берляндии по футболу 1910 года. К сожалению, он не нашел итоговый счет матча, зато нашел подробное текстовое описание хода всей игры. Всего в этом описании оказалось n строк, каждая из которых описывала один гол. Каждый гол обозначался названием забившей его команды. Помогите Васе — узнайте название команды, победившей в финале. Гарантируется, что матч не закончился вничью. Выходные данные Выведите название победившей команды. Напоминаем, что в футболе победившей считается команда, забившая больше мячей. | |
![]()
|
|
B. Письмо
реализация
Строки
*1100
Вася решил написать анонимное письмо, вырезая буквы из газетного заголовка. Ему известен заголовок s1 и текст, который он хочет послать, s2. Каждую отдельную букву из заголовка Вася может использовать не более одного раза. Васе не нужно вырезать из заголовка пробелы — он просто делает на их месте пропуски. Помогите ему — выясните, удастся ли ему составить требуемый текст. Выходные данные Если у Васи получится написать данное анонимное письмо, выведите YES, иначе выведите NO. | |
![]()
|
|
D. Префиксы и суффиксы
дп
Строки
строковые суфф. структуры
*2000
Дана строка s = s1s2...s|s|, где |s| — длина строки s, а si — ее i-й символ. Введем несколько определений: - Подстрокой s[i..j] (1 ≤ i ≤ j ≤ |s|) строки s называется строка sisi + 1...sj.
- Префиксом строки s длины l (1 ≤ l ≤ |s|) называется строка s[1..l].
- Суффиксом строки s длины l (1 ≤ l ≤ |s|) называется строка s[|s| - l + 1..|s|].
Требуется для каждого префикса строки s, который совпадает с суффиксом строки s, вывести, сколько раз он встречается в строке s как подстрока. Выходные данные В первой строке выведите целое число k (0 ≤ k ≤ |s|) — количество префиксов, которые совпадают с суффиксом строки s. Далее выведите k строк, в каждой строке выведите два целых числа li ci. Числа li ci обозначают, что префикс длины li совпадает с суффиксом длины li и встречается в строке s в качестве подстроки ci раз. Пары li ci выводите в порядке возрастания li. | |
![]()
|
|
B. Коля и тандемный повтор
Перебор
реализация
Строки
*1500
На день рождения Коле подарили строку s, состоящую из маленьких латинских букв. Он, недолго думая, дописал к ней еще k символов справа. После этого пришел Боря и сказал, что в новой строке, в качестве подстроки, есть тандемный повтор длины l. Насколько большим могло быть l? Определение тамдемного повтора дано в примечании. Выходные данные Выведите одно число — максимальную длину тандемного повтора, который мог встретится в новой строке. Примечание Тандемным повтором длины 2n называется строка s, в которой для любой позиции i (1 ≤ i ≤ n) выполняется si = si + n. В первом примере Коля мог получить строку aabaab, во втором — aaabbbbbb, в третьем — abracadabrabracadabra. | |
![]()
|
|
D. DZY любит строки
Бинарный поиск
Строки
хэши
*2500
DZY очень любит строки. Он коллекционирует особо ценные строки. В Китае многие люди любят использовать строки со своими инициалами, например: xyz, jcvb, dzy, dyh. Однажды DZY нашел особо ценную строку s. Услышав об этом, несколько пар хороших друзей пришло навестить DZY. Первого друга i-й пары зовут ai, второго друга пары зовут bi. Каждой паре стало интересно, есть ли в особо ценной строке подстрока, содержащая оба имени пары. Если такая существует, друзья хотели бы найти подстроку минимальной длины, чтобы запомнить ее на удачу. Пожалуйста, помогите DZY, для каждой пары найдите минимальную длину подстроки s, которая содержит ai и bi, или же укажите, что искомая подстрока не существует. Подстрока s это строка slsl + 1... sr для некоторых чисел l, r (1 ≤ l ≤ r ≤ |s|). Длина такой подстроки равна (r - l + 1). Строка p содержит некоторую другую строку q, если p имеет подстроку, равную q. Выходные данные Для каждой пары выведите строку, содержащую единственное целое число — минимальная длина требуемой подстроки. Если искомой подстроки не существует, выведите -1. Примечание Кратчайшие подстроки для первого примера таковы: xyz, dyhduxyz. Кратчайшие подстроки для второго примера таковы: ca, abc и abd. Кратчайшие подстроки для третьего примера таковы: baabca и abaa. | |
![]()
|
|
B. Про суффиксные структуры
реализация
Строки
*1400
Бизон-Чемпион не только бизон, но и любимец команды «Бизоны». На очередном соревновании «Бизонам» попалась следующая задача: «Даны два различных слова (строки из латинских букв) s и t. Необходимо из слова s получить слово t». Задача показалась ребятам простой, ведь они хорошо знают суффиксные структуры данных. Бизон Старший любит суффиксный автомат. Применяя его один раз к строке, он может удалить из этой строки любой один символ. Бизон Средний хорошо знает суффиксный массив. Применяя его один раз к строке, он может поменять местами два любых символа в этой строке. Суффиксным деревом ребята не владеют, а с его помощью можно сделать гораздо большее. Бизону-Чемпиону интересно, смогут ли «Бизоны» решить задачу. При этом, возможно, для решения задачи не требуются обе структуры данных. Выясните, смогут ли ребята решить задачу и если да, то как: можно ли решить ее только с помощью суффиксного автомата, только с помощью суффиксного массива или потребуются обе структуры? Обратите внимание, что структуры разрешается использовать неограниченное количество раз и в любом порядке. Выходные данные В единственную строку выведите ответ на задачу. Выведите «need tree» (без кавычек), если из слова s невозможно получить слово t, используя суффиксный массив и суффиксный автомат. Выведите «automaton» (без кавычек), если для решения задачи достаточно только суффиксного автомата. Выведите «array» (без кавычек), если для решения задачи достаточно только суффиксного массива. Выведите «both» (без кавычек), если для решения задачи необходимы обе эти структуры данных. Гарантируется, что если можно решить задачу только с использованием суффиксного массива, то решить задачу только с использованием суффиксного автомата невозможно. Аналогичное верно и для суффиксного автомата. Примечание В третьем примере можно действовать так: сначала превратить «both» в «oth», удалив первый символ с помощью суффиксного автомата, а потом сделать два обмена символов получившейся строки с помощью суффиксного массива и получить «hot». | |
![]()
|
|
A. Eevee
Перебор
реализация
Строки
*1000
Вы решаете кроссворд из задачи K с IPSC 2014. Вы уже решили почти весь кроссворд, осталось не разгаданным одно слово: в кого эволюционирует Eevee? Вы не очень хорошо знаете покемонов, но быстрый поиск в интернете помог вам узнать, что Eevee может эволюционировать в восемь разных покемонов: Vaporeon, Jolteon, Flareon, Espeon, Umbreon, Leafeon, Glaceon и Sylveon. Вы знаете длину слова в кроссворде, кроме того, вам уже известны некоторые буквы. Также известно, что этой длине и известным буквам удовлетворяет только один из покемонов, в которых эволюционирует Eevee. Ваша задача найти этого покемона. Выходные данные Выведите имя покемона, в которого Eevee может эволюционировать, который подходит под длину слова и известные буквы из входных данных. Используйте только строчные латинские буквы для вывода имени (в частности, не начинайте имя с заглавной буквы). Примечание Имена покемонов из задачи в формате, удобном для вставки в ваше решение: ["vaporeon", "jolteon", "flareon", "espeon", "umbreon", "leafeon", "glaceon", "sylveon"] {"vaporeon", "jolteon", "flareon", "espeon", "umbreon", "leafeon", "glaceon", "sylveon"} | |
![]()
|
|
E. Три строки
снм
Строки
строковые суфф. структуры
Структуры данных
*2400
Заданы три строки (s1, s2, s3). Для каждого целого l (1 ≤ l ≤ min(|s1|, |s2|, |s3|), найдите количество троек целых чисел (i1, i2, i3) таких, что три строки sk[ik... ik + l - 1] (k = 1, 2, 3) попарно равны между собой. Все найденные числа выведите по модулю 1000000007 (109 + 7). Если какие-то из обозначений вам не знакомы, прочтите примечание. Выходные данные Выведите min(|s1|, |s2|, |s3|) чисел, разделенных пробелом — ответы на задачу по модулю 1000000007 (109 + 7). Примечание Рассмотрим строку t = t1t2... t|t|, где ti обозначает i-й символ строки, а |t| обозначает длину строки t. Подстрокой t[i... j] (1 ≤ i ≤ j ≤ |t|) будем называть строку titi + 1... tj. | |
![]()
|
|
B. Много игр
Деревья
дп
игры
поиск в глубину и подобное
реализация
Строки
*1900
Андрей, Федя и Леша — очень изобретательные ребята. В очередной раз они придумали игру для двоих игроков со строками. Задан набор, состоящий из n непустых строк. Во время игры два игрока вместе строят слово, изначально это слово пустое. Игроки ходят по очереди. За свой ход игрок должен дописать в конец слова одну букву так, чтобы полученное слово было префиксом хотя бы одной строки из заданного набора. Проигрывает тот, кто не может сделать ход. Андрей и Леша решили сыграть в эту игру k раз. Причем, игрок, проигравший в i-й игре, делает первый ход в (i + 1)-й игре. Ребята решили, что победителем по сумме всех игр будет считаться тот, кто победил в последней (k-й) игре. Андрей и Леша уже начали играть, а Федя в это время решил посчитать: кто будет победителем, если оба игрока будут играть оптимально. Помогите ему. Выходные данные Если победит игрок, который ходит первым, то выведите «First», иначе выведите «Second» (кавычки выводить не нужно). | |
![]()
|
|
E. Яблов и игра
Бинарный поиск
кратчайшие пути
Строки
*3000
Яблов и Тостов любят играть. Сегодня они играют со строками по следующим правилам. Сперва Тостов называет Яблову две строки s и t, состоящие исключительно из букв 'A', 'B', 'C', 'D'. Затем Яблов должен как можно быстрее получить строку s. Изначально у него есть пустая строка, за одну секунду он может дописать к концу текущей строки любую непрерывную подстроку строки t. И вот Тостов и Яблов начинают играть в описанную игру. Тостов уже назвал Яблову строку t, а вот строку s он еще не придумал. Тостов считает, что строка s должна состоять из n символов. Конечно, он хочет придумать самую плохую строку для Яблова (такую, что Яблов проведет как можно больше времени, получая ее). Скажите Тостову, сколько времени Яблов проведет за игрой, если Тостов найдет для него самую худшую строку длины n? Считайте, что Яблов всегда действует оптимально и получает любую строку s за минимально возможное время. Выходные данные Выведите единственное целое число — максимальное возможное время, необходимое Яблову, чтобы получить какую-то строку s длины n. Примечание В первом примере Тостов может выбрать строку «AAAAA». Во втором примере Тостов может выбрать строку «DADDA». | |
![]()
|
|
A. Нет палиндромам!
жадные алгоритмы
Строки
*1700
Паша ненавидит палиндромы. Он считает строку s терпимой, если каждый ее символ — это одна из первых p букв латинского алфавита, и s не содержит ни одной подстроки-палиндрома длины 2 или больше. Паша нашел терпимую строку s длины n. Помогите ему найти лексикографически следующую терпимую строку той же длины, либо определите, что такой не существует. Выходные данные Если лексикографически следующая терпимая строка той же длины существует, выведите ее. В противном случае выведите «NO» (без кавычек). Примечание Строка s лексикографически больше (или просто больше) строки t той же длины, если существует число i, такое что s1 = t1, ..., si = ti, si + 1 > ti + 1. Лексикографически следующая терпимая строка — это лексикографически минимальная терпимая строка, большая данной. Палиндром — это строка, которая одинаково читается слева направо и справа налево. | |
![]()
|
|
D. Федя и реферат
графы
дп
поиск в глубину и подобное
Строки
хэши
*2400
После того, как вы помогли Феде найти друзей в игре «Call of Soldiers 3», он совсем перестал учиться. Сегодня преподаватель английского в качестве домашнего задания попросил Федю подготовить реферат. Федя не хотел готовить реферат, поэтому он попросил Лешу о помощи. Леша написал реферат за Федю, но Феде он совсем не понравился. Теперь Федя собирается немного изменить реферат, используя словарь синонимов английского языка. Федя не хочет менять смысл реферата, поэтому единственное изменение, которое он будет делать: менять слово на один из его синонимов, используя правило замены из словаря. Эту операцию Федя может выполнять любое количество раз. В итоге Федя хочет получить реферат, который, во-первых, содержит как можно меньше букв «R» (регистр не важен), а во-вторых, из всех рефератов с минимальным количеством букв «R» имеет минимальную длину (длина реферата — это сумма длин всех слов в нем). Помогите Феде получить требуемый реферат. Обратите внимание, что в этой задаче регистр букв не имеет значения. Например, если в словаре синонимов записано, что слово cat можно заметить на слово DOG, то разрешается заменить слово Cat на слово doG. Выходные данные Выведите два целых числа — минимальное количество букв «R» в полученном реферате и минимальная длина полученного реферата. | |
![]()
|
|
D. МУХ и стенки из кубиков
Строки
строковые суфф. структуры
*1800
Белые медведи Меньшиков и Услада из Санкт-Петербургского зоопарка и слоник Хорас из Киевского зоопарка где-то достали очень много деревянных кубиков. Из кубиков они стали строить башенки, ставя кубики один на другой, а башенки, поставленные в ряд, назвали стенкой. Стенка может состоять из башенок различных высот. Хорас первым закончил собирать свою стенку и назвал ее слоном, эта стенка состоит из w башенок. Медведи тоже закончили собирать свою стенку, но никак ее не назвали. Их стенка состоит из n башенок. Хорас посмотрел на стенку медведей, и его заинтересовало, в скольких участках этой стенки он может «увидеть слона». «Увидеть слона» можно на участке из w последовательных башенок, если высоты башенок на участке как последовательность совпадают с высотами башенок в стенке Хораса. Чтобы увидеть больше слонов Хорас может поднимать или опускать всю свою стенку целиком, в том числе Хорас может опустить свою стенку ниже уровня пола (посмотрите рисунки к тестовым примерам для лучшего понимая). От вас требуется посчитать количество участков, на которых можно «увидеть слона». Выходные данные Выведите количество участков в стенке медведей, на которых можно «увидеть слона». Примечание Слева на иллюстрации изображена стенка Хораса из примера, справа — стенка медведей. Серым цветом выделены места, в которых можно «увидеть слона».  | |
![]()
|
|
E. Dreamoon и строки
дп
Строки
*2200
У Dreamoon есть строка s и шаблон p. Сперва он удаляет ровно x символов из s, в результате чего получается строка s'. Затем он подсчитывает  , которое определяется как максимальное количество непересекающихся подстрок, равняющихся p, которые можно выделить в s'. Он хочет, чтобы это число было как можно больше. , которое определяется как максимальное количество непересекающихся подстрок, равняющихся p, которые можно выделить в s'. Он хочет, чтобы это число было как можно больше. Более формально, определим  как максимальное значение как максимальное значение  по всем s', которые можно получить, удалив ровно x символов из s. по всем s', которые можно получить, удалив ровно x символов из s. Dreamoon хочет знать  для всех x от 0 до |s|, где |s| обозначает длину строки s. для всех x от 0 до |s|, где |s| обозначает длину строки s. Выходные данные Выведите на единственной строке |s| + 1 целых чисел через пробел —  для всех x от 0 до |s|. для всех x от 0 до |s|. Примечание В первом примере соответствующие оптимальные s' после удаления от 0 до |s| = 5 символов из s таковы: {«aaaaa», «aaaa», «aaa», «aa», «a», «»}. Для второго примера оптимальные s' могут выглядеть как {«axbaxxb», «abaxxb», «axbab», «abab», «aba», «ab», «a», «»}. | |
![]()
|
|
D. Dreamoon и двоичное исчисление
дп
Строки
*2700
Dreamoon увидел большое целое число x, записанное на земле, теперь ему хочется вывести его в двоичной записи. Dreamoon успешно преобразовал x в двоичный формат. Теперь он собирается распечатать это число следующим образом. У него есть целое число n = 0 и он может выполнять две следующие операции неограниченное количество раз в любом порядке: - Распечатать двоичную запись n без ведущих нулей, результат печати добавляется справа к уже выведенной строке.
- Увеличить n на 1.
Определим идеальную последовательность как последовательность операций, которая может вывести двоичную запись x без ведущих нулей и заканчивается операцией 1. Dreamoon хочет знать, сколько существует различных идеальных последовательностей и какова длина (в операциях) наикратчайшей идеальной последовательности. Ответы могут быть очень большими, поэтому выводите их по модулю 1 000 000 007 (109 + 7). Определим строковое представление идеальной последовательности как строку из символов '1' и '2', где i-й символ в строке соответствует i-й выполненной операции. Две идеальные последовательности называются различными, если их строковые представления различны. Выходные данные В первой строке должно быть записано целое число — количество различных идеальных последовательностей по модулю 1 000 000 007 (109 + 7). Во второй строке должно быть записано целое число — минимальная длина идеальной последовательности по модулю 1 000 000 007 (109 + 7). Примечание В первом примере наикратчайшая и единственная идеальная последовательность — «222221» длины 6. Во втором примере существует три идеальных последовательности «21211», «212222222221», «222222222222222222222222221». Среди них кратчайшая имеет длину 5. | |
![]()
|
|
C. Взлом шифра
математика
Перебор
Строки
теория чисел
*1700
Поликарп участвует в соревновании по взлому нового защищенного мессенджера. Для победы в конкурсе осталось совсем немного. Тщательно изучив протокол взаимодействия, Поликарп пришел к выводу, что секретный ключ можно получить, если правильным образом порезать на две части публичный ключ приложения. Публичным ключом является длинное целое число, которое может состоять даже из миллиона цифр! Поликарпу надо найти такой способ порезать публичный ключ на две непустые части, что первая (левая) часть как отдельное число делится на a, а вторая (правая) часть как отдельное число делится на b. Обе части должны быть положительными числами, не имеющими лидирующих нулей. Значения a и b Поликарпу известны. Помогите Поликарпу и найдите любой из подходящих способов порезать публичный ключ. Выходные данные В первую строку выведите «YES» (без кавычек), если искомый способ существует. Далее в этом случае выведите две строки — левую и правую части после разреза. Записанные подряд (сначала левая, потом правая) эти части должны в точности составлять публичный ключ. Левая часть должна делиться на a, а правая — на b. Обе части должны быть целыми положительными числами, не имеющими ведущих нулей. Если ответов несколько, выведите любой из них. Если ответа не существует, то выведите в единственной строке «NO» (без кавычек). | |
![]()
|
|
B. Одержимость строкой
дп
Строки
*2000
Хамед недавно нашел строку t и неожиданно для себя крепко к ней привязался. Несколько дней он пытался найти все вхождения t в другие имеющиеся у него строки. Наконец, он устал и начал думать о следующей задаче. Вам дана строка s. Сколько существует способов извлечь k ≥ 1 неперекрывающихся подстрок из неё, таких, что в каждой из них содержится t как подстрока? Более формально, требуется подсчитать количество способов выбора двух последовательностей, a1, a2, ..., ak и b1, b2, ..., bk, удовлетворяющих следующим требованиям: - k ≥ 1
-
 -
 -
 -
 t является подстрокой строки saisai + 1... sbi (строка s индексируется с 1). t является подстрокой строки saisai + 1... sbi (строка s индексируется с 1). Так как количество способов может быть очень большим, выведите его по модулю 109 + 7. Выходные данные Выведите ответ единственной строкой. | |
![]()
|
|
B. Лекция
реализация
Строки
*1000
У вас новый преподаватель по теории графов и он очень быстро читает лекции. Чтобы успевать записывать, вы разработали следующий план. Вы знаете два языка, причём преподаватель читает лекцию на первом из них. Слова обоих языков состоят из маленьких латинских символов. Каждый язык представляет собой некоторый набор слов. В каждом языке все слова различаются, т. е. записываются различным образом. Более того, между словами этих языков установлено взаимно-однозначное соответствие, то есть для каждого слова каждого языка в другом языке существует ровно одно слово, которое имеет такое же значение. Каждое слово, сказанное преподавателем, вы можете написать либо на первом языке, либо на втором. Конечно, во время лекции каждое слово вы записываете на том языке, на котором данное слово записывается короче. В случае равенстве длин соответствующих слов вы отдаете предпочтение слову из первого языка. Вам задан текст лекции, которую прочитает вам преподаватель. Определите, как описанная лекция будет записана вами в конспект. Выходные данные Выведите ровно n строк — описание того, как вы запишите лекцию в свою тетрадь. Слова лекции требуется выводить в том же порядке, что и во входных данных. | |
![]()
|
|
B. Выравнивание по центру
реализация
Строки
*1200
Почти каждый текстовый редактор имеет встроенную функцию выравнивание по центру заданного текста. К выпуску четвертого релиза популярного в Берляндии редактора «Textpad» разработчики решили включить данную функциональность и в этот продукт. Вам положено в кратчайший срок реализовать выравнивание. Удачи! Выходные данные Отформатируйте заданный текст, выравняв его по центру. Окружите весь текст рамкой из символов «*» минимального размера. Если строка не может быть однозначно выравнена (например строка имеет четную длину при нечетной ширине всего блока), то такие строки надо размещать, попеременно округляя позицию к левому и правому краю (начинайте с округления в левую сторону). Внимательно изучите примеры для уточнения правил вывода ответа. | |
![]()
|
|
C. Наибольшая правильная скобочная подстрока
дп
жадные алгоритмы
Конструктив
сортировки
Строки
Структуры данных
*1900
И снова вам предлагается задача на правильные скобочные последовательности. Напомним, что скобочная последовательность называется правильной, если путем вставки в нее символов «+» и «1» можно получить из нее корректное математическое выражение. Например, последовательности «(())()», «()» и «(()(()))» — правильные, в то время как «)(», «(()» и «(()))(» — нет. Вам задана строка, состоящая из символов «(» и «)». Ваша задача найти её наидлиннейшую подстроку, которая является правильной скобочной последовательностью. Также вам надо найти количество таких подстрок. Выходные данные Выведите длину наибольшей подстроки, являющейся правильной скобочной последовательностью, и количество таких подстрок. Если искомых подстрок не существует, то выведите «0 1» в единственную строку выходных данных. | |
![]()
|
|
B. Выбор пары символов
Строки
*1500
Дана строка S, состоящая из N символов. Требуется найти количество упорядоченных пар целых чисел i и j таких, что: 1. 1 ≤ i, j ≤ N 2. S[i] = S[j], то есть i-ый символ строки S равен j-ому. Выходные данные Выведите одно число — количество пар i и j с требуемым свойством. Пары (x, y) и (y, x) следует считать различными, т. е. считаются упорядоченные пары. | |
![]()
|
|
B. Миша и смена хэндлов
снм
Строки
Структуры данных
*1100
Взломав сайт Codeforces, Миша решил дать возможность всем пользователям менять их хэндлы. Пользователь теперь может сменить свой хэндл сколько угодно раз. Но при этом каждый новый хэндл не должен совпадать ни с каким из уже занятых или занятых в прошлом хэндлов. У Миши есть список запросов пользователей на смену хэндлов. После их выполнения он хочет понять соответствие между исходными хэндлами пользователей и новыми. Помогите ему в этом. Выходные данные В первой строке выведите целое число n — количество пользователей, воспользовавшихся возможностью сменить хэндл. В последующих n строках выведите соответствие между старыми хэндлами пользователей и новыми. Каждая из них должна содержать по две строки old и new, разделенные пробелом, что означает следующее: до взлома сайта пользователь имел хэндл old, а после выполнения всех запросов получил хэндл new. Строки разрешается выводить в любом порядке. Каждый пользователь, менявший хэндл, должен встретиться в этом описании ровно один раз. | |
![]()
|
|
A. Подарок мистера Китаюта
Перебор
реализация
Строки
*1100
Мистер Китаюта любезно предоставил Вам строку s из строчных букв латинского алфавита. Он просит вас вставить ровно одну строчную букву латинского алфавита в s так, чтобы получился палиндром. Палиндром — это строка, которая читается одинаково в обоих направлениях. Например, «noon», «testset» и «a» — палиндромы, а «test» и «kitayuta» — нет. Вы можете выбрать любую строчную букву латинского алфавита и вставить её в любую позицию s, в частности, можно вставить в начало или в конец s. Букву надо вставить, даже если данная строка уже является палиндромом. Если возможно вставить одну строчную букву латинского алфввита в s так, чтобы получившаяся строка была палиндромом, выведите состояние строки после вставки. В противном случае выведите «NA». Если возможно получить более одного палиндрома, можно вывести любой из них. Выходные данные Если можно превратить строку s в палиндром, вставив одну строчную букву латинского алфавита, выведите итоговую строку в единственной строке. В противном случае выведите «NA» (без кавычек, регистр имеет значение). Если существует более одного решения, будет засчитано любое. Примечание В первом можно добавить «r> к концу строки «revive», чтобы получить палиндром «reviver». Во втором примере решений несколько. Например, «eve» также будет засчитан. В третьем примере невозможно превратить «kitayuta» в палиндром путем прибавления одной буквы. | |
![]()
|
|
E. Подарок мистера Китаюта
дп
Комбинаторика
матрицы
Строки
*3000
Мистер Китаюта любезно предоставил Вам строку s из строчных букв латинского алфавита. Он просит вас вставить ровно n строчных букв латинского алфавита в s так, чтобы получился палиндром. Палиндром — это строка, которая читается одинаково в обоих направлениях. Например, «noon», «testset» и «a» — палиндромы, а «test» и «kitayuta» — нет. Вы можете выбрать любые n строчных букв латинского алфавита и вставить каждую из них в любую позицию s, в частности, можно вставить в начало или в конец s. Надо вставить ровно n букв, даже если данную строку можно сделать палиндромом, вставив менее n букв. Найдите количество палиндромов, которые можно получить таким способом, по модулю 10007. Выходные данные Выведите количество палиндромов, которые можно получить, по модулю 10007. Примечание В первом примере можно получить палиндром «reviver», вставив «r» в конец «revive». Во втором примере можно получить следующие 28 палиндромов: «adada», «adbda», ..., «adzda», «dadad» and «ddadd». | |
![]()
|
|
B. Антон и та самая валюта
жадные алгоритмы
математика
Строки
*1300
Берляндия, 2016 год. Курс той самой валюты по отношению к бурлю настолько вырос, что для простоты вычислений его дробной частью стали пренебрегать, а сам курс теперь считается целым числом. Надёжные источники сообщили ворчливому финансисту Антону некоторую информацию о курсе той самой валюты по отношению к бурлю на завтра. Теперь Антон знает, что завтра курс будет четным числом, которое можно получить из сегодняшнего курса, поменяв в нём местами ровно две различные цифры. Из всех возможных значений, удовлетворяющих этим условиям, курс на завтра будет максимально возможным. Гарантируется, что на сегодняшний день курс — положительное нечётное число n. Помогите Антону определить курс той самой валюты на завтра! Выходные данные Если информация о завтрашнем курсе оказалась противоречивой, то есть ни одного целого числа, удовлетворяющего условию, не существует, выведите - 1. В противном случае, выведите курс той самой валюты по отношению к бурлю на завтра. Это должно быть максимально возможное число из тех, которые являются чётными, и которые получаются из сегодняшнего курса путём обмена ровно двух цифр. Запись завтрашнего курса не должна содержать ведущих нулей. | |
![]()
|
|
E. Мелодичная песня
математика
Строки
*2000
В седьмом классе Саша начал слушать музыку. Для того чтобы оценивать, какая из песен нравится ему больше, он ввел понятие мелодичности песни. Название песни — это слово из заглавных латинских букв. Мелодичность песни это мелодичность её названия. Назовем простой мелодичностью слова отношение количества гласных букв в слове к количеству всех букв в слове. Назовем мелодичностью слова сумму простых мелодичностей всех подстрок слова. Более формально, определим функцию vowel(c), равную 1, если c — гласная, и 0 иначе. Пусть si — i-й символ строки s, а si..j — подстрока слова s, начинающаяся с i-го символа и заканчивающаяся j-м символом (sisi + 1... sj, i ≤ j). Тогда простая мелодичность s определяется по формуле:  Мелодичность s равна  Найдите мелодичность данной песни. Гласными буквами считаются I, E, A, O, U, Y. Выходные данные Определите мелодичность песни с абсолютной или относительной погрешностью не более 10 - 6. Примечание В первом примере все буквы — гласные. Простая мелодичность каждой подстроки равна 1. Всего в слове длины 7 имеется 28 подстрок. Значит, мелодичность песни равна 28. | |
![]()
|
|
C. Уотто и механизм
Бинарный поиск
Строки
строковые суфф. структуры
Структуры данных
хэши
*2000
Недавно Уотто, хозяину магазина запчастей, поступил заказ на механизм, умеющий обрабатывать строки определённым образом. Изначально в память механизма загружаются n строк. Затем, механизм должен уметь отвечать на запросы следующего вида: «По данной строке s определить, есть ли в памяти механизма строка t, состоящая из того же количества символов, что и s, и отличающаяся от s ровно в одной позиции». Уотто уже собрал механизм, осталось только написать для него программу и проверить её корректность на данных n исходных строк и m запросах. Эту работу он решил поручить Вам. Выходные данные На каждый запрос выведите в отдельной строке «YES» (без кавычек), если в памяти механизма есть нужная строка, иначе выведите «NO» (без кавычек). | |
![]()
|
|
A. Виталий и строки
Конструктив
Строки
*1600
Виталий — прилежный студент, который за пять лет обучения в университете не пропустил ни одной пары, выполнял вовремя все домашние задания и всегда досрочно закрывал сессию. На последней паре преподаватель продиктовал Виталию две строки s и t одинаковой длины, состоящие из строчных букв латинского алфавита, причем строка s лексикографически меньше строки t. Виталию стало интересно — существует ли такая строка, которая лексикографически больше строки s и одновременно лексикографически меньше строки t. Искомая строка Виталия также должна состоять из строчных букв латинского алфавита и иметь длину, равную длинам строк s и t. Давайте поможем Виталию решить эту несложную задачу! Выходные данные Если не существует строки, удовлетворяющей заданным требованиям, выведите единственную строку «No such string» (без кавычек). Если же такая строка существует, выведите ее в первую строку выходных данных. Если подходящих строк несколько, разрешается вывести любую из них. Примечание По определению, строка s = s1s2... sn лексикографически меньше строки t = t1t2... tn, если существует такое i, что s1 = t1, s2 = t2, ... si - 1 = ti - 1, si < ti. | |
![]()
|
|
B. Таня и поздравление
жадные алгоритмы
реализация
Строки
*1400
Маленькая Таня решила поздравить папу с Днем рождения и подарить ему открытку. Она уже составила текст для поздравления — строку s длины n, состоящую из прописных и строчных букв латинского алфавита. Таня пока не умеет писать, поэтому она нашла газету и решила вырезать оттуда буквы и наклеить их в открытку, чтобы получилась строка s. В газете записана строка t, состоящая из прописных и строчных букв латинского алфавита. Известно, что длина строки t не меньше длины строки s. Возможно, что в газете не хватает каких-то букв для составления поздравления, а какие-то буквы могут оказаться лишними. Поэтому Таня хочет вырезать из газеты некоторые n букв и составить из них поздравление длины ровно n, чтобы оно было максимально похоже на s. Если буква в заданной позиции совпадает и по значению, и по регистру (в строке s и в той строке, что наклеит Таня), то она радостно кричит «УРА!», а если буква в заданной позиции совпадает только по значению, но не по регистру, то она произносит «ОПА». Таня хочет наклеить такую надпись, чтобы максимальное количество раз прокричать «УРА!», а если это можно сделать несколькими способами, то во вторую очередь она хочет максимизировать количество раз, которое она скажет «ОПА». Вам предстоит помочь Тане в составлении поздравления. Выходные данные Выведите два целых числа, разделенных пробелом, где: - первое число — сколько раз Таня прокричит «УРА!» при составлении поздравления,
- второе число — сколько раз Таня произнесет «ОПА» при составлении поздравления.
| |
![]()
|
|
A. Панграмма
реализация
Строки
*800
Слово или предложение на некотором языке называется панграммой, если в нем встречаются все символы алфавита этого языка хотя бы один раз. Панграммы часто используют в типографии для демонстрации шрифтов или тестирования средств вывода различных устройств. Вам дана строка, состоящая из маленьких и больших латинских букв. Проверьте, является ли эта строка панграммой. Считается, что строка содержит букву латинского алфавита, если эта буква встречается в верхнем или нижнем регистре. Выходные данные Выведите «YES», если строка является панграммой, и «NO» в противном случае. | |
![]()
|
|
C. Выравнивание ДНК
математика
Строки
*1500
Вася увлекся биоинформатикой. Он собирается написать статью про похожие циклические последовательности ДНК, и поэтому он придумал новый способ определения схожести циклических последовательностей. Пусть строки s и t имеют одинаковую длину n, тогда функция h(s, t) определяется как количество позиций, в которых соответствующие символы s и t совпадают. При помощи функции h(s, t), определяется функция расстояния по Василию ρ(s, t):  где  — это строка s, циклически сдвинутая на i символов влево. Например, ρ("AGC", "CGT") = h("AGC", "CGT") + h("AGC", "GTC") + h("AGC", "TCG") + h("GCA", "CGT") + h("GCA", "GTC") + h("GCA", "TCG") + h("CAG", "CGT") + h("CAG", "GTC") + h("CAG", "TCG") = 1 + 1 + 0 + 0 + 1 + 1 + 1 + 0 + 1 = 6Вася нашел в интернете строку s длины n. Теперь он хочет посчитать количество строк t, находящихся на максимальном расстоянии по Василию от строки s. Формально говоря, t должна удовлетворять равенству:  . . Вася не смог перебрать все возможные строки для нахождения ответа, поэтому ему нужна ваша помощь. Поскольку ответ может быть очень большим, посчитайте количество подходящих строк по модулю 109 + 7. Выходные данные Выведите одно число — ответ по модулю 109 + 7. Примечание Обратите внимание, что если для двух различных строк t1 и t2 значения ρ(s, t1) и ρ(s, t2) являются максимальными среди всех возможных строк, то обе строки необходимо учесть в итоговом количестве даже в том случае, когда одну из них можно получить циклическим сдвигом из другой. В первом примере существует ρ("C", "C") = 1, для остальных строк t длины 1 значение ρ(s, t) равно 0. Во втором примере ρ("AG", "AG") = ρ("AG", "GA") = ρ("AG", "AA") = ρ("AG", "GG") = 4. В третьем примере ρ("TTT", "TTT") = 27. | |
![]()
|
|
F. И снова правильная скобочная последовательность
жадные алгоритмы
Строки
строковые суфф. структуры
Структуры данных
хэши
*2700
У Поликарпа имеется конечная последовательность из открывающихся и закрывающихся скобок. Чтобы не уснуть на лекции, Поликарп развлекается со своей последовательностью. Он умеет выполнять две операции: - добавление любой скобки в любую позицию (в начало, в конец или между любыми двумя имеющимися скобками);
- циклический сдвиг — перемещение самой последней скобки из конца последовательности в начало.
Поликарп может применить к своей последовательности любое количество операций добавления и циклического сдвига в любом порядке. В результате он хочет получить правильную скобочную последовательность минимальной возможной длины. В случае если таких последовательностей несколько, Поликарпа интересует лексикографически наименьшая. Помогите ему найти такую последовательность. Правильной скобочной последовательностью называется последовательность открывающихся и закрывающихся скобок, из которой путем добавления символов «1» и «+» можно получить корректное арифметическое выражение. Каждой открывающейся скобке должна соответствовать закрывающаяся. Например, последовательности «(())()», «()», «(()(()))» правильные, а «)(», «(()» и «(()))(» — нет. Последовательность a1 a2... an лексикографически меньше последовательности b1 b2... bn, если найдется такой номер i от 1 до n, что ak = bk при 1 ≤ k < i и ai < bi. Считайте, что «(» < «)». Выходные данные Выведите правильную скобочную последовательность минимальной длины, которую Поликарп может получить при помощи своих операций. Если таких последовательностей несколько, выведите лексикографически наименьшую. Примечание Последовательность в первом примере уже является правильной, но чтобы получить лексикографически наименьший ответ, нужно выполнить четыре операции циклического сдвига. Во втором примере нужно добавить закрывающуюся скобку между второй и третьей скобками и совершить циклический сдвиг. Можно сначала совершить сдвиг, а потом добавить скобку в конце. | |
![]()
|
|
A. Виталий и пирожок
жадные алгоритмы
Строки
хэши
*1100
После тяжелого дня Виталий очень проголодался, он хочет съесть свой любимый пирожок с картошкой. Но всё не так просто. Виталий находится в первой комнате дома с n комнатами, расположенными в ряд и пронумерованными с единицы слева направо. Из первой комнаты можно попасть во вторую комнату, из второй комнаты в третью и так далее — из (n - 1)-й комнаты можно попасть в n-ю. Таким образом, в комнату номер x можно попасть только лишь из комнаты номер x - 1. Пирожок с картошкой находится в n-й комнате, в которую Виталию необходимо попасть. Между каждой парой последовательных комнат есть дверь. Чтобы попасть в комнату номер x из комнаты номер x - 1 необходимо открыть дверь между комнатами соответствующим ей ключом. Всего в доме существует несколько типов дверей (задаются прописными латинскими буквами) и несколько типов ключей (задаются строчными буквами латинского алфавита). Ключ типа t подходит к двери типа T тогда и только тогда, когда t и T это одна и та же буква, записанная в разных регистрах. Например, ключом f можно открывать двери F. В каждой из первых n - 1 комнат лежит ровно по одному ключу некоторого типа, которые Виталий может использовать, чтобы попасть в следующие комнаты. После того, как дверь открыта каким-то ключом, Виталий не достаёт ключ из замочной скважины и незамедлительно бежит в следующую комнату. Иными словами, каждым ключом можно открыть не более одной двери. Виталий понимает, что он может оказаться в какой-то комнате и у него не будет ключа, который открывает дверь в следующую комнату. Перед началом похода за пирожком с картошкой Виталий может купить любое количество ключей любого типа, чтобы гарантированно добраться до комнаты номер n. Зная план дома, Виталий хочет узнать, какое минимальное количество ключей ему нужно купить, чтобы точно добраться до комнаты номер n, в которой лежит очень вкусный пирожок с картошкой. Напишите программу, которая поможет Виталию максимально сэкономить. Выходные данные Выведите в первую строку целое число — минимальное количество ключей, которое Виталию необходимо приобрести, чтобы попасть из первой комнаты в комнату номер n. | |
![]()
|
|
B. Паша и строка
жадные алгоритмы
Конструктив
математика
Строки
*1400
На День рождения Паше подарили очень красивую строку s, состоящую из строчных латинских букв. Буквы в строке пронумерованы от 1 до |s| слева направо, где |s| — длина подаренной строки. Паше не совсем понравился подарок, и он решил его изменить. После Дня рождения в течение m дней Паша выполнял со своей строкой следующие преобразования — каждый день он выбирал целое число ai и переворачивал участок строки (отрезок) с позиции ai по позицию |s| - ai + 1. Гарантируется, что 2·ai ≤ |s|. Перед вами стоит следующая задача — определить, как будет выглядеть подаренная Паше строка через m дней. Выходные данные Выведите единственной строкой как будет выглядеть подаренная Паше строка s через m дней. | |
![]()
|
|
D. Ам Ням и ожерелье
Строки
строковые суфф. структуры
хэши
*2200
Как-то раз Ам Ням нашёл нитку с надетыми на неё n камешками разных цветов. Он решил отрезать первые несколько камней с этой нитки, чтобы сделать из них бусы и подарить своей подруге, Ам Нелли.  Ам Ням знает, что его подруга любит красивые узоры. Поэтому он хочет, чтобы камешки на бусах образовывали регулярный узор. Последовательность камешков S называется регулярной, если она представима в виде S = A + B + A + B + A + ... + A + B + A, где A и B — некоторые последовательности камешков, " + " обозначает конкатенацию последовательностей, слагаемых в этой сумме ровно 2k + 1, среди которых k + 1 слагаемое "A" и k слагаемых "B", причём слагаемые "A" и "B" чередуются. Ам Нелли знает, что её друг — увлекающийся математик, поэтому она с пониманием отнесётся, даже если какая-то из последовательностей A или B окажется пустой. Помогите Ом Ному определить, какими способами из найденной им нитки можно отрезать первые несколько камешков (не менее одного; возможно, все) таким образом, чтобы они образовывали регулярный узор. Отрезая камешки, Ам Ням не меняет их порядок. Выходные данные Выведите строку из n нулей и единиц. Позиция i (1 ≤ i ≤ n) должна либо содержать единицу, если первые i камешков на нитке образуют регулярную последовательность, либо ноль в противном случае. Примечание В первом тесте из условия регулярной является как последовательность из первых 6 камешков (если взять A = "", B = "bca"), так и последовательность из первых 7 камешков (если взять A = "b", B = "ca"). Во втором тесте из условия, например, последовательность из первых 13 камешков является регулярной, если взять A = "aba", B = "ba". | |
![]()
|
|
D. Тавас и Малекас
жадные алгоритмы
Строки
строковые суфф. структуры
хэши
*1900
Тавас — странное создание. Обычно, когда люди спят, от них доносится тихое "zzz", но от спящего Таваса доносится строка s длины n.  Сегодня Тавас уснул в гостях у Малекаса. Пока он спал, Малекас немного поработал со строкой s. У Малекаса есть своя любимая строка p. Он определил все позиции x1 < x2 < ... < xk, где p входит в s. Более формально, для каждого xi (1 ≤ i ≤ k) выполняется условие sxisxi + 1... sxi + |p| - 1 = p. Затем Малекас записал одну из подпоследовательностей x1, x2, ... xk (возможно, пустую) на бумажке. По определению, b — это подпоследовательность последовательности a тогда и только тогда, когда мы можем получить b из a, удалив некоторые элементы (возможно, удалив все или не удалив ничего вовсе). Когда Тавас проснулся, Малекас всё ему рассказал. Он не смог вспомнить строку s, но он знает, что и p, и s содержат только строчные буквы английского алфавита, а также у него есть подпоследовательность, записанная на бумажке. Тавасу стало интересно: сколько различных строк s подходит под имеющуюся информацию? Он спросил СаДДаса, но СаДДас недостаточно умен, чтобы решить задачу. Итак, Тавас попросил вас посчитать это количество для него. Ответ может быть очень большим, так что Тавас хочет, чтобы вы вывели его остаток от деления на 109 + 7. Выходные данные В единственной строке выведите ответ по модулю 1 000 000 007. Примечание В первом тесте из условия подходят все строки вида "ioioi?", где вместо вопросительного знака может стоять любая буква английского алфавита. Здесь |x| обозначает длину строки x. Обратите внимание, что такой строки может не существовать, в таком случае ответ — 0. | |
![]()
|
|
D. Сочинение песни
дп
Перебор
Строки
*2100
Одна из любимых забав Ёжика и его друга — это брать какое-нибудь предложение или песенку и заменять в них половину слов (а то и все) на имена друг друга. Вот близится День Рождения, и Ёжик решил подготовить своему другу особенный подарок — очень длинную песенку, в которой много раз будет повторяться его имя. Но вот беда — ему никак не удаётся сочинить хорошую песенку! Дело в том, что Ёжик уже точно решил, какой длины должно быть получившееся предложение (т.е. сколько букв в нём должно быть), и в каких позициях в этом предложении должно входить имя друга, а вот больше ни в какой позиции вхождения этого имени быть не должно. Кроме того, Ёжик решил ограничиться в этом предложении только первыми K буквами английского алфавита (так что это будет даже не предложение, а одно длинное слово). В итоге и правда получается достаточно сложная задача, поэтому Ёжик просит Вас помочь ему — написать программу, которая по заданной строке-имени P, длине N искомого слова, заданным позициям вхождения имени P в искомое слово и размеру алфавита K построит это слово. Вхождения имени, вообще говоря, могут перекрываться. Выходные данные Выведите искомое слово S. Если ответов несколько, выведите любой. Если решение не существует, выведите «No solution». | |
![]()
|
|
A. Набор строк
реализация
Строки
*1100
У вас есть строка q. Набор из k строк s1, s2, ..., sk называется красивым, если конкатенация этих строк даёт строку q (формально, s1 + s2 + ... + sk = q) и первые символы этих строк различны. Найдите любой красивый набор строк, либо сообщите, что красивого набора не существует. Выходные данные Если искомого набора не существует, тогда в единственной строке выведите «NO» (без кавычек). Иначе в первой строке выведите «YES» (без кавычек) и в следующих k строках выведите искомый красивый набор строк s1, s2, ..., sk. Если возможных ответов несколько, выведите любой из них. Примечание Во втором примере возможно два ответа: {"aaaca", "s"} и {"aaa", "cas"}. | |
![]()
|
|
E. Майк и друзья
Деревья
Строки
строковые суфф. структуры
Структуры данных
*2800
What-The-Fatherland — это странная страна! Все номера телефонов там представляют собой строки, состоящие из строчных букв латиницы. Вдвойне странно то, что один номер телефона может относиться к нескольким медведям! В этой стране есть рок-группа под названием CF, состоящая из n медведей (включая Майка), пронумерованных от 1 до n.  Номер телефона i-го члена CF — si. 17 мая в стране выходной под названием День звонков. В последний День Звонков каждый медведь позвонил по всем номерам, являющимся построками его номера (возможно, по некоторому номеру пришлось позвонить несколько раз). В частности, каждый позвонил себе (это действительно странная страна!). Обозначим как call(i, j) количество раз, которое i-й участник CF позвонил j-ому участнику CF. У Майка есть q запросов, которые он хочет задать вам. В каждом запросе он дает вам номера l, r и k, а вы должны назвать ему число  Выходные данные Выведите ответ на каждый запрос на отдельной строке. | |
![]()
|
|
A. Майк и факс
Перебор
реализация
Строки
*1100
Пока Майк гулял по метро, всё посыпалось из его рюкзака прямо на землю. В его рюкзаке было несколько факс-сообщений. Майк конкатенировал эти строки в некоторым порядке и теперь у него есть строка s.  Он не уверен, его ли это рюкзак или чужой. Он помнит, что в его рюкзаке было ровно k сообщений, каждое сообщение представляло собой строку-палиндром, и у всех этих строк была однаковая длина. Он просит вас помочь ему и сказать, свой ли рюкзак он подобрал. Проверьте, является ли данная строка s конкатенацией из k палиндромов одинаковой длины. Выходные данные Выведите "YES" (без кавычек), если юноша нес свой собственный рюкзак, в противном случае выведите "NO" (без кавычек). Примечание Палиндром — это строка, которая одинаково читается в обе стороны. Во втором примере сообщения в рюкзаке могут быть "saddas" и "tavvat". | |
![]()
|
|
A. Определение лиц
реализация
Строки
*900
Разработчикам Looksery необходимо написать эффективный алгоритм определения лиц на изображении. К сожалению, они сейчас заняты тем, что готовят для вас соревнование, поэтому вам придется сделать это за них. В рамках данной задачи изображением называется прямоугольная таблица, состоящая из строчных букв латинского алфавита. Лицом на изображении называется квадрат 2 на 2 элемента, такой, что из четырёх букв этого квадрата можно составить слово «face». Вам необходимо написать программу, которая определяет количество лиц на изображении. Квадраты, соответствующие лицам, могут пересекаться. Выходные данные В единственной строке выведите количество лиц на изображении. Примечание В первом примере на изображении находится одно лицо, расположенное в квадрате с верхним левым углом во второй строке и втором столбце:  Во втором примере на изображении также находится ровно одно лицо, его верхний левый угол находится во второй строке и первом столбце. В третьем примере изображены два лица:  В четвертом примере на изображении лиц нет. | |
![]()
|
|
A. Две подстроки
дп
жадные алгоритмы
Перебор
реализация
Строки
*1500
Дана строка s. Требуется определить, существуют ли в данной строке s две непересекающиеся подстроки "AB" и "BA" (подстроки могут идти в любом порядке). Выходные данные Выведите "YES" (без кавычек), если строка s содержит две непересекающиеся подстроки "AB" и "BA", и "NO" иначе. Примечание В первом примере входных данных, несмотря на то, что есть подстроки "AB" и "BA", их вхождения пересекаются, поэтому ответ — "NO". Во втором примере входных данных есть следующие вхождения подстрок: BACFAB. В третьем примере нет ни подстроки "AB", ни подстроки "BA". | |
![]()
|
|
B. ZgukistringZ
Конструктив
Перебор
реализация
Строки
*1800
Профессор GukiZ не всегда принимает строки такими, какие они есть. Получая строку, он иногда переставляет местами некоторые буквы в строке, таким образом, чтобы получалась новая строка. У GukiZ есть строки a, b, и c. Он хочет получить строку k, поменяв местами некоторые буквы в a, так, чтобы в k содержалось как можно больше непересекающихся подстрок, равных либо b, либо c. Подстрока строки x — это строка, сформированная непрерывным подотрезком символов из x. Две подстроки строки x пересекаются, если есть такая позиция i в строке x, которая принадлежит обеим этим подстрокам. GukiZ был разочарован, когда ни один из его учеников не смог решить эту задачу. Сможете помочь им и найти одну из возможных строк k? Выходные данные Найдите одну из возможных строк k, отвечающую описанию, данному в условии задачи. Если есть несколько возможных ответов, выведите любой. Примечание В третьем примере у данного оптимального решения есть три непересекающиеся подстроки, равные либо b, либо c в позициях 1 – 2 (ab), 3 – 4 (ab), 5 – 7 (aca). В этом примере существует много других оптимальных решений, одно из них: acaababbcc. | |
![]()
|
|
E. Ваня и скобки
дп
жадные алгоритмы
Перебор
Разбор выражений
реализация
Строки
*2100
Ваня делает домашнее задание по математике. У него есть выражение типа  , где x1, x2, ..., xn — цифры от 1 до 9, а знаком , где x1, x2, ..., xn — цифры от 1 до 9, а знаком  обозначается либо плюс '+' либо знак умножения '*'. Ване нужно поставить в этом выражении одну пару скобок так, чтобы максимизировать значение полученного выражения. обозначается либо плюс '+' либо знак умножения '*'. Ване нужно поставить в этом выражении одну пару скобок так, чтобы максимизировать значение полученного выражения. Выходные данные В первой строке выведите максимальное возможное значение выражения. Примечание Пояснение к первому тесту из условия. 3 + 5 * (7 + 8) * 4 = 303. Пояснение к второму тесту из условия. (2 + 3) * 5 = 25. Пояснение к третьему тесту из условия. (3 * 4) * 5 = 60 (также подходит множество других вариантов, например, (3) * 4 * 5 = 60). | |
![]()
|
|
A. Кёя и фотокниги
математика
Перебор
Строки
*900
Кёя Оотори продает фотокниги Гостевого клуба лицея Оран. У него есть 26 фотографий, обозначаемых строчными английскими буквами от 'a' до 'z'. Он собрал их в фото-книгу с некоторыми фотографиями в некотором порядке (возможно, некоторые фотографии повторяются). Таким образом, фото-книгу можно описать как строку, состоящую из строчных английских букв. Сейчас он хочет создать "особое издание" своей фото-книги, вставив одну дополнительную фотографию в произвольное место книги. Он хочет сделать как можно больше различных особых изданий своей фото-книги, чтобы получить больше денег. Он спрашивает у Харухи: сколько различных фото-книг может он сделать, вставляя одну дополнительную фотографию в уже имеющуюся фото-книгу? Пожалуйста, помогите Харухи решить эту задачу. Выходные данные Выведите единственное целое число, равное количеству различных фото-книг, которые может сделать Кёя Оотори, вставив одну дополнительную фотографию в имеющуюся фото-книгу. Примечание В первом примере можно сделать 'ab','ac',...,'az','ba','ca',...,'za', и 'aa', что даёт в итоге 51 различный вариант для фото-книги. | |
![]()
|
|
B. Охана прибирается в комнате
жадные алгоритмы
Перебор
Строки
*1200
Охана Мацумаэ пытается убраться в комнате, имеющей вид сетки размера n на n ячеек. Каждая ячейка изначально либо чистая, либо грязная. Охана может мести метлой по столбцам сетки. Её метла очень необычная: если она проводит ею по чистому квадрату, он становится грязным, а если она проводит по грязному квадрату, он становится чистым. Девушка хочет провести метлой по некоторым столбцам комнаты так, чтобы максимизировать количество полностью чистых строк. Разрешается проводить метлой только по всему столбцу, проводить метлой по части столбца запрещается. Выведите максимальное количество строк, которые она может сделать полностью чистыми. Выходные данные Выведите целое число, равное максимальному возможному количеству строк, являющихся полностью чистыми. Примечание В первом примере Охана может подмести 1-й и 3-й столбцы. От этого 1-й и 4-й ряд станут полностью чистыми. Во втором примере комната уже чистая, так что Охане ничего не надо делать. | |
![]()
|
|
E. Аня и полупалиндром
графы
Деревья
дп
Строки
строковые суфф. структуры
Структуры данных
*2300
Завтра Ане предстоит сдавать самый сложный экзамен по программированию, на котором ей необходимо получить отличную оценку. На последнем теоретическом занятии преподаватель ввел понятие полупалиндрома. Строка t является полупалиндромом, если для всех нечетных позиций i ( ) выполняется условие ti = t|t| - i + 1, где |t| — длина строки t, а нумерация позиций начинается с единицы. Например, строки "abaa", "a", "bb", "abbbaa" являются полупалиндромами, а строки "ab", "bba" и "aaabaa" — нет. ) выполняется условие ti = t|t| - i + 1, где |t| — длина строки t, а нумерация позиций начинается с единицы. Например, строки "abaa", "a", "bb", "abbbaa" являются полупалиндромами, а строки "ab", "bba" и "aaabaa" — нет. Аня узнала, что на экзамене она получит строку s, состоящую только из латинских символов a и b, а также число k. Для получения отличной оценки ей необходимо будет найти k-ю в лексикографическом порядке подстроку данной строки s среди тех подстрок, которые являются полупалиндромами. При этом, каждая подстрока в этом порядке учитывается столько раз, сколько раз она встречается в s. Преподаватель гарантирует, что данное число k не превышает количества подстрок данной строки, которые являются полупалиндромами. А вы сможете справиться с такой задачей? Выходные данные Выведите подстроку заданной строки, которая является k-й в лексикографическом порядке из тех подстрок заданной строки, которые являются полупалиндромами. Примечание По определению, строка a = a1a2... an лексикографически меньше строки b = b1b2... bm, если либо a является префиксом b и не совпадает с b, либо существует такое i, что a1 = b1, a2 = b2, ... ai - 1 = bi - 1, ai < bi. В первом примере подстроками-полупалиндромами являются следующие строки — a, a, a, a, aa, aba, abaa, abba, abbabaa, b, b, b, b, baab, bab, bb, bbab, bbabaab (список задан в лексикографическом порядке). | |
![]()
|
|
E. Простое задание
сортировки
Строки
Структуры данных
*2300
Это задание очень простое. Вам дана строка S длины n и q запросов, каждый запрос имеет формат i j k, что означает: отсортировать подстроку, состоящую из символов от i до j, в неубывающем порядке, если k = 1 или в невозрастающем порядке, если k = 0. Выведите итоговую строку после выполнения запросов. Выходные данные Выведите строку S после выполнения всех запросов. Примечание Объяснение к первому тесту: 




| |
![]()
|
|
B. Эквивалентные строки
разделяй и властвуй
сортировки
Строки
хэши
*1700
Сегодня на спецкурсе «Строки» Геральд узнал новое определение эквивалентности строк. Две строки a и b равной длины называются эквивалентными в одном из двух случаев: - Они равны.
- Если разделить строку a на две одинаковые по длине половины a1 и a2, а строку b — на две одинаковые по длине половины b1 и b2, то окажется, что верно одно из двух:
- a1 эквивалентно b1, а a2 эквивалентно b2
- a1 эквивалентно b2, а a2 эквивалентно b1
В качестве домашнего задания преподаватель выдал ученикам две строки и попросил определить, эквиваленты ли они. Геральд уже сделал это домашнее задание. Сделайте и вы! Выходные данные Выведите «YES» (без кавычек), если эти две строки эквивалентны, и «NO» (без кавычек) в противном случае. Примечание В первом примере первую строку можно разделить на строки "aa" и "ba", вторую – на строки "ab" и "aa". "aa" эквивалентно "aa"; "ab" эквивалентно "ba", так как "ab" = "a" + "b", "ba" = "b" + "a". Во втором примере первую строку можно разделить на строки "aa" и "bb", которые эквивалентны только сами себе. Поэтому строка "aabb" эквивалентна только сама себе и строке "bbaa". | |
![]()
|
|
A. Чат
жадные алгоритмы
Строки
*1000
Совсем недавно Вася научился печатать на клавиатуре и выходить в интернет. Он сразу же зашел в чат и решил поздороваться со всеми. Вася напечатал слово s. Считается, что у Васи получилось поздороваться, если из напечатанного слова можно удалить некоторые буквы так, чтобы получилось слово "hello". Например, если Вася напечатал слово "ahhellllloou", считается, что он поздоровался, а если он напечатал "hlelo", считается, что Васю не поняли, и ему не удалось поздороваться. По заданному слову s определите, удалось ли Васе поздороваться. Выходные данные Если Васе удалось поздороваться, выведите "YES", иначе выведите "NO". | |
![]()
|
|
D. Календарь
жадные алгоритмы
Строки
*2000
БерНефтьГазАлмазБанк имеет филиалы в n городах, причем n четно. Руководство банка хочет издать календарь с названиями всех этих городов, записанными в два столбца: календарь должен состоять из n / 2 строк одинаковой длины, каждая из которых содержит ровно два названия и ровно один разделитель между ними. При этом название каждого города нужно использовать в календаре ровно один раз. По историческим причинам в качестве разделителя слов в календаре используется символ d. Руководство БерНефтьГазАлмазБанка хочет показать, что для него одинаково важны все филиалы, поэтому порядок их следования в календаре должен быть беспрестрастным: если «склеить» все n / 2 строк словаря в одну так, чтобы между двумя словами из одной строки были разделители, а между разными строками календаря разделителей не было, получается лексикографически наименьшая возможная строка. Это равносильно тому, что нужно найти лексикографически наименьший календарь, причем сравнение календарей происходит построчно. Помогите БерНефтьГазАлмазБанку — составьте искомый календарь. Выходные данные Выведите n / 2 строк одинаковой длины — искомый календарь. Каждая строка должна содержать ровно 2 слова и ровно 1 разделитель между ними. Если решений несколько, выведите лексикографически минимальное. Лексикографическое сравнение строк реализует оператор < в современных языках программирования. | |
![]()
|
|
E. Кефа и часы
Строки
Структуры данных
хэши
*2500
Как-то попугай Кефа шел по улице, возвращаясь домой из ресторана, и увидел в кустах что-то блестящее. Подойдя поближе он понял, что это часы. Он решил отнести их в ломбард, чтобы на этом заработать. Там продавец сообщил ему, что на каждых часах есть серийный номер, представляющий собой строку из цифр от 0 до 9, и чем больше этот номер проходит проверок на подлинность, тем дороже часы. Проверка задаётся тремя целыми положительными числами l, r и d. Часы проходят проверку, если подстрока серийного номера с l по r имеет период d. Иногда продавец отвлекается, и Кефа изменяет в какой-то подстроке серийного номера все цифры на c, чтобы попытаться максимизировать прибыль с часов. У продавца и так много дел, а тут еще и Кефа мешает, поэтому он поручил вам написать программу для определения подлинности часов. Напомним, что число x называется периодом строки s (1 ≤ x ≤ |s|), если si = si + x для всех i от 1 до |s| - x. Выходные данные Для каждой проверки на отдельной строке выведите «YES», если часы прошли её, иначе выведите «NO». Примечание В первом тесте из условия будет произведено две проверки. В первой подстрока "12" проверяется на наличие периода 1, поэтому ответ — «NO». Во второй подстрока "88", проверяется на наличие периода 1, и у неё этот период есть, поэтому ответ — «YES». Во втором тесте из условия будет произведено три проверки. В первой рассматривается подстрока "3493", у которой нет периода 2. Перед второй проверкой строка приобретает вид "334334", поэтому на него ответ «YES». И наконец, в третьей проверке рассматривается подстрока "8334", у которой нет периода 1. | |
![]()
|
|
C. Марина и Вася
жадные алгоритмы
Конструктив
Строки
*1700
Марина любит строки одинаковой длины, а Вася любит, когда существует третья строка, отличающаяся от них ровно в t символах. Помогите Васе найти хотя бы одну такую строку. Более формально, вам дано даны две строки s1, s2 длины n и число t. Обозначим за f(a, b) количество символов, в которых отличаются строки a и b. Тогда вам требуется найти любую строку s3 длины n такую, что f(s1, s3) = f(s2, s3) = t. Если такой строки нет, то выведите - 1. Выходные данные Выведите строку длины n, отличающуюся от s1 и от s2 ровно в t символах. Ваша строка должна состоять только из строчных букв английского алфавита. Если же такой строки не существует, выведите -1. | |
![]()
|
|
F. Знаки числа Пи
дп
реализация
Строки
*3200
Василий совсем недавно узнал об удивительных свойствах числа π. В одной из статей, которые он прочитал, была высказана гипотеза, что, какую бы последовательность цифр мы не взяли, рано или поздно эта последовательность встретится среди знаков числа π. Таким образом, если взять, например, роман «Война и мир», и закодировать его произвольным образом с помощью цифр, то мы обязательно найдем роман среди знаков числа π. Василий был просто восхищен этим, поскольку это означает, что все книги, песни и программы уже написаны и зашифрованы в знаках числа π. Василия, конечно, немного насторожило то, что это только гипотеза, поэтому он решил проверить ее самостоятельно. Для этого Василий скачал из интернета архив с последовательностью знаков числа π с некоторой позиции, и стал проверять разные строки из цифр на наличие в скачанном архиве. Короткие строки цифр Василий находил быстро, но когда он брал длинные строчки, оказывалось, что их в архиве нет. Василий решил взять за определение, что строка длины d встречается наполовину, если в ней есть подстрока длины хотя бы  , которая есть в архиве. , которая есть в архиве. Для полноты картины Василий взял 2 больших числа x, y (x ≤ y), имеющих одинаковое количество цифр в десятичной записи, и теперь хочет найти количество чисел, находящихся в отрезке от x до y, которые встречаются в архиве наполовину. Помогите Василию вычислить остаток от деления этого значения на 109 + 7. Выходные данные Выведите количество чисел в отрезке от x до y, встречающихся наполовину в s, по модулю 109 + 7. | |
![]()
|
|
F. Duff в ярости
Строки
Структуры данных
*3000
Duff в ярости на своих друзей. От злости она просит Malek'а отнимать конфеты у её друзей безо всякого повода!  У неё n друзей. Её i-ого друга зовут si (их имена не обязательно уникальны). Она попросить Malek'а забрать конфеты у её друзей q раз. Она в ярости, но всё же она действует по определённым правилам. Когда она хочет попросить Malek'а забрать конфету у одного из её друзей, имеющего номер k, она выбирает два числа, l и r и говорит Malek'у взять ровно  конфет у друга, где occur(t, s) — это число вхождений строки t в строку s. конфет у друга, где occur(t, s) — это число вхождений строки t в строку s. Malek не может посчитать, сколько конфет надо забрать в каждом из запросов Duff. Поэтому он просит вас о помощи. Пожалуйста, скажите ему, сколько конфет взять в каждом запросе. Выходные данные Выведите ответ на каждый запрос в одной строке. | |
![]()
|
|
A. Слово
реализация
Строки
*800
Васю очень огорчает, что многие люди в интернете смешивают маленькие и большие буквы в одном слове. Поэтому он решил разработать расширение для своего любимого браузера, которое меняет регистр букв в каждом слове так, чтобы оно либо состояло только из маленьких букв, либо, наоборот, только из больших. При этом в слове должно измениться как можно меньше букв. Например, слово HoUse должно замениться на house, а слово ViP — на VIP. В случае, если в слове содержится одинаковое количество маленьких и больших букв, нужно заменить все буквы на маленькие. Например, maTRIx нужно заменить на matrix. Ваша задача — обработать указанным способом одно заданное слово. Выходные данные Выведите исправленное слово s. Если в заданном слове s строго больше заглавных букв, приведите его к верхнему регистру, иначе — к нижнему. | |
![]()
|
|
E. День рождения
Паросочетания
Строки
*3200
У маленькой Даши сегодня день рождения — ей исполнилось целых 8 лет! По такому случаю каждый из n её родственников и друзей подарил ей ленточку с праздничным поздравлением, причём, как оказалось, все поздравления отличаются друг от друга. Даша собрала все ленточки вместе и решила выкинуть некоторые из них так, чтобы оставшийся набор стал стильным. Именинница считает набор стильным, если ни одно поздравление не является подстрокой другого. Напомним, что подстрокой строки s называется непрерывный отрезок букв строки s. Помогите Даше оставить как можно больше ленточек, чтобы она могла хвастаться ими всем своим друзьям. Ленточки не разрешается поворачивать и переворачивать, то есть каждое поздравление может быть прочитано единственным способом. Выходные данные В первой строке выведите максимальный размер стильного набора. Во второй строке выведите номера участвующих в нём лент, считая, что они нумеруются с единицы в порядке следования во входных данных. Если стильных наборов максимального размера несколько, то выведите любой из них. Примечание В примере можно было также оставить ленты 3 и 4. | |
![]()
|
|
B. Ребрендинг
реализация
Строки
*1200
Название одной маленькой, но очень гордой корпорации состоит из n строчных английских букв. Корпорация решила провести ребрендинг — активную маркетинговую стратегию, включающую комплекс мероприятий по изменению бренда (как компании, так и производимого ею товара), либо его составляющих: названия, логотипа, слогана. Начать решили именно с названия. Для этого корпорация последовательно наняла m дизайнеров. Как только компания нанимает i-го дизайнера, тот сразу вносит свою лепту в создание нового имени корпорации следующим образом: он меняет в текущей версии названия все буквы xi на yi, а все буквы yi на xi, после чего получается новая версия. Возможно, каких-то из этих букв в строке нет, а также возможно, что xi совпадает с yi. Вариант имени, получившийся после работы последнего дизайнера, становится новым названием корпорации. Менеджер Аркадий лишь недавно устроился на работу в эту фирму, но уже проникся корпоративным духом и очень переживает за успех ребрендинга. Естественно, ему не терпится узнать, какое имя в итоге получит корпорация. Удовлетворите любопытство Аркадия — назовите ему окончательный вариант названия. Выходные данные Выведите окончательный вариант названия корпорации. Примечание Во втором примере название корпорации последовательно претерпевает следующие изменения:  




| |
![]()
|
|
E. Разрезание строки
Строки
строковые суфф. структуры
*3100
Дана непустая строка s и число k. Со строкой один раз проделывают следующую операцию: - Разбивают строку на не более чем k непустых подстрок, то есть представляют строку s в виде конкатенации (сцепления) набора строк s = t1 + t2 + ... + tm, 1 ≤ m ≤ k.
- Некоторые из строк ti заменяются строками tir, то есть их записью справа налево.
- Строки конкатенируются обратно в том же порядке, получается строка s' = t'1t'2... t'm, где t'i равно ti или tir.
Вам требуется определить лексикографически минимальную строку, которая может получиться в результате одного применения к строке s данной операции. Выходные данные В единственной строке выведите лексикографически минимальную строку s', которая может получиться в результате выполнения описанной операции. | |
![]()
|
|
E. Вилбур и строки
графы
дп
поиск в глубину и подобное
Строки
*2500
Теперь поросёнок Вилбур хочет поиграть со строками. Он нашёл таблицу размера n на m, состоящую только из цифр от 0 до 9. Ряды нумеруются от 1 до n, а столбцы от 1 до m. Вилбур начинает в какой-то клетке (x, y) и делает следующие ходы. Пусть в клетке (x, y) написана цифра d (0 ≤ d ≤ 9), тогда Вилбур должен сделать ход в ячейку (x + ad, y + bd), если эта ячейка находится внутри таблицы, и остаться на месте в противном случае. Перед совершением очередного хода Вилбур может, если сочтёт нужным, выписать на доску цифру, написанную в текущей клетке. Все выписанные цифры образую строчку, каждая новая цифра приписывает в конец текущей строки. У Вилбура есть q интересных ему строк. Для каждой строки si, Вилбур хочет узнать, можно ли так выбрать начальную позицию (x, y), что за конечное число ходов Вилбур может в итоге написать на доске строку si. Выходные данные Для каждой из q строк выведите "YES", если Вилбур может так выбрать начальную позицию (x, y), чтобы через какое-то конечно число ходов выписать на доску строку si. Если это невозможно, то выведите "NO". Примечание В первом примере дана таблица размера 1 на 1, в которой записана единственная цифра 0. Каждым ходом Вилбур будет оставаться в клетке (1, 1). Первую строку можно написать на доске, записывая друг за другом 0. Вторую строку нельзя записать, так как на в таблице нет 2. | |
![]()
|
|
B. Запросы на строке
реализация
Строки
*1300
Вам даны строка s и m запросов. Каждый запрос задаётся парой индексов li, ri и целым числом ki, и означает, что подстроку s[li... ri] нужно ki раз циклически сдвинуть вправо. Запросы нужно обрабатывать последовательно, друг за другом. Циклический сдвиг вправо обозначает перемещение последнего символа на место первого и сдвиг всех остальных символов направо на одну позицию. Например, если исходная строка s равна abacaba, то в случае запроса l1 = 3, r1 = 6, k1 = 1 получится строка abbacaa, если же после этого обработать запрос l2 = 1, r2 = 4, k2 = 2, то в результате получится строка baabcaa. Выходные данные Выведите строку, которая получится после обработки всех m запросов. Примечание Пример разобран в условии задачи. | |
![]()
|
|
A. Выделение чисел
реализация
Строки
*1600
Задана строка s. Будем называть словом любую наибольшую по включению последовательность подряд идущих символов, не включающую в себя символы ',' (запятая) и ';' (точка с запятой). Например, в строке «aba,123;1a;0» четыре слова: «aba», «123», «1a», «0». Слово может оказаться пустым: например, строка s=«;;» содержит три пустых слова, которые разделены символом ';'. Вам требуется найти в заданной строке все слова, являющиеся ЦЕЛЫМИ неотрицательными числами без лидирующих нулей, и по ним построить новую строку a. Строка a должна содержать слова, являющиеся числами, разделенные символом ',' (порядок чисел должен остаться таким же каким был в строке s). По оставшимся словам нужно построить строку b аналогичным образом (порядок слов должен остаться таким же как в строке s). В этой задаче "101", "0" — это ЦЕЛЫЕ числа, а "01" и "1.0" — нет. Например, для строки aba,123;1a;0 нужно построить строку a=«123,0» и строку равную b=«aba,1a». Выходные данные В первой строке выведите строку a, окруженную кавычками (ASCII 34), а во второй — строку b, окруженную кавычками. Если среди слов в строке s нет чисел, в первой строке выведите знак минус (ASCII 45). Если все слова в строке s являются числами, во второй строке выведите знак минус. Примечание Во втором примере строка s содержит 5 слов: «1», «», «01», «a0», «». | |
![]()
|
|
C. Сделай палиндром
жадные алгоритмы
Конструктив
Строки
*1800
Строка называется палиндромом, если она одинаково читается слева-направо и справа-налево. Например, строки «kazak», «oo», «r» и «mikhailrubinchikkihcniburliahkim» — палиндромы, а строки «abb» и «ij» — нет. Замена символа — это выбор позиции символа в строке и замена символа в этой позиции на произвольную другую строчную букву. Таким образом, при замене символа длина строки не изменяется. Задана строка s. Вы можете сначала заменить в строке s некоторые символы, а затем произвольным образом поменять местами порядок символов в строке. Изменение порядка не считается заменами. Необходимо получить палиндром за наименьшее количество замен. Если это возможно сделать несколькими способами, то нужно получить лексикографически наименьший палиндром. Таким образом в первую очередь необходимо минимизировать количество замененных символов, а среди таких способов найти какой наименьший лексикографически (алфавитно) палиндром можно получить в результате. Выходные данные Выведите лексикографически наименьший палиндром, который можно получить за наименьшее количество замен. | |
![]()
|
|
D. Ациклические органические составляющие
Деревья
поиск в глубину и подобное
снм
Строки
Структуры данных
хэши
*2400
Дано дерево T состоящее из n вершин (пронумерованных целыми числами от 1 до n). В каждой вершине записана некоторая буква. Корень дерева расположен в вершине 1. Рассмотрим поддерево дерево Tv некоторой вершины v. Вдоль любого просто пути, начинающегося в v и заканчивающегося в некоторой вершине  (возможно, в самой v), можно прочитать некоторую строку. Обозначим количество различных строк, которые можно прочитать таким способом как (возможно, в самой v), можно прочитать некоторую строку. Обозначим количество различных строк, которые можно прочитать таким способом как  . . Дополнительно: для каждой вершины v дано целое число cv. Нас интересуют вершины, в которых значение  как можно больше. как можно больше. Вы должны вычислить две величины — максимальное значение  и количество вершин v с максимальным и количество вершин v с максимальным  . . Выходные данные Выведите два числа — значение  для всех 1 ≤ i ≤ n и количество вершин v, для которых для всех 1 ≤ i ≤ n и количество вершин v, для которых  . . Примечание В первом примере дерево выглядит следующим образом: 
Наборы строк, которые могут быть прочитаны из вершин: 
Наконец, значения  таковы: таковы: 
Во втором примере значения  таковы: (5, 4, 2, 1, 1, 1).Различные строки, которые можно прочитать из вершины 2 таковы: таковы: (5, 4, 2, 1, 1, 1).Различные строки, которые можно прочитать из вершины 2 таковы:  ; обратите внимание, что ; обратите внимание, что  может быть прочитано как на пути до вершины 3, так и на пути до вершины 4. может быть прочитано как на пути до вершины 3, так и на пути до вершины 4. | |
![]()
|
|
C. Камушки
Строки
хэши
*2500
Под влиянием праздничной атмосферы Сайтама подарил Геносу два клеточных пути длины n (странненький подарок, даже для Сайтамы). Клеточный путь — это упорядоченная последовательность соседних клеток на бесконечной сетке. Две клетки называются соседними, если у них есть общая сторона. Например, клеточный путь может выглядеть так: (0, 0) → (0, 1) → (0, 2) → (1, 2) → (1, 1) → (0, 1) → ( - 1, 1). Обратите внимание, что клетки в этой последовательности могут повторяться, то есть путь может иметь самопересечения. Перемещение вдоль пути разрешено только в соседние клетки пути. Таким образом, из i-й позиции можно перейти только в (i - 1)-ю или (i + 1)-ю клетки. Обратите внимание, что из первой и последней ячеек клетчатого пути есть только один возможный ход. Дополнительно обратите внимание, что даже если j-я клетка пути совпадает с i-й, то всё равно можно произвести ходы только в (i - 1)-ю и (i + 1)-ю клетки. Например, из второй клетки приведённого выше пути можно пойти только в первую и третью клетки. Чтобы перемещение всегда определялось однозначно, в каждом из путей никогда не имеют повторяется одна и та же клетка на отрезке длины три. Например, в правильном клеточном пути не может быть подотрезка вида (0, 0) → (0, 1) → (0, 0) На первую клетку каждого клеточного пути кладётся по камушку. Генос хочет, чтобы оба камушка докатились до последней ячейки каждого клеточного пути, но всё не так просто. Каждый раз, когда Генос двигает один из камушков, второй камушек копирует его движение, если это возможно. Например, если один камушек движется на восток, то тогда другой камушек постарается тоже двигаться на восток. Под постарается имеется в виду, что если движение на восток возможно, то камушек сделает такое перемещение. Движение на север соответствует увеличению второй координаты на 1, а движение на юг — её уменьшению на 1. Аналогично движение на восток увеличивает первую координату на 1, а движение на запад уменьшает её на 1. Даны два правильных клеточных пути. Генос хочет знать, существует ли такая последовательность перемещений, что в итоге оба камушка окажутся в концах своих путей. Выходные данные Выведите "YES" (без кавычек), если можно добиться того, чтобы оба камушка одновременно находились на конечных клетках своих путей. В противном случае выведите "NO" (без кавычек). Примечание В первом примере, первый путь соответствует описанному в условии. Оба шарика могу оказаться в концах своих путей после следующей последовательности действий: NNESWWSWSW. Во втором примере, переместить оба шарика в концы соответствующих путей невозможно. | |
![]()
|
|
B. Сумма расстояний Хэмминга
Комбинаторика
Строки
*1500
Геносу нужна Ваша помощь. Сайтама попросил его решить следующую задачку по программированию: Обозначим как |s| длину некоторой строки s. Расстояние Хэмминга между двумя строками s и t одинаковой длины определяется как  , где si означает i-й символ строки s, а ti — i-й символ строки t. Например, расстояние Хэмминга между строкой "0011" и строкой "0110" равно |0 - 0| + |0 - 1| + |1 - 1| + |1 - 0| = 0 + 1 + 0 + 1 = 2. , где si означает i-й символ строки s, а ti — i-й символ строки t. Например, расстояние Хэмминга между строкой "0011" и строкой "0110" равно |0 - 0| + |0 - 1| + |1 - 1| + |1 - 0| = 0 + 1 + 0 + 1 = 2. Даны две строки a и b, найдите сумму расстояний Хэмминга между a и всеми подстроками b длины |a|. Выходные данные Выведите единственное целое число — сумму расстояний Хэмминга между a и всеми подстроками строки b длины |a|. Примечание В первом примере в строке b есть четыре подстроки длины |a|: "00", "01", "11", и "11". Расстояние между "01" и "00" равно |0 - 0| + |1 - 0| = 1. Расстояние между "01" и "01" равно |0 - 0| + |1 - 1| = 0. Расстояние между "01" и "11" равно |0 - 1| + |1 - 1| = 1. Последнее значение учитывается два раза, поскольку подстрока "11" встречается в b дважды. Сумма этих расстояний равна 1 + 0 + 1 + 1 = 3. Второй пример описан в условии задачи. | |
![]()
|
|
B. Тяжелая работа
Строки
*1300
После соревнования по сравнению чисел, учитель Шапура понял, что Шапур — настоящий гений, и никто не смог бы вычислять быстрее него даже используя супер компьютер! За несколько дней до соревнования, учитель провел очень простой экзамен, который сдавали все n его учеников. Учитель дал им 3 строки, и попросил конкатенировать их. Конкатенация строк означает их запись в каком-то порядке, одну за другой. Так же эту операцию иногда называют склеиванием. Например, при конкатенации Alireza и Amir мы можем получить или AlirezaAmir, или AmirAlireza, в зависимости от порядка конкатенации. К сожалению или к счастью, учитель забыл сказать ученикам порядок конкатенации, поэтому каждый выбрал тот порядок, который ему больше нравился. Учитель знает, что Шапур — гениальный математик, и поэтому он просит его проверить работы своих учеников. Шапур не любит заниматься такими скучными и бестолковыми вещами. Поэтому ему хочется поскорее закончить проверку и продолжить свою работу над решением 3-SAT за полиномиальное время. Учитель дал Шапуру несколько указаний, которые он должен выполнять. Вот что он сказал: - Как ты наверное знаешь, строки, которые я дал моим ученикам (включая тебя), состояли только из больших и маленьких букв персидского языка. Но чтобы усложнить твою работу, я поставил вместо них похожие большие и маленькие латинские буквы.
- Так как латинский алфавит гораздо меньше персидского алфавита, я добавил три новых символа: "-", ";" и "_". Эти символы — мое собственное изобретение, я назвал их знаки.
- Длины всех трех данных в начале строк не превосходят 100, а длины ответов моих учеников не превосходят 600
- Сын мой, не все ученики так гениальны, как ты. Вполне возможно, что они сделают небольшие ошибки — поменяют регистр некоторых букв. Например, они могут написать ALiReZaAmIR вместо AlirezaAmir. Не придирайся и не учитывай такие ошибки.
- Знаки, о которых я говорил тебе, не важны. Можешь не учитывать их, так как некоторым ученикам не нравятся знаки, а некоторые, наоборот, ставят их слишком много. Так что строка Iran;;-- должна считаться равной --;IRAN
- Ты должен определить для каждого ученика в отдельности, правильный ли его ответ. Пиши "WA", если ответ неправильный, или "ACC", если правильный.
- Все строки (как данные в начале, так и ответы учеников) непусты.
- И последнее — проверь все как можно скорее. У тебя осталось меньше 2 часов!
Выходные данные Для каждого ответа запишите на отдельной строке, правильный ли он. Выводите "WA", если он неправильный, или "ACC", если ответ правильный. | |
![]()
|
|
E. Перестановки алфавита
Строки
Структуры данных
*2500
Дана строка s длины n, состоящая из первых k строчных букв английского алфавита. Будем называть c-повтором некоторой строки q строку, состоящую из c копий строки q. Например, строка "acbacbacbacb" является 4-повтором строки "acb". Будем также говорить, что строка a содержит строку b как подпоследовательность, если строку b можно получить из a выкидыванием некоторых символов. Пусть p — строка, представляющая собой некоторую перестановку первых k строчных букв английского алфавита. Введём функцию d(p), равную наименьшему целому числу, такому что строка s является подпоследовательностью d(p)-повтора строки p. К строке s применяют m операций одного из двух типов: - Заменить все символы на позициях с li-й по ri-ю на символ ci.
- Для заданной p, являющейся перестановкой первых k букв английского алфавита, найти значение функции d(p).
Все операции выполняются последовательно, в порядке следования во входных данных. Ваша задача вывести значения функции d(p) для всех операций второго типа. Выходные данные Для каждого запроса второго типа выведите в отдельной строке значение функции d(pi). Примечание После первой операции строка станет равной abbbbba. Во второй операции в качестве ответа нужно взять 6-повтор строки abc: ABcaBcaBcaBcaBcAbc. После третьего запроса строка станет равной abbcbba. В четвертой операции в качестве ответа нужно взять 5-повтор строки cba: cbAcBacBaCBacBA. Заглавными буквами обозначены вхождения символов из строки s. | |
![]()
|
|
D. Новый год и древнее пророчество
дп
Строки
хэши
*2000
Маленький полярный медвежонок Лимак нашёл в снегу свитки с древним пророчеством. Никаких древних языков он не знает, поэтому в пророчестве ему не разобраться, зато он знает цифры! Один из фрагментов пророчества содержит последовательность из n цифр, причём первая из них не является нулём. Лимак полагает, что это последовательность каких-то годов. Пробелов и точек в записи нет, так что, возможно, древние люди их не использовали. Теперь Лимаку стало любопытно, какие же именно года фигурируют в фрагменте. Медвежонок сделал следующие три предположения: - Года записаны в порядке строгого возрастания;
- Каждый год обозначается целым положительным числом;
- Ведущие нули не используются.
Лимак хочет рассмотреть все возможные способы разбить данную последовательность цифр на числа (года), удовлетворяющие данным условиям. Он справится сам, без чьей либо помощи, однако попросил вас посчитать количество подходящих разбиений. Поскольку это число может быть достаточно большим, выведите его по модулю 109 + 7. Выходные данные Выведите количество способов корректно разбить последовательность цифр на числа по модулю 109 + 7. Примечание В первом примере существует 8 способов разбить исходную последовательность: - "123434" = "123434" (вся последовательность вполне может оказаться одним числом)
- "123434" = "1" + "23434"
- "123434" = "12" + "3434"
- "123434" = "123" + "434"
- "123434" = "1" + "23" + "434"
- "123434" = "1" + "2" + "3434"
- "123434" = "1" + "2" + "3" + "434"
- "123434" = "1" + "2" + "3" + "4" + "34"
Обратите внимание, что нельзя выполнить разбиение "123434" = "12" + "34" + "34", поскольку последовательность должна быть строго возрастающей. Во втором примере существует 4 способа: - "20152016" = "20152016"
- "20152016" = "20" + "152016"
- "20152016" = "201" + "52016"
- "20152016" = "2015" + "2016"
| |
![]()
|
|
A. Разбиение текста
Перебор
реализация
Строки
*1300
Вам задана строка s длины n и пара чисел p, q. Вам требуется разбить строку s на строки длины p и q. Например, строку "Hello" при p = 2, q = 3 можно разбить на две строки "Hel" и "lo" или на две строки "He" и "llo". Заметим, что допускается разбиение строки только на строки длины p или только на строки длины q (смотрите второй тестовый пример). Выходные данные Если разбить строку s на строки длины p и q невозможно выведите число "-1". В противном случае в первой строке выведите целое число k — количество строк в разбиении s. В следующих k строках выведите строки в разбиении. Каждая строка должна быть длины p или q. Строки нужно вывести в порядке появления в исходной строке s — слева направо. Если существует несколько решений, разрешается вывести любое из них. | |
![]()
|
|
E. Любитель кроссвордов
дп
Строки
хэши
*3200
Олег Петрович любит кроссворды и каждый четверг покупает в газетном киоске свой любимый журнал с кроссвордами и разными словесными головоломками. В последнем выпуске Олег Петрович обнаружил интересную головоломку, за решение которой в журнале обещали ценный приз. Ниже мы приводим её формальное описание. Поле для головоломки состоит из двух рядов по n клеток в каждом. Каждая клетка содержит ровно одну строчную английскую букву. Нужно найти и вычеркнуть на этом поле некоторое данное слово w, состоящее из k строчных английских букв. Решением головоломки является последовательность клеток поля c1, ..., ck, такая что: - Для всех i от 1 до k буква, записанная в клетке ci, совпадает с буквой wi;
- Все клетки в последовательности попарно различны;
- Для всех i от 1 до k - 1 клетки ci и ci + 1 имеют общую сторону.
Олег Петрович быстро нашёл решение для головоломки. Теперь ему интересно, сколько для нее существует различных решений. Олег Петрович не любит слишком большие числа, поэтому посчитайте ответ по модулю 109 + 7. Два решения ci и c'i считаются различными, если последовательности клеток не совпадают хотя бы в одной позиции, то есть найдётся такое j от 1 до k, что cj ≠ c'j. Выходные данные Выведите одно целое число — количество решений головоломки по модулю 109 + 7. | |
![]()
|
|
C. Беговой трек
Деревья
дп
жадные алгоритмы
Строки
*2000
На планете AMI-1511 живёт мальчик Айрат. У каждого из жителей этой планеты есть свое хобби, в частности, Айрат любит бегать, причём не просто так — он мечтает превратить бег в настоящее искусство. Для начала Айрат хочет сконструировать беговой трек с полотном t. Полотно для трека на AMI-1511 — последовательность из цветных блоков, где каждый блок обозначается строчной английской буквой. Таким образом, любое полотно представляется как строка некоторой длины. К сожалению, блоки отсутствуют в свободной продаже. Айрат нашёл в магазине неограниченное количество полотен для трека s, а ещё у него есть ножницы и клей. Айрат может купить некоторое количество полотен s, после чего вырезать из каждого ровно один непрерывный кусок (подстроку) и приклеить его в конец своего полотна, при этом он может развернуть новый кусок перед приклеиванием. Помогите Айрату посчитать, сколько минимум полотен s ему нужно купить, какие куски из них вырезать и в каком порядке склеить, чтобы получить желанное полотно t. Выходные данные В первой строке выведите минимальное число полотен n или -1, если собрать желанное полотно не представляется возможным. Если ответ не -1, то в следующих n строках выведите по два числа xi и yi — номера крайних блоков в вырезаемом куске. xi ≤ yi означает, что кусок приклеивается в исходном порядке, а xi > yi — что в развёрнутом. Куски выводите в том порядке, в котором их следует склеивать, чтобы получить строку t. Примечание В первом примере строка "cbaabc" = "cba" + "abc". Во втором примере: "ayrat" = "a" + "yr" + "at". | |
![]()
|
|
A. Сравнение длинных чисел
реализация
Строки
*900
Вам заданы два очень больших целых числа a, b (возможно с лидирующими нулями). Нужно определить какое из заданных чисел больше, либо определить, что они равны. Поскольку размер входных данных очень большой крайне не рекомендуется использовать посимвольное чтение. Используйте чтение строк или слов целиком. Рекомендуется для ввода и вывода данных использовать функции scanf, printf в языке C++, поскольку они работают значительно быстрее потоков cin, cout. Аналогично, рекомендуется использовать классы BufferedReader, PrintWriter вместо Scanner, System.out в языке Java. В языке Python2 не рекомендуется использовать функцию input(), вместо неё нужно использовать функцию raw_input(). Выходные данные Если a < b выведите символ "<", если a > b выведите символ ">". Если же числа равны выведите "=". | |
![]()
|
|
F. Дорогие строки
сортировки
Строки
строковые суфф. структуры
Структуры данных
*2700
Задан набор из n строк ti. Для каждой строки известна ее стоимость ci. Определим следующую функцию от строки  , где ps, i — число вхождений строки s в строку ti, а |s| — длина строки s. Найдите максимальное значение функции f(s) по всем строкам. , где ps, i — число вхождений строки s в строку ti, а |s| — длина строки s. Найдите максимальное значение функции f(s) по всем строкам. Обратите внимание, что s — это не обязательно строка из заданного набора t. Выходные данные В единственной строке выходного файла выведите целое число a — наибольшее значение функции f(s) по всем строкам s. Обращаем еще раз внимание, что строка s не обязательно из заданного набора t. | |
![]()
|
|
F. Ксоры на подотрезке
Деревья
Строки
Структуры данных
*2800
Вам задан массив из n целых чисел ai, а также m запросов. Каждый запрос описывается с помощью двух целых чисел (lj, rj). Определим функцию  . Функция определена только для u ≤ v. . Функция определена только для u ≤ v. Для каждого запроса выведите наибольшее значение функции f(ax, ay) по всем lj ≤ x, y ≤ rj, ax ≤ ay. Выходные данные Для каждого запроса выведите в отдельной строке целое число aj — наибольшее значение функции f(ax, ay) по всем lj ≤ x, y ≤ rj, ax ≤ ay. | |
![]()
|
|
B. Война корпораций
жадные алгоритмы
Конструктив
Строки
*1200
Давным-давно в далёкой-далёкой галактике противоборствовали две огромные IT-корпорации: Pineapple и Gogol. Противостояние длится уже многие годы, но близится переломный момент: компания Gogol разработала абсолютно новое устройство, не имеющее аналогов — планшет Lastus 3000. В этом устройстве используется впервые созданный искусственный интеллект (ИИ). Члены компании Pineapple пытались всеми силами отложить выход нового девайса. В конце концов, за неделю до выхода Lastus 3000 на рынок юристы обнаружили, что название искусственного интеллекта очень похоже на название телефона, который выпустила компания Pineapple 200 лет назад. Так как компания Pinapple обладает авторским правом на это название, она потребовала изменить имя искусственного интеллекта. Pineapple утверждает, что название их телефона присутствует в качестве подстроки в имени ИИ. Название этой технологии уже было выгравировано на всех планшетах, поэтому директор Gogol предложил вместо некоторых букв в названии ИИ поставить символ «#». Так как это довольно затратно, надо найти минимальное количество символов, которые нужно заменить на «#», чтобы имя ИИ больше не содержало название телефона Pineapple в качестве подстроки. Помогите компании Gogol решить эту задачу. Подстрокой называется непустая последовательность подряд идущих символов строки. Выходные данные Требуется вывести минимальное количество букв, которое надо заменить на символ «#» в названии ИИ, чтобы оно не содержало название телефона в качестве подстроки. Примечание В первом примере название ИИ можно заменить на «int#llect». Во втором примере название можно не менять. В третьем примере название ИИ можно поменять на «s#ris#ri». Обойтись меньшим количеством замен не получится. | |
![]()
|
|
C. Медведь и расстояние между строками
жадные алгоритмы
Строки
*1300
Лимак — маленький полярный медведь. Ему нравятся красивые строки — строки длины n, состоящие из маленьких английских букв. Расстоянием между двумя буквами будем называть разницу их позиций в алфавите. Например,  , а , а  . . Определим расстояние между двумя красивыми строками как сумму расстояний соответствующих букв. Например,  , а , а  . . У Лимака есть красивая строка s и целое число k. Вам требуется найти любую красивую строку s' такую, что  или определить, что такой строки не существует. или определить, что такой строки не существует. Рекомендуется для ввода и вывода данных использовать функции gets, scanf, printf в языке C++, поскольку они работают значительно быстрее чем getline, cin, cout. Аналогично, рекомендуется использовать классы BufferedReader, PrintWriter вместо Scanner, System.out в языке Java. Выходные данные Если не существует строки s', удовлетворяющей условиям задачи выведите "-1" (без кавычек). В противном случае, выведите любую красивую строку s' такую, что  . . | |
![]()
|
|
C. Фома Дор и скобки
дп
Строки
*2000
У Фомы Дора скоро день рождения, и его друг Габи решил подготовить ему подарок. Он знает, что Фома Дор без ума от правильных последовательностей из круглых скобок длины ровно n. Последовательность круглых скобок называется правильной, если выполнены следующие условия: - количество открывающих скобок в последовательности равно количеству закрывающих скобок
- для любого префикса последовательности количество открывающих скобок на этом префиксе не меньше количества закрывающих скобок на этом префиксе.
Габи купил строчку s длины m (m ≤ n) и хочет дополнить её до правильной скобочной последовательности длины n. Для этого он выберет какие-то последовательности скобок p и q и получит строку p + s + q, то есть припишет p в начало строки s и q в конец строки s. Теперь ему интересно, сколько существует пар строк p и q, таких что строка p + s + q является правильной скобочной последовательностью длины n. Вычислите это значение по модулю 109 + 7. Выходные данные Выведите количество пар строк p и q, таких что строка p + s + q является правильной скобочной последовательностью. Не забудьте, что требуется только вывести остаток от деления этого числа на 109 + 7. Примечание В первом примере подходят четыре различные пары: - p = "(", q = "))"
- p = "()", q = ")"
- p = "", q = "())"
- p = "", q = ")()"
Во втором примере единственным способом получить правильную последовательность будет выбрать пустые p и q. В третьем примере никакие p и q не сделают строчку p + s + q правильной скобочной последовательностью. | |
![]()
|
|
A. Кораблекрушение
реализация
сортировки
Строки
*900
Корабль наткнулся на риф и сейчас терпит крушение. Теперь весь экипаж должен быть срочно эвакуирован. Все n членов экипажа уже выстроились в один ряд (для удобства пронумеруем их всех слева направо натуральными числами от 1 до n) и ждут дальнейших указаний. Однако эвакуировать экипаж полагается не абы как, а в строгом порядке. А именно: Сначала корабль покидают те члены экипажа, которые являются крысами. Затем корабль покидают женщины и дети (и те, и другие имеют одинаковый приоритет). После этого с корабля эвакуируются все мужчины. Последним тонущий корабль покидает капитан. Если для каких-либо двух членов экипажа нельзя точно установить, кто должен покинуть корабль раньше по правилам из предыдущего абзаца, то раньше корабль покидает тот, который стоит левее в ряду (или, другими словами, тот, у которого номер в ряду меньше). Для каждого члена экипажа известно, кем он является, а так же его имя. Все члены экипажа имеют различные имена. Определите порядок эвакуации экипажа. Выходные данные Выведите n строк. i-ая из них должна содержать имя члена экипажа, который должен покинуть корабль i-ым по счету. | |
![]()
|
|
D. Мессенджер
реализация
Строки
строковые суфф. структуры
Структуры данных
хэши
*2100
Каждый сотрудник компании «Blake Technologies» пользуется специализированным приложением для мгновенного обмена сообщениями, которое носит название «Blake Messenger». Все сотрудники любят это приложение и пользуются им постоянно. Однако не всё так гладко, как хотелось бы. Многим не хватает очень важной функции — поиска по сообщениям. Поэтому было принято решение реализовать эту функцию в следующей версии мессенджера. К сожалению, из-за особенностей хранения сообщений разработчикам столкнулись с некоторыми проблемами... Все сообщения в приложении представляют собой строки, состоящие только из строчных букв английского алфавита. В целях снижения нагрузки эти строки передаются и хранятся в сжатом виде. Алгоритм сжатия работает следующим образом: строка s разбивается на n последовательных блоков одинаковых букв. Такую часть можно описать парой (li, сi), где li — длина i-й части, а ci — символ, который используется в i-й части. Таким образом, строку s можно записать в сжатом виде парами  . . Требуется написать программу, которая по заданным сжатым строкам t и s находит все вхождения строки s в строку t. Разработчики понимают, что таких вхождений может быть очень много, поэтому требуется вывести только количество различных позиций вхождений строки s в строку t. Напомним, что позиция p является позицией вхождения строки s в строку t тогда и только тогда, когда tptp + 1...tp + |s| - 1 = s, где ti — i-й символ строки t. Обратите внимание на то, что, к примеру, строка "aaaa" может быть сжата несколькими способами:  , ,  , ,  ... ... Выходные данные Выведите единственное целое число — количество вхождений строки s в строку t. Примечание В первом примере t = "aaabbccccaaacc", a s = "aabbc". Строка s входит в строку t только в одной позиции p = 2. Во втором тесте t = "aaabbbbbbaaaaaaacccceeeeeeeeaa", а s = "aaa". Строка s входит в строку t в следующих позициях: p = 1, p = 10, p = 11, p = 12, p = 13, p = 14. | |
![]()
|
|
C. Наименьшая конкатенация строк
сортировки
Строки
*1700
Вам задан набор из n строк a1, a2, ..., an. Вам нужно записать их друг за другом (конкатенировать) в некотором порядке так, чтобы получившаяся строка была лексикографически минимальной. Выведите лексикографически минимальную конкатенацию заданного набора строк. Выходные данные Выведите единственную строку a — лексикографически минимальную конкатенацию заданного набора строк. | |
![]()
|
|
C. Синдром шпиона 2
дп
реализация
сортировки
Строки
строковые суфф. структуры
Структуры данных
хэши
*1900
Яш хочет взломать используемый Сидхантом шифр. После долгих недель наблюдений он понял, что Сидхант шифрует предложения следующим образом: - Перевести все буквы в нижний регистр.
- Каждое слово в предложение заменить на развёрнутое.
- Удалить все пробелы.
Например, если взять предложение Kira is childish and he hates losing и применить к нему данный шифр, то получится строка ariksihsidlihcdnaehsetahgnisol Сейчас у Яша есть зашифрованная строка и список слов. Помогите ему найти какое-нибудь исходное предложение, составленное только из слов, встречающихся в списке. Обратите внимание, что любое слово может быть использовано в предложении сколько угодно раз. Выходные данные Выведите одну строчку, содержащую исходное предложение. Гарантируется, что хотя бы одно решение существует. Если решений несколько, то разрешается вывести любое. | |
![]()
|
|
B. Сборка генома в Берляндии
*особая задача
поиск в глубину и подобное
Строки
*1500
Перед берляндскими учёными встала важнейшая задача — восстановить по имеющимся частям коротких фрагментов ДНК геном динозавра! У берляндского динозавра геном совсем не похож на привычный нам: в нём могут встречаться 26 различных типов нуклеотидов, причём нуклеотид каждого типа может встречаться не более одного раза. Если присвоить всем нуклеотидам различные буквы английского алфавита, то геном берляндского динозавра будет представлять собой непустую строку, состоящую из строчных букв английского алфавита, такую что каждая буква встречается в ней не более одного раза. У учёных есть n фрагментов генома, которые представляют собой подстроки (непустые последовательности подряд идущих нуклеотидов) искомого генома. Перед вами стоит задача: помочь учёным восстановить геном динозавра. Гарантируется, что входные данные непротиворечивы и хотя бы одна подходящая строка всегда существует. Узнав, что вы сильный программист, учёные дополнительно попросили вас из подходящих строк выбрать ту, длина которой минимальна. Если и таких строк несколько, то их устроит любая. Выходные данные В единственной строке выходных данных выведите геном минимальной длины, который содержит все заданные части. Все нуклеотиды в геноме должны быть различными. Если подходящих строк несколько, выведите строку минимальной длины. Если подходящих строк минимальной длины также несколько, то разрешается вывести любую из них. | |
![]()
|
|
C. Псевдонимы серверов
*особая задача
Бинарный поиск
реализация
сортировки
Строки
Структуры данных
*2100
Существуют веб-сайты, доступные сразу по нескольким адресам. Например, долгое время на страницы Codeforces можно было заходить как используя хостнейм cf.m27.workers.dev, так и codeforces.ru. Вам задан список адресов страниц. Для упрощения будем считать, что все адреса имеют вид: http://<hostname>[/<path>], где: - <hostname> — имя сервера (состоит из слов, возможно, разделённых точками),
- /<path> — необязательная часть, где <path> состоит из слов, разделённых слешами.
Будем считать, что два <hostname> соответствуют одному и тому же веб-сайту, если для каждого запроса к первому <hostname> найдется такой же запрос ко второму и наоборот — для каждого запроса ко второму <hostname> найдется такой же запрос к первому. Изучите примеры из условия для лучшего понимания этого определения. Выделите все группы имён серверов, которые соответствуют одному сайту. Игнорируйте группы, которые состоят ровно из одного имени сервера. Обратите внимание, что формально два запроса http://<hostname> и http://<hostname>/ различаются. Выходные данные В первую строку выведите k — количество групп имен серверов, которые соответствуют одному сайту. Следует учитывать только такие группы, размер которых строго больше единицы. Далее в k строках выведите группы по одной в строке. Для каждой группы выведите все имена серверов в ней через пробел. Как группы, так и имена серверов в группе можно выводить в любом порядке. | |
![]()
|
|
E. Интеллектуальное развитие
дп
жадные алгоритмы
Строки
*2200
После того как Бесси уволили из газеты за незнание алфавита, она решила пойти учиться и устроилась в Академию Филе Миньон. У неё уже наблюдается определённый прогресс: она выучила первые k букв английского алфавита. Каждое утро Бесси идёт на учёбу вдоль дорожки, состоящей из m + n плиток. Чтобы помочь Бесси не растерять знания, профессор Муузинг нарисовал на каждой из первых m плиток одну из k первых строчных букв английского алфавита, получив строку t. Муузинг восхищён тем, какая Бесси способная ученица, поэтому разрешил ей самостоятельно заполнить буквами оставшиеся n плиток. Пусть в итоге получится строка s (|s| = m + n), состоящая из букв, написанных на плитках в порядке от дома к академии. Для любой последовательности индексов p1 < p2 < ... < pq можно определить соответствующую подпоследовательность строки s как строку sp1sp2... spq. Две подпоследовательности считаются различными, если различаются соответствующие им строки. Бесси хочет расставить буквы на оставшихся плитках таким образом, чтобы количество различных подпоследовательностей было как можно больше. Поскольку Бесси ещё продолжает учить алфавит, ей явно потребуется ваша помощь! Обратите внимание, что пустая подпоследовательность тоже учитывается в ответе. Выходные данные Определите максимальное количество различных подпоследовательностей, которое может быть у итоговой строки, после того как Бесси заполнит оставшиеся плитки первыми k буквами английского алфавита. Поскольку это число может быть достаточно большим, выведите его по модулю 109 + 7. Обратите внимание, что вас не просят максимизировать остаток от деления на 109 + 7! Требуется максимизировать изначальное значение, а потом вывести остаток. Примечание В первом примере оптимальный способ пометить буквами оставшиеся плитки даёт 8 различных подпоследовательностей: «» (пустая строка), «a», «c», «b», «ac», «ab», «cb» и «acb».  Во втором примере все плитки уже размечены буквами. Существует 10 различных подпоследовательностей: «» (пустая строка), «a», «b», «aa», «ab», «ba», «aaa», «aab», «aba» и «aaba». Обратите внимание, что некоторые строки, например «aa», могут быть прочитаны разными способами, но учитываются только один раз. | |
![]()
|
|
B. Медвежонок и сжатие
дп
Перебор
поиск в глубину и подобное
Строки
*1300
Полярный медвежонок Лимак терпеть не может длинные строки, поэтому предпочитает сжимать их. К тому же он ещё маленький и знает только первые шесть букв английского алфавита: 'a', 'b', 'c', 'd', 'e' и 'f'. Имеется q операций сжатия строк. Операции можно применять в любом порядке и каждую можно применить произвольное количество раз. Операция с номером i задаётся строкой ai длины два и строкой bi длины один. Все строки ai различны. Если у Лимака есть строка s, то он может применить к ней i-ю операцию, только если первые два символа этой строки совпадают со строкой ai. Применение операции заключается в отбрасывании этих двух символов и приписывании в начало строки bi. Для пояснения посмотрите примечание. Несложно заметить, что применение любой операции уменьшает длину строки s ровно на 1. Также для некоторых наборов операций возможно существование строки, сжатие которой невозможно, потому что первые две буквы не совпадают ни с одной из строк ai. Лимак хочет начать со строки длины n и применить n - 1 операцию, чтобы в итоге получить строку «a». Сколько существует подходящих строк, из которых можно получить «a»? Не забывайте, что Лимак может использовать только те буквы, которые ему знакомы. Выходные данные Выведите количество строк длины n, таких что Лимак сможет перевести в строку «a», используя только имеющиеся q операций. Примечание В первом примере существует 4 строки длины 3, из которых Лимак сможет получить строку «a»: "abb", "cab", "cca", "eea". Для сжатия первой строки Лимаку достаточно два раза применить первую операций (замена «ab» на «a»). Первое применение превратит строку «abb» в «ab», а второе превратит «ab» в «a». Остальные строки можно превратить в «a» следующим образом: - "cab"
 "ab" "ab"  "a" "a" - "cca"
 "ca" "ca"  "a" "a" - "eea"
 "ca" "ca"  "a" "a" Во втором примере единственной подходящей строкой является «eb». | |
![]()
|
|
F. Бумажная работа
Строки
строковые суфф. структуры
Структуры данных
*2600
Саша спокойной программировал, пока к нему не подошла Валентина и не попросила объяснить, зачем в коде нужны все эти круглые скобки. Он объяснил ей их назначение в общих чертах и дал задание, чтобы успеть закончить работу в срок. В этой задаче мы будет рассматривать только строки, состоящие из открывающих и закрывающих круглых скобок, то есть символов «(» и «)». Последовательность скобок называется правильной в следующих случаях: - Если она пустая;
- Если она состоит из правильной скобочной последовательности, заключённой между парой из открывающей скобки и закрывающей скобки;
- Если она состоит из двух правильных скобочных последовательностей, записанных одна за другой.
Например, последовательности круглых скобок «()()» и «((()))(())» являются правильными, а «)(()», «(((((» и «())» — нет. Саша взял листок и написал на нём некоторую строку s, состоящую только из открывающих и закрывающих круглых скобок, и попросил Валентину посчитать количество различных непустых подстрок строки s, являющихся правильными скобочными последовательностями. Другими словами, её задача состоит в том, чтобы посчитать количество непустых правильных скобочных последовательностей, встречающихся в s в качестве подстроки (не путать с подпоследовательностью). Когда Валентина закончила выполнять задание, Саша вдруг осознал, что сам не знает ответа. Помогите ему не ударить в грязь лицом и решите задачу! Выходные данные Выведите количество различных непустых правильных скобочных последовательностей, встречающихся в s в качестве подстроки. Примечание В первой примере существует 5 различных подстрок, которые следует посчитать: «()», «()()», «()()()», «()()()()» и «()()()()()». Во втором примере подходят 3 различные подстроки: «()», «(())» и «(())()». | |
![]()
|
|
A. Петя и Java
реализация
Строки
*1300
Маленький Петя недавно начал посещать кружок по программированию. Естественно, перед ним появилась задача выбрать язык, на котором он будет программировать. После долгих размышлений, он понял, что Java — лучший выбор. Главным аргументом в пользу выбора Java было то, что в ней есть очень большой целочисленный тип данных — BigInteger. Но после посещения занятий кружка, Петя понял, что не все задачи требует использования типа BigInteger. Как оказалось, в некоторых задачах намного удобнее использовать маленькие типы данных. Поэтому возникает вопрос: «Какой целочисленный тип использовать, если нужно хранить натуральное число n?» Петя знает лишь 5 целочисленных типов: 1) byte занимает 1 байт, позволяет хранить числа от - 128 до 127 2) short занимает 2 байта, позволяет хранить числа от - 32768 до 32767 3) int занимает 4 байта, позволяет хранить числа от - 2147483648 до 2147483647 4) long занимает 8 байт, позволяет хранить числа от - 9223372036854775808 до 9223372036854775807 5) BigInteger позволяет хранить любое целое число, но при этом не является примитивным типом, и операции с ним выполняются гораздо медленнее. Для всех указанных выше типов значения границ включаются в диапазон значений. Из этого списка Петя хочет выбрать самый маленький тип, в котором можно хранить натуральное число n. Так как BigInteger работает гораздо медленнее, Петя рассматривает его в последнюю очередь. Помогите ему. Выходные данные Выведите первый тип из списка "byte, short, int, long, BigInteger", в котором можно хранить натуральное число n, в соответствии с данными, приведенными выше. | |
![]()
|
|
C. Простые строки
дп
жадные алгоритмы
Строки
*1300
zscoder любит простые строки! Строка t называется простой, если любая пара соседних букв различается. Например, строки ab, aba, zscoder — простые, в то время как строки aa, add не являются таковыми. У zscoder есть строка s. Он хочет изменить в ней наименьшее количество букв, чтобы строка s стала простой. Помогите ему с этой задачей! Выходные данные Выведите простую строку s' — строку s после минимального количества изменений. Если существует несколько решений, можете вывести любое из них. Обратите внимание, что строка s' также должна состоять только из строчных английских букв. | |
![]()
|
|
E. Красивые подмассивы
Деревья
разделяй и властвуй
Строки
Структуры данных
*2100
Однажды ZSCoder выписал массив целых чисел a с элементами a1, a2, ..., an. Будем называть подмассивом массива a последовательность al, al + 1, ..., ar для некоторой пары целых чисел (l, r) таких, что 1 ≤ l ≤ r ≤ n. ZSCoder считает подмассив красивым, если значение операции побитового исключающего или (xor) по всем элементам подмассива не меньше k. Помогите ZSCoder-у найти количество красивых подмассивов массива a! Выходные данные Выведите одно целое число c — количество красивых подмассивов массива a. | |
![]()
|
|
A. Ребляндская лингвистика
дп
реализация
Строки
*1800
В Берляндском Государственном Институте Мира и Дружбы готовят первоклассных специалистов. И вы, как один из самых талантливых людей в Берляндии, обучаетесь именно в нём. Учёба нелегка, ведь от выпускников требуются фундаментальные знания в очень многих зачастую совершенно не связанных друг с другом областях. Например, среди прочего, вы должны хорошо знать лингвистику. И последние месяцы на этом предмете вы изучаете структуру иностранного для студентов Ребляндского языка. В этом языке слова строятся по следующей схеме. Сначала выбирается корень слова, состоящий не менее чем из пяти букв. Затем к слову приписывается несколько строк длиной 2 или 3 символа. Единственное ограничение — нельзя приписывать одну и ту же строку подряд два или более раз. Все эти строки считаются суффиксами слова (в смысле морфемы, а не последних нескольких символов, как вы, возможно, привыкли). Одно из упражнений, которое вы встретили в своём задании, выглядит следующим образом. Вам дано слово s, и вам необходимо найти все различные строки длины 2 или 3, которые могли оказаться его суффиксами, учитывая правила построения слов в Ребляндском языке. Две строки считаются различными, если у них разная длина или существует позиция, в которой в этих строках записаны различные символы. В задании также разобран следующий пример: дано слово abacabaca. Его возможно получить следующими способами:  , где надчеркиваниями обозначен корень слова, а «уголками» — суффиксы. Таким образом, множество возможных суффиксов для этого слова: {aca, ba, ca}. , где надчеркиваниями обозначен корень слова, а «уголками» — суффиксы. Таким образом, множество возможных суффиксов для этого слова: {aca, ba, ca}. Выходные данные В первой строке выведите целое число k — количество различных возможных суффиксов. В следующих k строках выведите сами суффиксы. Строки нужно выводить в лексикографическом (алфавитном) порядке. Примечание Первый тест разобран выше в основной части условия задачи. Во втором примере строка имеет длину 5. Так как корень имеет длину не менее 5, то никакая строка не может быть использована в качестве суффикса. | |
![]()
|
|
C. Кодовое слово
Комбинаторика
Строки
*2500
Знаменитый скульптор Кикассо — ребляндский шпион! Этим заголовком пестрят сегодня берляндские газеты. И теперь опальный скульптор находится в бегах. В этот раз маэстро нашёл убежище у вас, своего давнего друга. Как ни странно, у вас оказался защищённый бункер, который вы и предоставили скульптору. Вы установили для бункера такую систему защиты, что открыть его сможете лишь вы. Для этого необходимо решить задачу, простую для вас, но сложную для кого-либо ещё. Раз в день бункер формирует очередное кодовое слово s. Когда кто-нибудь пытается войти в бункер, на мониторе появляется целое число n. В ответ нужно ввести другое число — остаток от деления на 109 + 7 количества слов длины n, состоящих из строчных английских букв, таких, что они содержат строку s в качестве подпоследовательности. Подпоследовательностью строки a называют такую строку b, которая может быть получена из строки a удалением некоторого набора символов, возможно пустого. В частности, любая строка является своей подпоследовательностью. Например, строка «cfo» — это подпоследовательность строки «codeforces». Вы не успели реализовать алгоритм, который генерирует правильные ответы и это нужно срочно исправить. Займитесь этим. Выходные данные На каждый запрос типа 2 выведите в отдельной строке искомое количество по модулю 109 + 7. Примечание В тестовом примере к первому слову нам подходят слова вида "a?" и "?a", где ? — произвольный символ. Слов этих типов 26 в отдельности, но слово "aa" удовлетворяет обоим шаблонам, поэтому всего слов 51. | |
![]()
|
|
E. Редактор правильных скобочных последовательностей
снм
Строки
Структуры данных
*1700
Недавно Поликарп взялся за разработку текстового редактора правильных скобочных последовательностей (сокращенно ПСП). Напомним, что скобочная последовательность называется правильной, если путем вставки в нее символов «+» и «1» можно получить из нее корректное математическое выражение. Например, последовательности «(())()», «()» и «(()(()))» — правильные, в то время как «)(», «(()» и «(()))(» — нет. Каждая скобка в ПСП имеет парную ей. Например, в «(()(()))»: - для 1-й скобки — парная 8-я,
- для 2-й скобки — парная 3-я,
- для 3-й скобки — парная 2-я,
- для 4-й скобки — парная 7-я,
- для 5-й скобки — парная 6-я,
- для 6-й скобки — парная 5-я,
- для 7-й скобки — парная 4-я,
- для 8-й скобки — парная 1-я.
Редактор Поликарпа пока поддерживает лишь три операции при работе с ПСП. Курсор в редакторе занимает целиком позицию одной из скобок (а не позицию между скобками!). Вот три поддерживаемых операции: - «L» — передвинуть курсор влево на одну позицию,
- «R» — передвинуть курсор вправо на одну позицию,
- «D» — удалить скобку, в которой находится курсор, парную ей, а также все скобки между ними (то есть удалить подстроку от скобки до парной ей).
После операции «D» курсор перемещается на ближайшую скобку вправо (конечно, среди неудалённых). Если такой нет, то есть был удалён суффикс строки, то на ближайшую скобку влево (конечно, среди неудалённых). Ниже приведены рисунки нескольких возможных вариантов операции «D».  Всевозможные некорректные операции (сдвиг курсора за границы строки, удаление всей строки) пока Поликарпом не поддержаны. Поликарп очень гордится своей разработкой, а сможете ли вы реализовать функциональность его редактора? Выходные данные Выведите правильную скобочную последовательность, полученную в результате выполнения всех операций. Примечание В первом тестовом примере изначально курсор находится в позиции 5. Рассмотрим действия редактора подробнее: - команда «R» — курсор передвигается вправо в позицию 6;
- команда «D» — удаляются скобки с позиции 5 до позиции 6. После этого ПСП принимает вид (())(), курсор находится в позиции 5;
- команда «L» — курсор передвигается влево в позицию 4;
- команда «D» — удаляются скобки с позиции 1 до позиции 4. После этого ПСП принимает вид (), курсор находится в позиции 1.
Таким образом, ответ равен (). | |
![]()
|
|
F. Восстанови число
Конструктив
Перебор
Строки
*2300
Вася решил передать Кате очень большое число n. Для этого он сначала записал это число как строку, а затем дописал справа аналогичным образом число k, которое равно количеству цифр в числе n. Магическим образом при передаче этой записи Кате все цифры перемешались произвольным образом. Единственное, что помнит Вася, это некоторая непустая подстрока числа n (под подстрокой числа n следует понимать последовательность подряд идущих цифр из числа n). Вася понимает, что не всегда возможно однозначно восстановить число n, поэтому просит вас найти минимально возможное число, которое он мог передавать. Обратите внимание, что запись числа, которое Вася передал Кате, не могла начинаться с нуля, кроме случая, когда передаваемое число и было нулём (в этом случае оно записывалось как единственная цифра 0). Выходные данные Выведите минимальное число, которое мог передавать Вася. | |
![]()
|
|
B. Разнообразие - это хорошо
Конструктив
реализация
Строки
*1000
Однажды умный старец сказал Кариму, что разнообразие — это хорошо, и с тех пор Карим хочет, чтобы всё в его жизни было разнообразным. Недавно Кариму подарили строку s, состоящую из строчных букв английского алфавита. Поскольку Карим любит разнообразие, то он хочет, чтобы все подстроки строки s были различными. Подстрокой строки s называется некоторое количество последовательных символов данной строки. Например, подстроками строки «aba» являются «» (пустая подстрока), «a», «b», «a», «ab», «ba» и «aba». Если хотя бы две подстроки строки s совпадают, то Карим меняет символы в некоторых позициях на другие строчные буквы английского алфавита. Менять символы очень утомительно, поэтому Карим хотел бы сделать как можно меньше изменений. По данной строке s определите минимальное количество изменений, которое потребуется внести в строку, чтобы все её подстроки стали различными, или определите, что это невозможно. Выходные данные Если невозможно изменить строку s так, чтобы все её подстроки были различны, то выведите -1. В противном случае выведите минимальное количество изменений, которое позволит Кариму достичь цели. Примечание В первом примере одним из возможных решений будет заменить первый символ строки на «b». Во втором примере можно заменить первый символ на «a», а второй на «b», получив таким образом строку «abko». | |
![]()
|
|
C. Вася и строка
Бинарный поиск
дп
Строки
*1500
Школьник Вася получил в подарок на день рождения строку длины n, состоящую из букв «a» и «b». Вася называет привлекательностью строки максимальную длину подстроки (последовательности соседних символов), состоящей из одинаковых символов. Вася может поменять в исходной строке не более k символов. Какой максимальной привлекательности данной строки он сможет добиться? Выходные данные Выведите единственное целое число — максимальная привлекательность строки, которую Вася может получить, изменив в исходной строке не более k символов. Примечание В первом примере Вася может получить как строку «aaaa», так и строку «bbbb». Во втором примере оптимальный ответ достигается на строке «aaaaabaa» или на строке «aabaaaaa». | |
![]()
|
|
C. Ваня и надпись
битмаски
Комбинаторика
реализация
Строки
*1500
Ваня шёл по улице и увидел надпись «Hide&Seek». Поскольку Ваня — программист, ему сразу пришла идея воспользоваться операцией & (побитовое И) для этих двух слов в 64-ричной системе счисления (0..9A..Za..z-_) и получить новое слово. Теперь Ваня придумал некоторую строку s и задался вопросом, сколько существует различных пар слов длины |s| (длина строки s), побитовое И которых равно данному слову s? Поскольку ответ может быть очень большим, Ваня просит вас вычислить его по модулю 109 + 7. Для перевода букв слова в 64-ричную систему счисления Ваня использует следующее соответствие знаков и чисел: - цифрам от «0» до «9» соответствуют числа от 0 до 9;
- буквам от «A» до «Z» соответствуют числа от 10 до 35;
- буквам от «a» до «z» соответствуют числа от 36 до 61;
- символу «-» соответствует число 62;
- символу «_» соответствует число 63.
Выходные данные Выведите единственное целое число — количество возможных пар слов, побитовое И которых равняется строке s, по модулю 109 + 7. Примечание Для подробного описания функции побитовое И можно посмотреть соответствующую статью в Википедии. В первом примере возможны 3 варианта: - z&_ = 61&63 = 61 = z
- _&z = 63&61 = 61 = z
- z&z = 61&61 = 61 = z
| |
![]()
|
|
D. Алёна и строки
дп
Строки
*1900
Вернувшись из леса, Алёна начала читать книгу. Ее взгляд упал на строки s и t, длины которых равняются n и m соответственно. Как обычно, Алёне быстро наскучило читать, и она решила переключить внимание на строки s и t, которые показались ей очень похожими. У Алёны есть любимое целое положительное число k, но, так как она еще маленькая, k не превосходит 10. Девочка хочет выбрать k непересекающихся подстрок строки s, таких что они встречаются в строке t как непересекающиеся подстроки в том же порядке, что и в строке s, а их суммарная длина максимальна. Формально, Алёна хочет найти последовательность из k непустых строк p1, p2, p3, ..., pk, такую что: - строка s представима в виде конкатенации a1p1a2p2... akpkak + 1, где a1, a2, ..., ak + 1 — произвольная последовательность строк (возможно, пустых);
- строка t представима в виде конкатенации b1p1b2p2... bkpkbk + 1, где b1, b2, ..., bk + 1 — произвольная последовательность строк (возможно, пустых);
- сумма длин строк последовательности максимальна среди всех возможных вариантов.
Помогите Алёне справиться с непростой задачей и найти хотя бы суммарную длину строк искомой последовательности. Подстрока строки — это непрерывная последовательность букв строки. Выходные данные В единственной строке выведите одно целое неотрицательное число — суммарную длину строк в искомой последовательности. Гарантируется, что существует хотя бы одна искомая последовательность строк. Примечание Картинка, поясняющая второй пример из условия:  | |
![]()
|
|
B. s-палиндром
реализация
Строки
*1600
Назовём строку "s-палиндромом", если она симметрична относительно своей середины. Например, строка "oHo" является "s-палиндромом", а строка "aa" не является. Строка "aa" не является "s-палиндромом", поскольку вторая половина строки не является зеркальным отражением первой.  Английский алфавит Английский алфавит Вам задана строка s. Определите является ли она "s-палиндромом". Выходные данные Выведите "TAK", если строка s является "s-палиндромом" и "NIE" в противном случае. | |
![]()
|
|
C. Экспоненциальная запись
реализация
Строки
*1800
Вам задано положительное вещественное число x. Ваша задача преобразовать его в "простой экспоненциальный формат". Пусть x = a·10b, где 1 ≤ a < 10, тогда в общем случае "простой экспоненциальный формат" имеет вид "aEb". Если b равно нулю, то часть "Eb" должна быть опущена. Если a является целым числом, то оно должно быть записано без вещественной точки. Также a и b не должны содержать лидирующих нулей. Выходные данные Выведите одну строку — "простой экспоненциальный формат" заданного числа x. | |
![]()
|
|
D. Леген...
дп
матрицы
Строки
Структуры данных
*2500
Последнее время Барни проводил с Норой и ему кажется, что у него есть к ней чувства. Барни хочет отправить ей текстовое сообщение и сделать ее как можно счастливее.  Исходно уровень счастья Норы равен 0. Нора обожает любовные строчки вроде «Я запал на тебя» и подобные. Нора знает всего n любовных строчек, каждая из которых состоит только из строчных букв латинского алфавита, а некоторые из них могут совпадать (в написании, но различаться в произношении или значении). Каждый раз, когда Нора встречает i-ю из известных ей любовных строчек как непрерывную подстроку сообщения Барни, ее уровень счастья увеличивается на ai. Эти подстроки могут пересекаться, к примеру, в тексте aaab она встретит строку aa дважды, а строку ab один раз. В связи с ограничениями системы сообщений, текстовое сообщение Барни может содержать до l символов. Барни просит вас помочь ему сделать Нору как можно счастливее, это будет леген... Выходные данные Выведите единственное целое число — максимально возможный уровень счастья Норы после прочтения текстового сообщения Барни. Примечание Оптимальный ответ в первом примере из условия — hearth, содержащий каждую любовную строчку ровно по одному разу. Оптимальным ответом во втором примере из условия является строка artart. | |
![]()
|
|
B. Барникл
математика
Перебор
реализация
Строки
*1400
Барни, находясь в баре, загляделся на красивую девушку. Он хочет точным выстрелом пронзить ее стрелой любви, и поэтому ему нужно знать расстояние между ним и девушкой.  Барни попросил бармена Карла сообщить ему, чему равно это расстояние, но тот был так занят разговорами с другими посетителями, что написал значение расстояния (а это вещественное число) на салфетке. Однако, для этого Карл использовал экспоненциальную запись числа. Экспоненциальная запись некоторого вещественного числа x это запись в форме AeB, где A — некоторое вещественное число, B — целое число, а x равняется A × 10B. В нашей задаче A может принимать вещественные значения от 0 до 9, а B неотрицательно. Барни плохо знаком с экспоненциальной записью, поэтому он просит вас сообщить ему, чему равно расстояние в его обычной десятичной записи с минимально возможным количеством знаков после десятичной точки (или без десятичной точки, если его значение целое). Смотрите формат выходных данных для более подробной информации. Выходные данные В единственной строке выведите вещественное число x (искомое расстояние) в его десятичной записи. То есть, если x — целое число, выведите его значение без дробной части и десятичной точки и без ведущих нулей. В противном случае, выведите x в виде p.q, где p и q — целые числа, p не содержит ведущих нулей (но может быть равным нулю), а q не содержит нулей в конце своей записи (и не может быть равным нулю). | |
![]()
|
|
D. Палиндромность
Строки
хэши
*2200
Строка s длины n называется k-палиндромом, если она сама является палиндромом, а ее префикс и суффикс длины  являются (k - 1)-палиндромами. 0-палиндромом является любая строка (даже пустая). являются (k - 1)-палиндромами. 0-палиндромом является любая строка (даже пустая). Назовем палиндромностью строки s такое максимальное число k, для которого s является k-палиндромом. Например, палиндромность строки «abaaba» равна 3. Дана строка. Ваша задача — найти сумму палиндромностей всех ее префиксов. Выходные данные Выведите единственное число — сумму палиндромностей всех префиксов данной строки. | |
![]()
|
|
B. SMS
жадные алгоритмы
Разбор выражений
Строки
*1600
Маленький морж Клычок, как и все современные моржи, любит общаться с помощью SMS. Однажды он столкнулся с проблемой, что при отправке больших текстов они разделяются на части по n символов (размер одного SMS сообщения), и разрываются целые предложения или даже слова! Клычку это не понравилось, и перед ним встала задача разбить текст на сообщения самостоятельно таким образом, чтобы ни одно предложение не было разбито на части при отправке, и количество SMS сообщений для отправки было бы минимальным. Если два подряд идущих предложения находятся в разных сообщениях, то пробел между ними можно не учитывать (Клычок этот пробел не набирает). Текст маленького моржа имеет следующий вид: TEXT ::= SENTENCE | SENTENCE SPACE TEXT
SENTENCE ::= WORD SPACE SENTENCE | WORD END
END ::= {'.', '?', '!'}
WORD ::= LETTER | LETTER WORD
LETTER ::= {'a'..'z', 'A'..'Z'}
SPACE ::= ' '
Под SPACE следует подразумевать символ пробела. Сколько же сообщений отправил Клычок? Выходные данные В первой и единственной строке выведите количество SMS сообщений, которое потребуется Клычку. Если разбить текст невозможно, выведите "Impossible" без кавычек. Примечание Рассмотрим третий пример. Текст будет разбит на 3 сообщения: "Hello!", "Do you like fish?" и "Why?". | |
![]()
|
|
C. Они повсюду
Бинарный поиск
Строки
*1500
Юный тренер покемонов Сергей Б. обнаружил большой дом, состоящий из n квартир, выстроенных в ряд слева направо, причем в каждую квартиру можно зайти с улицы, из каждой квартиры можно выйти на улицу, а также из каждой квартиры можно зайти в соседнюю слева или справа квартиру. Из квартиры номер 1 можно попасть только в квартиру номер 2, а из квартиры номер n можно попасть только в квартиру номер n - 1. Так сложилось, что в каждой из этих квартир находится ровно один покемон какого-то типа. Возможно, что в каких-то квартирах находятся покемоны одинаковых типов. Сергей Б. попросил жителей дома пустить его к ним в квартиры, чтобы поймать покемонов. Посовещавшись, жители дома решили, что разрешат Сергею Б. зайти с улицы ровно в одну квартиру, посетить несколько квартир, а затем выйти из какой-то квартиры на улицу, причем они не разрешили Сергею Б. посещать никакую квартиру более одного раза. Сергей Б. очень обрадовался, но как человек интеллигентный, решил посетить как можно меньше квартир, но при этом, естественно, собрать покемонов всех типов, которые есть в доме (иначе зачем тогда это всё). Перед вами стоит задача помочь ему и определить это минимальное число квартир. Выходные данные Выведите минимальное число квартир, которые должен посетить Сергей Б., чтобы поймать покемонов всех типов, которые есть в доме. Примечание В первом тестовом примере Сергей Б. может, например, начать с квартиры 1 и закончить в квартире 2. Во втором тестовом примере Сергей Б. может, например, начать с квартиры 4 и закончить в квартире 6. В третьем тестовом примере Сергей Б. должен начать с квартиры 2 и закончить в квартире 6. | |
![]()
|
|
C. Сложная загадка
дп
Строки
*1600
Василий очень любит разные загадки. Сегодня он нашёл загадку, которую не смог решить сам, поэтому он просит вас помочь ему. У Василия есть n строк, состоящих из строчных букв английского алфавита. Он хочет, чтобы строки располагались в лексикографическом порядке (как в словаре), но при этом не хочет менять их местами. Единственное, что Василий может делать, это разворачивать строки (первая буква становится последней, вторая предпоследней и так далее). Чтобы развернуть i-ю строку Василию, надо потратить ci единиц энергии. Василия интересует минимальное количество энергии, которое необходимо потратить, чтобы строки шли в лексикографическом порядке. Строка A лексикографически меньше строки B, если она короче B (|A| < |B|) и является её префиксом, либо ни одна из них не является префиксом другой, и в первой позиции, где они различаются, в строке A стоит символ с меньшим номером. В данной задаче две одинаковые строки на соседних позициях не нарушают порядок лексикографической сортировки. Выходные данные Если, разворачивая какие-либо из данных строк, невозможно добиться, чтобы они следовали в лексикографическом порядке, то выведите - 1. В противном случае выведите минимальное количество энергии, которое придётся потратить Василию. Примечание Во втором примере можно развернуть строку 2 или строку 3. На разворот строки 3 тратится меньше энергии, поэтому правильным ответом будет развернуть её. В третьем примере обе строки не изменяются после разворота и расположены в неправильном порядке, поэтому ответом является - 1. В четвёртом примере обе строки состоят из букв «a», но в отсортированном порядке строка «aa» должна располагаться раньше строки «aaa», поэтому ответ - 1. | |
![]()
|
|
A. Циклический сдвиг букв
жадные алгоритмы
Конструктив
реализация
Строки
*1200
Выходные данные Выведите лексикографически минимальную строку, которую можно получить из s, сдвинув ровно одну непустую подстроку. Примечание Строка s называется лексикографически меньшей, чем строка t такой же длины, если существует такое 1 ≤ i ≤ |s|, что s1 = t1, s2 = t2, ..., si - 1 = ti - 1, а si < ti. | |
![]()
|
|
A. Слишком длинные слова
Строки
*800
Иногда некоторые слова вроде «localization» или «internationalization» настолько длинны, что их весьма утомительно писать много раз в каком либо тексте. Будем считать слово слишком длинным, если его длина строго больше 10 символов. Все слишком длинные слова можно заменить специальной аббревиатурой. Эта аббревиатура строится следующим образом: записывается первая и последняя буква слова, а между ними — количество букв между первой и последней буквой (в десятичной системе счисления и без ведущих нулей). Таком образом, «localization» запишется как «l10n», а «internationalization» как «i18n». Вам предлагается автоматизировать процесс замены слов на аббревиатуры. При этом все слишком длинные слова должны быть заменены аббревиатурой, а слова, не являющиеся слишком длинными, должны остаться без изменений. Выходные данные Выведите n строк. В i строке должен находиться результат замены i-го слова из входных данных. | |
![]()
|
|
F. Операции над множеством строк
интерактив
Перебор
Строки
строковые суфф. структуры
Структуры данных
хэши
*2400
Вам нужно обработать m запросов над множеством строк D. Каждый запрос одного из трёх типов: - Добавить строку s в множество D. Гарантируется, что эта строка ранее не добавлялась в множество.
- Удалить строку s из множества D. Гарантируется, что эта строка находится в множестве D.
- Для заданной строки s найти количество вхождений строк из множества D. Если некоторая строка p из множества D имеет несколько вхождений в s вы должны посчитать их все.
Заметим, что вам требуется решить задачу в режиме online. Это значит, что вы не можете сразу считать все входные данные. Вы можете считать очередной запрос только после того как выведите ответ на последний запрос третьего типа. Используйте функции fflush в языке C++ и BufferedWriter.flush в языке Java после каждого вывода вашей программы. Выходные данные Для каждого запроса третьего типа выведите одно целое число c — требуемое количество вхождений в строку s. | |
![]()
|
|
B. Мемори и трезубец
реализация
Строки
*1100
Мемори гуляет по декартовой плоскости, начиная в точке начала координат. У неё есть последовательность действий s: - Символ «L» означает шаг на единицу влево.
- Символ «R» означает шаг на единицу вправо.
- Символ «U» означает шаг на единицу вверх.
- Символ «D» означает шаг на единицу вниз.
Мемори хочет, чтобы, последовательно исполнив все команды, она снова оказалась в точке начала координат. У неё есть специальный трезубец, который за одно применение может изменить любой символ в строке s на один из символов «L», «R», «U» или «D». Однако пользоваться трезубцем нелегко, поэтому Мемори хочет минимизировать количество его применений или определить, что добиться желаемого невозможно в принципе. Выходные данные Если невозможно изменить строку так, чтобы Мемори заканчивала путешествие в точке начала координат, то выведите -1 в единственной строке выходных данных. В противном случае выведите минимальное требуемое количество изменений. Примечание В первом примере Мемори сначала идёт направо, потом снова направо, затем вверх. Можно показать, что эту последовательность инструкций невозможно изменить таким образом, чтобы она возвращала Мемори в начало координат. Во втором примере Мемори сначала идёт вверх, потом вниз, потом вверх, потом направо. Одним из возможных решений является изменение строки s на «LDUR», для этого потребуется внести только одно изменение. | |
![]()
|
|
E. Али идет за покупками
*особая задача
Перебор
Строки
*1800
Али Кучулу собирается пойти за подарками к Наврузу, древнему персидскому празднику, иранскому новому году. Когда Али вошел в магазин, он сразу понял, что когда-то хозяин магазина тоже был программистом. Но программистом много денег не заработаешь, и ему пришлось сменить работу. Хозяин сказал Али, что тот может взять бесплатно что угодно, если ответит на простой вопрос за 10 секунд. Правда, чтобы увидеть вопрос, нужно было заплатить 3 томана. Али сразу же согласился, и хозяин магазина дал ему листок бумаги, на котором было задание. Оно было очень простым: Пусть строка A — ababababababab. Какая непустая подстрока A встречается в ней чаще всего? Али тут же ответил: a. Но хозяин сказал, что это неправильно, и попросил его дочитать условие до конца: Если есть несколько таких подстрок, выберите самую длинную из них. Если их все равно несколько, выберите ту из них, что идет позже других в алфавитном порядке. Правильный ответ был ab. Сейчас Али просит вас решить эту задачу для других строк. А у вас есть для этого компьютер и странный язык. Выходные данные В первую строку выведите ответ. | |
![]()
|
|
B. Пароли
математика
реализация
сортировки
Строки
*1100
Ваня собирается зайти на свой любимый сайт Codehorses. Всего Ваня использует n различных паролей для сайтов, однако, какой именно пароль он указывал при регистрации на Codehorses, он не помнит. Ваня будет вводить пароли в порядке неубывания их длин, а пароли одинаковой длины — в произвольном порядке. Как только Ваня введет правильный пароль, он сразу окажется авторизован на сайте. Ваня не будет вводить один и тот же пароль несколько раз. На ввод любого пароля Ваня тратит одну секунду. Однако, если Ваня k раз введет неправильный пароль, то следующую попытку ввода он сможет совершить только через 5 секунд. Каждую попытку ввода Ваня совершает незамедлительно, то есть всегда, когда у него есть возможность вводить очередной пароль, Ваня этим занят. Сообщите, сколько секунд потребуется Ване, чтобы зайти на Codehorses, в лучшем для него случае (если он потратит минимально возможное количество секунд) и в худшем для него случае (если он потратит максимально возможное количество секунд). Выходные данные Выведите два целых числа — время (в секундах), которое потребуется Ване для авторизации на Codehorses в лучшем для него случае и худшем для него случае соответственно. Примечание Рассмотрим первый тест. Так как все пароли одинаковой длины, Ваня может ввести правильный пароль как первым, так и последним. Если он вводит правильный пароль первым, то он тратит на это ровно 1 секунду. Следовательно, ответ в лучшем случае равен 1. Если же он вводит его последним, до этого он введёт остальные 4 пароля. Он потратит 2 секунды на ввод первых 2 неправильных паролей, после этого ему придется подождать 5 секунд, так как он ввёл 2 неправильных пароля. Потом он потратит ещё 2 секунды на ввод 2 неправильных паролей, опять подождёт 5 секунд и наконец введёт верный пароль, потратив на это ещё 1 секунду. Итого в худшем случае он сможет авторизоваться за 15 секунд. Рассмотрим второй тест. Как бы Ваня ни вводил пароли, он не сможет добиться того, чтобы доступ к сайту заблокировался. Так как необходимый пароль имеет длину 2, Ваня в любом случае введёт сначала все пароли длины 1, потратив на это 2 секунды. Затем, в лучшем случае, он сразу введёт необходимый пароль, и ответ в лучшем случае будет равен 3, а в худшем случае сначала введёт неверный пароль длины 2, и только потом верный, и потратит 4 секунды. | |
![]()
|
|
B. Стихотворный шаблон
реализация
Строки
*1200
Вам задан текст, состоящий из n строк. Каждая строка содержит несколько слов, состоящих из строчных английских букв, разделённых пробелами. Назовём слогом строчку, содержащую ровно одну гласную букву и некоторое (возможно, нулевое) количество согласных. Гласными буквами принято считать «a», «e», «i», «o», «u», «y». Каждое слово в тексте, в котором есть хотя бы одна гласная буква, можно разбить на слоги. При этом каждая буква слова должна попасть ровно в один слог. Например, слово «mamma» можно разбить на слоги как «ma» и «mma», «mam» и «ma», и «mamm» и «a». Слова, целиком состоящие из согласных букв, будем игнорировать. Стихотворным шаблоном для данного текста называется последовательность p1, p2, ..., pn из n неотрицательных целых чисел. Текст подходит под стихотворный шаблон, если для каждого i от 1 до n можно разбить все слова в i-й строке на слоги так, чтобы суммарное количество слогов равнялось бы pi. Определите, подходит ли заданный текст под заданный стихотворный шаблон. Выходные данные В единственной строке выведите «YES» (без кавычек), если текст подходит под заданный шаблон, и «NO» в противном случае. Примечание В первом примере слова можно разбить на слоги следующим образом: in-tel
co-de
ch al-len-ge
Поскольку в слове «ch» в третьей строке нет ни одной гласной буквы, оно игнорируется при подсчете количества слогов. В итоге мы получаем по 2 слога в первых двух строках и 3 слога в третьей. | |
![]()
|
|
D. Генерация наборов
Бинарный поиск
Деревья
жадные алгоритмы
поиск в глубину и подобное
Строки
Структуры данных
*1900
Вам задан набор Y из n различных целых положительных чисел y1, y2, ..., yn. Назовём набор X из n различных целых положительных чисел x1, x2, ..., xn генератором для Y, если из набора X можно получить набор Y, применяя к элементам набора X следующие две операции: - Умножить произвольное число xi на два, то есть заменить xi на 2·xi.
- Умножить произвольное число xi на два и прибавить единицу, то есть заменить xi на 2·xi + 1.
Обратите внимание, не требуется, чтобы все числа в наборе X были различны после выполнения каждой операции. Наборы в данной задаче сравниваются как множества чисел. Другими словами, два набора различных чисел X и Y совпадают, если, выписав оба набора в отсортированном порядке, мы получим одинаковые массивы. Заметьте, что любой набор чисел (или его перестановка) сам является одним из своих генераторов. По заданному набору Y найдите его генератор, в котором максимальное число минимально. Выходные данные Выведите n чисел — генератор для заданного набора Y, в котором максимальное число как можно меньше. Если подходящих наборов несколько, разрешается вывести любой из них. | |
![]()
|
|
B. Анализ текстового документа
Разбор выражений
реализация
Строки
*1100
Современные текстовые редакторы обычно показывают некоторую информацию для текущего редактируемого документа — например, количество слов, количество страниц или количество знаков. В этой задаче вам предстоит реализовать похожую функциональность. Задана строка, состоящая только из: - прописных и строчных букв английского алфавита,
- символов подчёркивания (они используются в качестве разделителей),
- круглых скобок (как открывающих, так и закрывающих).
Гарантируется, что каждая открывающая скобка имеет парную закрывающую, идущую следом. Аналогично, каждая закрывающая скобка имеет парную открывающую, которая расположена до неё. Для каждой пары соответствующих скобок верно, что между ними нет каких-либо других скобок. Иными словами, каждая скобка в строке входит в пару «открывающая-закрывающая», и такие пары не вкладываются друг в друга. Например, допустимой строкой является: «_Hello_Vasya(and_Petya)__bye_(and_OK)». Словом называется нерасширяемая последовательность подряд идущих букв, то есть последовательность букв, такая что слева и справа от неё находится скобка или символ подчёркивания, или соответствующий символ отсутствует. Пример выше содержит семь слов: «Hello», «Vasya», «and», «Petya», «bye», «and» и «OK». Напишите программу, которая найдет: - длину самого длинного слова вне скобок (выведите 0, если слов вне скобок нет),
- количество слов внутри скобок (выведите 0, если слов внутри скобок нет).
Выходные данные Выведите два числа: - длину самого длинного слова вне скобок (выведите 0, если слов вне скобок нет),
- количество слов внутри скобок (выведите 0, если слов внутри скобок нет).
Примечание В первом примере слова «Hello», «Vasya» и «bye» записаны вне скобок, а слова «and», «Petya», «and» и «OK» — внутри. Обратите внимание, что слово «and» встречается дважды, и учитывать в ответе его тоже следует два раза. | |
![]()
|
|
D. Плотная подпоследовательность
жадные алгоритмы
Строки
Структуры данных
*1900
Вам дана строка s, состоящая из строчных английских букв, и целое число m. Выберем из данной строки некоторые символы так, чтобы в любой непрерывный подотрезок длины m попал хотя бы один выбранный символ. Заметьте, что здесь выбираются именно позиции символов, а не сами символы. Затем из символов, которые стоят на выбранных позициях, собирается новая строка. При этом необходимо использовать все символы на выбранных позициях, но их разрешается переставлять как угодно. Формально, мы выбираем некоторую подпоследовательность индексов 1 ≤ i1 < i2 < ... < it ≤ |s|. Выбранная последовательность должна удовлетворять условию: для любого j, такого что 1 ≤ j ≤ |s| - m + 1, среди выбранных индексов найдется хотя бы один, который принадлежит отрезку [j, j + m - 1], то есть существует k от 1 до t, такое что j ≤ ik ≤ j + m - 1. Затем мы выбираем некоторую перестановку p выбранных индексов и составляем новую строчку sip1sip2... sipt. Найдите лексикографически минимальную строку, которую можно получить с помощью описанных действий. Выходные данные Выведите лексикографически минимальную строку, которую можно получить с помощью описанных действий. Примечание В первом примере мы можем выбрать подпоследовательность {3} и составить строку «a». Во втором примере мы можем выбрать подпоследовательность {1, 2, 4} и составить из символов на этих позициях строку «aab». | |
![]()
|
|
C. Спрятанное слово
Конструктив
Перебор
реализация
Строки
*1600
Определим игровое поле как таблицу из 2 рядов и 13 столбцов. В каждой клетке таблицы записана заглавная буква английского алфавита. Некоторые клетки могут содержать одинаковые буквы. Рассмотрим пример таблицы:
ABCDEFGHIJKLM
NOPQRSTUVWXYZ
Назовём две клетки соседними, если у них есть общая сторона или общий угол. В приведённом примере клетка «A» является соседней с клетками с буквами «B», «N» и «O». Клетка не является соседней сама себе. Последовательность клеток называется путём, если любые две соседние клетки последовательности являются соседними клетками поля. В приведённом примере «ABC» является путём, также как и «KXWIHIJK». Последовательность клеток «MAB» путём не является, так как «M» не соседняя с «A». Одна клетка может входить в путь несколько раз (но не может занимать две соседние позиции в пути, так как клетка не является соседней сама себе). Вам дана строка s, состоящая из 27 заглавных букв английского алфавита. Каждая заглавная буква английского алфавита встречается в s хотя бы один раз. Требуется построить какую-нибудь таблицу, содержащую какой-нибудь путь, такой что если выписать буквы в клетках вдоль этого пути, получится строка s. Если решения не существует выведите «Impossible». Выходные данные Выведите две строки, каждая из которых содержит 13 заглавных букв английского алфавита, определяющие строки таблицы. Если правильных решений несколько, выведите любое из них. Если решений не существует, выведите «Impossible». | |
![]()
|
|
B. Сумма чека
Разбор выражений
реализация
Строки
*1600
Василий вышел из магазина и ему стало интересно пересчитать сумму в чеке. Чек представляет собой строку, в которой названия покупок и их цены записаны подряд без пробелов. Чек имеет вид «name1price1name2price2...namenpricen», где namei (название i-го продукта) — это непустая строка длины не более 10, состоящая из строчных букв латинского алфавита, а pricei (цена i-го продукта) — это непустая строка, состоящая из точек и цифр. Продукты с одинаковым названием могут иметь разные цены. Цена каждого продукта записана в следующем формате. Если продукт стоит целое количество рублей, то копейки не пишутся. Иначе, после записи количества рублей к цене приписывается точка, за которой следом ровно двумя цифрами записаны копейки (если копеек менее 10, то используется лидирующий ноль). Также, каждые три разряда (от менее значимых к более значимым) в записи рублей разделяются точками. Лишние лидирующие нули недопустимы, запись цены всегда начинается с цифры и заканчивается цифрой. Например, записи цен: - «234», «1.544», «149.431.10», «0.99» и «123.05» являются корректными,
- «.333», «3.33.11», «12.00», «.33», «0.1234» и «1.2» не являются корректными.
Напишите программу, которая по содержимому чека найдет суммарную цену всех покупок. Выходные данные Выведите суммарную цену всех покупок строго в том же формате, в котором задаются цены покупок во входных данных. | |
![]()
|
|
E. Игры на диске
Строки
строковые суфф. структуры
Структуры данных
хэши
*2300
У Толи было n компьютерных игр, и он решил записать их на один диск. После этого он решил написать маркером названия всех своих игр на этом диске по кругу по часовой стрелке друг за другом. Названия всех игр были различные, а длина каждого названия была ровно k. Написанные названия на диске не перекрываются между собой. После того, как Толя написал названия всех игр, на диске получилась циклическая строка длины n·k. Прошло несколько лет и Толя уже и забыл, какие игры записаны на его диске. Он помнит, что всего в то время было g популярных игр, и на его диске могут быть только лишь эти игры, причем каждая из g игр может быть записана на диске не более одного раза. Перед вами стоит задача восстановить любой корректный список игр, которые Толя мог записать на свой диск. Выходные данные Если ответа не существует, выведите «NO» (без кавычек). В противном случае, выведите в первую строку «YES» (без кавычек). Во вторую строку выведите n целых чисел — номера популярных игр, записанных на диске Толи. Выводить игры нужно в порядке их записи на диске, то есть по часовой стрелке, при этом начинать вывод можно с любой игры. Помните, что каждая популярная игра могла быть записана на диск не более одного раза. Если ответов несколько, разрешается вывести любой из них. | |
![]()
|
|
A. Интервью с Олегом
реализация
Строки
*900
Поликарп взял у Олега интервью и записал его себе в блокнот без знаков препинания и пробелов, чтобы сэкономить время и успеть все записать. В итоге, интервью представляет собой строку s, состоящую из n строчных букв латинского алфавита. В речи Олега есть слово-паразит ogo, а также все слова, которые получаются из слова ogo приписыванием справа к нему слога go. Например, слова ogo, ogogo, ogogogo являются паразитами, а слова go, og, ogog, ogogog и oggo — не являются. Слова-паразиты имеют максимальный возможный размер, то есть, например, в речи ogogoo нельзя считать, что слово-паразит это ogo, а goo является частью обыкновенной фразы интервью. В данном случае словом-паразитом является подстрока ogogo. До печати Поликарпу необходимо заменить каждое слово-паразит на последовательность из трёх звездочек. Обратите внимание, что независимо от длины слова-паразита оно заменяется ровно на три звёздочки. Поликарп быстро справился с этой задачей. А сможете ли это сделать вы? Время пошло! Выходные данные Выведите текст интервью после замены каждого слова-паразита на «***». Допустимо, что в ответе подстрока «***» будет идти подряд несколько раз. Примечание В первом примере одно слово-паразит ogogo, поэтому интервью для печати выглядит как «a***b». Во втором примере два слова-паразита ogo и ogogogo, поэтому интервью без слов-паразитов выглядит как «***gmg***». | |
![]()
|
|
A. Ночь в музее
реализация
Строки
*800
Гриша, подобно персонажу известной кинокомедии, нашел себе ночную работу в музее естественной истории. В первую же смену ему выдали его главное орудие труда — эмбоссер — и приказали провести инвентаризацию всей экспозиции. Эмбоссер представляет собой устройство для «печати» текста на пластиковой ленте. Текст набирается последовательно, буква за буквой. В устройство входят колесо с нанесёнными по кругу строчными буквами английского алфавита, неподвижная засечка, которая указывает на текущую букву, и кнопка, печатающая выбранную букву. За одно действие можно повернуть колесо с алфавитом на одну букву влево либо вправо по циклу. Изначально засечка эмбоссера указывает на букву a. Остальные буквы расположены так, как показано на рисунке.  После внесения предмета в базу Гриша должен с помощью эмбоссера выдавить на пластиковой ленте название и прикрепить его к экспонату. Возвращать колесо обратно в позицию, соответствующую букве a, не требуется. Наш герой боится, что некоторые особо устрашающие экспонаты могут ожить и начать за ним свою охоту, поэтому он хочет как можно быстрее напечатать все названия. Помогите ему: для данного названия экспоната определите минимальное количество поворотов колеса, необходимое для его печати. Выходные данные Выведите единственное целое число — минимальное количество поворотов колеса, за которое Гриша сможет напечатать название экспоната. Примечание  Для набора слова из первого примера необходимо сделать следующую последовательность поворотов: - от a до z (1 поворот против часовой стрелки),
- от z до e (5 поворотов по часовой стрелке),
- от e до u (10 поворотов против часовой стрелки),
- от u до s (2 поворотa против часовой стрелки).
Итого потребуется 1 + 5 + 10 + 2 = 18 поворотов. | |
![]()
|
|
A. Антон и Даник
реализация
Строки
*800
Антону нравится играть в шахматы. Поэтому он часто играет в эту увлекательную игру со своим другом Даником. Однажды, Антон с Даником сыграли n партий подряд. Для каждой партии друзьям известно, кто в ней победил — Антон или Даник. При этом ни одна из партий не окончилась вничью. Антону стало интересно, кто же выиграл больше раз — он или Даник? Помогите Антону и определите это. Выходные данные Если Антон выиграл большее количество партий, чем Даник, выведите «Anton» (без кавычек). Если Даник выиграл большее количество партий, чем Антон, выведите «Danik» (без кавычек). Если Антон и Даник выиграли поровну партий, выведите «Friendship» (без кавычек). Примечание В первом примере Антон выиграл 6 партий, а Даник — всего одну. Следовательно, ответ — «Anton». Во втором примере Антон выиграл 3 партии, а Даник — 4. Значит, ответ — «Danik». В третьем Антон и Даник выиграли по 3 партии. Поэтому ответ — «Friendship». | |
![]()
|
|
A. Остап и Кузнечик
реализация
Строки
*800
В пути до Рио-де-Жaнeйро Остап развлекается, играя с кузнечиком, которого он взял с собой в специальной коробочке. Остап строит для кузнечика полосу препятствий длиной n, некоторые клетки полосы свободные, а другие полностью заняты. В одну из свободных клеток Остап помещает кузнечика, а в другую — маленькое насекомое, которое кузнечик хочет съесть. Известно, что за один прыжок кузнечик может переместиться в любую свободную клетку на расстоянии в точности k от текущей, при этом для прыжка кузнечика не имеет значения, свободны или пусты промежуточные клетки. Например, если k = 1, то кузнечик может прыгать только в соседнюю клетку, а если k = 2, то через клетку. Определите, существует ли последовательность корректных прыжков, которая приводит кузнечика в клетку с насекомым. Выходные данные Если существует последовательность прыжков (каждый длины k), приводящая кузнечика из его начальной клетки в клетку с насекомым, то выведите «YES» (без кавычек) в единственной строке выходных данных. В противном случае выведите «NO» (без кавычек). Примечание В первом примере кузнечику достаточно совершить один прыжок вправо, тогда он сразу попадёт из позиции 2 в позицию 4. Во втором примере кузнечик совершает прыжки только в соседние клетки, но путь до насекомого свободен — кузнечик может добраться до него за 5 прыжков влево. В третьем примере кузнечик не может совершить ни одного прыжка. В четвёртом примере кузнечик может прыгать только по клеткам с нечётными координатами, поэтому он никогда не доберётся до насекомого. | |
![]()
|
|
E. Коровоконг повелевает циклическими сдвигами
Строки
*3200
Учитель Коровоконга узнал, что тот весьма неплохо управляется с циклическими сдвигами, и придумал для него новую сложную задачу. Вам дана последовательность из n строк s1, s2, ..., sn, которую мы обозначим как A. Последовательность строк X называется стабильной, если выполнено условие, описанное ниже. Для начала, сообщением назовём конкатенацию произвольного конечного количества элементов последовательности X. Любой элемент последовательности может быть использован произвольное количество раз, и конкатенация также происходит в произвольном порядке. Обозначим через SX множество всех возможных сообщений, которые можно построить по данной последовательности. Разумеется, это множество содержит бесконечно много элементов, если исходная последовательность X непуста. Сообщение называется хорошим, если выполняются следующие условия: - Допустим сообщение является конкатенацией k строк w1, w2, ..., wk, где каждое wi является элементом X.
- Рассмотрим все |w1| + |w2| + ... + |wk| возможных циклических сдвигов этой строки. Обозначим через m количество этих циклических сдвигов, являющихся элементами SX.
- Сообщение является хорошим, если и только если m в точности равно k.
Последовательность X называется стабильной, если и только если все элементы SX являются хорошими. Пусть f(L) равно 1, если L является стабильной последовательностью, и 0 в противном случае. Вычислите сумму f(L) по всем L, являющимся непустыми непрерывными подпоследовательностями A (всего существует  непрерывных подпоследовательностей). непрерывных подпоследовательностей). Выходные данные Выведите одно целое число, равное количеству непустых непрерывных подпоследовательностей, являющихся стабильными. Примечание В первом примере требуется рассмотреть 10 непрерывных подпоследовательностей. Не являются стабильными [«a», «ab», «b»], [«ab», «b», «bba»] и [«a», «ab», «b», «bba»]. Остальные семь являются стабильными. Например, X = [«a», «ab», «b»] не является стабильной, поскольку у сообщения «ab» + «ab» = «abab» четыре циклических сдвига [«abab», «baba», «abab», «baba»], все из которых являются элементами SX. | |
![]()
|
|
A. Коровоконг изучает циклические сдвиги
реализация
Строки
*900
Коровоконг учится произносить слова! Однажды учитель дал ему новое слово, которое необходимо научиться правильно произносить. Будучи исполнительным студентом, Коровоконг сразу же выполнил задание. Теперь Коровоконг хочет образовать новые слова, используя данное. Для этого он берёт текущее слово и переставляет его последнюю букву в начало. Такую операцию он называет циклическим сдвигом. Он может применить эту операцию произвольное количество раз, например, последовательно применяя циклический сдвиг к слову «abracadabra», он получит слова «aabracadabr», «raabracadab» и так далее. Теперь Коровоконг хочет знать, сколько различных слов он может получить, применяя операцию циклического сдвига. Изначальную строку также необходимо учитывать. Выходные данные Выведите одно целое число, равное количеству различных строк, которые можно получить, применяя операцию циклического сдвига к строке из входных данных. Примечание В первом примере Коровоконг может получить строки «abcd», «dabc», «cdab» и «bcda». Во втором примере не имеет значения, сколько раз Коровоконг применит операцию циклического сдвига, он сможет получить только строку «bbb». В третьем примере Коровоконг может получить две строки «yzyz» и «zyzy». | |
![]()
|
|
B. Расшифровка
реализация
Строки
*900
Поликарп без ума от шифрования, поэтому он пишет Свете сообщения в зашифрованном виде. Медианной буквой в слове он называет ту, которая находится в середине слова. Если слово четной длины, то медианная буква та, которая стоит левее из двух средних букв. Медианная буква выделена в следующих примерах: contest, info. Если слово состоит из одной буквы, то, по определению выше, она и будет его медианной буквой. Поликарп шифрует каждое слово следующим образом: он выписывает медианную букву слова, затем удаляет эту букву из слова и повторяет процесс до тех пор, пока в слове есть хоть одна буква. Например, слово volga он зашифрует в слово logva. Вам задано слово s, зашифрованное Поликарпом, а ваша задача — расшифровать его. Выходные данные Выведите слово, которое зашифровал Поликарп. Примечание В первом примере Поликарп зашифровал слово volga. Сначала он выписал букву l, стоящую в позиции 3, после чего его слово приняло вид voga. После этого, Поликарп выписал букву o, стоящую в позиции 2, а его слово стало равным vga. Затем, Поликарп выписал букву g, стоящую во второй позиции, после этого слово изменилось на va. Потом он выписал букву v, а затем букву a. Таким образом, зашифрованное слово выглядит как logva. Во втором примере Поликарп зашифровал слово no. Сначала он выписал букву n, слово стало равным o, и он выписал букву o. Таким образом, в этом примере, слово и его зашифровка выглядят одинаково. В третьем примере Поликарп зашифровал слово baba. Сначала он выписал букву a, стоящую в позиции 2, после чего слово стало равным bba. Затем он выписал букву b, стоящую в позиции 2, а его слово приняло вид ba. После этого он выписал сначала букву b, стоящую в позиции 1, слово приняло вид a, и он выписал эту букву a. Таким образом, зашифрованное слово выглядит как abba. | |
![]()
|
|
B. Расшифровка генома мамонта
реализация
Строки
*900
Расшифровка генома берляндского мамонта подходит к концу! Одна из немногих оставшихся задач — восстановление нераспознанных нуклеотидов в найденной цепочке s. Каждый нуклеотид кодируется прописной буквой латинского алфавита: 'A', 'C', 'G' или 'T'. Нераспознанный нуклеотид кодируется знаком вопроса '?'. Таким образом, s — это строка, состоящая из букв 'A', 'C', 'G', 'T' и символов '?'. Известно, что в расшифрованном геноме берляндского мамонта количества нуклеотидов каждого из четырех видов равны между собой. Требуется расшифровать геном и заменить каждый нераспознанный нуклеотид на один из четырёх так, чтобы количества нуклеотидов каждого из четырёх типов стали равны между собой. Выходные данные Если расшифровать геном возможно, выведите его расшифровку. Если существует много вариантов расшифровки, то выведите любой из них. Если искомой замены не существует, то выведите три знака равно подряд «===» (без кавычек). Примечание В первом примере можно заменить первый знак вопроса на букву 'A', второй знак вопроса на букву 'G', в третий — на букву 'T', тогда каждого нуклеотида в геноме будет по 2. Во втором примере геном уже корректно расшифрован и каждого нуклеотида в нём ровно по одному. В третьем и четвертом примерах корректно расшифровать геном невозможно. | |
![]()
|
|
E. Комментарии
поиск в глубину и подобное
Разбор выражений
реализация
Строки
*1700
Редкая статья в интернете обходится без возможности комментирования. Вот и на сайте, который написал Поликарп, у каждой статьи есть лента комментариев. Каждый комментарий на сайте Поликарпа — это непустая строка из строчных или прописных латинских букв. Комментарии имеют древовидную структуру, то есть у каждого комментария, кроме корневых (то есть комментариев самого верхнего уровня) есть ровно один родительский комментарий. При сохранении комментариев на жесткий диск Поликарп использует следующий формат. Каждый комментарий он записывает так: - сначала следует текст комментария;
- затем следует количество комментариев, для которых он является родительским (то есть тех, которые даны в ответ на этот комментарий);
- после этого следуют комментарии, для которых этот является родительским (запись комментариев происходит по такому же алгоритму).
Все элементы в записи выше разделяются единичными запятыми. Аналогично, комментарии первого уровня Поликарп записывает через запятую. Например, если комментарии имели вид:  то первый будет записан как «hello,2,ok,0,bye,0», второй как «test,0», а третий как «one,1,two,2,a,0,b,0». Вся ветка комментариев будет записана как: «hello,2,ok,0,bye,0,test,0,one,1,two,2,a,0,b,0». По заданной ветке комментариев в формате описанном выше выведите комментарии в другом формате: - сначала выведите d — максимальную глубину вложенности комментариев;
- затем выведите d строк, i-я из них соответствует комментариям вложенности i;
- для i-й строки выведите комментарии вложенности i в порядке их появления в записи Поликарпа, разделённые единичными пробелами.
Выходные данные Выведите комментарии в формате, описанном в условии. Для каждого уровня вложенности комментарии выводите в том же порядке, в котором они заданы во входных данных. Примечание Первый пример разобран в условии. | |
![]()
|
|
B. Санта-Клаус и проверка клавиатуры
реализация
Строки
*1500
Санта-Клаус решил разобрать свою клавиатуру, чтобы её почистить. После того, как он поставил все клавиши обратно, он с ужасом понял, что что-то не так: некоторые пары клавиш перепутаны между собой! Таким образом, Санта-Клаус подозревает, что каждая клавиша либо стоит на своём месте, либо заняла место другой, а та другая — на месте первой. Для того, чтобы убедиться в этом, найти ошибку и восстановить верное расположение, Санта-Клаус набрал текст своей любимой скороговорки, смотря только на надписи на клавиатуре. Вам даны любимая скороговорка Санта-Клауса и строка, которая получилась в результате набора. Определите, какие пары клавиш Санта-Клаус мог перепутать. Каждая клавиша должна принадлежать не более чем одной паре перепутанных клавиш. Выходные данные Если предположение Санта-Клауса неверно и клавиатура требует починки и её нельзя починить, поменяв местами буквы в нескольких непересекающихся парах, выведите одно число «-1» (без кавычек). Иначе в первой строке выведите число k (k ≥ 0) — количество пар букв, которые нужно поменять местами. Затем в следующих k строках выведите по две буквы, разделённые пробелом — буквы, которые необходимо поменять местами на клавиатуре. Все выведенные буквы должны быть различны. Если ответов несколько, выведите любой. Как пары, так и буквы в парах можно выводить в любом порядке. Каждая буква должна присутствовать не более чем в одной паре. Санта-Клаус считает, что клавиши расположены корректно, если он может набрать на клавиатуре текст своей любимой скороговорки без ошибок. | |
![]()
|
|
B. Стена Facetook
Разбор выражений
реализация
Строки
*1500
Facetook — широко известная социальная сеть. Недавно в ней появилась новая функция — стена с приоритетами. Эта функция позволяет сортировать всех ваших друзей по коэффициенту дружбы. Чем больше вы общаетесь с другом, тем больше будет его коэффициент дружбы. На коэффициент дружбы влияет 3 типа действий: - 1. человек X написал на стене человек Y ("X posted on Y's wall") — 15 очков;
- 2. человек X прокомментировал сообщение человека Y ("X commented on Y's post") — 10 очков;
- 3. человеку X понравилось сообщение человека Y ("X likes Y's post") — 5 очков.
X и Y — два различных имени. Каждое действие увеличивает коэффициент дружбы между X и Y (и наоборот) на данное количество очков (коэффициент дружбы между X и Y равен коэффициенту дружбы между Y и X). Вам дано n действий в формате, описанном выше. Выведите все различные имена, которые встречаются в списке действий, в отсортированном порядке в соответствие с коэффициентом дружбы с вами. Выходные данные Выведите m строк, где m — количество различных имен во входных данных (исключая вас). Каждая строка должна содержать ровно одно имя. Имена должны быть отсортированы в по убыванию коэффициента дружбы с вами (т. е. люди с большим коэффициентом дружбы должны идти раньше). Если два или больше человек имеют одинаковый коэффициент дружбы, выводите их в алфавитном (лексикографическом) порядке. Учтите, что нужно выводить все имена, присутствующие во входных данных (исключая вас), даже если человек имеет нулевой коэффициент дружбы с вами. Лексикографическое сравнение реализует оператор "<" в современных языках программирования. Строка a лексикографически меньше строки b, если либо a является префиксом b, либо существует такое i (1 ≤ i ≤ min(|a|, |b|)), что ai < bi, а для любого j (1 ≤ j < i) aj = bj, где |a| и |b| обозначают длины строк a и b соответственно. | |
![]()
|
|
C. Владик и чат
дп
Конструктив
Перебор
реализация
Строки
*2200
Недавно Владик нашел себе новое увлечение — написание ботов для социальных сетей. Ботов он хочет писать не простых, а с использованием машинного обучения. Поэтому он собрался обучать ботов на данных. Первым делом он решил выкачать t чатов. Владик написал скрипт, который должен был выкачать все чаты. По каким-то неизвестным причинам переписки выкачались неполными, а точнее у некоторых сообщений оказался неизвестен отправитель. Зато известно, что если пользователь отсылал несколько сообщений подряд, то они объединялись в одно. То есть нет двух подряд сообщений в одном чате с одним и тем же автором. Ещё известно, что отправитель сообщения не упоминал себя в сообщении. Владик хочет восстановить отправителя для каждого сообщения с неизвестным отправителем, так чтобы у любых двух последовательных сообщений одного чата были разные отправители, и никакой отправитель не упоминал бы себя в своих сообщениях. Он не придумал как это делать, поэтому просит вас помочь ему. Помогите Владику восстановить отправителей сообщений для каждого чата! Входные данные В первой строке входных данных находится единственное целое число t (1 ≤ t ≤ 10) — количество выкачанных чатов. Далее задано t чатов. Каждый чат задан в следующем формате. В первой строке каждого описания записано целое число n (1 ≤ n ≤ 100) — количество пользователей в чате. В следующей строке находятся n различных имен пользователей разделенных пробелом. Каждое имя пользователя состоит из прописных и строчных латинских букв и цифр, причем имя не может начинаться на цифру. Два имени пользователя различаются даже тогда, когда они различаются только регистром букв. Длина имени положительна и не превышает 10 символов. В следующей строке дано целое число m (1 ≤ m ≤ 100) — количество сообщений в чате. В следующих m строках находятся сообщения в одном из следующих форматов, по одному на строке: - <имя отправителя>:<текст сообщения> — формат сообщения, для которого известен отправитель. Имя отправителя должно присутствовать в списке имен пользователей чата.
- <?>:<текст сообщения> — формат сообщения, для которого неизвестен отправитель.
Текст сообщения может состоять из маленьких и больших латинских букв, цифр, '.' (точка), ',' (запятая), '!' (восклицательный знак), '?' (вопросительный знак) или ' ' (пробел). Текст сообщения не содержит пробелов в конце. Длина текста сообщения положительна и не превышает 100 символов. Определим, что значит упоминание пользователя в сообщении. Пользователь упоминается в сообщении, если он содержится в сообщении в качестве слова. Иными словами так, что соседний слева и соседний справа от имени символы либо отсутствуют либо не равны латинской букве и цифре. Например, сообщение «Vasya, masha13 and Kate!» может содержать упоминания пользователей «Vasya», «masha13», «and» и «Kate», но не «masha». Гарантируется, что в каждом чате, заданном во входных данных, для всех известных пользователей выполняется, что пользователь не упоминает сам себя в сообщении и нет двух подряд идущих сообщений с одним и тем же известным отправителем. Выходные данные Во входные данные следует вывести информацию о t чатах в следующем формате: Если нет ни одного способа восстановить неизвестных отправителей в чате, то для такого чата следует вывести «Impossible». Иначе следует вывести m сообщений в формате: <имя отправителя>:<текст сообщения> Если возможных ответов несколько, следует вывести любой. | |
![]()
|
|
E. Даша и циклическая таблица
битмаски
бпф
Деревья
Перебор
Строки
*2600
Даша увлекается всякими сложными головоломками — кубик Рубика 3 × 3 × 3, 4 × 4 × 4, 5 × 5 × 5 и тому подобное. На этот раз у неё есть циклическая таблица размера n × m клеток из строчных букв латинского алфавита. Каждая клетка таблицы имеет координаты (i, j) (0 ≤ i < n, 0 ≤ j < m). Цикличность этой таблицы заключается в том, что правее клетки (i, j) находится клетка  , а ниже находится клетка , а ниже находится клетка  . . Также у Даши есть шаблон. Шаблоном является нециклическая таблица размера r × c клеток. Каждая клетка шаблона является либо строчной буквой латинского алфавита либо символом вопроса. Каждая клетка шаблона имеет координаты (i, j) (0 ≤ i < r, 0 ≤ j < c). Задачей головоломки является определение всех позиций вхождения шаблона в циклическую таблицу. Определим позицию вхождения шаблона в циклическую таблицу. Позиция (i, j) циклической таблицы является позицией вхождения, если для каждого (x, y), что 0 ≤ x < r и 0 ≤ y < c, выполняется одно из двух условий: - Клетка шаблона с координатами (x, y) является символом вопроса.
- Клетка циклической таблицы с координатами
 равняется клетке шаблона с координатами (x, y). равняется клетке шаблона с координатами (x, y). Даша прекрасно справилась с решением этой головоломки, впрочем как и со всеми остальными головоломками. Посмотрим, сможете ли вы это сделать. Выходные данные Выведите n строк. Каждая из этих n строк должна содержать по m символов. Каждый из этих символов должен быть равен '0' или '1'. На позиции j строки i (0-индексация) выходных данных должен находиться символ '1', если позиция (i, j) является позицией вхождения, иначе символ '0'. | |
![]()
|
|
B. Польшар и Игра
Бинарный поиск
жадные алгоритмы
игры
сортировки
Строки
Структуры данных
*1100
Польшар играет со Врагошаром в некоторую игру. Правила просты. Игроки по очереди называют слова, называть слово, которое уже прозвучало, нельзя. Начинает Польшар. Проигрывает тот шар, который не может сказать ранее неназванного слова. Вам даны списки слов, известных Польшару и Врагошару. Определите, кто выиграет, если оба играют оптимально? Выходные данные В единственной строке выведите ответ: «YES», если выиграет Польшар, и «NO» иначе. Оба шара играют оптимально. Примечание В первом примере Польшар знает намного больше слов и выиграет без труда. Во втором примере если Польшар скажет вначале kremowka, то Врагошар не сможет использовать это слово. Единственное, что может сделать Врагошар — сказать wiedenska. Польшар скажет wadowicka и выиграет. | |
![]()
|
|
C. Фестиваль близко!
сортировки
Строки
Структуры данных
хэши
*1900
В это время года близок фестиваль и вы можете видеть празднующих людей повсюду в Гималаях. В Гималаях есть n школ. Школа i учит gi покемонов. В Гималаях существуют m различных типов покемонов, типы пронумерованы от 1 до m. На площадке фестиваля организован специальный эволюционный лагерь, в котором каждый покемон может эволюционировать. Тип покемона может измениться после того, как покемон эволюционирует, однако, если два покемона были одного типа до эволюционирования, то они будут одного типа после. Также, если два покемона были различных типов до эволюционирования, то они будут различными и после него. Возможно, что покемон не поменяет свой тип после эволюционирования. Формально, планом эволюционирования называется перестановка f чисел {1, 2, ..., m}, при этом f(x) = y означает, что покемон типа x эволюционирует в тип y. Руководители школ заинтригованы специальным лагерем, и все из них хотят эволюционировать всех своих покемонов. Устав Гималаев гласит, что в каждой школе количество покемонов каждого типа до эволюционирования должно быть равно количеству покемонов этого типа после эволюционирования. Руководители хотят найти количество различных планов эволюционирования, удовлетворяющих уставу Гималаев. Два плана эволюционирования f1 и f2 считаются различными, если как минимум один тип покемонов эволюционирует в разные типы в этих двух планов, то есть существует i такое, что f1(i) ≠ f2(i). Ваша задача — найти число различных планов эволюционирования таких, что если все покемоны во всех школах эволюционируют, количество покемонов каждого типа в каждой из школ останется таким же. Так как это число может быть большим, выведите остаток от его деления на 109 + 7. Выходные данные Выведите остаток от деления числа удовлетворяющих уставу планов эволюционирования на 109 + 7. Примечание В первом примере единственный корректный план эволюционирования выглядит так:  Во втором примере подходит любая перестановка чисел (1, 2, 3). В третьем примере есть два корректных плана:   В четвертом примере единственный корректный план эволюционирования выглядит так:  | |
![]()
|
|
D. Умение переводить
дп
жадные алгоритмы
Конструктив
математика
Строки
*2000
Александр учится переводить числа из десятичной системы счисления в любую другую, однако он не знает латинских букв, поэтому любую цифру он записывает только десятичным числом, то есть вместо буквы A он запишет число 10. Таким образом, переводя число 475 из десятичной системы в шестнадцатеричную, он получил 11311 (475 = 1·162 + 13·161 + 11·160). Александр жил спокойно, пока не попробовал перевести число обратно в десятичную систему счисления. Саша помнит, что работал с небольшими числами, поэтому просит найти минимальное десятичное число, при переводе которого в систему счисления с основанием n он получил бы число k. Выходные данные Выведите число x (0 ≤ x ≤ 1018) — ответ на задачу. Примечание В первом тесте 12 могло получится при переводе двух чисел в 13-ричную систему счисления 12 = 12·130 или 15 = 1·131 + 2·130. | |
![]()
|
|
C. Две строки
Бинарный поиск
Строки
хэши
*2100
Даны строки a и b. Требуется удалить наименьшее количество подряд идущих символов из строки b так, чтобы она стала подпоследовательностью строки a. Возможно, не придётся удалять ни одного символа, а, возможно, придётся удалить все символы из строки b, чтобы она стала пустой. Подпоследовательностью строки s называется любая такая строка, которую можно получить вычёркиванием из s нуля или более символов (не обязательно идущих подряд). Выходные данные В единственной строке выведите подпоследовательность строки a, получившуюся в результате удаления из строки b наименьшего количества подряд идущих символов. Если ответ содержит нулевое количество символов, выведите «-» (знак минус). Примечание В первом примере строки a и b вообще не имеют общих символов, поэтому наидлиннейшая строка, которую можно получить — пустая. Во втором примере ac является подпоследовательностью строки a, в то же время эту строку можно получить, удалив последовательно идущие символы cepted из строки b. | |
![]()
|
|
B. Обфускация кода
жадные алгоритмы
реализация
Строки
*1100
Костя очень любит писать контесты на Codeforces. Правда, его расстраивает, что его постоянно взламывают. Поэтому перед очередным контестом он решил обфусцировать свой код (то есть изменить его так, чтобы сделать менее читабельным). Обфускация происходит так. Сперва Костя смотрит на первый идентификатор в своей программе и заменяет все его вхождения на букву a, затем смотрит на следующий, который ещё не был заменён, и заменяет все его вхождения на букву b, и так далее. Костя — хороший программист, поэтому в его изначальной программе не бывает однобуквенных имён. Кроме того, в любой его программе не более 26 различных идентификаторов. Вам дан список идентификаторов из некоторой программы в том порядке, в котором они встречаются в программе, с удалёнными пробелами и символами переноса строки. Определите, могла ли эта программа получиться в результате обфускации Костей. Выходные данные Если данная программа могла получиться в результате обфускации Костей, выведите «YES» (без кавычек), иначе выведите «NO». Примечание В первом примере, один из возможных списков идентификаторов такой: «number string number character number string number». Обфускация такой программы выглядела бы следующим образом: - заменить все вхождения number на a, в результате получается «a string a character a string a»,
- заменить все вхождения string на b, в результате получается «a b a character a b a»,
- заменить все вхождения character на c, в результате получается «a b a c a b a»,
- все идентификаторы заменены, поэтому обфускация завершается.
| |
![]()
|
|
A. Махмуд и наибольшая не общая подпоследовательность
Конструктив
Строки
*1000
Когда Махмуд и Ехаб готовились к Международной олимпиаде по информатике, они встретились с задачей о наибольшей общей подпоследовательности. Они ее решили, а после этого Ехаб задал Махмуду другую задачу. Дано две строки a и b, найдите длину их наибольшей не общей подпоследовательности, то есть такой строки, которая является подпоследовательностью одной строки и не является подпоследовательностью другой. Подпоследовательность некоторой строки это последовательность букв, которая встречается в том же порядке в строке, не обязательно подряд. Например, строки «ac», «bc», «abc» и «a» являются подпоследовательностями строки «abc», а строки «abbc» и «acb» — нет. Пустая строка является подпоследовательностью любой строки, любая строка является подпоследовательностью ее самой. Выходные данные Если наибольшей не общей подпоследовательности не существует, выведите «-1». Иначе выведите длину наибольшей не общей подпоследовательности строк a и b. Примечание В первом примере можно выбрать «defgh» из строки b как наибольшую подпоследовательность b, которая не встречается в строке a. | |
![]()
|
|
C. Махмуд и сообщение
дп
жадные алгоритмы
Перебор
Строки
*1700
Махмуд написал сообщение s длины n. Он хочет послать его своему другу Моазу как подарок на день рождения, потому что тот очень любит строки. Он написал сообщение на магической бумаге, но был очень удивлен, когда увидел, что некоторые буквы исчезли после написания. А все потому, что эта магическая бумага не разрешает символу номер i латинского алфавита находится в строке длиной более чем ai. Например, если a1 = 2, то невозможно использовать символ 'a' на этой бумаге в строке длиной 3 или более. Строку «aa» возможно написать, в то время как строку «aaa» — нет. Махмуд решил разбить сообщение не несколько подстрок, и написать каждую из них на отдельном листке магической бумаги так, чтобы каждая подстрока удовлетворяла ограничению бумаги. Сумма длин подстрок должна быть равна n, и подстроки не должны накладываться друг на друга. Например, если a1 = 2, и Махмуд хочет отправить строку «aaa», он может разбить ее на подстроки «a» и «aa» и использовать 2 магических листка, или, например, на «a», «a» и «a» и использовать 3 магических листка бумаги. Он не может разбить сообщение на «aa» и «aa», т. к. сумма длин этих строк больше, чем n. Он может разбить сообщение на единственную подстроку, если она удовлетворяет ограничениям. Подстрока строки s — это строка, состоящая из нескольких последовательных букв из строки s, например, строки «ab», «abc» и «b» являются подстроками строки «abc», в то время как «acb» и «ac» — не являются. Любая строка является подстрокой самой себя. Пока Махмуд думал о том, как же разбить сообщение, Ехаб сказал ему, что существует много способов сделать это. После этого Махмуд задал вам три вопроса: - Сколько существует способов разбить сообщение на подстроки, при условии, что все подстроки удовлетворяют ограничениям магической бумаги, сумма их длин равна n, и они не накладываются? Вы должны вычислить ответ по модулю 109 + 7.
- Какая наибольшая длина может быть у какой-то подстроки какого-то корректного разбиения?
- На какое минимальное число подстрок можно разбить сообщение?
Два разбиения считаются различными, если множества позиций разбиений различаются. Например, разбиения «aa|a» и «a|aa» считаются различными разбиениями сообщения «aaa». Выходные данные Выведите три строки. В первой строке выведите число способов разбить сообщение на подстроки и удовлетворить всем ограничениям по модулю 109 + 7. Во второй строке выведите наибольшую длину подстроки среди всех подстрок всех возможных разбиений. В третьей строке выведите минимальное число подстрок, на которое можно разбить сообщение. Примечание В первом примере можно разбить сообщение тремя способами: Самые длинные подстроки — «aa» и «ab» длины 2. Наименьшее число подстрок — 2 в разбиениях «a|ab» и «aa|b». Заметьте, что «aab» — некорректное разбиение, потому что буква 'a' встречается в подстроке длины 3, в то время как a1 = 2. | |
![]()
|
|
K. Степан и гласные
*особая задача
реализация
Строки
*1600
Степан любит при написании слов повторять гласные буквы несколько раз, например, вместо слова «pobeda» он может написать «pobeeeedaaaaa». Сереже это не нравится, и он хочет написать программу, которая форматирует слова, написанные Степаном, и преобразует все подряд идущие повторяющиеся гласные в одну. Гласными буквами являются буквы «a», «e», «i», «o», «u» и «y». Есть исключения: если буквы «e» или «o» идут подряд ровно 2 раза, как в словах «feet» и «foot», то их не следует заменять на одну. Например, слово «iiiimpleeemeentatiioon» в отформатированном виде выглядит как «implemeentatioon». Сережа занят, поэтому вам предстоит написать программу форматирования за него. Выходные данные Выведите одну строку — слово, написанное Степаном, в отформатированном виде, согласно условию задачи. | |
![]()
|
|
A. Серийный убийца
Перебор
реализация
Строки
*900
Наш любимый детектив Шерлок занят поиском серийного убийцы, который убивает одного человека каждый день. Используя свой дедуктивный метод, он узнал, что у киллера есть стратегия для выбора следующей жертвы. В первый день у убийцы есть две потенциальных жертвы. Он выбирает одну из них, убивает ее и заменяет ее новой потенциальной жертвой. Та же процедура повторяется каждый день. Таким образом, каждый день у убийцы есть две потенциальных жертвы, из которых он выбирает. Шерлок знает имена потенциальных жертв в первый день. Кроме этого, он знает, кого убили в каждый день и кто — новая потенциальная жертва, заменившая убитую. Вам необходимо вычислить для каждого дня две потенциальные жертвы, из которых киллер выбирал в этот день, ведь Шерлок надеется найти в этой информации какую-то закономерность. Выходные данные Выведите n + 1 строку, i-я строка должна содержать имена двух людей, из которых убийца выбирает жертву в i-й день. (n + 1)-я строка должна содержать два имени, из которых будет выбрана следующая жертва. В каждой строке два имени могут быть выведены в любом порядке. Примечание В первом примере изначально потенциальные жертвы это ross и rachel. - После дня 1: ross убит, и появляется joey.
- После дня 2: rachel убит, и появляется phoebe.
- После дня 3: phoebe убит, и появляется monica.
- После дня 4: monica убит, и появляется chandler.
| |
![]()
|
|
D. Облако хештегов
Бинарный поиск
жадные алгоритмы
реализация
Строки
*1800
Вася ведёт публичную страницу организации «Мышь и клавиатура», где постоянно публикует различные новости из мира спортивного программирования. Для удобства поиска по новостям Вася прикрепляет к каждой из них список хештегов. В данной задаче хештегом называется строка, состоящая из маленьких букв английского алфавита и ровно одного символа '#', расположенного в начале строки. Длиной хештега будем называть количество символов в нём, без учёта символа '#'. Начальство Васи распорядилось, что хештеги у каждой новости должны быть расположены в лексикографическом порядке (для пояснения смотрите примечания). Поскольку Васе не хочется менять порядок хештегов в уже написанной новости, он решил удалить у некоторых хештегов некоторый суффикс (какое-то количество последних символов), при этом можно даже удалить весь текст хештега, оставив только символ '#', но сам символ '#' удалять нельзя. Из всех возможных вариантов такого удаления Вася хочет выбрать тот, в котором суммарно будет удалено минимальное количество символов. Если и таких вариантов несколько, то разрешается использовать любой из них. Выходные данные Выведите полученные после удаления символов хештеги. Примечание Слово a1, a2, ..., am длины m лексикографически не превосходит слова b1, b2, ..., bk длины k, если выполняется одно из двух: - либо в первой позиции i, такой что ai ≠ bi, символ ai идёт раньше по алфавиту, чем символ bi, то есть в первой различающейся позиции символ слова a меньше символа слова b;
- либо, если такой позиции i нет, и m ≤ k, то есть второе слово начинается с первого либо совпадает с ним
Про последовательность слов говорят, что они идут в лексикографическом порядке, если каждое слово в нём (кроме последнего) лексикографически не превосходит следующего за ним. Для слов, состоящих из маленьких латинских букв, лексикографический порядок совпадает с алфавитным порядком расположения слов в словаре. Хештег, состоящий только из символа '#', лексикографически не больше любого другого хештега. Поэтому в третьем примере мы не можем оставить два первых слова и сократить два вторых. | |
![]()
|
|
A. Игра на строке
Бинарный поиск
жадные алгоритмы
Строки
*1700
Любимое занятие Насти — вычеркивать буквы из слова, чтобы получилось другое слово. Но получается это у нее довольно плохо, потому что она еще маленькая. Поэтому ей всегда помогает ее старший брат Сергей. Сергей дал Насте слово t и хочет, чтобы из него получилось слово p. Настя начинает вычеркивать буквы в некотором порядке (последовательно, строго в этом порядке), который задан перестановкой номеров букв слова t: a1... a|t|. Длину слова x мы обозначаем |x|. Заметим, что после вычеркивания буквы нумерация не меняется. Например, если t = «nastya» и a = [4, 1, 5, 3, 2, 6] тогда вычеркивания образуют следующую последовательность слов: «nastya»  «nastya» «nastya»  «nastya» «nastya»  «nastya» «nastya»  «nastya» «nastya»  «nastya» «nastya»  «nastya». «nastya». Этот порядок изначально известен Сергею. Его задача состоит в том, чтобы в некоторый момент времени остановить сестру и закончить вычеркивание самому, получив после этого слово p. Так как Насте нравится это занятие, Сергей хочет остановить ее как можно позже. Ваша задача — сообщить, сколько букв может вычеркнуть Настя до того, как ее остановит Сергей. Гарантируется, что слово p можно получить вычеркиванием букв из t. Выходные данные Выведите одно число — максимальное число букв, которые может вычеркнуть Настя. Примечание В первом примере последовательность вычеркивания букв Настей выглядит так: «ababcba»  «ababcba» «ababcba»  «ababcba» «ababcba»  «ababcba» «ababcba» Продолжать вычеркивать Настя не может, потому что из «ababcba» нельзя получить «abb». Таким образом, Настя может вычеркнуть только три буквы в свой последовательности. | |
![]()
|
|
C. Петрович — полиглот
Деревья
Перебор
поиск в глубину и подобное
снм
Строки
хэши
*2500
Петрович обожает изучать новые языки, но самое любимое его увлечение — составление своих собственных. Языком Петрович называет множество слов, а словом — последовательность маленьких букв латинского алфавита. Каждое утро Петрович составляет свой новый язык. Хранить все языки в явном виде очень сложно, поэтому Петрович придумал веник — специальную структуру данных для хранения языка, представляющую собой подвешенное дерево, на ребрах которого написаны буквы. Перед придумыванием языка веник представляет одну вершину — корень. При добавлении нового слова в язык Петрович встает в корень веника и обрабатывает буквы слова по одной. Пусть Петрович стоит в вершине u. Если из u есть ребро, на котором написана текущая буква, он переходит по нему. Иначе же, Петрович добавляет ребро из u в новую вершину v, пишет на нем текущую букву и переходит по этому ребру. Размером веника Петрович называет количество вершин в нем. Вечером, приходя со смены, Петрович не может понять язык, придуманный утром: он ему кажется слишком сложным. Тогда Петрович старается упростить свой язык. Упрощением языка Петрович называет удаление букв из некоторых слов языка. Формально, Петрович фиксирует некоторое целое положительное число p, берет все слова, содержащие хотя бы p букв, и выкидывает из каждого из них букву с номером p. Буквы в слове Петрович предпочитает нумеровать, начиная с 1. Петрович считает, что при упрощении языка хотя бы одно слово должно измениться, то есть в языке должно быть хотя бы слово с длиной хотя бы p. Так как Петрович стремится сделать язык, придуманный утром, как можно проще, он старается подобрать число p таким образом, чтобы минимизировать размер веника, в котором он будет хранить язык. Петровичу надоело заниматься одним и тем же каждый вечер, поэтому он обратился за помощью к вам. Напишите программу, которая будет находить минимальный размер веника, который может получиться в результате упрощения языка, придуманного Петровичем, и число p, которое нужно выбрать, чтобы получить такой размер. Выходные данные В первой строке выведите минимальный возможный размер веника, который может получиться в результате упрощения языка. Во второй строке выведите число p, которое следует выбрать Петровичу для получения минимального размера. Если таких чисел p несколько, выведите минимальное из них. Примечание 
Веник из второго примера может быть составлен из множества слов «piece», «of», «pie», «pretty», «prefix». После упрощения языка с p = 2 получается язык из слов «pece», «o», «pe», «petty», «pefix». Этот язык и задаёт веник минимального возможного размера. | |
![]()
|
|
A. Хайку
реализация
Строки
*800
Хайку — жанр традиционной японской лирической поэзии. Стихотворение хайку состоит из 17 слогов, которые разбиты на три фразы, содержащие 5, 7 и 5 слогов соответственно (первая фраза должна содержать ровно 5 слогов, вторая — ровно 7 слогов, а третья — ровно 5). Мастерством хайку считается в этих трех фразах описать момент. В маленьком стихотворении каждое слово на счету, поэтому для хайку характерна символичность — каждое слово приобретает особую весомость, значимость. Сказать многое малым количеством слов — главный принцип хайку. В данной задаче для простоты мы будем считать, что количество слогов в фразе равно количеству гласных букв в ней. Гласными буквами считаются только «a», «e», «i», «o» и «u». Имеются три фразы некоторого стихотворения. Определите — являются они хайку или нет. Выходные данные Выведите «YES» (без кавычек) если стихотворение является хайку. Иначе выведите «NO» (тоже без кавычек). | |
![]()
|
|
D. Иннокентий и футбольная лига
2-sat
графы
жадные алгоритмы
кратчайшие пути
реализация
Строки
*1900
Иннокентий — президент только что созданной футбольной лиги в Байтландии. Первая задача, которая стоит перед ним — обеспечить трансляцию всех матчей лиги по телевидению. Как вы, возможно, знаете, во время футбольного матча на экране отображаются сокращенные названия команд и текущий счет. Конечно, будет странно, если сокращенные названия клубов соперников совпадут, поэтому Иннокентий должен придумать. как сократить название каждого из клубов лиги до трех букв так, чтобы у всех команд лиги были разные названия. Название каждого клуба состоит из двух слов: названия команды и города, в котором располагается клуб, например, «DINAMO BYTECITY». Иннокентий не хочет сильно искажать название, поэтому он хочет выбрать сокращенное название для каждого из клубов таким образом, чтобы: - либо сокращенное название клуба совпадало с первыми тремя буквами названия команды, например, для вышеприведенный команды это «DIN»,
- либо первые две буквы сокращенного названия клуба совпадали с первыми двумя буквами названия команды, а третья — с первой буквой города команды. Например, для вышеприведенный команды это «DIB».
Кроме этого, если для какой-то команды x выбран второй вариант названия, то не должно быть команды, у которой выбран первый вариант сокращенного названия, совпадающий с первым вариантом названия команды x. Например, если сокращенное название вышеприведенной команды это «DIB», то никакая команда, у которой выбран первый вариант сокращенного названия, не должна иметь сокращенного названия «DIN». При этом возможно, что какая-то команда получит название «DIN», где «DI» — первые две буквы названия команды, а «N» — первая буква города. Конечно, никакие две команды не должны иметь одинакового сокращенного названия. Помогите Иннокентию выбрать сокращенное название для каждой из команд. Если это невозможно, сообщите об этом. Если возможных ответов несколько, Иннокентия устроит любой из них. Если для некоторой команды совпадают оба варианта сокращенного названия, то Иннокентий все равно будет формально считать, что выбран только один из этих вариантов. Выходные данные Если выбрать сокращенные названия, удовлетворив требованиям Иннокентия, невозможно, выведите единственную строку «NO». Иначе в первую строку выведите «YES». Далее выведите n строк, в каждой строке выведите выведите сокращенное название очередного клуба. Выводите клубы в том же порядке, в каком они заданы во входных данных. Если возможных ответов несколько, выведите любой. Примечание В первом примере можно выбрать первый вариант названия для обеих команд. Во втором примере невозможно подобрать названия, т. к. по условию нельзя у одной команды выбрать первый вариант названия, а у второй выбрать второй вариант названия, если первые варианты названий у этих команд совпадают. В третьем примере можно выбрать вторые варианты названий у первых двух команд, и первый вариант — у третьей команды. В четвертом примере обратите внимание на то, что разрешается, чтобы выбранное название некоторой команды x совпадало с первым вариантом названия y, если первый вариант названия x не совпадает с первым вариантом названия y. | |
![]()
|
|
A. Антон и многогранники
реализация
Строки
*800
Любимые геометрические фигуры Антона — правильные многогранники. Напомним, что правильных многогранников всего пять видов: - Тетраэдр. У тетраэдра 4 треугольных грани.
- Куб. У куба 6 квадратных граней.
- Октаэдр. У октаэдра 8 треугольных граней.
- Додекаэдр. У додекаэдра 12 пятиугольных граней.
- Икосаэдр. У икосаэдра 20 треугольных граней.
Все пять видов многогранников показаны на рисунке ниже:  У Антона есть целая коллекция из n многогранников. Однажды ему стало интересно, сколько суммарно граней у всех фигур в его коллекции. Помогите Антону найти это число! Выходные данные Выведите одно целое число — суммарное число граней у всех многогранников в коллекции Антона. Примечание В первом примере у Антона есть один икосаэдр, один куб, один тетраэдр и один додекаэдр. У икосаэдра 20 граней, у куба — 6, у тетраэдра — 4 и, наконец, у додекаэдра — 12. Итого 20 + 6 + 4 + 12 = 42 грани. | |
![]()
|
|
D. Бог рэпа
Деревья
поиск в глубину и подобное
Строки
Структуры данных
хэши
*3400
Рик влюблен в Юнити. Но и мистер Мисикс также любит Юнити. Поэтому Рик и мистер Мисикс «любовные соперники». Юнити нравится рэп, поэтому было решено, что они должны участвовать в рэп игре (баттле), чтобы выбрать лучшего. Рик слишком ботаник, поэтому вместо этого он собирается сделать свой текст используя его оригинальный алгоритм на лирике песни «Rap God».  Его алгоритм немного сложен. Он делает дерево с n вершинами, пронумерованными от 1 до n. На каждом ребре дерева написана маленькая латинская буква. Он определил str(a, b), как строку сформированную написанием всех букв, одну за другой, на кратчайшем пути от a до b (длина строки равна расстоянию от a до b). Заметьте, что str(a, b) это, записанная задом наперед, строка str(b, a). Также строка str(a, a) является пустой строкой. Чтобы сделать лучший текст, ему необходимо отвечать на некоторые запросы, но он не ученый-компьютерщик и не может ответить на эти запросы, поэтому он просит вас помочь ему. Каждый запрос характеризуется двумя вершинами x и y (x ≠ y). Ответом на этот запрос является кол-во таких вершин z, что z ≠ x, z ≠ y и str(x, y) лексикографически больше, чем str(x, z). Строка x = x1x2...x|x| лексикографически больше, чем строка y = y1y2...y|y|, если |x| > |y| и x1 = y1, x2 = y2, ..., x|y| = y|y|, или существует такое r (r < |x|, r < |y|), что x1 = y1, x2 = y2, ..., xr = yr и xr + 1 > yr + 1. Символы сравниваются, как их ASCII коды (или как их позиции в алфавите). Помогите Рику заполучить девушку. Выходные данные Для каждого запроса выведите ответ в одну строку. Примечание Дерево для первого теста из условия:  Дерево для второго теста из условия:  В этом тесте: - str(8, 1) = poo
- str(8, 2) = poe
- str(8, 3) = po
- str(8, 4) = pop
- str(8, 5) = popd
- str(8, 6) = popp
- str(8, 7) = p
Поэтому для первого запроса  и для третьего запроса и для третьего запроса  это ответ. это ответ. | |
![]()
|
|
C. Скучные строки
дп
жадные алгоритмы
Строки
Структуры данных
хэши
*1800
После того как лиса Кейл вышла из автобуса, она обнаружила, что ошиблась маршрутом. Теперь она была в каком-то странном и незнакомом городе. К счастью, ей вскоре повстречался ее друг — бобром Таро. Лиса поинтересовалась у бобра, как ей пройти к замку. Однако, бобер ответил ей лишь строкой s, которую лиса Кейл постаралась запомнить. У Кейл — особенные отношения со строками. Например, n строк b1, b2, ... , bn она считает скучными. По этой причине ей никогда не удается запомнить строку, которая содержит хотя бы одну скучную в качестве подстроки. Таким образом, лиса Кейл опасается, что ей не удастся запомнить строку s целиком, а получится только запомнить некоторую ее подстроку (такую, которая не содержит скучных слов). Ваша задача помочь Кейл, найдите наидлиннейшую подстроку s такую, что подстрока не содержит ни одного скучного слова. Выходные данные В первую строку выведите два разделенных пробелом целых числа len и pos, где len — длина искомой наидлиннейшей подстроки, а pos — индекс первого (самого левого) символа из s в искомой подстроке (нумерация от 0). Число pos должно находиться в границах от 0 до |s| - len включительно, где |s| обозначает длину строки s. Если решений несколько, то выведите любое. Примечание В первом примере искомой подстрокой является «traight_alon». Во втором примере искомой подстрокой является пустая строка. В третьем примере искомой подстрокой является либо «nagio» либо «oisii». | |
![]()
|
|
C. Минимальная строка
жадные алгоритмы
Строки
Структуры данных
*1700
На день рождения Пете подарили строку s длиной до 105 символов. Он взял еще две пустые строки t и u и решил сыграть в игру. По правилам в игре допускается два варианта ходов: - Изъять символ из начала строки s и приписать его в конец строки t.
- Изъять символ из конца t и приписать его в конец строки u.
В результате Петя хочет, чтобы строка u была лексикографически минимальна, а s и t — пусты. Напишите программу, которая поможет Пете выиграть в игру. Выходные данные Выведите полученную строку u. | |
![]()
|
|
A. Майк и палиндром
Конструктив
Перебор
Строки
*1000
У Майка имеется строка s состоящая только из маленьких букв латинского алфавита. Он хочет изменить ровно один символ из строки так, чтобы результирующая строка стала палиндромом. Палиндром это строка, которая читается в две стороны одинаково. Например строки «z», «aaa», «aba», «abccba» палиндромы, а строки «codeforces», «reality», «ab» нет. Выходные данные Выведите «YES» (без кавычек), если Майк может изменить ровно один символ так, что результирующая строка станет палиндромом, или выведите «NO» (без кавычек) иначе. | |
![]()
|
|
B. Майк и строки
дп
Перебор
Строки
*1300
У Майка есть n строк s1, s2, ..., sn. Каждая строка состоит из маленьких букв латинского алфавита. За один ход он может выбрать строку si, удалить первый символ и вставить его в конец этой строки. Например, если у него имеется строка «coolmike», то за один ход он может преобразовать эту строку в строку равную «oolmikec». Теперь Майк задается вопросом: какое минимальное количество ходов необходимо сделать, чтобы все строки стали равными. Выходные данные Выведите минимальное количество ходов, которое необходимо сделать, чтобы все строки стали равными, или выведите - 1, если решения не существует. Примечание В первом тестовом примере оптимальным образом будет преобразовать все строки в строку «zwoxz». | |
![]()
|
|
A. Поезд и Петя
Строки
*1200
Пете очень интересно ездить в поездах. Так интересно, что он засыпает. Однажды летом мальчик Петя ехал на поезде из города А в город Б и, как обычно, спал. Потом он проснулся, начал смотреть в окно и заметил, что на каждой станции есть флаг определенного цвета. Мальчик начал запоминать последовательность цветов флагов, которые он видел. Однако вскоре он опять уснул. К сожалению, его покой длился не долго и он вновь проснулся и продолжил запоминать цвета. Потом он уснул, и в этот раз сон длился до конца поездки. Уже на вокзале он рассказал родителям о своем занятии и выписал две последовательности цветов, которые увидел в первый и второй период бодрствования, соответственно. Родители знают, что Петя любит фантазировать. Они предоставили вам список цветов флагов станций, которые последовательно посещает поезд по пути из А в Б, и попросили узнать, мог ли Петя увидеть эти последовательности на пути из А в Б, или из Б в А. Помните, что у Пети было ровно два периода бодрствования. Цвета родители обозначили строчными латинскими буквами. Одинаковые буквы обозначают одинаковые цвета, а разные буквы — разные цвета. Выходные данные Выведити одно из четырех слов без кавычек: - «forward» — если Петя мог увидеть такие последовательности только на пути из А в Б;
- «backward» — если Петя мог увидеть такие последовательности только на пути из Б в А;
- «both» — если Петя мог увидеть такие последовательности как на пути из А в Б, так и на пути из Б в А;
- «fantasy» — если Петя не мог увидеть такие последовательности.
Примечание Считается, что поезд все время движется, так что один и тот же флаг невозможно увидеть два раза. На станциях А и Б флагов нет. | |
![]()
|
|
B. Весомые Клавиши
жадные алгоритмы
Конструктив
Строки
*900
Вы нашли странную функцию f. Функция принимает две строки s1 и s2. Эти строки могут состоять только из строчных букв латинского алфавита, а их длины должны совпадать. Результатом функции f будет другая строка той же длины. Символ i результата равен минимальному из i-го символа s1 и i-го символа s2. Например, f(«ab», «ba») = «aa», а f(«nzwzl», «zizez») = «niwel». Вы нашли две строки x и y совпадающей длины, состоящие только из строчных букв латинского алфавита. Найдите любую строку z такую, что f(x, z) = y, или выведите -1, если такой строки z не существует. Выходные данные Если не существует строки z такой, что f(x, z) = y, выведите -1. Иначе выведите строку z такую, что f(x, z) = y. Если существует несколько возможных ответов, выведите любой из них. Строка z должна быть той же длины, что и строки x и y и состоять только из строчных букв латинского алфавита. Примечание Первый пример разобран в условии. Другое возможное решение во втором примере — «zizez» В третьем примере нет решений. Другими словами, не существует строки z такой, что f(«ab», z) = «ba». | |
![]()
|
|
G. Ложные Новости (простая)
реализация
Строки
*800
Поскольку сегодня первое апреля, Хайди подозревает, что новости, о которых она сегодня читает, являются ложными. Она не хочет выглядеть глупо перед другими участниками. Она знает, что новость является ложной, если в ней содержится строка «heidi» в качестве подпоследовательности. Помогите Хайди определить, является ли данный фрагмент новости истинным, но, пожалуйста, будьте предельно осторожны... Выходные данные Выведите «YES» (без кавычек), если строка s содержит последовательность «heidi» в качестве подпоследовательности. В противном случае, выведите «NO» (без кавычек). Примечание Строка s содержит другую строку p как подпоследовательность, если возможно удалить некоторое (возможно нулевое) количество символов из s и получить p. | |
![]()
|
|
H. Ложные Новости (средняя)
Конструктив
Строки
*2200
Спасибо за помощь, Хайди уверена, что никто ее не одурачит. Она решила отправить несколько ложных новостей на страницу HC2 в Facebook. Однако она хочет иметь возможность сообщить комитету HC2 о том, что заметка ложная, используя скрытую секретную фразу в заметке. Чтобы сделать этот метод безошибочным, она хочет, чтобы фраза появлялась в записи n раз. Она просит вас разработать запись (строку) s и скрытую фразу p, так что p появляется в s как подпоследовательность ровно n раз. Выходные данные Выведите две непустые строки s и p, разделенных пробелом. Каждая строка должна состоять из букв (a-z и A-Z: допускаются как строчные, так и прописные буквы) и иметь длину не более 200. Число вхождений p в s в качестве подпоследовательности должно быть точно n. Если существует несколько возможных решений, выведите любое из них. Гарантируется, что существует хотя бы одно решение. Примечание Вхождение p в качестве последовательности s следует рассматривать как набор позиций s таких, что буквы в этих позициях в порядке p. Количество вхождений является числом таких множеств. Например, ab появляется 6 раз как последовательность в aaabb, для следующих наборов позиций: {1, 4}, {1, 5}, {2, 4}, {2, 5}, {3, 4}, {3, 5} (то есть мы должны выбрать одну из букв a и одну из букв b). | |
![]()
|
|
G. Гимн Берляндии
дп
Строки
*2300
У Берляндии невероятно богатая и славная история. Чтобы повысить уровень осведомленности о ней среди молодого поколения, Король Берляндии распорядился сочинить гимн. Несмотря на то, что в прошлом у Берляндии было огромное множество достойных побед, есть одна наиболее важная. Король желает упомянуть ее в гимне как можно большее количество раз. Он уже сочинил немалую часть гимна, осталось лишь заполнить некоторые места, которые ему никак не удаются. Король просит вас помочь с его работой. Гимн Берляндии — это строка s, состоящая из не более чем 105 строчных латинских букв и знаков вопроса. Самая важная победа — это строка t, состоящая из не более чем 105 строчных латинских букв. Необходимо заменить все знаки вопроса строчными латинскими буквами так, чтобы максимизировать количество вхождений строки t в s. Обратите внимание, что вхождения строки t в s могут пересекаться. В третьем примере рассмотрен такой случай. Выходные данные Выведите максимальное количество вхождений строки t, которое можно достичь, заменив все знаки вопроса в строке s не строчные латинские буквы. Примечание В первом примере полученная строка s — "winlosewinwinlwinwin" Во втором примере полученная строка s — "glorytoreorand". Последняя буква в строке может быть выбрана произвольно. В третьем примере вхождения строки t пересекаются между собой. Строка s с максимальным количеством вхождений t — "abcabcab". | |
![]()
|
|
B. Форматирование последовательности
реализация
Строки
*1700
Поликарп очень аккуратен. Даже числовые последовательности он набирает аккуратно, не то что его одноклассники. Если он видит последовательность, в которой нет пробела после запятой, стоят два пробела подряд или присутствует еще какая-либо неаккуратность, он тут же начинает ее исправлять. Например, запись «1,2 ,3,..., 10» он исправит на «1, 2, 3, ..., 10». В этой задаче задана строка s, которая составлена последовательной записью частей, каждая из которых может быть: - положительным целым числом произвольной длины (лидирующие нули недопустимы),
- символом «запятая» («,»),
- символом «пробел» (« »),
- многоточием («...» — т.е. тремя точками, записанными подряд).
Поликарп хочет добавлением и удалением пробелов в строке s добиться того, чтобы: - после каждой запятой шел ровно один пробел (если запятая является последним символом строки, то это правило к ней не применимо),
- перед каждым многоточием был ровно один пробел (если многоточие начинает строку, то это правило к нему не применимо),
- если два подряд идущих числа разделялись исключительно пробелами (одним или более), то следует оставить ровно один из них,
- других пробелов быть не должно.
Автоматизируйте труд Поликарпа — напишите программу, которая будет обрабатывать заданную строку s. Выходные данные Выведите строку s после обработки. Вывод вашей программы должен посимвольно совпадать с ожидаемым ответом. Вывод строки допустимо заканчивать как с заключительным переводом строки, так и без него. | |
![]()
|
|
C. Пылкий поток любви
дп
Перебор
Строки
*1600
День рождения Надеко приближается! Так как она украсила комнату для вечеринки, длинная гирлянда из бумажных гвоздик была повешена на видную часть стены. Койому, брату Надеко, она понравится! Надеке все еще не нравится гирлянда, поэтому она решила ее снова улучшить. Гирлянда состоит из n частей, пронумерованных слева направо от 1 до n, и i-я из этих частей имеет цвет si, обозначенный строчной латинской буквой. Надеко перекрасит не более m частей в любой цвет (по-прежнему обозначенный строчной латинской буквой). После этого, она найдет все подотрезки, состоящие только из частей цвета c — любимого цвета Койоми — и будет называть длину самого большого такого подотрезка койомностью гирлянды. Пусть, например, гирлянда имеет цвета «kooomo», а любимый цвет Койоми — «o». Среди всех подотрезков, содержащих только цвет «o», самым длинным является «ooo», его длина равна 3. Поэтому койомность этой гирлянды равна 3. Проблема в том, что Надеко не уверена в любимом цвете Койоми, поэтому она постоянно меняет свои планы на предстоящую работу. У нее есть q планов, каждый определяется парой из числа mi и строчной буквы ci, значения которых были объяснены раньше. Вам предстоит найти максимальную койомность, достижимую после изменения гирлянды в соответствии с каждым из планов. Выходные данные Выведите q строк: для каждого плана выведите одно целое число на отдельной строке — максимально возможную койомность, достижимую после изменения гирлянды в соответствии с этим планом. Примечание В первом примере есть три плана: - В первом плане можно перекрасить не более чем 1 часть. Перекрасив часть цвета «y» в цвет «o», получим «kooomi», койомность которой равна 3 — максимально возможной;
- Во втором плане можно перекрасить не более чем 4 части, получив гирлянду «oooooo», койомность которой равна 6;
- В третьем случае можно перекрасить не более 4 частей, два способа «mmmmmi» и «kmmmmm» являются оптимальными с койомностью, равной 5.
| |
![]()
|
|
B. Решение кроссворда
Перебор
реализация
Строки
*1000
Вскоре Лехе наскучило считать наибольшие общие делители двух факториалов. Поэтому он решил заняться разгадыванием кроссвордов. Как известно, это очень интересное занятие, но может быть и очень сложным время от времени. В ходе разгадывания одного из кроссвордов Лехе пришлось решить несложную задачу. А сможете ли вы? У Лехи есть две строки s и t. Теперь хакер хочет изменить строку s так, чтобы она встречалась в t в качестве подстроки. Все изменения должны иметь вид: Леха выбирает некоторую позицию в строке s и заменяет символ в этой позиции на знак вопроса «?». Хакер уверен, что знак вопроса «?» при сравнении может играть роль произвольного символа. Например, если в результате он получит строку s=«ab?b», то она встретится в t=«aabrbb» как подстрока. Гарантируется, что длина строки s не превосходит длины строки t. Помогите хакеру Лехе заменить в s минимальное количество символов на знаки вопроса «?» так, чтобы результат встречался в t в качестве подстроки. Символ «?» при сравнении следует считать равным любому другому символу. Выходные данные В первую строку выведите целое число k — минимальное количество символов, которые нужно заменить. Во второй строке выведите k различных целых чисел — позиции букв в строке s, которые нужно заменить. Позиции выводите в любом порядке. Если ответов несколько, разрешается вывести любой из них. Нумерация позиций начинается с единицы. | |
![]()
|
|
F. Сжатие строки
дп
Строки
строковые суфф. структуры
хэши
*2400
Иван хочет написать письмо своему другу. Письмо — строка s, состоящая из строчных латинских букв. К сожалению, как только Иван начал писать письмо, он понял, что оно слишком длинное, и писать его целиком придётся очень долго. Поэтому он хочет написать сжатую версию строки s вместо самой строки. Сжатая версия строки s — последовательность строк c1, s1, c2, s2, ..., ck, sk, где ci — десятичная запись числа ai (без лидирующих нулей), а si — некоторая строка из строчных латинских букв. Если Иван запишет строку s1 ровно a1 раз, потом s2 ровно a2 раз, и так далее, у него получится строка s. Длина сжатой версии равна |c1| + |s1| + |c2| + |s2|... |ck| + |sk|. Среди всех сжатых версий Иван хочет выбрать такую, что её длина минимальна. Помогите Ивану определить минимально возможную длину. Выходные данные Выведите одно целое число — минимальную длину сжатой версии строки s. Примечание В первом примере Иван выберет следующую версию: c1 — 10, s1 — a. Во втором примере Иван выберет следующую версию: c1 — 1, s1 — abcab. В третьем примере Иван выберет следующую версию: c1 — 2, s1 — c, c2 — 1, s2 — z, c3 — 4, s3 — ab. | |
![]()
|
|
A. Восстановление строки
жадные алгоритмы
сортировки
Строки
Структуры данных
*1700
У Ивана была строка s, состоящая из строчных букв латинского алфавита. Но его подруга Юля решила пошутить над ним и спрятала строку s. Иван решил, что не будет искать строку, а просто сделает новую. Иван помнит о строке s следующую информацию. Он помнит, что строка ti встречается в строке s количество раз ki или больше, а также помнит ровно ki позиций, с которых начинается вхождение строки ti в строку s — это позиции xi, 1, xi, 2, ..., xi, ki. При этом количество строк ti, про которые помнит Иван, равно n. Перед вами стоит задача восстановить лексикографически минимальную строку s такую, что она удовлетворяет всей информации, которую помнит Иван. Как строки ti, так и строка s могут содержать только строчные буквы латинского алфавита. Выходные данные Выведите лексикографически минимальную строку, которая удовлетворяет всей информации, которую помнит Иван. | |
![]()
|
|
B. Раскладки клавиатуры
реализация
Строки
*800
В Берляндии распространены две раскладки для клавиатур, которые различаются только порядком следования букв на клавишах. Все остальные клавиши совпадают. В Берляндии используют алфавит, который содержит 26 букв и совпадает с английским. Вам будут заданы две строки по 26 букв в каждой — все клавиши первой и второй раскладки в порядке слева направо сверху вниз. Также вам будет задан набранный текст, который состоит из прописных и строчных букв английского алфавита и цифр. Известно, что он был набран по ошибке в первой раскладке, хотя хотели набрать его во второй. Выведите этот текст, если бы использовалась вторая раскладка, а не первая при его наборе. Так как все клавиши кроме буквенных совпадают, то регистр букв и символы отличные от букв остаются неизменными. Выходные данные Выведите текст, если бы он был набран во второй раскладке. | |
![]()
|
|
B. Петя и ЕГЭ
реализация
Строки
*1600
Настали тяжелые времена. Сегодня Пете нужно набрать на экзамене по информатике 100 баллов. Все задачи на экзамене Пете кажутся простыми, но он боится, что не успеет сделать одну из них за такой маленький промежуток времени, поэтому он обратился к вам за помощью. В условии даётся шаблон (строка, состоящая из строчных латинских букв, символов «?» и «*»). Известно, что символ «*» встречается в шаблоне не более одного раза. Также в условии даны n строк-запросов, и для каждой необходимо определить, подходит ли она под данный шаблон, или нет. Все было бы хорошо, но специальные символы в шаблоне в этой задаче действуют не так, как обычно! Строка подходит под шаблон, если можно в шаблоне заменить каждый из символов «?» на одну хорошую строчную латинскую букву, а символ «*» (если он есть) — на любую, в том числе пустую, строку из плохих строчных латинских букв так, чтобы результат совпал со строкой. В условии также даны буквы, считающиеся хорошими. Плохими являются все остальные буквы латинского алфавита. Выходные данные Выведите n строк: в i-й строке необходимо вывести «YES», если i-я строка-запрос удовлетворяет шаблону, и «NO» в противном случае. Вы можете выводить каждую из букв в любом регистре. Примечание Объяснение первого теста. Символ «?» можно заменять на хорошие буквы «a» и «b», поэтому видно, что на первый запрос ответ «YES», а на второй запрос ответ «NO», потому что третья буква не может совпасть. Объяснение второго теста. - Первый запрос: «NO», потому что символ «*» можно заменять на строку из плохих букв, а единственный способ совпасть со строкой-запросом — заменить его на строку «ba», где оба символа — хорошие.
- Второй запрос: «YES», потому что «?» можно заменить на соответствующие хорошие буквы, а «*» — на пустую строку, и строки совпадут.
- Третий запрос: «NO», потому что «?» нельзя заменять на плохие буквы.
- Четвертый запрос: «YES», потому что «?» можно заменить на хорошие символы «a», а «*» — на строку из плохих букв «x».
| |
![]()
|
|
D. Палиндромная характеристика
дп
Перебор
Строки
хэши
*1900
Палиндромная характеристика строки s длины |s| — это последовательность из |s| целых чисел, k-е из которых равно количеству непустых подстрок строки s, являющихся k-палиндромами. Строка является 1-палиндромом тогда и только тогда, когда она читается одинаково как слева-направо, так и справа-налево. Строка является k-палиндромом (k > 1) тогда и только тогда, когда: - Её левая половина равна правой половине.
- Её левая и правая половины не пусты и являются (k - 1)-палиндромами.
Левая половина строки t — это её префикс длины ⌊|t| / 2⌋, а правая — её суффикс той же длины. ⌊|t| / 2⌋ обозначает длину строки t, делённую на 2, округленную вниз. Обратите внимание, что каждая подстрока учитывается столько раз, сколько встречается как подстрока. Так, например, в строке «aaa» подстрока «a» встречается 3 раза. Выходные данные Выведите |s| целых чисел — палиндромную характеристику строки s. Примечание В первом примере 1-палиндромами являются подстроки «a», «b», «b», «a», «bb», «abba», 2-палиндромом является подстрока «bb». 3- и 4-палиндромы у этой строки отсутствуют. | |
![]()
|
|
A. Разнообразие
жадные алгоритмы
реализация
Строки
*1000
Вычислите, какое наименьшее число символов надо поменять в строке s, чтобы в ней стало не менее k различных букв, либо выведите, что это сделать невозможно. Строка s состоит только из маленьких латинских букв, и заменять буквы можно также только на маленькие латинские. Выходные данные Выведите одну строчку с минимальным количеством букв, которые необходимо заменить, либо слово «impossible» (без кавычек), если это сделать невозможно. Примечание В первом примере в строке есть 6 различных букв, поэтому ничего менять не требуется. Во втором примере в строке изначально есть 4 различных буквы: {'a', 'h', 'o', 'y'}. Для получения 5 различных букв необходимо заменить одну из букв 'o' на букву, которая в строке не встречается, например на {'b'}. В третьем примере получить 7 различных букв невозможно, поскольку длина строки 6. | |
![]()
|
|
A. Дневник Тома Реддла
Перебор
реализация
Строки
*800
Гарри Поттер стремится уничтожить крестражи Сами-Знаете-Кого. Первый крестраж, о котором Гарри узнал из Тайной Комнаты — это дневник Тома Реддла. Он был у Джинни и заставил её открыть Тайную Комнату. Гарри хочет узнать, как много разных людей видели дневние, чтобы убедиться, что они не находятся под его влиянием. У него есть n имён людей, которые видели дневник в порядке, в котором они читали его. Гарри хочет для каждого человека узнать, видел ли он дневник ранее. Формально, для имени si в i-й строке, выведите «YES» (без кавычек) если существует индекс j, такой что si = sj и j < i, иначе выведите «NO» (без кавычек). Выходные данные Выведите n строк, в каждой из которых выведите «YES» или «NO» (без кавычек), в зависимости от того, встречалось ли это имя ранее. Вы можете вывести любую букву как заглавной, так и строчной. Примечание В примере 1 для i = 5 существует j = 3 такое, что si = sj и j < i, поэтому ответ для i = 5 равен «YES». | |
![]()
|
|
B. Похожие слова
Деревья
дп
Строки
хэши
*2300
Назовем словом непустую последовательность, состоящую из строчных букв латинского алфавита. Префиксом слова x называется слово y, которое можно получить из x удалением нуля или более последних букв x. Назовем два слова похожими, если одно из них можно получить из другого, удалив в нем первую букву. Дано множество слов S. Требуется найти размер максимального множества непустых слов X, удовлетворяющего следующим условиям: - каждое слово из X является префиксом некоторого слова из S;
- в X нет двух похожих слов.
Выходные данные Для каждого теста выведите на отдельной строке число m — размер максимального искомого множества X. | |
![]()
|
|
F. Махмуд, Ехаб и последнее испытание
Строки
Структуры данных
*2900
Махмуд и Ехаб справились со всеми задачами Доктора Зло, поэтому он дал им пароль от двери, которая выведет их из злой страны. Когда они попытались открыть дверь, на ней отобразилась задача, которую надо решить, чтобы спастись (да, дверь цифровая, Доктор Зло любит современные технологии). Если они не решат её, все старания будут напрасными, и Махмуд и Ехаб никогда не покинут злую страну. Вы поможете им? Махмуду и Ехабу дали n строк s1, s2, ... , sn, пронумерованных от 1 до n, и q запросов. Каждый запрос относится к одному из двух типов: - 1 a b (1 ≤ a ≤ b ≤ n), Для всех отрезков [l;r], для которых (a ≤ l ≤ r ≤ b) найдите максимальное значение выражения:
(r - l + 1) * LCP(sl, sl + 1, ... , sr - 1, sr) где LCP(str1, str2, str3, ... )— это длина наибольшего общего префикса строк str1, str2, str3, ... . - 2 x y (1 ≤ x ≤ n) где y — строка состоящая из строчных букв английского алфавита. Необходимо заменить строку на позиции x на строку y.
Выходные данные Для каждого запроса первого типа выведите ответ на него в новой строке | |
![]()
|
|
B. Поликарп и буквы
Перебор
реализация
Строки
*1000
Поликарп любит строчные буквы и недолюбливает прописные. Однажды он получил строку s, состоящую только из строчных и прописных букв английского алфавита. Пусть A — множество индексов строки. Назовем его симпатичным, если: - в индексах из A стоят различные строчные буквы;
- в строке нет таких прописных (заглавных) букв, которые расположены между элементами из A (иными словами, не существует такого j, что s[j] — прописная буква и a1 < j < a2 для некоторых a1 и a2 из A).
Напишите программу, которая найдет наибольшее количество элементов симпатичного множества индексов. Выходные данные Выведите наибольшее количество элементов симпатичного множества индексов для строки s. Примечание В первом примере искомыми позициями могут являться позиции 6 и 8 или позиции 7 и 8. В позициях 6 и 7 стоит буква 'a', в позиции 8 стоит буква 'b'. Пара позиций 1 и 8 не подходит, так как между ними стоит прописная буква 'B'. Во втором примере искомыми позициями, например, являются позиции 7, 8 и 11. Существуют и другие способы выбрать симпатичное множество, состоящее из трёх элементов. В третьем примере строка s не содержит строчных букв, следовательно, ответ равен 0. | |
![]()
|
|
A. Разблокируйте
Перебор
реализация
Строки
*900
По мере развития технологий производители стараются сделать экран разблокировки телефона настолько удобным, насколько возможно. Чтобы разблокировать новый телефон, домашнему щенку Аркадия Му-му надо пролаять пароль. Пароль представляется телефоном в виде строки из двух строчных латинских букв. Каштанка, заклятый враг Му-му, хочет разблокировать ее телефон, чтобы получить некоторую важную информацию. Однако, она может пролаять лишь n различных слов, каждое из которых может быть представлено как строка из двух строчных латинских букв. Каштанка хочет пролаять несколько слов (не обязательно различных) одно за другим так, чтобы произнести строку, которое содержит пароль как подстроку. Определить, возможно разблокировать телефон таким образом, или нет. Выходные данные Выведите «YES», если Каштанка может пролаять несколько слов друг за другим так, чтобы получившаяся строка содержала пароль, и «NO» иначе. Вы можете выводить каждую букву в любом регистре (заглавную или строчную). Примечание В первом примере пароль равен «ya», Каштанка может пролаять «oy», затем «ah» и затем «ha», образовав в итоге строку «oyahha», которая содержит пароль. Поэтому ответ «YES». Во втором примере Каштанка не может получить строку, содержащую пароль как подстроку. Обратите внимание, она может пролаять, например, «ht», затем «tp», получив «http», но эта строка не содержит «hp» как подстроку. В третьем примере строка «hahahaha» содержит «ah» как подстроку. | |
![]()
|
|
D. Огромные строки
битмаски
дп
Перебор
реализация
Строки
*2200
Дано n строк s1, s2, ..., sn, состоящих из символов 0 и 1. Далее m раз создается новая строка как конкатенация уже имеющихся. Формально, на i-м шаге конкатенация saisbi записывается в новую строку sn + i (нумерация шагов ведется с 1). После каждой операции вам нужно найти максимальное положительное целое число k такое, что в полученной строке встречаются все возможные строки из 0 и 1 длины k (а таких различных строк 2k) как подстроки. Если такого k не существует, выведите 0. Выходные данные Выведите m строк, содержащие по одному целому числу — ответы на запросы после операций. Примечание В первой операции создается строка "0110". Для k = 1 две возможные бинарные строки длины k — это "0" и "1", они обе являются подстроками новой строки. Для k = 2 и больше существуют строки длины k, не встречающиеся в получившейся строке (для k = 2 такая строка — это "00"). Поэтому ответ равен 1. Во второй операции создается строка "01100". Теперь присутствуют все строки длины k = 2. В третьей операции создается строка "1111111111". В ней нет нулей, поэтому ответ равен 0. | |
![]()
|
|
B. Вася и Типы
реализация
Строки
*1800
Программист Вася изучает новый язык программирования &K*. Язык &K* по своему синтаксису напоминает языки семейства C, однако он гораздо более мощный, и поэтому правила реальных C-подобных языков к нему не применимы. Для полного понимания условия внимательно прочитайте описание языка ниже, и следуйте ему, а не аналогичным правилам в реальных языках программирования. В &K* есть очень мощная технология указателей — к имеющемуся типу X можно приписать звездочку после него и получить тип X * . Это называется операцией взятия указателя. А есть противоположная операция — к любому типу X, являющемуся указателем, можно приписать слева амперсанд и получить тип &X, на который ссылается X. Это называется операцией разыменовывания. В языке &K* есть только два базовых типа данных — void и errtype. Также в этом языке есть операторы typedef и typeof. - Оператор "typedef A B" определяет новый тип данных B, эквивалентный типу A. В A могут быть звездочки и амперсанды, а в B — не могут. Например, оператор typedef void** ptptvoid создаст новый тип ptptvoid, который может использоваться в качестве void**.
- Оператор "typeof A" возвращает тип A, приведённый к void, т. е. возвращает эквивалентный ему тип void**...* с необходимым количеством звёздочек (возможно и нулевым). То есть после определения типа ptptvoid, как показано выше, оператор typeof ptptvoid вернёт void**.
Попытка разыменовать тип void приводит к ошибке: особому типу данных errtype. Для errtype верно следующее соотношение: errtype* = &errtype = errtype. Попытка использовать не объявленный ранее тип данных так же приведет к типу errtype. С помощью typedef можно определить один тип несколько раз. Из всех определений силу имеет только последнее. Однако все типы, которые были определены с его использованием ранее, не меняются. Заметим также, что операция разыменовывания имеет меньший приоритет, чем операция взятия указателя, иными словами &T * всегда равно T. Учтите, что операторы выполняются последовательно, один за другим. Пусть у нас есть два оператора "typedef &void a" и "typedef a* b". Сначала a принимает значение errtype, а затем b принимает значение errtype* = errtype, но не &void* = void (см. пример 2). Вася еще не до конца понимает эту мощную технологию, поэтому он попросил вас помочь в ней разобраться. Напишите программу, которая обрабатывает эти операторы и операции. Выходные данные На каждый оператор typeof выведите в отдельной строке ответ на этот оператор — тип, который вернул данный оператор. Примечание Разберем второй пример. После первых двух запросов typedef тип b эквивалентен void*, а с — void**. Следующий запрос typedef переопределяет b — теперь он равен &b = &void* = void. Тип с при этом не меняется. После чего тип с определяется как &&b* = &&void* = &void = errtype. На тип b это никак не влияет, поэтому следующий typedef определяет c, как &void* = void. Далее тип b снова переопределяется как &void = errtype. Отметим, что тип c в следующем запросе определяется именно как errtype******* = errtype, а не &void******* = void******. Тоже самое происходит и в последнем typedef. | |
![]()
|
|
F. Запрещённые индексы
снм
Строки
строковые суфф. структуры
*2400
Дана строка s, состоящая из n строчных латинских букв. Некоторые индексы в этой строке являются запрещёнными. Вам необходимо найти такую строку a, что значение |a|·f(a) является максимально возможным, где f(a) — количество вхождений a в s, заканчивающихся в индексах, не являющихся запрещёнными. Например, если s — aaaa, a — aa и индекс 3 — запрещённый, то f(a) = 2, так как a встречается в s три раза (начиная с индексов 1, 2 и 3), но одно из этих вхождений (то, которое начинается в индексе 2) заканчивается в запрещённом индексе. Посчитайте максимально возможное значение |a|·f(a). Выходные данные Выведите максимально возможное значение |a|·f(a). | |
![]()
|
|
A. Леша и сломаный контест
реализация
Строки
*1100
Как-то раз Леша готовил контест про своих друзей и случайно удалил его. К счастью, все задачи сохранились, но теперь их нужно найти среди других задач. Но задач слишком много, чтобы сделать это вручную. Леша просит Вас написать программу, которая по названию задачи определит, принадлежит ли задача этому контесту. Известно, что задача принадлежит контесту тогда и только тогда, когда в ней содержится имя одного друга Леши в качестве подстроки ровно один раз. Его друзей зовут «Danil», «Olya», «Slava», «Ann» и «Nikita». Имена чувствительны к регистру. Выходные данные Выведете «YES», если задача принадлежит контесту, и «NO» в противном случае. Вы можете выводить ответ в любом регистре. | |
![]()
|
|
E. Field of Wonders
реализация
Строки
*1500
Polycarpus takes part in the "Field of Wonders" TV show. The participants of the show have to guess a hidden word as fast as possible. Initially all the letters of the word are hidden. The game consists of several turns. At each turn the participant tells a letter and the TV show host responds if there is such letter in the word or not. If there is such letter then the host reveals all such letters. For example, if the hidden word is "abacaba" and the player tells the letter "a", the host will reveal letters at all positions, occupied by "a": 1, 3, 5 and 7 (positions are numbered from left to right starting from 1). Polycarpus knows m words of exactly the same length as the hidden word. The hidden word is also known to him and appears as one of these m words. At current moment a number of turns have already been made and some letters (possibly zero) of the hidden word are already revealed. Previously Polycarp has told exactly the letters which are currently revealed. It is Polycarpus' turn. He wants to tell a letter in such a way, that the TV show host will assuredly reveal at least one more letter. Polycarpus cannot tell the letters, which are already revealed. Your task is to help Polycarpus and find out the number of letters he can tell so that the show host will assuredly reveal at least one of the remaining letters. Output Output the single integer — the number of letters Polycarpus can tell so that the TV show host definitely reveals at least one more letter. It is possible that this number is zero. Note In the first example Polycarpus can tell letters "b" and "c", which assuredly will be revealed. The second example contains no letters which can be told as it is not clear, which of the letters "v" or "s" is located at the third position of the hidden word. In the third example Polycarpus exactly knows that the hidden word is "aba", because in case it was "aaa", then the second letter "a" would have already been revealed in one of previous turns. | |
![]()
|
|
H. Palindromic Cut
Перебор
реализация
Строки
*1800
Kolya has a string s of length n consisting of lowercase and uppercase Latin letters and digits. He wants to rearrange the symbols in s and cut it into the minimum number of parts so that each part is a palindrome and all parts have the same lengths. A palindrome is a string which reads the same backward as forward, such as madam or racecar. Your task is to help Kolya and determine the minimum number of palindromes of equal lengths to cut s into, if it is allowed to rearrange letters in s before cuttings. Output Print to the first line an integer k — minimum number of palindromes into which you can cut a given string. Print to the second line k strings — the palindromes themselves. Separate them by a space. You are allowed to print palindromes in arbitrary order. All of them should have the same length. | |
![]()
|
|
D. Оценочная строка
Комбинаторика
математика
Строки
*2100
В университете, где учится Вася, оценки представляют собой строки одинаковой длины, причем оценка x считается лучше чем y, если строка y лексикографически меньше строки x. Недавно в этом университете прошла важная контрольная, по которой Вася получил оценку a. Из-за большого количества студентов, преподаватель не может запомнить оценку каждого, но он точно помнит оценку b такую, что все студенты получили оценку строго меньше чем b. Вася недоволен своей оценкой и хочет её исправить. Для этого он может как угодно поменять местами символы в строке соответствующей его оценке. Сейчас Васю интересует количество различных способов улучшить свою оценку так, чтобы преподаватель не заподозрил неладного. Более формально: даны две строки одинаковой длины a и b, требуется вычислить количество различных строк c таких, что: 1) c может быть получена из a путем перестановки некоторых символов, то есть c является перестановкой a 2) a лексикографически меньше c 3) c лексикографически меньше b Если длина строки x равна длине строки y, то x лексикографически меньше y, если существует такое i, что x1 = y1, x2 = y2, ..., xi - 1 = yi - 1, xi < yi. Так как ответ может быть очень большим, вычислите только остаток от деления ответа на 109 + 7. Выходные данные Требуется вывести одно целое число — остаток от деления количества различных строк удовлетворяющих условию задачи на 109 + 7. Примечание В первом тесте из строки abc можно получить строки acb, bac, bca, cab, cba, все они больше строки abc, но меньше строки ddd. Поэтому ответ равен 5. Во втором тесте любая строка, которую можно получить из abcdef, будет больше строки abcdeg. Поэтому ответ равен 0. | |
![]()
|
|
C. Телефонные номера
реализация
Строки
*1400
У Васи есть несколько телефонных книг, в которые он записаны телефонные номера его друзей. У каждого из его друзей может быть один телефонный номер, а может быть и несколько. Вася решил упорядочить информацию о телефонах друзей. Вам будет задано n строк — все записи из телефонных книг Васи. Каждая запись начинается с имени друга. Затем следует количество телефонных номеров в текущей записи, а затем сами телефонные номера. Возможно, что в одной и той же записи записано несколько одинаковых телефонов. Также Вася считает, что если телефонный номер a является суффиксом телефонного номера b (то есть номер b заканчивается на номер a), и оба номера записаны Васей, как номера одного и того же человека, то номер a записан без кода города и его учитывать не следует. Перед вами стоит задача вывести упорядоченную информацию о телефонах друзей Васи, объединив разные записи в телефонных книгах для одних и тех же людей. Допустимо, что два разных человека имеют один и тот же номер. Если один человек имеет два номера x и y, причём x является суффиксом y (то есть y оканчивается на x), то выводить номер x не нужно. Если в телефонных книгах Васи номер какого-то друга записан несколько раз в одинаковом формате, учитывать его нужно ровно один раз. Ознакомьтесь с примерами, для лучшего понимания условия и формата вывода. Выходные данные Выведите упорядоченную информацию о телефонных номерах друзей Васи. Сначала выведите m — количество друзей, которые встречаются в телефонных книгах Васи. Следующие m строк должны содержать записи в следующем формате «имя количество номера». Номера следует разделять пробелом. Каждая такая запись должна содержать все телефонные номера очередного друга. Друзей можно выводить в любом порядке, телефонные номера для одной записи также можно выводить в любом порядке. | |
![]()
|
|
F. Удаление букв
Строки
Структуры данных
*2100
У Пети есть строка длины n, состоящая из прописных и строчных букв латинского алфавита, а также из цифр. Он выполняет со своей строкой по очереди m операций. Каждая операция описывается двумя целыми числами l и r и одним символом c — Петя удаляет из своей строки все символы c, находящиеся между позициями l и r, включительно. Очевидно, что после каждой операции длина строки либо не изменяется, либо уменьшается. Определите как будет выглядеть строка Пети после выполнения m операций. Выходные данные Выведите строку Пети после выполнения всех m операций. Если после выполнения всех операций строка Пети станет пустой, выведите пустую строку. Примечание В первом примере после выполнения первой операции из строки удалятся обе буквы «a», и строка примет вид «bc». После выполнения второй операции из строки удалится буква «c» (стоящая на второй позиции), и строка примет вид «b». Во втором примере после выполнения первой операции из строки удаляется «0», находящийся во второй позиции. После этого строка примет вид «Az». После выполнения второй операции строка не изменится. | |
![]()
|
|
B. Африканский кроссворд
реализация
Строки
*1100
Африканский кроссворд представляет собой прямоугольную таблицу n × m, в каждую ячейку которой вписана ровно одна буква. В этой таблице (еще ее называют сеткой) зашифровано некоторое слово, которое нужно расшифровать. Чтобы решить кроссворд, нужно вычеркнуть все повторяющиеся буквы в строках и в столбцах. Другими словами, буква должна быть вычеркнута в том и только в том случае, когда в соответствующих ей строке или столбце помимо нее есть еще хотя бы одна такая же буква. Причем все такие буквы вычеркиваются одновременно. Когда все повторяющиеся буквы будут вычеркнуты, оставшиеся буквы следует выписать в одну строчку. Раньше идут те буквы, которые находятся выше, если они в одной строке — раньше идет та буква, которая левее. Полученное слово является ответом. Вам предлагается решить африканский кроссворд и вывести слово, которое в нем зашифровано. Выходные данные В единственной строке выведите зашифрованное слово. Гарантируется, что ответ состоит хотя бы из одной буквы. | |
![]()
|
|
E. Максимальные вопросы
дп
Строки
Структуры данных
*2100
У мальчика Васи в блокноте были записаны две строки s длины n и t длины m, состоящие из букв «a» и «b» латинского алфавита. Причем Вася знает, что строка t имеет вид «abab...», то есть на нечетных позициях строки стоит буква «a», а на четных — «b». Вдруг утром Вася обнаружил, что кто-то испортил его строку s. Некоторые буквы s были заменены на символ «?». Назовем последовательность позиций i, i + 1, ..., i + m - 1 вхождением строки t в s, если 1 ≤ i ≤ n - m + 1 и t1 = si, t2 = si + 1, ..., tm = si + m - 1. Мальчик оценивает красоту строки s, как максимальное количество непересекающихся вхождений строки t в нее. Вася может заменить некоторые из символов «?» на «a» или «b» (символы на разных позициях можно заменять на разные буквы). Вася хочет произвести замены так, чтобы красота строки s была максимально возможной. Из всех таких вариантов он хочет заменить как можно меньше символов «?». Найдите, сколько замен он должен сделать. Выходные данные Выведите единственное целое число — минимальное количество замен, которое должен сделать Вася, чтобы сделать красоту строки s максимально возможной. Примечание В первом примере строка t имеет вид «a». Единственный оптимальный вариант — заменить все символы «?» на «a». Во втором примере используя две замены можно получить строку «aba?aba??». Больше двух вхождений получить нельзя. | |
![]()
|
|
E. Обмены в строке
Перебор
реализация
Строки
хэши
*2200
Изначально была дана строка s длины n, состоящая из строчных латинских букв. Её скопировали ровно k раз, получив при этом k одинаковых строк s1, s2, ..., sk. После этого в каждой из них поменяли местами ровно одну пару символов (возможно, одинаковых, но находящихся на разных позициях). Вам необходимо по заданным k строкам s1, s2, ..., sk восстановить любую подходящую строку s. Обратите внимание, что суммарная длина всех строк не превосходит 5000 (то есть k·n ≤ 5000). Выходные данные В единственной строке выведите любую подходящую строку s, либо же «-1» (без кавычек), если такой строки не существует. Примечание В первом тестовом примере строка s1 получается из строки acab перестановкой местами 2 и 4 символов, строка s2 получается перестановкой 1 и 2 символов, а строка s3 — 3 и 4 символов. Во втором тестовом примере s1 получается из строки kbub перестановкой 3 и 4 символов, s2 — перестановкой 2 и 4 символов, а s3 — перестановкой 1 и 3 символов. В третьем тестовом примере невозможно получить никакую строку, удовлетворяющую условиям. | |
![]()
|
|
E. Перевороты
дп
Строки
строковые суфф. структуры
*3300
В Берляндии ураган и это стихийное бедствие не обошло стороной предместье Строксвиль. Вы мчитесь в него, чтобы проверить, всё ли в порядке с вашей любимой строкой. Ураган немного потрепал её, перевернув несколько её непересекающихся подстрок. У вас сохранилась фотография строки до урагана и вы хотите привести её в исходное состояние, перевернув обратно наименьшее возможное число её подстрок, но для этого сперва нужно определиться, какие подстроки нужно перевернуть. У вас есть строка s — исходное состояние вашей строки и строка t — то, какой она стала после того, как ураган перевернул некоторые её подстроки. Ваша задача выбрать k непересекающихся подстрок строки t таких что если их развернуть, вы получите строку s и число k при этом наименьшее возможное. Выходные данные В первой строке выведите число k — наименьшее возможное число подстрок, которые надо перевернуть. В следующих k строках выведите по два числа li, ri в каждой, обозначающие, что нужно перевернуть строку с li по ri символы (строки 1-индексированные). Указанные подстроки не должны пересекаться. Если вариантов ответа несколько, выведите любой. Если решения не существует, выведите -1. | |
![]()
|
|
E. Перевороты
дп
Строки
строковые суфф. структуры
*3300
В Берляндии ураган и это стихийное бедствие не обошло стороной предместье Строксвиль. Вы мчитесь в него, чтобы проверить, всё ли в порядке с вашей любимой строкой. Ураган немного потрепал её, перевернув несколько её непересекающихся подстрок. У вас сохранилась фотография строки до урагана и вы хотите привести её в исходное состояние, перевернув обратно наименьшее возможное число её подстрок, но для этого сперва нужно определиться, какие подстроки нужно перевернуть. У вас есть строка s — исходное состояние вашей строки и строка t — то, какой она стала после того, как ураган перевернул некоторые её подстроки. Ваша задача выбрать k непересекающихся подстрок строки t таких что если их развернуть, вы получите строку s и число k при этом наименьшее возможное. Выходные данные В первой строке выведите число k — наименьшее возможное число подстрок, которые надо перевернуть. В следующих k строках выведите по два числа li, ri в каждой, обозначающие, что нужно перевернуть строку с li по ri символы (строки 1-индексированные). Указанные подстроки не должны пересекаться. Если вариантов ответа несколько, выведите любой. Если решения не существует, выведите -1. | |
![]()
|
|
E. Перевороты
дп
Строки
строковые суфф. структуры
*3300
В Берляндии ураган и это стихийное бедствие не обошло стороной предместье Строксвиль. Вы мчитесь в него, чтобы проверить, всё ли в порядке с вашей любимой строкой. Ураган немного потрепал её, перевернув несколько её непересекающихся подстрок. У вас сохранилась фотография строки до урагана и вы хотите привести её в исходное состояние, перевернув обратно наименьшее возможное число её подстрок, но для этого сперва нужно определиться, какие подстроки нужно перевернуть. У вас есть строка s — исходное состояние вашей строки и строка t — то, какой она стала после того, как ураган перевернул некоторые её подстроки. Ваша задача выбрать k непересекающихся подстрок строки t таких что если их развернуть, вы получите строку s и число k при этом наименьшее возможное. Выходные данные В первой строке выведите число k — наименьшее возможное число подстрок, которые надо перевернуть. В следующих k строках выведите по два числа li, ri в каждой, обозначающие, что нужно перевернуть строку с li по ri символы (строки 1-индексированные). Указанные подстроки не должны пересекаться. Если вариантов ответа несколько, выведите любой. Если решения не существует, выведите -1. | |
![]()
|
|
E. Перевороты
дп
Строки
строковые суфф. структуры
*3300
В Берляндии ураган и это стихийное бедствие не обошло стороной предместье Строксвиль. Вы мчитесь в него, чтобы проверить, всё ли в порядке с вашей любимой строкой. Ураган немного потрепал её, перевернув несколько её непересекающихся подстрок. У вас сохранилась фотография строки до урагана и вы хотите привести её в исходное состояние, перевернув обратно наименьшее возможное число её подстрок, но для этого сперва нужно определиться, какие подстроки нужно перевернуть. У вас есть строка s — исходное состояние вашей строки и строка t — то, какой она стала после того, как ураган перевернул некоторые её подстроки. Ваша задача выбрать k непересекающихся подстрок строки t таких что если их развернуть, вы получите строку s и число k при этом наименьшее возможное. Выходные данные В первой строке выведите число k — наименьшее возможное число подстрок, которые надо перевернуть. В следующих k строках выведите по два числа li, ri в каждой, обозначающие, что нужно перевернуть строку с li по ri символы (строки 1-индексированные). Указанные подстроки не должны пересекаться. Если вариантов ответа несколько, выведите любой. Если решения не существует, выведите -1. | |
![]()
|
|
E. Перевороты
дп
Строки
строковые суфф. структуры
*3300
В Берляндии ураган и это стихийное бедствие не обошло стороной предместье Строксвиль. Вы мчитесь в него, чтобы проверить, всё ли в порядке с вашей любимой строкой. Ураган немного потрепал её, перевернув несколько её непересекающихся подстрок. У вас сохранилась фотография строки до урагана и вы хотите привести её в исходное состояние, перевернув обратно наименьшее возможное число её подстрок, но для этого сперва нужно определиться, какие подстроки нужно перевернуть. У вас есть строка s — исходное состояние вашей строки и строка t — то, какой она стала после того, как ураган перевернул некоторые её подстроки. Ваша задача выбрать k непересекающихся подстрок строки t таких что если их развернуть, вы получите строку s и число k при этом наименьшее возможное. Выходные данные В первой строке выведите число k — наименьшее возможное число подстрок, которые надо перевернуть. В следующих k строках выведите по два числа li, ri в каждой, обозначающие, что нужно перевернуть строку с li по ri символы (строки 1-индексированные). Указанные подстроки не должны пересекаться. Если вариантов ответа несколько, выведите любой. Если решения не существует, выведите -1. | |
![]()
|
|
E. Перевороты
дп
Строки
строковые суфф. структуры
*3300
В Берляндии ураган и это стихийное бедствие не обошло стороной предместье Строксвиль. Вы мчитесь в него, чтобы проверить, всё ли в порядке с вашей любимой строкой. Ураган немного потрепал её, перевернув несколько её непересекающихся подстрок. У вас сохранилась фотография строки до урагана и вы хотите привести её в исходное состояние, перевернув обратно наименьшее возможное число её подстрок, но для этого сперва нужно определиться, какие подстроки нужно перевернуть. У вас есть строка s — исходное состояние вашей строки и строка t — то, какой она стала после того, как ураган перевернул некоторые её подстроки. Ваша задача выбрать k непересекающихся подстрок строки t таких что если их развернуть, вы получите строку s и число k при этом наименьшее возможное. Выходные данные В первой строке выведите число k — наименьшее возможное число подстрок, которые надо перевернуть. В следующих k строках выведите по два числа li, ri в каждой, обозначающие, что нужно перевернуть строку с li по ri символы (строки 1-индексированные). Указанные подстроки не должны пересекаться. Если вариантов ответа несколько, выведите любой. Если решения не существует, выведите -1. | |
![]()
|
|
E. Перевороты
дп
Строки
строковые суфф. структуры
*3300
В Берляндии ураган и это стихийное бедствие не обошло стороной предместье Строксвиль. Вы мчитесь в него, чтобы проверить, всё ли в порядке с вашей любимой строкой. Ураган немного потрепал её, перевернув несколько её непересекающихся подстрок. У вас сохранилась фотография строки до урагана и вы хотите привести её в исходное состояние, перевернув обратно наименьшее возможное число её подстрок, но для этого сперва нужно определиться, какие подстроки нужно перевернуть. У вас есть строка s — исходное состояние вашей строки и строка t — то, какой она стала после того, как ураган перевернул некоторые её подстроки. Ваша задача выбрать k непересекающихся подстрок строки t таких что если их развернуть, вы получите строку s и число k при этом наименьшее возможное. Выходные данные В первой строке выведите число k — наименьшее возможное число подстрок, которые надо перевернуть. В следующих k строках выведите по два числа li, ri в каждой, обозначающие, что нужно перевернуть строку с li по ri символы (строки 1-индексированные). Указанные подстроки не должны пересекаться. Если вариантов ответа несколько, выведите любой. Если решения не существует, выведите -1. | |
![]()
|
|
A. Газетный заголовок
жадные алгоритмы
Строки
*1500
В Моржландии выпускается газета с названием s1, состоящем из строчных букв латинского алфавита. Маленький морж Клычок хочет купить несколько таких газет, вырезать из них названия, склеить их друг за другом и стереть некоторые буквы так, чтобы получилось слово s2. Считается, что когда Клычок стирает какую-то букву, на ее месте не образуется пустое место. То есть строка остается неразрывной и по-прежнему состоит только из маленьких букв латинского алфавита. Например, заголовок газеты — «abc». Взяв два таких заголовка и склеив, получится «abcabc». Если стереть буквы на позициях 1 и 5 получится слово «bcac». Какое наименьшее количество газетных заголовков s1 понадобится Клычку, чтобы он мог их склеить, стереть несколько букв и получить слово s2? Выходные данные Если получить слово s2 описанным выше способом невозможно, выведите «-1» (без кавычек). Иначе выведите наименьшее количество газетных заголовков s1, которое понадобится, чтобы получить слово s2. | |
![]()
|
|
F. Подстроки в строке
битмаски
Перебор
Строки
строковые суфф. структуры
Структуры данных
*3000
Дана строка s, обработайте q запросов, каждый из которых имеет один из следующий типов: - 1 i c — Изменить i-й символ в строке на c.
- 2 l r y — Рассмотрим подстроку строки s, начинающуюся с символа с номером l и заканчивающуюся на символ с номером r. Выведите количество раз, которые y входит в неё как подстрока.
Выходные данные Для каждого запроса типа 2 выведите ответ в отдельной строке. Примечание В первом тестовом примере изначально строка aba встречается 3 раза как подстрока на подотрезке [1, 7]. После запроса первого типа строка становится равной ababcbaba и строка aba встречается только один раз как подстрока на отрезке [1, 7]. | |
![]()
|
|
E. Обратная сторона
Деревья
Строки
строковые суфф. структуры
Структуры данных
*3400
Все знают, что Одиннадцать обладает некоторыми сверхспособностями. Поэтому Хоппер уговорила ее закрыть врата на Обратную сторону силой мысли. Монстры с Обратной стороны любят перемещаться между мирами, поэтому они собираются атаковать Хоппер и Одиннадцать, чтобы остановить их. Монстры живут на дереве из n вершин, пронумерованных от 1 до n. На каждом ребре написана строчная латинская буква.  Обратная сторона — магический мир. В нем живут m видов монстров, пронумерованных от 1 до m. У каждого вида монстров есть специальное слово, которое дает ему силу. Специальное слово вида i равно si. Всего на Обратной стороне q монстров. Каждый сейчас находится в одной вершине и собирается дойти до некоторой другой вершины. Если монстр типа k идет от вершины i до вершины j, его сила увеличивается на количество раз, когда он видел свое специальное слово (sk) как подстроку на своем пути. Более формально: Пусть f(i, j) — строка, которую мы получим, если выпишем все буквы на ребрах на кратчайшем пути из i в j. Тогда сила монстра увеличивается на количество вхождений sk в f(i, j). Хоппер и Одиннадцать хотят подготовиться, поэтому для каждого монстра они хотят определить силу, которую приобретет монстр после передвижения. Выходные данные Выведите q строк. В i-й из этих строк выведите силу i-го монстра после передвижения. | |
![]()
|
|
B. Радиостанция
реализация
Строки
*900
После того, как друзья спалили оборудование радиостанции, школьное управление дало им задания в качестве наказания. Задачей Дастина было добавлять комментарии к файлам конфигурации nginx на школьном сайте. В школе n серверов. Каждый сервер имеет имя и ip-адрес (имена не обязательно различны, ip-адреса обязательно различны). Дастин знает ip-адрес и имя каждого сервера. Для простоты, предположим, что все команды nginx имеют вид «command ip;», где command — строка из строчных букв латинского алфавита, а ip — адрес одного из школьных серверов.  Каждый ip-адрес имеет вид «a.b.c.d», где a, b, c и d являются неотрицательными целыми числами, не превосходящими 255 (без лидирующих нулей). Конфигурационный файл nginx, к которому Дастин должен добавить комментарии, имеет m команд. Никто никогда не помнит, какие ip-адреса у каких серверов, поэтому, чтобы конфигурационный файл было удобнее читать, Дастин должен после каждой команды дописать имя сервера, которому принадлежит данный ip-адрес. Формально, если строчка имела вид «command ip;», то Дастин должен заменить ее на «command ip; #name», где name — имя сервера, ip-адрес которого равняется ip. Дастин ничего не знает о nginx, поэтому он запаниковал, и его друзья попросили вас выполнить задачу. Выходные данные Выведите m строк — команды в конфигурационном файле после того, как Дастин выполнит свою задачу. | |
![]()
|
|
C. Идеальная защита
Деревья
жадные алгоритмы
Строки
Структуры данных
*1800
У Алисы есть важное сообщение M, состоящее из нескольких неотрицательных целых чисел, которое она хочет сохранить в тайне от Евы. Алиса знает, что единственный теоретически защищенный способ шифрования — использование одноразового ключа. Алиса сгенерировала случайный ключ K с длиной, равной длине сообщения. Алиса затем вычислила побитовое исключающее ИЛИ каждого соответствующего элемента массива и ключа ( , где , где  обозначает операцию побитового исключающего ИЛИ) и сохранила зашифрованное сообщение A. Алиса умная. Будь как Алиса. обозначает операцию побитового исключающего ИЛИ) и сохранила зашифрованное сообщение A. Алиса умная. Будь как Алиса. Например, пусть Алиса хочет сохранить сообщение M = (0, 15, 9, 18), и она сгенерировала ключ K = (16, 7, 6, 3). Тогда зашифрованное сообщение равно A = (16, 8, 15, 17). Алиса понимает, что она не может хранить ключ вместе с зашифрованным сообщением. Поэтому Алиса послала ключ K Бобу и удалила свою копию. Алиса умная. Действительно, будь как Алиса. Боб понимает, что зашифрованное сообщение защищено только до тех пор, пока ключ является секретным. Поэтому Боб случайным образом поменял местами элементы ключа перед тем, как сохранить его. Боб думает, что в таком случае, даже если Ева получит и зашифрованное сообщение, и ключ, она не сможет прочитать исходное сообщение. Боб не умный. Не будь как Боб. В примере выше Боб мог, например, выбрать перестановку (3, 4, 1, 2), перемешать элементы в соответствии с ней и сохранить ключ P = (6, 3, 16, 7). Прошел год, и Алиса теперь хочет расшифровать свое сообщение. Только сейчас Боб понял, что это невозможно. Так как он поменял местами элементы ключа случайным образом, сообщение утеряно навсегда. Мы уже сказали, что Боб не очень умный? Боб хочет получить хотя бы какую-то информацию из сообщения. Так как он не очень умный, он попросил у вас помощи. Вам известны зашифрованное сообщение A и произвольно перемешанный ключ P. Каково лексикографически минимальное сообщение, которое могло быть зашифровано подобным образом? Формально, по данным A и P найдите лексикографически минимальное сообщение O такое, что существует перестановка π такая, что  для всех i. для всех i. Напомним, что последовательность S лексикографически меньше последовательности T, если существует такая позиция i, что Si < Ti, а для всех j < i выполняется Sj = Tj. Выходные данные Выведите одну строку с N целыми числами — лексикографически минимально возможное сообщение O. Напомним, что все числа в нем должны быть неотрицательны. Примечание В первом примере решением является (10, 3, 28), потому что  , ,  и и  . Другие возможные перестановки ключа дают сообщения (25, 6, 10), (25, 3, 15), (10, 21, 10), (15, 21, 15) и (15, 6, 28), все из которых лексикографически больше, чем оптимальное решение. . Другие возможные перестановки ключа дают сообщения (25, 6, 10), (25, 3, 15), (10, 21, 10), (15, 21, 15) и (15, 6, 28), все из которых лексикографически больше, чем оптимальное решение. | |
![]()
|
|
D. Выбор строк
Конструктив
реализация
Строки
*2500
Выходные данные Выведите строку из Q символов, где i-й символ равен «1», если ответ на i-й запрос «Да», и «0» иначе. Примечание В первом запросе мы можем получить нужную строку, например, используя следующие шаги:  . . В третьем запросе просят получить из строки AAB строку A, но в этом случае невозможно избавиться от буквы «B». | |
![]()
|
|
A. Проверка логина
*особая задача
Строки
*1200
При регистрации в некоторой социальной сети пользователям предлагается придумать себе удобный логин, чтобы легко было оставить свой контакт для связи, напечатать его на визитках и так далее. Логином может быть любая последовательность строчных и заглавных латинских букв, цифр и символов нижнего подчеркивания («_»). Однако, чтобы усложнить жизнь мошенникам и уменьшить число нелепых ситуаций из-за невнимательности пользователей, запрещено регистрировать логин, если он похож на хотя бы один из уже существующих логинов. А именно, два логина s и t считаются похожими, если один можно логин s из логина t путем некоторого количества последовательных применений следующих операций: - изменить регистр любой буквы (т. е. заменить строчную букву на заглавную или наоборот);
- заменить букву «O» (заглавная латинская буква) на цифру «0» или наоборот;
- заменить цифру «1» (один) на любую из букв «l» (строчная латинская буква «L»), «I» (заглавная латинская буква «i») или наоборот, или же заменить одну из этих букв на другую.
Например, логины «Codeforces» и «codef0rces», а также «OO0OOO00O0OOO0O00OOO0OO_lol» и «OO0OOO0O00OOO0O00OO0OOO_1oI» считаются похожими, а логины «Codeforces» и «Code_forces» — нет. Вам дан список уже существующих логинов в социальной сети, среди которых нет похожих, и запрос пользователя на регистрацию нового логина. Проверьте, есть ли среди существующих логинов хотя бы один похожий на логин, который хочет зарегистрировать пользователь. Выходные данные Выведите «Yes» (без кавычек), если пользователь может зарегистрировать новый логин, то есть среди уже имеющихся логинов нет похожих. В противном случае, выведите «No» (без кавычек). Примечание В пером примере пользователь может зарегистрировать свой логин, поэтому нужно вывести «Yes». Во втором примере пользователь хочет зарегистрировать логин, состоящий из трёх нулей. Ему не удастся это сделать, так как есть логин (третий из списка существующих), который состоит из строчной буквы o, заглавной буквы O и ещё одной строчной буквы o. В третьем примере пользователь хочет зарегистрировать логин «_i_. Ему не удастся это сделать, так как есть логин «_1_» (второй из списка существующих). | |
![]()
|
|
D. Автодополнение
*особая задача
Деревья
Строки
*1900
Аркадий работает копирайтером. Сегодня ему нужно написать некоторый текст, который он уже продумал до мельчайших подробностей, но еще не набрал. Для набора текста Аркадий использует свою любимый текстовый редактор. Аркадий набирает слова, знаки препинания и пробельные символы один за другим, для набора каждой буквы и каждого знака (в том числе перевода строки) требуется одно нажатие клавиши на клавиатуре. При этом, когда Аркадий набрал непустой префикс некоторого слова (в том числе слово полностью), его редактор подсказывает возможное автоматическое дополнение для текущего слова: слово из числа тех, которые Аркадий набрал до этого, префикс которого совпадает с текущим набранным префиксом, если такое слово уникально. Например, если Аркадий уже набрал слова «codeforces», «coding» и еще раз «codeforces», то, если он наберет префикс «cod», то редактор ему ничего не подскажет, а если он наберет префикс «code», редактор подскажет «codeforces». При этом не важно, собирается ли Аркадий набрать слово «codeforces» или, например, «codebest». Одним нажатием клавиши Аркадий может использовать подсказку, то есть дополнить текущий префикс до слова, предложенного редактором, при этом никаких других символов после слова автоматически не ставится и можно продолжить набирать слово. Какое минимальное число нажатий на клавиши необходимо Аркадию для того, чтобы набрать текст, если он не может перемещать курсор и стирать уже написанные буквы и другие символы? Формально словом называется непрерывная последовательность латинских букв, с обоих концов ограниченная пробелами, знаками препинания, началом или концом строки или текста. Аркадий использует только строчные буквы. Например, в тексте «it's well-known that tic-tac-toe is a paper-and-pencil game for two players, x and o.» 20 слов. Выходные данные Выведите одно целое число — минимальное количество нажатий на клавиши, которое должен сделать Аркадий. Примечание В первом примере нужно воспользоваться автодополнением для первого слова «snowboarding» после того, как набран префикс «sn», и для второго слова «snowboarding» после того, как набран префикс «snowb». Суммарно это экономит 7 нажатий. Во втором примере все равно, пользоваться автодополнением, или нет. В третьем нужно можно воспользоваться автодополнением для второго слова после набора «t», для третьего слова — после набора «t», затем набрать его до конца, далее слова «thun» надо набирать полностью, а для набора «thunder» необходимо набирать «thund», затем пользоваться автодополнением, кроме того, надо пользоваться автодополнением для вторых слов «lightning» и «feel» после набора одной буквы. | |
![]()
|
|
B. Игра со строкой
реализация
Строки
Теория вероятностей
*1600
Вася и Коля играют в игру со строкой по следующим правилам. Сначала Коля загадывает строку s, состоящую из строчных латинских букв, и равновероятно выбирает из отрезка [0, len(s) - 1] целое число k. Он сообщает строку s Васе, а затем циклически сдвигает её на k символов влево, то есть получает новую строку t = sk + 1sk + 2... sns1s2... sk. Вася не знает ни числа k, ни итоговой строки t, но хочет угадать число k. Для этого он может попросить Колю открыть первую букву получившейся строки, а затем, увидев её, еще одну букву на некоторой позиции, которую Вася может выбрать. Вася уже понял, что не может гарантировать себе победу, однако, он хочет узнать вероятность своего выигрыша при оптимальной игре. Вам необходимо помочь ему в этом. Заметим, что целью Васи является однозначное определение числа k, значит, если после открытия второй буквы остается не менее двух циклических сдвигов исходной строки s, удовлетворяющих известной информации, Вася считается проигравшим. Конечно же, в каждый момент игры Вася пытается максимизировать вероятность своего выигрыша, насколько это возможно. Выходные данные Выведите одно вещественное число — ответ на задачу. Ответ будет считаться верным, если его абсолютная или относительная ошибка не будет превосходить 10 - 6. Формально, пусть ваш ответ равен a, а ответ жюри — b. Ваш ответ считается правильным, если  . . Примечание В первом примере после открытия первой буквы Вася может попросить открыть вторую букву, и после этого циклический сдвиг определяется однозначно. Во втором примере если первой буквой в циклическом сдвиге t будет «t» или «c», то у Васи не получится угадать сдвиг, открыв лишь одну другую букву. В то же время, если первой буквой будет «i» или «a», то, открыв четвертую букву, можно однозначно определить циклический сдвиг. | |
![]()
|
|
G. Палиндромное разбиение
дп
Строки
строковые суфф. структуры
*2900
Дана строка s, найдите число способов разбить s на подстроки так, что если в разбиении содержится k подстрок (p1, p2, p3, ..., pk), то pi = pk - i + 1 для всех i (1 ≤ i ≤ k) и k чётно. Так как число таких разбиений может быть велико, выведите ответ по модулю 109 + 7. Выходные данные Выведите одно целое число — количество требуемых разбиений по модулю 109 + 7. Примечание В первом тестовом примере единственным корректным разбиением является ab|cd|cd|ab. Во втором тестовом примере корректными разбиениями являются ab|b|ab|ab|ab|ab|b|ab, ab|b|abab|abab|b|ab и abbab|ab|ab|abbab. | |
![]()
|
|
E. Интересный замок
Конструктив
Строки
*2300
Добро пожаловать в очередную задачу про взлом кодового замка! Исследователи Уитфилд и Мартин наткнулись на необычный сейф, внутри которого, по слухам, находятся несметные богатства, среди которых можно найти решение задачи дискретного логарифма! На сейфе, разумеется, установлен кодовый замок, на экране которого в каждый момент времени показывается строка, состоящая из n маленьких букв английского алфавита. Изначально на экране показывается строка s. Уитфилд и Мартин выяснили, что сейф откроется, когда на экране окажется строка t. Строку на экране можно изменять с помощью операции «shift x». Для того, чтобы применить эту операцию, исследователи выбирают число x от 0 до n включительно. После этого текущая строка p = αβ изменяется на строку βRα, где длина β равна x, а длина α равна n - x. Иными словами, суффикс строки p длины x разворачивается и переставляется в начало строки. Например, применение операции «shift 4» заменит строку «abcacb» на строку «bcacab», поскольку α = ab, β = cacb, βR = bcac. Исследователи боятся, что если применить слишком много операций «shift», то замок заблокируется навсегда. Они просят вас найти способ получить на экране строку t, используя не более чем 6100 операций. Выходные данные Если нельзя получить t из s, используя не более 6100 операций «shift», выведите единственное число - 1. Иначе в первой строке выведите количество операций k (0 ≤ k ≤ 6100). В следующей строке выведите k чисел xi, соответствующих операциям «shift xi» (0 ≤ xi ≤ n), в том порядке, в котором их нужно применить. | |
![]()
|
|
D. Спасение любви
графы
жадные алгоритмы
поиск в глубину и подобное
снм
Строки
*1600
Валя и Толя — идеальная пара, но даже у них бывают ссоры. Недавно Валя обиделась на своего кавалера, так как он пришел к ней в футболке, надпись на которой отличается от надписи на ее свитере. Теперь она не хочет с ним видеться, а Толя сидит целыми днями в своей комнате и плачет над ее фотографиями. Эта история так и осталась бы такой печальной, если бы в нее не вмешалась добрая швея-волшебница (бабушка Толи). Ее сердце разрывается, когда она видит молодых людей в ссоре, и поэтому она срочно хочет все исправить. Бабушка уже тайно забрала Валин свитер и Толину футболку, осталось только сделать надписи на них одинаковыми. Для этого она может за одну единицу маны купить заклинание, которое позволяет менять некоторые буквы на одежде. Ваша задача — рассчитать, какое минимальное количество маны придется потратить бабушке Толи для спасения любви молодых людей. Более формально, надписи на Валином свитере и Толиной футболке — это две строчки одинаковой длины n, состоящие только из строчных букв латинского алфавита. За одну единицу маны бабушка может купить заклинание вида (c1, c2) (где c1 и c2 — произвольные строчные буквы латинского алфавита), с помощью которого она может сколько угодно раз менять букву c1 на c2 (и наоборот) как на Валином свитере, так и на Толиной футболке. Вам требуется найти минимальное количество маны, позволяющее приобрести набор заклинаний, с помощью которого можно сделать надписи одинаковыми. Также вам необходимо вывести соответствующий набор заклинаний. Выходные данные В первой строке выведите одно целое число — минимальное количество маны t для спасения любви молодых. В следующих t строках выведите по две строчные буквы латинского алфавита через пробел — заклинания, которые нужно приобрести бабушке Толи. Заклинания и буквы в заклинаниях можно выводить в любом порядке. Если оптимальных ответов несколько, выведите любой. Примечание В первом примере достаточно купить два заклинания: («a»,«d») и («b»,«a»). Тогда первые буквы совпадут, когда мы поменяем букву «a» на «d». Вторые совпадут, когда поменяем «b» на «a». Третьи совпадут, когда поменяем сначала «b» на «a», потом «a» на «d». | |
![]()
|
|
A. Восстановление пароля
реализация
Строки
*900
Игорь К. всегда доверял своему любимому Антивирусу Кашпировского. Поэтому, когда ему пришло сообщение в QIP Infinium от одного из одногруппников, содержащее ссылку на "прикольную флэшку о свином гриппе", он, не особо задумываясь, скачал ее. Антивирус не ругался, поэтому "флэшка" была запущена. Тут же QIP Infinium выдал сообщение: "Неправильный логин/пароль". Зайдя со своего запасного ISQ-аккаунта, Игорь К. посмотрел данные основного. Имя и фамилия заменились на соответственно "H1N1" и "Infected", а в разделе "Дополнительно" был странный двоичный код длиной 80 символов, состоящий из нулей и единичек. "Взломали", — подумал Игорь К. и, запустив браузер Internet Exploiter, быстро напечатал адрес своего любимого поисковика. Вскоре он выяснил, что это действительно был вирус, меняющий пароли у пользователей ISQ. К счастью, он обнаружил, что тот двоичный код на самом деле был зашифрованным паролем, где каждая группа из 10 символов обозначала одну из десятичных цифр. Соответственно, настоящий пароль состоял из 8 десятичных цифр. Помогите Игорю К. восстановить его ISQ-аккаунт. Выходные данные Выведите одну строку из 8 символов — пароль от ISQ-аккаунта Игоря К. Гарантируется, что решение существует. | |
![]()
|
|
C. Телефонные номера
Конструктив
реализация
Строки
*1500
И где здесь телефонные номера? Дана строка s из строчных букв английского алфавита и число k. Найдите лексикографически минимальную строку t, имеющую длину k, множество букв которой является подмножеством множества букв s и s лексикографически меньше t. Гарантируется, что ответ существует. Обратите внимание, что под множеством букв строки подразумевается множество, а не мультимножество. В частности, множество букв строки abadaba это {a, b, d}. Строка p считается лексикографически меньше строки q, если p — префикс q, не равный q или существует i такое, что pi < qi и для всех j < i выполнено pj = qj. Например, abc лексикографически меньше abcd , abd лексикографически меньше abec, afa лексикографически не меньше ab и a лексикографически не меньше a. Выходные данные Выведите строку t, удовлетворяющую условиям, описанным выше. Гарантируется, что ответ существует. Примечание В первом примере список строк t длины 3, подходящих под условие, что множество букв t — подмножество множества букв s, таков: aaa, aab, aac, aba, abb, abc, aca, acb, .... Из них лексикографически больше abc: aca, acb, .... Лексикографически минимальная из них — aca. | |
![]()
|
|
C. Преобразование строки
жадные алгоритмы
Строки
*1300
Вам задана строка s, состоящая из |s| строчных латинских букв. За один ход вы можете заменить любой символ строки на следующий в алфавитном порядке (a будет заменена на b, s будет заменена на t и так далее). Вы не можете заменить букву z ни на какую другую. Ваша задача состоит в том, чтобы за какое-то количество ходов (не обязательно минимальное) получить строку abcdefghijklmnopqrstuvwxyz (английский алфавит) как подпоследовательность. Подпоследовательностью строки является такая строка, которая получена удалением символов на некоторых позициях. Вы должны вывести строку, которая получается из исходной и содержит в себе английский алфавит в качестве подпоследовательности, либо же сказать, что это невозможно. Выходные данные Если вы можете получить строку, которая получается из исходной и содержит в себе английский алфавит в качестве подпоследовательности, выведите её. Иначе выведите «-1» (без кавычек). | |
![]()
|
|
A. Хоккей
реализация
Строки
*1600
Петя очень любит хоккей. Однажды, глядя хоккейный матч, он заснул. Ему приснился сон, в котором ему поручили переделать название хоккейной команды. Так, Пете дали исходное название команды w и набор запрещенных подстрок s1, s2, ..., sn. Все эти строки состоят из больших и маленьких букв латинского алфавита. Строка w имеет длину |w|, ее символы пронумерованы от 1 до |w|. Сначала Петя должен найти в строке w все вхождения запрещенных подстрок, причем регистр букв при поиске вхождений не учитывается. То есть строки «aBC» и «ABc» считаются эквивалентными. После этого Петя должен произвести замену всех букв, покрывающихся вхождениями. Более формально: букву в позиции i необходимо заменить на любую другую, если для позиции i в строке w найдется такая пара индексов l, r (1 ≤ l ≤ i ≤ r ≤ |w|), что подстрока w[l ... r] является элементом набора s1, s2, ..., sn, не учитывая регистр букв при сравнении строк. При замене регистр буквы должен сохраниться. Пете не разрешается заменять буквы, которые не покрывает ни одна запрещенная подстрока. Буква letter (как большая, так и маленькая) у хоккеистов считается счастливой. Поэтому Петя должен так произвести замены, чтобы эта буква встречалась в итоговой строке как можно больше раз. Помогите ему — найдите лексикографически минимальную новую строку с максимальным возможным количеством счастливых букв. Обратите внимание, что процесс замен не повторяется, а происходит лишь один раз. То есть если после Петиных замен в строке появились новые вхождения плохих подстрок, Петя не обращает на них внимание. Выходные данные В единственной строке выведите лексикографически минимальную строку с максимальным количеством букв letter, которую получит Петя. Лексикографическое сравнение реализует оператор < в современных языках программирования. Строка a лексикографически меньше строки b, если a является префиксом b, или существует такое i (1 ≤ i ≤ |a|), что ai < bi, а для любого j (1 ≤ j < i) aj = bj. |a| обозначает длину строки a. | |
![]()
|
|
B. Набор строки
реализация
Строки
*1400
Задана строка s, состоящая из n строчных латинских букв. Вам необходимо набрать эту строку на вашей клавиатуре. Изначально у вас есть пустая строка. Пока вы не набрали необходимую строку, вы можете применять следующую операцию: - дописать символ в конец строки.
Кроме того, не более одного раза вы можете применить дополнительную операцию: cкопировать строку и приписать её к самой себе. Например, если вы хотите набрать строку abcabca, вы можете набрать её за 7 операций, если будете выписывать символы один за другим. Или вы можете набрать её за 5 операций, если вы сначала наберёте строку abc, затем скопируете её и допишете последний символ. Если вам нужно набрать строку aaaaaaaaa, наилучший вариант — набрать 4 символа первой операцией, потом скопировать и приписать строку, и затем дописать последний символ. Выведите минимальное количество операций, которое необходимо, чтобы набрать заданную строку. Выходные данные Выведите единственное целое число — минимальное количество ходов, которое необходимо, чтобы набрать заданную строку. Примечание Первый тест описан в условии задачи. Во втором тесте вы можете только выписывать символы один за другим. | |
![]()
|
|
D. Ножницы
Перебор
Строки
*2600
Женя недавно обзавелся крайне полезным в хозяйстве инструментом — k-ножницами для резки строк. С их помощью можно вырезать из произвольной строки s (длины не менее 2·k) две непересекающиеся подстроки длины ровно k, которые затем склеиваются (с сохранением порядка). Например, 2-ножницами из строки abcde можно вырезать подстроки ab и de и склеить их в abde, а вырезать ab и bc не получится. Разумеется, перед применением ножницы стоит проверить на чем-то, что не жалко испортить. Порывшись в бумагах, Женя раздобыл две строки s и t. Ему сразу же стало интересно: правда ли, что можно применить его ножницы к строке s так, чтобы в получившейся вырезке t содержалась в качестве подстроки? Выходные данные Если ответ не существует, выведите «No». В противном случае в первой строке выведите «Yes», а во второй — два числа L и R, означающие индексы, в которых начинаются вырезанные подстроки (в 1-индексации). Если возможных ответов несколько, выведите любой. Примечание В первом примере можно вырезать подстроки, начинающиеся по индексам 1 и 5. Получившаяся вырезка baaaab содержит подстроку aaaa. Во втором примере получившаяся вырезка равняется bccb. | |
![]()
|
|
A2. Death Stars (medium)
Строки
хэши
*2000
The stardate is 1983, and Princess Heidi is getting better at detecting the Death Stars. This time, two Rebel spies have yet again given Heidi two maps with the possible locations of the Death Star. Since she got rid of all double agents last time, she knows that both maps are correct, and indeed show the map of the solar system that contains the Death Star. However, this time the Empire has hidden the Death Star very well, and Heidi needs to find a place that appears on both maps in order to detect the Death Star. The first map is an N × M grid, each cell of which shows some type of cosmic object that is present in the corresponding quadrant of space. The second map is an M × N grid. Heidi needs to align those two maps in such a way that they overlap over some M × M section in which all cosmic objects are identical. Help Heidi by identifying where such an M × M section lies within both maps. Output The only line of the output should contain two space-separated integers i and j, denoting that the section of size M × M in the first map that starts at the i-th row is equal to the section of the second map that starts at the j-th column. Rows and columns are numbered starting from 1. If there are several possible ways to align the maps, Heidi will be satisfied with any of those. It is guaranteed that a solution exists. Note The 5-by-5 grid for the first test case looks like this:
mayth
eforc
ebewi
thyou
hctwo
| |
![]()
|
|
A. Футбол
реализация
Строки
*900
Петя очень любит футбол. Однажды, глядя футбольный матч, он записывал на листе бумаги текущее положение игроков. Для простоты он изобразил ситуацию в виде строки из нулей и единиц. Ноль соответствует игрокам одной команды, единица — игрокам другой команды. Если есть как минимум 7 игроков некоторой команды, стоящих подряд, то эта ситуация считается опасной. Например, ситуация 00100110111111101 — опасная, а 11110111011101 — нет. Вам задана текущая ситуация. Определите, является ли она опасной. Выходные данные Выведите «YES» если ситуация опасная. В противном случае выведите «NO». | |
![]()
|
|
D. Частота строки
Строки
строковые суфф. структуры
хэши
*2500
Дана строка \(s\). Требуется ответить на \(n\) запросов. \(i\)-й запрос состоит из целого числа \(k_i\) и строки \(m_i\), ответом является минимальная длина строки \(t\) такой, что \(t\) является подстрокой \(s\) и строка \(m_i\) входит в \(t\) как подстрока не менее \(k_i\) раз. Подстрокой строки называется любая последовательность подряд идущих символов в этой строке. Гарантируется, что для любых двух запросов строки \(m_i\) из этих запросов различны. Выходные данные Для каждого запроса выведите ответ на него в отдельной строке. Если строка \(m_{i}\) встречается в \(s\) менее \(k_{i}\) раз, выведите -1. | |
![]()
|
|
E. Короткий код
Деревья
дп
жадные алгоритмы
Строки
Структуры данных
*2200
Код Аркадия содержит \(n\) переменных. Каждая переменная имеет уникальное имя, состоящее только из английских строчных (маленьких) букв. Однажды Аркадий решил укоротить свой код. Он хочет заменить имя каждой переменной его непустым префиксом таким образом, что новые имена останутся попарно различными (но новое имя какой-либо переменной может совпадать со старым именем этой или другой переменной). Среди всех таких возможных замен он хочет найти такую, для которой суммарная длина названий переменных будет минимальной. Строка \(a\) является префиксом строки \(b\), если вы можете удалить несколько (возможно, ни одного) символа с конца строки \(b\) и получить \(a\). Найдите минимальную возможную суммарную длину новых имён. Выходные данные Выведите одно целое число — минимально возможную суммарную длину новых названий переменных. Примечание В первом примере одним из наилучших вариантов будет сокращение имён в порядке их ввода до "cod", "co", "c". Во втором примере можно укоротить последнее имя до "aac" и первое имя до "a" без изменения других имён переменных. | |
![]()
|
|
A. Арамейский манускрипт
реализация
Строки
*900
В арамейском языке слова могут обозначать только обьекты. У слов в арамейском языке есть несколько особых свойств: - Слово является корнем, если оно в нём нет двух одинаковых букв.
- Корень и все его перестановки обозначают один и тот же самый объект.
- Корнем \(x\) слова \(y\) является любое слово, которое содержит все различные буквы, встречающиеся в \(y\), ровно по одному разу каждая. Например, «a» является корнем слов «aaaa», «aa», «aaa»; корнем слов «aabb», «bab», «baabb», «ab» является «ab».
- Все слова в арамейском языке обозначают тот же самый объект, что и его корень.
Вам в руки попал древний манускрипт на арамейском. Определите, сколько различных объектов упомянуто в нём. Выходные данные Выведите одно целое число — число различных объектов, упомянутых в древнем арамейском манускрипте. Примечание В первом примере упомянуты два объекта. Соответствующие им корни — «a»,«ab». Во втором примере упомянут лишь один объект с корнем «amer». Остальные слова являются перестановками слова «amer». | |
![]()
|
|
D. Куро, НОД, побитовое исключающее ИЛИ, сумма и все-все-все
Бинарный поиск
битмаски
Деревья
дп
жадные алгоритмы
математика
Перебор
снм
Строки
Структуры данных
теория чисел
*2200
Куро играет в обучающую игру про числа. Основные математические операции в этой игре — наибольший общий делитель, побитовое исключающее ИЛИ и сумма двух чисел. Куро так любит эту игру, что проходит уровень за уровнем изо дня в день. К сожалению, Куро уезжает в отпуск и будет неспособна продолжить череду решений. Поскольку Кэти — надёжный человек, Куро попросил её прийти к нему домой в этот день и поиграть за него. Изначально дан пустой массив \(a\). Игр состоит из \(q\) запросов двух разных типов. Запросы первого типа просят Кэти добавить число \(u_i\) в массив \(a\). Запросы второго типа просят Кэти найти такое число \(v\), принадлежащее массиву \(a\), что \(k_i \mid GCD(x_i, v)\), \(x_i + v \leq s_i\), и \(x_i \oplus v\) максимально, где \(\oplus\) обозначает операцию побитового исключающего ИЛИ, \(GCD(c, d)\) обозначает наибольший общий делитель целых чисел \(c\) и \(d\), а \(y \mid x\) означает, что \(x\) делится на \(y\), или же вывести -1, если таких чисел в массиве нет. Поскольку вы программист, Кэти просит вас написать программу, которая будет автоматически и точно выполнять внутриигровые запросы, чтобы выполнить поручения Куро. Давайте поможем ей! Выходные данные Для каждого запроса типа \(2\) выведите запрашиваемое число \(v\) или -1, если таких чисел не найдено, в отдельной строке. Примечание В первом примере необходимо выполнить пять запросов: - Первый запрос просит вас добавить \(1\) в \(a\). Теперь \(a\) — \(\left\{1\right\}\).
- Второй запрос просит вас добавить \(2\) в \(a\). Теперь \(a\) — \(\left\{1, 2\right\}\).
- Третий запрос просит вас найти ответ с \(x = 1\), \(k = 1\) и \(s = 3\). И \(1\), и \(2\) удовлетворяют условиям на \(v\), так как \(1 \mid GCD(1, v)\) и \(1 + v \leq 3\). Поскольку \(2 \oplus 1 = 3 > 1 \oplus 1 = 0\), ответом на этот запрос будет \(2\).
- Четвёртый запрос просит вас найти ответ с \(x = 1\), \(k = 1\) и \(s = 2\). Только \(v = 1\) удовлетворяет условия \(1 \mid GCD(1, v)\) и \(1 + v \leq 2\), поэтому ответом на этот запрос будет \(1\).
- Пятый запрос просит вас найти ответ с \(x = 1\), \(k = 1\) и \(s = 1\). В \(a\) нет удовлетворяющих условиям элементов, поэтому мы выводим -1 как ответ на этот запрос.
| |
![]()
|
|
A. Антипалиндром
Перебор
реализация
Строки
*900
Строка называется палиндромом, если она одинаково читается слева направо и справа налево. Например, строки «kek», «abacaba», «r» и «papicipap» — палиндромы, а строки «abb» и «iq» — нет. Подстрокой \(s[l \ldots r]\) (\(1 \leq l \leq r \leq |s|\)) строки \(s = s_{1}s_{2} \ldots s_{|s|}\) называется строка \(s_{l}s_{l + 1} \ldots s_{r}\). Девушка Анна очень боится палиндромов, поэтому она предпочитает, чтобы ее называли Анн. Таким же образом в своем воображении она меняет слова-палиндромы на другие слова. А именно, она меняет слово \(s\) на самую длинную подстроку, которая не является палиндромом. Если же все совсем плохо и все подстроки слова \(s\) являются палиндромами, она и вовсе пропускает это слово из виду. Не так давно во время чтения книги Анн увидела слово \(s\). Скажите, в слово какой длины оно превратилось в ее воображении? Выходные данные Если существует подстрока строки \(s\), которая не является палиндромом, выведите длину самой длинной такой подстроки. Иначе выведите \(0\). Обратите внимание, самых длинных подстрок, не являющихся палиндромами, может быть несколько, однако их длина определяется однозначно. Примечание «mew» не является палиндромом, поэтому подстрока максимальной длины строки «mew», не являющаяся палиндромом, это вся строка. Таким образом, ответ на первый тест из примера это \(3\). Строка «uffuw», не являющаяся палиндромом, является подстрокой длины \(5\) строки «wuffuw», таким образом ответ на второй тест из примера это \(5\). Все подстроки строки «qqqqqqqq» состоят из одинаковых букв, поэтому являются палиндромами, таким образом, у этой строки не существует подстроки, не являющейся палиндромом, и ответ на третий тест из примера это \(0\). | |
![]()
|
|
F. Изоморфные строки
Строки
хэши
*2300
Вам дана строка s длины n, состоящая из строчных букв латинского алфавита. Для двух заданных строк s и t назовем S — множество всех различных букв строки s и T множество всех различных букв строки t. Строки s и t называются изоморфными если их длины равны и существует взаимо-однозначное соответствие (биекция) f между S и T для которого f(si) = ti. Формально: - f(si) = ti для всех индексов i,
- для любого символа
 существует ровно один символ существует ровно один символ  , что f(x) = y, , что f(x) = y, - для любого символа
 существует ровно один символ существует ровно один символ  , что f(x) = y,. , что f(x) = y,. Например, строки «aababc» b «bbcbcz» изоморфные. Аналогично, строки «aaaww» и «wwwaa» изоморфные. Но следующие пары строк неизоморфны: «aab» и «bbb», «test» и «best». Обработайте m запросов, каждый состоит из трех целых чисел x, y, len (1 ≤ x, y ≤ n - len + 1). Для каждого запроса проверьте, правда ли две подстроки s[x... x + len - 1] и s[y... y + len - 1] изоморфны. Выходные данные Для каждого запроса на отдельной строке выведите «YES», если подстроки s[xi... xi + leni - 1] и s[yi... yi + leni - 1] изоморфны, и «NO» в противном случае. Примечание Запросы в примере следующие: - подстроки «a» и «a» изоморфны: f(a) = a;
- подстроки «ab» и «ca» изоморфны: f(a) = c, f(b) = a;
- подстроки «bac» и «aba» неизоморфны, так как f(b) и f(c) должны быть равны a одновременно;
- подстроки «bac» и «cab» изоморфны: f(b) = c, f(a) = a, f(c) = b.
| |
![]()
|
|
A. Весенний микс
реализация
Строки
*900
Откройте шторы, и вы увидите прекрасный вид. Канно наслаждается видом около реки, наполненным светлыми оттенками. Это не мандарины, а цветы.— Как жаль, что уже поздняя весна, — с сожалением вздыхает Мино, — еще одна прохладная ночь, и они исчезнут. — Но ведь сейчас эти краски выглядят лучше всего? — впечатленный пейзажем Канно оптимистичен. Поле может быть представлено как ряд из клеток, каждая из которых либо содержит цветок аврорового, ванильного или солнечно-желтого цвета, либо пустая. Когда цветок увядает, он пропадает из своей клетки и раскидывает лепестки своего цвета в две соседние клетки (или за границу поля, если эта клетка крайняя). Лепестки, падающие за границу поля, сразу становятся не видны. Помогите Канно определить, возможно ли такое, что после того, как некоторые (возможно, все или ни одного) цветки увянут, как минимум в одной клетке будут находится все три цвета, если учитывать опавшие лепестки и еще не увядшие цветы. Обратите внимание, цветы могут увядать в любом порядке. Выходные данные Выведите «Yes», если возможно, что все три цвета появятся в какой-то клетке, и «No» в противном случае. Вы можете выводить каждую из букв в любом регистре (строчную или заглавную). Примечание В первом примере если цветки ванильного и солнечно-желтого цвета увянут, то они оставят свои лепестки в центральной клетке, где в таком случае будут находиться все три цвета. Во втором примере все три цвета не могут находиться в одной клетке, поскольку этого нельзя добиться, например, для аврорового и ванильного цветов. | |
![]()
|
|
B. Речной прилив
Конструктив
Строки
*1200
Прогуливаясь вдоль реки, Мино молча что-то записывает.— Время, — вслух думает Мино. — Что? — Время не ждет. Приливы тоже, — объясняет Мино. — Мое имя всегда напоминает мне об этом. — Что же ты записываешь? — Приливы, ты же видишь. У всего есть свой период, и мне кажется, этот я нашел, — уверенно заявил Мино. Канно не уверен в записях Мино. Заметки о приливе можно выразить как строку \(s\) из символов «0», «1» и «.», где «0» означает отсутствие прилива, «1» означает наличие прилива, а «.» означает, что записей в этот день нет (возможно, прилив был, возможно, не было). Вы должны помочь Мино определить, возможно ли, что после замены каждого символа «.» независимо на «0» или «1» данное число \(p\) не является периодом получившейся строки. Если ответ утвердительный, то найдите одну из таких возможных замен. В данной задаче положительное целое число \(p\) является периодом строки \(s\), если для всех \(1 \leq i \leq \lvert s \rvert - p\) символы \(i\) и \((i + p)\) строки \(s\) совпадают. Здесь \(\lvert s \rvert\) обозначает длину строки \(s\). Выходные данные Выведите одну строку: если возможно, что \(p\) не является периодом строки после замены, выведите получившуюся строку после одной из таких замен; иначе выведите «No» (без кавычек, буквы можете выводить в любом регистре (строчные или заглавные)). Примечание В первом примере \(7\) не является периодом получившейся строки, так как \(1\)-й и \(8\)-й символы отличаются. Во втором примере \(6\) не является периодом получившейся строки, так как \(4\)-й и \(10\)-й символы отличаются. В третьем примере \(9\) всегда является периодом, потому что единственное условие для этого — совпадение первого и последнего символа — уже удовлетворено. Обратите внимание, в первом и втором примере существует несколько правильных ответов, вы можете вывести любой. | |
![]()
|
|
A. Помогите Тридевятому царству
Строки
*800
В Тридевятом царстве, Тридесятом государстве жили-были Царь, Царевич, Король, Королевич, Сапожник, Портной и много других граждан. И жили они, не тужили, пока не пришла в Тридевятое царство беда лихая. Поселились в нем АСМ-щики. Одна из главных бед, связанных с этими странными существами, состояла в том, что любили они числа высокой точности. Поэтому в Тридевятом царстве было уже несколько случаев попадания купцов к лекарю после очередной просьбы АСМ-щика продать, скажем, ровно 0.273549107 бочки пива. Чтобы как-то бороться с этой бедой, Царь издал приказ о необходимости произведения округления всех чисел до ближайшего целого с целью упрощения вычислений. Более подробно, приказ состоял в следующем: - Если целая часть числа не оканчивается цифрой 9, а дробная часть числа строго меньше 0.5, округленное число совпадает с целой частью числа.
- Если целая часть числа не оканчивается цифрой 9, а дробная часть числа не меньше 0.5, округленное число получается прибавлением 1 к последней цифре целой части числа.
- Если целая часть числа оканчивается цифрой 9, для произведения округления необходимо идти к Василисе Премудрой. Только она одна во всем Тридевятом царстве умеет делать хитрую операцию переноса в следующий разряд.
Купцам этот алгоритм показался очень сложным, и они прибежали к вам — АСМ-щикам. Поможете им программой, выполняющей округления в соответствии с царским указом? Выходные данные Если последняя цифра целой части числа не равна 9, выведите округленное число без лидирующих нулей. В противном случае выведите сообщение «GOTO Vasilisa.» (без кавычек). | |
![]()
|