| Условие задачи | | Прогресс | Попытки, все/успешные |
|
Темы:
Компоненты сильной связности
Применение обхода в глубину
Алгоритмы на графах
Поиск компонент связности
В далёком заснеженном города Снежнокрибирске очень мало пеших тропинок, так как город просто не успевает их чистить, потому люди передвигаются в основном только на внедорожниках: ездят в магазин, отвозят детей в школу, ездят на работу и так далее.
В один из последних дней перед зимними каникулами ребятам в школе задали проект на каникулы, который можно делать как самому, так и в группе, но не более 3 человек. Но так как проект связан с совместной работой, а в городе нет никакой связи: ни телефонной, ни интернета, то ребята решили собираться у кого-нибудь дома, чтобы делать проект вместе. Так как проект может делать до трёх человек, то ученики составили карту своих домов в городе, а также отметили на них тропинки. У них встал вопрос о том, как делать большинство проектов максимальным возможным количеством человек, но так, чтобы как можно меньше учеников делали проект одни. Помогите ребятам по описанию карты их города и тропинкам составить возможный план, как им лучше распределить проекты между собой.
Формат входных данных
На первой строке подаются два числа N, M (1 <= N,M <= 100) – количество домов и тропинок между ними соответственно.
Далее на M строках подаются дорожки в виде номеров домов (если существует дорога 1-2, то значит существует дорожка и 2-1).
Формат выходных данных
Выведите на первой строке количество учеников, которые делают проект в одиночку.
На второй – количество групп учеников, делающих проект в паре.
На третьей – количество групп учеников, делающих проект втроём.
Примечание: ребята стараются разбиться на группы по максимуму человек (по 3), если остался кто-то один, но он мог делать проект не один, то стараемся минимизировать одиночек.
| |
![]()
|
88/
31
|
|
Темы:
Алгоритмы на графах
Секретный бункер уходит на N этажей вниз. Под нижним этажом бункера находится сверхсекретная лаборатория. Злобный диверсант хочет вывести лабораторию из строя, залив её водой (даже очень небольшого количества воды хватит, чтобы запоганить сверхточные приборы). Для этого он использует лужицы воды, остающиеся от жизнедеятельности обитателей бункера. В лужицах i-го этажа находится Ei воды. Диверсанту известно, что если на нём скопится больше Сi воды, то перегородка не выдержит и вся вода сольется на этаж ниже. Он может проделать отверстия в некоторых перегородках, по которым вода также стечет вниз. Проделать отверстие в полу i-го этажа стоит Pi у.е. Помогите диверсанту уничтожить лабораторию с минимальными материальными затратами.
Входные данные
Первая строка содержит натуральное число N (1 <= N <= 50000) - количество этажей в бункере, в следующих N строках находятся тройки целых чисел Ci, Ei, Pi (0 < Ei <= Ci < 1000000; E1+E2+...+EN < 2000000000; Pi > 0; P1+P2+...+PN < 2000000000). Этажи нумеруются сверху вниз.
Выходные данные
В первой строке выдать количество денег, которое придется потратить злобному диверсанту, в следующих строках выведите номера этажей, в полу которых следует проделать отверстия.
| |
![]()
|
2/
2
|
|
Темы:
Алгоритмы на графах
В ЛКШ построили аттракцион "Лабиринт знаний". Лабиринт представляет собой N комнат, занумерованных от 1 до N, между некоторыми из которых есть двери. Когда человек проходит через дверь, показатель его знаний изменяется на определенную величину, фиксированную для данной двери. Вход в лабиринт находится в комнате 1, выход - в комнате N. Каждый ЛКШонок проходит лабиринт ровно один раз и попадает в группу в зависимости от набранных знаний (при входе в лабиринт этот показатель равен нулю). Ваша задача показать наилучший результат.
Входные данные
Первая строка входного файла содержит целые числа N (1 <= N <= 2000) - количество комнат и M (1 <= M <= 10000) - количество дверей. В каждой из следующих M строк содержится описание двери - номера комнат, из которой она ведет и в которую она ведет, а также целое число, которое прибавляется к количеству знаний при прохождении через дверь (это число по модулю не превышает 10000). Двери могут вести из комнаты в нее саму, между двумя комнатами может быть более одной двери.
Выходные данные
В выходной файл выведите ":)" - если можно получить неограниченно большой запас знаний, ":(" - если лабиринт пройти нельзя, и максимальное количество набранных знаний в противном случае.
| |
![]()
|
2/
1
|
|
Темы:
Алгоритмы на графах
Пусть нам известны степени (количество ребер, инцидентных данной вершине) всех вершин неориентированного графа. Требуется построить неориентированный граф без петель и кратных ребер с заданными степенями вершин или сказать, что это невозможно.
Формат входных данных
Первая строка входного файла содержит натуральное число N (1 <= N <= 500), а во второй строке N чисел - степени вершин.
Формат выходных данных
В первой строке выходного файла выдать слово 'Yes', если граф построить можно, или 'No', если нет. Если построить возможно, то выдать в следующей строке количество ребер, далее список ребер, заданных парой вершин.
| |
![]()
|
20/
4
|
|
Темы:
Комбинаторика
Алгоритмы на графах
Динамическое программирование
Однажды Юрик оказался в лесу у костра, где собрались \(n\) человек. Оказалось, что некоторые из них знакомы друг с другом. Для удобства пронумеруем людей целыми числами от \(1\) до \(n\). Обозначим как \(d_i\) количество людей, сидящих у костра, с которыми знаком \(i\)-й человек. Неожиданно оказалось, что два человека с номерами \(i\) и \(j\) (\(i \ne j\)) знакомы друг с другом тогда и только тогда, когда \(d_i = d_j\).
Вернувшись домой, Юрик задумался, какое минимальное количество пар людей могли быть знакомы, чтобы выполнялось это условие?
Формат входных данных
Единственная строка содержит одно целое число \(n\) (\(1 \le n \le 5\,000\)) — количество людей.
Формат выходных данных
Выведите одно целое число — минимальное количество пар знакомых людей.
Замечание
Рассмотрим первый пример из условия. Возможны следующие варианты:
-
Любые два человека знакомы друг с другом. В этом случае количество пар знакомых людей равно \(\frac{4 \cdot 3}{2} = 6\).
-
Некоторые три человека попарно знакомы друг с другом, четвертый человек не знаком ни с кем. В этом случае количество пар знакомых людей равно \(3\).
| |
![]()
|
3/
3
|
|
Темы:
Алгоритмы на графах
Арифметические алгоритмы (Теория чисел)
Применение обхода в глубину
Обход в глубину
Дано дерево на n вершинах (связный неориентированный ациклический граф c n−1 рёбрами), где у каждого ребра есть вес w. Назовём простой путь длины k возрастающим , если существует такое целое x>=2, что вес первого ребра пути делится на x, второго ребра — делится на x2, ……, вес k-го ребра делится на xk.
Требуется найти максимальную длину k возрастающего пути, где k — количество рёбер в нём.
Входные данные
В первой строке вводится единственное целое число n (1 <= n <= 100000) - число вершин в дереве.
В следующих n−1 строках вводятся по три целых числа u, v, w ( 1<= v <= n, 1<= w <= n, u ≠ v, 1 <= w <= 107) - номера вершин, которые соединяет очередное ребро, и его вес.
Выходные данные
Выведите одно целое число k - максимальную длину возрастающего пути.
Примечание
Простым путем называется такой путь, что все вершины в нем различны.
В 1-м примере есть путь длины 2: 3 — 1 — 2. Тогда для него подходящий x = 2. Можно показать, что возрастающего пути большей длины не существует.
Во 2-м примере есть путь длины 3: 3 — 4 — 5 — 6. Тогда для него подходящий x = 2. Можно показать, что возрастающего пути большей длины не существует.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4
1 2 8
1 3 6
1 4 3
|
2
|
| 2 |
6
1 2 2
2 3 4
3 4 2
4 5 4
5 6 8
|
3
|
| |
![]()
|
5/
2
|
|
Темы:
Динамическое программирование на таблицах
Элементарная геометрия
Алгоритмы на графах
Дед Мороз за ночь должен посетить N городов. У него есть двумерный план расположения всех городов. План нарисован в декартовой системе координат, в которой точкой (0, 0) обозначено место старта Деда Мороза. Каждый город на плане отмечен точкой с координатой (Xi, Yi). Также на карте обозначены M точек с координатами (Pi, Qi), в которых расположены ускорители. Чтобы успеть разнести все подарки, Дед Мороз может воспользоваться ускорителем, который увеличивает его скорость в два раза (а может им и не пользоваться).
Дед Мороз в Новогоднюю ночь начинает с места старта, посещает все N городов и возвращается обратно.
Начальная скорость Деда Мороза равна 1. Найдите наименьшее время, необходимое Деду Морозу, чтобы посетить все города и вернуться обратно. Временем, при котором он раскладывает все подарки будем пренебрегать!
Входные данные
Первая строка входных данных содержит два целых числа N и M (1 <= N <= 12, 0 <= M <=5). Следующие N строк содержат координаты городов (Xi, Yi). Далее идут M строк с координатами ускорителей (Pi, Qi). Все координаты различны и среди них нет координаты (0, 0).
Выходные данные
Выведите ответ на задачу, с точностью не менее 6 знаков после запятой.
Примеры
| № |
Входные данные |
Выходные данные |
Примечание |
| 1 |
2 1
1 1
0 1
1 0 |
2 1
1 1
0 1
1 0 |
Вот один из оптимальных способов разнести все подарки
- Пройти расстояние 1 от начала координат до ускорителя 1 со скоростью 1, затратив время 1.
- Пройти расстояние 1 от ускорителя 1 до города 1 со скоростью 2, затратив время 0,5.
- Пройти расстояние 1 от города 1 до города 2 со скоростью 2, затратив время 0,5.
- Пройти расстояние 1 от города 2 до начала координат со скоростью 2, затратив время 0,5.
|
| 2 |
2 1
1 1
0 1
100 0 |
3.4142135624 |
Вот один из оптимальных способов разнести все подарки
- Пройти расстояние 1.41... от начала координат до города 1 со скоростью 1, затратив время 1.41....
- Пройти расстояние 1 от города 1 до города 2 со скоростью 1, затратив время 1.
- Пройти расстояние 1 от города 2 до начала координат со скоростью 1, затратив время 1.
|
| 3 |
1 2
4 4
1 0
0 1 |
4.3713203436 |
Вот один из оптимальных способов разнести все подарки
- Пройти расстояние 1 от начала координат до ускорителя 1 со скоростью 1, затратив время 1.
- Пройти расстояние 1,41... от ускорителя 1 до ускорителя 2 со скоростью 2, затратив время 0,707....
- Пройти расстояние 5 от ускорителя 2 до города 1 со скоростью 4, затратив время 1,25.
- Пройти расстояние 5,65... от города 1 до начала координат со скоростью 4, затратив время 1,41....
|
| |
![]()
|
18/
2
|
|
Темы:
Алгоритмы на графах
Кратчайшие пути в графе
Давилон - самый крупный город на Луне. На Давилоне есть собственная система метро, состоящая из N станций и M железнодорожных линий. Станции пронумерованы от 1 до N. Каждой линией управляет компания. У каждой компании есть идентификационный номер. I-я (1<=i<=M) линия соединяет станцию pi и qi двунаправленно. Промежуточной станции нет. Этой линией управляет компания ci . Можно делать пересадки на станции, где доступно несколько линий. Система оплаты проезда, используемая в этой системе метро, немного странная. Когда пассажир использует только те линии, которые обслуживаются одной и той же компанией, тариф составляет 1 сантик (валюта Давилона). Каждый раз, когда пассажир переходит на линию, которой управляет компания, отличная от текущей линии, с пассажира взимается дополнительная плата за проезд в размере 1 сантик. В случае, если пассажир, перешедший с линии компании А на линию другой компании, снова переходит на линию компании А, дополнительный тариф взимается снова. Незнайка сейчас на станции 1 и хочет добраться до станции N на метро. Найдите минимально необходимый тариф.
Входные данные
В первой строке задается два целых числа N (2<=N<=105) и M (0<=M<=2*105). В каждой из следующих M строк записаны по 3 числа: pi, qi и ci; 1<=pi<=N (1<=i<=M), 1<=qi<=N, 1<=ci<=106, pi ≠ qi.
Выходные данные
Выведите минимальный требуемый тариф. Если добраться до станции N на метро невозможно, выведите -1.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
3 3
1 2 1
2 3 1
3 1 2 |
1 |
Используйте линии компании 1:
1 → 2 → 3.
Стоимость проезда 1 сантик. |
| 2 |
8 11
1 3 1
1 4 2
2 3 1
2 5 1
3 4 3
3 6 3
3 7 3
4 8 4
5 6 1
6 7 5
7 8 5 |
2 |
Сначала используйте линии компании 1:
1 → 3 → 2 → 5 → 6.
Затем используйте линии компании 5:
6 → 7 → 8.
Стоимость проезда 2 сантика. |
| 3 |
2 0 |
-1 |
|
| |
![]()
|
64/
4
|
|
Темы:
Алгоритмы на графах
Кратчайшие пути в графе
Обход в ширину
Вам дано дерево с N вершинами. Здесь дерево - это разновидность графа, а точнее, связный неориентированный граф с N−1 ребром, где N - количество его вершин. I-е ребро (\(1<=i<=N-1\)) соединяет вершины ai и bi и имеет длину ci.
Вам также дано Q запросов и целое число K. Для каждого j-го запроса (\(1<=j<=Q\)) найдите длину кратчайшего пути от вершины xj к вершине yj через вершину K.
Входные данные
В первой строке записано целое число N (\(3<=N<=10^5\)). В следующих N строках записаны вершины ai и bi (\(1<=a_i,b_i<=N\), \(1<=i<=N-1\)) и длина между ними ci (\(1<=c_i<=10^9\), \(1<=i<=N-1\))
Далее идут два числа Q и K (\(1<=Q<=10^5\), \(1<=K<=N\)). В последних Q строках записаны целые числа xj, yj (\(x_j \neq y_j\),\(x_j \neq K\), \(y_j \neq K\) \(1<=j<=Q\), ).
Заданный граф является деревом.
Выходные данные
Выведите ответы на запросы в Q строках. В j-й строке выведите ответ на j-й запрос.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
5
1 2 1
1 3 1
2 4 1
3 5 1
3 1
2 4
2 3
4 5 |
3
2
4 |
Кратчайшие пути для трех запросов следующие:
Запрос 1: Вершина 2 → Вершина 1 → Вершина 2 → Вершина 4: Длина 1 + 1 + 1 = 3
Запрос 2: Вершина 2 → Вершина 1 → Вершина 3: Длина 1 + 1 = 2
Запрос 3: Вершина 4 → Вершина 2 → Вершина 1 → Вершина 3 → Вершина 5: Длина 1 + 1 + 1 + 1 = 4 |
| 2 |
7
1 2 1
1 3 3
1 4 5
1 5 7
1 6 9
1 7 11
3 2
1 3
4 5
6 7 |
5
14
22 |
Путь для каждого запроса должен проходить через вершину K = 2. |
| 3 |
10
1 2 1000000000
2 3 1000000000
3 4 1000000000
4 5 1000000000
5 6 1000000000
6 7 1000000000
7 8 1000000000
8 9 1000000000
9 10 1000000000
1 1
9 10 |
17000000000 |
|
| |
![]()
|
9/
6
|
|
Темы:
Алгоритмы на графах
Кратчайшие пути в графе
Дан неориентированный связный взвешенный граф с N вершинами и M ребрами, который не содержит ни петель, ни двойных ребер. I-е (\(1<=i<=M\)) ребро соединяет вершину ai и вершину bi на расстоянии ci. Будем считать, что петля - это ребро, где \(a_i=b_i\) (\(1<=i<=M\)), а двойные ребра - это два ребра, где \((a_i,b_i)=(a_j,b_j) \) или \((a_i,b_i)=(b_j,a_j)\) (\(1<=i<j<=M\)). Связный граф - это граф, в котором есть путь между каждой парой разных вершин. Найдите количество ребер, которые не входят ни в один кратчайший путь между любой парой различных вершин.
Входные данные
В первой строке задаются два целых числа N и M (\(2<=N<=100\), \(N-1<=M<=min(N \cdot (N-1)/2,1000)\)). Далее идет M строк по три целых числа в каждой строке: ai, bi, ci (\(1<=a_i, b_i<=N\), \(1<=c_i<=1000\)). Данный граф не содержит петель и двойных ребер. Данный граф является связанным.
Выходные данные
Выведите количество ребер в графе, которые не входят ни в один кратчайший путь между любой парой различных вершин.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснения |
| 1 |
3 3
1 2 1
1 3 1
2 3 3
|
1
|
В данном графе кратчайшие пути между всеми парами различных вершин следующие:
Кратчайший путь от вершины 1 к вершине 2: вершина 1 → вершина 2, длина пути равна 1.
Кратчайший путь от вершины 1 к вершине 3: вершина 1 → вершина 3, длина пути равна 1.
Кратчайший путь из вершины 2 в вершину 1: вершина 2 → вершина 1, длина пути равна 1.
Кратчайший путь от вершины 2 к вершине 3: вершина 2 → вершина 1 → вершина 3, длина пути равна 2.
Кратчайший путь от вершины 3 до вершины 1: вершина 3 → вершина 1, длина пути равна 1.
Кратчайший путь от вершины 3 к вершине 2: вершина 3 → вершина 1 → вершина 2, длина пути равна 2.
Таким образом, единственное ребро, которое не содержится ни в одном кратчайшем пути, - это ребро длины 3, соединяющее вершину 2 и вершину 3, поэтому на выходе должно быть 1. |
| 2 |
3 2
1 2 1
2 3 1
|
0
|
Каждое ребро содержится в некотором кратчайшем пути между парой различных вершин. |
| |
![]()
|
6/
3
|
|
Темы:
Интерактивные задачи
Мосты
Алгоритмы на графах
– Это что за остановка – Бологое иль Поповка? – А с платформы говорят: – Это город Ленинград.
«Вот какой рассеянный», Самуил Маршак
Пытаясь спастись от мира спортивного программирования, Алина сбежала на вокзал и уехала прочь на ночной электричке. Минуты медленно уплывали в даль, и уставшую девочку клонило в сон. Ей снился город-сказка, где не надо программировать, а можно гулять, мечтать и наслаждаться жизнью. Внезапно дождь из интерактивных задач разрушил эту идиллию.
Проснувшись и открыв окно, Алина задалась вопросом весьма философского свойства: «Где я?». С перрона потерявшейся девочке сообщили, что этот город, не похожий ни на что вокруг, представляет собой неориентированный граф на n вершинах и m ребрах. Сeй невероятный факт, однако, нисколько не удивил Алину. Она давно мечтала побывать в одном таком городе — Петербурге. Его уникальной отличительной особенностью является то, что хотя бы половина его ребер — мосты (определение дано в конце условия). Так как никакие другие города Алине не интересны, она решила ограничиться расспросом находящихся на платформе эрудированных путешественников. Любой из их них может по данной вершине v сообщить любое ещё не названное ребро, исходящее из нее, или же заявить об отсутствии таковых.
Алина неуверена в своих силах, поэтому попросила вас помочь ей определить, попала ли она в Петербург. Так как её поезд скоро продолжит свой путь, задать больше 3n вопросов не получится.
Обратите внимание, что в графе могут присутствовать петли и кратные ребра.
Протокол взаимодействия
В первой строке стандартного потока ввода даны два целых числа n и m (1 ≤ n, m ≤ 100000 ) — число вершин и ребер в графе соответственно.
Для того, чтобы узнать очередное ребро, исходящее из u-й вершины (1 ≤ u ≤ n), нужно вывести « ? u ». После этого ваша программа на вход получит целое число v (−2 ≤ v ≤ −1 или 1 ≤ v ≤ n) — v=a+b−u, если существует ребро ab, которое инцидентно вершине u и ещё не было названо , −1, если такого ребра не существует и −2, если вы превысили допустимое число запросов. В последнем случае ваша программа должна немедленно завершиться, в ином случае жюри не гарантирует корректность полученного вами вердикта.
Вам разрешается задать не более 3n вопросов.
Чтобы сообщить, что ответ найден, требуется вывести « ! Yes » или « ! No », в зависимости от того, является ли загаданный граф Петербургом. В случае положительного ответа выведите \( {m \over 2}\) строк, по два целых числа ui и vi в каждой (1 ≤ ui, vi ≤ n), обозначающих, что ребро (ui, vi) является мостом. Любое ребро в приведенном списке должно встречаться не более одного раза (кратные ребра считаются различными).
Запрос на вывод ответа не входит в ограничение на 3n запросов.
Примечание
В условии в примере взаимодействия вводимые и выводимые данные расположены для удобства восприятия в хронологическом порядке, при реальном взаимодействии никакие «лишние» переводы строк возникать не должны.
Ввод-вывод в примерах демонстрирует пример взаимодействия вашей программы с проверяющей системой.
В первом примере был загадан граф на трех вершинах с ребрами (1, 2) , (2, 3) и (3, 1) .
Во втором примере была загадан граф на четырех вершинах с ребрами (1, 2) , (2, 3) , (3, 4) и (2, 3) .
Ребро, соединяющее вершины u и v, называется мостом, если после его удаления между вершинами u и v не существует пути.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 3
2
2
-1
3
-1
-1 |
? 3
? 1
? 2
? 1
? 1
? 3
! No |
| 2 |
4 4
2
3
2
-1
4
-1
-1
-1 |
? 1
? 2
? 3
? 1
? 3
? 3
? 2
? 4
! Yes
1 2
3 4 |
| |
![]()
|
18/
0
|
|
Темы:
Алгоритмы на графах
Есть N городов. Есть также шоссе K и железные дороги L, проходящие между городами. Каждое i-я шоссе двунаправленно соединяет рi и qi города, а каждая i-я железная дорога двунаправленно соединяет ri и si города. Нет двух шоссе, соединяющих одну и ту же пару городов. Точно так же, никакие две железные дороги не соединяют одну и ту же пару городов. Будем считать, что города A и B соединены шоссе, если до города B можно добраться из города A по некоторому количеству шоссе. Здесь любой город считается соединенным с собой шоссе. Аналогичным образом, мы также определим возможность сообщения железными дорогами. Для каждого города найдите количество городов, соединенных с этим городом как шоссе, так и железными дорогами.
Входные данные
Входные данные поступают в следующем формате:
N K L
p1 q1
...
pK qK
r1 s1
...
rl sL
Ограничения:
\(2<=N<=2\cdot10^5 \\ 1<=K,L<=10^5 \\ 1<=p_i,q_i,r_i,s_i<=N\\ p_i <q_i \\ r_i<s_i \\ Когда\ i \neq j, (p_i,q_i)\neq(p_j,q_j) \\ ?Когда\ i \neq j, (r_i,s_i)\neq(r_j,s_j)\)
Выходные данные
Выведите N целых чисел в одной строке, разделяя каждое число одним пробелом. Каждое i число должно обозначать количество городов, соединенных с i-м городом как шоссе, так и железными дорогами.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснения |
| 1 |
4 3 1
1 2
2 3
3 4
2 3 |
1 2 2 1 |
Все четыре города связаны между собой дорогами.
Железной дорогой соединены только второй и третий города. Таким образом, ответы для городов 1,2,2 и 1 соответственно. |
| 2 |
4 2 2
1 2
2 3
1 4
2 3 |
1 2 2 1 |
|
| 3 |
7 4 4
1 2
2 3
2 5
6 7
3 5
4 5
3 4
6 7 |
1 1 2 1 2 2 2 |
|
| |
![]()
|
/
|
|
Темы:
Динамическое программирование
Алгоритмы на графах
Обход в глубину
Динамическое программирование на графах
В тридесятом государстве есть N деревень. Некоторые пары деревень соединены дорогами. В целях экономии, “лишних” дорог нет, т.е. из любой деревни в любую можно добраться по дорогам единственным образом.
Новейшие исследования показали, что тридесятое государство находится в сейсмически опасной зоне. Поэтому глава государства захотел узнать, какой именно ущерб может принести его державе землетрясение. А именно, он хочет узнать, какое минимальное число дорог должно быть разрушено, чтобы образовалась изолированная от остальных группа ровно из P деревень такая, что из любой деревни из этой группы до любой другой деревни из этой группы по-прежнему можно будет добраться по неразрушенным дорогам (группа изолирована от остальных, если никакая неразрушенная дорога не соединяет деревню из этой группы с деревней не из этой группы).
Вы должны написать программу, помогающую ему в этом.
Формат входных данных
Первая строка входного файла содержит два числа: N и P (1 ≤ P ≤ N ≤ 150). Все остальные строки содержат описания дорог, по одному на строке: описание дороги состоит из двух номеров деревень (от 1 до N), которые эта дорога соединяет. Все числа во входном файле разделены пробелами и/или переводами строки.
Формат выходных данных
В выходной файл выведите единственное число — искомое количество дорог.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
3 2
1 2
3 2 |
1 |
|
| 2 |
11 6
1 2
1 3
1 4
1 5
2 6
2 7
2 8
4 9
4 10
4 11 |
2 |
группа деревень (1, 2, 3, 6, 7, 8) окажется изолированной от остальных, если разрушить дороги 1–4 и 1–5. |
| |
![]()
|
11/
1
|
|
Темы:
Минимальный каркас
Алгоритмы на графах
С целью подготовки к проведению олимпиады по информатике мэр решил обеспечить надежным электроснабжением все школы города. Для этого необходимо провести линию электропередач от альтернативного источника электроэнергии “Майбуття” к одной из школ города (к какой неважно), а также соединить линиями электропередач некоторые школы между собой.
Считается, что школа имеет надежное электроснабжение, если она напрямую связана с источником “Майбуття”, либо с одной из тех школ, которые имеют надежное электроснабжение.
Известна стоимость соединения между некоторыми парами школ. Мэр города решил выбрать одну из двух наиболее экономичных схем электроснабжения (стоимость схемы равняется сумме стоимостей соединений пар школ).
Напишите программу, которая вычисляет стоимость двух наиболее экономных схем альтернативного электроснабжения школ.
Входные данные
В первой строке входного файла находятся два натуральных числа, разделенных пробелом: N (3 <= N <= 100), количество школ в городе, и M – количество возможных соединений между ними. В каждой из последующих M строк находятся по три числа: Ai, Bi, Ci, разделенных пробелами, где Ci - стоимость прокладки линии электроснабжения (1 <= Ci <= 300) от школы Ai до школы Bi (i=1,2,…,N).
Выходные данные
В единственной строке выходного файла должны содержаться два натуральных числа S1 и S2, разделенных пробелом – две наименьшие стоимости схем (S1 <= S2). S1=S2 тогда и только тогда, когда существует несколько схем надежного электроснабжения наименьшей стоимости.
Гарантируется, что для входных данных существует две различные схемы надёжного электроснабжения.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5 8
1 3 75
3 4 51
2 4 19
3 2 95
2 5 42
5 4 31
1 2 9
3 5 66
|
110 121 |
| |
![]()
|
140/
22
|
|
Темы:
Алгоритмы на графах
Найдите суммарную длину всех дорог в городе Новые Васюки. Схема дорог задана в виде весовой матрицы графа. На некоторых дорогах введено одностороннее движение. Если длины дорог из пункта А в пункт Б разные, это означает, что есть две разные дороги.
Входные данные
В первой строке вводится количество перекрёстков в Новых Васюках N ( 1 ≤ N ≤ 1000 ). В следующих N строках записано по N чисел, разделённых пробелами – длины дорог между каждой парой перекрёстков. Ноль означает, что дороги между этими перекрёстками нет.
Выходные данные
Программа должна вывести одно число – суммарную длину дорог. Дороги с двусторонним движением нужно считать только один раз.
|
Ввод |
Вывод |
|
5
0 2 3 4 0
2 0 5 0 7
3 6 0 8 0
0 0 0 0 0
0 7 0 9 0
|
44 |
| |
![]()
|
730/
414
|
|
Темы:
Алгоритмы на графах
Напишите программу, которая считает количество дорог в городе Новые Васюки. Схема дорог задана как матрица смежности графа. На некоторых дорогах введено одностороннее движение.
Входные данные
В первой строке вводится количество перекрёстков в Новых Васюках N ( 1 ≤ N ≤ 1000 ). В следующих N строках записано по N чисел, разделённых пробелами – элементы матрицы смежности графа, который описывает схему дорог.
Выходные данные
Программа должна вывести одно число – количество дорог в Новых Васюках. Дороги с двусторонним движением нужно считать только один раз.
|
Ввод |
Вывод |
|
5
0 1 1 1 0
1 0 1 0 1
1 1 0 1 0
0 0 0 0 0
0 1 0 1 0
|
7 |
| |
![]()
|
669/
378
|
|
Темы:
Деревья
Алгоритмы на графах
Строки
Динамическое программирование
Газораспределительная система одного региона устроена следующим образом. Она
содержит n узлов, пронумерованных от 1 до n, некоторые узлы соединены односторонними
трубами. Узел с номером 1 соответствует центральному газохранилищу.
Система узлов описывается числами от p2, p3, …, pn. Для всех i от 2 до n узел с
номером pi соединен односторонней трубой с узлом i, газ по этой трубе передается от узла pi
к узлу i. Известно, что возможно доставить газ по трубам от центрального газохранилища до
любого узла системы (возможно, с использованием промежуточных узлов). В системе
используются трубы различных типов, тип трубы обозначается буквой английского алфавита
от «a» до «z». Труба, соединяющая узел pi с узлом i, имеет тип ci.
Для проверки качества труб используется специальный робот. Он помещается в
систему труб в одном из узлов и перемещается по трубам, каждый раз проверяя трубу, по
которой он перемещается. Робот может перемещаться по трубам только в том же
направлении, в котором по трубе передается газ. Совершив одно или несколько
перемещений по трубам между узлами, робот извлекается из системы труб.
Каждый запуск робота должен соответствовать одной из m заданных спецификаций,
пронумерованных от 1 до m. Спецификация с номером t представляет собой строку st,
состоящую из строчных букв английского алфавита. Запуск соответствует спецификации st,
если количество перемещений робота по трубам во время запуска совпадает с длиной st, и
для всех j от 1 до длины st на j-м шаге робот перемещается по трубе, тип которой совпадает с
st[j] —символом на позиции j в спецификации.
Если запуск робота соответствует спецификации с номером t, то стоимость этого
запуска составляет wt. Оператору системы необходимо проверить все трубы, для этого
можно запускать робот несколько раз. Каждый раз выбирается спецификация и маршрут
робота по трубам, соответствующие выбранной спецификации. Необходимо проверить все
трубы так, чтобы суммарная стоимость запусков робота для проверки качества труб была
минимальна. Одну и ту же трубу можно проверять несколько раз.
Требуется написать программу, которая по описанию системы труб и списку
спецификаций определяет минимальную суммарную стоимость запусков робота, в
результате которых все трубы будут проверены, а также список необходимых для этого
запусков (по требованию).
Формат входных данных
В первой строке входных данных находятся три целых числа n, m и t — количество
узлов системы труб, количество спецификаций запусков робота и параметр, указывающий,
требуется ли вывести список запусков робота или только их минимальную суммарную
стоимость (1 ≤ n ≤ 500, 1 ≤ m ≤ 105, t равно 0 или 1).
В последующих (n – 1) строках содержится информация о трубах, (i – 1)-я из этих
строк содержит разделенные пробелом значения pi и ci, где pi — целое число, задающее
номер узла, из которого ведет труба в i-й узел, а ci — строчная буква английского алфавита,
задающая тип этой трубы (1 ≤ pi ≤ i – 1).
В последующих m строках содержится информация о спецификациях, i-я из этих
строк содержит разделенные пробелом целое число wi — стоимость запуска робота в
соответствии с этой спецификацией, и состоящую из строчных букв английского алфавита
строку si — саму спецификацию (1 ≤ wi ≤ 10 9). Суммарная длина строк si не превышает 10 6.
Формат выходных данных
Первая строка выходных данных должна содержать одно число — минимальную
суммарную стоимость запусков робота, в результате которых все трубы будут проверены.
Если проверить все трубы невозможно, требуется вывести «–1».
Если t = 0, то больше ничего выводить не требуется.
Если t = 1 и проверить трубы возможно, то далее следует вывести список описаний
запусков робота. В этом случае вторая строка выходных данных должна содержать
число k — количество запусков робота, которое необходимо выполнить для проверки труб. В
следующих k строках необходимо вывести по три целых числа ai, bi и ci — номер узла, в
котором начинается запуск, номер узла, в котором заканчивается запуск, и номер
спецификации, которой соответствует запуск.
Если оптимальных способов проверки несколько, требуется вывести любой из них.
| Ввод |
Вывод |
|
3 3 0
1 a
2 b
3 a
4 b
2 a
|
6 |
|
7 3 1
1 a
2 a
3 b
3 b
1 b
6 b
3 aab
5 b
2 ab
|
15
4
1 4 1
2 5 3
1 6 2
6 7 2
|
Пояснение к примеру
Система труб, заданная во втором примере входных данных, и оптимальный способ
проверки всех труб для этого случая приведены на рисунке ниже.
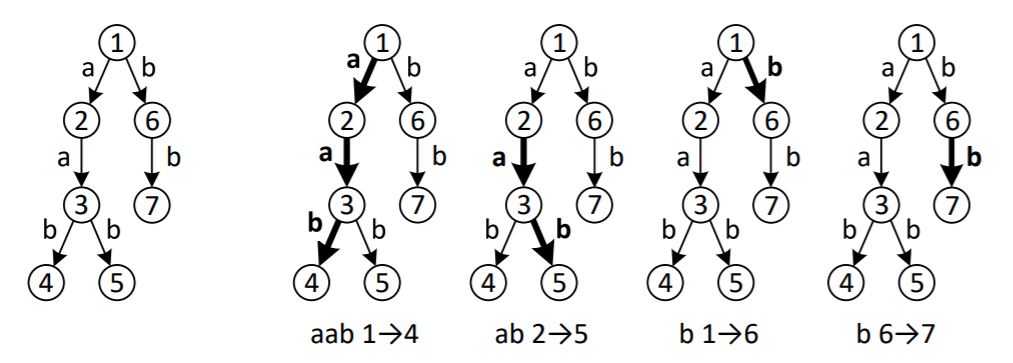
Необходимо обратить внимание на следующие моменты:
- трубу можно проверять несколько раз, так в приведенном примере дважды
проверена труба из узла 2 в узел 3;
- одну и ту же спецификацию разрешается использовать несколько раз, в
приведенном примере вторая спецификация используется дважды, для
проверки труб из узла 1 в узел 6 и из узла 6 в узел 7;
- робот может перемещаться по трубам только в том же направлении, по
которому по трубе передается газ, спецификацию «ab» нельзя использовать
для проверки труб по маршруту 2→1→6, так как робот не может
переместиться из узла 2 в узел 1.
| |
![]()
|
/
|
|
Темы:
Минимальный каркас
Структуры данных
Дерево отрезков, RSQ, RMQ
Обход в глубину
Алгоритмы на графах
Фермер Джон обнаружил, что разные типы коров любят разные типы травы. Однако он должен правильно их высаживать, чтобы не навредить.
Ферма Джона состоит из NN (1≤N≤200,000), полей, и MM пар полей соединены двунаправленными дорожками (1≤M≤200,000). Используя эти дорожки, можно пройти от любого поля к любому другому полю. Каждая дорожка имеет целочисленную длину в интервале 1…1,000,000. Любая пара полей соединена не более чем одной прямой дорожкой.
В каждом поле ФД изначально посадил один из KK типов травы (1≤K≤N). Через некоторое время, однако, он может решить изменить тип травы на некоторых из полей. Он называет это операцией "обновления".
После каждого обновления, ФД хочет знать длину кратчайшего пути между двумя полями, имеющими различные типы травы. То есть, среди всех пар полей, имеющих различные типы травы, он хочет узнать, какие два поля ближайшие друг к другу. Гарантируется, что всегда имеется как минимум одна пара полей с различными типами травы.
В 30 процентах тестов каждое поле непосредственно соединено не более чем с 10 дорожками.
ФОРМАТ ВВОДА:
Первая строка ввода содержит четыре целых числа N, M, K, Q, где Q - количество операций обновления (1≤Q≤200,000). Следующие M строк описывают дорожки. Каждая строка содержит три целых числа A, B, L, указывающих, что есть дорожка между полями A, B и её длина L. (A, B - целые числа в интервале 1…N). Следующая строка указывает начальный тип травы для каждого поля (N целых чисел в интервале 1…K). Затем идут Q строк, каждая из которых описывает одну операцию обновления двумя целыми числами A и B, означающими, что на поле A типе травы изменён на B.
ФОРМАТ ВЫВОДА:
Для каждой операции обновления выведите длину кратчайшего пути между двумя полями с различными типами травы, после применения этой операции обновления.
| Ввод |
Вывод |
|
3 2 3 4
1 2 3
2 3 1
1 1 2
3 3
2 3
1 2
2 2
|
1
3
3
1
|
| |
![]()
|
5/
1
|
|
Темы:
Алгоритмы на графах
Конструктив
Комбинаторика
Boolean satisfiability problem (SAT) is known to be a very hard problem in computer science. In this problem you are given a Boolean formula, and you need to find out if the variables of a given formula can be consistently replaced by the values true or false in such a way that the formula evaluates to true. SAT is known to be NP-complete problem. Moreover, it is NP-complete even in case of 3-CNF formula (3-SAT). However, for example, SAT problem for 2-CNF formulae (2-SAT) is in P.
#SAT is the extension of SAT problem. In this problem you need to check if it is possible, and count the number of ways to assign values to variables. This problem is known to be #P-complete even for 2-CNF formulae. We ask you to solve #1-DNF-SAT, which is #SAT problem for 1-DNF formulae.
You are given a Boolean formula in 1-DNF form. It means that it is a disjunction (logical or) of one or more clauses, each clause is exactly one literal, each literal is either variable or its negation (logical not). Formally:
 Your task is to find the number of ways to replace all variables with values true and false (all occurrences of the same variable should be replaced with same value), such that the formula evaluates to true.
Input
The only line of the input file contains a logical formula in 1-DNF form (not longer than 1000 symbols). Logical operations are represented by ‘|’ (disjunction) and ‘~’ (negation). The variables are ‘A’ . . . ‘Z’ and ‘a’ . . . ‘z’ (uppercase and lowercase letters are different variables). The formula contains neither spaces nor other characters not mentioned in the grammar.
Output
Output a single integer — the answer for #SAT problem for the given formula
| Input |
Output |
| a |
1 |
| B|~B |
2 |
| c|~C |
3 |
| i|c|p|c |
7 |
| |
![]()
|
27/
11
|
|
Темы:
Обход в ширину
Структуры данных
Алгоритмы на графах
В научно-исследовательском институте чародейства и волшебства пожар! Во время опыта Кор- неева В. П. по превращению всей морской и океанской воды планеты в живую воду произошло короткое замыкание, и теперь его кабинет объят пламенем. Задача первостепенной важности — спасти из огня ценные лабораторные приборы, в особенности единственный в своём роде диван- транслятор µ-поля. Ваша задача — перенести диван-транслятор из кабинета Корнеева в запасную лабораторию изучения µ-поля.
НИИЧАВО состоит из N кабинетов, соединённых M коридорами. Кабинеты пронумерованы це- лыми числами от 1 до N, при этом кабинет Корнеева имеет номер A, а лаборатория изучения µ-поля расположена в кабинете номер B. Благодаря специальному искажению пространства внутри инсти- тута, все коридоры имеют одинаковую длину, которую можно пройти за 1 минуту, если двигаться быстрым шагом.
Ситуация усугубляется тем, что диван-транслятор — прибор, очень чувствительный к резким пе- репадам температуры. Внутри каждого коридора НИИЧАВО поддерживается свой температурный режим. Если абсолютная величина разности температур в двух последовательных коридорах на пути из кабинета Корнеева в лабораторию окажется больше D градусов, то диван-транслятор пе- рейдёт в нестабильное состояние, что может привести к катастрофическим последствиям. Обратите внимание, что на своём пути вы не заходите в сами кабинеты, а только переходите из коридора в коридор, поэтому климат внутри кабинетов не влияет на диван-транслятор. В силу причин магиче- ского характера, войдя в коридор, вы обязаны дойти до его конца, иными словами, останавливаться или разворачиваться посреди коридора запрещено. По каждому коридору можно перемещаться в обоих направлениях.
Определите, за какое минимальное время можно добраться из кабинета Корнеева до запасной лаборатории, не допуская резкого перепада температур. В рамках данной задачи вам предлагается ответить на поставленный вопрос для нескольких пар значений A и B.
Формат входных данных
В первой строке входных данных следуют три целых числа N, M и D (2 <= N <= 100 000, 1 <= M <= 200 000, 0 <= D <= 2 · 108 ), обозначающие количество кабинетов, количество коридоров в НИИЧАВО и максимальный допустимый перепад температур для дивана-транслятора в граду- сах. В последующих M строках находятся описания коридоров. Каждая строка содержит по три целых числа ui , vi , ti — номера двух кабинетов, соединённых i-м коридором, и значение температуры в этом коридоре, выраженное в градусах (1 <= ui , vi <= N, −109 <= ti <= 109 ). Как вы уже могли понять, НИИЧАВО — весьма необычное заведение, поэтому между двумя кабинетами может пролегать несколько коридоров, возможно с разными температурами, а некоторые коридоры могут соединять кабинет с самим собой. Гарантируется, что коридоры перечислены во входном файле в порядке неубывания ti . В следующей строке находится целое число Q (1 <= Q <= 50) — количество пар A и B, которые вам требуется обработать. В каждой из последующих Q строк находятся по два целых числа Ai , Bi , обозначающих номер кабинета Корнеева и номер кабинета, в котором расположена лаборатория (1 <= Ai , Bi <= N, Ai != Bi).
Формат выходных данных
Для каждого набора данных выведите в отдельной строке минимальное количество минут, ко- торое требуется потратить, чтобы добраться из кабинета Корнеева до лаборатории, либо выведите −1, если сделать это, используя допустимый для дивана-транслятора маршрут, невозможно.
Примеры
| Ввод |
Вывод |
6 9 5
6 6 -42
1 2 4
2 3 6
3 2 7
2 5 11
6 1 12
1 3 15
3 4 16
5 6 18
2
1 5
4 2 |
4
-1 |
6 9 7
6 6 -42
1 2 4
2 3 6
3 2 7
2 5 11
6 1 12
1 3 15
3 4 16
5 6 18
1
4 2 |
5 |
Замечание
Пояснение к тестам из условия. В обоих тестах план НИИЧАВО выглядит следующим образом:
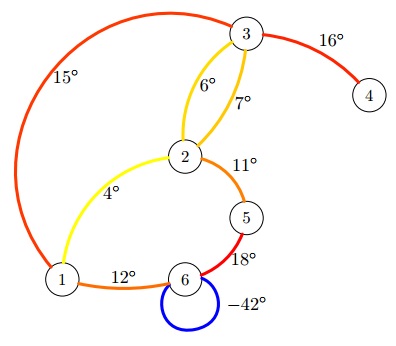
Рассмотрим первый тест, в нём D = 5. В первом наборе A = 1, B = 5. В качестве воз- можного маршрута может выступить следующая последовательность переходов по коридорам:
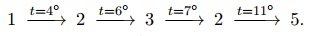 Третьим шагом можно вернуться в кабинет 2 и по тому же коридору с t = 6 . Третьим шагом можно вернуться в кабинет 2 и по тому же коридору с t = 6 .
Во втором наборе A = 4, B = 2. Способа добраться из кабинета 4 в кабинет 2, ни разу не допустив перепад температуры больше, чем в 5 градусов, не существует.
Во втором тесте D = 7. В единственном наборе A = 4, B = 2 cтартовый и конечный кабинет те же, что и во втором наборе первого теста из условия, но допустимый перепад температур больше, благодаря чему подходит следующий маршрут: 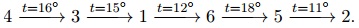
| |
![]()
|
26/
11
|
|