| | | |
|
Коровы
Потоки
Пете необходимо переправить стадо коров через болото. Для переправы можно использовать доски, которые соединяют кочки. После того, как на кочке кто-нибудь побывал, она тонет. Вам требуется переправить максимальное количество коров через болото.
Входные данные
В первой строке входного файла записано число досок N (0 <= N <= 1000). Далее для каждой доски записаны координаты кочек - концов доски (-231 <= Xi,Yi <= 231). Затем записаны координаты начальной и конечной точек (точки различны и доски, их соединяющей нет). Все числа во входном файле целые.
Выходные данные
Вывести максимально количество коров, которых можно переправить
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
8
0 0 1 0
1 0 2 1
1 0 2 -1
2 1 3 0
2 -1 3 0
1 0 4 0
3 0 4 0
0 0 3 0
0 0
4 0 |
2 |
| |
![]()
|
|
Пешки
Потоки
В первом классе Глеб увлекался шахматами. К тому моменту он знал только лишь как ходит пешка: она может бить по диагонали влево-наверх и вправо-наверх, и ходить на клетку вверх только если та клетка не занята другой фигурой. Поэтому он придумал свой вариант шахмат.
Игра идёт на доске с \(N\) строками и \(M\) столбцами (\(1 \le N \le 100\), \(1 \le M \le 100\)) по следующим правилам. В нижней строке, имеющей номер 1, стоит \(P\) белых пешек, белых фигур на доске больше нет. На остальной части доски стоят разные чёрные фигуры (их названия Глеб не знает). Ходят только белые, цель — достичь хотя бы одной пешкой самой верхней строки, имеющей номер \(N\) (Глеб слышал, что в этой ситуации из пешки можно сделать ферзя, а с такой силой он безусловно сможет побить все остальные чёрные фигуры).
Как и в настоящих шахматах, если пешка Глеба бьёт чёрную фигуру, то она становится на её место, а побитая фигура убирается с доски. Считается, что Глеб выиграл, если он сумел достичь хотя бы одной пешкой самой верхней строки, в противном случае он проиграл. Помогите ему по заданной конфигурации всех фигур определить, сможет ли он выиграть.
Формат входных данных
Сначала вводятся четыре целых числа \(N\), \(M\), \(P\), \(K\) (\(1 \le N \le 100\), \(1 \le M \le 100\), \(0 \le P \le M\), \(1 \le K \le (N - 1)M\). Далее записано \(P\) различных чисел — номера столбцов \(p_j\) (\(1 \le p_j \le M\)), в которых стоят белые пешки. Далее идут \(K\) различных пар целых чисел — номера строк и столбцов чёрных фигур \(r_i\), \(c_i\) (\(2 \le r_i \le N\), \(1 \le c_i \le M\)).
Формат выходных данных
Если хотя бы одна пешка сможет достичь последнего ряда, выведите YES, в противном случае выведите NO.
| |
![]()
|
|
K задач (A)
Потоки
Паросочетания
K участникам сборов для решения было предложено K задач. Участники решили разделить задачи между собой, решить каждому по одной задаче, а затем обменяться решениями (они не учли, что система ejudge способна отследить данный факт J). Известно ориентировочное время, за которое каждый из участников сборов может решить каждую из предложенных задач.
Помогите участникам сборов распределить задачи так (по одной каждому участнику), чтобы суммарное время, потраченное на их решение было минимальным.
Входные данные
Во входном файле сначала записано число K (0 < K < 101) и далее K2 неотрицательных целых чисел, не превосходящие 20000, описывающих матрицу K x K, времен решения каждым из участников каждой из задач.
Выходные данные
В файл выведите суммарное минимальное время решения всех задач, при условии, что каждый участник решит ровно одну задачу.
| |
![]()
|
|
Кубики
Потоки
Паросочетания
Родители подарили Пете набор детских кубиков. Поскольку Петя скоро пойдет в школу, они купили ему кубики с буквами. На каждой из шести граней каждого кубика написана буква.
Теперь Петя хочет похвастаться перед старшей сестрой, что научился читать. Для этого он хочет сложить из кубиков ее имя. Но это оказалось довольно сложно сделать - ведь разные буквы могут находиться на одном и том же кубике и тогда Петя не сможет использовать обе буквы в слове. Правда одна и та же буква может встречаться на разных кубиках. Помогите Пете!
Дан набор кубиков и имя сестры. Выясните, можно ли выложить ее имя с помощью этих кубиков и если да, то в каком порядке следует выложить кубики.
Входные данные
В первой строке вводится число N (1 <= N <= 100) - количество кубиков в наборе у Пети. Во второй строке задано имя Петиной сестры - слово, состоящие только из больших латинских букв, не длиннее 100 символов. Следующие N строк содержат по 6 букв (только большие латинские буквы), которые написаны на соответствующем кубике.
Выходные данные
В первой строке выведите "YES" если выложить имя Петиной сестры данными кубиками можно, "NO" в противном случае.
В случае положительного ответа, во второй строке выведите M различных чисел из диапазона 1…N, где M - количество букв в имени Петиной сестры. i-е число должно быть номером кубика, который следует положить на i-е место при составлении имени Петиной сестры. Кубики нумеруются с 1, в том порядке, в котором они заданы во входных данных. Если решений несколько, выведите любое. Разделяйте числа пробелами.
| |
![]()
|
|
G. Разрешенные буквы
Потоки
Паросочетания
жадные алгоритмы
*2400
графы
битмаски
Поликарп недавно запустил свою новую идею для стартапа. Ниша довольно свободна, вектор развития звучит еще как многообещающе, поэтому он довольно легко нашел себе инвесторов для поддержки компании. Однако он так и не смог выбрать название стартапа! На самом деле, Поликарп придумал название, но некоторые изменения ему точно не помешают. Теперь он хочет поменять местами некоторые буквы, чтобы получить лучшее название. Буквы не обязательно должны стоять рядом. К тому же, каждый из инвесторов выбрал себе по позиции в названии и утвердил список букв, которые могут там стоять. Позиции, выбранные инвесторами попарно различны. Если некоторые позиции не выбраны ни одним инвестором, то там может стоять любая буква. Наконец, Поликарп уверен, что минимальное лексикографически название — лучшее название. (Ну так а почему, думаете, Google решил стать Alphabet?) Формально, вам дана строка, состоящая из строчных латинских букв от «a» to «f». Можно менять местами буквы на любых позициях произвольное количество раз (можно и ноль). Какое минимальное лексикографически название получить такое, что буква на каждой позиции в нем находится среди разрешенных букв? Если Поликарп не может получить ни одного корректного названия, то выведите «Impossible». Выходные данные Если Поликарп не может составить никакого корректного названия, то выведите «Impossible». В противном случае выведите минимальное лексикографически название, которое Поликарп может получить с помощью обменов букв в строке \(s\), такое, что буква на каждой позиции в нем находится среди разрешенных букв. | |
![]()
|
|
D. Вася и матрица
Потоки
Конструктив
математика
*1800
Сегодня Вася сдает экзамен по математике. Чтобы получить хорошую оценку, Вася должен угадать загаданную учителем матрицу! Вася знает, что в матрице n строк и m столбцов. Для каждой строки ему известен xor (побитовое исключающее или) всех элементов в этой строке. Последовательность a1, a2, ..., an задает xor элементов строки под номером 1, 2, ..., n, соответственно. Аналогично, для каждого столбца Вася знает xor всех элементов в столбце. Последовательность b1, b2, ..., bm обозначает xor элементов в столбцах под номерами 1, 2, ..., m, соответственно. Помогите Васе! Найдите матрицу, которая соответствует этим ограничениям, или скажите, что такой матрицы не существует. Выходные данные Если не существует матрицы, удовлетворяющей заданным ограничениям, в первой строке выведите «NO». Иначе в первой строке выведите «YES», а затем n строк по m чисел в каждой ci1, ci2, ... , cim (0 ≤ cij ≤ 2·109) — описание матрицы. Если существует несколько подходящих матриц — разрешено вывести любую из них. | |
![]()
|
|
G. Рыбы
Потоки
Деревья
Структуры данных
*3400
Группа исследователей изучает популяцию рыб в естественной системе рек и озер. Система состоит из \(n\) озёр, соединённых между собой \(n - 1\) реками. Каждая река имеет целочисленную длину (в километрах) и допускает перемещение в обоих направлениях. От любого озера можно добраться до любого другого по рекам (иными словами, система представляет собой дерево). В озёрах живёт неизвестное количество рыб, неотличимых друг от друга. В день \(1\) рыбы произвольно распределены по озёрам. Рыбы могут перемещаться между озёрами по рекам. Рыба может проплыть реку длиной \(l\) километров за \(l\) дней. Также любая рыба, которая посещает какое-либо озеро, может оставаться в нём любое количество дней. В наблюдаемый период в системе не появляется новых рыб, и присутствующие рыбы не исчезают. В любом озере в любой момент времени может находиться сколь угодно большое количество рыб одновременно. Исследователи провели несколько наблюдений. \(j\)-е из этих наблюдений определило, что в день \(d_j\) в озере \(p_j\) находилось не менее \(f_j\) различных рыб. Помогите исследователям определить наименьшее возможное общее количество рыб, проживающих в озёрах, которое не противоречило бы сделанным наблюдениям. Выходные данные Выведите одно число — наименьшее общее количество рыб, не противоречащее наблюдениям. Примечание В первом примере одна из рыб могла проплыть через озёра \(2\), \(1\) и \(4\), а вторая — через озёра \(3\), \(1\) и \(2\). Во втором примере одна рыба не могла быть замечена во всех наблюдениях одновременно, но две рыбы, плывущие по маршрутам \(2 \to 1 \to 4\) и \(3 \to 1 \to 5\), могли. В третьем примере одна рыба могла приплыть из озера \(1\) в озеро \(5\), а остальные могли все время находиться в одном и том же озере: две рыбы в озере \(4\), шесть рыб в озере \(5\), одна рыба в озере \(3\). Система озер показана на рисунке ниже. 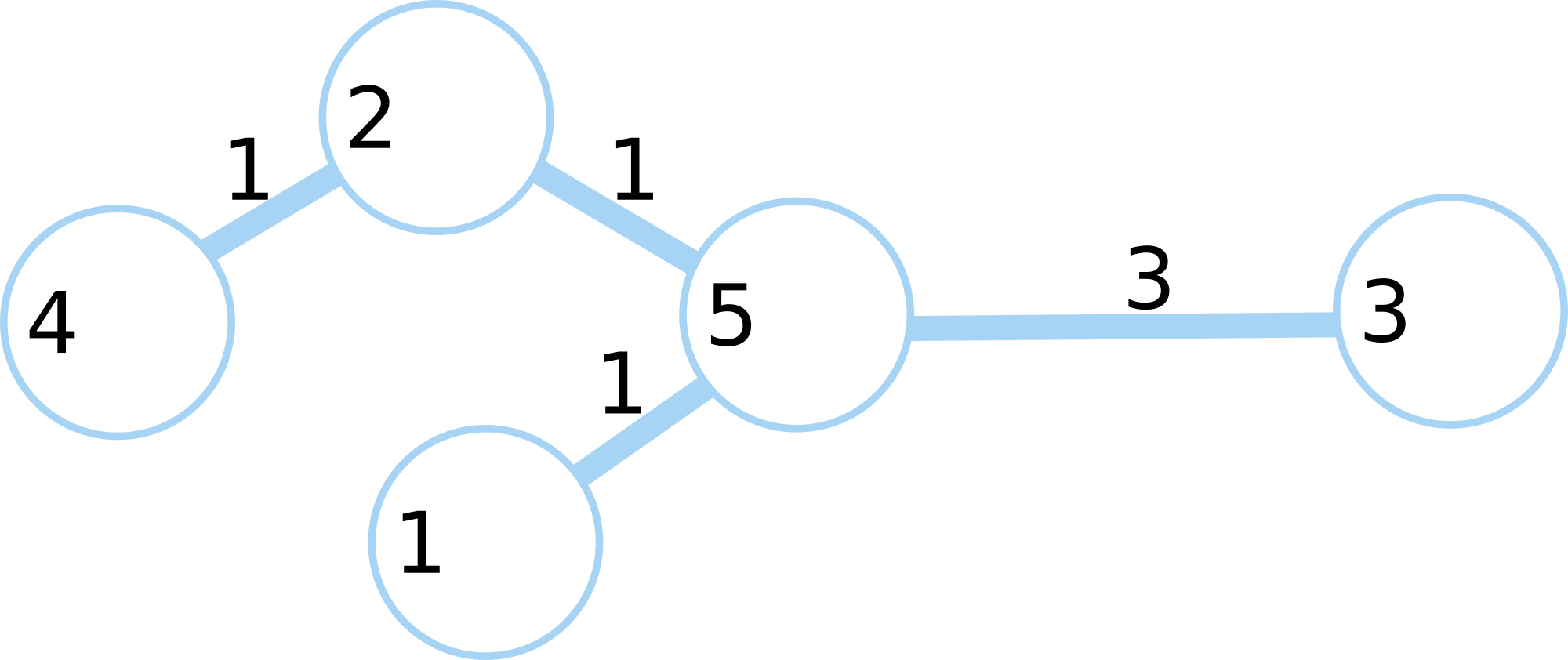 | |
![]()
|
|
E. Закупка множеств
Потоки
Паросочетания
*2900
СЪЕЛ ОУЖАС. Рабочее название задачи Вирус Хексадесимал очень любит играть с числовыми множествами — пересекать их, объединять. В один прекрасный день она с удивлением обнаружила, что Сказзи, ее ручной сферический кот, объединил все множества в одно и съел результат! Надо было срочно что-то делать, и Хексадесимал полетела на рынок. На рынке продается n числовых множеств. Вирус хочет купить такой набор множеств, что количество множеств в нем будет равно количеству чисел в его объединении. Из всех подходящих наборов множеств она готова выбрать только самый дешевый. Но не все так просто! Поскольку в Мэйнфрейме царит рынок совершенной конкуренции, то известно, что объединение любых k множеств содержит не менее k различных чисел (для любого целого положительного k). Помогите вирусу выбрать подходящий набор множеств. Этот набор может быть пустым. Выходные данные Выведите одно число — минимальную стоимость покупки такого набора из k множеств, что объединение множеств этого набора содержит ровно k чисел (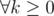 ). ). | |
![]()
|
|
B. Little C любит 3 II
Потоки
Паросочетания
Перебор
Конструктив
*2200
Little C очень любит число «3». Он любит все, что с ним связано. Сейчас он играет в игру на шахматной доске \(n \times m\). Клетку в строке \(x\) и в столбце \(y\) назовем \((x,y)\). Исходно, шахматная доска пуста. Каждый раз он ставит две шахматные фигуры на две различные пустые клетки, Манхэттенское расстояние между которыми равно \(3\). Манхэттенским расстоянием между клетками \((x_i,y_i)\) и \((x_j,y_j)\) назовем \(|x_i-x_j|+|y_i-y_j|\). Он хочет расставить таким образом как можно больше шахматных фигур на доске. Пожалуйста, помогите ему найти максимальное количество фигур которое он может так расставить. Выходные данные Выведите единственное целое число — максимально количество шахматных фигур, которое сможет расставить Little C. Примечание В первом примере Манхэттенское расстояние между любыми двумя клетками меньше чем \(3\), поэтому ответ \(0\). Во втором примере, одно из возможных решений это \((1,1)(3,2)\), \((1,2)(3,3)\), \((2,1)(1,3)\), \((3,1)(2,3)\). | |
![]()
|
|
A. Последний шанс
Потоки
Паросочетания
Деревья
Структуры данных
графы
*2500
2969-й год. Прошло 1000 лет с момента посадки на луну. Человечество колонизировало Гиперпространство и жило в гармонии. Жило, пока мы не поняли, что мы не одни. Не очень далеко от Земли многочисленный космический флот инопланетян готовит атаку на Землю. Впервые за долгое время человечеству угрожает реальная опасность. Повсюду паника и кризис. Ученые со всей солнечной системы встретились и обсуждают возможный выход из ситуации. Но пока все усилия тщетны. Последняя надежда Земли — ВЫ! К счастью, Земля имеет мощную систему защиты, созданную специалистами из MDCS. Флот инопланетян содержит \(N\) кораблей на одной линии. Система защиты состоит из трех типов вооружения: - SQL-ракеты: каждая SQL-ракета может уничтожить не более одного корабля инопланетян из заданного для каждой ракеты набора.
- лучи Познания: каждому лучу Познания сопоставлен отрезок \([l,r]\), он может уничтожить не более одного корабля инопланетян из этого отрезка.
- OMG-базука: каждая OMG-базука имеет ровно три цели и может уничтожить либо ровно ноль, либо ровно два корабля. Кроме того, система прицеливания является «умной», поэтому множества трех целей для любых двух OMG-базук не пересекаются (таким образом, каждый корабль находится под прицелом не более чем одной OMG-базуки).
Ваша задача — найти такой план атаки на корабли инопланетян, чтобы уничтожить максимально возможное количество кораблей. Каждый уничтоженный корабль должен быть уничтожен ровно одним оружием. Выходные данные Первая строка должна содержать максимальное количество уничтоженных кораблей \(X\). Каждая из следующих \(X\) строк должна содержать два целых числа \(A\) и \(B\), где \(A\) — номер оружия, а \(B\) — номер корабля, уничтоженного оружием \(A\). Примечание SQL-ракета может уничтожить только четвертый корабль. OMG-базука может уничтожить два из 1-го, 4-го или 5-го кораблей, а луч Познания может уничтожить любой корабль из отрезка \([1,4]\). Максимальное количество уничтоженных кораблей равно 4, один из возможных планов — SQL-ракета уничтожает 4-й корабль, OMG-базука уничтожает 1-й и 5-й корабли, а луч Познания уничтожает 2-й корабль. | |
![]()
|
|
F. Электрическая схема
Потоки
Паросочетания
*2700
Паша — начинающий техник, но уже поставил себе большую цель собрать собственный компьютер. Первая непростая задача — научиться собирать электрическую схему. Схема, которую собрал Паша, состоит из несколько проводов. Каждый провод — это отрезок, который соединяет две точки на плоскости с целыми координатами, лежащими в диапазоне \([1, 10^9]\). В схеме есть провода двух цветов: - красные провода: эти провода должны иметь вид горизонтального отрезка, то есть если провод соединяет две точки \((x_1, y_1)\) и \((x_2, y_2)\), то выполнено, что \(y_1 = y_2\);
- синие провода: эти провода должны иметь вид вертикального отрезка, то есть если провод соединяет две точки \((x_1, y_1)\) и \((x_2, y_2)\), то выполнено, что \(x_1 = x_2\).
Обратите внимание, что если провод соединяет две одинаковые точки, то он может быть как красным, так и синим. Также в Пашиной схеме никакие два провода одного цвета не могут пересекаться, то есть любые два отрезка проводов одного цвета не могут содержать общих точек. Недоработка Пашиной схемы состоит в том, что его провода не были изолированы, и поэтому в точках пересечения проводов разных цветов возникли искры, которые Паша увидел. Он записал все точки, в которых он увидел искру. У него получилось множество из \(n\) различных точек. После чего он разобрал схему и пошёл спать. Утром, когда Паша увидел на листочке множество из \(n\) точек, в которых он увидел искру, ему стало интересно, сколько проводов он использовал, собрав эту схему. К сожалению, он ничего не запомнил, поэтому он решил узнать, какое минимальное количество проводов он мог использовать в своей схеме. Помогите ему узнать это число, а также расположить эти провода так, чтобы в получившейся схеме искры возникли в тех же самых точках. Выходные данные Выведите описание электрической схемы в следующем формате: Сначала выведите \(h\) — количество горизонтальных красных проводов (\(0 \leq h\)). В следующих \(h\) строках выведите по \(4\) целых числа \(x_1\), \(y_1\), \(x_2\), \(y_2\) — координаты двух точек \((x_1, y_1)\) и \((x_2, y_2)\), которые соединяет очередной красный провод. Поскольку отрезки горизонтальные, должно быть выполнено \(y_1 = y_2\). Также должно быть выполнено \(1 \leq x_1, y_1, x_2, y_2 \leq 10^9\). Потом выведите \(v\) — количество вертикальных синих проводов (\(0 \leq v\)). В следующих \(v\) строках выведите по \(4\) целых числа \(x_1\), \(y_1\), \(x_2\), \(y_2\) — координаты двух точек \((x_1, y_1)\) и \((x_2, y_2)\), которые соединяет синий очередной провод. Поскольку отрезки вертикальные, должно быть выполнено \(x_1 = x_2\). Также должно быть выполнено \(1 \leq x_1, y_1, x_2, y_2 \leq 10^9\). Никакие два отрезка одного цвета не должны иметь общих точек. Множество точек, в которых Паша мог увидеть искру, если бы он построил такую схему, должно совпадать с данным во входных данных множеством точек. Количество отрезков \((h + v)\) должно быть минимально возможным. Можно легко показать, что ответ всегда существует. Если существует несколько возможных ответов, выведите любой. Примечание В первом примере Паша мог собрать такую схему: 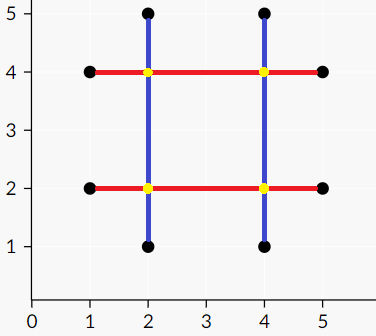 В этой схеме по \(2\) провода каждого цвета: красные из \((5, 2)\) в \((1, 2)\) и из \((1, 4)\) в \((5, 4)\), синие из \((2, 1)\) в \((2, 5)\) и из \((4, 5)\) в \((4, 1)\). Заметим, что он увидит искры ровно в тех точках, которые он записал (обозначены желтым цветом на картинке). Например, искру в точке \((2, 4)\) он увидит, так как в этой точке пересекаются второй красный провод и первый синий. Можно доказать, что нужно не меньше \(4\)-х проводов, чтобы получить схему, нужную Паше. | |
![]()
|
|
E. Политика
Потоки
*2600
графы
В стране есть \(n\) городов. Два кандидата борются за пост президента страны. Выборы состоятся в скором будущем и оба кандидата уже спланировали как они собираются соединить города дорогами. Каждый из планов соединяет города используя ровно \(n - 1\) дорогу. Иначе говоря, каждый план представляет из себя дерево. Оба кандидата также выбрали предлагаемую столицу среди \(n\) городов (\(x\) у первого кандидата, и \(y\) у второго), которая может как совпадать, так и нет. В каждом городе можно построить порт (в одном городе можно построить не более одного порта). Порт, построенный в \(i\)-м городе принесёт \(a_i\) денег. Однако, у каждого кандидата есть свои специфичные требования, выглядящие следующим образом: - \(k\) \(x\), что означает, что кандидат хочет построить ровно \(x\) портов в поддереве вершины \(k\) (дерево подвешено за столицу, которую выбрал этот кандидат).
Выясните, какую наибольшую выручку можно получить, удовлетворив требованиям обоих кандидатов, или выведите -1, если это невозможно сделать. Дополнительно гарантируется, что каждый из кандидатов указал свои специфичные требования относительно своей столицы. Входные данные Первая строка содержит целые числа \(n\), \(x\) и \(y\) (\(1 \le n \le 500\), \(1 \le x, y \le n\)) — количество городов, столица у первого кандидата и столица у второго кандидата соответственно. Следующая строка содержит целые числа \(a_1, a_2, \ldots, a_n\) (\(1 \le a_i \le 100\,000\)) — прибыль, которую принесёт постройка порта в соответствующем городе. Каждая из следующих \(n - 1\) строк содержит целые числа \(u_i\) и \(v_i\) (\(1 \le u_i, v_i \le n\), \(u_i \ne v_i\)), обозначающие рёбра между вершинами в дереве первого кандидата. Каждая из следующих \(n - 1\) строк содержит целые числа \(u'_i\) и \(v'_i\) (\(1 \le u'_i, v'_i \le n\), \(u'_i \ne v'_i\)), обозначающие рёбра между вершинами в дереве второго кандидата. Следующая строка содержит одно целое число \(q_1\) (\(1 \le q_1 \le n\)), обозначающее количество специфичных требований первого кандидата. Каждая из следующих \(q_1\) строк содержит целые числа \(k\) и \(x\) (\(1 \le k \le n\), \(1 \le x \le n\)) — номер города и количество портов в его поддереве. Следующая строка содержит одно целое число \(q_2\) (\(1 \le q_2 \le n\)), обозначающее количество специфичных требований второго кандидата. Каждая из следующих \(q_2\) строк содержит целые числа \(k\) и \(x\) (\(1 \le k \le n\), \(1 \le x \le n\)) — номер города и количество портов в его поддереве. Гарантируется, что заданные рёбра задаут корректные деревья, что каждый кандидат задал специфичное требование про каждый город не более одного раза и что каждый кадидат задал специфичные требования относительно своей столицы. То есть город \(x\) есть в требованиях первого кандидата, а город \(y\) — в требованиях второго. Выходные данные Выведите ровно одно целое число — наибольшую прибыль, которую можно получить, удовлетворив специфичным требованиям обоих кандидатов или -1, если это сделать невозможно. Примечание В первом примере оптимально построить порты в городах \(2\), \(3\) и \(4\), что удовлетворяет всем требованиям обоих кандидатов и приносит прибыль \(2 + 3 + 4 = 9\). Во втором примере оптимально построить порты в городах \(2\) и \(3\), что удовлетворяет всем требованиям обоих кандидатов и приносит прибыль \(99 + 99 = 198\). В третьем примере не возможно построить порты таким образом, чтобы удовлетворить всем требованиям, а значит ответ -1. | |
![]()
|
|
I. Privatization of Roads in Berland
Потоки
Паросочетания
*2400
графы
There are \(n\) cities and \(m\) two-way roads in Berland, each road connecting two distinct cities. Recently the Berland government has made a tough decision to transfer ownership of the roads to private companies. In total, there are \(100500\) private companies in Berland, numbered by integers from \(1\) to \(100500\). After the privatization, every road should belong to exactly one company. The anti-monopoly committee demands that after the privatization each company can own at most two roads. The urbanists of Berland also stated their opinion: each city should be adjacent to the roads owned by at most \(k\) companies. Help the government to distribute the roads between the companies so that both conditions are satisfied. That is, each company gets at most two roads, and each city has roads of at most \(k\) distinct companies adjacent to it. Output Print \(t\) lines: the \(i\)-th line should contain the answer for the \(i\)-th test case. For a test case, print a sequence of integers \(c_1, c_2, \dots, c_m\) separated by space, where \(c_i\) (\(1 \le c_i \le 100500\)) is the company which owns the \(i\)-th road in your plan. If there are multiple solutions, output any of them. If there is no solution for a test case, print \(c_1=c_2=\ldots=c_m=0\). | |
![]()
|
|
G. Петя и граф
Потоки
*2400
графы
У Пети есть простой граф (т. е. граф без петель и кратных ребер), состоящий из \(n\) вершин и \(m\) ребер. Вес \(i\)-й вершины равен \(a_i\). Вес \(i\)-го ребра равен \(w_i\). Подграфом графа будем называть некоторое множество вершин графа и некоторое множество ребер графа, причем множество ребер должно удовлетворять условию: оба конца каждого ребра из множества должны принадлежать выбранному множеству вершин. Весом подграфа является сумма весов входящих в него ребер минус сумма весов входящих в него вершин. Вам нужно найти подграф данного графа максимального веса. Заданный граф не содержит петель и кратных ребер. Выходные данные В единственной строке выведите целое число — максимальный вес подграфа заданного графа. Примечание В первом тестовом примере оптимальный подграф состоит из вершин \({1, 3, 4}\) и имеет вес \(4 + 4 + 5 - (1 + 2 + 2) = 8\). Во втором тестовом примере оптимальный подграф – пустой. | |
![]()
|
|
F. Вася и бесконечные кредиты
Потоки
Паросочетания
дп
*2600
сортировки
графы
Вася решил купить себе шикарную новую машину. К сожалению, ему немного не хватает денег. Сейчас у него есть 0 бурлей. В местном банке есть \(n\) предложений по кредитам. Каждое предложение описывается тремя числами \(a_i\), \(b_i\) и \(k_i\). Предложения пронумерованы от \(1\) до \(n\). Если Вася пользуется \(i\)-м предложением, то банк выдает ему \(a_i\) бурлей в начале месяца, а потом забирает по \(b_i\) бурлей в конце каждого из \(k_i\) следующих месяцев (включая месяц, в который кредит был взят). Вася может брать предложения в любом порядке. В каждый месяц Вася может брать не более одного кредитного предложения. К тому же каждое кредитное предложение может быть использовано не более одного раза. Несколько кредитов могут быть активны в одно и то же время. Это подразумевает, что Вася платит банку сумму \(b_i\) по всем \(i\) активных кредитов в конце каждого из месяцев. Вася хочет купить машину в середине некоторого месяца. Он просто берет все деньги, которые у него есть на текущий момент, и покупает машину ровно этой цены. Васю не особо заботит, сколько он должен будет заплатить банку после покупки машины. Он просто уедет на своей машине из страны, так что банк не сможет его найти. Какая максимальная цена может быть у новой машины? Выходные данные Выведите одно целое число — максимальную цену машины. Примечание В первом примере оптимальная последовательность взятых кредитов такова: 4 \(\rightarrow\) 3. Количество бурлей у Васи меняется следующим образом: 5 \(\rightarrow\) 32 \(\rightarrow\) -86 \(\rightarrow\) .... Он забирает деньги в середине второго месяца (32 бурля) и покупает машину. Отрицательное число бурлей значит, что Вася должен заплатить банку эту сумму денег. Во втором примере оптимальная последовательность взятых кредитов такова: 3 \(\rightarrow\) 1 \(\rightarrow\) 2. Количество бурлей у Васи меняется следующим образом: 0 \(\rightarrow\) 300 \(\rightarrow\) 338 \(\rightarrow\) 1337 \(\rightarrow\) 236 \(\rightarrow\) -866 \(\rightarrow\) .... | |
![]()
|
|
B. Алена и узкий холодильник
Бинарный поиск
Потоки
жадные алгоритмы
сортировки
*1300
Недавно Алена купила миниатюрный холодильник, который может быть представлен как таблица из \(h\) строк и \(2\) столбцов. Изначально в холодильнике лишь одна полка в самом низу, но Алена может установить любое число полок внутрь холодильника между любыми двумя рядами. Все полки имеют ширину в две клетки, не занимают места по вертикали, но разделяют холодильник на верхнюю и нижнюю части. 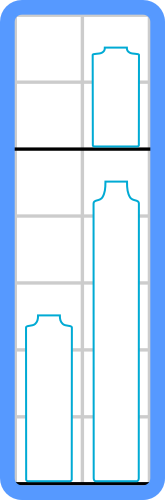 Пример холодильника с \(h = 7\) и двумя полками. Полки показаны черным. Рисунок соответствует первому примеру. Пример холодильника с \(h = 7\) и двумя полками. Полки показаны черным. Рисунок соответствует первому примеру. У Алены есть \(n\) бутылок молока, она хочет поставить их в холодильник. Высота \(i\)-й бутылки равна \(a_i\) клеток, а ширина любой бутылки равна \(1\) клетке. Алена может поставить бутылку на полку, если высота свободного пространства над этой полкой не меньше высоты бутылки. Она не может ставить бутылки друг на друга (если, конечно, между ними нет полки). Бутылки не могут занимать общие клетки в таблице. Алена хочет найти максимальное целое число \(k\) такое, что она может одновременно поставить бутылки с номерами \(1\), \(2\), ..., \(k\) в холодильник. Найдите это наибольшее \(k\). Выходные данные Выведите одно целое число \(k\) — максимальное целое число такое, что Алена может одновременно поставить бутылки с номерами \(1\), \(2\), ..., \(k\) в холодильник. Если Алена может поставить все бутылки, выведите \(n\). Легко понять, что Алена всегда может поставить хотя бы одну бутылку в холодильник. Примечание Один из оптимальных способов постановки бутылок в холодильник в первом примере показан на рисунке в условии. Один из оптимальных способов постановки бутылок в холодильник во втором примере показан на рисунке ниже.  Один из оптимальных способов постановки бутылок в холодильник во третьем примере показан на рисунке ниже.  | |
![]()
|
|
E. Максимизировать mex
Потоки
Паросочетания
*2400
графы
В колледже учатся \(n\) студентов, также в колледже есть \(m\) клубов, пронумерованных от \(1\) до \(m\). У каждого студента известен его потенциал \(p_i\) и номер клуба \(c_i\), членом которого он является. Изначально каждый студент является членом ровно одного клуба. Скоро в колледже состоится технический фестиваль, который продлится \(d\) дней. Каждый день в рамках фестиваля будет проведено соревнование по программированию. Каждый день утром, ровно один студент решает покинуть свой клуб. После того как студент покинул свой клуб, он больше не присоединится ни к какому клубу снова. Каждый день в полдень, директор колледжа выбирает по одному студенту из каждого клуба (в случае если в каком-то клубе нет ни одного студента, из этого клуба не будет выбран никто) и составляет из них команду на этот день. Силой команды называется mex потенциалов студентов, которые в неё входят. Директор хочет выяснить наибольшую возможную силу команды в каждый из следующих \(d\) дней. Таким образом, каждый день директор выбирает команду так, чтобы максимизировать силу команды. Для мультимножества \(S\), его mex определён как наименьший неотрицательный элемент не входящий в \(S\). Например, mex мультимножества \(\{0, 1, 1, 2, 4, 5, 9\}\) равн \(3\), mex мультимножества \(\{1, 2, 3\}\) равен \(0\), а mex \(\varnothing\) (пустого множества) равен \(0\). Выходные данные Для каждого из \(d\) дней, выведите наибольшую возможную силу команды в этот день. Примечание Рассмотрим первый пример: В первый день студент \(3\) покидает свой клуб. Теперь, остались студенты \(1\), \(2\), \(4\) и \(5\). Мы можем выбрать студентов \(1\), \(2\) и \(4\) чтобы получить максимальную силу команды, равную \(3\). Заметим, что мы не можем выбрать команду из студентов \(1\), \(2\) и \(5\), так как студенты \(2\) и \(5\) состоят в одном клубе. Также мы не можем выбрать команду \(1\), \(3\) и \(4\), так как студент \(3\) уже покинул свой клуб. Во второй день студент \(2\) покидает свой клуб. Теперь, остались студенты \(1\), \(4\) и \(5\). Мы можем выбрать студентов \(1\), \(4\) и \(5\) чтобы получить максимальную возможную силу, то есть \(1\). В третий день, остаются только студенты \(1\) и \(5\). Мы можем выбрать студентов \(1\) и \(5\) чтобы получить наибольшую возможную силу команды, то есть \(1\). В четвёртый день, остался только студент \(1\). Мы можем выбрать студента \(1\), чтобы получить максимальную возможную силу команды, то есть \(1\). В пятый день не осталось ни одного клуба, в котором бы состоял хотя бы один студент, а значит максимальная возможная сила равна \(0\). | |
![]()
|
|
G. Ограничения
Потоки
дп
графы
*2700
Вы планируете строить дома на улице. На улице есть \(n\) мест, где вы можете построить дома. Все они пронумерованы слева направо от \(1\) до \(n\). В каждом из них вы можете построить дом с целочисленной высотой от \(0\) до \(h\). За каждый дом вы получаете прибыль в размере \(a^2\) долларов, где \(a\) — высота этого дома. У города есть \(m\) ограничений. \(i\)-е ограничение говорит о том, что если самый высокий дом от \(l_i\) до \(r_i\) строго больше, чем \(x_i\), вы должны заплатить штраф в размере \(c_i\) долларов. Вы хотели бы построить дома, чтобы максимизировать свою чистую прибыль (прибыль минус штрафы). Определите максимально возможную прибыль. Выходные данные Выведите одно целое число — максимальную прибыль, которую вы можете получить. Примечание В первом примере оптимальным является строительство домов высотой \([1, 3, 2]\). Мы получаем прибыль в размере \(1^2+3^2+2^2 = 14\). Мы не нарушаем никаких ограничений, поэтому никаких штрафов нет, поэтому общая прибыль составляет \(14 - 0 = 14\). Во втором примере оптимально строить дома высотой \([10, 8, 8, 10]\). Мы получаем прибыль в размере \(10^2+8^2+8^2+10^2 = 328\), и мы нарушаем второе ограничение и платим штраф в \(39\) долларов, таким образом, общая прибыль составляет \(328-39 = 289\). Обратите внимание, что даже при отсутствии ограничения на дом \(1\), мы все равно не можем иметь высоту выше \(10\) метров. | |
![]()
|
|
H. Фондовая биржа
Бинарный поиск
Потоки
графы
*3500
Предупреждение: в этой задаче необычное ограничение по памяти! Боб решил, что он не будет тратить свои лучшие года, создавая программное обеспечение для больших компаний, а вместо этого он будет зарабатывать на хлеб на Рейкьявикской фондовой бирже. Рейкьявикская фондовая биржа — единственная настоящая фондовая биржа в мире. Там есть только один вид транзакций — взять одну акцию вида \(x\) и обменять ее на другую акцию вида \(y\), но это можно сделать, только если цена акции \(x\) не меньше цены акции \(y\). Всего есть \(2n\) видов акций, пронумерованных от \(1\) до \(2n\), которые интересны Бобу. У Боба есть по одной акции видов от \(1\) до \(n\), а хотел бы в будущем владеть по одной акции видов от \(n+1\) до \(2n\). Боб смог спрогнозировать цену каждой акции — в момент времени \(t \geq 0\) одна акция вида \(i\) будет стоить \(a_i \cdot \lfloor t \rfloor + b_i\). Сейчас \(t = 0\). Помогите Бобу найти минимально возможный момент времени, когда он сможет владеть по одной акции видов от \(n+1\) до \(2n\) и минимальное количество транзакций, которые нужно совершить, чтобы получить эти акции. Можете считать, что фондовая биржа имеет неограниченное количество акций каждого вида в любой момент времени. Выходные данные Если Боб не может достичь своей цели, то выведите \(-1\). Иначе выведите два целых числа \(T\) и \(E\), где \(T\) — минимальное возможное время, когда Боб может достичь своей цели, а \(E\) — минимальное количество транзакций, необходимых для достижения цели в момент времени \(T\). Примечание В первом примере Боб может просто ждать, когда будет \(t = 3\) и обе акции будут иметь одинаковую цену, и сделать транзакцию. Во втором примере оптимальная стратегия выглядит так: нужно обменять акцию вида \(2\) на акцию вида \(1\) в момент времени \(t = 1\), после этого нужно обменять первую акцию вида \(1\) на акцию вида \(3\) в момент времени \(t = 5\) (когда они обе стоят \(15\)), а вторую в момент времени \(t = 6\) обменять на акцию вида \(4\) (когда они стоят \(18\) и \(17\) соответственно). Обратите внимание, что он может достичь своей цели за две транзакции, но это он может сделать только в момент времени \(t = 9\), когда он наконец сможет обменять акцию вида \(2\) на акцию вида \(3\). В третьем примере Боб никогда не сможет достичь своей цели, так как акция второго вида всегда дороже акции первого. | |
![]()
|
|
B2. Доктор встречает Вейдера (средняя)
Потоки
Паросочетания
сортировки
графы
*2200
кратчайшие пути
Благодаря помощи Доктора, повстанцам удалось украсть достаточно золота, чтобы запустить полномасштабную атаку на эмперию! Однако Дарт Вейдер ищет возможности отомстить и забрать назад своё золото. Повстанцы спрятали золото на различных базах по всей галактике. Дарт Вейдер и Империя собираются послать свои космические корабли в атаку на эти базы. Галактика может быть представлена как неориентированный граф из \(n\) планет (вершин) и \(m\) червоточин (рёбер), каждая соединяющая две планеты. Всего у империи есть \(s\) космических кораблей, а у повстанцев есть \(b\) баз, расположенных на различных планетах галактики. У каждого космического корабля есть его местоположение \(x\), обозначающее индекс планеты, на которой он находится, его сила атаки \(a\) и определённый уровень топлива \(f\). У каждой базы есть местоположение \(x\) и уровень защиты \(d\). Космический корабль может атаковать базу если выполнены оба следующих условия: - Сила атаки космического корабля больше или равна уровня защиты базы,
- Уровень топлива космического корабля больше или равен кратчайшему расстоянию (количество червоточин) между планетой космического корабля и планетой с базой
Вейдер очень требователен к своим атакующим формациям. Он требует, чтобы каждый космический корабль атаковал не более одной базы, и чтобы каждая база была атакована не более чем одним космическим кораблем. Вейдер знает, что повстанцы спрятали \(k\) золота в каждой базе, так что он назначит космическим кораблям базы для атаки таким образом, чтобы максимизировать число атакованных баз. Таким образом, для каждой атакованной базы повстанцы теряют по \(k\) золота. Однако повстанцы имеют возможность создать произвольное количество фейковых баз. С помощью Доктора, эти базы будут существовать за пределами пространства и времени, так что все корабли смогут достичь и атаковать их. Более того, фейковые базы всегда будут казаться очень заманчивыми, то есть они гарантировано будут атакованы каким-то кораблём. Разумеется, фейковые базы не содержат золота, но создание одной такой базы стоит \(h\) золота. Какое минимальное количество золота повстанцы потеряют, если они создадут оптимальное количество фейковых баз? Выходные данные Выведите одно целое число — минимальную цену в золоте. Примечание Один из способов минимизировать стоимость — это построить \(4\) фейковые базы, тем самым итоговая стоимость равна \(4 \times 3 = 12\). По одному имперскому кораблю будет назначено на атаку каждой фейковой базы, тем самым будет атаковано ноль настоящих баз. | |
![]()
|
|
B3. Доктор встречает Вейдера (сложная)
Потоки
*2700
кратчайшие пути
Повстанцы сохранили достаточно золота, чтобы подготовить полномасштабную атаку. Теперь ситуация перевернулась и повстанцы запускают космические корабли, чтобы атаковать базы Империи! Галактика может быть представлена как неориентированый граф из \(n\) планет (вершин) и \(m\) червоточин (рёбра), каждая из которых соединяет две планеты. Всего есть \(s\) космических кораблей повстанцев и \(b\) баз Империи, расположеных на различных планетах галактики. Каждый космический корабль имеет местоположение \(x\), обозначающее индекс планеты, на которой он расположен, силу атаки \(a\), определённый уровень энергии \(f\) и цена эксплуатации \(p\). Каждая база имеет местоположение \(x\), силу защиты \(d\) и определённый уровень золота \(g\). Космический корабль может атаковать базу, если выполняются оба следующих условия: - Сила атаки космического корабля больше или равна силе защиты базы
- Уровень топлива космического корабля больше или равен кратчайшему расстоянию (количеству червоточин) между планетой космического корабля и планетой, на которой расположена база.
Повстанцы очень гордые бойцы. Например, если космический корабль не может атаковать ни одну базу, ни один пилот повстанцев не согласится управлять им. Если космический корабль управляется, то прибыль, которую производит этот корабль, равна золоту базы, которую он атакует, минус цену за эксплуатацию этого корабля. Обратите внимание, что эта величина может быть отрицательной. Пилот корабля выберет ту базу для атаки, которая максимизирует полученную прибыль. Дарт Вейдер любит казаться богатым. Поэтому всякий раз, когда база подвергается нападению, он немедленно пополняет эту базу новым золотом, вместо похищенного. Тем самым, с точки зрения повстанцев, разные корабли могут свободно атаковать одну и ту же базу, в таком случае все атакующие получат золото от этой базы. Повстанцы попросили Хайди и Доктора определить какой набор кораблей следует использовать, чтобы получить максимальную суммарную прибыль. Однако, так как война продолжалась достаточно долго времени, то между пилотами возникли различные нерушимые связи, и некоторые из них отказываются управлять кораблём, если их друзья не управляют своими кораблями. В частности есть список из \(k\) зависимостей вида \(s_1, s_2\), обозначающие, что корабль \(s_1\) можно использовать только если корабль \(s_2\) тоже используется. Выходные данные Выведите одно целое число — максимальную суммарную прибыль, которую можно получить. Примечание Оптимальной стратегией является выбрать корабли 1, 2, and 4, которые будут атаковать базы 1, 1 и 2 соответственно. | |
![]()
|
|
G. Сходка
Потоки
графы
*2500
Глава одной очень секретной организации решил собрать всех участников организации на встречу. Все они живут в одном и том же городе, который можно рассматривать как \(n\) перекрестков, соединенных \(m\) улицами. По улицам можно перемещаться в обоих направлениях. Встреча пройдет в доме главы около перекрестка \(1\). На встречу, помимо главы, приглашены \(k\) человек, состоящих в организации; \(i\)-й из них живет у перекрестка \(a_i\). Все приглашенные одновременно получат приглашение и начнут движение к месту встречи. В начале каждой минуты каждый человек находится на каком-то перекрестке. Он или она может подождать минуту на этом перекрестке, или за минуту пройти по улице до другого перекрестка (очевидно, можно идти только по тем улицам, на одном из концов которой стоит человек). В начале первой минуты каждый человек находится на перекрестке, около которого живет. Как только человек достигает перекрестка \(1\), он или она сразу же приходит в дом главы организации. Очевидно, глава хочет, чтобы все пришли как можно раньше. Но так как организация очень секретная, глава не хочет, чтобы движение ее участников привлекло слишком много внимания. Определим недовольство главы следующим образом: - в самом начале недовольство равно \(0\);
- когда участник встречи приходит к перекрестку \(1\), недовольство увеличивается на \(c \cdot x\), где \(c\) — некоторая заданная константа, а \(x\) — количество минут, которое потребовалось человеку, чтобы достичь перекрестка \(1\);
- когда \(x\) участников организации идут по одной и той же улице в одну и ту же минуту в одном и том же направлении, к недовольству прибавляется \(dx^2\), где \(d\) — некоторая заданная константа. Например, если два человека идут по одной и той же улице в одну и ту же минуту в одном и том же направлении, к недовольству добавляется \(4d\) (не \(5d\)).
Перед отправкой сообщения о встрече глава организации может отправить каждому сообщение, каким путем ему надо двигаться и на каких перекрестках ждать. Помогите главе разработать такой план, при котором все достигают перекрестка \(1\), и недовольство минимально возможно. Выходные данные Выведите одно целое число — минимальное недовольство главы организации после того, как все придут к перекрестку \(1\). Примечание Лучший план действий в первом примере — следующий: - первый человек идет по улице \(2\) к перекрестку \(2\), затем идет по улице \(1\) к перекрестку \(1\) и приходит на встречу;
- второй человек ждет минуту на перекрестке \(3\), затем идет по улице \(2\) к перекрестку \(2\), затем идет по улице \(1\) к перекрестку \(1\) и приходит на встречу;
- третий человек ждет две минуты на перекрестке \(3\), затем идет по улице \(2\) к перекрестку \(2\), затем идет по улице \(1\) к перекрестку \(1\) и приходит на встречу;
- четвертый человек ждет три минуты на перекрестке \(3\), затем идет по улице \(2\) к перекрестку \(2\), затем идет по улице \(1\) к перекрестку \(1\) и приходит на встречу;
| |
![]()
|
|
E. Покраска прямоугольника 2
Потоки
Паросочетания
графы
*2500
Есть клетчатый квадрат размера \(n \times n\). Некоторые клетки квадрата покрашены в черный цвет, остальные клетки покрашены в белый. За одну операцию разрешается выбрать некоторый прямоугольник и перекрасить все его клетки в белый цвет. За перекраску прямоугольника размера \(h \times w\) взимается штраф в размере \(\min(h, w)\). Требуется за минимальный суммарный штраф покрасить все клетки в белый цвет. Квадрат большой, поэтому зададим мы его в сжатом виде. Множество чёрных клеток является объединением \(m\) прямоугольников. Выходные данные Выведите одно число — минимальный суммарный штраф покраски всего квадрата в белый цвет. Примечание На картинке вы можете видеть два примера и некоторые из оптимальных способов их покрасить. 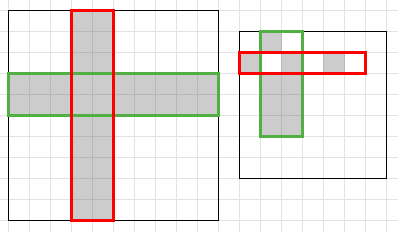 | |
![]()
|
|
D. Остров Сокровищ
Потоки
дп
поиск в глубину и подобное
*1900
хэши
Сокровища! Кто не мечтал о них в детстве? Именно так подумал юный Вася и отправился в длительное путешествие к Острову Сокровищ. Остров Сокровищ представляет собой прямоугольное поле \(n \times m\), окруженное океаном. Пронумеруем строки поля последовательными целыми числами от \(1\) до \(n\) сверху вниз, а столбцы последовательными целыми числами от \(1\) до \(m\) слева направо. Обозначение \((r, c)\) соответствует клетке, расположенной в строке \(r\) и столбце \(c\). В некоторых клетках острова растут непроходимые леса, а остальные клетки свободные и проходимые. Сокровище закопано в клетке \((n, m)\). Вася высадился с корабля в клетку \((1, 1)\). Теперь он хочет добраться до сокровища. Вася сильно спешит за сокровищем, поэтому может перемещаться только в клетку в следующей строке (вниз) или следующем столбце (вправо), то есть из клетки \((x, y)\) он может сделать ход только в клетки \((x+1, y)\) и \((x, y+1)\). Конечно, Вася не может заходить в клетки, где растёт непроходимый лес. Злая Ведьма узнала о планах Васи завладеть сокровищами и хочет ему помешать. До начала движения Васи она с помощью своей магии может вырастить непроходимые леса в клетках, которые ранее были свободными. Ведьма может вырастить непроходимый лес в любых клетках, кроме клетки \((1, 1)\), где уже высадился Вася, и клетки \((n, m)\), где закопаны сокровища. Помогите Злой Ведьме определить, на каком минимальном количестве клеток ей придётся вырастить непроходимый лес, чтобы Вася не смог добраться до сокровища? Выходные данные Выведите одно целое число \(k\) — минимальное количестве клеток, в которых Злой Ведьме нужно вырастить непроходимый лес, чтобы Вася не смог добраться до сокровища. Примечание Следующая картинка изображает осторов в третьем примере. Синим отмечены возможные пути Васи из клетки \((1, 1)\) в клетку \((n, m)\), красным отмечены клетки, на которых ведьма может вырастить непроходимый лес, чтобы Вася не смог добраться из \((1, 1)\) в \((n, m)\). 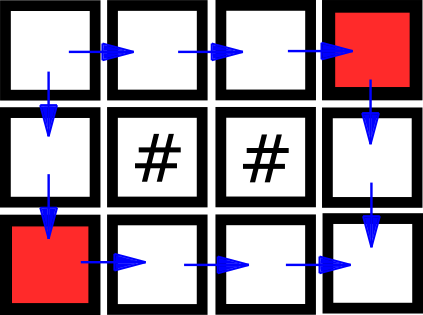 | |
![]()
|
|
K. Projectors
Потоки
графы
*3100
There are \(n\) lectures and \(m\) seminars to be conducted today at the Faculty of Approximate Sciences. The \(i\)-th lecture starts at \(a_i\) and ends at \(b_i\) (formally, time of the lecture spans an interval \([a_i, b_i)\), the right bound is exclusive). The \(j\)-th seminar starts at \(p_j\) and ends at \(q_j\) (similarly, time of the seminar spans an interval \([p_j, q_j)\), the right bound is exclusive). There are \(x\) HD-projectors numbered from \(1\) to \(x\) and \(y\) ordinary projectors numbered from \(x + 1\) to \(x + y\) available at the faculty. Projectors should be distributed in such a way that: - an HD-projector is used in each lecture;
- some projector (ordinary or HD) is used in each seminar;
- a projector (ordinary or HD) can only be used in one event at the same moment of time;
- if a projector is selected for an event, it is used there for the whole duration of the event;
- a projector can be reused in some following event, if it starts not earlier than current event finishes.
You are to find such distribution of projectors, if it exists. Again, note that the right bound of the event's time range is not inclusive: if some event starts exactly when another event finishes, the projector can be reused (suppose that it is instantly transported to the location of the event). Output For each test case, print YES if it is possible to distribute projectors in order to meet all requirements, or NO otherwise. In case of positive answer, output one additional line containing \(n + m\) integers. The first \(n\) integers should be not less than \(1\) and not greater than \(x\), and the \(i\)-th of them should be the index of HD projector used in the \(i\)-th lecture. The last \(m\) integers should be not less than \(1\) and not greater than \(x + y\), and the \(j\)-th of them should be the index of projector used in the \(j\)-th seminar. If there are multiple answers, print any of them. | |
![]()
|
|
L. Road Construction
Потоки
графы
*2300
There are \(N\) cities in the country of Numbata, numbered from \(1\) to \(N\). Currently, there is no road connecting them. Therefore, each of these \(N\) cities proposes a road candidate to be constructed. City \(i\) likes to connect with city \(A_i\), so city \(i\) proposes to add a direct bidirectional road connecting city \(i\) and city \(A_i\). It is guaranteed that no two cities like to connect with each other. In other words, there is no pair of integers \(i\) and \(j\) where \(A_i = j\) and \(A_j = i\). It is also guaranteed that any pair of cities are connected by a sequence of road proposals. In other words, if all proposed roads are constructed, then any pair of cities are connected by a sequence of constructed road. City \(i\) also prefers the road to be constructed using a specific material. Each material can be represented by an integer (for example, \(0\) for asphalt, \(1\) for wood, etc.). The material that can be used for the road connecting city \(i\) and city \(A_i\) is represented by an array \(B_i\) containing \(M_i\) integers: \([(B_i)_1, (B_i)_2, \dots, (B_i)_{M_i}]\). This means that the road connecting city \(i\) and city \(A_i\) can be constructed with either of the material in \(B_i\). There are \(K\) workers to construct the roads. Each worker is only familiar with one material, thus can only construct a road with a specific material. In particular, the \(i^{th}\) worker can only construct a road with material \(C_i\). Each worker can only construct at most one road. You want to assign each worker to construct a road such that any pair of cities are connected by a sequence of constructed road. Output If it is not possible to assign each worker to construct a road such that any pair of cities are connected by a sequence of constructed road, simply output -1 in a line. Otherwise, for each worker in the same order as input, output in a line two integers (separated by a single space): \(u\) and \(v\) in any order. This means that the worker constructs a direct bidirectional road connecting city \(u\) and \(v\). If the worker does not construct any road, output "0 0" (without quotes) instead. Each pair of cities can only be assigned to at most one worker. You may output any assignment as long as any pair of cities are connected by a sequence of constructed road. Note Explanation for the sample input/output #1 We can assign the workers to construct the following roads: - The first worker constructs a road connecting city \(1\) and city \(2\).
- The second worker constructs a road connecting city \(2\) and city \(3\).
- The third worker constructs a road connecting city \(3\) and city \(4\).
- The fourth worker does not construct any road.
- The fifth worker constructs a road connecting city \(4\) and city \(2\).
Therefore, any pair of cities are now connected by a sequence of constructed road. Explanation for the sample input/output #2 There is no worker that can construct a road connecting city \(1\), thus city \(1\) is certainly isolated. | |
![]()
|
|
E. Пилюли
Потоки
Перебор
*2900
Доктор прописал своему пациенту лекарство. Лекарство имеет вид пилюль, каждая из которых состоит из оболочки и целебного порошка. Оболочка состоит из двух половинок, каждая из которых имеет один из четырех цветов — синий, красный, белый или желтый. Доктор хочет сложить 28 пилюль в прямоугольную коробочку размера 7 × 8. При этом каждая пилюля занимает ровно две соседние ячейки, а в любой ячейке находится ровно одна из половин пилюли. Таким образом, получается четырехцветная картинка размера 7 × 8. Доктор полагает, что пациент скорее выздоровеет, если картинка, получаемая из пилюль, будет особенной. К сожалению, это не такая простая задача расположить пилюли в коробочке таким образом, чтобы получилась требуемая картинка. Поэтому доктор обратился к вам за помощью. У доктора имеется некоторый запас пилюль каждого из 10 типов раскраски. Лекарство внутри них одинаковое, поэтому не имеет значения, какие 28 из них будут находиться в коробочке. Расположите пилюли в коробочке так, чтобы получилась требуемая картинка. Если расположить пилюли требуемым образом невозможно, то расположите их таким образом, чтобы количество совпадений цветов по всем 56 ячейкам в итоговой расстановке и картинке доктора было наибольшим. Выходные данные В первой строке выведите наибольшее количество ячеек, для которых цвет совпадает. Далее выведите 13 строк по 15 символов в каждой — расположение пилюль в наилучшей расстановке. На пересечениях нечетных строк и нечетных столбцов должны располагаться символы «B», «R», «W» и «Y». На всех остальных позициях должны быть символы «.», «-» и «|». Используйте «-» и «|» для того, чтобы показать, какие половинки оболочки связаны в единую пилюлю. Смотрите примеры для более ясного понимания. Если возможных решений несколько — выведите любое. | |
![]()
|
|
F. Экономические проблемы
Потоки
Деревья
Структуры данных
дп
поиск в глубину и подобное
*2400
графы
Электросеть дворцов в Берляндии состоит из 2-х сетей: основной и запасной. Провода во дворцах сделаны из дорогого материала, поэтому их продажа будет отличной идеей! Каждая из сетей (основная и запасная) имеет главный узел (он имеет номер \(1\)), из которого ток поступает на другие узлы сети. Все узлы доступны от главного по единственному пути. В обеих сетях количество узлов, из которых ток не распространяется дальше, равно \(n\). Иными словами, каждая из сетей является отдельным корневым ориентированным деревом с \(n\) листьями и с корнем в вершине \(1\). В каждом дереве свои вершины и своя независимая нумерация вершин. Кроме электросетей во дворце есть \(n\) приборов, каждый из которых соединён с одним из узлов основной и с одним из узлов запасной сети. Приборы соединяются только с такими узлами, из которых ток не распространяется далее (то есть, которые являются листьями). Каждый такой узел (лист дерева) соединён ровно с одним прибором. 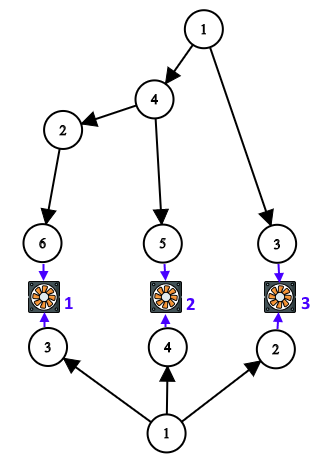 В этом примере основная сеть содержит \(6\) узлов (изображена сверху), а запасная — \(4\) узла (изображена снизу). Количество приборов равно \(3\), они пронумерованы синим цветом. В этом примере основная сеть содержит \(6\) узлов (изображена сверху), а запасная — \(4\) узла (изображена снизу). Количество приборов равно \(3\), они пронумерованы синим цветом. Гарантируется, что вся электросеть (две сети и \(n\) приборов) может быть изображена на схеме способом, аналогичным картинке выше: - основная сеть будет составлять дерево сверху, в котором все провода ведут в направлении «сверху вниз»,
- запасная сеть будет составлять дерево снизу, в котором все провода ведут в направлении «снизу вверх»,
- приборы — горизонтальный ряд между ними, пронумерованный от \(1\) до \(n\) слева направо,
- провода между узлами сетей изображены непересекающимися отрезками.
Формально, для каждого дерева существует такой обход в глубину из вершины \(1\), что его листья посещаются в порядке их присоединения к приборам \(1, 2, \dots, n\) (то есть сначала узел, присоединенный к прибору \(1\), затем узел, присоединенный к прибору \(2\), и так далее). Предприниматель хочет продать (удалить) максимальное количество проводов так, чтобы на каждый прибор поступал ток из хотя бы одной сети. Иначе говоря, для каждого прибора должен существовать путь до главного узла сети (основной или запасной), проходящий по проводам сети от этого главного узла. Выходные данные Выведите единственное целое число — максимальное количество проводов, которые можно удалить из сети так, чтобы каждый прибор продолжил получать электрический ток. Примечание Для первого примера ниже на картинке изображен один из возможных вариантов решения (красным цветом отмечены провода, которые можно удалить): 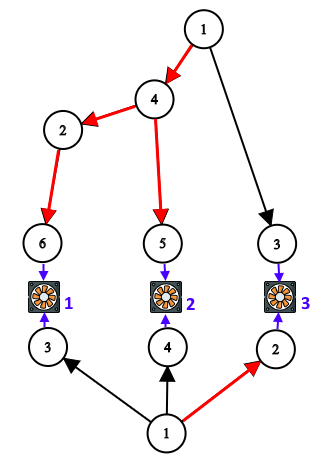 Второй и третий примеры изображены ниже: 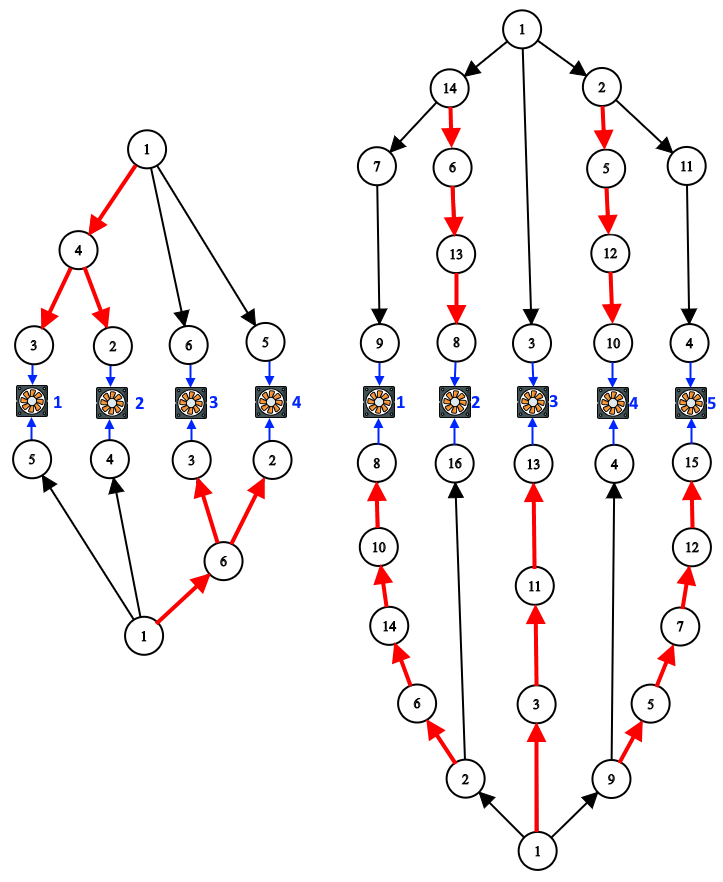 | |
![]()
|
|
E. Красивая лига
Потоки
Паросочетания
Конструктив
*2700
Футбольная лига недавно стартовала в Красивой долине. Всего \(n\) команд участвует в этой лиге. Пронумеруем их для удобства целыми числами от \(1\) до \(n\). Всего будет проведено ровно \(\frac{n(n-1)}{2}\) матчей: каждая команда будет играть со всеми оставшимися командами ровно по одному разу. В каждом матче всегда есть победившая и проигравшая команда, ничьих не бывает. После того, как все матчи будут сыграны, организаторы посчитают количество красивых троек. Тройка команд \((A, B, C)\) называется красивой, если команда \(A\) победила команду \(B\), команда \(B\) победила команду \(C\) и команда \(C\) победила команду \(A\). Мы рассматриваем только тройки различных команд, порядок команд внутри тройки имеет значение. Красотой лиги назовем количество красивых троек. В данный момент, \(m\) матчей уже было проведено и их результаты уже известны. Какая максимальная красота лиги может быть в итоге, после проведения оставшихся матчей? Также найдите возможные результаты оставшихся \(\frac{n(n-1)}{2} - m\) матчей, при которых красота лиги максимально возможная. Выходные данные Выведите \(n\) строк, в каждой из них строку, содержащую ровно \(n\) символов. Каждый символ должен быть равен \(0\) или \(1\). Обозначим за \(a_{ij}\) \(j\)-е число в \(i\)-й строке. Для всех \(1 \leq i \leq n\) должно быть выполнено \(a_{ii} = 0\). Для всех пар команд \(i \neq j\) число \(a_{ij}\) обозначает результат матча между командой с номером \(i\) и командой с номером \(j\): - Если \(a_{ij}\) это \(1\), то \(i\)-я команда победила \(j\)-ю команду;
- Иначе \(j\)-я команда победила \(i\)-ю команду;
- Также, должно быть выполнено, что \(a_{ij} + a_{ji} = 1\).
Также заметьте, что результаты \(m\) матчей, которые уже были сыграны, не могут быть изменены в вашей лиге. Красота лиги, представленной в качестве ответа должна быть максимально возможной. Если существует несколько лиг, подходящих под условия и красота которых максимальна, вы можете найти любую из них. Примечание Красота лиги в первом тесте равна \(3\), потому что есть ровно три красивые тройки команд: \((1, 2, 3)\), \((2, 3, 1)\), \((3, 1, 2)\). Красота лиги во втором тесте равна \(6\) потому что существует шесть красивых троек команд: \((1, 2, 4)\), \((2, 4, 1)\), \((4, 1, 2)\), \((2, 4, 3)\), \((4, 3, 2)\), \((3, 2, 4)\). | |
![]()
|
|
F. Красно-синий граф
Потоки
Конструктив
*2900
Вам задан двудольный граф: первая доля графа содержит \(n_1\) вершин, вторая — \(n_2\) вершин, а также в графе \(m\) ребер. Граф может содержать кратные ребра. Первоначально, все ребра графа бесцветные. Каждое ребро вы можете либо оставить бесцветным (это бесплатно), либо покрасить в красный (стоимость данного действия \(r\) монет), либо покрасить в синий (за \(b\) монет). Никакое ребро не может быть покрашено в оба цвета одновременно. Также в графе вершины разбиваются на три типа — бесцветные, красные и синие. Цветные вершины добавляют дополнительные ограничения на раскраску ребер: - у каждой красной вершины количество смежных с ней красных ребер должно быть строго больше, чем смежных с ней синих ребер;
- у каждой синей вершины количество смежных с ней синих ребер должно быть строго больше, чем смежных с ней красных ребер.
Бесцветные вершины не накладывают никаких ограничений. Ваша задача — раскрасить некоторые (возможно, никакие) ребра так, чтобы выполнялись заданные ограничения, и среди всех возможных раскрасок выбрать такую, суммарная стоимость которой минимальна. Выходные данные Если не существует раскраски ребер, которая удовлетворяет всем заданным ограничениям, — выведите \(-1\). Иначе, выведите число \(c\), обозначающее минимальную суммарную стоимость раскраски, и строку из \(m\) символов. \(i\)-й символ должен быть U, если \(i\)-е ребро осталось бесцветным, R, если \(i\)-е ребро покрашено в красный, или B, если \(i\)-е ребро покрашено в синий. Если существует несколько оптимальных раскрасок — выведите любое. | |
![]()
|
|
G. Корова и тренировка
Потоки
графы
кратчайшие пути
*3100
Фермер Джон намерен заставить Бесси тренироваться больше! Бесси сейчас пасется на ферме, которая состоит из \(n\) полей, соединенных между собой \(m\) ориентированными дорогами. Нужно потратить \(w_i\) времени, чтобы пройти по соответствующей дороге. Бесси в данный момент находится на поле \(1\) и вернется к себе домой на поле \(n\) в конце дня. Фермер Джон планирует увеличить время прохождения по некоторым дорогам. Он может увеличить время прохождения каждой дороги на неотрицательное число, но суммарная прибавка не должна превосходить \(x_i\) для \(i\)-го плана. Определите, какому максимальному числу может быть равна длина кратчайшего пути из \(1\) в \(n\) для каждого из \(q\) независимых планов. Выходные данные Для каждого плана выведите максимальную длину кратчайшего пути, которую может достичь Фермер Джон, если суммарная прибавка не превосходит \(x_i\). Ваш ответ будет считаться верным, если абсолютная или относительная погрешность не будет превосходить \(10^{-6}\). Формально, пусть Ваш ответ равен \(a\), а ответ жюри равен \(b\). Вас ответ засчитается тогда и только тогда, когда\(\frac{|a - b|}{\max{(1, |b|)}} \le 10^{-6}\). | |
![]()
|
|
E. Биты старой Англии
Потоки
графы
*2700
Еще одна характерная черта языка Shakespeare — то, что переменные называются именами персонажей пьес Шекспира, а все действия над ними (изменение значений, вывод на печать и так далее) производятся в виде диалога с другими персонажами. Кроме того, новые значения переменных задаются довольно громоздко, поэтому их использование обычно стараются свести к минимуму. Нам нужно вывести на печать заданную последовательность n натуральных чисел. Для этого у нас есть m персонажей-переменных и два вида действий над ними: - variable=integer
- print(variable)
В качестве variable может выступать любая из m переменных. Переменные обозначаются строчными латинскими буквами от «a» до «z» включительно. В качестве integer может выступать любое натуральное число. Будем считать штрафом за использование первого типа действия количество установленных бит в числе integer. Штраф за использование второго типа действия — 0. Найдите и выведите программу, в которой суммарный штраф будет минимален. Выходные данные Выведите количество строк и цену в оптимальной программе. Далее выведите саму программу, по одной команде на строку. Если таких программ несколько, то выведите любую (надо минимизировать только цену). | |
![]()
|
|
F. Призыв существ
Потоки
Паросочетания
Конструктив
дп
жадные алгоритмы
сортировки
*2500
Поликарп играет в компьютерную игру. В этой игре игроки призывают армии магических существ и сражаются с армиями существ других игроков. Поликарп может призвать \(n\) разных существ, \(i\)-е существо изначально имеет силу \(a_i\); кроме того, когда Поликарп призывает его, оно увеличивает на \(b_i\) силу всех ранее призванных существ (исключая себя). Поликарп может призывать существ в любом порядке. Однако под контролем Поликарпа может находиться не более \(k\) существ одновременно. Поэтому, помимо призыва существ, он может уничтожать ранее призванных существ. Каждое существо может быть призвано (а, значит, и уничтожено) не более одного раза. Цель Поликарпа — собрать максимально сильную армию существ. Он хочет, чтобы после всех его действий суммарная сила всех призванных (но не уничтоженных) им существ была максимально возможной. Помогите Поликарпу составить оптимальную последовательность действий, чтобы собрать максимально сильную армию! Выходные данные Для каждого набора тестовых данных выведите оптимальную последовательность действий в следующем формате: Сначала выведите \(m\) — количество действий, которые должен совершить Поликарп (\(0 \le m \le 2n\)). После этого выведите \(m\) целых чисел \(o_1\), \(o_2\), ..., \(o_m\), где \(o_i\) описывает \(i\)-е действие следующим образом: если \(i\)-е действие — это «призвать существо \(x\)», то \(o_i = x\), а если \(i\)-е действие — это «уничтожить существо \(x\)», то \(o_i = -x\). Каждое существо может быть призвано не более одного раза и не может быть уничтожено, если оно еще не призвано (или уже уничтожено). После каждого действия под контролем Поликарпа должно быть не более \(k\) существ. Если оптимальных последовательностей действий несколько, выведите любую из них. Примечание Рассмотрим пример из условия. В первом наборе тестовых данных можно сначала вызвать существо \(2\) с силой \(7\), затем призвать существо \(1\), которое увеличит силу предыдущего существа на \(3\), после этого уничтожить существо \(1\) и поставить существо \(5\). В итоге у Поликарпа будут два существа с силой \(10\). Во втором наборе тестовых данных у Поликарпа не может быть более одного существа под контролем, поэтому достаточно выбрать самое сильное существо и призвать его. В третьем наборе тестовых данных Поликарп может призвать всех существ, никого не уничтожая. | |
![]()
|
|
H1. Пропускная способность платы (простая версия)
Потоки
дп
жадные алгоритмы
*3300
Это более простая версия задачи H без запросов на изменение. Лестер и Делберт работают в компании-производителе электроники. Сейчас они трудятся над микроплатой, которая должен соединять две независимые части большого суперкомпьютера. Плата строится на основе макета в виде сетки. В макете \(n\) рядов и \(m\) столбцов, и на каждом пересечении ряда и столбца находится контакт. Также, на каждой из сторон макета расположены порты, которые можно подсоединять к ближайшему контакту. На левой и правой стороне находится по \(n\) портов, а на верхней и нижней — по \(m\) портов. Каждый из портов снаружи соединён с одной из частей суперкомпьютера, и раскрашен в красный либо синий цвет. 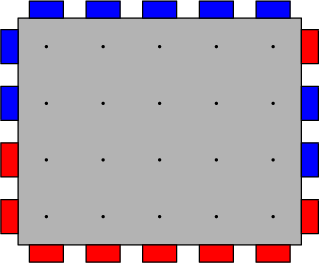 Порты можно соединять проводами внутри платы. Однако, есть несколько требований: - Каждый провод должен соединять красный и синий порт, и каждый порт может быть соединён не более чем одним проводом.
- Каждый участок провода должен быть горизонтальным либо вертикальным, и повороты возможно только в одном из контактов.
- Чтобы избежать интерференции, провода не должны иметь общих частей ненулевой длины (однако, они могут проходить через общие контакты). Кроме того, провод не может покрывать один участок ненулевой длины дважды.
Пропускной способностью платы называется наибольшее количество соединений между красными и синими портами, которого можно достичь, соблюдая условия выше. Например, плата, изображенная выше, имеет пропускную способность \(7\), и один из способов построить семь соединений изображён ниже. 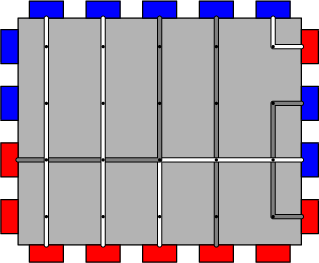 До этого места условия обеих версий задачи совпадают. Различия начинаются ниже. Помогите Лестеру и Делберту найти пропускную способность платы с данной конфигурацией. Выходные данные Выведите одно число — пропускную споособность заданной платы. | |
![]()
|
|
F. Особенные ребра
Потоки
графы
*3200
У коалы Коа есть ориентированный граф \(G\) с \(n\) вершинами и \(m\) ребрами. Каждое ребро имеет пропускную способность, связанную с ним. Ровно \(k\) ребер графа, пронумерованные от \(1\) до \(k\), являются особенными, такие ребра изначально имеют пропускную способность, равную \(0\). Коа задаст вам \(q\) запросов. В каждом запросе она даст вам \(k\) целых чисел \(w_1, w_2, \ldots, w_k\). Это означает, что пропускная способность \(i\)-го особенного ребра становится равной \(w_i\) (а другие пропускные способности остаются неизменными). Коа задается вопросом: чему равен максимальный поток, из вершины \(1\) в вершину \(n\) после каждого такого запроса? Помогите ей! Выходные данные Для \(i\)-го запроса выведите одно целое число \(res_i\) — максимальный поток из вершины \(1\) в вершину \(n\) с учетом специальных весов ребер \(i\)-го запроса. Примечание Для второго примера следующие изображения соответствуют первым двум запросам (слева направо соответственно). Для каждого ребра указана пара поток/пропускная способность, обозначающая поток, проталкиваемый через ребро, и пропускную способность ребра. Специальные ребра окрашены в красный цвет. 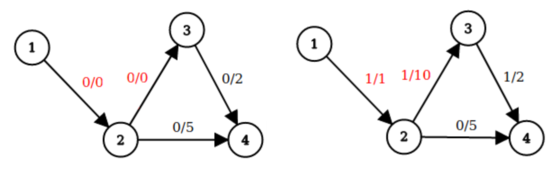 Как вы можете видеть, в первом запросе максимальный поток от вершины \(1\) к вершине \(4\) равен \(0\), а во втором запросе равен \(1\). | |
![]()
|
|
E. Кирпичи
Потоки
Паросочетания
*2800
графы
Кирпич — прямоугольник с целыми сторонами шириной \(1\) или высотой \(1\) (или и то и другое). Дана сетка \(n\times m\), и каждая ячейка окрашена в черный или белый цвет. Замощение — это способ поместить кирпичи на сетку так, чтобы каждая черная ячейка была покрыта ровно одним кирпичом, а каждая белая ячейка не была покрыта кирпичом. Другими словами, кирпичи размещаются только в черных ячейках, покрывают все черные ячейки, и никакие два кирпича не перекрываются. 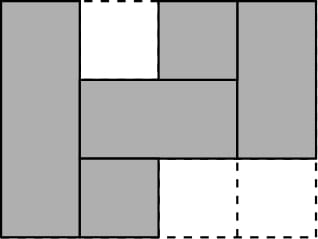 Пример замощения с первого примера с использованием \(5\) кирпичей. Существует также замощение из \(4\) кирпичей. Пример замощения с первого примера с использованием \(5\) кирпичей. Существует также замощение из \(4\) кирпичей. Какое минимальное количество кирпичей необходимо для замощения данной сетки? Выходные данные Выведите единственное целое число — минимальное количество требуемых кирпичей. Примечание Сетка с первого примера может быть замощена \(4\)-мя кирпичами, размещенными вертикально. Сетка с третьего примера может быть замощена такими \(18\) кирпичами: 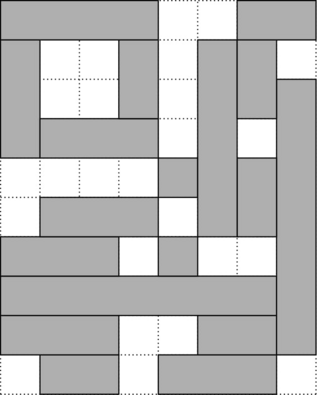 | |
![]()
|
|
H. Разноцветные тройки
Бинарный поиск
Потоки
Структуры данных
жадные алгоритмы
*3300
Вам дана последовательность \(a_1, a_2, \ldots, a_n\) неотрицательных целых чисел. Вам нужно найти наибольшее число \(m\) троек \((i_1, j_1, k_1)\), \((i_2, j_2, k_2)\), ..., \((i_m, j_m, k_m)\) таких, что выполняются следующие условия: - \(1 \leq i_p < j_p < k_p \leq n\) для всех \(p\) среди \(1, 2, \ldots, m\);
- \(a_{i_p} = a_{k_p} = 0\), \(a_{j_p} \neq 0\);
- значения \(a_{j_1}, a_{j_2}, \ldots, a_{j_m}\) различны;
- значения \(i_1, j_1, k_1, i_2, j_2, k_2, \ldots, i_m, j_m, k_m\) различны.
Выходные данные Для каждого набора выходных данных выведите одно целое число \(m\): наибольшее количество троек, которое вы можете найти. Примечание В первых двух примерах не хватает элементов даже для одной тройки, так что ответ \(0\). Во втором примере вы можете выбрать одну тройку \((1, 2, 3)\). В четвертом примере можно выбрать две тройки \((1, 3, 5)\) и \((2, 4, 6)\). В пятом примере можно выбрать одну тройку \((1, 2, 3)\). Мы не можем выбрать тройки \((1, 2, 3)\) и \((4, 5, 6)\) одновременно, так как \(a_2 = a_5\). | |
![]()
|
|
F. Понты
Потоки
Паросочетания
реализация
жадные алгоритмы
*3300
В очередной скучный день карантина BThero принялся изучать матрицы размера \(n \times m\). Строки матрицы нумеруются от \(1\) до \(n\) сверху вниз, а столбцы нумеруются от \(1\) до \(m\) слева направо. Клетка в \(i\)-й строке и \(j\)-м столбце обозначается \((i, j)\). Для каждой клетки \((i, j)\) матрицы у BThero были два значения: - ценность данной клетки, которая выражается одним положительным целым числом;
- направление данной клетки, которое выражается одним из символов L, R, D, U. Данные символы означают переходы в соседние клетки \((i, j - 1)\), \((i, j + 1)\), \((i + 1, j)\), \((i - 1, j)\), соответственно. Никакой переход не вел за границу матрицы.
Назовем клетку \((i_2, j_2)\) достижимой из \((i_1, j_1)\), если, начав из клетки \((i_1, j_1)\) и переходя в соседнюю клетку в соответствии с направлением текущей клетки, мы рано или поздно посетим \((i_2, j_2)\). BThero решил создать еще одну матрицу из имеющихся двух. Для клетки \((i, j)\) обозначим \(S_{i, j}\) как множество достижимых из нее клеток (включая саму клетку \((i, j)\)). Значение новой матрицы в клетке \((i, j)\) будет равно сумме ценностей всех клеток из \(S_{i, j}\). Быстро посчитав новую матрицу, BThero разослал ее всем своим друзьям. Однако он не сохранил обе изначальные матрицы! Помогите ему восстановить любые две изначальные матрицы, из которых могла получиться заданная. Выходные данные Для каждого набора, если ответа не существует выведите одну единственную строку NO. Иначе выведите строку YES и две матрицы в таком же формате, как и во вводе. - Первая матрица должна быть матрицей ценностей, а вторая должна быть матрицей направлений.
- Все числа в матрице ценностей должны быть положительными.
- Все буквы в матрице направлений должны быть допустимыми. Никакой переход не должен указывать за границы матрицы.
| |
![]()
|
|
B. Valuable Paper
Бинарный поиск
Потоки
Паросочетания
*1900
графы
The pandemic is upon us, and the world is in shortage of the most important resource: toilet paper. As one of the best prepared nations for this crisis, BubbleLand promised to help all other world nations with this valuable resource. To do that, the country will send airplanes to other countries carrying toilet paper. In BubbleLand, there are \(N\) toilet paper factories, and \(N\) airports. Because of how much it takes to build a road, and of course legal issues, every factory must send paper to only one airport, and every airport can only take toilet paper from one factory. Also, a road can't be built between all airport-factory pairs, again because of legal issues. Every possible road has number \(d\) given, number of days it takes to build that road. Your job is to choose \(N\) factory-airport pairs, such that if the country starts building all roads at the same time, it takes the least amount of days to complete them. Output If there are no solutions, output -1. If there exists a solution, output the minimal number of days to complete all roads, equal to maximal \(d\) among all chosen roads. | |
![]()
|
|
E. Камень, ножницы, бумага
Потоки
Перебор
Конструктив
математика
*1800
жадные алгоритмы
Аня и Боря решили сыграть в игру «Камень, ножницы, бумага». Игра состоит из раундов, каждый из раундов проводится независимо от остальных. В каждом раунде оба игрока одновременно показывают один из трех предметов: камень, ножницы или бумагу. При этом, если оба игрока показали одинаковые предметы, то в раунде объявляется ничья. В противном случае, действуют следующие правила: - если один игрок показал камень, а другой ножницы, то игрок, показавший камень, объявляется победителем раунда, а другой игрок — проигравшим;
- если один игрок показал ножницы, а другой бумагу, то игрок, показавший ножницы, объявляется победителем раунда, а другой игрок — проигравшим;
- если один игрок показал бумагу, а другой камень, то игрок, показавший бумагу, объявляется победителем раунда, а другой игрок — проигравшим.
Аня и Боря решили, что они сыграют ровно \(n\) раундов описанной игры. Аня решила, что она \(a_1\) раз покажет камень, \(a_2\) раз покажет ножницы и \(a_3\) раз покажет бумагу. Боря решил, что он \(b_1\) раз покажет камень, \(b_2\) раз покажет ножницы и \(b_3\) раз покажет бумагу. При этом ни Аня, ни Боря еще не выбрали последовательность, в которой будут показывать предметы. Гарантируется, что \(a_1 + a_2 + a_3 = n\) и \(b_1 + b_2 + b_3 = n\). Перед вами стоит задача определить два числа: - минимальное количество раундов, которое может выиграть Аня;
- максимальное количество раундов, которое может выиграть Аня.
Выходные данные Выведите два целых числа — минимальное и максимальное количество раундов, которое может выиграть Аня. Примечание В первом примере Аня может не выиграть ни одного раунда, если покажет, например, сначала ножницы, а потом бумагу, а Боря покажет камень, а потом ножницы. В лучшем случае Аня выиграет один раунд, если, например, сначала покажет бумагу, а потом ножницы, а Боря покажет камень, а потом ножницы. Во втором примере Аня может не выиграть ни одного раунда, если, например, Боря в каждом раунде будет показывать те же предметы, что и Аня. В третьем примере Аня всегда показывает бумагу, а Боря всегда показывает камень, поэтому Аня в любом случае выиграет все три раунда. | |
![]()
|
|
G. Миллиард оттенков серого
Потоки
графы
*3300
Вы должны покрасить оттенками серого плитки стены размера \(n\times n\). Стена состоит из \(n\) рядов плиток, в каждом по \(n\) плиток. Плитки на границе стены (т.е. в первом ряду, последнем ряду, первом столбце и последнем столбце) уже покрашены, и вы не должны менять их цвет. Все остальные плитки не покрашены. Некоторые из плиток сломаны, их нельзя красить. Гарантируется, что плитки на границе не сломаны. Вы должны покрасить все не сломанные плитки, которые еще не покрашены. Когда вы красите плитку, вы можете выбрать один из \(10^9\) оттенков серого, пронумерованных от \(1\) до \(10^9\). Вы можете покрасить несколько плиток одним и тем же оттенком. Формально, раскраска стены эквивалентна присвоению оттенка (целое число от \(1\) до \(10^9\)) каждой неокрашенной плитке, которая еще не закрашена. Контраст между двумя плитками равен модулю разности между оттенками двух плиток. Общий контраст стены является суммой контрастов по всем парам соседних несломанных плиток (две плитки соседние, если они имеют общую сторону). Вычислите минимально возможный суммарный контраст стены. Выходные данные Выведите единственное целое число — минимально возможный суммарный контраст стены. Примечание Пояснение первого примера: Первоначальная конфигурация плиток (плитки, которые нужно покрасить, обозначаются ?):
1 7 6
4 ? 6
1 1 1
Возможный способ покраски плитки, достигающий минимально возможного суммарного контраста в \(26\):
1 7 6
4 5 6
1 1 1
Пояснение второго примера: Так как все плитки либо покрашены, либо сломаны, делать нечего. Общий контраст составляет \(396\). Пояснение третьего примера: Первоначальная конфигурация плиток (плитки, которые нужно покрасить, обозначены ?):
6 6 5 4 4
6 ? ? ? 4
7 ? ? ? 3
8 ? ? ? 2
8 8 1 2 2
Возможный способ покраски плитки достигает минимально возможного контраста в \(34\):
6 6 5 4 4
6 6 5 4 4
7 7 5 3 3
8 8 2 2 2
8 8 1 2 2
| |
![]()
|
|
G. Очередное взвешивание графа
Потоки
математика
дп
*2600
поиск в глубину и подобное
графы
битмаски
Дан ориентированный ацикличный граф (ориентированный граф, не содержащий циклов) из \(n\) вершин и \(m\) дуг. \(i\)-я дуга ведет из вершины \(x_i\) в вершину \(y_i\) и имеет вес \(w_i\). Ваша задача — для каждой вершины \(v\) выбрать некоторое целое число \(a_v\), после чего на каждой дуге \(i\) записать такое число \(b_i\), что \(b_i = a_{x_i} - a_{y_i}\). Вы должны выбрать числа таким образом, чтобы: - все \(b_i\) были положительны;
- значение выражения \(\sum \limits_{i = 1}^{m} w_i b_i\) было минимально возможным.
Можно показать, что для любого ориентированного ацикличного графа с неотрицательными \(w_i\) такой способ выбрать числа существует. Выходные данные Выведите \(n\) целых чисел \(a_1\), \(a_2\), ..., \(a_n\) (\(0 \le a_v \le 10^9\)), которые необходимо записать на вершинах, чтобы все \(b_i\) были положительны, и значение выражения \(\sum \limits_{i = 1}^{m} w_i b_i\) было минимально возможным. Если ответов несколько — выведите любой. Можно показать, что ответ всегда существует, и хотя бы один из оптимальных ответов удовлетворяет ограничениям \(0 \le a_v \le 10^9\). | |
![]()
|
|
C. Шеф Монокарп
Потоки
Паросочетания
математика
дп
*1800
жадные алгоритмы
сортировки
Шеф Монокарп только что поставил \(n\) блюд на плиту. Он знает, что оптимальное время готовки \(i\)-го блюда равно \(t_i\) минут. В любую положительную целую минуту \(T\) Монокарп может снять не более одного блюда с плиты. Если достать \(i\)-е блюдо в некоторую минуту \(T\), то его испорченность будет равна \(|T - t_i|\) — модуль значения разности между \(T\) и \(t_i\). Как только блюдо снято с плиты, его уже нельзя поставить обратно. Монокарп должен снять все блюда с плиты. Какую минимальную суммарную испорченность он может получить? Выходные данные На каждый набор входных данных выведите одно целое число — минимальную суммарную испорченность блюд, которую может получить Монокарп, когда снимет все блюда с плиты. Помните, что Монокарп может снимать блюда только в положительные целые минуты и не более одного в минуту. Примечание В первом наборе входных данных Монокарп может снять блюда в минуты \(3, 1, 5, 4, 6, 2\). Тогда суммарная испорченность будет равна \(|4 - 3| + |2 - 1| + |4 - 5| + |4 - 4| + |6 - 5| + |2 - 2| = 4\). Во втором наборе входных данных Монокарп может снять блюда в минуты \(4, 5, 6, 7, 8, 9, 10\). В третьем наборе входных данных Монокарп может снять блюдо в минут \(1\). В четвертом наборе входных данных Монокарп может снять блюда в минуты \(5, 1, 2, 4, 3\). В пятом наборе входных данных Монокарп может снять блюда в минуты \(1, 3, 4, 5\). | |
![]()
|
|
C. Инженер Артем
Потоки
Конструктив
*2000
2-sat
бпф
китайская теорема об остатках
Артем строит нового робота. У него есть таблица \(a\), состоящая из \(n\) строк и \(m\) столбцов. Ячейка, расположенная на \(i\)-й сверху строке и \(j\)-м слева столбце, содержит значение \(a_{i,j}\). Если две соседние ячейки таблицы содержат одинаковое значение, то робот ломается. Таблица называется хорошей, если никакие две соседние клетки не содержат одинаковое значение. Две клетки называются соседними, если они имеют общую сторону. Артем хочет увеличить значения в некоторых ячейках на один, чтобы сделать \(a\) хорошей. Более формально, найдите хорошую таблицу \(b\), которая удовлетворяет следующему условию: - Для всех подходящих (\(i,j\)) выполняется или \(b_{i,j} = a_{i,j}\), или \(b_{i,j} = a_{i,j}+1\).
Для данных ограничений можно показать, что такая таблица \(b\) всегда существует. Если таких таблиц несколько, вы можете вывести любую из них. Пожалуйста, обратите внимание, что нет необходимости минимизировать количество ячеек, значения в которых вы увеличите. Выходные данные Для каждого набора входных данных выводите \(n\) строк, каждая из которых содержит \(m\) целых чисел. \(j\)-м числом в \(i\)-й строке выведите \(b_{i,j}\). Примечание Для каждого набора входных данных из примера можно проверить, что никакие две соседние ячейки не имеют одинакового значения, и что \(b\) равен \(a\) с некоторыми значениями, увеличенными на единицу. | |
![]()
|
|
E. Четыре точки
Тернарный поиск
Потоки
Перебор
Конструктив
математика
реализация
геометрия
жадные алгоритмы
*2400
Вам заданы четыре различные целые точки \(p_1\), \(p_2\), \(p_3\) и \(p_4\) на коодинатной плоскости \(\mathit{XY}\). За один шаг вы можете выбрать одну из точек \(p_i\) и сдвинуть ее в одном из четырех направлений на единицу. Другими словами, если вы выбрали точку \(p_i = (x, y)\), вы можете передвинуть ее в \((x, y + 1)\), \((x, y - 1)\), \((x + 1, y)\) или \((x - 1, y)\). Ваша задача — сдвинуть точки таким образом, чтобы они образовали квадрат со сторонами параллельными осям \(\mathit{OX}\) и \(\mathit{OY}\) (квадрат со стороной \(0\) разрешен). Какое минимальное количество шагов вам нужно, чтобы получить такой квадрат? Выходные данные Для каждого набора входных данных, выведите единственное число — минимальное количество шагов, необходимых для получения квадрата. Примечание В первом наборе входных данных, один из оптимальных ответов изображен ниже:  Каждая точка будет сдвинута два раза, поэтому ответ \(2 + 2 + 2 + 2 = 8\). Во втором наборе, один из оптимальных ответов изображен ниже: 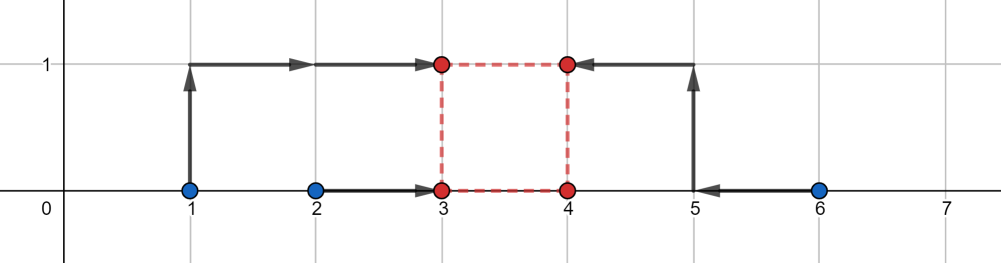 Ответ равен \(3 + 1 + 0 + 3 = 7\). В третьем наборе, один из оптимальных ответов изображен ниже: 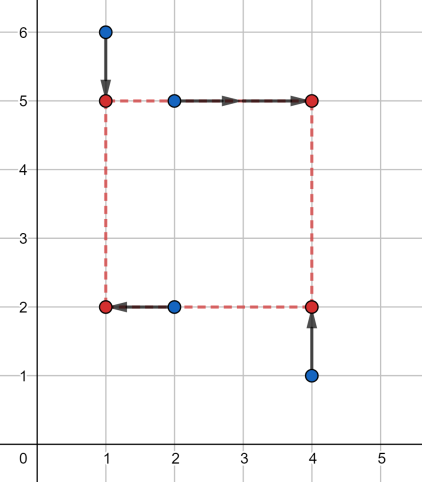 Ответ равен \(1 + 1 + 2 + 1 = 5\). | |
![]()
|
|
F. Странное множество
Потоки
математика
*2700
Обратите внимание на необычное ограничение по памяти. Задано целое число \(n\) и две последовательности \(a_1, a_2, \dots, a_n\) и \(b_1, b_2, \dots, b_n\). Назовем множество целых чисел \(S\) такое, что \(S \subseteq \{1, 2, 3, \dots, n\}\) странным, если для каждого элемента \(i\) из \(S\) выполняется следующее условие: для каждого \(j \in [1, i - 1]\), если \(a_j\) делит \(a_i\), то \(j\) также входит в \(S\). Пустое множество является странным. Стоимостью множества \(S\) назовем величину \(\sum\limits_{i \in S} b_i\). Вам необходимо найти максимальную возможную стоимость странного множества. Выходные данные Выведите одно целое число — максимальную стоимость странного множества. Примечание Для первого примера странное множество с максимальной стоимостью выглядит следующим образом — \(\{1, 2, 4, 8, 9\}\). Для второго примера странным множеством с максимальной стоимостью является пустое множество. | |
![]()
|
|
E. Парный платёж
Бинарный поиск
Потоки
Перебор
Конструктив
дп
графы
*2200
кратчайшие пути
В стране \(n\) городов и \(m\) двунаправленных дорог. Дороги в стране формируют неориентированный взвешенный граф. Граф может быть несвязным. У каждой дороги есть свой параметр \(w\). Вы можете ездить по дорогам, но правительство издало новый закон: вы можете проезжать только по двум дорогам сразу (проехать из города \(a\) в город \(b\), и из города \(b\) в город \(c\)) и вы должны будете заплатить \((w_{ab} + w_{bc})^2\) денег, чтобы проехать по этим дорогам. Для каждого города \(t\) найдите, можно ли добраться до него из города \(1\), и какое наименьшее количество денег необходимо потратить, чтобы добраться из \(1\) в \(t\). Выходные данные Для каждого города \(t\) выведите одно целое число. Если нет корректного пути из \(1\) в \(t\) выведите \(-1\). Иначе выведите минимальное необходимое количество денег, чтобы добраться из \(1\) в \(t\). Примечание Граф в первом примере выглядит так. 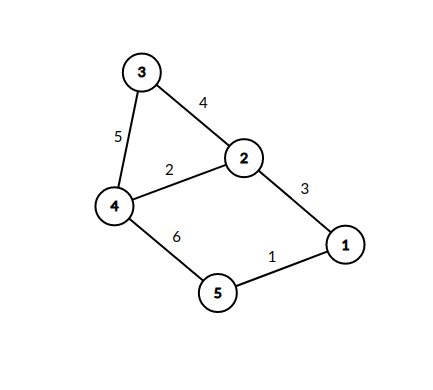
Во втором примере путь из \(1\) в \(3\) проходит через \(2\), так что результирующая стоимость поездки будет \((1 + 2)^2 = 9\). 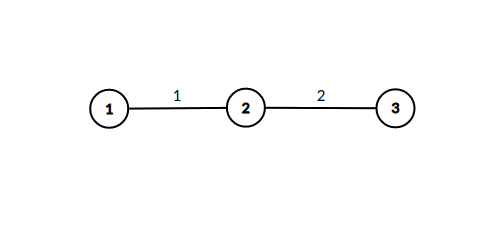
| |
![]()
|
|
I. Вторжение демонов
Потоки
*особая задача
*3100
Даларан — летающий город магии. Он состоит из \(n\) парящих островов, соединенных \(m\) мостами (каждый мост можно пересечь в обоих направлениях). По этим мостам можно добраться до каждого острова. Было бы обидно, если бы какой-нибудь магический эксперимент пошел ужасно неправильно и этот великолепный город был бы разрушен, верно? Ну, теперь угадайте, что случилось. На острове \(1\) был открыт портал в мир демонов. Сейчас начало \(1\)-го дня катастрофы, и все \(k\) магов собрались на острове \(1\) (они пытались закрыть портал, но поняли, что это невозможно). В начале \(2\)-го дня гигантская орда демонов выйдет из портала, захватит остров \(1\) и убьет каждого мага, оставшегося на этом острове. В течение каждого дня \(i\), если остров \(v\) был захвачен демонами к началу дня, орда демонов будет путешествовать по всем таким мостам, одним из концов которых является \(v\), захватывать каждый остров, который они достигнут, и убивать каждого мага, которого они встретят на своем пути. Каждый мост содержит ровно один волшебный камень. Каждый маг в начале дня может выполнить одно из следующих действий: - потратить один день для пересечения одного из мостов, соединенных с островом, где в настоящее время находится маг. Проходя через мост, маг может забрать с него магический камень (если таковой имеется; каждый магический камень может быть поднят не более чем одним магом). Если мост будет пройден демонами в тот же день, или к началу следующего дня тот остров, на который отправляется маг, будет уже захвачен демонической ордой (даже если они прибудут туда в тот же момент), и маг будет убит.
- выполнить ритуал телепортации, чтобы добраться до безопасного места за пределами Даларана. Этот ритуал потребляет два магических камня (и не может быть выполнен, если у мага меньше двух камней).
Каждый магический камень распадается за \(2\) дня — если его поднять в середине дня \(i\), он распадается в середине дня \(i + 2\). Если камень распался, то его нельзя использовать в ритуале телепортации. Посчитайте максимальное количество магов, которые смогут добраться до безопасного места. Выходные данные Выведите одно целое число — максимальное количество магов, которые смогут добраться до безопасного места. | |
![]()
|
|
G. Звездная ночь в кемпинге
Потоки
Конструктив
графы
*3300
У подножия горы Лиюшань будут установлены \(n\) палаток, для тех, кто желает испытать радость от единения с природой, спокойствия ночи и яркого звездного неба. Палатка номер \(i\) будет расположена в точке \((x_i, y_i)\) и будет иметь вес \(w_i\). Палатка считается важной, если оба \(x_i\) и \(y_i\) являются четными. Вам нужно убрать некоторые из палаток так, чтобы для каждой оставшейся важной палатки \((x, y)\) не существовало \(3\) другие палатки \((x'_1, y'_1)\), \((x'_2, y'_2)\) и \((x'_3, y'_3)\), такие что оба условия выполнены: - \(|x'_j-x|, |y'_j - y|\leq 1\) для всех \(j \in \{1, 2, 3\}\).
- Эти четыре палатки образуют параллелограмм (или прямоугольник), и одна из его сторон параллельна оси \(x\).
Максимизируйте сумму весов оставшихся палаток. Выходные данные Выведите одно целое число — максимальную сумму весов оставшихся палаток. Примечание Иллюстрация для второго примера. Черные треугольники обозначают важные палатки. Этот пример также показывает все \(8\) запрещенных паттернов. 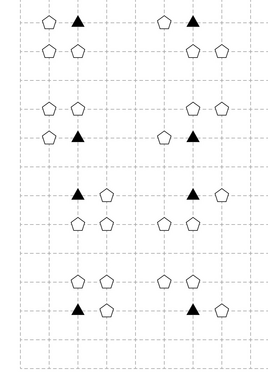 | |
![]()
|
|
F. Сундуки и ключи
Потоки
Перебор
дп
поиск в глубину и подобное
битмаски
*3200
Алиса и Боб играют в игру. У Алисы есть \(n\) сундуков с сокровищами (в \(i\)-м лежит \(a_i\) монет) и \(m\) ключей (\(j\)-й из которых она может продать Бобу за \(b_j\) монет). Сначала Алиса вешает некоторые замки на сундуки. Есть \(m\) типов замков, замок \(j\)-го типа можно открыть только \(j\)-м ключом. Чтобы повесить замок типа \(j\) на \(i\)-й сундук, Алиса должна заплатить \(c_{i,j}\) долларов. Алиса может повесить произвольное количество различных замков на каждый сундук (возможно, ноль). Затем Боб покупает у Алисы несколько ключей (возможно, ноль или все) и открывает все сундуки, которые он может открыть (он может открыть сундук, если у него есть ключи от всех замков на этом сундуке). Прибыль Боба — это разность между суммарным количеством монет в открытых сундуках и суммарным количеством монет, которые он тратит на покупку ключей у Алисы. Если прибыль Боба строго положительная (больше ноля), то он выигрывает игру. Иначе Алиса выигрывает игру. Алиса хочет повесить замки на некоторые сундуки так, чтобы она выиграла игру вне зависимости от ключей, которые Боб купит (Боб не может получить положительную прибыль). Разумеется, она хочет потратить как можно меньше долларов на покупку замков. Помогите ей определить, может ли она выиграть игру, а если может, то сколько долларов ей придется потратить на замки. Выходные данные Если Алиса не может гарантированно выиграть (как бы она ни выбирала замки, Боб всегда сможет получить положительную прибыль), то выведите \(-1\). Иначе выведите одно целое число — минимальное количество долларов, которые необходимо потратить Алисе, чтобы выиграть вне зависимости от действий Боба. Примечание В первом примере Алиса должна повесить замки \(1\) и \(3\) типов на первый сундук и замки \(2\) и \(3\) типов на второй сундук. Во втором примере Алиса должна повесить замки \(1\) и \(2\) типов на первый сундук и замок \(3\) типа на второй сундук. | |
![]()
|
|
D. Кресла
Потоки
Паросочетания
дп
*1800
жадные алгоритмы
В ряд стоят \(n\) кресел, пронумерованных от \(1\) до \(n\) слева направо. Некоторые кресла заняты людьми (не более одного человека на кресло), остальные свободны. Количество занятых мест не превосходит \(\frac{n}{2}\). По некоторым причинам вы хотите пересадить людей. Если \(i\)-е кресло занято, а \(j\)-е — нет, вы можете попросить человека, сидящего в \(i\)-м кресле, пересесть в \(j\)-е кресло. Время, которое потребуется на перемещение из \(i\)-го кресла в \(j\)-е, равно \(|i - j|\) минутам. Эту операцию можно проводить любое количество раз, но операции должны выполняться последовательно, то есть вы не можете попросить человека пересесть, пока человек, которого вы попросили в предыдущей операции, еще не закончил перемещение. Вы бы хотели добиться следующей ситуации: все кресла, которые были заняты в самом начале, должны оказаться свободными. За какое минимальное время вы сможете это сделать? Выходные данные Выведите одно целое число — минимальное количество минут, за которое вы можете добиться следующей ситуации: все кресла, которые были заняты в самом начале, должны оказаться свободными. Примечание В первом примере возможна следующая последовательность действий: - попросить человека пересесть из кресла \(1\) в кресло \(2\) за \(1\) минуту;
- попросить человека пересесть из кресла \(7\) в кресло \(6\) за \(1\) минуту;
- попросить человека пересесть из кресла \(4\) в кресло \(5\) за \(1\) минуту.
Во втором примере возможна следующая последовательность действий: - попросить человека пересесть из кресла \(1\) в кресло \(4\) за \(3\) минуты;
- попросить человека пересесть из кресла \(2\) в кресло \(6\) за \(4\) минуты;
- попросить человека пересесть из кресла \(4\) в кресло \(5\) за \(1\) минуту;
- попросить человека пересесть из кресла \(3\) в кресло \(4\) за \(1\) минуту.
В третьем примере ни одно место не занято, поэтому вам не надо тратить время. | |
![]()
|
|
F. Гоблины и гномы
Потоки
Паросочетания
Перебор
дп
*2800
Монокарп играет в компьютерную игру «Гоблины и гномы». В этой игре он управляет подземным городом гномов, защищающимся от орд гоблинов. Подземный город состоит из \(n\) залов и \(m\) односторонних туннелей, соединяющих некоторые пары залов. Структура туннелей такова, что, выйдя из какого-то зала, нельзя вернуться в него обратно по тоннелям. На город готовится \(k\) атак гоблинов, в \(i\)-й атаке город атакуют \(i\) гоблинов. Цель Монокарпа — выдержать все \(k\) атак. \(i\)-я атака происходит следующим образом: сначала \(i\) гоблинов появляются в каких-то залах города и грабят их, при этом в каждом зале появляется не более одного гоблина. После этого гоблины начинают перемещаться из зала в зал по туннелям, попутно грабя каждый зал на своем пути. Гоблины очень жадные и хитрые, а поэтому планируют выбирать свои стартовые залы и пути так, что никакие два гоблина не пройдут через один и тот же зал. При этом, среди всех возможных планов атаки они выбирают такой, что позволяет в сумме разграбить максимальное количество залов. После того как гоблины разграбили максимальное количество залов, они покидают город. Если в результате атаки все залы оказались разграблены — Монокарп проигрывает. Иначе гномам удается восстановить город. Если какой-то зал оказался разграблен в ходе атаки, то в ходе следующих атак он все равно представляет интерес для гоблинов (гномы успевают восстановить его). Перед каждой атакой у Монокарпа есть время для подготовки. Монокарп может готовиться бесконечно долго (он сам решает, когда вызвать каждую атаку), но чем дольше он готовится к атаке, тем меньше очков он получает. Если Монокарп готовился к \(i\)-й атаке \(t_i\) минут, то после нее он получает \(\max(0, x_i - t_i \cdot y_i)\) очков (естественно, если он не проигрывает). Во время подготовки к атаке Монокарп может блокировать туннели. За одну минуту он может заблокировать либо все туннели, ведущие в некоторый зал, либо все туннели, ведущие из некоторого зала. Если Монокарп заблокировал какой-то туннель во время подготовки к атаке, то этот туннель остается заблокированным и во время следующих атак. Помогите Монокарпу выдержать все \(k\) атак гоблинов и набрать максимальное количество очков! Выходные данные Выведите оптимальную последовательность действий Монокарпа в следующем формате: В первой строке выведите целое число \(a\) (\(k \le a \le 2n + k\)) — количество действий, которые совершает Монокарп. Во второй строке выведите сами эти действия в том порядке, в котором Монокарп их выполняет. \(i\)-е действие описывается целым числом \(b_i\) (\(-n \le b_i \le n\)) в следующем формате: - если \(b_i > 0\), то Монокарп блокирует все туннели, ведущие из зала \(b_i\);
- если \(b_i < 0\), то Монокарп блокирует все туннели, ведущие в зал \(|b_i|\);
- если \(b_i = 0\), то Монокарп вызывает очередную атаку гоблинов.
Нельзя повторять одно и то же действие по блокировке \(b_i\) несколько раз. Каждый раз, когда Монокарп вызывает очередную атаку гоблинов, он должен выдержать ее (у гоблинов не должно быть возможности разграбить все залы города). Монокарп должен выдержать ровно \(k\) атак и получить максимально возможное количество очков. Если существует несколько оптимальных последовательностей действий — выведите любую из них. Примечание В первом примере Монокарп сначала блокирует все туннели, ведущие в зал \(2\), а потом — все туннели, ведущие в зал \(3\), после чего вызывает все атаки. Он готовился к атаке \(1\) две минуты, поэтому он получает за нее \(98\) очков. К остальным атакам он не готовился, поэтому получает максимально возможные очки за них (\(200\), \(10\) и \(100\)). Суммарно он набирает \(408\) очков. Во втором примере Монокарп сразу вызывает первую атаку и получает за нее \(100\) очков. Перед второй атакой он блокирует все туннели, ведущие в зал \(3\). Это означает, что он готовится к ней одну минуту и получает \(195\) очков за нее. К третьей атаке Монокарп не готовится и получает \(10\) очков. Перед четвертой атакой он блокирует туннели, ведущие из зала \(1\), это означает, что он готовится к атаке одну минуту и получает за нее \(99\) очков. Суммарно он набирает \(404\) очка. В третьем примере Монокарпу не важно, сделает он одно действие или несколько перед единственной атакой, так как он в любом случае не получит за нее очков. А потому блокирует все туннели в городе, потратив на это целых \(5\) минут и переживает атаку, не получив за нее очков. | |
![]()
|
|
D. Секретный Санта
Потоки
Конструктив
математика
*1600
жадные алгоритмы
графы
В компании ВКонтакте в декабре традиционно проводится мероприятие под названием «Секретный Санта». Суть его в следующем. В мероприятии участвуют \(n\) сотрудников, пронумерованных от \(1\) до \(n\). Каждому сотруднику \(i\) назначается другой сотрудник \(b_i\), которому сотрудник \(i\) должен сделать новогодний подарок. При этом каждый сотрудник назначается ровно одному другому сотруднику, и никто не назначается сам себе (но возможно, что два сотрудника окажутся назначены друг другу). Формально, все \(b_i\) должны быть различными целыми числами от \(1\) до \(n\), и для любого \(i\) должно выполняться \(b_i \ne i\). Как правило, назначение происходит случайным образом. Но в качестве эксперимента у участников мероприятия спросили, кому бы они хотели сделать подарок. Каждый сотрудник \(i\) сказал, что желает сделать подарок сотруднику \(a_i\). Найдите такое корректное назначение \(b\), что как можно больше пожеланий сотрудников окажется выполнено. Выходные данные Для каждого набора входных данных выведите две строки. В первой строке выведите целое число \(k\) (\(0 \le k \le n\)) — число выполненных пожеланий в вашем назначении. Во второй строке выведите \(n\) различных целых чисел \(b_1, b_2, \ldots, b_n\) (\(1 \le b_i \le n\); \(b_i \ne i\)) — номера сотрудников, назначенных сотрудникам \(1, 2, \ldots, n\). Число \(k\) должно быть равно числу индексов \(i\) таких, что \(a_i = b_i\), и должно быть максимальным возможным. Если существует несколько решений, выведите любое из них. Примечание В первом наборе входных данных существует два корректных назначения — \([3, 1, 2]\) и \([2, 3, 1]\). В первом случае будет выполнено два пожелания, а во втором — одно. Таким образом, \(k = 2\), и верным ответом является только назначение \([3, 1, 2]\). | |
![]()
|
|
I. Экскурсии
Потоки
Паросочетания
Конструктив
*особая задача
поиск в глубину и подобное
графы
Ирина работает в экскурсионной компании Саратова. Сегодня она собирается организовать экскурсии по городам Саратов и Энгельс. Всего существует \(n_1\) достопримечательность в Саратове и \(n_2\) достопримечательность в Энгельсе. Города разделены рекой, но есть \(m\) автобусных маршрутов, которые проходят по мостам и позволяют туристам добраться из Саратова в Энгельс и обратно. Маршрут \(i\)-го автобуса проходит от \(x_i\)-й достопримечательности в Саратове до \(y_i\)-й достопримечательности в Энгельсе, а также в обратном направлении. Ирина хочет спланировать экскурсии на текущий день. Экскурсионные поездки начинаются в Саратове утром, продолжаются в Энгельсе днем и заканчиваются в Саратове вечером. Каждый турист начинает свой экскурсионный день с какой-нибудь достопримечательности Саратова, \(k_i\) туристов начинают с \(i\)-й достопримечательности. Затем гиды везут их в Энгельс: на каждой достопримечательности Саратова гид выбирает автобусный маршрут, ведущий от этой достопримечательности в Энгельс, и все туристы, отправляющиеся с этой достопримечательности, отправляются в Энгельс по этому автобусному маршруту. После завершения экскурсий в Энгельсе происходит то же самое: для каждой достопримечательности в Энгельсе гид выбирает автобусный маршрут, ведущий от этой достопримечательности в Саратов, и все туристы с этой достопримечательности отправляются в Саратов по этому автобусному маршруту. Этот процесс может привести к такой ситуации, что некоторые туристы вернутся к той же достопримечательности в Саратове, с которой они начали утром. Очевидно, туристам это не нравится, поэтому Ирина хочет выбрать, куда гиды повезут туристов (как по дороге из Саратова в Энгельс, так и по дороге из Энгельса в Саратов), чтобы минимально возможное количество туристов вернулось к той же достопримечательности, с которой они начали. Помогите Ирине найти оптимальный план! Выходные данные Выведите одно целое число — минимально возможное количество туристов, которые вернутся к тому же месту, откуда они начали. | |
![]()
|
|
B. Грегор и игра в пешки
Потоки
Паросочетания
реализация
дп
поиск в глубину и подобное
жадные алгоритмы
графы
*800
Дана шахматная доска размера \(n\) на \(n\). Клетка на пересечении \(i\)-й сверху ряду и \(j\)-го слева столбца обозначается как \((i,j)\). На данный момент у Грегора есть несколько пешек в \(n\)-м ряду. Также в \(1\)-м ряду стоят вражеские пешки. За один шаг Грегор перемещает одну из своих пешек. Пешка может ходить на одну клетку вверх (из \((i,j)\) в \((i-1,j)\)), если клетка назначения не занята другой пешкой. В дополнение, пешка может переместиться на одну клетку вверх по диагонали (из \((i,j)\) в \((i-1,j-1)\) или в \((i-1,j+1)\)), если и только если в этой клетке стоит вражеская пешка. Вражеская пешка в таком случае убирается с доски. Грегор хочет узнать, какое максимальное количество его пешек может достичь \(1\)-го ряда. Заметьте, что в этой игре ходит только Грегор, вражеские пешки никогда не перемещаются. Также, когда пешка Грегора достигает \(1\)-го ряда, она останавливается и больше не может перемещаться. Выходные данные Для каждого набора входных данных выведите одно целое число: максимальное количество пешек Грегора, которые могут достичь \(1\)-го ряда. Примечание В первом примере Грегор может просто переместить вперед все его \(3\) пешки. Таким образом, ответ равен \(3\). Во втором примере Грегор может гарантировать, что все его \(4\) пешки достигнут вражеского ряда, следуя раскрашенным путям как показано ниже. Помните — только Грегор делает ходы в этой «игре»! 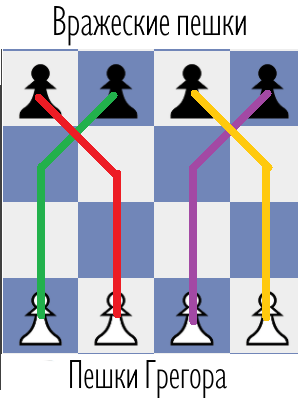 В третьем примере единственная пешка Грегора застряла перед вражеской пешкой и не может достигнуть желаемого ряда. В четвертом примере у Грегора нет пешек, поэтому ответ равен \(0\). | |
![]()
|
|
D. Бридж-клуб
Потоки
Паросочетания
*2800
жадные алгоритмы
графы
В местном бридж-клубе сейчас спорят на \(n\) различных тем, пронумерованных от \(0\) до \(n-1\), и, вот совпадение, в клубе состоят ровно \(2^n\) игроков, пронумерованных от \(0\) до \(2^n-1\). Никакие два игрока не имеют полностью совпадающих взглядов на все \(n\) тем, а именно, у \(i\)-го игрока положительный взгляд на \(j\)-ю тему, если \(i\ \&\ 2^j > 0\), и отрицательный взгляд иначе. Здесь \(\&\) обозначает операцию побитового И. Вы хотите организовать турнир по бриджу, в котором примут участие не более чем \(k\) пар игроков (в бридж играют командами из двух игроков). Вы можете составлять пары игроков произвольным образом (каждый игрок должен быть не более чем в одной паре), но с одним условием: два игрока не могут быть в одной паре, если у них различные взгляды на \(2\) или более из данных \(n\) тем. Вы знаете, что \(i\)-й игрок заплатит вам \(a_i\) долларов, если примет участие в турнире. Вычислите максимальную сумму, которую можно получить, выбрав команды оптимальным образом. Выходные данные Выведите одно целое число: максимальную сумму, которую вы можете получить, если составите команды оптимальным образом. Примечание В первом примере оптимальное решение — поставить в пару \(0\)-го и \(2\)-го игрока, что принесет \(8 + 5 = 13\) долларов. Хотя \(0\)-й и \(5\)-й игроки принесли бы вместе \(8 + 10 = 18\) долларов, мы их не можем объединить в команду, так как их взгляды отличаются в \(2\) из \(3\) тем. Во втором примере можно объединить в команду \(0\)-го и \(1\)-го игрока, а также \(2\)-го и \(3\)-го игрока, что в сумме даст \(7 + 4 + 5 + 7 = 23\) долларов. | |
![]()
|
|
F2. Алиса и перекрашивание 2
Потоки
Паросочетания
Конструктив
*2800
жадные алгоритмы
Разница между версиями заключается в стоимости операций. Решение для одной версии не будет работать для другой! У Алисы есть таблица размером \(n \times m\), изначально все ее клетки окрашены в белый цвет. Клетка на пересечении \(i\)-й строки и \(j\)-го столбца обозначается как \((i, j)\). Алиса может выполнять следующие операции: Выбрать любой подпрямоугольник, содержащий клетку \((1, 1)\), и инвертировать цвета всех его клеток. (Инвертировать означает изменить цвет клетки с белого на черный или с черного на белый). Эта операция стоит \(1\) монету. Выбрать любой подпрямоугольник, содержащий клетку \((n, 1)\), и инвертировать цвета всех его клеток. Эта операция стоит \(3\) монеты. Выбрать любой подпрямоугольник, содержащий клетку \((1, m)\), и инвертировать цвета всех его клеток. Эта операция стоит \(4\) монеты. Выбрать любой подпрямоугольник, содержащий клетку \((n, m)\), и инвертировать цвета всех его клеток. Эта операция стоит \(2\) монеты.
Напомним, что подпрямоугольник — это все клетки \((x, y)\) с \(x_1 \le x \le x_2\), \(y_1 \le y \le y_2\) для некоторых \(1 \le x_1 \le x_2 \le n\), \(1 \le y_1 \le y_2 \le m\). Алиса хочет получить свою любимую раскраску с помощью этих операций. Какое наименьшее количество монет ей придется потратить? Можно показать, что всегда можно преобразовать исходную таблицу в любую другую. Выходные данные Выведите наименьшее количество монет, которое Алиса должна будет потратить, чтобы получить свою любимую раскраску. Примечание В первом примере оптимально просто применить четвертую операцию один раз к прямоугольнику, содержащему клетки \((2, 2), (2, 3), (3, 2), (3, 3)\). Это обойдется в \(2\) монеты. | |
![]()
|
|
H. Оленьи игры
Бинарный поиск
Потоки
Структуры данных
Конструктив
графы
разделяй и властвуй
кратчайшие пути
*3000
На северном полюсе проживают \(n\) оленей, и все они соревнуются за первые позиции в таблице лидеров на главной странице CodeNorses (популярный сайт по спортивным оленьим играм). Довольно примечательно, что лидерство в таблице зависит от вклада и напрямую не связано с уровнем навыков в самих оленьих играх, однако для оленей таблица все равно крайне важна. На текущий момент, у \(i\)-го оленя вклад равен \(a_i\). Вы хотите повлиять на таблицу лидеров с помощью нескольких операций. За одну операцию вы можете выбрать оленя и либо увеличить, либо уменьшить его вклад на \(1\). Отрицательные вклады разрешены. При этом у вас есть \(m\) ограничений на получившиеся вклады. Каждое ограничение задается упорядоченной парой \((u, v)\), означающей, что в финальный вклад оленя \(u\) должен быть меньше или равен финального вклада оленя \(v\). Ваша задача — сделать наименьшее количество операций так, чтобы все ограничения были выполнены. Выходные данные Выведите \(n\) целых чисел \(b_1,\ldots, b_n\) (\(-10^{15}\le b_i\le 10^{15}\)), где \(b_i\) будет равно финальному вкладу \(i\)-го оленя после применения всех операций. Если существует несколько решений с наименьшим количеством операций, выведите любое из них. Можно доказать, что всегда существует оптимальное решение с \(|b_i|\le 10^{15}\) для всех \(i\). | |
![]()
|
|
C. Деление на два и перестановка
Потоки
Паросочетания
Конструктив
математика
*1100
жадные алгоритмы
Вам дан массив \(a\), состоящий из \(n\) целых положительных чисел. Над ним вы можете совершать операции. За одну операцию можно заменить любой элемент массива \(a_i\) на \(\lfloor \frac{a_i}{2} \rfloor\), то есть на целую часть от деления \(a_i\) на \(2\) (округление вниз). Проверьте, можно ли за произвольное количество операций (возможно, \(0\)) сделать так, чтобы массив \(a\) стал перестановкой чисел от \(1\) до \(n\) — то есть содержал все числа от \(1\) до \(n\), каждое по одному разу. Например, если \(a = [1, 8, 25, 2]\), \(n = 4\), то ответ положительный. Можно поступить так: - Заменим \(8\) на \(\lfloor \frac{8}{2} \rfloor = 4\), тогда \(a = [1, 4, 25, 2]\).
- Заменим \(25\) на \(\lfloor \frac{25}{2} \rfloor = 12\), тогда \(a = [1, 4, 12, 2]\).
- Заменим \(12\) на \(\lfloor \frac{12}{2} \rfloor = 6\), тогда \(a = [1, 4, 6, 2]\).
- Заменим \(6\) на \(\lfloor \frac{6}{2} \rfloor = 3\), тогда \(a = [1, 4, 3, 2]\).
Выходные данные Для каждого набора входных данных в отдельной строке выведите: - YES, если можно сделать так, чтобы массив \(a\) стал перестановкой чисел от \(1\) до \(n\),
- NO в противном случае.
Вы можете выводить YES и NO в любом регистре (например, строки yEs, yes, Yes и YES будут распознаны как положительный ответ). Примечание Первый тест разобран в тексте условия задачи. Во втором тесте получить искомый массив невозможно. | |
![]()
|
|
F. Сделай его двудольным!
Потоки
Паросочетания
теория чисел
графы
*3400
Дан неориентированный граф, состоящий из \(n\) вершин, пронумерованных от \(1\) до \(n\). Вершина \(i\) имеет значение \(a_i\), все \(a_i\) попарно различны. Между вершинами \(u\) и \(v\) есть ребро, если либо \(a_u\) делит \(a_v\), либо \(a_v\) делит \(a_u\). Найдите минимальное количество вершин, которое нужно удалить, чтобы граф стал двудольным. При удалении вершины удаляются все инцидентные ей ребра. Выходные данные Для каждого набора входных данных выведите одно число — минимальное количество вершин, которое нужно удалить, чтобы граф стал двудольным. | |
![]()
|
|
C. Автоматное программирование
Потоки
*2400
графы
В один замечательный день в компанию «X» завезли k автоматов. И не простых автоматов, а автоматов-программистов! Это был последний неудачный шаг перед переходом на андроидов-программистов, но это уже совсем другая история. В компании сейчас n задач, для каждой из которых известно время начала ее выполнения si, длительность ее выполнения ti и прибыль компании от ее завершения ci. Любой автомат может выполнять любую задачу, ровно одну в один момент времени. Если автомат начал выполнять задачу, то он занят все моменты времени с si по si + ti - 1 включительно и не может переключиться на другую задачу. Вам требуется выбрать набор задач, которые можно выполнить с помощью этих k автоматов и который принесет максимальную суммарную прибыль. Выходные данные Выведите n целых чисел x1, x2, ..., xn. Число xi должно быть равно 1, если задачу i следует выполнить, и 0 в противном случае. Если оптимальных решений несколько, то выведите любое из них. Примечание В первом примере задания требуют выполнения в моменты времени 2 ... 8, 1 ... 3 и 4 ... 4, соответственно. Первое задание пересекается со вторым и третьим, поэтому можно выполнять либо его одно (прибыль 5), либо второе и третье (прибыль 6). | |
![]()
|
|
J. Training Camp
Потоки
графы
You are organizing a training camp to teach algorithms to young kids. There are \(n^2\) kids, organized in an \(n\) by \(n\) grid. Each kid is between \(1\) and \(n\) years old (inclusive) and any two kids who are in the same row or in the same column have different ages. You want to select exactly \(n\) kids for a programming competition, with exactly one kid from each row and one kid from each column. Moreover, kids who are not selected must be either older than both kids selected in their row and column, or younger than both kids selected in their row and column (otherwise they will complain). Notice that it is always possible to select \(n\) kids satisfying these requirements (for example by selecting \(n\) kids who have the same age). During the training camp, you observed that some kids are good at programming, and the others are not. What is the maximum number of kids good at programming that you can select while satisfying all the requirements? Input The first line contains \(n\) (\(1 \leq n \leq 128\)) — the size of the grid. The following \(n\) lines describe the ages of the kids. Specifically, the \(i\)-th line contains \(n\) integers \(a_{i,1}, \, a_{i,2}, \, \dots, \, a_{i, n}\) (\(1 \le a_{i,j} \le n\)) — where \(a_{i,j}\) is the age of the kid in the \(i\)-th row and \(j\)-th column. It is guaranteed that two kids on the same row or column have different ages, i.e., \(a_{i,j} \ne a_{i,j'}\) for any \(1\le i\le n\), \(1\le j < j'\le n\), and \(a_{i,j} \ne a_{i',j}\) for any \(1\le i < i'\le n\), \(1\le j\le n\). The following \(n\) lines describe the programming skills of the kids. Specifically, the \(i\)-th line contains \(n\) integers \(c_{i,1}, \, c_{i,2}, \, \dots, \, c_{i, n}\) (\(c_{i,j} \in \{0, \, 1\}\)) — where \(c_{i,j}=1\) if the kid in the \(i\)-th row and \(j\)-th column is good at programming and \(c_{i,j}=0\) otherwise. Output Print the maximum number of kids good at programming that you can select while satisfying all the requirements. Note In the first sample, it is not possible to select the two kids good at programming (in row \(1\) and column \(1\), and in row \(2\) and column \(3\)), because then you would have to select the kid in row \(3\) and column \(2\), and in that case two kids would complain (the one in row \(1\) and column \(2\), and the one in row \(3\) and column \(1\)). A valid selection which contains \(1\) kid good at programming is achieved by choosing the \(3\) kids who are \(1\) year old. In the second sample, there are \(10\) valid choices of the \(n\) kids that satisfy the requirements, and each of them selects exactly \(2\) kids good at programming. | |
![]()
|
|
F. Поток минимальной стоимости?
Потоки
Структуры данных
жадные алгоритмы
сортировки
графы
*2700
Вам даны два массива \(a\) и \(b\) целых чисел (\(b_i \neq 0\) и \(|b_i| \leq 10^9\)). Массив \(a\) отсортирован в неубывающем порядке. Стоимость подмассива \(a[l:r]\) определяется следующим образом: Вам даны \(q\) запросов в виде двух целых чисел \(l\) и \(r\). Вы должны вычислить стоимость подмассива \(a[l:r]\) для каждого запроса, по модулю \(10^9 + 7\). Если вы не знаете, что означает минимальная стоимость максимального потока, обратитесь сюда. Выходные данные Для каждого запроса \(l_i\), \(r_i\) — выведите стоимость подмассива \(a[l_i:r_i]\) по модулю \(10^9 + 7\). Примечание В первом запросе, максимально возможный поток составляет \(1\), т.е. одна единица из источника в \(2\), затем одна единица из \(2\) в \(3\), затем одна единица из \(3\) в сток. Стоимость потока равна \(0 \cdot 1 + |2 - 4| \cdot 1 + 0 \cdot 1 = 2\). Во втором запросе, максимально возможный поток снова составляет \(1\), т.е. от источника к \(7\), от \(7\) к \(6\) и от \(6\) к стоку со стоимостью \(0 \cdot |10 - 10| \cdot 1 + 0 \cdot 1 = 0\). В третьем запросе, граф показан слева с пропускной способностью, указанной вне скобок, и стоимостью, указанной в скобках. Изображение справа показывает поток через каждое ребро в оптимальной конфигурации. 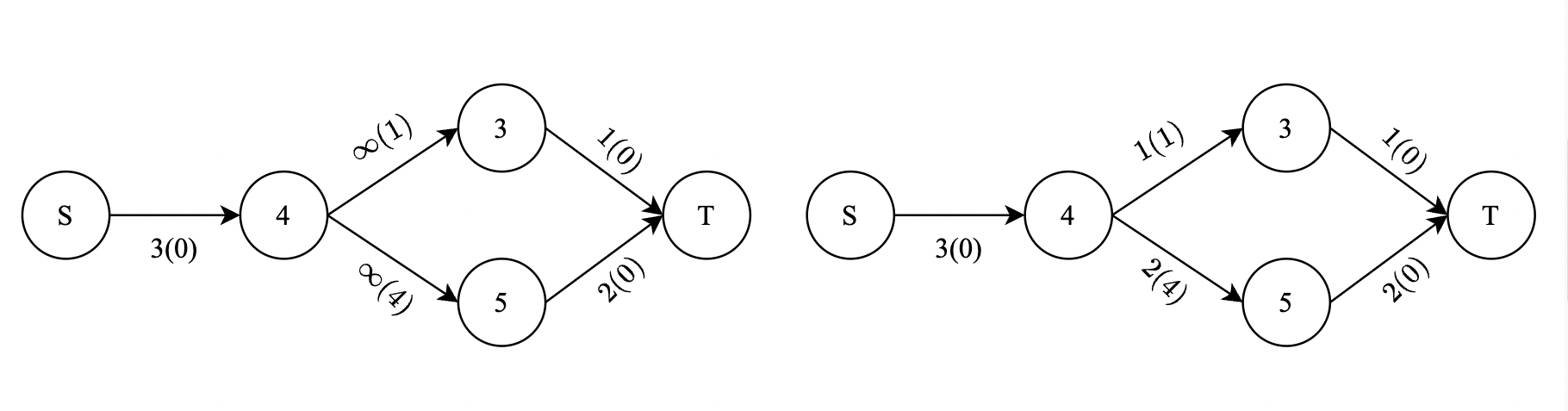 Максимальный поток составляет \(3\) при стоимости \(0 \cdot 3 + 1 \cdot 1 + 4 \cdot 2 + 0 \cdot 1 + 0 \cdot 2 = 9\). В четвертом запросе, сеть потока выглядит следующим образом: 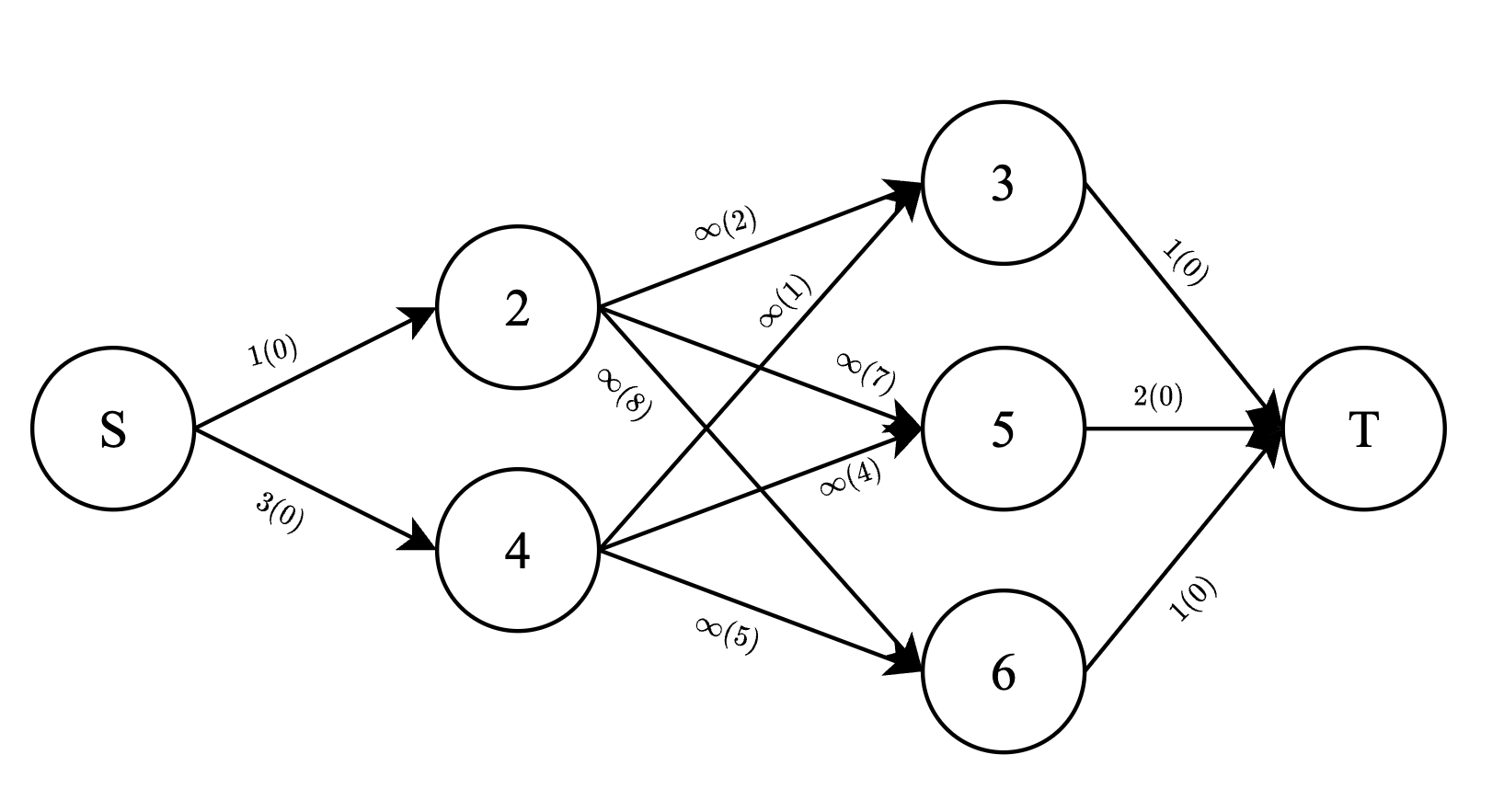 Минимальная стоимость максимального потока достигается следующим образом: 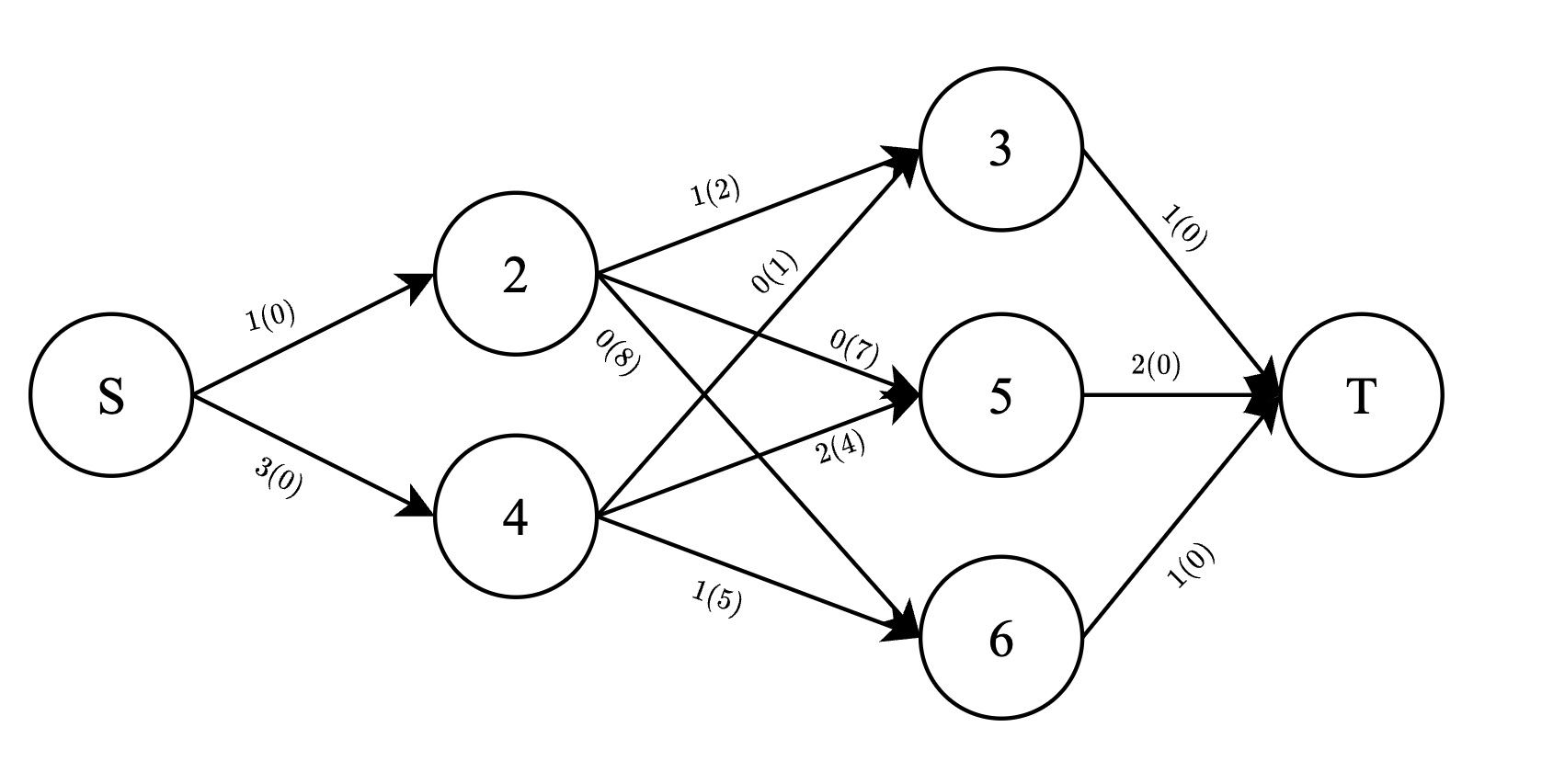 Максимальный поток в этой сети равен 4, а минимальная стоимость такого потока равна 15. | |
![]()
|
|
G. Алгоритм Люсине
Потоки
Паросочетания
Конструктив
математика
теория чисел
*2800
Принято считать, что самый известный алгоритм нахождения наибольшего общего делителя двух чисел придумал Евклид, однако на самом деле этот алгоритм придумала именно Тётя Люсине. Вы, должно быть, уже не удивились, ведь она — величайший ум человечества. И теперь она решила модернизировать этот алгоритм, привнеся в него немного креатива. А в вас есть эта жилка креатива? Рассмотрим алгоритм Люсине для нахождения наибольшего общего делителя, где \(t\) это некоторый список:
function Euclid(a, b):
if a < b:
swap(a, b)
if b == 0:
return a
r = остаток от деления a на b
if r > 0:
добавить r в конец t
return Euclid(b, r)
Существует массив \(p\) пар положительных целых чисел, каждое из них не больше \(m\). Изначально список \(t\) пустой. Описанная выше функция запускается на каждой паре из массива \(p\). После этого вам даётся перестановка элементов \(t\). Вам необходимо найти массив \(p\) любого размера не больше \(2 \cdot 10^4\) такой, что по описанному алгоритму из него получится массив \(t\), или сказать, что это невозможно. Выходные данные - Если ответа не существует, выведите \(-1\).
- Если ответ существует, в первой строке выведите \(k\) (\(1 \le k \le 2 \cdot 10^4\)) — размер массива \(p\), т. е. количество пар в вашем ответе. \(i\)-я из следующих \(k\) строк должна содержать два целых числа \(a_i\) и \(b_i\) (\(1 \le a_i, b_i \le m\)) — \(i\)-я пара массива \(p\).
Если существуют несколько решений, вы можете вывести любой из них. Примечание В первом тесте рассмотрим массив \(t\) для каждой из пар: - \((19,\, 11)\): \(t = [8, 3, 2, 1]\);
- \((15,\, 9)\): \(t = [6, 3]\);
- \((3,\, 7)\): \(t = [1]\).
Тогда в итоге \(t = [8, 3, 2, 1, 6, 3, 1]\), что совпадает с входным массивом \(t\) с точностью до перестановки. Во втором тесте невозможно найти такой массив пар \(p\), в котором все числа не превосходят \(10\) и \(t = [7, 1]\). В третьем тесте для пары \((15,\, 8)\) массив \(t\) будет \([7, 1]\). | |
![]()
|
|
C. Qpwoeirut и город
Потоки
реализация
дп
*1400
жадные алгоритмы
Qpwoeirut занялся архитектурой и решил перестроить свой город. Город состоит из \(n\) зданий, расположенных в ряд. Здание \(i\) (\(1 \le i \le n\)) имеет высоту \(h_i\) этажей. Вы можете считать, что все этажи в этой задаче имеют одинаковую высоту. Иными словами, здание \(i\) выше здания \(j\) тогда и только тогда, когда количество этажей \(h_i\) в здании \(i\) больше количества этажей \(h_j\) в здании \(j\). Здание \(i\) классное, если оно выше (\(i-1\))-го здания и (\(i+1\))-го здания одновременно (и оба этих здания существуют). В частности, \(1\)-е и \(n\)-е здания не могут быть классными. Qpwoeirut хочет максимизировать количество классных зданий. Чтобы сделать это, он может строить новые этажи на уже существующих зданиях, тем самым делая их выше. Обратите внимание, что Qpwoeirut не может удалять уже существующие этажи. Так как новые этажи очень дорогие, Qpwoeirut хочет минимизировать количество новых этажей. Найдите минимальное количество этажей, которое ему придётся построить, чтобы максимизировать количество классных зданий. Выходные данные Для каждого набора входных данных выведите одно число: минимальное количество этажей, которое Qpwoeirut должен построить, чтобы максимизировать количество классных зданий. Примечание В первом наборе входных данных оптимально построить \(2\) новых этажа на втором здании, в результате чего оно станет выше обоих соседних зданий. Высоты зданий будут равны \([2, \underline{3}, 2]\). Во втором наборе входных данных количество классных зданий уже максимально, поэтому Qpwoeirut может ничего не делать. В третьем наборе входных данных оптимально построить \(2\) этажа на третьем здании и \(1\) этаж на пятом здании. Количество классных зданий будет равно двум. Высоты зданий будут равны \([3, 1, \underline{6}, 5, \underline{6}, 2]\). Можно показать, что нельзя сделать более \(2\) классных зданий или сделать \(2\) классных здания, построив не более \(3\) этажей. В четвёртом наборе входных данных можно сделать классным второе либо третье здание. В обоих случаях надо построить \(3\) новых этажа. Высоты зданий будут равны \([4, 2, \underline{4}, 3, 5, 3, 6, 1]\) либо \([4, \underline{5}, 1, 3, 5, 3, 6, 1]\). | |
![]()
|
|
F. Мультимножество строк
Потоки
Деревья
Перебор
математика
дп
графы
битмаски
meet-in-the-middle
*2500
бпф
Вам даны три целых числа \(n\), \(k\) и \(f\). Рассмотрим все бинарные строки (то есть все строки, состоящие из символов \(0\) и/или \(1\)) длины от \(1\) до \(n\). Для каждой такой строки \(s\) вы должны выбрать целое число \(c_s\) от \(0\) до \(k\). Мультимножество из бинарных строк длины ровно \(n\) считается красивым, если для каждой бинарной строки \(s\) длины от \(1\) до \(n\) выполняется следующее: количество строк в мультимножестве, для которых \(s\) является префиксом, не превосходит \(c_s\). Например, пусть \(n = 2\), \(c_{0} = 3\), \(c_{00} = 1\), \(c_{01} = 2\), \(c_{1} = 1\), \(c_{10} = 2\) и \(c_{11} = 3\). Мультимножество строк \(\{11, 01, 00, 01\}\) является красивым, так как: - для строки \(0\) существует \(3\) строки из мультимножества, для которых \(0\) — префикс, и \(3 \le c_0\);
- для строки \(00\) существует одна строка из мультимножества, для которой \(00\) — префикс, и \(1 \le c_{00}\);
- для строки \(01\) существует \(2\) строки из мультимножества, для которых \(01\) — префикс, и \(2 \le c_{01}\);
- для строки \(1\) существует одна строка из мультимножества, для которой \(1\) — префикс, и \(1 \le c_1\);
- для строки \(10\) существует \(0\) строк из мультимножества, для которых \(10\) — префикс, и \(0 \le c_{10}\);
- для строки \(11\) существует одна строка из мультимножества, для которой \(11\) — префикс, и \(1 \le c_{11}\).
А теперь — сама задача. Вы должны посчитать количество способов выбрать числа \(c_s\) для всех бинарных строк \(s\) длины от \(1\) до \(n\) таким образом, чтобы максимальный возможный размер красивого мультимножества был равен ровно \(f\). Выходные данные Выведите одно целое число — количество способов выбрать числа \(c_s\) для всех бинарных строк \(s\) длины от \(1\) до \(n\) таким образом, чтобы максимальный возможный размер красивого мультимножества был равен ровно \(f\). Так как ответ может быть очень большим, выведите его по модулю \(998244353\). Примечание В первом примере есть три способа выбрать значения \(c_s\): - \(c_0 = 0\), \(c_1 = 2\), тогда максимальное красивое мультимножество — \(\{1, 1\}\);
- \(c_0 = 1\), \(c_1 = 1\), тогда максимальное красивое мультимножество — \(\{0, 1\}\);
- \(c_0 = 2\), \(c_1 = 0\), тогда максимальное красивое мультимножество — \(\{0, 0\}\).
| |
![]()
|
|
F. Мадока и первая сессия
Потоки
Паросочетания
Конструктив
реализация
графы
*2500
О нет, на первой же сессии Мадоке попался билет со следующей сложной задачей: Дано число \(n\) и \(m\) пар чисел (\(v_i, u_i\)). А также есть массив \(b_1, b_2, \ldots, b_n\), изначально заполненный нулями. Затем для каждого индекса \(i\), где \(1 \leq i \leq m\), выполняется либо \(b_{v_i} := b_{v_i} - 1\) и \(b_{u_i} := b_{u_i} + 1\), либо \(b_{v_i} := b_{v_i} + 1\) и \(b_{u_i} := b_{u_i} - 1\). Обратите внимание, что ровно одна из этих операций должна быть выполнена для каждого \(i\). Также дан массив \(s\) размера \(n\), состоящий только из \(0\) и \(1\). И массив \(a_1, a_2, \ldots, a_n\), где гарантируется, что если \(s_i = 0\), то \(a_i = 0\). Помогите Мадоке и определите, можно ли выполнить операции выше таким образом, чтобы для каждого \(i\), где \(s_i = 1\), выполнялось \(a_i = b_i\). И если возможно, то как это сделать. Выходные данные Выведите в первой строке «YES», если можно выполнить операции нужным образом, и «NO» в противном случае. Вы можете выводить каждую букву в любом регистре (например, «YES», «Yes», «yes», «yEs» будут распознаны как положительный ответ). В случае, если вы вывели «YES», выведите \(m\) пар целых чисел. Если для пары \((v_i, u_i)\) нужно выполнить \(b_{v_i} := b_{v_i} - 1\) и \(b_{u_i} := b_{u_i} + 1\), выведите \((v_i, u_i)\). Иначе выведите \((u_i, v_i)\). Если существует несколько способов получить правильный ответ, можно вывести любой из них. Пары можно выводить в любом порядке. Примечание В первом примере массив \(b\) будет меняться следующим образом: \([0,0,0,0,0] \rightarrow [-1,0,0,1,0] \rightarrow [-2,0,0,1,1] \rightarrow [-2,0,1,0,1] \rightarrow [-2,0,2,0,0] \rightarrow [-2,0,2,1,-1]\). \(a_i = b_i\) для всех индексов \(i\) от \(1\) до \(5\). Во втором примере нам достаточно, чтобы в конце \(b_2 = 1\), поскольку только \(s_2 = 1\). В третьем примере входных данных нельзя выполнить операции нужным образом. | |
![]()
|
|
F. Уменьшение паросочетания
Потоки
Паросочетания
Перебор
Конструктив
*2800
поиск в глубину и подобное
графы
интерактив
Дан двудольный граф с \(n_1\) вершинами в первой доле, \(n_2\) вершинами во второй доле и \(m\) ребрами. Максимальное паросочетание в таком графе — максимальный по размеру набор ребер, такой, что ни одна вершина не инцидентна более чем одному выбранному ребру. Вам нужно обрабатывать запросы двух видов к этому графу: - \(1\) — удалить минимально возможное количество вершин так, чтобы размер максимального паросочетания уменьшился ровно на \(1\), и вывести список удаленных вершин. Затем найти любое максимальное паросочетание в полученном графе и вывести сумму номеров ребер, входящих в это паросочетание;
- \(2\) — запрос этого типа может быть задан только после запроса типа \(1\). В качестве ответа на этот запрос вы должны вывести список номеров ребер, входящих в выбранное в предыдущем запросе паросочетание.
Обратите внимание, что вы должны решить эту задачу в режиме online. Это означает, что вы не можете считать все входные данные сразу. Вы можете считать каждый запрос только после вывода ответа на последний запрос. Используйте функции fflush в C++ и BufferedWriter.flush в Java после каждого вывода в вашей программе. Выходные данные Для запроса типа \(1\) выведите три строки: - в первой строке выведите количество удаляемых вершин;
- во второй строке выведите список вершин, которые вы удаляете, следующим образом: если вы удаляете вершину \(x\) из первой доли, выведите \(x\); если вы удаляете вершину \(y\) из второй доли, выведите \(-y\) (номер со знаком минус);
- в третьей строке выведите сумму номеров ребер, которые принадлежат некоторому максимальному паросочетанию. Ребра нумеруются от \(1\) до \(m\).
Для запроса типа \(2\) выведите две строки: - в первой строке выведите одно число — размер максимального паросочетания;
- во второй строке выведите номера ребер, формирующих максимальное паросочетание. Обратите внимание, что сумма этих номеров должна быть равна числу, которое вы вывели в конце предыдущего запроса типа \(1\);
После вывода ответа на запрос не забудьте сбросить буфер вывода. Протокол взаимодействия В этой задаче вы можете получить вердикт «Решение зависло», так как ее нужно решать в режиме online. Если это случилось, то либо вы не следуете формату вывода, либо нарушаете какое-то из ограничений задачи. Вы можете считать, что это эквивалентно вердикту «Неправильный ответ». Для вашего удобства в примере из условия вывод для запросов разделен строкой ===. Ваше решение не должно выводить эту строку; она добавлена только для того, чтобы было проще понять, где ответ на какой запрос. | |
![]()
|
|
F. Рыбаки
Потоки
Паросочетания
жадные алгоритмы
*3100
С рыбалки вернулось \(n\) рыбаков. \(i\)-й рыбак поймал рыбу размера \(a_i\). Рыбаки выберут какой-то порядок, в котором они будут рассказывать, какого размера они поймали рыбу (порядок — это просто перестановка размера \(n\)). Рыбаки не совсем честны, и во время рассказа могут «увеличить» размер пойманной рыбы. Формально, пусть рыбаки рассказывают про пойманную ими рыбу в порядке \([p_1, p_2, p_3, \dots, p_n]\). Пусть \(b_i\) — размер рыбы, названный \(i\)-м рыбаком в выбранном порядке. Значения \(b_i\) считаются следующим образом: - первый рыбак в выбранном порядке просто честно называет размер пойманной рыбы, то есть \(b_1 = a_{p_1}\);
- каждый следующий рыбак хочет назвать минимальное значение, которое будет строго больше значения, названного предыдущим рыбаком, а также делится на размер пойманной этим рыбаком рыбы. То есть для \(i > 1\) значение \(b_i\) равно минимальному целому числу, которое одновременно строго больше \(b_{i-1}\) и делится на \(a_{p_i}\).
Например, пусть \(n = 7\), \(a = [1, 8, 2, 3, 2, 2, 3]\). Если выбранный порядок рыбаков \(p = [1, 6, 7, 5, 3, 2, 4]\), тогда: - \(b_1 = a_{p_1} = 1\);
- \(b_2\) — минимальное целое число, которое делится на \(2\) и превосходит \(1\), то есть \(2\);
- \(b_3\) — минимальное целое число, которое делится на \(3\) и превосходит \(2\), то есть \(3\);
- \(b_4\) — минимальное целое число, которое делится на \(2\) и превосходит \(3\), то есть \(4\);
- \(b_5\) — минимальное целое число, которое делится на \(2\) и превосходит \(4\), то есть \(6\);
- \(b_6\) — минимальное целое число, которое делится на \(8\) и превосходит \(6\), то есть \(8\);
- \(b_7\) — минимальное целое число, которое делится на \(3\) и превосходит \(8\), то есть \(9\).
Вы хотите выбрать такой порядок, в котором рыбаки будут называть размер пойманной рыбы, чтобы минимизировать значение \(\sum\limits_{i=1}^{n} b_i\). Выходные данные Выведите одно целое число — минимально возможное значение \(\sum\limits_{i=1}^{n} b_i\), если выбрать порядок рыбаков оптимально. | |
![]()
|
|
G. Кирилл и компания
Потоки
Перебор
дп
поиск в глубину и подобное
графы
*2200
кратчайшие пути
битмаски
Кирилл живёт на связном неориентированном графе из \(n\) вершин и \(m\) рёбер в вершине с номером \(1\). В один прекрасный вечер он собрал у себя \(f\) друзей, \(i\)-й друг живёт в вершине \(h_i\). Таким образом, в настоящий момент все друзья находятся в вершине \(1\), каждый должен добраться домой — \(i\)-й друг должен попасть в вершину \(h_i\). Вечер подошёл к концу и настала пора расходиться. Оказалось, что у \(k\) (\(k \le 6\)) из его друзей нет машин и им придётся идти пешком, если их никто не подвезёт. Один друг с машиной может подвезти любое количество друзей без машин, но только если он может подвезти их, проехав по одному из кратчайших путей до своего дома. Например, в графе ниже, друг из вершины \(h_i=5\) может подвезти друзей из следующих наборов вершин: \([2, 3]\), \([2, 4]\), \([2]\), \([3]\), \([4]\), но не может подвезти друга из вершины \(6\) или набор \([3, 4]\). 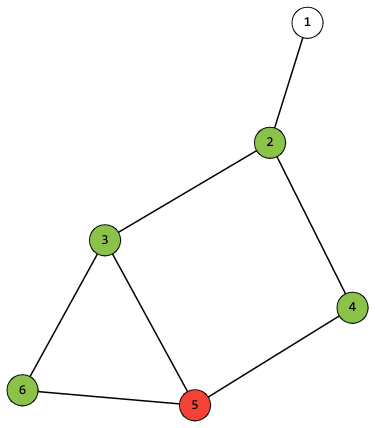 Вершины в которых живут друзья без машин выделены зелёным, а с машинами — красным. Вершины в которых живут друзья без машин выделены зелёным, а с машинами — красным. Кирилл хочет, чтобы как можно меньшему числу друзей пришлось идти пешком. Помогите ему найти минимально возможное количество. Входные данные Первая строка входных данных содержит целое число \(t\) (\(1 \le t \le 10^3\)) — количество наборов входных данных в тесте. Первая строка набора содержит два целых числа \(n\) и \(m\) (\(2 \le n \le 10^4\), \(n-1 \le m \le min (10^4, \)\( \frac{n \cdot (n - 1)}{2} \)\()\)) — количество вершин и рёбер соответственно. Следующие \(m\) строк набора содержат описание рёбер, по два целых числа \(u\) и \(v\) (\(1 \le u, v \le n\), \(u \ne v\)) — номера вершин, соединённых ребром. Гарантируется, что в графе нет петель и кратных рёбер. Дальше следует строка набора, содержащая число \(f\) (\(1 \le f \le 10^4\)) — количество друзей Кирилла. Следующая строка набора содержит \(f\) целых чисел: \(h_1, h_2, \dots, h_f\) (\(2 \le h_i \le n\)) — вершины, в которых они живут. Некоторые вершины могут повторяться. Следующая строка набора содержит число \(k\) (\(1 \le k \le min(6, f)\)) — количество друзей без машин. Последняя строка каждого набора содержит \(k\) целых чисел: \(p_1, p_2, \dots, p_k\) (\(1 \le p_i \le f\), \(p_i < p_{i+1}\)) — номера друзей без машин. Гарантируется, что сумма \(n\) по всем наборам не превосходит \(10^4\), как и суммы \(m\) и \(f\). Выходные данные Выведите \(t\) строк, каждая из которых содержит ответ на соответствующий набор входных данных. В качестве ответа выведите единственное число — минимально возможное количество друзей, которым придётся идти пешком. Примечание Первый набор входных данных первого примера разобран в условии. Во втором наборе входных данных первого примера в вершине \(5\) живут два друга с машинами, один может подвезти друзей из вершин \(2\) и \(3\), а второй из вершины \(4\), не подвезут только друга из вершины \(6\). | |
![]()
|
|
G. Подготовка к олимпиаде
Бинарный поиск
Потоки
Структуры данных
реализация
геометрия
дп
сортировки
*3500
Антон решил подготовиться к очередной олимпиаде. Чтобы Антону было интереснее, Илья подготовил для него \(n\) задач. Сдать \(i\)-ю задачу можно только в первые \(d_{i}\) дней, причем сдавать несколько задач в один и тот же день нельзя. Илья оценил полезность \(i\)-й задачи как \(r_{i}\), и разделил задачи на три темы, тема \(i\)-й задачи равна \(type_{i}\). Антон хочет решить ровно \(a\) задач на первую тему, ровно \(b\) на вторую тему и ровно \(c\) задач на третью тему (и каждая из этих задач должна быть решена не позже своего дедлайна). Скажите Антону, сможет ли он это сделать, и если сможет, то выведите максимальную суммарную полезность задач, которые он решит. Выходные данные Для каждого набора входных данных выведите единственное число: \(-1\), если решить нужный набор задач невозможно, и максимальную полезность решенных задач в противном случае. Примечание В первом наборе входных данных выгодно решить \(2\)-ю и \(4\)-ю задачи. Во втором наборе входных данных ответа не существует. В третьем наборе входных данных оптимально решить \(2\)-ю, \(3\)-ю и \(4\)-ю задачи. В последнем наборе входных данных оптимально решить \(1\)-ю, \(2\)-ю и \(4\)-ю задачи. | |
![]()
|
|
E. Очередная задача на подсчёт массивов
Бинарный поиск
Потоки
Деревья
Структуры данных
математика
дп
разделяй и властвуй
*2300
Позиция первого максимума на отрезке \([l; r]\) массива \(x = [x_1, x_2, \ldots, x_n]\) это наименьшее целое число \(i\), такое что \(l \le i \le r\) и \(x_i = \max(x_l, x_{l+1}, \ldots, x_r)\). Вам дан массив \(a = [a_1, a_2, \ldots, a_n]\) длины \(n\). Найдите количество массивов \(b = [b_1, b_2, \ldots, b_n]\) длины \(n\), удовлетворяющих следующим требованиям: - \(1 \le b_i \le m\) для всех \(1 \le i \le n\);
- для всех пар \(1 \le l \le r \le n\), позиция первого максимума на отрезке \([l; r]\) массива \(b\) равна позиции первого максимума на отрезке \([l; r]\) массива \(a\).
Так как это количество может быть очень большим, выведите его по модулю \(10^9+7\). Выходные данные Для каждого набора входных данных выведите одно число: количество массивов \(b\), удовлетворяющих требованиям выше, по модулю \(10^9+7\). Примечание В первом наборе входных данных следующие \(8\) массивов удовлетворяют требованиям из условия: - \([1,2,1]\);
- \([1,2,2]\);
- \([1,3,1]\);
- \([1,3,2]\);
- \([1,3,3]\);
- \([2,3,1]\);
- \([2,3,2]\);
- \([2,3,3]\).
Во втором наборе входных данных следующие \(5\) массивов удовлетворяют требованиям из условия: - \([1,1,1,1]\);
- \([2,1,1,1]\);
- \([2,2,1,1]\);
- \([2,2,2,1]\);
- \([2,2,2,2]\).
| |
![]()
|
|
A. Access Levels
Потоки
Паросочетания
*2400
битмаски
снм
BerSoft is the biggest IT corporation in Berland, and Monocarp is the head of its security department. This time, he faced the most difficult task ever. Basically, there are \(n\) developers working at BerSoft, numbered from \(1\) to \(n\). There are \(m\) documents shared on the internal network, numbered from \(1\) to \(m\). There is a table of access requirements \(a\) such that \(a_{i,j}\) (the \(j\)-th element of the \(i\)-th row) is \(1\) if the \(i\)-th developer should have access to the \(j\)-th document, and \(0\) if they should have no access to it. In order to restrict the access, Monocarp is going to perform the following actions: - choose the number of access groups \(k \ge 1\);
- assign each document an access group (an integer from \(1\) to \(k\)) and the required access level (an integer from \(1\) to \(10^9\));
- assign each developer \(k\) integer values (from \(1\) to \(10^9\)) — their access levels for each of the access groups.
The developer \(i\) has access to the document \(j\) if their access level for the access group of the document is greater than or equal to the required access level of the document. What's the smallest number of access groups Monocarp can choose so that it's possible to assign access groups and access levels in order to satisfy the table of access requirements? Output The first line should contain a single integer \(k\) — the smallest number of access groups Monocarp can choose so that it's possible to assign access groups and access levels in order to satisfy the table of access requirements. The second line should contain \(m\) integers from \(1\) to \(k\) — the access groups of the documents. The third line should contain \(m\) integers from \(1\) to \(10^9\) — the required access levels of the documents. The \(i\)-th of the next \(n\) lines should contain \(k\) integers from \(1\) to \(10^9\) — the access level of the \(i\)-th developer on each of the access groups. If there are multiple solutions, print any of them. Note In the first example, we assign the documents to different access groups. Both documents have level \(2\) in their access group. This way, we can assign the developers, who need the access, level \(2\), and the developers, who have to have no access, level \(1\). If they had the same access group, it would be impossible to assign access levels to developers \(1\) and \(3\). Developer \(1\) should've had a lower level than developer \(3\) in this group to not be able to access document \(1\). At the same time, developer \(3\) should've had a lower level than developer \(1\) in this group to not be able to access document \(2\). Since they can't both have lower level than each other, it's impossible to have only one access group. In the second example, it's possible to assign all documents to the same access group. | |
![]()
|
|
F. MCF
Потоки
*2800
Вам дан граф из \(n\) вершин и \(m\) ориентированных дуг. Дуга под номером \(i\) идет из вершины \(x_i\) в вершину \(y_i\), имеет пропускную способность \(c_i\) и вес \(w_i\). Ни одна дуга не входит в вершину \(1\); также ни одна дуга не выходит из вершины \(n\). В графе нет циклов отрицательного веса (невозможно переместиться из вершины в нее же саму таким образом, что суммарный вес всех ребер, которые мы прошли, будет отрицательным). Вы должны каждой дуге назначить величину потока (целое число между \(0\) и пропускной способностью дуги, включительно). Для каждой вершины, кроме \(1\) и \(n\), суммарная величина потока на дугах, входящих в нее, должна быть равна суммарной величине потока на дугах, исходящих из нее. Пусть величина потока на \(i\)-й дуге равна \(f_i\), тогда стоимость потока можно вычислить как \(\sum \limits_{i = 1}^{m} f_i w_i\). Вам нужно найти комбинацию величин потока, которая минимизирует стоимость. Говорите, это баян? Ну, у нас есть дополнительные ограничения на поток по каждой дуге: - если \(c_i\) — четное число, \(f_i\) тоже должна быть четным числом;
- если \(c_i\) — нечетное число, \(f_i\) тоже должна быть нечетным числом.
Получится ли у вас решить эту задачу? Выходные данные Если потока, удовлетворяющего ограничениям задачи, не существует, выведите Impossible. Иначе выведите две строки: - в первой строке должно быть одно слово Possible;
- во второй строке — \(m\) целых чисел \(f_1, f_2, \dots, f_m\).
Если ответов несколько, выведите любой из них. Обратите внимание, что вы должны минимизировать стоимость потока. | |
![]()
|
|
D. Косия и игра
Потоки
Паросочетания
Структуры данных
Конструктив
реализация
*2000
поиск в глубину и подобное
графы
снм
игры
Косия и Махиру играют в игру с тремя массивами \(a\), \(b\) и \(c\) длины \(n\). Каждый элемент \(a\), \(b\) и \(c\) — целое число от \(1\) до \(n\) включительно. Игра состоит из \(n\) раундов. В \(i\)-м раунде они делают следующие ходы: - Пусть \(S\) — мультимножество \(\{a_i, b_i, c_i\}\).
- Косия удаляет один из элементов \(S\) по своему выбору.
- Затем Махиру выбирает одно из двух оставшихся в \(S\) чисел.
Пусть \(d_i\) — число, выбранное Махиру в \(i\)-м раунде. Если \(d\) является перестановкой\(^\dagger\), Косия выигрывает. Иначе выигрывает Махиру. Сейчас выбраны только массивы \(a\) и \(b\). Являясь ярым поклонником Косии, вы хотите выбрать массив \(c\) так, чтобы Косия выиграла. Вычислите количество таких \(c\) по модулю \(998\,244\,353\). Обратите внимание, что Косия и Махиру играют оптимально. \(^\dagger\) Перестановкой длины \(n\) является массив, состоящий из \(n\) различных целых чисел от \(1\) до \(n\) в произвольном порядке. Например, \([2,3,1,5,4]\) — перестановка, но \([1,2,2]\) не перестановка (\(2\) встречается в массиве дважды) и \([1,3,4]\) тоже не перестановка (\(n=3\), но в массиве встречается \(4\)). Выходные данные Выведите одно целое число — количество массивов \(c\), при которых выигрывает Косия, по модулю \(998\,244\,353\). Примечание В первом примере есть \(6\) массивов \(c\), при которых выигрывает Косия: \([1, 2, 3]\), \([1, 3, 2]\), \([2, 2, 3]\), \([2, 3, 2]\), \([3, 2, 3]\), \([3, 3, 2]\). Во втором примере можно показать, что нет массивов \(c\), при которых выигрывает Косия. | |
![]()
|
|
F. Двойная сортировка II
Потоки
Паросочетания
поиск в глубину и подобное
графы
*2500
Даны две перестановки \(a\) и \(b\), обе размера \(n\). Перестановка размера \(n\) — это массив из \(n\) элементов, в который каждое целое число от \(1\) до \(n\) входит ровно один раз. Элементы в каждой перестановке пронумерованы от \(1\) до \(n\). Вы можете выполнять следующую операцию любое количество раз: - выбрать целое число \(i\) от \(1\) до \(n\);
- обозначим за \(x\) такое целое число, что \(a_x = i\). Поменять местами \(a_i\) и \(a_x\);
- обозначим за \(y\) такое целое число, что \(b_y = i\). Поменять местами \(b_i\) и \(b_y\).
Вы должны отсортировать обе перестановки в порядке возрастания (то есть должны выполняться условия \(a_1 < a_2 < \dots < a_n\) и \(b_1 < b_2 < \dots < b_n\)) за минимальное количество операций. Обратите внимание, что обе перестановки должны быть отсортированы после того, как вы выполните выбранную вами последовательность операций. Выходные данные Сначала выведите одно целое число \(k\) (\(0 \le k \le 2n\)) — минимальное количество операций, за которое можно отсортировать обе перестановки. Обратите внимание: можно показать, что \(2n\) операций всегда достаточно. Затем выведите \(k\) целых чисел \(op_1, op_2, \dots, op_k\) (\(1 \le op_j \le n\)), где \(op_j\) — значение \(i\), выбранное для \(j\)-й операции. Если ответов несколько, выведите любой из них. | |
![]()
|
|
A. Li Hua и лабиринт
Потоки
Конструктив
реализация
жадные алгоритмы
графы
*800
Имеется прямоугольный лабиринт размером \(n\times m\). Обозначим \((r,c)\) как клетку в \(r\)-й строке сверху и \(c\)-м столбце слева. Две клетки называются соседними, если они имеют общую сторону. Путь — это последовательность пустых клеток, в которой любые две подряд идущие клетки являются соседними. Каждая клетка изначально пуста. Li Hua может выбрать несколько клеток (кроме \((x_1, y_1)\) и \((x_2, y_2)\)) и поместить в каждую из них препятствие. Он хочет узнать минимальное количество препятствий, которые нужно поставить, чтобы не существовало пути из \((x_1, y_1)\) в \((x_2, y_2)\). Предположим, что вы Li Hua. Пожалуйста, решите эту задачу. Выходные данные Для каждого набора входных данных выведите минимальное количество препятствий, которое нужно поставить на поле, чтобы не существовало пути из \((x_1, y_1)\) в \((x_2, y_2)\). Примечание В первом наборе входных данных можно поставить препятствия на \((1,3), (2,3), (3,2), (4,2)\). Тогда путь из \((2,2)\) в \((3,3)\) не будет существовать. | |
![]()
|
|
F. Встречи панд
Потоки
Структуры данных
дп
*3500
Красные панды приехали в город, чтобы встретиться со своими родственниками, синими пандами! Город представлен в виде числовой оси. Панды уже запланировали свою встречу, но график постоянно меняется. Вам дано \(q\) обновлений вида x t c. - Если \(c < 0\), это означает, что дополнительно \(|c|\) красных панд входят на числовую ось в позиции \(x\) и времени \(t\). Затем каждую секунду они могут независимо перемещаться на одну единицу в любом направлении по числовой оси или не перемещаться вовсе.
- Если \(c > 0\), это означает, что дополнительно \(c\) синих панд проверяют позицию \(x\) на наличие красных панд в момент времени \(t\). Если синяя панда не встречает красную панду в этом конкретном месте и времени, она сразу печально покидает числовую ось. Если красная панда есть на позиции в то время, когда синяя панда ее проверяет, они становятся друзьями и покидают числовую ось. Каждая красная панда может стать другом не более чем одной синей панды и наоборот.
Запросы представлены в порядке неубывания значений \(x\). После каждого запроса выведите максимальное количество пар друзей, которое может быть сформировано, если красные панды движутся в оптимальном порядке на основе всех событий, представленных во входных данных до этого обновления (включительно). Движения красных панд могут меняться от обновления к обновлению. Выходные данные После каждого обновления выведите максимальное количество пар друзей, которое может быть сформировано. Примечание В первом примере количество пар друзей после каждого обновления может быть оптимизировано следующим образом: - \(3\) синих панды проверяют наличие красных панд на позиции \(0\) в момент времени \(6\). Нигде нет красных панд, поэтому пар друзей не возникает.
- \(5\) красных панд появляются на позиции \(4\) в момент времени \(2\). \(4\) из них могут переместиться на позицию \(0\) в момент времени \(6\), где \(3\) из них могут стать друзьями с \(3\) существующими синими пандами.
- \(6\) красных панд появляются на позиции \(7\) в момент времени \(4\). Новые синие панды не добавляются, поэтому максимальное количество пар друзей остается \(3\).
- \(100\) синих панд появляются на позиции \(10\) в момент времени \(5\). Ни одна красная панда не может достичь их в момент времени \(5\), поэтому новых пар друзей не создается.
- \(7\) синих панд появляются на позиции \(10\) в момент времени \(8\). \(6\) красных панд на позиции \(7\) в момент времени \(4\), вместе с \(1\) красной пандой на позиции \(4\) в момент времени \(2\), могут достичь \(7\) синих панд на позиции \(10\) в момент времени \(8\), добавляя \(7\) новых пар друзей. Это приводит к общему количеству пар друзей, равному \(10\).
| |
![]()
|
|
F. Четыре масти
Бинарный поиск
Потоки
жадные алгоритмы
битмаски
*3200
Игра в берландский покер проводится следующим образом. Участвуют \(n+1\) человек: \(n\) игроков, пронумерованных от \(1\) до \(n\), и дилер. У дилера есть колода, содержащая карты четырех разных мастей (количество карт каждой масти необязательно одинаковое); количество карт в колоде нацело делится на \(n\). Дилер раздает все карты игрокам, что каждый игрок получает одинаковое количество карт, и все карты колоды розданы. После раздачи карт каждый игрок выбирает одну из четырех мастей (независимо) и сбрасывает все карты из своей руки, которые не принадлежат к выбранной им масти. Победителем игры становится игрок, у которого на руках осталось максимальное количество карт. Количество очков, которые получает победитель, равно \(x - y\), где \(x\) — количество карт в руке победителя, а \(y\) — максимальное количество карт среди всех других игроков; все остальные получают \(0\) очков. Обратите внимание, это означает, что если есть несколько игроков с максимальным количеством карт, каждый получает \(0\) очков. Поскольку каждый игрок хочет максимизировать свои шансы на победу, он выберет масть с максимальным количеством карт в своей руке. Монокарп — дилер. Он уже раздал несколько карт игрокам; \(i\)-й игрок получил \(a_{i,j}\) карт масти \(j\). Обратите внимание, что количество карт на руках игроков в данный момент необязательно должно быть одинаковым. У Монокарпа в колоде осталось \(b_1, b_2, b_3, b_4\) карт мастей \(1, 2, 3, 4\) соответственно. Он должен раздать их игрокам таким образом, чтобы после раздачи всех карт у каждого игрока стало одинаковое количество карт. Для каждого игрока подсчитайте максимальное количество очков, которое он может получить среди всех возможных способов раздачи оставшихся карт в соответствии с правилами игры. Выходные данные Выведите \(n\) целых чисел, \(i\)-е из них — максимальное количество очков, которое может получить \(i\)-й игрок среди всех возможных способов раздачи оставшихся карт. | |
![]()
|
|
G. Grouped Carriages
Бинарный поиск
Потоки
Структуры данных
*2100
дп
жадные алгоритмы
Pak Chanek observes that the carriages of a train is always full on morning departure hours and afternoon departure hours. Therefore, the balance between carriages is needed so that it is not too crowded in only a few carriages. A train contains \(N\) carriages that are numbered from \(1\) to \(N\) from left to right. Carriage \(i\) initially contains \(A_i\) passengers. All carriages are connected by carriage doors, namely for each \(i\) (\(1\leq i\leq N-1\)), carriage \(i\) and carriage \(i+1\) are connected by a two-way door. Each passenger can move between carriages, but train regulation regulates that for each \(i\), a passenger that starts from carriage \(i\) cannot go through more than \(D_i\) doors. Define \(Z\) as the most number of passengers in one same carriage after moving. Pak Chanek asks, what is the minimum possible value of \(Z\)? Output An integer representing the minimum possible value of \(Z\). Note One strategy that is optimal is as follows: - \(5\) people in carriage \(1\) move to carriage \(4\) (going through \(3\) doors).
- \(3\) people in carriage \(5\) move to carriage \(3\) (going through \(2\) doors).
- \(2\) people in carriage \(6\) move to carriage \(5\) (going through \(1\) door).
- \(1\) person in carriage \(6\) moves to carriage \(7\) (going through \(1\) door).
The number of passengers in each carriage becomes \([2,4,5,5,4,5,4]\). | |
![]()
|
|
G. Два символа, два цвета
Бинарный поиск
Потоки
Структуры данных
дп
жадные алгоритмы
*3100
Дана строка, состоящая из символов 0 и/или 1. Вам нужно покрасить каждый символ этой строки в один из двух цветов: красный или синий. Если вы покрасите \(i\)-й символ в красный цвет, вы получите \(r_i\) монет. Если вы покрасите его в синий цвет, вы получите \(b_i\) монет. После покраски строки из нее удаляются все символы синего цвета. Затем в полученной строке подсчитывается количество инверсий (т. е. количество пар символов, в которых левый символ в паре — 1, а правый символ — 0). За каждую инверсию вы должны заплатить \(1\) монету. Какое максимальное количество монет вы можете заработать? Выходные данные Для каждого набора входных данных выведите одно целое число — максимальное количество монет, которое вы можете заработать. Примечание Пояснения для наборов входных данных в примере из условия (синие символы подчеркнуты, красные — нет): - \(0100\underline{0}1\underline{0}\);
- \(10\underline{11}1\);
- \(\underline{0}1\underline{00000000}\);
- \(0\underline{1}010000\).
| |
![]()
|
|
E. Задача про матрицу
Потоки
*2400
графы
Вам дана матрица \(a\), состоящая из \(n\) строк и \(m\) столбцов. Каждый элемент матрицы равен \(0\) или \(1\). Вы можете выполнять следующую операцию любое количество раз (возможно, ни одного): выбрать элемент матрицы и заменить его на \(0\) или \(1\). Также вам даны два массива \(A\) и \(B\) (длиной \(n\) и \(m\) соответственно). После выполнения операций матрица должна удовлетворять следующим условиям: - количество единиц в \(i\)-й строке матрицы должно быть ровно \(A_i\) для каждого \(i \in [1, n]\).
- количество единиц в \(j\)-м столбце матрицы должно быть ровно \(B_j\) для каждого \(j \in [1, m]\).
Вычислите минимальное количество операций, которое вам нужно выполнить. Выходные данные Выведите одно целое число — минимальное количество операций, которые вам нужно выполнить, или -1, если это невозможно. | |
![]()
|
|
F2. Винный завод (сложная версия)
Потоки
Структуры данных
дп
*2800
жадные алгоритмы
матрицы
Это сложная версия задачи. Единственное различие между двумя версиями заключается в ограничениях на \(c_i\) и \(z\). Вы можете делать взломы, только если обе версии задачи решены. Даны три массива \(a\), \(b\) и \(c\). \(a\) и \(b\) имеют длину \(n\), а \(c\) — длину \(n-1\). Обозначим за \(W(a,b,c)\) количество литров вина, произведённых в результате следующего процесса. Построим \(n\) водонапорных башен. Изначально \(i\)-я водонапорная башня имеет \(a_i\) литров воды, и перед ней стоит волшебник с силой \(b_i\). Кроме того, для каждого \(1 \le i \le n - 1\) существует клапан, соединяющий водонапорную башню \(i\) с \(i + 1\), и имеющий пропускную способность \(c_i\). Для каждого \(i\) от \(1\) до \(n\) в этом порядке происходит следующее: - Волшебник, стоящий перед водонапорной башней \(i\), забирает из башни не более \(b_i\) литров воды и превращает забранную воду в вино.
- Если \(i \neq n\), то не более \(c_i\) литров воды, оставшейся в водонапорной башне \(i\), вытекает через клапан в водонапорную башню \(i + 1\).
Дано \(q\) обновлений. В каждом обновлении вам будут даны целые числа \(p\), \(x\), \(y\) и \(z\), означающие следующие изменения: \(a_p := x\), \(b_p := y\) и \(c_p := z\). После каждого обновления найдите значение \(W(a,b,c)\). Обратите внимание, что предыдущие обновления массивов \(a\), \(b\) и \(c\) сохраняются во всех последующих обновлениях. Выходные данные Выведите \(q\) строк, каждая из которых содержит одно целое число, равняющееся \(W(a, b, c)\) после каждого обновления. Примечание Первое обновление не вносит никаких изменений в массивы. - Для \(i = 1\), в башне 1 находится \(3\) литра воды, и \(1\) литр воды превращается в вино. Оставшиеся \(2\) литра воды перетекают в башню 2.
- Для \(i = 2\), в башне 2 находится \(5\) литров воды, и \(4\) литра воды превращаются в вино. Оставшийся \(1\) литр воды попадает в башню 3.
- Для \(i = 3\), в башне 3 находится \(4\) литра воды, и \(2\) литра воды превращаются в вино. Несмотря на то, что осталось \(2\) литра воды, в башню 4 может попасть только \(1\) литр воды.
- Для \(i = 4\), в башне 4 находится \(4\) литра воды. Все \(4\) литра воды превращаются в вино.
Следовательно, \(W(a,b,c)=1 + 4 + 2 + 4 = 11\) после первого обновления. Второе обновление изменяет массивы на \(a = [3, 5, 3, 3]\), \(b = [1, 1, 2, 8]\) и \(c = [5, 1, 1]\). - Для \(i = 1\), в башне 1 находится \(3\) литра воды, и \(1\) литр воды превращается в вино. Оставшиеся \(2\) литра воды перетекают в башню 2.
- Для \(i = 2\), в башне 2 находится \(7\) литров воды, и \(1\) литр воды превращается в вино. Несмотря на то, что осталось \(6\) литров воды, только \(1\) литр воды может попасть в башню 3.
- Для \(i = 3\), в башне 3 находится \(4\) литра воды, и \(2\) литра воды превращаются в вино. Несмотря на то, что осталось \(2\) литра воды, только \(1\) литр воды может попасть в башню 4.
- Для \(i = 4\), в башне 4 находится \(4\) литра воды. Все \(4\) литра воды превращаются в вино.
Следовательно, \(W(a,b,c)=1 + 1 + 2 + 4 = 8\) после второго обновления. Третье обновление изменяет массивы на \(a = [3, 5, 0, 3]\), \(b = [1, 1, 0, 8]\) и \(c = [5, 1, 0]\). - Для \(i = 1\), в башне 1 находится \(3\) литра воды, и \(1\) литр воды превращается в вино. Оставшиеся \(2\) литра воды перетекают в башню 2.
- Для \(i = 2\), в башне 2 находится \(7\) литров воды, и \(1\) литр воды превращается в вино. Несмотря на то, что осталось \(6\) литров воды, только \(1\) литр воды может попасть в башню 3.
- Для \(i = 3\) в башне 3 находится \(1\) литр воды, и \(0\) литров воды превращается в вино. Несмотря на то, что в башне остался \(1\) литр воды, в башню 4 вода не поступает.
- Для \(i = 4\), в башне 4 находится \(3\) литра воды. Все \(3\) литра воды превращаются в вино.
Следовательно, \(W(a,b,c)=1 + 1 + 0 + 3 = 5\) после третьего обновления. | |
![]()
|
|
G. Влад и проблемы в МИТ
Потоки
Деревья
реализация
дп
поиск в глубину и подобное
жадные алгоритмы
*1900
графы
У Владислава есть сын, который очень хотел поступить в МИТ. Общежитие колледжа в МИТ (Молдавский институт технологий) можно представить в виде дерева с \(n\) вершинами, где каждая вершина представляет собой комнату с ровно одним студентом. Дерево — это связный неориентированный граф с \(n\) вершинами и \(n-1\) ребром. Сегодня ночью есть три типа студентов: - студенты, которые хотят веселиться и слушать музыку (обозначены \(\texttt{P}\)),
- студенты, которые хотят спать и наслаждаться тишиной (обозначены \(\texttt{S}\)), и
- студенты, которым не важно, что делать ночью (обозначены \(\texttt{C}\)).
Изначально все рёбра представляют собой тонкие стены, которые позволяют музыке проходить через них, поэтому когда веселящийся студент включает музыку, её можно услышать в каждой комнате. Однако мы можем установить толстые стены на любые рёбра — толстые стены не позволяют музыке проходить через них. Университет хочет установить несколько толстых стен, чтобы каждый веселящийся студент мог слушать музыку, и ни один спящий студент не мог её услышать. Поскольку университет потерял много денег в судебном процессе о правах на наименование, они просят вас найти минимальное количество толстых стен, которые им придется использовать. Выходные данные Для каждого набора входных данных выведите одно целое число — искомое минимальное количество толстых стен. Примечание В первом случае мы можем установить одну толстую стену между комнатами \(1\) и \(2\), как показано ниже. Мы не можем установить \(0\) стен, так как тогда музыка из комнаты 3 дойдет до комнаты 2, где студент хочет спать, поэтому ответ равен \(1\). Существуют и другие допустимые решения. 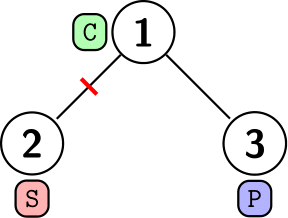 | |
![]()
|
|
H. Лучший стажер фермера Джона
Потоки
Деревья
Структуры данных
дп
*3500
Руби только что получила место стажера на ферме Фермера Джона, победив в соревновании по программированию! В обязанности Руби входит обслуживание персикового дерева Фермера Джона — дерева, состоящего из \(n\) вершин, с корнем в вершине \(1\). В каждой вершине изначально содержится \(a_i = 0\) персиков. Могут происходить два вида событий: - Событие роста в вершине \(x\): Руби должна выбрать либо родителя \(x\), либо любую вершину в поддереве \(x\), и увеличить количество персиков в ней на единицу.
- Событие сбора урожая в вершине \(x\): Руби должна выбрать одну вершину, которая находится в поддереве \(x\), и уменьшить количество содержащихся в ней персиков на единицу. Обратите внимание, что это не тот же набор вершин, что и в событии роста.
Обратите внимание, поддерево вершины \(x\) включает в себя саму вершину \(x\). Руби также дан массив \(b\) длины \(n\). Персиковое дерево считается здоровым, если \(a_i \ge b_i\) для каждой вершины \(i\). Руби предлагается выполнить \(q\) операций двух типов: - 1 x v — Выполнить \(v\) событий роста на вершине \(x\). Руби не обязательно выбирать одну и ту же вершину для увеличения в каждом событии роста.
- 2 x v — Выполнить \(v\) событий сбора урожая на вершине \(x\). Руби не обязательно выбирать одну и ту же вершину для уменьшения в каждом событии сбора урожая.
Для каждого префикса операций она просит вас определить, может ли она выполнить эти операции в некотором порядке так, чтобы получившееся (после всех этих операций) персиковое дерево было здоровым. Обратите внимание, что Руби не может выполнять событие сбора урожая, которое сделает некоторое \(a_i\) отрицательным. Каждый префикс операций независим, то есть для данной операции Руби может выбрать разные вершины для выполнения событий на каждом префиксе, содержащем эту операцию. Выходные данные Для каждого набора входных данных выведите \(q\) строк. Строка \(i\) должна содержать «YES», если Руби может сделать персиковое дерево здоровым после выполнения операций \(1, 2, \ldots, i\) в любом порядке. В противном случае она должна содержать «NO». Вы можете выводить ответ в любом регистре (верхнем или нижнем). Например, строки «YEs», «Yes», «Yes» и «YES» будут распознаны как положительные ответы. Примечание Для префикса, содержащего операции \(1, 2, \ldots, 5\) в первом примере, Руби может выполнять операции в следующем порядке: - Руби выполняет операцию \(2\) и решает увеличить \(a_4\) на \(9\) и \(a_5\) на \(8\).
- Руби выполняет операцию \(1\) и решает увеличить \(a_1\) на \(5\), \(a_3\) на \(2\), \(a_6\) на \(4\) и \(a_8\) на \(3\).
- Руби выполняет операцию \(3\) и решает увеличить \(a_2\) на \(7\).
- Руби выполняет операцию \(4\) и решает уменьшить \(a_2\) на \(1\).
- Руби выполняет операцию \(5\) и решает увеличить \(a_7\) на \(1\).
| |
![]()
|
|
I. Выращивание деревьев
Бинарный поиск
Потоки
Конструктив
жадные алгоритмы
графы
*3200
Вам дан неориентированный связный простой граф с \(n\) вершинами и \(m\) ребрами, где ребро \(i\) соединяет вершины \(u_i\) и \(v_i\). С каждым ребром связаны два положительных параметра \(a_i\) и \(b_i\). Кроме того, вам дано целое число \(k\). Неотрицательный массив \(x\) длины \(m\) называется генератором \(k\)-остовного-дерева, если он удовлетворяет следующим условиям: - Рассмотрим неориентированный мультиграф с \(n\) вершинами, в котором ребро \(i\) клонировано \(x_i\) раз (т.е. существует \(x_i\) ребер, соединяющих \(u_i\) и \(v_i\)). Можно разбить ребра этого графа на \(k\) остовных деревьев, где каждое ребро принадлежит ровно одному остовному дереву\(^\dagger\).
Стоимость такого массива \(x\) определяется как \(\sum_{i = 1}^m a_i x_i^2 + b_i x_i\). Найдите минимальную стоимость генератора \(k\)-остовного-дерева. \(^\dagger\) Остовное дерево (мульти)графа — это подмножество ребер графа, которые образуют дерево, соединяющее все вершины графа. Выходные данные Для каждого набора входных данных выведите одно целое число: минимальную стоимость генератора \(k\)-остовного-дерева. Примечание В первом наборе входных данных допустимым генератором \(1\)-остовного-дерева является \(x = [1, 1, 1, 1, 0]\), как показано на следующем рисунке. Стоимость этого генератора равна \((1^2 \cdot 5 + 1 \cdot 5) + (1^2 \cdot 5 + 1 \cdot 7) + (1^2 \cdot 6 + 1 \cdot 2) + (1^2 \cdot 3 + 1 \cdot 5) + (0^2 \cdot 4 + 0 \cdot 9) = 38\). Можно доказать, что ни один другой генератор не имеет меньшей стоимости. 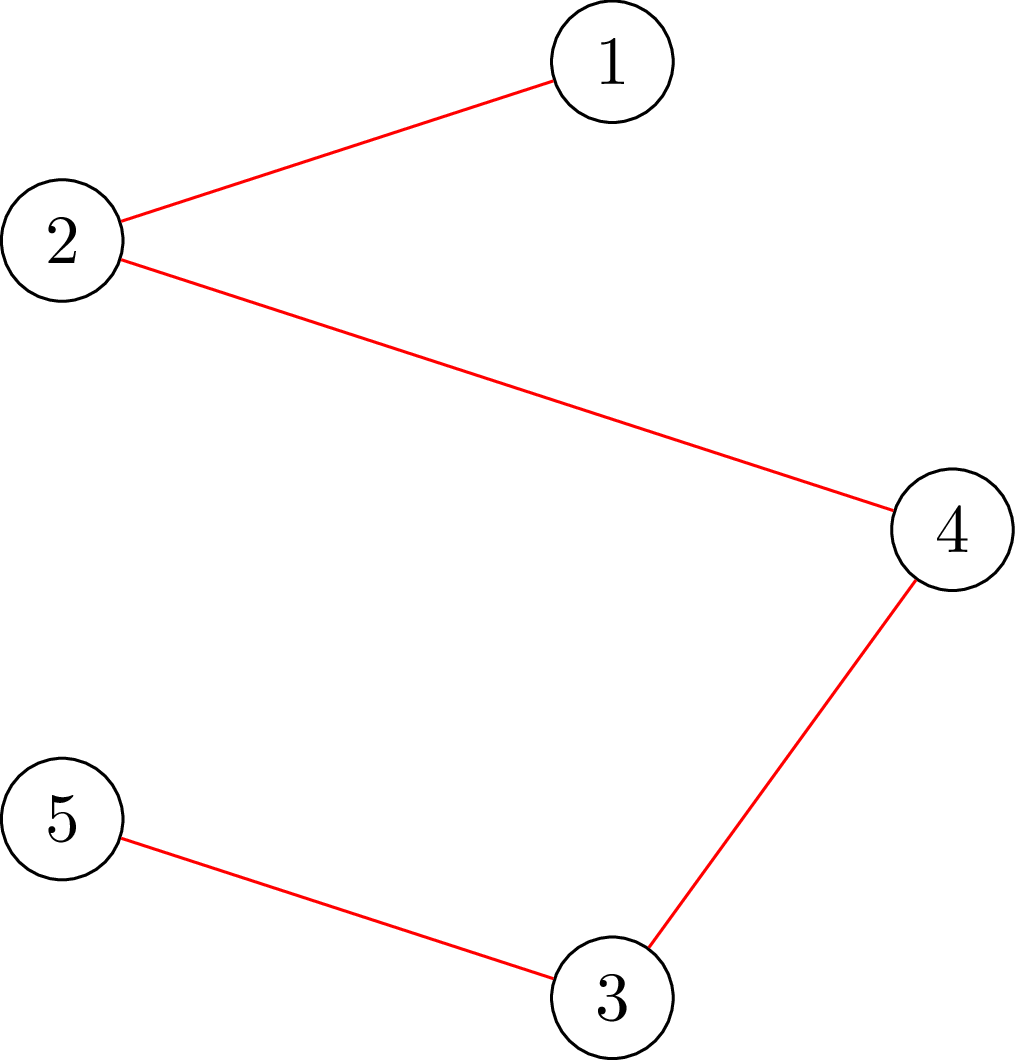 Разбиение \(1\)-остовного-дерева \(x = [1, 1, 1, 1, 0]\) Разбиение \(1\)-остовного-дерева \(x = [1, 1, 1, 1, 0]\) Во втором наборе входных данных допустимым генератором \(3\)-остовного-дерева является \(x = [2, 3, 2, 2, 3]\), как показано на следующем рисунке. Стоимость этого генератора равна \((2^2 \cdot 5 + 2 \cdot 5) + (3^2 \cdot 5 + 3 \cdot 7) + (2^2 \cdot 6 + 2 \cdot 2) + (2^2 \cdot 3 + 2 \cdot 5) + (3^2 \cdot 4 + 3 \cdot 9) = 191\). Можно доказать, что ни один другой генератор не имеет меньшей стоимости. 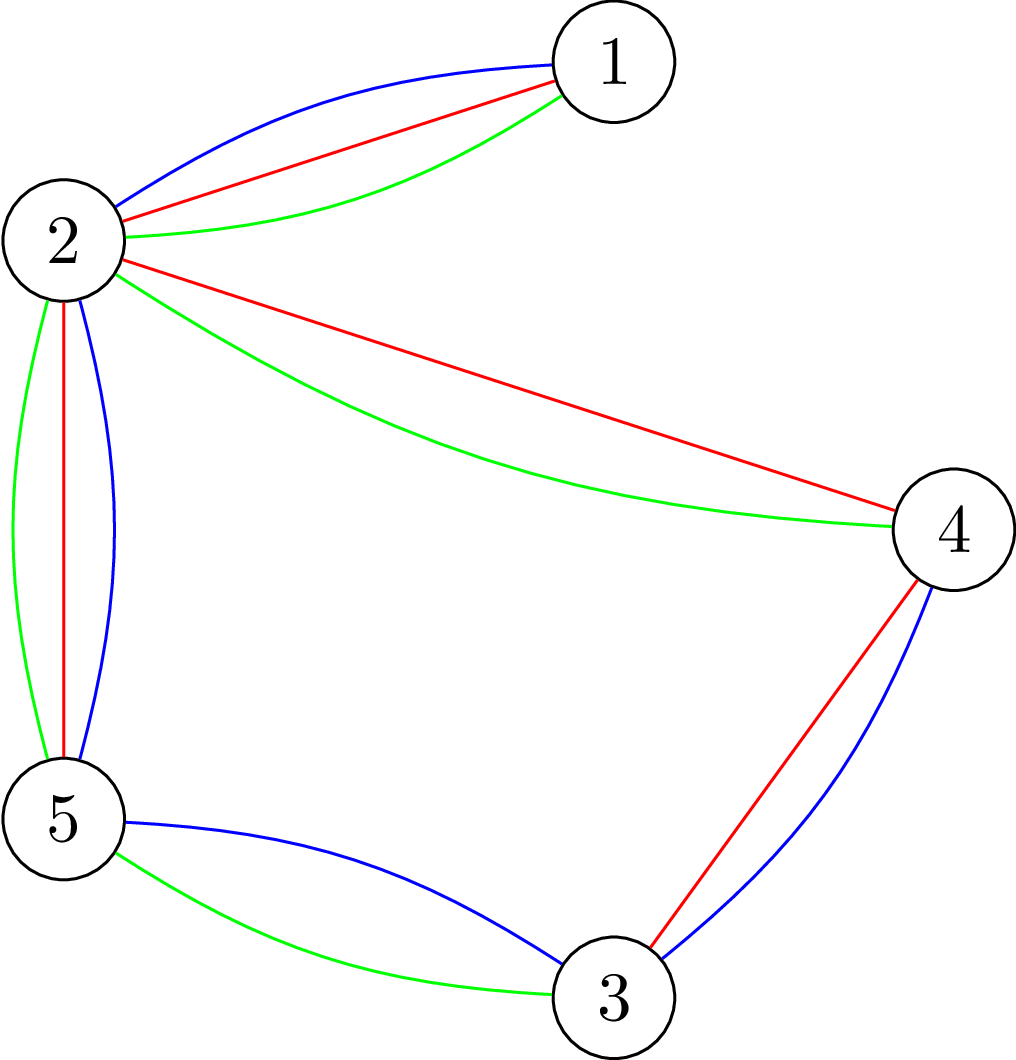 Разбиение \(3\)-остовного-дерева \(x = [2, 3, 2, 2, 3]\) Разбиение \(3\)-остовного-дерева \(x = [2, 3, 2, 2, 3]\) | |
![]()
|
|
H. Самая безбашенная оборона
Потоки
Паросочетания
Перебор
Конструктив
дп
*2300
кратчайшие пути
битмаски
Вы играете в очень популярную игру в жанре Tower Defense «Runnerfield 2». В ней игрок выставляет защитные башни, которые атакуют врагов, идущих от некоторой начальной точки до базы игрока. Вам дано клетчатое поле размера \(n \times m\), на котором уже расставлены \(k\) башен и проложен маршрут, через который будут идти враги. Клетка на пересечении \(x\)-й строки и \(y\)-го столбца обозначается как \((x, y)\). Каждую секунду башня наносит \(p_i\) единиц урона всем врагам в радиусе её действия. Например, если враг расположен в клетке \((x, y)\), а башня в \((x_i, y_i)\), и её радиус равен \(r\), тогда врагу будет нанесён урон \(p_i\), если \((x - x_i) ^ 2 + (y - y_i) ^ 2 \le r ^ 2\). Враги идут из клетки \((1, 1)\) в клетку \((n, m)\), посещая каждую клетку пути ровно один раз. Враг моментально перемещается на соседнюю по горизонтали или вертикали клетку, однако перед этим он проводит в текущей клетке одну секунду. Если в эту секунду его здоровье стало равно нулю или ниже нуля, то враг больше не может перемещаться. Игрок проигрывает, если враг смог добраться до клетки \((n, m)\) и может сделать ещё одно перемещение. По умолчанию все башни обладают нулевым радиусом действия, но игрок может сделать радиус башни равным целому числу \(r\) (\(r > 0\)) за это здоровье всех врагов увеличится на \(3^r\), однако каждое \(r\) может быть использовано не более чем для одной башни. Допустим, враг имел \(h\) единиц базового здоровья. Если радиусы башен \(2\), \(4\) и \(5\), то его здоровье в начале пути будет \(h + 3 ^ 2 + 3 ^ 4 + 3 ^ 5 = h + 9 + 81 + 243 = h + 333\). Выбор радиусов происходит один раз до появления врагов и не может быть изменён после начала игры. Найдите максимальное количество базового здоровья \(h\), при котором возможно установить радиусы так, чтобы игрок не проиграл при прохождении врага со здоровьем \(h\) (без учёта прибавок за радиусы башен). Выходные данные Для каждого набора входных данных в отдельной строке выведите максимальное количество базового здоровья \(h\), при котором возможно установить радиусы так, чтобы игрок не проиграл при прохождении врага со здоровьем \(h\) (без учёта прибавок за радиусы башен). Если невозможно выбрать радиусы даже для врага с \(1\) единицей базового здоровья, выведите «0». Примечание В первом примере нет смысла увеличивать радиус башни, так как она не сможет нанести достаточное количество урона монстру даже с \(1\) единицей здоровья. Во втором примере радиус башни равен \(1\), она наносит урон монстру в клетках \((1, 1)\) и \((2, 2)\). В третьем примере радиус башни равен \(2\), она наносит урон монстру на всех клетках пути. Если базовое здоровье врага \(1491\), то после прибавки за радиус башни его здоровье будет \(1491 + 3 ^ 2 = 1500\), что в точности будет равно урону, который ему нанесёт башня за три секунды. В четвёртом примере у башни \((1, 2)\) радиус \(1\), а у башни \((3, 1)\) радиус \(2\). | |
![]()
|
|
F. Конференция
Потоки
Структуры данных
*3300
Вас попросили организовать очень важную конференцию об искусстве. Первый шаг — выбрать даты. Конференция должна длиться некоторое число подряд идущих дней. Каждый день на конференции должен выступать один лектор, причём один и тот же лектор не может выступать более одного раза. Вы опросили \(n\) потенциальных лекторов по поводу их доступности. Лектор \(i\) указал, что сможет выступить в любой день с \(l_i\) по \(r_i\) включительно. Некоторый отрезок дней можно выбрать в качестве дат конференции в том случае, если существует способ на каждый из дней отрезка назначить доступного в этот день лектора, при этом назначив каждого лектора не более чем на один день. Для каждого \(k\) от \(1\) до \(n\) найдите, сколько есть способов выбрать отрезок из \(k\) подряд идущих дней в качестве дат конференции. Выходные данные Выведите \(n\) целых чисел, где \(k\)-е число обозначает число способов выбрать отрезок из \(k\) подряд идущих дней в качестве дат конференции. Примечание В первом примере конференцию из одного дня можно устроить в любой из дней с \(1\) по \(6\). Конференцию из двух дней можно устроить с дня \(2\) по день \(3\), а также с дня \(4\) по день \(5\). Во втором примере, несмотря на то, что сразу пятеро лекторов выразили желание выступить на конференции, все они доступны только в дни с \(1\) по \(3\), поэтому устроить конференцию длиннее трёх дней не выйдет. | |
![]()
|
|
F. Запросы Светлячка
Потоки
Структуры данных
математика
*1700
битмаски
Светлячку дан массив \(a\) длины \(n\). Пусть \(c_i\) обозначает \(i\)-й циклический сдвиг\(^{\text{∗}}\) массива \(a\). Она создает новый массив \(b\) так, что \(b = c_1 + c_2 + \dots + c_n\), где \(+\) представляет собой конкатенацию\(^{\text{†}}\). Затем она задает вам \(q\) запросов. Для каждого запроса выведите сумму всех элементов в подмассиве \(b\), который начинается с \(l\)-го элемента и заканчивается \(r\)-м, включая оба конца. Выходные данные Для каждого запроса выведите ответ на новой строке. Примечание Для первого набора входных данных, \(b = [1, 2, 3, 2, 3, 1, 3, 1, 2]\). | |
![]()
|
|
G. Переменный урон
Потоки
Структуры данных
*3000
Монокарп собирает армию в компьютерной игре, чтобы сразиться с драконом. Армия состоит из двух частей: героев и защитных артефактов. У каждого героя один параметр — его здоровье. У каждого защитного артефакта тоже один параметр — его прочность. Перед началом боя Монокарп раздает артефакты героям так, чтобы каждый герой получил не более одного артефакта. Бой состоит из раундов, которые проходят следующим образом: - сначала дракон наносит каждому герою урон, равный \(\frac{1}{a + b}\) (вещественное число без округления), где \(a\) — количество живых героев, а \(b\) — количество активных артефактов;
- после этого все герои со здоровьем \(0\) или меньше умирают;
- наконец, некоторые артефакты деактивируются. Артефакт с прочностью \(x\) деактивируется, когда происходит одно из следующего: герой, держащий артефакт, либо умирает, либо получает суммарно \(x\) урона (от начала боя). Если артефакт не выдан ни одному из героев, он считается неактивным с самого начала битвы.
Бой заканчивается, если в живых не осталось ни одного героя. Изначально армия пуста. Приходит \(q\) запросов: добавить в армию героя со здоровьем \(x\) или артефакт с прочностью \(y\). После каждого запроса найдите максимальное количество раундов, которые Монокарп может продержаться, если оптимально распределит артефакты. Выходные данные Выведите \(q\) целых чисел. После каждого запроса выведите максимальное количество раундов, которые Монокарп может продержаться, если оптимально распределит артефакты. Примечание Рассмотрим первый пример. - Добавляется артефакт с прочностью \(5\). Так как героев пока нет, бой сразу же заканчивается.
- Добавляется герой со здоровьем \(4\). Монокарп может дать ему артефакт с прочностью \(5\). Сначала идут раунды, в которых герою наносится \(\frac{1}{1 + 1} = \frac{1}{2}\) урона. Через \(8\) таких раундов суммарно будет нанесено \(4\) урона, и герой умрет, а артефакт деактивируется. Больше в живых нет героев, так что бой заканчивается за \(8\) раундов.
- Добавляется герой со здоровьем \(10\). Пусть теперь артефакт с прочностью \(5\) будет у этого героя. Тогда за первые \(12\) раундов героям будет нанесено \(12 \cdot \frac{1}{2 + 1} = 4\) урона, и первый герой умрет. У второго героя осталось \(6\) здоровья, а у артефакта \(1\) прочности. Теперь урон равен \(\frac{1}{2}\), поэтому еще за \(2\) раунда артефакт деактивируется. У второго героя осталось \(5\) здоровья. За еще \(5\) раундов умрет второй герой. Поэтому ответ равен \(12 + 2 + 5 = 19\).
| |
![]()
|
|
E. Лучшая подпоследовательность
Потоки
Паросочетания
поиск в глубину и подобное
графы
битмаски
*2500
Задан целочисленный массив \(a\) размера \(n\). Скажем, что ценность массива равна его размеру минус количество единичных бит в побитовом ИЛИ всех элементов массива. Например, для массива \([1, 0, 1, 2]\) побитовое ИЛИ равно \(3\) (содержит \(2\) единичных бита), а ценность массива равна \(4-2=2\). Ваша задача — вычислить максимально возможную ценность некоторой подпоследовательности заданного массива. Выходные данные Для каждого набора входных данных выведите максимально возможную ценность некоторой подпоследовательности заданного массива. | |
![]()
|
|
I. Вызов дисперсии
Потоки
жадные алгоритмы
графы
*3400
Кевин недавно узнал определение дисперсии. Для массива \(a\) длины \(n\) дисперсия \(a\) определяется следующим образом: - Пусть \(x=\dfrac{1}{n}\displaystyle\sum_{i=1}^n a_i\), т.е. \(x\) — это среднее арифметическое массива \(a\);
- Тогда дисперсия \(a\) равна \(\) V(a)=\frac{1}{n}\sum_{i=1}^n(a_i-x)^2. \(\)
Теперь Кевин даст вам массив \(a\), состоящий из \(n\) целых чисел, а также целое число \(k\). Вы можете выполнять следующую операцию над \(a\): - Выберите отрезок \([l,r]\) (\(1\le l\le r\le n\)), затем для каждого \(l\le i\le r\) увеличьте \(a_i\) на \(k\).
Для каждого \(1\le p\le m\) вам нужно найти минимально возможную дисперсию \(a\) после выполнения ровно \(p\) операций, независимо для каждого \(p\). Для простоты вам нужно только вывести ответы, домноженные на \(n^2\). Можно доказать, что результаты всегда являются целыми числами. Выходные данные Для каждого теста выведите \(m\) целых чисел в одной строке, где \(p\)-е целое число обозначает минимально возможную дисперсию \(a\) после выполнении ровно \(p\) операций, домноженную на \(n^2\). Примечание В первом наборе входных данных: - Для \(p = 1\) вы можете выполнить операцию на \([1, 1]\), изменив \(a\) с \([1, 2, 2]\) на \([2, 2, 2]\). Поскольку все элементы равны, дисперсия равна \(0\).
- Для \(p = 2\) вы можете выполнить операцию на \([1, 3]\), а затем на \([1, 1]\), изменив \(a\) с \([1, 2, 2]\) на \([2, 3, 3]\), а затем на \([3, 3, 3]\). Поскольку все элементы равны, дисперсия равна \(0\).
Во втором наборе входных данных: - \(p=1\): \([\underline{1,}\,2,2]\to [3,2,2]\);
- \(p=2\): \([1,\underline{2,2}] \to [\underline{1,}\,4,4] \to [3,4,4]\).
В третьем наборе входных данных: - \(p=1\): \([10,\underline{1,1,1,1,10,1,1,1,1}]\to[10,2,2,2,2,11,2,2,2,2]\);
- \(p=2\): \([10,1,1,1,1,10,\underline{1,1,1,1}] \to [10,\underline{1,1,1,1},10,2,2,2,2] \to [10,2,2,2,2,10,2,2,2,2]\).
В восьмом наборе входных данных для всех \(p\) оптимально выполнить операцию над всем массивом \(p\) раз. | |
![]()
|
|
H. Galactic Council
Потоки
*3000
Monocarp plays a computer game. In this game, he maintains a space empire. The empire is governed by \(n\) political parties. Initially, every party has political power equal to \(0\), and there is no ruling party. During each of the next \(m\) turns, the following happens: - initially, Monocarp has to choose which party he supports. He can support any party, except for the ruling party. When Monocarp supports a party, its political power is increased by \(1\). If Monocarp supports the \(i\)-th party during the \(j\)-th turn, his score increases by \(a_{i,j}\) points;
- then, the elections happen, and the party with the maximum political power is chosen as the ruling party (if there are multiple such parties, the party with the lowest index among them is chosen). The former ruling party is replaced, unless it is chosen again;
- finally, an event happens. At the end of the \(j\)-th turn, the party \(p_j\) must be the ruling party to prevent a bad outcome of the event, otherwise Monocarp loses the game.
Determine which party Monocarp has to support during each turn so that he doesn't lose the game due to the events, and the score he achieves is the maximum possible. Initially, Monocarp's score is \(0\). Output If Monocarp loses the game no matter how he acts, print one integer \(-1\). Otherwise, print \(m\) integers \(c_1, c_2, \dots, c_m\) (\(1 \le c_j \le n\)), where \(c_j\) is the index of the party Monocarp should support during the \(j\)-th turn. If there are multiple answers, print any of them. | |
![]()
|
|
D. Задача про НОД
Потоки
Перебор
математика
теория чисел
*1800
Даны три числа \(l\), \(r\) и \(G\). Найдите два числа \(A\) и \(B\) (\(l \le A \le B \le r\)), такие, что их наибольший общий делитель равен \(G\), а расстояние \(|A - B|\) максимально. Если существует несколько таких пар, выберите ту, где \(A\) минимально. Если подходящих пар нет, выведите «-1 -1». Выходные данные Для каждого набора входных данных выведите два целых числа \(A\) и \(B\) — ответ на задачу, либо «-1 -1», если подходящей пары чисел не существует. | |
![]()
|
|
D. За императора!
Потоки
графы
*3100
В Древнем Риме был разработан план по уничтожению варваров, но для его реализации каждый город должен быть проинформирован о нем. Северная часть Римской Империи состоит из \(n\) городов, соединенных \(m\) односторонними дорогами. Изначально в \(i\)-м городе находится \(a_i\) гонцов, и каждый гонец может свободно перемещаться между городами по существующим дорогам. Гонец может взять с собой копию плана и информировать города, которые он посещает, а также может делать неограниченное количество копий для других гонцов в городе, в котором он находится. В начале вы сделаете несколько копий планов и доставите их выбранным вами гонцам. Ваша цель — сделать так, что каждый город будет посещен гонцом с планом. Найдите наименьшее количество копий планов, которые вам нужно произвести изначально, чтобы гонцы доставили их в каждый город, или определите, что это невозможно сделать. Выходные данные Выведите одну строку, содержащую одно целое число — наименьшее количество гонцов, которым вам нужно в начале дать копию плана, или \(-1\), если невозможно проинформировать все города. | |
![]()
|
|
H1. Кевин и камни (простая версия)
Потоки
Паросочетания
графы
*3500
Это простая версия задачи. Отличие между версиями заключается в том, что в этой версии вам нужно только определить, существует ли корректная последовательность операций. Вы можете делать взломы только в том случае, если решили все версии этой задачи. У Кевина есть неориентированный граф с \(n\) вершинами и \(m\) рёбрами. Изначально некоторые вершины содержат камни, которые Кевин хочет переместить на новые позиции. Кевин может выполнять следующую операцию: - Для каждого камня на \(u_i\) выбрать соседнюю вершину \(v_i\). Одновременно переместить каждый камень из \(u_i\) на соответствующую ему \(v_i\).
В любой момент каждая вершина может содержать не более одного камня. Определите, существует ли корректная последовательность операций, которая перемещает камни из начального состояния в целевое. Выходные данные Для каждого набора входных данных на отдельной строке выведите «Yes» или «No» — существует ли допустимая последовательность операций. Вы можете выводить каждую букву в любом регистре (строчную или заглавную). Например, строки «yEs», «yes», «Yes» и «YES» будут приняты как положительный ответ. | |
![]()
|
|
H2. Кевин и камни (сложная версия)
Потоки
графы
*3500
Это сложная версия задачи. Отличие между версиями заключается в том, что в этой версии вам нужно вывести корректную последовательность операций, если она существует. Вы можете делать взломы только в том случае, если решили все версии этой задачи. У Кевина есть неориентированный граф с \(n\) вершинами и \(m\) рёбрами. Изначально некоторые вершины содержат камни, которые Кевин хочет переместить на новые позиции. Кевин может выполнять следующую операцию: - Для каждого камня на \(u_i\) выбрать соседнюю вершину \(v_i\). Одновременно переместить каждый камень из \(u_i\) на соответствующую ему \(v_i\).
В любой момент каждая вершина может содержать не более одного камня. Определите, существует ли корректная последовательность операций, которая перемещает камни из начального состояния в целевое. Выведите корректную последовательность операций, содержащую не более \(2n\) операций, если она существует. Можно доказать, что если существует корректная последовательность, то существует и корректная последовательность, содержащая не более \(2n\) операций. Выходные данные Для каждого набора входных данных на отдельной строке выведите «Yes» или «No» — существует ли допустимая последовательность операций. Вы можете выводить каждую букву в любом регистре (строчную или заглавную). Например, строки «yEs», «yes», «Yes» и «YES» будут приняты как положительный ответ. Если существует корректная последовательность операций, во второй строке выведите единственное целое число \(k\) (\(0 \leq k \leq 2n\)), обозначающее количество операций. Предположим, что в исходном состоянии имеется \(c\) камней. Каждая из следующих \(k + 1\) строк должна содержать \(c\) различных целых чисел, представляющих положение камней до операций и после каждой операции. Эти позиции должны удовлетворять следующим требованиям: - Расположение камней в первой строке соответствует исходному состоянию из входных данных в любом порядке.
- Расположение камней в последней строке соответствует целевому состоянию из входных данных в любом порядке.
- Для всех \(i\) (\(1\leq i\leq k\)) и \(j\) (\(1\leq j\leq c\)) убедитесь, что \(j\)-е целое число в \(i\)-й строке и \(j\)-е целое число в \((i+1)\)-й строке соответствуют соседним вершинам в графе. Другими словами, камень перемещается из своего предыдущего положения в следующее.
Если существует несколько решений, выведите любое из них. | |
![]()
|
|
G. Фабрика перестановок
Потоки
Паросочетания
геометрия
графы
*3500
Даны две перестановки \(p_1,p_2,\ldots,p_n\) и \(q_1,q_2,\ldots,q_n\) длины \(n\). За одну операцию вы можете выбрать два целых числа \(1\leq i,j\leq n,i\neq j\) и поменять местами \(p_i\) и \(p_j\). Стоимость операции равна \(\min (|i-j|,|p_i-p_j|)\). Найдите минимальную стоимость последовательности операций, в результате которых для всех \(1\leq i\leq n\) выполняется равенство \(p_i = q_i\), и выведите последовательность с минимальной стоимостью. Перестановкой длины \(n\) является массив, состоящий из \(n\) различных целых чисел от \(1\) до \(n\) в произвольном порядке. Например, \([2,3,1,5,4]\) — перестановка, но \([1,2,2]\) не перестановка (\(2\) встречается в массиве дважды) и \([1,3,4]\) тоже не перестановка (\(n=3\), но в массиве встречается \(4\)). Выходные данные Для каждого набора входных данных выведите общее количество операций \(k\) (\(0\le k\le n^2\)) в первой строке. Затем выведите \(k\) строк, каждая из которых содержит два целых числа \(i,j\) (\(1\le i,j\le n\), \(i\neq j\)) — операцию обмена \(p_i\) и \(p_j\). Операции выводите в порядке выполнения. Можно показать, что ни одна оптимальная последовательность операций не имеет длину больше \(n^2\). Примечание Во втором наборе входных данных вы можете поменять местами \(p_1,p_3\), что будет стоить \(\min(|1-3|,|1-3|)=2\). Тогда \(p\) станет равно \(q\), а общая стоимость равна \(2\). В третьем наборе входных данных вы можете выполнить следующие операции: Изначально, \(p=[2,1,4,3]\). - Поменять местами \(p_1,p_4\), что будет стоить \(\min(|1-4|,|2-3|)=1\), в результате чего \(p=[3,1,4,2]\).
- Поменять местами \(p_2,p_4\), что будет стоить \(\min(|2-4|,|1-2|)=1\), в результате чего \(p=[3,2,4,1]\).
- Поменять местами \(p_1,p_3\), что будет стоить \(\min(|1-3|,|3-4|)=1\). Тогда \(p\) станет равно \(q\). Общая стоимость равна \(3\).
| |
![]()
|
|
E. Планарный граф
Потоки
геометрия
графы
*3000
Граф называется планарным, если он может быть изображен на плоскости так, что его ребра пересекаются только в вершинах. Точкой сочленения называется такая вершина неориентированного графа, при удалении которой число компонент связности графа увеличивается. Мостом называется такое ребро неориентированного графа, при удалении которого число компонент связности графа увеличивается. Задан связный неориентированный планарный граф, состоящий из n вершин, пронумерованных от 1 до n, уложенный на плоскость. Граф не имеет мостов, точек сочленения, петель и кратных ребер. Также заданы q запросов. Каждый запрос представляет из себя цикл в графе. Ответ на запрос — количество вершин графа, которые (если нарисовать граф и цикл на плоскости) находятся внутри цикла, либо на нем самом. Напишите программу, которая по заданному графу и запросам отвечает на каждый из запросов. Выходные данные Для каждого запроса выведите единственное целое число — количество вершин внутри цикла, либо на нем самом. Ответы на запросы выводите в том порядке, в котором запросы заданы во входных данных. Числа разделяйте пробельными символами. | |
![]()
|
|
E. Собираем строку
Потоки
*2000
графы
Вам очень нужно собрать некоторую строку t. Для этого Вы заранее приготовили n некоторых строк s1, s2, ..., sn. Чтобы собрать строку t, Вам разрешатся выполнить ровно |t| (|t| — длина строки t) операций с этими строками. Каждая операция имеет следующий вид: - выбрать любую непустую строку из строк s1, s2, ..., sn;
- выбрать произвольный символ выбранной строки и записать его на листок бумаги;
- удалить выбранный символ из выбранной строки.
Заметьте, что после применения описанной операции общее количество символов в строках s1, s2, ..., sn уменьшится на 1. Считается, что вы собрали строку t, если символы, записанные на листок бумаги, в порядке применения операций образуют строку t. Однако есть и другие ограничения. Для каждой строки si Вам известно число ai — максимальное количество символов, которое разрешается удалить из строки si. Также известно, что каждая операция, в результате которой из строки si удаляется символ, имеет цену i рублей. То есть, операция над строкой s1 самая дешевая (она стоит 1 рубль), а операция над строкой sn — самая дорогая (она стоит n рублей). Вам нужно посчитать, какое наименьшее количество денег (в рублях) потребуется, чтобы собрать строку t по описанным правилам. Считайте, что стоимость сборки строки t — это сумма цен использованных Вами операций. Выходные данные Выведите единственное число — наименьшее количество денег (в рублях), которое потребуется, чтобы собрать строку t. Если решения не существует, выведите -1. Примечание Пояснения к примерам: В первом примере из первой строки нужно взять символы «b» и «z» по цене 1 рубль, из второй строки символы «a», «e» и «b» по цене 2 рубля. Стоимость строки t в таком случае 2·1 + 3·2 = 8. Во втором примере из первой строки нужно взять два символа «a» по цене 1 рубль, из второй строки символ «c» по цене 2 рубля, из третьей строки два символа «a» по цене 3 рубля, из четвертой строки два символа «b» по цене 4 рубля. Стоимость строки t в таком случае 2·1 + 1·2 + 2·3 + 2·4 = 18. В третьем примере решения не существует, потому что ни из одной строки невозможно получить символ «y». | |
![]()
|
|
C. Неисправный Поток
Потоки
Конструктив
*2100
жадные алгоритмы
графы
Эмускальд считает себя мастером алгоритмов по нахождению потока. Он только что завершил самую искусную из всех своих программ: она вычисляет максимальный поток в неориентированном графе. Граф состоит из n вершин и m ребер. Вершины пронумерованы от 1 до n. Вершины 1 и n — исток и сток, соответственно. Однако, его алгоритм максимального потока, похоже, немного неисправен: для каждого ребра он находит только величину потока, протекающего по этому ребру, но не направление, в котором течет поток. Помогите ему для каждого ребра найти направление, в котором должен протекать поток по этому ребру, чтобы в итоге получился корректный максимальный поток. Более формально: дан неориентированный граф, в котором для каждого неориентированного ребра (ai, bi) задана величина ci. Вы должны ориентировать все ребра так, чтобы выполнялись следующие условия: - для каждой вершины v (1 < v < n), сумма ci входящих ребер равняется сумме ci исходящих ребер;
- вершина номер 1 не имеет входящих ребер;
- полученный ориентированный граф не имеет циклов.
Выходные данные Выведите m строк, в каждой строке должно быть по целому числу di, равному 0, если направление i-го ребра равняется ai → bi (поток протекает от вершины ai к вершине bi), и равному 1 в противном случае. Считайте, что ребра пронумерованы от 1 до m в том порядке, в котором они заданы во входных данных. Если существует несколько решений, выведите любое из них. Примечание В первом тестовом примере 10 единиц потока проходят по пути  , а 5 единиц потока проходят прямо от истока к стоку: , а 5 единиц потока проходят прямо от истока к стоку:  . . | |
![]()
|
|
E. Бинарное дерево на плоскости
Потоки
Деревья
*2400
Корневое дерево — это ориентированный ациклический граф, в котором есть одна вершина (корень), из которой существует ровно один путь до любой другой вершины. Корневое дерево называется бинарным, если каждая вершина имеет не более двух исходящих дуг. Когда бинарное дерево рисуют на плоскости, все дуги должны быть направлены сверху вниз. То есть для каждой дуги из u в v должно выполняться: yu > yv. Вам даны координаты всех вершин дерева. Ваша задача — соединить эти вершины дугами так, чтобы получилось бинарное корневое дерево, и суммарная длина дуг была минимальна. Все дуги построенного дерева должны быть направлены сверху вниз. Выходные данные Если невозможно построить бинарное дерево на данных точках, выведите «-1». Иначе выведите одно вещественное число — суммарную длину дуг в минимальном бинарном дереве. Ответ будет засчитан, если абсолютная или относительная погрешность не превосходит 10 - 6. | |
![]()
|
|
D. Максимальная сумма k подотрезков
Потоки
Структуры данных
реализация
*2800
графы
Рассмотрим последовательность целых чисел a1, a2, ..., an. Вам требуется выполнять запросы двух типов: - Формат запроса «0 i val». В ответ на запрос нужно выполнить присвоение: ai = val.
- Формат запроса «1 l r k». В ответ на запрос нужно вывести максимальную сумму не более чем k непересекающихся подотрезков последовательности al, al + 1, ..., ar. Формально, вам нужно выбрать не более чем k пар целых чисел (x1, y1), (x2, y2), ..., (xt, yt) (l ≤ x1 ≤ y1 < x2 ≤ y2 < ... < xt ≤ yt ≤ r; t ≤ k) таких, чтобы сумма ax1 + ax1 + 1 + ... + ay1 + ax2 + ax2 + 1 + ... + ay2 + ... + axt + axt + 1 + ... + ayt была как можно больше. Обратите внимание, что требуется выбрать не более чем k подотрезков. В частности, можно выбрать 0 подотрезков. В таком случае описанная сумма считается равной нулю.
Выходные данные Для каждого запроса на подсчет максимальной суммы не более чем k непересекающихся подотрезков выведите ответ — максимальную сумму. Ответы на запросы выводите в порядке следования запросов во входных данных. Примечание В первом запросе первого примера можно выбрать единственную пару (1, 9). Таким образом, описанная сумма будет равна 17. Взгляните на второй запрос первого примера. Как выбрать два подотрезка? (1, 3) и (7, 9)? Нет, конечно: сумма (1, 3) и (7, 9) равняется 20, в то время как при оптимальном выборе (1, 7) и (9, 9) сумма равняется 25. Ответ на третий запрос равняется 0, мы предпочитаем ничего не выбирать, если на данном интервале все числа отрицательные. | |
![]()
|
|
E. Биолог
Потоки
*2300
SmallR — биолог. Результаты ее последнего исследования показывают, как изменить пол собак на противоположный. Другими словами, она может сделать собаку женского пола мужского пола и наоборот. SmallR собирается продемонстрировать эту технику. У SmallR есть n собак, затраты на изменение пола каждой собаки могут быть различными. Предположим, что собаки пронумерованы от 1 до n, тогда стоимость изменения пола для собаки номер i равняется vi юаням. Кстати, подобный эксперимент требует некоторого препарата, который годен только один день. Так что эксперимент должен проходить в течение одного дня, и пол каждой собаки может быть изменен не более одного раза. Эксперимент привлек грандиозное внимание со стороны всех слоев общества. Есть m богатых людей, которые с подозрением относятся к этому эксперименту. Они все хотят заключить пари со SmallR. Если SmallR добьется успеха, то i-ый богач заплатит SmallR wi юаней. Но странно, что у них есть специальный метод для определения успешности эксперимента SmallR. Каждый из i богачей заранее выберет некоторых ki собак и один определенный пол. Он будет думать, что эксперимент SmallR успешен тогда и только тогда, когда на следующий день все выбранные ki собак будут иметь назначенный пол. В противном случае, он будет думать, что эксперимент SmallR провалился. Если в результате эксперимента SmallR не удовлетворит условия богачей, которые не являются ее друзьями, то ей не надо платить им деньги в качестве компенсации. Но если она не удовлетворит условия своего хорошего друга, то она должна заплатить g юаней ему в качестве извинений за ее провал. SmallR надеется получить как можно больше денег в результате эксперимента. Пожалуйста, выясните, какую максимальную сумму денег может заработать SmallR. Кстати, вполне возможно, что она не может получить никаких денег или даже потерпит убыток. Тогда, пожалуйста, высчитайте минимальное количество потерянных ей денег. Выходные данные Выведите единственное целое число — максимальная прибыль SmallR (целое число может быть отрицательным, если SmallR потеряет деньги). | |
![]()
|
|
C1. Уборка
Потоки
*2200
Умный Бобер следит за своим внешним видом, а особое внимание уделяет обуви, потому имеет огромное количество пар кроссовок от самых известных лесных брендов. Он старается аккуратно складывать свои ботинки, чтобы каждая пара стояла рядышком. Но к концу недели из-за достаточно активного образа жизни в его гардеробной образуется беспорядок. Умный Бобер из ABBYY является не только самым эрудированным бобром в округе, но еще и самым хозяйственным. Например, по понедельникам Умный Бобер устраивает генеральную уборку в своем жилище. Настало утро понедельника. Тратить на уборку весь день Умный Бобер не хочет, да еще и дел много, в тренажерный зал успеть нужно, потому желает прибраться как можно скорее. И вот полы вымыты, пыль вытерта — время прибраться в гардеробной. Но как только Умный Бобер вошел в гардеробную — все планы на день были вмиг разрушены: там царил полный хаос и казалось, что невозможно справиться даже за неделю. Обнадежьте нашего героя: подскажите ему, какое минимальное количество ботинок должно изменить свое положение, чтобы в гардеробной наступил порядок. Гардеробная имеет прямоугольную форму и разделена на n × m равных квадратов, причем в каждом квадрате лежит ровно по одному ботинку. Каждая пара обуви пронумерована уникальным числом от 1 до 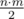 . Квадрат с координатами (i, j) содержит целое число — номер пары, которой принадлежит ботинок, лежащий в нем. Умный Бобер считает, что в гардеробной порядок, только когда каждая пара кроссовок лежит рядом. Будем считать, что пара кроссовок в квадратах (i1, j1) и (i2, j2) лежит рядом, если |i1 - i2| + |j1 - j2| = 1. . Квадрат с координатами (i, j) содержит целое число — номер пары, которой принадлежит ботинок, лежащий в нем. Умный Бобер считает, что в гардеробной порядок, только когда каждая пара кроссовок лежит рядом. Будем считать, что пара кроссовок в квадратах (i1, j1) и (i2, j2) лежит рядом, если |i1 - i2| + |j1 - j2| = 1. Выходные данные Выведите ровно одно целое число — минимальное число кроссовок, которые должны поменять свое местоположение. Примечание 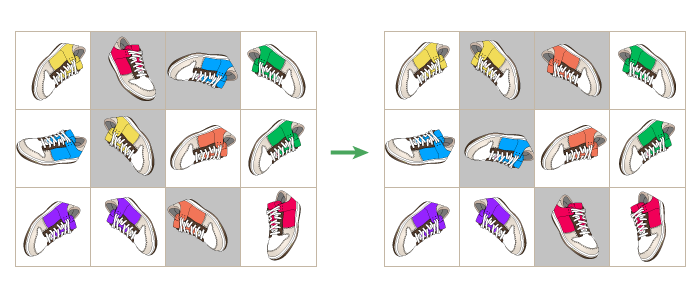 Второй пример. Второй пример. | |
![]()
|
|
B. Ciel и дуэль
Потоки
дп
жадные алгоритмы
*1900
Лиса Ciel играет в карты со своим другом Jiro. У Jiro есть n карт, у каждой карты есть два атрибута: позиция position (атака или защита) и сила strength. У лисы Ciel есть m карт, аналогично, у каждой карты есть два атрибута. Известно, что позиция всех карт Ciel — это атака. Пришло время Ciel атаковать! Она может выполнить следующую операцию много раз: - Выбрать одну из своих карт X, которая не была выбрана ранее.
- Если у Jiro нет живых карт, он получит урон, равный (силе X). В противном случае, Ciel надо выбрать у Jiro одну живую карту Y, тогда:
- Если позиция Y — атака, то должно выполняться условие (сила X) ≥ (сила Y). После этой атаки карта Y умрет и Jiro получит урон, равный (сила X) - (сила Y).
- Если позиция Y — защита, то должно выполняться условие (сила X) > (сила Y). После этой атаки карта Y умрет, но Jiro не получит повреждений.
Ciel может в любой момент закончить атаковать Jiro (то есть она не обязана использовать все свои карты). Помогите Ciel посчитать максимальную сумму урона, которую можно нанести Jiro. Выходные данные Выведите целое число: максимальный ущерб, который можно нанести Jiro. Примечание В первом тесте все карты Ciel имеют одинаковую силу. Оптимальнее всего сначала напасть на карту «ATK 2000», уничтожить эту карту, тогда Jiro получит 2500 - 2000 = 500 единиц урона. Затем используем вторую карту для уничтожения карты «DEF 1700». Jiro не получает урона. Теперь у Jiro нет карт и можно использовать третью карту — нападаем на Jiro, он получает 2500 урона. Таким образом, ответ равняется 500 + 2500 = 3000. Во втором тесте нужно использовать карту «1001» для атаки на карту «ATK 100», затем с помощью карты «101» напасть на карту «ATK 10». После этого у Ciel еще есть карты, но она может закончить атаковать. Таким образом, общий урон равен (1001 - 100) + (101 - 10) = 992. В третьем случае заметьте, что Ciel может уничтожить карту «ATK 0» картой с силой, равной 0. Но не может уничтожить карту «DEF 0» картой с силой, равной 0. | |
![]()
|
|
E. Насосные станции
Потоки
Деревья
Перебор
поиск в глубину и подобное
жадные алгоритмы
графы
разделяй и властвуй
*2900
Безумный ученый Майк устроился на работу. Его задача — управлять системой насосных станций для перекачки воды. Система состоит из n насосных станций, которые пронумерованы целыми числами от 1 до n. Некоторые пары станций соединены двунаправленными трубами, по которым может течь вода в том или другом направлении (но одновременно только в одном). Для каждой трубы задана пропускная способность — наибольшее количество литров воды, которое может через нее протекать в течение одного часа. Каждая насосная станция может перекачивать входящую воду из одних станций в другие станции по трубам при условии, что за один час общее входящее в эту станцию количество литров воды равняется общему исходящему из этой станции количеству литров воды. В обязанности Майка входит перекачивание воды между станциями. Из станции a в станцию b по трубам (возможно, через другие станции) в течение одного часа можно пустить какое-то количество литров воды согласно правилам, описанным выше. В течение этого времени вода из других станций не может втекать в станцию a, и не может вытекать из станции b, при том из станции a может вытекать любое количество воды, и в станцию b может втекать любое количество воды. Если из станции a за час в общем было выкачано x литров воды, то Майк получает к зарплате x бублей. Чтобы получить зарплату, Майк по контракту должен работать n - 1 дней. В первый день он выбирает две станции v1 и v2, и в течение одного часа перекачивает определённое количество воды из v1 в v2. Далее в i-тый день Майк выбирает до этого ни разу не выбранную станцию vi + 1, и в течение одного часа перекачивает определенное количество воды из станции vi в станцию vi + 1. При этом количество перекачиваемой воды в i-тый день не зависит от количества перекачиваемой воды в (i - 1)-ый день. Для своих проектов Майку нужно заработать как можно больше бублей. Помогите Майку найти такую перестановку номеров станций v1, v2, ..., vn, при которой Майк может заработать наибольшую возможную зарплату. Выходные данные В первой строке выведите одно целое число — наибольшее значение зарплаты, которую может получить Майк. В второй строке через пробелы выведите перестановку из n чисел от 1 до n — номера станций последовательности v1, v2, ..., vn. Если существует несколько ответов, выведите любой. | |
![]()
|
|
E. Петя и трубопровод
Потоки
графы
*2300
кратчайшие пути
Мальчик Петя мечтает вырасти и стать Главным Сантехником Берляндии. Уже сейчас он обдумывает задачи, которые ему наверняка придется решать в будущем. К сожалению, Петя еще слишком неопытен, и потому одну из таких задач (вызывающую у Пети наибольший интерес) предстоит решить Вам. В столице Берляндии есть n резервуаров для воды, пронумерованных целыми числами от 1 до n. Эти резервуары некоторым образом соединены однонаправленными трубами, причем любая пара резервуаров соединена не более чем одной трубой в каждом из направлений. Каждая труба характеризуется своей толщиной — строго положительным целым числом, которое определяет, сколько литров воды в единицу времени эта труба может пропустить. Вода в город поступает из главного водохранилища, имеющего номер 1. Пройдя по некоторому пути из труб, она должна попасть в сточный резервуар, снабженный очистной системой (он имеет номер n). Петя хочет увеличить толщину некоторого поднабора труб суммарно не более чем на k единиц толщины таким образом, чтобы толщина каждой трубы осталась целочисленной. Помогите ему определить, какое максимальное количество воды может протекать в единицу времени из главного водохранилища в сточный резервуар после осуществления такой операции. Выходные данные Выведите единственное целое число — максимальное количество воды, которое может протекать в единицу времени из главного водохранилища в сточный резервуар. Примечание В первом тесте можно увеличить толщину трубы из 1-го во 2-ой резервуар на 7 единиц. Во втором тесте толщину трубы из 1-го во 2-ой резервуар нужно увеличить на 4 единицы, из 2-го в 3-ий — на 3 единицы, из 3-го в 4-ый — на 2 единицы и из 4-ого в 5-ый — на 1 единицу. | |
![]()
|
|
D. Электростанция Нанами
Потоки
*2900
Нанами любит играть в игры, и у нее это шикарно получается. Сегодня она играла в новую игру, требующую управления электростанцией. Задача Нанами — следить за генераторами завода и получать максимальную производительность. На заводе есть n генераторов. Каждому генератору надо установить определенный уровень работы. Уровень работы генератора — это целое число (возможно, равное нулю или отрицательное), при этом уровень i-го генератора должен быть между li и ri (обе границы включительно). Производительность генератора зависит от уровня работы генератора x как квадратичная функция f(x). Каждый генератор имеет свою функцию производительности, функция i-го генератора fi(x). Однако есть еще m ограничений на уровни генераторов. Пусть уровень i-го генератора равен xi. Каждое ограничение имеет вид: xu ≤ xv + d, где u и v — идентификаторы двух различных генераторов, а d — целое число. Игра показалась Нанами скучной, но сдаваться не в ее правилах. Поэтому она решила написать программу, которая посчитает для нее оптимальный ответ (максимально-возможную суммарную производительность). Как ни странно, в итоге работа по написанию программы досталась вам. Выходные данные Выведите единственную строку, содержащую единственное целое число — максимальную производительность всех генераторов. Гарантируется, что существует хотя бы одна корректна конфигурация. Примечание В первом примере f1(x) = x, f2(x) = x + 1, а f3(x) = x + 2, поэтому нужно максимизировать сумму уровней генераторов. Ограничения равны x1 ≤ x2, x2 ≤ x3, и x3 ≤ x1, что на самом деле обозначает: x1 = x2 = x3. Оптимальная конфигурация уровней генераторов, x1 = x2 = x3 = 2, дает нам производительность 9. Во втором примере ограничения равны |xi - xi + 1| ≤ 3 при 1 ≤ i < n. Одна из оптимальных конфигураций равна x1 = 1, x2 = 4, x3 = 5, x4 = 8 и x5 = 7. | |
![]()
|
|
E. Оптимальный поток
Потоки
Конструктив
математика
*3000
Рассмотрим сеть, состоящую из n вершин, пронумерованных от 1 до n. Некоторые пары вершин соединены ребрами. Пара вершин может быть соединена несколькими ребрами, тем не менее, не существует ребра, соединяющего какую-то вершину саму с собой. Каждое ребро имеет бесконечную пропускную способность (в обоих направлениях), однако в один момент времени ребро может пропускать поток только в одном из направлений. Стоимость пропускания потока по ребру пропорциональна квадрату пропускаемого потока. Точнее, для каждого ребра задана характеристика (вес), стоимость пропускания x потока по ребру с весом w равна w·x2. Известно, что сеть связна (между любой парой вершин есть путь по ребрам). Более того, сеть устроена таким образом, что при удалении любой вершины, она останется связной. Вам нужно пропустить k (k > 0) потока из вершины 1 в вершину n. Другими словами, вы хотите для каждого ребра выбрать величину (не обязательно целочисленную) и направление, проходящего по этому ребру потока, так, чтобы для вершины 1 значение [сумма всех входящих потоков минус сумма всех выходящих потоков] равнялось - k, для вершины n это значение равнялась k, а для всех остальных вершин оно равнялось 0. Желая минимизировать стоимость пропускания k потока, вы нарисовали диаграмму сети и дали задание одному из подчиненных. Недавно, последний сказал, что он нашел оптимальное решение задачи и нарисовал его, но, к сожалению, пролил кофе на рисунок. Поэтому некоторые данные утрачены (вполне возможно, даже части изначальной диаграммы и значение k). Имея все сохранившиеся данные, вам нужно определить, могло ли решение подчиненного быть оптимальным. Другими словами, определите, существуют ли корректная сеть, значение k (оно должно быть положительным) и оптимальное решение, которые не противоречат никакой сохранившейся информации. Дополнительно, если это возможно, определите эффективность решения подчиненного. Эффективность решения равна суммарной стоимости деленой на k. Выходные данные Если решение подчиненного точно не является оптимальным, выведите строку «BAD x», где x — это номер первого ребра, которое противоречит оптимальности решения. Если решение подчиненного может быть оптимальным, то выведите эффективность этого решения, округленную до ближайшего целого числа, если ее можно определить. Если определить эффективность нельзя выведите строку "UNKNOWN". Примечание Обратите внимание, что, несмотря на то, что заданные веса и потоки целочисленные, веса и потоки неизвестных ребер могут быть вещественными. | |
![]()
|
|
C. Расшифровка
Потоки
Паросочетания
*2300
Недавно на уроке во время контрольной Мария Ивановна перехватила записку от Саши к Оле. Мария Ивановна очень хочет знать, что в записке, но, к сожалению, записка зашифрована. Мария Ивановна знает, что её ученики для шифровки заменяют каждую букву исходного сообщения на какую-то другую. Замена происходит таким образом, что одинаковые буквы всегда заменяются одной и той же буквой, а разные — разными. Мария Ивановна подозревает, что записка — это ответы к контрольному тесту (ведь её длина случайно оказалась равной длине строки с правильными ответами). Однако она знает, что ответы Саши не обязательно полностью правильны. На каждый вопрос возможен один из K вариантов ответа. Естественно, Мария Ивановна знает правильные ответы. Мария Ивановна решила расшифровать записку таким способом, чтобы максимизировать количество правильных ответов Саши. Однако, она очень занята, поэтому попросила Вас помочь ей в этом пустяковом деле. Выходные данные В первой строке выведите единственное число — максимально возможное количество правильных ответов у Саши. Во второй строке выведите расшифровку — строчку длины K, где по порядку для каждой буквы из шифра учеников указано, какому ответу она соответствует. Если несколько расшифровок дают правильный ответ, выведите любую. | |
![]()
|
|
C. Массив и операции
Потоки
Паросочетания
*2100
теория чисел
Вы выписали на листок массив из n целых положительных чисел a[1], a[2], ..., a[n] и m хороших пар целых чисел (i1, j1), (i2, j2), ..., (im, jm). Каждая хорошая пара (ik, jk) удовлетворяет условиям: ik + jk — нечетное число и 1 ≤ ik < jk ≤ n. За одну операцию вы можете выполнить последовательность действий: - взять одну из хороших пар (ik, jk) и некоторое целое число v (v > 1), которое делит оба числа a[ik] и a[jk];
- разделить оба числа на v, т. е. выполнить присваивания:
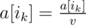 и и  . . Определите, какое максимальное количество операций можно последовательно совершить над данным массивом. Обратите внимание, что одну пару можно использовать несколько раз в описанных операциях. Выходные данные Выведите единственное целое число — ответ на задачу. | |
![]()
|
|
E. Лиса и ужин
Потоки
*2300
Лиса Ciel участвует в вечеринке в Простом королевстве. На вечеринку приглашены n лис (включая саму Ciel). i-й из приглашённых лис ai лет. Ужин будет проходить за несколькими круглыми столами. Требуется распределить лис по столам так, что: - Каждая лиса окажется за некоторым столом.
- За каждым столом сидит не менее 3 лис.
- Сумма возрастов любых двух соседних лис за каждым столом должна быть простым числом.
Если k лис f1, f2, ..., fk сидят за столом по часовой стрелке, то для 1 ≤ i ≤ k - 1 fi и fi + 1 соседние, а также f1 и fk тоже являются соседними. Если можно распределить лис требуемым образом, найдите способ сделать это. Выходные данные Если распределить лис указанным образом невозможно, выведите «Impossible» (без кавычек). В противном случае, в первой строке выведите целое число m ( ) — количество столов. ) — количество столов. Затем выведите m строк. Каждая строка должна начинаться с целого числа k, количества лис за столом, затем должны следовать k чисел — индексы лис, сидящих за этим столом, по часовой стрелке. Если возможных распределений несколько, выведите любое. Примечание В первом примере можно усадить всех лис за один стол указанным образом. Их возрасты: 3 – 8 – 9 – 4, суммы возрастов соседних лис: 11, 17, 13 и 7, все эти числа являются простыми. Во втором примере это невозможно: сумма 2 + 2 = 4 не является простым числом. | |
![]()
|
|
F1. Скейгербосс
Потоки
*2700
Ктулху решил поймать Скейгербосса. Скейгербосс узнал об этом и решил спрятаться в стае своих скейгеров. Каждый скейгер за исключением Скейгербосса является мужской или женской особью. Пол Скейгербосса — "другой". Скейгеры гуляют по двухмерной карте, разбитой на единичные клетки. Скейгер выглядит милым ботаном, если он находится в одной клетке с ровно одним другим скейгером некоторого пола, отличного от его собственного. Ктулху не сможет поймать Скейгербосса, если все скейгеры на карте будут выглядеть милыми ботанами. Скейгеры двигаются с разными скоростями. Для каждого скейгера известно количество времени, требуемое для того, чтобы он перешел в соседнюю клетку. Клетки являются соседними, если у них есть общая сторона. В любой момент времени в клетке, в которой нет препятствия, может находиться произвольное количество скейгеров. Скейгеры не могут перемещаться в клетки, в которых есть препятствия. Посчитайте минимальное время, необходимое для того, чтобы все скейгеры на карте выглядели милыми ботанами, если они перемещаются оптимально для достижения этой цели. Выходные данные Выведите минимально возможное время, требуемое для того, чтобы все скейгеры выглядели милыми ботанами, или -1, если это невозможно. Примечание Рассмотрим первый пример. Скейгеры прячутся на карте размером 4x4. Скейгербосс изначально находится в клетке (2, 1) и может перемещаться из клетки в соседнюю за 1 единицу времени. Кроме него, на карте есть 2 мужских и 3 женских особи. Одна из женских особей находится в клетке (1, 1), а все остальные особи находятся в клетке (2, 1). Все они перемещаются в соседние клетки за 2 единицы времени. Если Скейгербосс и женская особь из клетки (1, 1) перейдут в клетку (1, 2), а одна женская и одна мужская особь из числа оставшихся перейдут в клетку (1, 1), тогда все скейгеры станут выглядеть милыми ботанами, и на это потребуется всего 2 единицы времени. | |
![]()
|
|
E. Солдат и путешествия
Потоки
математика
*2100
графы
В стране есть n городов и m двусторонних дорог между ними. У каждого города есть армия. Армия i-го города состоит из ai солдат. В стране объявлена мобилизация. В результате неё каждый солдат должен либо остаться в своем городе, либо перейти в один из соседних городов, то есть перейти по не более чем одной дороге. Проверьте, возможно ли, чтобы после перехода в i-м городе было ровно bi солдат. Выходные данные Если требуемое невозможно, выведите единственное слово: "NO". В противном случае выведите слово "YES", а затем выведите n строк, в каждой строке выведите по n целых чисел. Число в i-й строке и j-м столбце должно обозначать, сколько солдат должно перейти из города i в город j (если i ≠ j), либо сколько солдат должно остаться в городе i (если i = j). Если возможных ответов несколько, выведите любой из них. | |
![]()
|
|
H. Новый Год и забытое дерево
Потоки
Конструктив
графы
*3200
Деревом называется связный неориентированный граф из n вершин и n - 1 ребра. Вершины пронумерованы от 1 до n. Лимак — белый медвежонок, и его медвежья семья каждый год собирает новогоднее дерево. Год назад дерево получилось особенно замечательным, поэтому они решили запомнить его и собрать такое же в этом году. Эта миссия была поручена Лимаку. Запомнить всё дерево и не забыть в течение года было бы слишком сложно, поэтому Лимак решил записать его рёбра в своем блокноте. Он взял ручку и записал n - 1 строку, по два целых числа в каждой — индексы двух вершин, соединённых общим ребром. И вот новый год уже совсем близко, семья попросила Лимака восстановить прошлогоднее дерево. И тут начались проблемы. Год назад он был ещё очень маленьким медвежонком, и не знал ни цифр, ни алфавита, поэтому он просто заменил все цифры на вопросительные знаки — единственный известный ему символ. Это означает, что для каждого индекса вершины, записанного в его блокноте, он знает только количество цифр в его записи. По крайней мере, он уверен, что все индексы записывались без ведущих нулей. Лимак очень не хочет всех разочаровать, поэтому он попросил вас построить какое-нибудь дерево, отвечающее его записям в блокноте. Найдите такое дерево и выведите его рёбра в любом порядке. Если Лимак допустил ошибку, и подходящего дерева не существует, то выведите "-1" (без кавычек). Выходные данные Если подходящего дерева нет, выведите "-1" (без кавычек). В противном случае, выведите любое дерево, подходящее под записи Лимака. Выведите n - 1 строк, каждая строка должна содержать два целых числа — номера вершин, соединённых ребром. Ребра можно выводить в любом порядке. | |
![]()
|
|
E. Вселенское Зло
Потоки
дп
*2700
В результате таинственных экспериментов Пинки и Брейна в Большом Адронном Коллайдере открылись порталы — чёрные дыры — в параллельное измерение, откуда сразу же Вселенское Зло протянуло свои зловещие щупальца. Брейн быстро оценил ситуацию и понял, что, чем больше щупалец выберется на свободу, тем выше его шансы повелевать миром. Конструкция Коллайдера представляет собой квадратную сетку, свёрнутую в цилиндр, и состоящую из n строк и m столбцов такую, какая показана на рисунке ниже: 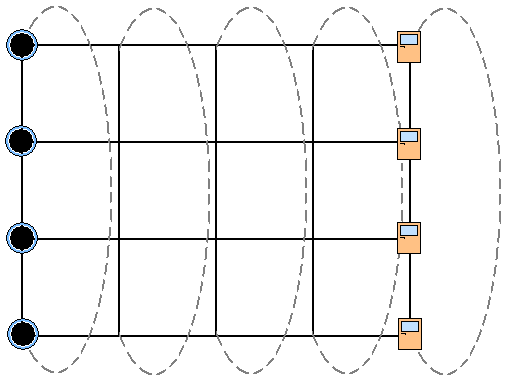 В данном примере n = 4, m = 5. Пунктирными линиями обозначены коридоры, которые замыкают каждый столбец в кольцо, то есть соединяют n-ную и 1-ую строки сетки. В самом левом столбце этой сетки находятся порталы, из которых готовы вылезти щупальца Вселенского Зла. В самом правом столбце расположены выходы из сооружения. Щупальца могут выбраться только через эти выходы. Отрезки, соединяющие узлы этой сетки — это коридоры. Брейн рад бы выпустить все щупальца, но вот незадача: из порталов может вылезти бесконечное количество щупалец, каждое щупальце обладает бесконечной длиной и некоторой толщиной, а объёмы коридоров, увы, весьма ограничены. Брейн навскидку смог оценить максимальное количество щупалец, которое может пролезть через каждый коридор. Теперь помогите мышкам определить, какое максимальное количество щупалец Вселенского Зла выберется из Большого Адронного Коллайдера. Выходные данные Выведите одно число — количество щупалец Вселенского Зла, которыми будут повелевать Пинки и Брейн. Пожалуйста, не используйте спецификатор %lld для чтения или записи 64-х битовых чисел на С++. Рекомендуется использовать поток cout (также вы можете использовать спецификатор %I64d). | |
![]()
|
|
F. Медведь и справедливое множество
Потоки
графы
*2500
Лимак — медведь гризли. Он большой и страшный. Прогуливаясь по лесу, вы случайно встретились с ним. Это не лучшее, что могло с вами произойти. Он съест все ваши печеньки, если вы не продемонстрируете ему свои математические навыки. Лимак решил дать вам головоломку, чтобы проверить вас. Всем известно, что у Лимака, как и любого другого медведя, есть множество чисел. Вам известна некоторая информация об этом множестве: - Элементами этого множества являются различные положительные числа.
- Количество элементов в этом множестве равно n. Число n кратно 5.
- Все элементы множества находятся в промежутке от 1 до b включительно: медведи не знают чисел больших b.
- Для каждого r из {0, 1, 2, 3, 4} множество медведя содержит ровно
 элементов, которые дают остаток r при делении на 5. (Таким образом, в множестве элементов, которые дают остаток r при делении на 5. (Таким образом, в множестве  элементов кратных 5, элементов кратных 5,  элементов вида 5k + 1, элементов вида 5k + 1,  элементов вида 5k + 2 и так далее.) элементов вида 5k + 2 и так далее.) Лимак загадочно улыбнулся вам и дал q подсказок об этом множестве. i-я подсказка выглядит следующим образом: "Количество элементов в множестве со значениями в промежутке от 1 до upToi включительно равно quantityi." Вот-вот Лимак расскажет вам настоящую головоломку, но что-то явно не так... Эта улыбка была очень странной. Вы заподозрили причину этого. Может Лимак обманул вас? Или он всё-таки честный медведь гризли? Вам заданы числа n, b, q и подсказки, определите мог ли Лимак быть честным с вами, то есть существует ли хотя бы одно множество с такими ограничениями. Если такое возможно выведите ''fair". В противном случае выведите ''unfair". Выходные данные Выведите ''fair" если существует хотя бы одно множество, удовлетворяющее всем свойствам и подсказкам. В противном случае выведите ''unfair". Примечание В первом примере всем условиям удовлетворяет только множество {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. Во втором примере также существует только одно множество, удовлятворяющее всем условиям: {6, 7, 8, 9, 10, 11, 12, 13, 14, 15}. Легко видеть, что третий пример противоречив. Таким образом, Лимак вас обманул :-( | |
![]()
|
|
D. Медвежья доставка
Бинарный поиск
Потоки
графы
*2200
Маленький золотой медвежонок Нивел долго жил в лесу. Созерцать деревья ежедневно ему в какой-то момент порядком надоело, и он переехал в большой город. В городе Нивел устроился управляющим медвежьей доставки. Город, в котором он поселился, можно представить как ориентированный граф из n вершин и m рёбер. У каждого ребра есть пропускная способность, равная максимальному количеству веса, который можно пронести по этому ребру в рамках одного цикла доставки. Доставка заключается в том, что каждый имеющийся у Нивела медвежонок несёт в своих лапках груз из вершины 1 в вершину n. Суммарный вес, пронесённый всеми медвежатами по ребру, не должен превышать пропускной способности этого ребра. В подчинении у Нивела ровно x медвежат. Чтобы всё было честно, никто из медвежат не должен отдыхать и каждый медвежонок должен доставить из 1 в n груз одинакового веса. Однако медвежата вполне могут пойти разными дорогами. Нивел хочет определить, какой максимальный суммарный вес может быть доставлен из вершины 1 в вершину n. Выходные данные Выведите единственное вещественное число — максимальный суммарный вес, который можно доставить из вершины 1 в вершину n, используя ровно x медвежат, каждый из которых пронесёт одинаковый вес. Ваш ответ будет считаться правильным, если его абсолютная или относительная ошибка не будет превосходить 10 - 6. А именно: пусть ваш ответ равен a, а ответ жюри — b. Проверяющая программа будет считать ваш ответ правильным, если 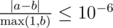 . . Примечание Доступны три медвежонка. Двое из них могут пойти по пути 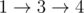 , а третий по пути , а третий по пути  . Хотя медвежонок, идущий по пути . Хотя медвежонок, идущий по пути  , мог бы нести одну единицу веса, из-за зашкаливающей честности он не может взять с собой больше 0.5 единиц веса. Таким образом, суммарно будет доставлено 1.5 единиц веса. Обратите внимание, что, используя всего двух медвежат, можно было бы доставить 2 единицы веса, но Нивел обязан использовать всех трёх. , мог бы нести одну единицу веса, из-за зашкаливающей честности он не может взять с собой больше 0.5 единиц веса. Таким образом, суммарно будет доставлено 1.5 единиц веса. Обратите внимание, что, используя всего двух медвежат, можно было бы доставить 2 единицы веса, но Нивел обязан использовать всех трёх. | |
![]()
|
|
D. Капитан Америка
Потоки
жадные алгоритмы
*3100
Стив Роджерс в восторге от новых щитов, которые ему выдали в S.H.I.E.L.D. Осталось только их раскрасить. Всего щитов n, i-й из которых расположен в точке (xi, yi) координатной плоскости. Вполне возможно, что два или более щита расположены в одной точке. Стив хочет покрасить каждый щит в красный или синий цвет. Покраска щита в красный стоит r долларов, а покраска в синий стоит b долларов. Дополнительно покраска Стива должна удовлетворять m условиям. Каждое условие описывается тремя целыми числами ti, li и di: - Если ti = 1, то модуль разницы между количеством красных и количеством синих щитов на прямой x = li не должен превосходить di.
- Если ti = 2, то модуль разницы между количеством красных и количеством синих щитов на прямой y = li не должен превосходить di.
Стив поручил вам найти корректную раскраску минимальной стоимости. Выходные данные Если удовлетворить все ограничения невозможно, то выведите -1 в первой и единственной строке выходных данных. В противном случае сначала выведите минимальную суммарную стоимость покраски всех щитов. Во второй строке выведите строку длины n, состоящую из букв «r» и «b». i-й из этих символов должен быть равен «r», если i-й щит следует покрасить в красный цвет в оптимальном ответе, и «b», если его следует покрасить в синий. Если оптимальных решений несколько, выведите любое из них. | |
![]()
|
|
D. Неправильный поток
Потоки
*2900
На экзамене в магистратуру Кибер-Механического факультета МГУ Саше попался билет про алгоритм Форда-Фалкерсона. Этот билет он знал очень хорошо, потому что неоднократно встречал алгоритм на олимпиадах. В качестве задачи к билету была дана сеть с уже частично построенным потоком, на которой надо было продемонстрировать работу алгоритма. Саша быстро написал билет и приступил было к задаче, как вдруг понял, что описание сети некорректное! Ему был дан ориентированный граф G(V, E), в котором выделены две вершины s и t, называемые сток и исток. Обозначим за n количество вершин в графе, то есть n = |V|, а за m — количество рёбер в графе, то есть m = |E|. В рамках данной задачи будем полагать истоком вершину с номером 1, а стоком — вершину с номером n. Дополнительно, на рёбрах графа определена функция пропускных способностей c(e) и функция потока f(e). Функция f(e) определяет корректный поток, если выполнены следующие условия: - Для любого ребра
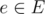 поток по данному ребру неотрицателен и не превосходит c(e), то есть 0 ≤ f(e) ≤ c(e). поток по данному ребру неотрицателен и не превосходит c(e), то есть 0 ≤ f(e) ≤ c(e). - Для любой вершины
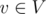 , не являющейся стоком или истоком (v ≠ s и v ≠ t), суммарный поток по всем рёбрам, входящим в v, равен суммарному потоку по всем рёбрам, выходящим из v. Другими словами, поток не скапливается в вершине v. , не являющейся стоком или истоком (v ≠ s и v ≠ t), суммарный поток по всем рёбрам, входящим в v, равен суммарному потоку по всем рёбрам, выходящим из v. Другими словами, поток не скапливается в вершине v. Было понятно, что экзамен готовили в последнюю ночь, и поэтому в условие закралось много опечаток. Саша подошёл к преподавателю и попросил исправить сеть и дать корректную задачу, на что получил ответ — студенты магистратуры должны уметь исправить сеть сами. Чтобы Саша не упростил себе задачу, преподаватель сказал, что сумма всех изменений должна быть минимальной. Направление рёбер менять нельзя, их нельзя удалять или добавлять. Разрешается изменять только пропускные способности c(e) и величины потока f(e), причём все величины должны остаться целочисленными и неотрицательными. Полученное описание сети не обязательно должно быть максимальным потоком, его Саша позже найдет сам. Найдите минимальную сумму всех изменений функций f(e) и c(e), которые придётся сделать Саше, чтобы функция потока стала корректной. Суммарное изменение считается как сумма абсолютной разницы, то есть если новые функции равны f * (e) и c * (e), то считается, что было внесено 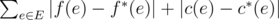 изменений. изменений. Выходные данные Выведите одно целое число — минимальную сумму изменений, которые надо сделать Саше, чтобы получить корректное описание сети. Примечание В первом тестовом примере поток изначально правильный. Обратите внимание, что поток не максимальный, но максимальность и не требуется. Во втором тестовом примере поток по единственному ребру превосходит пропускную способность. Существует два оптимальных решения: увеличить пропускную способность до 2 или уменьшить величину потока до 1. В третьем тестовом примере в вершину 2 входит одна единица потока, а выходит две. Одно из возможных решений — уменьшить величину потока по второму ребру на 1. В четвертом примере в графе есть изолированная циркуляция, и, согласно определению, этот поток корректен. | |
![]()
|
|
G. Падение
Потоки
*2400
Вы упали в какую-то дыру и после нескольких часов беспамятства обнаружили себя в подземном городе. Во время одной из ежедневных прогулок в неизвестность вы встретили двух забавных скетелов Санца и Ппариуса, который почему то решили составить вам компанию и выдали вам несколько загадок. В один из дней, Санц сделал для вас кроссворд. Да не просто кроссворд, а 1D кроссворд! Вам дано m слов и строка длины n. Также дан массив p, который для каждого слова определяет его стоимость — i-е слово стоит pi очков. Как только вы встречаете в строке одно из m слов, вы получаете соответствующее количество очков. Каждая позиция в строке может быть использована не более чем x раз. Различные вхождения одного и того же слова могут быть учтены несколько раз, но не более чем один раз на каждое вхождение. Если слово является подстрокой другого слова, то есть можно учитывать несколько раз (при условии выполнения требования на использование позиций не более чем x раз). Чтобы решить данный пазл, требуется сказать Санцу максимально возможный счёт, который можно набрать. Нет необходимости покрывать все позиции, главное максимизировать свой счёт. Кроссворд и слова состоят только из строчных букв английского алфавита. Выходные данные Выведите одно целое число — максимальное количество очков, которое можно получить. Примечание Например, для строки «abacba», слов «aba» (6 очков) и «ba» (3 очка), и x = 3, мы можем заработать 12 очков — слово «aba» встречается один раз, а слово «ba» дважды. Обратите внимание, что для x = 1 можно получить не более 9 очков, поскольку нельзя одновременно взять «aba» и первое вхождение «ba». | |
![]()
|
|
B. Кактусофобия
Потоки
поиск в глубину и подобное
*2400
Дерево — это связный неориентированный граф без циклов. Реберный кактус — связный неориентированный граф без петель и кратных ребер, в котором каждое ребро лежит не более чем на одном простом цикле. У Васи есть реберный кактус, в котором каждое ребро покрашено в какой-то цвет. Вася хочет убрать из кактуса минимальное число ребер так, чтобы получилось дерево. При этом Вася хочет, чтобы количество различных цветов среди оставшихся ребер было максимально. Помогите ему узнать, сколько различных цветов может остаться в графе. Выходные данные Выведите одно целое число — максимальное количество различных цветов, которое можно оставить в графе. | |
![]()
|
|
E. Односторонняя реформа
Потоки
Конструктив
поиск в глубину и подобное
жадные алгоритмы
графы
*2200
В Берляндии есть n городов и m двунаправленных дорог, которыми соединены некоторые пары городов. Известно, что между каждой парой городов существует не более одной дороги, а также никакая дорога не соединяет город сам с собой. Допустимо, что между некоторыми парами городов не существует пути по дорогам от одного до другого. Дорожный министр решил провести в Берляндии реформу и заориентировать все дороги в стране, то есть сделать каждую дорогу односторонней. При этом министр хочет максимизировать количество таких городов, чтобы количество дорог, начинающихся в этих городах, было равно количеству дорог, которые в них заканчиваются. Выходные данные Для каждого набора входных данных выведите сначала искомое максимальное количество таких городов, что количество дорог, начинающихся в этих городах, было равно количеству дорог, которые в них заканчиваются. В следующих m строках выведите заориентированные дороги. Сначала выводите номер города, в котором дорога начинается, а затем номер города, в котором дорога заканчивается. Если ответов несколько, выведите любой из них. Дороги в каждом наборе входных данных разрешается выводить в любом порядке. Каждая дорога должна быть выведена ровно один раз. | |
![]()
|
|
E. Транспортировка товаров
Потоки
дп
жадные алгоритмы
*2900
Вдоль трассы с односторонним движением расположены n городов. Города пронумерованы числами от 1 до n в порядке проезда вдоль трассы. В i-м городе было произведено pi единиц товара и может быть продано не более чем si единиц товара. Для каждой пары городов i и j, таких что 1 ≤ i < j ≤ n, можно не более одного раза перевезти не более чем c единиц товара из города i в город j. Заметьте, что товар можно перевозить только из города с меньшим номером в город с большим номером. Перевозить товары между городами можно в любом порядке. Определите, какое максимальное количество произведённого товара суммарно может быть продано во всех городах после некоторой последовательности перевозок. Выходные данные Выведите одно число — максимальное количество товара, которое может быть продано во всех городах после некоторой последовательности перевозок. | |
![]()
|
|
D. Распределение футболок
Потоки
Конструктив
*1800
жадные алгоритмы
В качестве сувениров на соревновании по программированию было решено вручить футболки. Всего в типографии были напечатаны футболки шести размеров: S, M, L, XL, XXL, XXXL (размеры перечислены в порядке возрастания). Для каждого размера от S до XXXL вам известно количество футболок такого размера. Во время регистрации организаторы попросили каждого из n участников указать размер футболки. Если участник колебался между двумя размерами, то он мог указать два соседних — это означает, что ему подойдет футболка любого из двух размеров. Напишите программу, которая определит, возможно ли из напечатанных в типографии футболок сделать подарок каждому участнику соревнования. Конечно, каждому участнику должна достаться футболка его размера: - требуемого размера, если указан один размер;
- любого из двух размеров, если указаны два соседних размера.
В случае положительного ответа программа должна найти любой из вариантов раздачи футболок. Выходные данные Если ответа не существует выведите «NO» (без кавычек). В противном случае, в первой строке выведите «YES» (без кавычек). В следующих n строках выведите размеры футболок, которые получат участники. Порядок участников должен совпадать с тем порядком, который задан во входных данных. Если решений несколько, выведите любое. | |
![]()
|
|
I. Olympiad in Programming and Sport
Потоки
дп
*2000
жадные алгоритмы
графы
| |
![]()
|
|
E. Чемпионат
Потоки
Конструктив
математика
жадные алгоритмы
*2900
Остап Бендер решил в очередной раз дать сеанс одновременной игры по шахматам. В этот раз он тщательно готовился, поэтому следил за ходом одного крупного турнира по шахматам. В турнире принимали участие m шахматистов, каждый сыграл с каждым ровно одну партию. В случае победы участник получал 2 очка, ничьей — 1 очко, поражения — 0 очков. Остап не хотел держать в голове всю турнирную таблицу, поэтому для каждого участника он вычислил итоговое количество набранных им очков (то есть сумму его очков по всем партиям, в которых он принимал участие). Далее Остап упорядочил участников по невозрастанию набранных очков и запомнил результаты первых n из этого списка. Теперь у великого комбинатора возник вопрос, а ничего ли он не напутал и действительно ли существует турнирная таблица, по которой могли быть получены данные n чисел? Другими словами, можно ли так назначить исходы всех попарных встреч для m шахматистов, что после вычисления итоговой суммы для каждого, упорядочивания и отбрасывания последних m - n останется набор чисел, в точности совпадающий с тем, что помнит Остап? Выходные данные Если не существует турнира, по которому Остап мог получить данный набор чисел, выведите «no» в единственной строке выходных данных. В противном случае в первой строке выходных данных выведите «yes», а следующих m строках — сам турнир. Каждая строка описания турнира должна состоять из m символов «X», «W», «D» и «L». Символ «X» всегда ставится на главной диагонали (и только там), то есть в i-й позиции i-й строки, символ «W» в j-й позиции i-й строки означает, что игрок номер i обыграл игрока номер j, символы «D» и «L» на соответствующей позиции означают ничью и поражение соответственно. Выведенная таблица должна быть непротиворечива, а набор чисел, состоящий из баллов n участников с наилучшим счётом, должен совпадать с набором, указанным во входных данных. Если подходящих ответов несколько, разрешается вывести любой из них. | |
![]()
|
|
E. Гоша выходит на охоту
Потоки
Перебор
Структуры данных
Теория вероятностей
математика
дп
сортировки
*3000
Гоша выходит на охоту. Его цель — поймать как можно больше покемонов. У Гоши есть a покеболов и b ультраболов. Всего покемонов n. Они пронумерованы числами от 1 до n. Про i-го покемона Гоша знает, что если бросить в него покеболом, то с вероятностью pi данный покемон будет пойман. Если бросить в i-го покемона ультраболом, то он будет пойман с вероятностью ui. В каждого покемона можно бросить не более чем одним болом каждого типа. Охота происходит следующим образом: Гоша сначала выбирает не более чем a покемонов, в которых он будет бросать покеболами, и не более чем b покемонов, в которых он будет бросать ультраболами. После этого Гоша бросает в выбранных покемонов выбранными болами. Если он бросает в покемона и покеболом, и ультраболом, то данный покемон будет пойман, если он будет пойман хотя бы одним из двух болов. Результаты бросков независимы. Гоша хочет узнать, чему равно математическое ожидание количества пойманных покемонов, если он будет действовать оптимально. Иными словами, он хочет узнать максимально возможное математическое ожидание. Выходные данные Выведите максимально возможное математическое ожидание количества пойманных покемонов. Ответ будет считаться правильным, если его относительная или абсолютная погрешность не превышает 10 - 4. | |
![]()
|
|
E. Эвакуация
Потоки
графы
*2300
кратчайшие пути
Опять они там что-то напортачили... В одном из ядерных реакторов исследовательской станции идет неуправляемая реакция и скоро произойдет взрыв, который уничтожит всю станцию. Станция представляет собой квадрат n × n разбитый на блоки 1 × 1. Каждый блок является или реактором или лабораторией. Реакторов может быть несколько и ровно один из них собирается взорваться. Реакторы можно считать непроходимыми блоками, по лабораториям же можно перемещаться. Между любыми двумя лабораториями, которые находятся в соседних блоках, имеется коридор. Блоки считаются соседними, если имеют общее ребро. В каждой из лабораторий имеется некоторое количество ученых и некоторое количество спасательных капсул. Как только ученый залезает в капсулу, он считается спасенным. В каждую капсулу помещается не более одного ученого. Реактор, который скоро взорвется, поврежден и из него вытекает токсичная охлаждающая жидкость в соседние блоки. Блок, в котором расположен этот реактор, считается зараженным. Каждую минуту охлаждающая жидкость растекается по лабораториям через коридоры. Если в какую-то минуту один из блоков заражен, то на следующую минуту все соседние лаборатории также оказываются заражены. Как только лаборатория оказывается заражена, все ученые в ней, которые находятся не в спасательных капсулах, погибают. Через блоки с реакторами охлаждающая жидкость не распространяется. До взрыва осталось ровно t минут. Любой ученый за одну минуту может переместиться по коридору в соседнюю лабораторию, если она не заражена. По любому коридору одновременно могут перемещаться неограниченное количество ученых в обоих направлениях. Считается, что ученые внутри лаборатории перемещается без затрат времени. Кроме того, любой ученый может залезть в спасательную капсулу мгновенно. Также считается, что любой ученый в данную минуту всегда успевает сделать свои действия (переместиться из данной лаборатории в соседнюю или залезть в спасательную капсулу) до того, как лаборатория окажется заражена. Определите максимальное количество ученых, которым удастся спастись. Выходные данные Выведите одно целое число — максимальное количество ученых, которым удастся спастись. Примечание Во втором примере события могли происходить следующим образом: 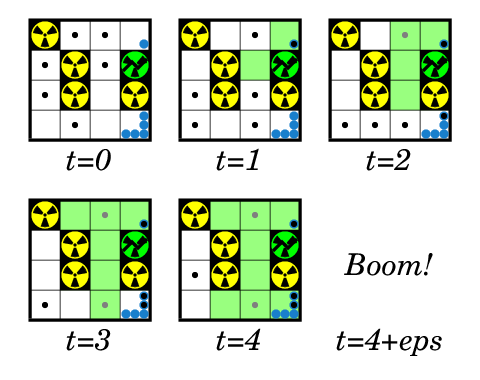 | |
![]()
|
|
E. Альт
Потоки
Деревья
Структуры данных
графы
*3200
Альт — планета в галактике «Энкор». Люди управляют этой планетой, но по некоторым причинам здесь нет собак, на их планете. Поэтому люди в депрессии и грустят. Рик и Морти вселенские филантрописты и они хотят сделать людей на планете Альт счастливыми. Альт имеет n городов пронумерованных от 1 до n и n - 1 двунаправленных дорог, пронумерованных от 1 до n - 1. От любого города до любого можно доехать используя эти дороги. На Альте есть два типа людей: - Стражи. Страж живет в доме вдоль дороги и охраняет дорогу.
- Граждане. Гражданин живет дома, внутри города, и работает в офисе, в другом городе.
Каждый человек на Альте является либо стражем либо гражданином. Вдоль каждой дороги живет один страж.  Рик и Морти обратились ко всем людям на Альте, и вот что они получили: - m граждан живет на Альте.
- Гражданин номер i живет в городе номер xi и работает в городе номер yi.
- Каждый день гражданин едет по дорогам вдоль кратчайшего пути от его дома на работу.
- Гражданин будет счастлив, если и только если он будет иметь щенка, или все стражи вдоль пути на его работу будут иметь щенка (он видит щенков у стражей на каждой дороге и он счастлив).
- Страж всегда счастлив.
Вам необходимо сказать Рику и Морти минимальное количество щенков необходимое, чтобы сделать всех на Альте счастливыми, и также предоставить оптимальный путь раздать щенков. Выходные данные В первой строке выведите целое число k — суммарное необходимое количество щенков (1 ≤ k ≤ n). Во второй строке выведите число q — количество щенков, которых необходимо раздать гражданам, за которым следует q различных чисел a1, a2, ..., aq — номера граждан, которым необходимо раздать щенков (0 ≤ q ≤ min(m, k), 1 ≤ ai ≤ m). В третьей строке выведите число e — количество щенков, которых необходимо раздать стражам, за которым следует e различных целых чисел b1, b2, ..., be — номера дорог, стражам которых необходимо раздать щенков (0 ≤ e ≤ min(n - 1, k), 1 ≤ bi ≤ n - 1). Сумма q и e должна быть равна k. Примечание Карта Альта для первого тестового примера (числа, написанные на дорогах, это их номера): 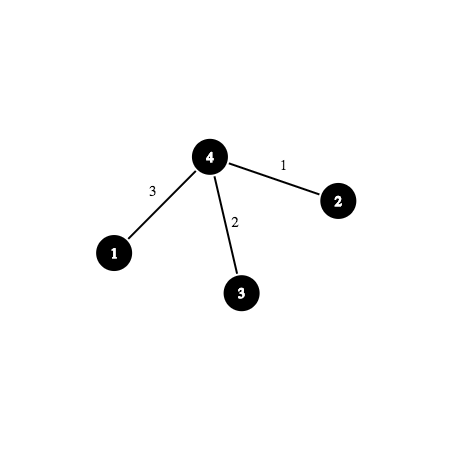 Карта Альта для второго тестового примера (числа, написанные на дорогах, это их номера): 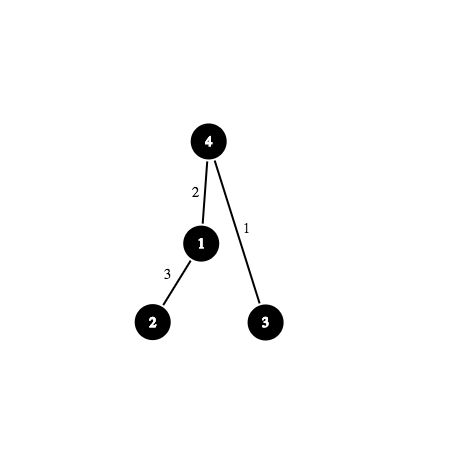 | |
![]()
|
|
G. Олег и шахматы
Потоки
Паросочетания
Структуры данных
разделяй и властвуй
*3400
Обычный клиент банка Олег решает интересную шахматную задачу: расставить на шахматной доске n × n наибольшее число ладей, чтобы они не били друг друга. Напомним, что ладья, которая стоит в клетке (a, b), бьет ладью, стоящую в клетке (x, y), тогда и только тогда, когда a = x или b = y. К сожалению (или радости?) Олега ответ в этой задаче всегда получался равным n, поэтому вскоре задача ему наскучила. Он решил её усложнить, удалив некоторые клетки из шахматной доски. Удалив клетку, Олег подразумевает, что на нее нельзя ставить ладью, однако, бить «сквозь» удаленные клетки ладьи могут. Олег удаляет клетки группами, а именно, он раз за разом выбирает некоторый прямоугольник по сторонами, параллельными осям координат, и удаляет все клетки в нем. Формально, если он выбрал некоторый прямоугольник, левая нижняя и правая верхняя клетки которого имеют координаты (x1, y1) и (x2, y2), соответственно, то он удаляет все такие клетки (x, y) что x1 ≤ x ≤ x2 и y1 ≤ y ≤ y2. Гарантируется, что никакую клетку два раза Олег удалять не будет, то есть все выбранные прямоугольники не пересекаются. Эту версию задачи Олег решить не смог, а его друг, к которому он часто обращается за советами, — аналитик Игорь — сейчас очень занят на конференции, и не может помочь Олегу. Вы — последняя надежда Олега! Помогите ему: по заданному размеру доски и прямоугольникам, клетки в которых удалены, выясните, какое максимальное число ладей можно расставить на доске так, чтобы никакая ладья не била никакую другую. Выходные данные В единственной строке выведите максимальное число ладей, которое Олег сможет расставить на поле так, чтобы они не били друг друга. Примечание Ниже приведено изображения поля и пример расстановки ладей на нем в первом примере. 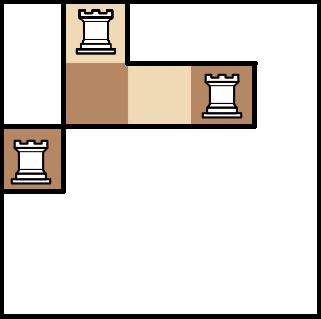
| |
![]()
|
|
C. Хайди и Библиотека (сложная)
Потоки
*2600
графы
Хорошие времена в библиотеке Хайди закончились. Читатели подключились к интернету и совсем перестали посещать библиотеку. Кроме этого в книжном магазине стали брать дополнительную плату за некоторые книги. А именно, если в предыдущих версиях каждая книга могла быть куплена за 1 CHF, теперь цена книги i составляет ci CHF. Выходные данные В единственной строке выведите минимальную стоимость покупки книг в книжном магазине, которые необходимы для удовлетворения запросов всех посетителей. Примечание Первые три примера повторяются, но четвертый является новым. В четвертом примере, покупая книгу 3, Хайди должна избавиться от книги 1 или от книги 2. Хотя книга 2 будет запрошена позже, чем книга 1, Хайди сохранит ее, потому что очень дорого покупать снова книгу 2. | |
![]()
|
|
N. Первоапрельская задача (средняя)
Бинарный поиск
Потоки
*2400
графы
Сурки должны подготовить k задач для HC2 за n дней. Каждую задачу нужно распечатать после того, как она будет подготовлена. Подготовить задачу в день номер i (не более одной задачи в день) стоит ai CHF, а распечатать задачу в день i (тоже не более одной задачи в день) стоит bi CHF. Конечно, нельзя распечатать задачу до того, как она была подготовлена (но распечатать в тот же день, что и подготовить, позволительно). Какова минимальная стоимость подготовки и распечатки всех задач? Выходные данные Выведите минимальную суммарную стоимость подготовки и печати k задач, которая равна минимально возможной сумме ai1 + ai2 + ... + aik + bj1 + bj2 + ... + bjk, где 1 ≤ i1 < i2 < ... < ik ≤ n, 1 ≤ j1 < j2 < ... < jk ≤ n и i1 ≤ j1, i2 ≤ j2, ..., ik ≤ jk. Примечание В примере одно из возможных решений — подготовить первую задачу в день 1 и распечатать ее в день 1, подготовить вторую задачу в день 2 и распечатать в день 4, подготовить третью задачу в день 3 и распечатать в день 5, подготовить четвертую задачу в день 6 и распечатать в день 8. | |
![]()
|
|
O. Первоапрельская задача (сложная)
Бинарный поиск
Потоки
Структуры данных
*2900
Планы для HC2 довольно надуманны: остаётся чуть более чем 500 000 дней до HC2 3387, например, и, соответственно, мы планируем сделать несколько сотен тысяч задач в соответствующем году (мы надеемся, что соревнования по программированию станут более популярными). Суркам нужно приступать к работе, и они могли бы использовать хороший план ... Выходные данные Выходные данные те же, что и в средней версии этой задачи. | |
![]()
|
|
F. Карточная игра
Бинарный поиск
Потоки
*2400
графы
Компьютерные коллекционные карточные игры недавно стали очень популярны. Вот и Вова решил попробовать сыграть в одну такую. В коллекции Вовы n карт, каждая из которых характеризуется своей силой pi, магическим числом ci и уровнем li. Вова хочет собрать колоду с суммарной силой не менее k, однако магические числа, записанные на картах, могут не позволить ему это сделать — нельзя взять в колоду две карты, если сумма магических чисел, записанных на них, является простым числом. Также Вова не может брать в колоду карты, уровень которых выше уровня его персонажа. Сейчас у персонажа Вовы 1-й уровень. Помогите Вове определить, до какого уровня ему необходимо развиться, чтобы собрать колоду необходимой силы. Выходные данные Если Вова не сможет собрать колоду необходимой силы, выведите - 1. Иначе выведите минимальный уровень, при котором это возможно. | |
![]()
|
|
D. Две мелодии
Потоки
дп
*2600
Алиса — начинающий композитор, и сейчас она собирается написать очередной шедевр. И даже не один, а сразу два! У Алисы есть лист с n нотами на нем. Она хочет выбрать две такие непустые непересекающиеся подпоследовательности, что обе образуют мелодии и сумма их длин максимальна. Подпоследовательность — это последовательность, которую можно получить из другой последовательности путем удаления некоторых элементов, не меняя порядок оставшихся элементов. Подпоследовательность образует мелодию, когда два соседних элемента либо отличаются на 1, либо сравнимы по модулю 7. Напишите программу, которая найдет максимальную сумму длин двух таких непустых непересекающихся подпоследовательностей, что обе образуют мелодии. Выходные данные Выведите максимальную сумму длин двух таких непустых непересекающихся подпоследовательностей, что обе образуют мелодии. Примечание В первом примере подпоследовательности [1, 2] и [4, 5] дадут суммарную длину 4. Во втором примере подпоследовательности [62, 48, 49] и [60, 61] дадут суммарную длину 5. Если выбрать первой подпоследовательностью [62, 61], то максимальная возможная длина второй мелодии будет 2, и результат будет 4, что не является максимальным ответом. | |
![]()
|
|
G. Четыре мелодии
Потоки
*2600
графы
От автора: возможно, некоторые из вас помнят задачу «Две мелодии» с Educational Codeforces Round 22. Пришло время сделать её немного сложнее! Алиса — начинающий композитор, и недавно она записала два трека, ставшие очень популярными. Теперь у неё целая толпа фанатов, и все они ждут, когда Алиса запишет что-то ещё. На этот раз для записи треков Алисе потребуются четыре мелодии. У Алисы есть лист с n нотами на нем. Она хочет выбрать четыре такие непустые непересекающиеся подпоследовательности, что все они образуют мелодии и сумма их длин максимальна. Подпоследовательность — это последовательность, которую можно получить из другой последовательности путем удаления некоторых элементов, не меняя порядок оставшихся элементов. Подпоследовательность образует мелодию, когда два соседних элемента либо отличаются на 1, либо сравнимы по модулю 7. Напишите программу, которая найдет максимальную сумму длин четырёх таких непустых непересекающихся подпоследовательностей, что все они образуют мелодии. Выходные данные Выведите максимальную сумму длин четырёх таких непустых непересекающихся подпоследовательностей, что все они образуют мелодии. Примечание В первом примере можно составить 4 мелодии, взяв любые 4 ноты (по одной ноте в каждой мелодии). Во втором примере есть одна мелодия длины 2 — {1, 2}. Остальные ноты используются в оставшихся трёх мелодиях (по одной ноте в мелодии). | |
![]()
|
|
E. Максимальный поток
Потоки
графы
*3000
Дан ориентированный граф, состоящий из n вершин и m ребер, с выделенными вершинами s и t. При этом, в вершину s не входит ни одного ребра, а из вершины t не выходит ни одного ребра. Изначально у каждого ребра была целая пропускная способность ci > 0. В сети с истоком s и стоком t был построен некоторый максимальный поток, и на ребре номер i записали fi — сколько единиц потока течет по этому ребру. Затем все пропускные способности ci и величины fi потока стерли, оставив лишь направление ребра и индикаторы gi: течет ли по ребру поток, т.е. 1, если fi > 0, и 0 иначе. По графу и индикаторам gi определите, каково минимально возможное число насыщенных ребер в этой сети (ребро i является насыщенным, если fi = ci), и постройте соответствующую сеть c максимальным потоком в ней. Поток в ориентированном графе задается величинами потока fi на каждом ребре такими, что выполняются условия: - для каждой вершины, кроме истока и стока, сумма потока на входящих и выходящих из нее ребрах одинакова
- для каждого ребра 0 ≤ fi ≤ ci
Максимальный поток — такой поток, в котором разность между суммой величин потоков на ребрах, выходящих из истока, и суммой величин потоков на ребрах, входящих в исток (таких в этой задаче нет), максимальна. Выходные данные В первой строке выведите целое число k — минимальное число ребер, которые должны быть насыщены в максимальном потоке. В каждой из следующих m строк выведите два целых числа fi, ci (1 ≤ ci ≤ 109, 0 ≤ fi ≤ ci) — поток по ребру номер i и пропускную способность ребра номер i. Эти данные должны задавать корректный максимальный поток в сети с такими пропускными способностями, ровно для k ребер должно выполняться fi = ci, а также fi > 0 должно выполняться тогда и только тогда, когда во входных данных для gi = 1. Если возможных ответов несколько, выведите любой из них. Примечание Иллюстрация к примеру из условия. Темным обозначены насыщенные ребра, пунктиром — ребро, по которому не идет поток (gi = 0). Число на ребре — номер данного ребра в списке. 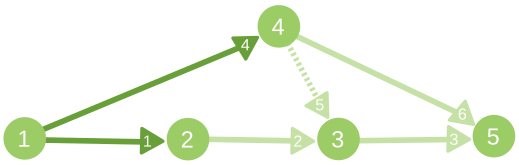 | |
![]()
|
|
J. Посвящение в студенты
Бинарный поиск
Потоки
*2400
графы
Скоро в Берляндском университете состоится посвящение первокурсников в студенты. Организаторы посвящения придумывают программу этого праздника. По их мнению, было бы хорошо, если бы новоиспечённые студенты подарили друг другу небольшие сувениры. Когда они озвучили эту идею первокурсникам, то выяснили следующее: - некоторые пары первокурсников уже знакомы друг с другом;
- каждый первокурсник согласен дарить сувениры только тем, с кем он уже знаком;
- каждый первокурсник не хотел бы дарить много сувениров.
Организаторы записали все пары знакомых между собой первокурсников и теперь хотят определить для каждого первокурсника, кому он должен подарить сувениры. По мнению организаторов, в каждой паре знакомых между собой первокурсников ровно один должен подарить сувенир другому. Первокурсники уже решили назвать самым невезучим того, кому придётся дарить наибольшее количество сувениров. Организаторы в ответ пообещали, что самый невезучий будет минимально невезучим: конечно, ему придётся дарить наибольшее количество сувениров по сравнению с остальными, но это количество будет минимально возможным. Организаторам очень некогда, и они обратились к вам с просьбой определить для каждой пары знакомых первокурсников, кто кому должен подарить сувенир. Выходные данные В первой строке выведите единственное целое число — минимальное количество сувениров, которые подарит самый невезучий первокурсник. В каждой из следующих m строк выведите по одной паре номеров знакомых между собой первокурсников. Первым в паре выводите номер того первокурсника, который будет дарить сувенир. Пары можно выводить в любом порядке. Если существует несколько решений, выведите любое из них. | |
![]()
|
|
D. Shake It!
Потоки
Комбинаторика
дп
графы
*2900
Открывая тайную дверь, раскрой нескончаемый переменчивый сказочный мир. Назовем миром неориентированный граф G, во множестве вершин которого V(G) есть две особые вершины s(G) и t(G). Начальный мир имеет множество вершин {s(G), t(G)} и ребро между ними. С начальным миром произошло n изменений. В каждом изменении была добавлена новая вершина w во множество V(G), выбрано существующее ребро (u, v), и добавлены два новых ребра (u, w) и (v, w) во множество ребер E(G). Обратите внимание, некоторые ребра могут быть выбраны в более, чем одном изменении. Известно, что в итоговом графе минимальный s-t разрез равен m, то есть, нужно удалить хотя бы m ребер, чтобы s(G) и t(G) оказались в разных компонентах связности. Найдите число непохожих миров, которые могли получиться, по модулю 109 + 7. Два мира называются похожими, если они изоморфны и есть изоморфизм, который не переобозначает вершины s и t. Формально, два мира G и H считаются похожими, если между их множествами вершин существует биекция 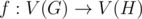 такая, что: такая, что: - f(s(G)) = s(H);
- f(t(G)) = t(H);
- Две вершины u и v в графе G соседние в G, если и только если f(u) и f(v) соседние в H.
Выходные данные Выведите одно число — число непохожих миров, которые могли получиться, по модулю 109 + 7. Примечание В первом примере следующие 6 миров попарно непохожи и удовлетворяют всем ограничениям, s(G) обозначена зеленым, t(G) обозначена синим, один из минимальных разрезов обозначен голубым. 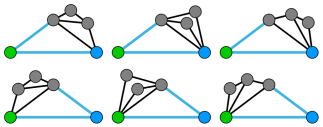 Во втором примере следующие 3 мира удовлетворяют ограничениям. 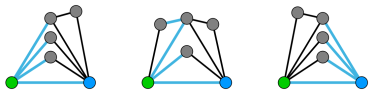 | |
![]()
|
|
D. Путь исследования
Бинарный поиск
Потоки
Паросочетания
*2100
кратчайшие пути
Участники Bubble Cup X собрались после соревнования и обсуждают, как лучше всего узнать страну-организатор и города в ней. После небольшого исследования карты Сербии участники выяснили следующий факт: в стране есть V городов, которые пронумерованы от 1 до V, и E двусторонних дорог, соединяющих города. У каждой дороги есть вес (время, необходимое для прохода по этой дороге). На Bubble Cup есть N команд, поэтому участники придумали следующий план: каждая из N команд начнет свой путь в одном из V городов, возможно, некоторые команды будут иметь одинаковую начальную позицию. Они хотят найти минимальное время T такое, что каждая команда может двигаться в течении этих T минут, и количество различных городов, в которых окажутся команды, как минимум K (потому что они будут исследовать только город, в котором окажутся в конце). Команда не обязана двигаться все время, если им нравится какой-то город, они могут остаться в нем и подождать, пока время пройдет. Помогите участникам определить это минимальное время T такое, что участники закончат в минимум K различных городах, или выведите -1, если решения нет. Обратите внимание, что между некоторыми городами может быть больше одной дороги. Выходные данные Выведите единственное число — минимальное время, в течение которого команды могут двигаться, чтобы закончить в хотя бы K различных городах, или выведите -1, если решения не существует. Если решение существует, результат будет не больше 1731311. Примечание В примере три команды начинают из города 5, две начинают из города 2. Если они будут двигаться 3 минуты, то возможно следующее: две команды в городе 2, одна команда в городе 5, одна команда в городе 3, и одна команда в городе 1. Видно, что всего есть четыре города, в которых команды закончили путешествие. | |
![]()
|
|
F. Почти перестановка
Потоки
*2200
Недавно Иван заметил массив a во время отладки одной программы. Сейчас Иван не может вспомнить этот массив полностью, но ему хотелось бы его восстановить, так как устранить баг до сих пор не получается, но, возможно, тот массив может помочь в устранении. Иван прекрасно помнит, что в массиве было n элементов, и каждый из них был не меньше 1 и не больше n. Также он помнит q фактов про массив. Существуют два типа фактов, которые помнит Иван: - 1 li ri vi — для каждого x, такого, что li ≤ x ≤ ri, ax ≥ vi;
- 2 li ri vi — для каждого x, такого, что li ≤ x ≤ ri, ax ≤ vi.
Также Иван считает, что этот массив был перестановкой, но в этом Иван совсем не уверен. Он хочет восстановить такой массив, который бы соответствовал q фактам, в которых Иван точно уверен, и был бы похож на перестановку. Формально, Иван определил стоимость (cost) массива как:  , где cnt(i) равно количеству вхождений i в массив. , где cnt(i) равно количеству вхождений i в массив.
Помогите Ивану определить минимально возможную величину cost массива, который бы соответствовал заданным фактам! Выходные данные Если факты противоречат друг другу и не существует массива, который бы им соответствовал, выведите -1. Иначе выведите минимально возможное значение величины cost. | |
![]()
|
|
F. Аня и книги
Потоки
Структуры данных
хэши
*2300
В любимом магазине Ани продается целых n книг по математике и экономике, пронумерованных от 1 до n. В каждой книге содержится неотрицательное число задач. Сегодня там проходит акция: любой подотрезок отрезка с l по r можно купить по фиксированной цене. Аня решила, что хочет купить непустой подотрезок, на который действует акция, такой, что в нем ровно на k задач по математике больше, чем по экономике. Заметьте, что k может быть положительным, отрицательным или нулем. К сожалению, Аня не уверена, на какой отрезок распространяется акция, но у нее есть q предположений. Для каждого из них она хочет заранее знать количество вариантов купить подотрезок, удовлетворяющий условию (ведь от этого зависит время, которое она потратит на выбор). Сейчас Аня слишком занята решением других задач, поэтому просит вашей помощи. Определите для каждого предположения, сколько существует подотрезков данного отрезка таких, что задач по математике там ровно на k больше, чем по экономике. Выходные данные Выведите q строк, в i-й из которых количество подходящих подотрезков для i-го предположения Ани. Примечание В первом примере Ане подойдут подотрезки [1;1], [2;2], [3;3], [2;4], если они попадают в отрезок, на который действует скидка, так как для них верно, что количество задач по математике на 1 больше, чем количество задач по экономике. Поэтому для каждого предположения мы должны посчитать количество этих подотрезков, являющихся частью данного отрезка. Отрезки [1;1] и [2;2] — подотрезки [1;2]. Отрезки [1;1], [2;2] и [3;3] — подотрезки [1;3]. Отрезки [1;1], [2;2], [3;3], [2;4] — подотрезки [1;4]. Отрезок [3;3] — подотрезок [3;4] | |
![]()
|
|
F. Распалиндруй!
Потоки
жадные алгоритмы
графы
*2500
Строка a длины m называется антипалиндромной тогда и только тогда, когда m четное, и для каждого i (1 ≤ i ≤ m) ai ≠ am - i + 1. У Ивана есть строка s из n строчных латинских букв; n четно. Он хочет построить некоторую строку t, которая будет антипалидромной перестановкой букв строки s. Также Иван определяет красоту индекса i как bi, а красоту строки t как сумму bi по всем таким индексам i, что si = ti. Помогите Ивану определить максимальную красоту строки t, которую он может получить. Выходные данные Выведите одно число — максимальную возможную красоту строки t. | |
![]()
|
|
E. Удаление отрезков
Потоки
Структуры данных
реализация
*2000
снм
У Васи есть массив целых чисел, состоящий из n элементов. Вася производит с массивом следующие операции: каждый раз он находит самый длинный отрезок подряд идущих одинаковых чисел (если таких несколько, то Вася выберет самый левый из них) и удаляет его из массива. Например, если массив Васи имеет вид [13, 13, 7, 7, 7, 2, 2, 2], то после одной операции массив примет вид: [13, 13, 2, 2, 2]. Определите количество описанных операций, которое произведёт Вася до того момента, как его массив станет пустым (то есть Вася удалит из него все элементы). Выходные данные Выведите количество операций, которые произведет Вася, чтобы удалить из массива все элементы. Примечание В первом примере Вася сначала удалит две пятёрки, стоящие во второй и третьей позициях. После этого массив будет выглядеть как [2, 2]. Во время второй операции Вася удалит две двойки, стоящие в первой и второй позициях. После этого массив станет пустым, и Вася закончит выполнение операций. Во втором примере Васе нужно пять операций, чтобы удалить все элементы из массива. Во время каждой операции он будет удалять самый левый элемент из массива. В третьем примере Васе нужно три операции, чтобы удалить все элементы из массива. Во время первой операции он удалит все числа 4, во время второй — все числа 100, а во время третьей — все числа 2. В четвёртом примере во время первой операции Вася удалит два первых числа 10. После этого массив примет вид [50, 10, 50, 50]. Затем во время второй операции Вася удалит два крайних правых числа 50, массив примет вид [50, 10]. Во время третьей операции — число 50, массив примет вид [10]. Во время последней четвертой операции он удалит единственное число 10. После этого массив Васи станет пустым. | |
![]()
|
|
G. Очередная задача про максимальный поток
Потоки
Структуры данных
графы
*2700
В этой задаче вам придётся иметь дело с очень специфичной ориентированной сетью (взвешенным ориентированным графом). Сеть состоит из двух частей: части A и части B. Каждая часть состоит из n вершин; i-ю вершину части A будем обозначать как Ai, а i-ю вершину части B — как Bi. Для каждого i (1 ≤ i < n) существует ориентированное ребро из Ai в Ai + 1, а также из Bi в Bi + 1. Пропускные способности этих рёбер заданы во входных данных. Также может быть несколько рёбер, ведущих из A в B (но нет таких рёбер, которые ведут из B в A). Вам необходимо посчитать величину максимального потока из A1 в Bn в данной сети. Пропускные способности рёбер, ведущих из Ai в Ai + 1, также могут иногда меняться, и вам нужно пересчитывать величину потока после этих изменений. Вся остальная часть сети фиксирована (не происходит никаких изменений в части B, никаких изменений рёбер, ведущих из A в B, никакие рёбра не добавляются и не удаляются). Посмотрите на пример и пояснение к нему, чтобы лучше понять структуру сети. Выходные данные Сначала выведите величину максимального потока в исходной сети. Затем выведите q чисел, i-е из которых должно быть равно величине максимального потока после i-го изменения. Примечание В примере до всех изменений сеть выглядит так:  | |
![]()
|
|
F. Параметрическая циркуляция
Бинарный поиск
Потоки
*3100
Вова недавно познакомился с таким комбинаторным объектом, как циркуляция в графе. Напомним определение: пусть задан ориентированный граф \(G = (V, E)\). Тогда циркуляцией \(f\) называется такой набор неотрицательных действительных чисел \(f_e\) (\(e \in E\)), что для любой вершины \(v \in V\) выполняется условие консервативности \(\)\sum\limits_{e \in \delta^{-}(v)} f_e = \sum\limits_{e \in \delta^{+}(v)} f_e\(\) где \(\delta^{+}(v)\) обозначает множество рёбер, входящих в вершину \(v\), а \(\delta^{-}(v)\) — множество рёбер, исходящих из вершины \(v\). Иными словами, в любую вершину входит столько же потока, сколько из неё исходит. Будем также называть допустимой \(lr\)-циркуляцией такую циркуляцию \(f\), что для любого ребра выполнено соотношение \(l_e \leq f_e \leq r_e\), где \(l_e\) и \(r_e\) для каждого ребра \(e \in E\) это два неотрицательных действительных числа, задающих нижнюю и верхнюю границу для величины циркуляции по ребру \(e\). Вова полон исследовательского духа, а ещё он не умеет вовремя останавливаться при обдумывании новых тем, с которыми он познакомился. Сейчас он размышляет над следующим естественным вопросом — пусть граф фиксирован, а каждая величина \(l_e\) и \(r_e\) сама по себе является линейной функцией действительного переменного \(t\): \(\)l_e(t) = a_e t + b_e\(\) \(\)r_e(t) = c_e t + d_e\(\) Обратите внимание, переменная \(t\) — общая для всех рёбер. Предположим, что \(t\) выбирается случайным образом из равномерного распределения на отрезке \([0, 1]\). Какова тогда вероятность, что в данном графе существует допустимая \(lr\)-циркуляция? Выходные данные Выведите единственное действительное число — вероятность того, что в данном графе существует допустимая \(lr\)-циркуляция при условии, что \(t\) выбирается из равномерного распределения на отрезке \([0, 1]\). Ваш ответ будет засчитан, если его абсолютная погрешность относительно ответа жюри не превосходит \(10^{-6}\). Примечание В первом тесте из условия циркуляция из условий консервативности следует, что величина \(f_e\) должна быть одинаковой по всем трём рёбрам. Вне зависимости от выбора \(t\) единственное допустимое значение циркуляции по последнему ребру — это \(4\), поэтому искомая вероятность есть \(\)P(4 \in [3, -4t + 7]~~\&~~4 \in [-2t + 5, t + 6]) = 0.25\(\) | |
![]()
|
|
D. Одноразовые камни
Бинарный поиск
Потоки
жадные алгоритмы
*1900
Много лягушек хотят пересечь реку. Река имеет ширину \(w\), но лягушки могут прыгать только на расстояние \(l\), причём \(l < w\). Кроме того, лягушки могут прыгать на расстояния, меньшие \(l\), но не на расстояния большие. К счастью, в реке есть камни, которые могут помочь пересечь реку. Камни расположены на целых расстояниях от берегов. На расстоянии \(i\) от берега, на котором сейчас находятся лягушки, находится \(a_i\) камней. Каждый камень может быть использован только одной лягушкой, после чего он тонет. Какое максимальное количество лягушек может пересечь реку, если они могут прыгать только по камням? Выходные данные Выведите одно целое число — максимальное количество лягушек, которые могут пересечь реку. Примечание В первом примере две лягушки могут использовать два разных камня на расстоянии \(5\), а ещё одна может использовать камни на расстояниях \(3\) и \(8\). Во втором примере то, что на расстоянии \(5\) находятся два разных камня, не улучшает ответ. Есть три разных пути: \(0 \to 3 \to 6 \to 9 \to 10\), \(0 \to 2 \to 5 \to 8 \to 10\), \(0 \to 1 \to 4 \to 7 \to 10\). | |
![]()
|
|
F. Минимальное k-покрытие
Потоки
графы
*2500
Задан двудольный неориентированный граф G = (U, V, E), U — множество вершин в первой доле, V — множество вершин во второй доле, E — множество ребер. Могут встречаться кратные ребра. Назовем некоторое подмножество его ребер 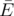 k-покрытием тогда и только тогда, когда в графе k-покрытием тогда и только тогда, когда в графе 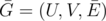 каждой вершине инциндентно не менее k ребер. Минимальным k-покрытием называется такое k-покрытие, что размер множества каждой вершине инциндентно не менее k ребер. Минимальным k-покрытием называется такое k-покрытие, что размер множества  минимален. минимален. Ваша задача — найти минимальное k-покрытие для каждого 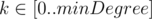 , где minDegree — это минимальная степень какой-либо вершины в графе G. , где minDegree — это минимальная степень какой-либо вершины в графе G. Выходные данные Для каждого 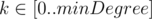 выведите подмножество ребер (минимальное k-покрытие) в отдельной строке. выведите подмножество ребер (минимальное k-покрытие) в отдельной строке. Первое число cntk в k-й строке — это количество ребер в минимальном k-покрытии графа. Затем идут cntk целых чисел — оригинальные номера ребер, которые принадлежат минимальному k-покрытию, эти номера должны быть попарно различны. Ребра пронумерованы от 1 до m в таком же порядке, в котором встречаются во входных данных. | |
![]()
|