| | | |
|
SNTP
Разбор случаев
Для того чтобы компьютеры поддерживали актуальное время, они могут обращаться к серверам точного времени SNTP (Simple Network Time Protocol). К сожалению, компьютер не может просто получить время у сервера, потому что информация по сети передаётся не мгновенно: пока сообщение с текущим временем дойдёт до компьютера, оно потеряет свою актуальность. Протокол взаимодействия клиента (компьютера, запрашивающего точное время) и сервера (компьютера, выдающего точное время) выглядит следующим образом:
1) Клиент отправляет запрос на сервер и запоминает время отправления A (по клиентскому времени).
2) Сервер получает запрос в момент времени B (по точному серверному времени) и отправляет клиенту сообщение, содержащее время B.
3) Клиент получает ответ на свой запрос в момент времени C (по клиентскому времени) и запоминает его. Теперь клиент, из предположения, что сетевые задержки при передаче сообщений от клиента серверу и от сервера клиенту одинаковы, может определить и установить себе точное время, используя известные значения A, B, C.
Вам предстоит реализовать алгоритм, с точностью до секунды определяющий точное время для установки на клиенте по известным A, B и C. При необходимости округлите результат до целого числа секунд по правилам арифметики (в меньшую сторону, если дробная часть числа меньше ½, иначе в большую сторону).
Возможно, что, пока клиент ожидал ответа, по клиентскому времени успели наступить новые сутки, однако известно, что между отправкой клиентом запроса и получением ответа от сервера прошло менее 24 часов.
Программа получает на вход три временные метки A, B, C, по одной в каждой строке. Все временные метки представлены в формате «hh:mm:ss», где «hh» – это часы, «mm» – минуты, «ss» – секунды. Часы, минуты и секунды записываются ровно двумя цифрами каждое (возможно, с дополнительными нулями в начале числа).
Программа должна вывести одну временную метку в формате, описанном во входных данных, – вычисленное точное время для установки на клиенте. В выводе не должно быть пробелов, пустых строк в начале вывода.
| Ввод |
Вывод |
Примечание |
15:01:00
18:09:45
15:01:40 |
18:10:05 |
Клиент отправил запрос в 15:01:00 по своим часам, сервер получил запрос в 18:09:45 по своим часам. Клиент получил ответ в 15:01:40, в этот момент точное время будет 18:10:05. |
| |
![]()
|
|
Часы
Условный оператор
Задачи на моделирование
Разбор случаев
Наручные часы на электронных чернилах могут показывать текущее время в нескольких разных формах. Одна из форм - это имитация механических часов со стрелками. Циферблат часов разделен на 12 больших часовых делений, а каждое из них - на 5 малых делений. Угол между малыми делениями на циферблате равен 6. Для экономии энергии перерисовка изображения происходит один раз в минуту, когда необходимо переместить минутную стрелку. Часовая стрелка также движется дискретно, перемещаясь через каждые 12 минут на одно малое деление. Таким образом в 12:35 часовая стрелка будет указывать на 2-е малое деление справа от 12 часов, а минутная будет указывать на 7 часов. Угол между стрелками в этот момент равен 162º. В 12:36 часовая стрелка переместится на 3-е малое деление после 12 часов, а минутная — на следующее малое деление после 7 часов. Угол между стрелками часов при этом не изменится.
Напишите программу, которая вычисляет величину "внутреннего" (меньшего) угла между часовой и минутной стрелкой в заданный момент времени.
Первая строка ввода содержит два целых числа, разделенных одним пробелом — время на часах, часы H и минуты M (\(1 <= H <= 12, 0 <= M <= 59\)).
Вывести одно целое число в диапазоне от 0 до 180 — величину угла между стрелками в градусах.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
12 35 |
162 |
| |
![]()
|
|
Комфортабельные коровы
Очередь
Разбор случаев
Пастбище Фермера Юрика может рассматриваться как огромная 2D-решётка ячеек (шахматная доска). Изначально пастбище пустое.
Фермер Юрик добавит N (\(1<=N<=10^5\)) коров на пастбище одну за другой. i-ая корова займёт ячейку (xi,yi), которая отличается от ячеек, занятых всеми другими коровами (\(0<=x_i,y_i<=1000\)).
Корова называется "комфортабельной", если она имеет ровно трёх соседей по горизонтали и вертикали. Комфортабельные коровы дают меньше молока, поэтому Фермер Юрик хочет добавлять коров пока нет комфортабельных (включая ту которую он добавит). Заметим, что добавляемые коровы не обязательно должны иметь координаты x и y в интервале \(0…1000\).
Для каждого i в интервале \(1…N\), выведите минимальное количество коров, которое он должен добавить, чтобы не осталось комфортабельных коров, если считать, что на пастбище находятся только коровы \(1…i\).
Входные данные
Первая строка содержит целое число N. Каждая из следующих N строк содержит по 2 разделённых пробелом целых числа (x, y), указывающих координаты ячейки с коровой.
Выходные данные
Минимальное количество коров, которое Фермер Юрик должен добавить, для каждого i в интервале \(1…N\), на отдельной строке.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
9
0 1
1 0
1 1
1 2
2 1
2 2
3 1
3 2
4 1 |
0
0
0
1
0
0
1
2
4 |
Для i=4, Фермер Юрик должен добавить корову в позицию (2,1),
чтобы сделать корову в позиции (1,1) некомфортабельной.
Для i=9, лучшее что Фермер может сделать - добавить коров в позиции (2,0), (3,0), (2,−1), (2,3).
|
| |
![]()
|
|
Нью-Кэпитал
Обход в ширину
Разбор случаев
В стране из предыдущей задачи много специалистов не только по защите детей, но и про проектированию городов. Поэтому, чтобы решить проблему пробок в перенаселенной столице раз и навсегда, было решено построить новую столицу и перенести все правительство туда. Сказано — сделано.
Улицы в новой столице образуют правильную прямоугольную сетку, в которой все улицы пересекаются ровно через одну местную единицу длины. Вертикально идущие улицы называются улицами, а горизонтально идущие — аллеями. Всего в городе получилось 2000 улиц и 2000 аллей, поэтому, чтобы не придумывать много новых названий, их все просто пронумеровали. Улицы пронумеровали с запада на восток числами от −1000 до 999, а аллеи — с юга на север, тоже числами от −1000 до 999. Центром города считаются кварталы на пересечении улиц и аллей с номерами от −100 до 100.
Чтобы увеличить пропускную способность дорог в городе, было решено сделать все улицы и аллеи односторонними. По улицам с четными номерами разрешается ехать только с севера на юг, а по улицам с нечетными номерами — только с юга на север. Аналогично, по аллеям с четными номерами можно ехать только с востока на запад, а с нечетными — только с запада на восток.
Сколько местных единиц длины придется проезжать мэру новой столицы каждый вечер, возвращаясь из мэрии города домой? И мэрия, и дом мэра находятся в центре города. Мэр едет домой кратчайшим путем, соблюдая, впрочем, правила дорожного движения.
Входные данные
В первой строке даны два числа x1 и y1 — номер улицы и номер аллеи, на пересечении которых находится мэрия. В второй строке даны два числа x2 и y2 — номер улицы и номер аллеи, на пересечении которых находится дом мэра. Все числа целые и не превосходят по модулю 100.
Выходные данные
Выведите одно число: длину кратчайшего пути от мэрии до дома мэра на автомобиле.-
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
0 0
1 1 |
4 |
| 2 |
3 5
2 4 |
4 |
| |
![]()
|
|
Выбор конфет
Одномерные массивы
Разбор случаев
Скоро у Гарри Поттера день рождения! Гермиона хочет приготовить для него необычный подарок. Она хочет подарить Гарри набор из n волшебных конфет. Каждая конфета характеризуется её вкусом — целым числом ti . Удовольствие , которое получит Гарри от набора конфет — это сумма вкусов всех конфет в этом наборе. Обратите внимание, что вкусы конфет, как и удовольствие Гарри, не обязательно должны быть положительными.
У Гермионы есть огромная коробка с конфетами, в которой для каждого целого числа t от - 109 до 109 лежит ровно одна конфета со вкусом t . Гермиона хочет взять из этой коробки n конфет, из которых будет состоять набор для Гарри.
Гермиона хочет, чтобы Гарри получил от подаренного ему набора конфет удовольствие, в точности равное целому числу s . Помогите ей выбрать подходящий набор или определите, что это невозможно.
Входные данные
Первая строка входных данных содержит единственное целое число n ( 1 ≤ n ≤ 100 ) — количество конфет, которое хочет Гермиона положить в набор. Вторая строка входных данных содержит единственное целое число s ( - 109 ≤ s ≤ 109 ) — удовольствие, которое должен получить Гарри от набора.
Выходные данные
Если составить желаемый набор из имеющихся у Гермионы конфет невозможно, выведите « NO ». Иначе, в первой строке выведите « YES », а во второй строке в произвольном порядке n чисел — вкусы конфет в искомом наборе. Если правильных ответов несколько, выведите любой из них.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
10 |
YES
500000000 -500000000 10 |
| |
![]()
|
|
Проверка автомата
Разбор случаев
Андрюша — юный инженер. Сейчас он конструирует современный автомат для преобразования чисел. В процессе конструирования к автомату добавляются все новые и новые блоки, и Андрюше интересно, как будет работать автомат после каждой такой модификации.
Автомат представляет собой последовательность из блоков двух типов: максимизаторов и минимизаторов . На каждом блоке написано некоторое натуральное число x . Максимизатор принимает на вход натуральное число a и подает на выход число max ( x , a ) . Минимизатор принимает на вход натуральное число a и подает на выход число min ( x , a ) .
Автомат работает следующим образом: он принимает некоторое натуральное число, которые подает на вход первому блоку, затем то, что получилось на выходе у первого блока, подается на вход второго блока, и так далее. В итоге автомат возвращает число, получившееся на выходе у последнего блока. Иначе говоря, автомат просто последовательно пропускает данное ему число через все блоки.
Изначально в автомате нет ни одного блока, и он просто возвращает число, которое принимает.
Андрюша последовательно выполняет действия с автоматом. Действия бывают трех типов:
- Добавить в конец последовательности блоков автомата максимизатор, на котором написано число x .
- Добавить в конец последовательности блоков автомата минимизатор, на котором написано число x .
- Подать на вход автомату число x . В этом случае Андрюша хочет узнать, что автомат вернет на выход.
Андрюша уже запланировал, какие действия и в каком порядке он будет совершать. Напишите программу, которая определит результат работы автомата Андрюши, чтобы он мог убедиться в его исправности!
Входные данные
Первая строка входных данных содержит единственное целое число n ( 1 ≤ n ≤ 4·105 ) — суммарное количество действий Андрюши.
В каждой из следующих n строк содержится по два целых числа t и x ( 1 ≤ t ≤ 3 , 1 ≤ x ≤ 109 ), где t — это тип очередного действия. Если t = 1 , то Андрюша хочет добавить к автомату максимизатор, на котором написано число x . Если t = 2 , то Андрюша хочет добавить к автомату минимизатор, на котором написано число x . Если t = 3 , то Андрюша хочет подать на вход автомату число x и узнать, что получится на выходе.
Выходные данные
Для каждого действия третьего типа выведите в отдельной строке одно число, которое должно получиться на выходе автомата после этого действия.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
7
3 5
1 5
3 2
3 7
2 7
3 8
3 6 |
5
5
7
7
6 |
| |
![]()
|
|
Карты на троих
Простые игры
Разбор случаев
Антонин, Бальбин и Цезарь играют в игру "Карты на троих", алгоритм которой следующий:
- сначала у каждого из трех игроков есть колода, состоящая из некоторого количества карт. На каждой карточке написана буква a, b или c. Порядок карт в колодах не может быть изменен;
- игроки ходят по очереди. Антонин ходит первым;
- если в колоде текущего игрока есть хотя бы одна карта, ему необходимо сбросить верхнюю карту в колоде;
- следующий ход переходит к игроку, имя которого начинается с буквы на сброшенной карте (a - Антонин, b - Бальбин, c - Цезарь);
- если колода текущего игрока пуста, игра заканчивается, и текущий игрок выигрывает игру.
Вам выдаются начальные колоды игроков (Sa, Sb, Sc). Состояние колоды Антонина записано в строке Sa, где i-й (\(1<=i<=len(S_a)\)) символ это буква в i-й карты в колоде. Строка Бальбина (Sb) и строка Цезаря (Sс) описываются таким же образом.
Определите победителя в игре.
Формат входных данных
На вход подаются три ненулевых строки Sa, Sb и Sc, каждая с новой строки. Длина каждой строки не более 100 символов. Каждая строка состоит только из букв a, b или c.
Формат выходных данных
Если выиграл Антонин. то выведите букву A, если Бальбин - букву B, если Цезарь - букву C.
Примечание
В первом тестовом примере игра будет развиваться следующим образом:
Антонин сбрасывает верхнюю карту своей колоды, a. Антонин делает следующий ход.
Антонин сбрасывает верхнюю карту своей колоды, с. Цезарь следующий.
Цезарь сбрасывает верхнюю карту своей колоды, с. Цезарь следующий.
Цезарь сбрасывает верхнюю карту своей колоды: a. Антонин делает следующий ход.
Антонин сбрасывает верхнюю карту своей колоды: a. Антонин делает следующий ход.
Колода Антонина пуста. Игра заканчивается, и Антонин выигрывает игру.
| |
![]()
|
|
Плот
Разбор случаев
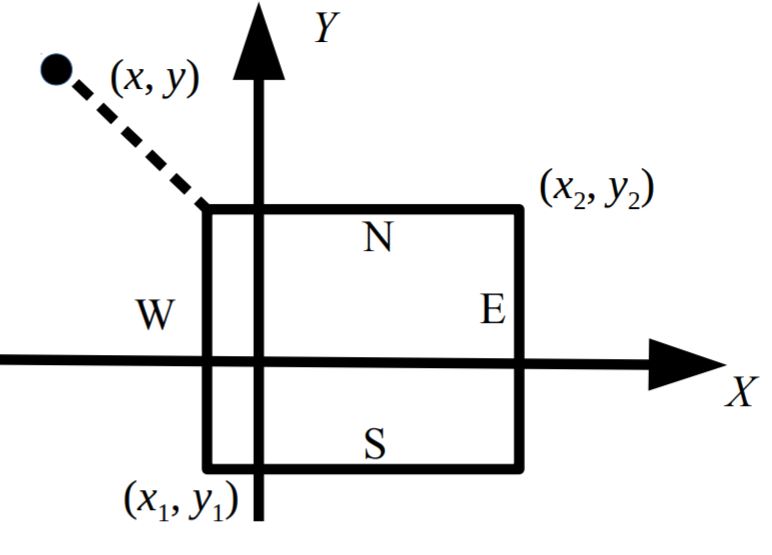
Посередине озера плавает плот, имеющий форму прямоугольника. Стороны плота направлены вдоль параллелей и меридианов. Введём систему координат, в которой ось OX направлена на восток, а ось ОY – на север. Пусть юго-западный угол плота имеет координаты (x1, y1), северо-восточный угол – координаты (x2, y2).
Пловец находится в точке с координатами (x, y). Определите, к какой стороне плота (северной, южной, западной или восточной) или к какому углу плота (северо-западному, северо-восточному, юго-западному, юго-восточному) пловцу нужно плыть, чтобы как можно скорее добраться до плота.
Программа получает на вход шесть чисел в следующем порядке: x1, y1 (координаты юго-западного угла плота), x2, y2 (координаты северо-восточного угла плота), x, y (координаты пловца). Все числа целые и по модулю не превосходят 100. Гарантируется, что x1 < x2, y1 < y2, x ≠ x1, x ≠ x2, y ≠ y1, y ≠ y2, координаты пловца находятся вне плота.
Если пловцу следует плыть к северной стороне плота, программа должна вывести символ «N», к южной – символ «S», к западной – символ «W», к восточной – символ «E». Если пловцу следует плыть к углу плота, нужно вывести одну из следующих строк: «NW», «NE», «SW», «SE».
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
-1
-2
5
3
-4
6 |
NW |
 |
| |
![]()
|
|
Делимость
Разбор случаев
Сегодня в школе на уроке математики проходят делимость. Чтобы продемонстрировать свойства делимости, учитель выписал на доске все целые числа от 1 до
N в несколько групп, при этом если одно число делится на другое, то они обязательно оказались в разных группах. Например, если взять N = 10, то получится 4 группы.
- Первая группа: 1.
- Вторая группа: 2, 7, 9.
- Третья группа: 3, 4, 10.
- Четвёртая группа: 5, 6, 8.
Вы уже догадались, что, поскольку любое число делится на 1, одна группа всегда будет состоять только из числа 1, но в остальном подобное разбиение можно выполнить различными способами. От вас требуется определить минимальное число групп, на которое можно разбить все числа от 1 до N в соответствии с приведённым выше условием.
Программа получает на вход одно натуральное число N, не превосходящее 109, и должна вывести одно число – искомое минимальное количество групп.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
10 |
4 |
| |
![]()
|
|
Уравнения математической магии
Битовые операции
Разбор случаев
Колоссально! — воскликнул горбоносый. — Программист! Нам нужен именно программист.
Аркадий и Борис Стругацкие, Понедельник начинается в субботу
Изучая книгу «Уравнения математической магии» Роман Ойра-Ойра и Кристобаль Хунта обнаружили интересное уравнение: a−(a⊕x)−x=0 для заданного a, где знаком ⊕ обозначено побитовое исключающее ИЛИ (XOR) двух чисел (эта операция обозначается как ^ или xor во многих современных языках программирования). Поскольку данное уравнение предназначалось для решения на машине Алдан-3, все вычисления производились над целыми неотрицательными числами по модулю 232. Ойра-Ойра быстро нашел x, являющееся решением, однако Кристобалю Хунте результат Ойры-Ойры показался недостаточно интересным, поэтому он спросил коллегу, сколько всего существует решений данного уравнения. Так как все вычисления производятся по модулю 232, Кристобаля Хунту интересует количество таких решений x, что 0 ≤ x ≤ 232. Такая задача оказалась для Ойры-Ойры слишком сложной, поэтому он обратился за помощью к Вам.
Входные данные
В первой строке задано одно целое число a (0 ≤ a ≤ 232−1).
Выходные данные
Выведите одно целое число — количество неотрицательных решений уравнения.
Примечание
Определим операцию побитового ИЛИ (XOR). Пусть даны два целых неотрицательных числа x и y, рассмотрим их двоичные записи (возможно с ведущими нулями): xk...x2x1x0 и yk...y2y1y0. Здесь xi это i-й бит числа x, а yi это i-й бит числа y. Пусть r=x⊕y — результат операции XOR над числами x и y. Тогда двоичной записью r будет rk...r2r1r0, где:
\(r_i = \begin{cases} 1, & \quad \text{если } x_i \neq y_i \\ 0, & \quad \text{если } x_i = y_i \end{cases} \)
В первом примере решениями уравнения являются 0 и 2147483648=231, так как 0−(0⊕0)−0=0−0−0=0 и 0−(0⊕ 2147483648)−2147483648=−4294967296=−232=0 по модулю 232.
Во втором примере решениями уравнения являются 0, 2, 2147483648=231 и 2147483650=231+2.
В третьем примере решениями являются все x, для которых выполнено 0 ≤ x ≤ 232.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
0 |
2 |
| 2 |
2 |
4 |
| 3 |
4294967295 |
4294967296 |
| |
![]()
|
|
Голосование
Циклы
Разбор случаев
Конструктив
Коротышки решили взять в полет на Луну либо Незнайку либо Пончика. Не сумев договориться, они решили проголосовать. Незнайка и Пончик наблюдают краткий отчет о голосовании. Коротышки показывают Незнайке и Пончику соотношение текущего количества голосов, полученных Незнайкой и Пончиком, но не фактическое количество голосов. Незнайка и Пончик посмотрели отчет N раз, и когда они смотрели его в i-й (1<=i<=N) раз, соотношение было Pi:Ni. Известно, что Незнайка и Пончик имели хотя бы один голос, когда впервые увидели отчет. Найдите минимально возможное общее количество голосов, полученных Незнайкой и Пончиком, когда они проверили отчет в N-й раз. Можно предположить, что количество голосов, полученных Незнайкой и Пончиком, никогда не уменьшается.
Входные данные
В первой строке задается целое число N (1<=N<=1000). В следующих N строках записано по 2 числа Pi и Ni (1<=Pi,Ni<=1000). Pi и Ni - взаимно простые числа.
Выходные данные
Выведите минимально возможное общее количество голосов. Гарантируется, что правильный ответ - не более 1018.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
3
2 3
1 1
3 2 |
10 |
Количество голосов, полученных Пончиком и Незнайкой, изменяется так 2,3 → 3,3 → 6,4.
Общее количество голосов в конце составляет 10, что является минимально возможным числом. |
| 2 |
4
1 1
1 1
1 5
1 100 |
101 |
Возможно, что ни Пончик ни Незнайка не получили голосов между моментом, когда они смотрели отчет, и моментом, когда они смотрели его в следующий раз. |
| 3 |
5
3 10
48 17
31 199
231 23
3 2 |
6930 |
|
| |
![]()
|
|
Социальное дистанцирование I
Условный оператор
Простые задачи на перебор
Разбор случаев
Ужасная болезнь поражает коров. Фермер Джон хочет их защитить.
Амбар ФД - это узкое длинное здание, содержащее N стойл в ряд (2≤N≤105). Некоторые из этих стойл уже заняты коровами, некоторые - свободны. Прочитав о необходимости социального дистанцирования, ФД хочет максимизировать D, где D, это расстояние между двумя ближайшими занятыми стойлами. Например, если стойла 3 и 8 ближайшие, которые заняты, тогда D=5.
Две новых коровы пополнили стадо ФД и он должен решить, в какое не занятое стойло разместить каждую из них. Определите, ка к он должен разместить этих коров, чтобы в результате D, стало максимальным из возможных. ФД не может передвигать никакую из имеющихся коров, он может только назначить стойла новым коровам.
Входные данные
Первая строка ввода содержит N. Следующая строка содержит строку длиной N из 0 и 1, описывающая последовательность стойл в амбаре. 0 означает пустое стойло, 1 означает занятое стойло. В строке имеется как минимум два нуля, что достаточно для размещения двух коров.
Выходные данные
Выведите наибольше значение D (наименьшее расстояние между двумя занятыми стойлами), которое ФД может получить добавлением двух новых коров оптимальным образом.
Примеры
| № |
Входные данные |
Выходные данные |
|
| 1 |
14
10001001000010 |
2 |
В этом примере ФД может добавить коров так: 10x010010x0010 где x показывает новых коров. В этом случае D=2. Невозможно разметить коров так, чтобы получить D больше. |
| |
![]()
|
|
Лягушки
Разбор случаев
Три лягушки сидят на числовой прямой в трёх различных точках с целочисленными координатами a, b, c. Лягушки боятся отступать слишком далеко друг от друга, поэтому прыгать может только одна из крайних лягушек (такая, что слева или справа от нее нет других лягушек) и только в целочисленную точку между двумя другими лягушками, если такая есть. Заметим, что в некоторых положениях ни одна из лягушек прыгнуть не может, назовем их стабильными .
Требуется по заданному начальному положению лягушек определить минимальное и максимальное число прыжков, которые могут совершить лягушки, пока не попадут в какое-нибудь стабильное положение.
Входные данные
В трёх строках заданы три различных целых числа - a, b, c (1 <= a, b, c <= 1018), исходные позиции лягушек.
Обратите внимание, что входные данные могут быть больше, чем возможное значение 32-битной целочисленной переменной, поэтому необходимо использовать 64-битные целочисленные типы данных (тип int64 в языке Pascal, тип long long в C и C++, тип long в Java и C#). Язык Python будет корректно работать и с типом int.
Выходные данные
Выведите два числа - минимальное и максимальное число прыжков, за которое лягушки могут достичь стабильного состояния.
Примечание
В первом примере из условия лягушка с позиции 4 может прыгнуть на позицию 2 и образовать стабильное положение (1,2,3). Можно показать, что больше одного прыжка они сделать не смогут.
Во втором тесте из условия лягушка с позиции 1 может прыгнуть на позицию 4, а затем лягушка с позиции 10 может прыгнуть на позицию 3, тем самым придя в стабильное положение (2,3,4) за два прыжка. Можно показать, что больше 7 прыжков по описанным правилам лягушки сделать не могли.
В третьем тесте из условия лягушки уже находятся в стабильном положении, поэтому прыгать не смогут.
В четвёртом тесте из условия лягушка с позиции 1 может прыгнуть на позицию 4, а затем лягушка с позиции 5 может прыгнуть на позицию 3, тем самым придя в положение (2,3,4) за два прыжка. Можно показать, что больше двух прыжков лягушки сделать не могли.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1
3
4
|
1
1
|
| 2 |
1
10
2
|
2
7
|
| 3 |
1
2
3
|
0
0
|
| 4 |
2
1
5
|
2
2
|
| |
![]()
|
|
Счастливчики
Условный оператор
Разбор случаев
Вам дали сумму денег в рублях и попросили разделить эту сумму между всеми детьми. Назовем Счастливчиками тех детей, которые получат ровно по 8 рублей при дележе денег по следующим правилам:
- Все деньги должны быть распределены.
- Каждый должен получить как минимум 1 рубль.
- Никто не должен получить 4 рубля (это совсем не счастливая сумма).
Определите максимальное количество Счастливчиков, если вы разделите деньги в соответствии с вышеупомянутыми правилами. Если нет способа разделить деньги, верните -1.
Входные данные
В первой строке записана сумма денег (money - целое число), которую вам дали. Вторая строка содержит количество детей (children - целое число), между которыми необходимо разделить данную сумму.
Ограничения
1 <= money <= 2002 <= children <= 30
Выходные данные
Выведите максимальное количество Счастливчиков.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
20
3 |
1 |
| 2 |
16
2 |
2 |
| |
![]()
|
|
Не летное положение
Разбор случаев
Три скворца сидят на ветке дерева. Ветку дерева будем считать числовой прямой. С учетом этого, можно сказать, что скворцы сидят в трёх разных точках с целочисленными координатами a, b, c. Когда скорцам становится скучно, один из крайних скворцов перелетает на другое место (скворец считается крайним, если слева или справа нет другого скворца). Причем, из-за того, что скворцы не хотят улетать друг от друга слишком далеко, скворец, который решил сменить положение, перелетает только в целочисленную точку между двумя другими скворцами, если такая есть. Скворцы могут менять свое положение до тех пор пока их положение не станет "не летным". "Не летным" называется положение, при котором ни один из скорцов не может перелететь и сесть между двумя другими в целочисленную точку.
По начальному положению скворцов определите минимальное и максимальное число перелетов, которые могут совершить скворцы, пока не попадут в какое-нибудь "не летное" положение.
Входные данные
В трёх строках заданы три различных целых числа - a, b, c (1 <= a, b, c <= 1018), исходные позиции скворцов.
Выходные данные
Выведите два числа - минимальное и максимальное число перелетов, за которое скворцы могут достичь "не летного" положения.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1
3
4
|
1
1
|
| 2 |
1
10
2
|
2
7
|
| 3 |
1
2
3
|
0
0
|
| 4 |
2
1
5
|
2
2
|
| |
![]()
|
|
Kotlin Island
Разбор случаев
Задача на реализацию
There is an urban myth that Peter the Great wanted to make a rectangular channel-grid engineering masterpiece not only from Vasilyevskiy island, but also from Kotlin island (where the town of Kronstadt is located nowadays).
The following mathematical model was (allegedly) presented to the tsar. The island is considered a rectangular grid h cells high and w cells wide. Each cell is dry land initially but can become water.
Technologies of those days allowed engineers to dig a channel across the entire island. In that case an entire row or an entire column of cells became water. If some of these cells already were water, their status did not change.
Your task is to propose a plan of the island which has exactly n connected components of dry land cells.
Input
The only line of the input contains three integers h, w, and n — grid’s height, width and the desired number of connected components (1 ≤ h, w ≤ 100; 1 ≤ n ≤ 109 )
Output
If there is no valid plan containing n connected components, output a single word “Impossible”. Otherwise output h lines of length w depicting the plan. Dot (‘.’) represents a dry land cell, hash (‘#’) represents a water cell.
| Input |
Output |
| 3 5 4 |
..#..
#####
..#.. |
| 2 1 1 |
# . |
| 5 3 10 |
Impossible |
| |
![]()
|
|
Auxiliary Project
Разбор случаев
Вывод формулы
Anna has just finished her course project. She has a lot of seven-segment LED displays as leftovers and a small power source. Each display consumes power proportionally to the number of lit segments, e.g. ‘9’ consumes twice more power than ‘7’.

Anna wonders what is the maximum possible sum of digits she is able to achieve, if her power source is able to light n segments, and she wants to light exactly n segments.
Input
The single line of the input contains one integer n — the number of segments that should be lit (2 ≤ n ≤ 106 ).
Output
Output a single integer — the maximum possible sum of digits that can be displayed simultaneously.
| Input |
Output |
| 4 |
4 |
| 7 |
11 |
| 6 |
14 |
In the first example, a single ‘4’ should be displayed (‘7’ has greater value, but has only three segments). In the second example ‘4’ and ‘7’ should be displayed, in the third one — two ‘7’s.
| |
![]()
|
|
Падающее домино
Структуры данных
Префиксные суммы(минимумы, ...)
Разбор случаев
Вася обожает выставлять сложные фигуры из костяшек домино и, толкнув одну из них, смот- реть, как вся конструкция падает. Однако, он сделал уже так много фигур, что решил придумать что-то новое.
Для своей новой идеи он использует костяшки не только длиной 2, но и более длинные (и более короткие). Все костяшки выстраиваются в одну линию на расстоянии 1, а цель игры опрокинуть все костяшки толкнув наименьшее количество костяшек.
Каждую костяшку можно толкнуть влево или вправо, падая она опрокидывает все костяшки, находящиеся на расстоянии строго меньшем высоты падающей костяшки. При этом те костяшки, которые упали в результате падения на них других костяшек также падают в ту же сторону и, в свою очередь, могут опрокидывать и другие костяшки и так далее.
Формат входных данных
В первой строке записано натуральное число N (0 <= N <= 1 000 000) количество костяшек. Во второй строке записано N натуральных чисел Hi (1 <= Hi <= 1 000 000) высоты костяшек.
Формат выходных данных
Выведите число M наименьшее количество костяшек, которые нужно толкнуть, чтобы вся конструкция упала.
В следующих M строках выведите описание костяшек, которые необходимо толкнуть: номер костяшки (нумерация начинается с единицы и идет слева-направо), а также направление толчка: букву L для толчка влево и R для толчка вправо. Номер костяшки и букву разделяйте пробелом.
Порядок вывода костяшек, которые нужно толкнуть, может быть произвольным. Если решений несколько выведите любое из них
Система оценки
Решения, верно работающие при N <= 1000, будут набирать не менее половины баллов.
| Ввод |
Вывод |
6
1 2 1 4 1 3 |
1
6 L |
7
1 2 4 1 2 3 2 |
2
3 R
2 L |
Замечание
В первом примере последняя костяшка толкается влево, опрокидывая костяшки с номерами 4 и 5 (их высоты 4 и 1 соответственно). Костяшка номер 4 также падает налево и опрокидывает костяшки с номерами 1, 2 и 3.
Во втором примере костяшка номер 3 толкается вправо, опрокидывая костяшки номер 4, 5 и 6.
Костяшка номер 6 также падает вправо и опрокидывает костяшку номер 7. После этого костяшка
номер 2 толкается влево и опрокидывает костяшку номер 1.
| |
![]()
|
|
ПТИЦЫ
Разбор случаев
Всеволод Юрьевич устроился работать охранником на склад. Работа монотонная, и от скуки Всеволод Юрьевич считает ворон и других птиц, пролетающих мимо будки охраны. За годы работы он обнаружил следующую закономерность. Вороны летают поодиночке, начиная с 8:00 утра с периодичностью P1 минут, а после 8:00 вечера летать перестают. Утки пролетают стайками по N штук, начиная с 10:00 утра, с периодичностью P2 минут и перестают летать после 5:00 вечера. Голуби летают поодиночке с 7:00 утра до 8:00 вечера с периодичностью P3 минут. Три раза в день Всеволоду Юрьевичу приходится отвлечься от своего занятия ровно на полтора часа, чтобы принять на склад товар. Приемка начинается ровно в 11:00, 15:00 и 17:00. Сколько птиц (M) Всеволод Юрьевич насчитает за смену, если смена начинается в 6:00 утра и заканчивается в 6:00 утра на следующий день?
Во всех временных интервалах левый конец входит в него, а правый - нет. Например, одна из приемок начинается в 11:00 и Всеволод Юрьевич не считает птиц пролетающих в моменты с 11:00 до 12:29 включительно, а птиц, пролетающих в 12:30 - считает.
Формат входных данных
В строке указываются 4 целых положительных числа не превышающих 10000 каждое: P1, P2, N, P3, разделенные пробелом.
Формат выходных данных
В единственной строке указывается целое число M – количество птиц, которых Всеволод Юрьевич насчитает за смену при указанных условиях входа.
| Ввод |
Вывод |
| P1 P2 N P3 |
M |
| 23 57 5 7 |
123 |
| |
![]()
|
|
Два массива
Сортировка слиянием
Разбор случаев
Вывод формулы
Алиса со своим отцом профессором Селезневым записывают на листочке числа определенной последовательности. У Алисы каждый i-й член последовательности равен i2, у профессора Селезнева i-й член последовательности равен i3. Они решили создать новую возрастающую последовательность путем объединения двух своих последовательностей. При этом, если в обоих последовательностях есть одинаковое число, то в новой последовательности оно присутствует только один раз.
Алиса и профессор просят вас угадать i-е число в новой объединенной последовательности.
Входные данные
В единственной строке входного файла дано натуральное число i (1 <= i <= 107).
Выходные данные
Выведите i-е число новой последовательности.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1 |
1 |
| 2 |
2 |
4 |
| 3 |
4 |
9 |
| |
![]()
|
|
Помогаем природе
Разбор случаев
Разбор случаев
Участникам, использующим язык Python3, рекомендуется отправлять решения на проверку с использованием интерпретатора PyPy3.
Маленький Леон живет в лесу. Недавно он заметил, что некоторые деревья возле его любимой тропинки засыхают, а другие наоборот слишком увлажнены. Леон очень любит свой лес, поэтому решил научиться контролировать уровень влажности почвы, чтобы спасти деревья.
Возле тропинки растут \(n\) деревьев, текущие уровни влажности которых заданы массивом \(a_1, a_2, \dots, a_n\). Леон научился трем способностям, которые помогут ему осушать и поливать почву.
-
Он может выбрать позицию \(i\) и уменьшить уровень влажности деревьев \(1, 2, \dots, i\) на \(1\).
-
Он может выбрать позицию \(i\) и уменьшить уровень влажности деревьев \(i, i + 1, \dots, n\) на \(1\).
-
Увеличить уровень влажности всех деревьев на \(1\).
Леон хочет узнать минимальное число действий, которое необходимо совершить, чтобы каждое дерево имело уровень влажности равный \(0\).
Формат входных данных
В первой строке вводится одно целое число \(n\) (\(1 \leq n \leq 200\,000\)).
Во второй строке вводятся \(n\) целых чисел \(a_1, a_2 \ldots a_n\) (\(-10^9 \leq a_i \leq 10^9\)) — изначальные уровни влажности деревьев.
Формат выходных данных
Выведите одно целое число — минимальное число действий.
В первом примере из условия достаточно \(2\) раза применить операцию прибавления \(1\) ко всему массиву.
Во втором примере из условия можно \(4\) раза применить операцию вычитания на префиксе длины \(3\) и получить массив \(6, 0, 3\).
После этого \(6\) раз применить операцию вычитания на префиксе длины \(1\) и \(3\) раза операцию вычитания на суффиксе длины \(1\). Итого, количество действий составит \(4 + 6 + 3 = 13\). Можно показать, что меньшим количеством действий обойтись нельзя, поэтому \(13\) — это ответ.
| |
![]()
|
|
Помогаем природе
Разбор случаев
Разбор случаев
Участникам, использующим язык Python3, рекомендуется отправлять решения на проверку с использованием интерпретатора PyPy3.
Маленький Леон живет в лесу. Недавно он заметил, что некоторые деревья возле его любимой тропинки засыхают, а другие наоборот слишком увлажнены. Леон очень любит свой лес, поэтому решил научиться контролировать уровень влажности почвы, чтобы спасти деревья.
Возле тропинки растут \(n\) деревьев, текущие уровни влажности которых заданы массивом \(a_1, a_2, \dots, a_n\). Леон научился трем способностям, которые помогут ему осушать и поливать почву.
-
Он может выбрать позицию \(i\) и уменьшить уровень влажности деревьев \(1, 2, \dots, i\) на \(1\).
-
Он может выбрать позицию \(i\) и уменьшить уровень влажности деревьев \(i, i + 1, \dots, n\) на \(1\).
-
Увеличить уровень влажности всех деревьев на \(1\).
Леон хочет узнать минимальное число действий, которое необходимо совершить, чтобы каждое дерево имело уровень влажности равный \(0\).
Формат входных данных
В первой строке вводится одно целое число \(n\) (\(1 \leq n \leq 200\,000\)).
Во второй строке вводятся \(n\) целых чисел \(a_1, a_2 \ldots a_n\) (\(-10^9 \leq a_i \leq 10^9\)) — изначальные уровни влажности деревьев.
Формат выходных данных
Выведите одно целое число — минимальное число действий.
В первом примере из условия достаточно \(2\) раза применить операцию прибавления \(1\) ко всему массиву.
Во втором примере из условия можно \(4\) раза применить операцию вычитания на префиксе длины \(3\) и получить массив \(6, 0, 3\).
После этого \(6\) раз применить операцию вычитания на префиксе длины \(1\) и \(3\) раза операцию вычитания на суффиксе длины \(1\). Итого, количество действий составит \(4 + 6 + 3 = 13\). Можно показать, что меньшим количеством действий обойтись нельзя, поэтому \(13\) — это ответ.
| |
![]()
|
|
Олег и двоичные последовательности
Обход в глубину
Применение обхода в глубину
Разбор случаев
Олег очень любит двоичные последовательности — последовательности из нулей и единиц. Совсем недавно он написал в тетради очередную двоичную последовательность из n элементов.
Для выписанной последовательности Олег посчитал Z-функцию.
Z-функцией последовательности s1, . . . , sn называется массив z[1..n], в котором:
• z[1] = 0;
• Если i > 1, то z[i] равно длине наибольшего общего префикса последовательности s и суффикса последовательности s, начинающегося с i-й позиции. Иначе говоря, z[i] равно максимальному k, такому что s1 = si , s2 = si+1, . . . , sk = si+k−1.
Например, для последовательности s = h0, 0, 1, 1, 0, 0, 1i Z-функция следующая: z = h0, 1, 0, 0, 3, 1, 0i.
Записав в тетради последовательность и ее Z-функцию, Олег лег спать. Пока он спал, его младший брат Егор прокрался в комнату и закрасил фломастером последовательность и некоторые значения Z-функции. Проснувшись, Олег заинтересовался, сколько различных двоичных последовательностей он мог вечером написать в тетради, чтобы незакрашенные значения Z-функции были правильными.
Найдите число искомых последовательностей и выведите его по модулю 109 + 7. Заметьте, что Олег мог и ошибиться при вычислении Z-функции, в этом случае ни одна последовательность не подходит и ответ равен 0.
Формат входных данных
В первой строке входного файла находится целое число n — длина исходной двоичной последовательности (1 ≤ n ≤ 1000). Во второй строке входного файла находятся n целых чисел z[1], . . . , z[n], где z[i] — значение Z-функции в позиции i, или −1, если значение в i-й позиции было закрашено (−1 ≤ z[i] ≤ n).
Формат выходных данных
В выходной файл выведите единственное число — остаток от деления числа подходящих двоичных последовательностей на число 109 + 7.
| Ввод |
Вывод |
3
0 0 1 |
2 |
4
0 0 1 0 |
0 |
3
0 3 -1 |
0 |
3
-1 -1 -1 |
8 |
Пояснение
В первом примере подходят последовательности {0, 1, 0 } и { 1, 0, 1 }.
Во втором примере не существует ни одной двоичной последовательности длины 4 с заданной Z-функцией.
В третьем примере z[2] = 3, что противоречит определению Z-функции, поэтому ответ 0.
В четвертом примере подходит любая двоичная последовательность длины 3.
| |
![]()
|
|
Телефонные номера
Строки
Разбор случаев
Задача на реализацию
Неотъемлемой частью программного обеспечения любого мобильного телефона является записная книжка. В самых первых мобильных телефонах в ней можно было хранить лишь имена абонентов и их телефонные номера. В более современных моделях в ней можно также хранить множество другой полезной информации — электронный адрес человека, его фотографию, ссылки на его страницы в социальных сетях и дату его рождения. Однако, при реализации даже самой простой версии этой программы, позволяющей работать только с телефонными номерами, разработчики иногда сталкиваются с некоторыми сложностями.
Будем считать, что любой телефонный номер состоит из 11 цифр и делится на три части, каждая из которых является числом без ведущих нулей. Первая часть состоит из одной, двух или трех цифр и является кодом страны, в которой этот телефон зарегистрирован. Вторая часть может состоять из трех, четырех или пяти цифр, и может являться или кодом региона, в котором зарегистрирован номер, или кодом мобильного оператора, которому этот номер принадлежит. Третья часть состоит из всех оставшихся цифр номера и является номером конкретного абонента.
При отображении телефонного номера на экране телефона, части этого номера принято отделять друг от друга различными символами так, чтобы номер было проще прочитать и запомнить. Так, перед кодом страны обычно ставится символ «+», код региона или оператора берется в скобки, номер абонента разделяется символами «-» на несколько частей. При этом, то, на сколько частей он разбивается, напрямую зависит от количества цифр в нем:
• если номер абонента состоит из трех цифр, то он представляет собой одну часть, состоящую из трех цифр;
• если номер абонента состоит из четырех цифр, то он разбивается на две части, каждая из которых состоит из двух цифр;
• если номер абонента состоит из пяти цифр, то он разбивается на две части, первая из которых состоит из трех цифр, а вторая — из двух;
• если номер абонента состоит из шести цифр, то он разбивается на три части, каждая из которых состоит из двух цифр;
• если номер абонента состоит из семи цифр, то он разбивается на три части, первая из которых состоит из трех цифр, а все остальные — из двух.
Естественно, что человек, заносящий новый номер в записную книжку своего телефона, не станет задумываться об этих правилах, а просто введет его как последовательность из 11 цифр. Однако, перед отображением номера на экране, программное обеспечение телефона должно выяснить, какая часть этого номера является кодом страны, какая — кодом региона или оператора, а какая — номером абонента, и отформатировать номер по правилам, описанным выше. Чтобы сделать эту задачу разрешимой, в память телефона записывается информация о том, какие в данный момент существуют коды государств и какие в этих государствах существуют коды операторов или регионов. Вам необходимо реализовать программу, которая, имея эту информацию, будет правильно форматировать номера, сохраненные в записной книжке телефона.
Формат входных данных
Первая строка файла содержит одно целое число n (1 ≤ n ≤ 100) — количество государств, информация про телефонные коды которых записана в память телефона. Далее следуют n описаний этих государств, разделенных переводами строк. Первая строка описания каждого государства содержит два целых числа c и k (1 ≤ c ≤ 999, 1 ≤ k ≤ 100) — телефонный код этого государства и количество операторов или регионов, существующих в этом государстве. Следующие k строк описания этого государства содержат целые числа, каждое из которых не меньше 100 и не больше 99999 — коды операторов или регионов, зарегистрированных в этом государстве.
Следующая строка входного файла содержит одно целое число m (1 ≤ m ≤ 10 000) — количество телефонных номеров, которые необходимо отформатировать. Следующие m строк содержат сами номера — строки, состоящие ровно из 11 цифр.
Гарантируется, что ни один данный вам номер невозможно разбить на код государства, код оператора или региона и номер абонента более, чем одним способом.
Формат выходных данных
Выведите номера, данные вам во входном файле, отформатированными по правилам, описанным в условии. Каждый номер необходимо вывести в отдельной строке. Номера необходимо выводить в том же порядке, в котором они были перечислены во входном файле. Вместо номеров, корректного разбиения которых на код государства, код оператора или региона и номер абонента не существует, необходимо вывести слово «Incorrect».
| Ввод |
Вывод |
2
7 3
981
3517
812
351 3
34712
1234
963
8
79818266456
35196328463
78122472557
01234567890
73517960326
35134712239
35112342013
78120203040 |
+7(981)826-64-56
+351(963)284-63
+7(812)247-25-57
Incorrect
+7(3517)96-03-26
+351(34712)239
+351(1234)20-13
Incorrect |
| |
![]()
|
|
Призы
Целые числа
Разбор случаев
Организаторы Всероссийской командной олимпиады школьников по программированию всегда ответственно относятся ко всем этапам проведения соревнования. Недавно организаторам были доставлены футболки для участников олимпиады. Они были сложены в ящик, который является кубом со стороной в один метр. Ящик был поставлен в углу комнаты прямоугольной формы размером m × n метров. Чтобы никто случайно не забрал ящик, на его верхней грани красной краской написали слово «ВКОШП».
Сегодня организаторам вдруг понадобилось переставить этот ящик в противоположный угол комнаты. Но, к сожалению, ящик оказался настолько тяжелым, что никто не мог сдвинуть его с места. Выяснилось, что все, что можно сделать с ящиком — перекатить его через ребро нижней грани. Соответствующее ребро при этом остается на том же месте, а нижней становится другая смежная с этим ребром грань.
Перед организаторами олимпиады встала следующая задача. Им необходимо перекатить ящик из угла комнаты, в котором он стоит, в противоположный угол. При этом даже перекатывать ящик очень тяжело, поэтому организаторы решили минимизировать количество перекатываний ящика.
Но когда они уже собрались начать транспортировку, обнаружилась еще одна проблема. Красная надпись «ВКОШП» каждый раз, касаясь пола, оставляет на нем следы. Поэтому среди всех вариантов транспортировки, минимизирующих количество перекатываний, организаторы решили выбрать тот, при котором надпись «ВКОШП» окажется на нижней грани куба минимальное число раз.
Помогите организаторам — посчитайте, сколько раз надпись «ВКОШП» коснется пола при оптимальном перекатывании куба с футболками.
Формат входных данных
В первой строке задано два числа n и m (1 ≤ n, m ≤ 109 ) — размеры комнаты в метрах.
Формат выходных данных
Выведите одно число — сколько раз надпись «ВКОШП» окажется на нижней грани при оптимальном перемещении ящика.
Пояснение
В первом примере необходимо одно перекатывание, надпись, которая исходно была на верхней грани, окажется на боковой грани, но пола не коснется.
Во втором примере необходимо четыре перекатывания. В любом случае хотя бы один раз надпись «ВКОШП» коснется пола. Один из способов сделать перекатывания так, чтобы это произошло один раз, следующий. Сначала два раза перекатим куб в одном направлении (он окажется в соседнем углу комнаты). Сейчас надпись «ВКОШП» находится на нижней грани и касается пола. Затем перекатим куб еще два раза в перпендикулярном направлении. Теперь куб находится в требуемом положении.
| |
![]()
|
|
Полные квадраты
Рекурсия
Целые числа
Разбор случаев
Вывод формулы
С целью поиска закономерностей иногда полезно сгенерировать длинную последовательность по определенным правилам. Известно, например, что последовательность 0, 0+ 1, 0+ 1+ 3, 0+ 1+ 3+ 5,
. . . , 0 + 1 + 3 + . . . + (2n − 1), . . ., составленная из сумм нескольких первых нечетных натуральных чисел, состоит из квадратов целых чисел: 0, 1, 4, 9, . . . , n2, . . ..
Обобщим эту последовательность следующим образом: будем использовать вместо начального значения не ноль, а число k. Получим последовательность: k, k + 1, k + 1 + 3, k + 1 + 3 + 5, . . . ,k+ 1+ 3+. . .+ (2n−1), . . .. В отличие от случая k = 0, в этой последовательности могут встречаться не только полные квадраты. Необходимо найти минимальное целое неотрицательное число, квадрат которого встречается в этой последовательности.
Требуется написать программу, которая по заданному целому числу k определяет, квадрат какого минимального неотрицательного целого числа встречается в описанной последовательности,
либо выясняет, что в ней вообще не встречается полных квадратов.
Формат входных данных
В единственной строке содержится целое число k — начальное число в последовательности
(−1012 <= k <= 1012).
Обратите внимание, что для считывания и хранения такого большого числа необходимо использовать 64-битный тип данных.
Формат выходных данных
Выведите минимальное неотрицательное целое число, квадрат которого встречается в описанной
последовательности. Если в последовательности не встречается квадратов целых чисел, выведите
«none».
| Ввод |
Вывод |
| 0 |
0 |
| -5 |
2 |
| 2 |
none |
| |
![]()
|
|
Ряд чисел
Целые числа
Разбор случаев
Легенда гласит, что Карл Фридрих Гаусс, учась в школе, смог быстро посчитать сумму целых чисел от 1 до 100, заметив, что 1 + 100 = 2 + 99 = … = 50 + 51. Теперь решите задачу посложнее: можно ли перед каждым из чисел от 1 до N расставить знаки «+» или «–» так, чтобы сумма получившихся чисел была равна 0? Например, для N = 3 сумма –1 –2 +3 будет равна 0, а для N = 2 этого сделать нельзя. Программа получает на вход целое неотрицательное число N, не превосходящее 105.
Программа должна вывести последовательность из N символов «+» или «–», соответствующих знакам, которые нужно расставить перед числами от 1 до N так, чтобы сумма получившихся чисел была равна 0. Если задача имеет несколько решений, нужно вывести один (лобой) ответ. Если задача не имеет решения для данного N, нужно вывести
одно слово «IMPOSSIBLE».
| Ввод |
Вывод |
Примечание |
| 3 |
--+ |
Правильным ответом будет также «++-» |
| 2 |
IMPOSSIBLE |
|
| |
![]()
|
|
Римские числа
Строки
Разбор случаев
Задача на реализацию
Один древнеримский торговец брал несколько раз ссуду в древнеримском банке. Каждый раз банкир записывал размер выданной ссуды на листе пергамента, используя римские числа. Но ввиду дороговизны пергамента запись производилась плотно и все числа оказались записанными подряд, без разделителей. Когда торговец пришёл возвращать ссуду, оказалось, что невозможно установить разбиение записи на числа.
Например, если на пергаменте записана строка «XIIV», её можно разбить на римскиечисла разными способами, например, XI + IV = 11 + 4 = 15 или XII + V = 12 + 5 = 17, возможны и другие варианты разбиения.
Торговец хочет вернуть как можно меньше денег, поэтому он хочет так разбить строку цифр на римские числа, чтобы сумма всех чисел была как можно меньше.
Программа получает на вход строку, длина которой не превосходит 250 символов. Строка состоит только из заглавных латинских букв I, V, X, L, С, D, M.
Программа должна вывести единственное число – минимально возможную сумму, которую можно получить при разбиении данной строки на последовательность корректных римских чисел. Ответ нужно вывести арабскими цифрами в десятичной системе счисления.
Правила записи римских чисел
Римскими цифрами можно записать целые числа от 1 до 3999. Число представляется в виде суммы тысяч, сотен, десятков и единиц. Далее из следующей таблицы берётся по одному элементу, соответствующему тысячам, сотням, десяткам, единицам ровно в таком порядке.
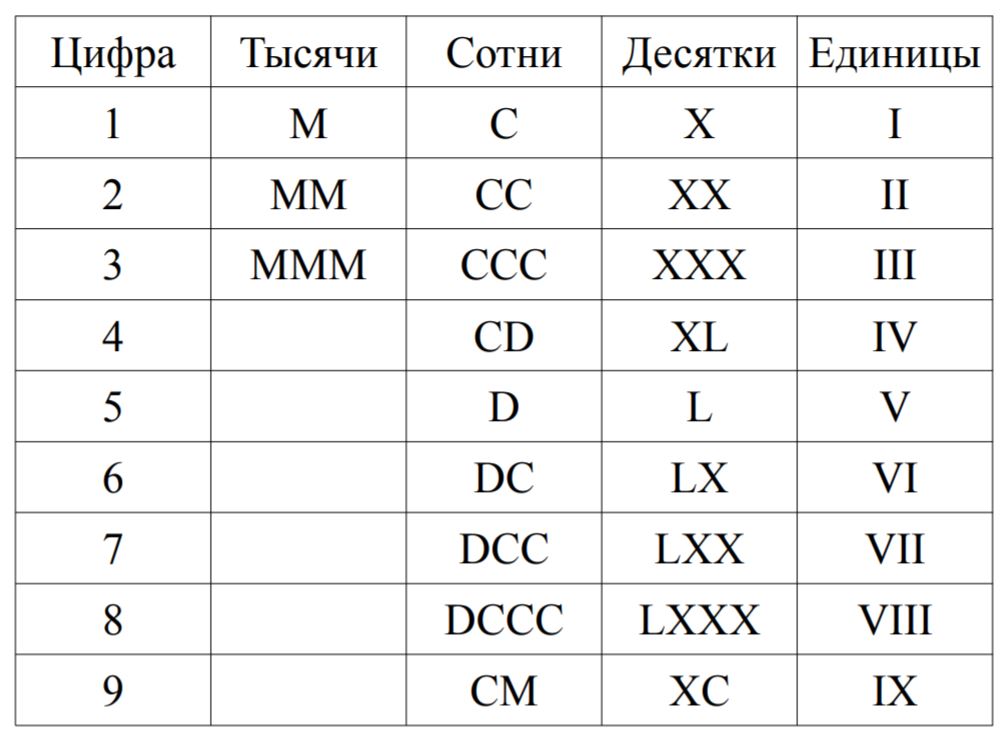
Если число тысяч, сотен, десятков, единиц равно 0, то из соответствующего столбца ничего не берётся. Например, число 1990 записывается, как 1000 + 900 + 90 = MCMXС.
| |
![]()
|
|
Пирожные
Разбор случаев
Для праздничного чаепития необходимо купить n пирожных. В магазине продается всего два вида пирожных, причем пирожных одного вида осталось a штук, а пирожных другого вида осталось b штук. Пирожные одного вида считаются одинаковыми. Сколькими способами можно купить ровно n пирожных?
Формат входных данных
В первой строке входных данных записано число n — количество пирожных, которое нужно купить, во второй и третьей строке записаны числа a и b — количество пирожных каждого из двух видов, которые есть в магазине. Все числа — целые, от 1 до 100.
Формат выходных данных
Программа должна вывести одно целое число — количество различных способов купить n пирожных.
| Ввод |
Вывод |
Примечание |
5
3
10 |
4 |
В примере из условия купить 5 пирожных можно 4 способами: 0 пирожных первого вида и 5 пирожных второго вида, 1 пирожное первого вида и 4 пирожных второго вида, 2 пирожных первого вида и 3 пирожных второго вида, 3 пирожных первого вида и 2 пирожное второго вида. Больше способов нет, так как в магазине есть только 3 пирожных первого вида. |
| |
![]()
|
|
Дневник дождя
Разбор случаев
Задача на реализацию
Петя живёт в Санкт-Петербурге и увлекается метеорологией. Из научного интереса он решил подтвердить или опровергнуть мнение о том, что в Санкт-Петербурге постоянно идёт дождь. Для этого Петя завёл дневник дождя и раз в неделю в воскресенье оставляет в нём запись с информацией о том, идёт ли дождь. Каждую запись Петя подписывает номером текущего дня в месяце, дни в месяце нумеруются с 1 до числа дней в этом месяце (от 28 до 31 в разных месяцах).
Сегодня Петя открыл дневник, чтобы сделать очередную запись, и обнаружил, что он сделал последнюю запись две недели назад, а в прошлое воскресенье забыл занести информацию в дневник. Петя помнит, что неделю назад шёл дождь, и он решил сделать две записи: за сегодняшний день и за прошлое воскресенье. Он знает номер текущего дня в месяце \(n\) и видит, каким числом \(m\) подписана запись две недели назад. Каким числом Петя должен подписать запись за прошлую неделю?
Формат входных данных
В первой строке вывода даны два целых числа \(n\) и \(m\) (\(1 \le n, m \le 31\)) — номер текущего дня месяца и число, которым подписана запись две недели назад.
Формат выходных данных
Выведите единственное число – каким числом должна быть подписана запись неделю назад.
| |
![]()
|
|
Весы
Разбор случаев
У учителя физики есть четыре гири и чашечные весы. Он пытается заставить весы находиться в равновесии, поставив все гири на чашки весов. Весы находятся в равновесии, если суммарный вес гирь на обеих чашках одинаковый.
Помогите учителю физики уравновесить весы или убедитесь, что это невозможно.
Формат входных данных
Входные данные содержат четыре строки, каждая из них содержит вес одной из гирь — натуральное число, не превышающее \(100\).
Формат выходных данных
Если уравновесить весы невозможно, выведите единственное число \(-1\).
Иначе выведите две строки. На первой строке выведите веса гирь, которые необходимо разместить на левой чаше весов. На второй строке выведите веса гирь, которые необходимо разместить на правой чаше весов.
Если есть несколько способов уравновесить весы, можно вывести любой из них.
| |
![]()
|