| | | |
|
Пазл
Динамическое программирование
Динамическое программирование
Паросочетания
Жадный алгоритм
Участникам, использующим язык Python3, рекомендуется отправлять решения на проверку с использованием интерпретатора PyPy3.
Школьники Алиса и Ибрагим — лучшие друзья. У Ибрагима скоро день рождения, и по этому поводу Алиса решила подарить ему новый пазл. Пазл можно представить в виде матрицы из \(2\) строк и \(n\) столбцов, каждый элемент которой \(0\) или \(1\). За один ход можно поменять местами два элемента, стоящие в соседних клетках.
Более формально, будем считать, что строки матриц пронумерованы сверху вниз от \(1\) до \(2\), а столбцы — слева направо от \(1\) до \(n\). Обозначим клетку на пересечении строки \(x\) и столбца \(y\) за \((x, y)\). Будем считать две клетки \((x_1, y_1)\) и \((x_2, y_2)\) соседними, если \(|x_1 - x_2| + |y_1 - y_2| = 1\).
Алисе не нравится, какой рисунок образуют клетки пазла в данный момент. Она придумала свой рисунок, с которым и планирует подарить Ибрагиму новый пазл, но для этого нужно привести пазл в соответствующее состояние.
В конце учебного года у Алисы очень плотное расписание, и она не хочет тратить на эту задачу много времени. Помогите Алисе найти минимальное количество ходов, за которое она может получить свой рисунок, или скажите, что это невозможно.
Формат входных данных
В первой строке вводится одно целое число \(n\) (\(1 \leq n \leq 200\,000\)) — количество столбцов в пазле.
Следующие две строки описывают рисунок, образованный пазлом в данный момент. В каждой строке вводятся \(n\) целых чисел, каждое из которых равно \(0\) или \(1\).
Следующие две строки описывают желаемый рисунок Алисы в том же формате.
Формат выходных данных
Если Алиса не ошиблась и её рисунок можно получить, найдите и выведите минимальное необходимое количество ходов, иначе выведите \(-1\).
В первом примере из условия подойдет следующая последовательность обменов:
\((2, 1), (1, 1)\)
\((1, 2), (1, 3)\)
\((2, 2), (2, 3)\)
\((1, 4), (1, 5)\)
\((2, 5), (2, 4)\)
Можно показать, что меньшим числом обменов обойтись нельзя, поэтому ответ равен \(5\).
Во втором примере из условия никакая последовательность ходов не приводит пазл к нужному виду.
| |
![]()
|
|
K задач (A)
Потоки
Паросочетания
K участникам сборов для решения было предложено K задач. Участники решили разделить задачи между собой, решить каждому по одной задаче, а затем обменяться решениями (они не учли, что система ejudge способна отследить данный факт J). Известно ориентировочное время, за которое каждый из участников сборов может решить каждую из предложенных задач.
Помогите участникам сборов распределить задачи так (по одной каждому участнику), чтобы суммарное время, потраченное на их решение было минимальным.
Входные данные
Во входном файле сначала записано число K (0 < K < 101) и далее K2 неотрицательных целых чисел, не превосходящие 20000, описывающих матрицу K x K, времен решения каждым из участников каждой из задач.
Выходные данные
В файл выведите суммарное минимальное время решения всех задач, при условии, что каждый участник решит ровно одну задачу.
| |
![]()
|
|
Кубики
Потоки
Паросочетания
Родители подарили Пете набор детских кубиков. Поскольку Петя скоро пойдет в школу, они купили ему кубики с буквами. На каждой из шести граней каждого кубика написана буква.
Теперь Петя хочет похвастаться перед старшей сестрой, что научился читать. Для этого он хочет сложить из кубиков ее имя. Но это оказалось довольно сложно сделать - ведь разные буквы могут находиться на одном и том же кубике и тогда Петя не сможет использовать обе буквы в слове. Правда одна и та же буква может встречаться на разных кубиках. Помогите Пете!
Дан набор кубиков и имя сестры. Выясните, можно ли выложить ее имя с помощью этих кубиков и если да, то в каком порядке следует выложить кубики.
Входные данные
В первой строке вводится число N (1 <= N <= 100) - количество кубиков в наборе у Пети. Во второй строке задано имя Петиной сестры - слово, состоящие только из больших латинских букв, не длиннее 100 символов. Следующие N строк содержат по 6 букв (только большие латинские буквы), которые написаны на соответствующем кубике.
Выходные данные
В первой строке выведите "YES" если выложить имя Петиной сестры данными кубиками можно, "NO" в противном случае.
В случае положительного ответа, во второй строке выведите M различных чисел из диапазона 1…N, где M - количество букв в имени Петиной сестры. i-е число должно быть номером кубика, который следует положить на i-е место при составлении имени Петиной сестры. Кубики нумеруются с 1, в том порядке, в котором они заданы во входных данных. Если решений несколько, выведите любое. Разделяйте числа пробелами.
| |
![]()
|
|
G. Разрешенные буквы
Потоки
Паросочетания
жадные алгоритмы
*2400
графы
битмаски
Поликарп недавно запустил свою новую идею для стартапа. Ниша довольно свободна, вектор развития звучит еще как многообещающе, поэтому он довольно легко нашел себе инвесторов для поддержки компании. Однако он так и не смог выбрать название стартапа! На самом деле, Поликарп придумал название, но некоторые изменения ему точно не помешают. Теперь он хочет поменять местами некоторые буквы, чтобы получить лучшее название. Буквы не обязательно должны стоять рядом. К тому же, каждый из инвесторов выбрал себе по позиции в названии и утвердил список букв, которые могут там стоять. Позиции, выбранные инвесторами попарно различны. Если некоторые позиции не выбраны ни одним инвестором, то там может стоять любая буква. Наконец, Поликарп уверен, что минимальное лексикографически название — лучшее название. (Ну так а почему, думаете, Google решил стать Alphabet?) Формально, вам дана строка, состоящая из строчных латинских букв от «a» to «f». Можно менять местами буквы на любых позициях произвольное количество раз (можно и ноль). Какое минимальное лексикографически название получить такое, что буква на каждой позиции в нем находится среди разрешенных букв? Если Поликарп не может получить ни одного корректного названия, то выведите «Impossible». Выходные данные Если Поликарп не может составить никакого корректного названия, то выведите «Impossible». В противном случае выведите минимальное лексикографически название, которое Поликарп может получить с помощью обменов букв в строке \(s\), такое, что буква на каждой позиции в нем находится среди разрешенных букв. | |
![]()
|
|
F. Сессия в БГУ
Бинарный поиск
Паросочетания
поиск в глубину и подобное
*2400
графы
снм
Поликарп учится в Берляндском государственном университете. Совсем скоро ему предстоит сдать сессию. Он должен сдать \(n\) экзаменов. Для каждого экзамена \(i\) известны два дня: \(a_i\) — день основной сдачи экзамена, \(b_i\) — день пересдачи (\(a_i < b_i\)). В один день Поликарп может сдавать не более одного экзамена. Для каждого экзамена Поликарп самостоятельно выбирает, в какой из двух дней его сдать. Необходимо сдать все \(n\) экзаменов. Поликарп хочет сдать сессию как можно быстрее. Выведите минимальный номер дня, в который Поликарп сможет сдать все \(n\) экзаменов, либо выведите -1, если сдать сессию полностью невозможно. Выходные данные Если Поликарп не сможет сдать все \(n\) экзаменов, выведите -1. В противном случае выведите минимальный номер дня, когда Поликарп сможет это сделать. | |
![]()
|
|
E. Закупка множеств
Потоки
Паросочетания
*2900
СЪЕЛ ОУЖАС. Рабочее название задачи Вирус Хексадесимал очень любит играть с числовыми множествами — пересекать их, объединять. В один прекрасный день она с удивлением обнаружила, что Сказзи, ее ручной сферический кот, объединил все множества в одно и съел результат! Надо было срочно что-то делать, и Хексадесимал полетела на рынок. На рынке продается n числовых множеств. Вирус хочет купить такой набор множеств, что количество множеств в нем будет равно количеству чисел в его объединении. Из всех подходящих наборов множеств она готова выбрать только самый дешевый. Но не все так просто! Поскольку в Мэйнфрейме царит рынок совершенной конкуренции, то известно, что объединение любых k множеств содержит не менее k различных чисел (для любого целого положительного k). Помогите вирусу выбрать подходящий набор множеств. Этот набор может быть пустым. Выходные данные Выведите одно число — минимальную стоимость покупки такого набора из k множеств, что объединение множеств этого набора содержит ровно k чисел (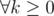 ). ). | |
![]()
|
|
B. Little C любит 3 II
Потоки
Паросочетания
Перебор
Конструктив
*2200
Little C очень любит число «3». Он любит все, что с ним связано. Сейчас он играет в игру на шахматной доске \(n \times m\). Клетку в строке \(x\) и в столбце \(y\) назовем \((x,y)\). Исходно, шахматная доска пуста. Каждый раз он ставит две шахматные фигуры на две различные пустые клетки, Манхэттенское расстояние между которыми равно \(3\). Манхэттенским расстоянием между клетками \((x_i,y_i)\) и \((x_j,y_j)\) назовем \(|x_i-x_j|+|y_i-y_j|\). Он хочет расставить таким образом как можно больше шахматных фигур на доске. Пожалуйста, помогите ему найти максимальное количество фигур которое он может так расставить. Выходные данные Выведите единственное целое число — максимально количество шахматных фигур, которое сможет расставить Little C. Примечание В первом примере Манхэттенское расстояние между любыми двумя клетками меньше чем \(3\), поэтому ответ \(0\). Во втором примере, одно из возможных решений это \((1,1)(3,2)\), \((1,2)(3,3)\), \((2,1)(1,3)\), \((3,1)(2,3)\). | |
![]()
|
|
A. Последний шанс
Потоки
Паросочетания
Деревья
Структуры данных
графы
*2500
2969-й год. Прошло 1000 лет с момента посадки на луну. Человечество колонизировало Гиперпространство и жило в гармонии. Жило, пока мы не поняли, что мы не одни. Не очень далеко от Земли многочисленный космический флот инопланетян готовит атаку на Землю. Впервые за долгое время человечеству угрожает реальная опасность. Повсюду паника и кризис. Ученые со всей солнечной системы встретились и обсуждают возможный выход из ситуации. Но пока все усилия тщетны. Последняя надежда Земли — ВЫ! К счастью, Земля имеет мощную систему защиты, созданную специалистами из MDCS. Флот инопланетян содержит \(N\) кораблей на одной линии. Система защиты состоит из трех типов вооружения: - SQL-ракеты: каждая SQL-ракета может уничтожить не более одного корабля инопланетян из заданного для каждой ракеты набора.
- лучи Познания: каждому лучу Познания сопоставлен отрезок \([l,r]\), он может уничтожить не более одного корабля инопланетян из этого отрезка.
- OMG-базука: каждая OMG-базука имеет ровно три цели и может уничтожить либо ровно ноль, либо ровно два корабля. Кроме того, система прицеливания является «умной», поэтому множества трех целей для любых двух OMG-базук не пересекаются (таким образом, каждый корабль находится под прицелом не более чем одной OMG-базуки).
Ваша задача — найти такой план атаки на корабли инопланетян, чтобы уничтожить максимально возможное количество кораблей. Каждый уничтоженный корабль должен быть уничтожен ровно одним оружием. Выходные данные Первая строка должна содержать максимальное количество уничтоженных кораблей \(X\). Каждая из следующих \(X\) строк должна содержать два целых числа \(A\) и \(B\), где \(A\) — номер оружия, а \(B\) — номер корабля, уничтоженного оружием \(A\). Примечание SQL-ракета может уничтожить только четвертый корабль. OMG-базука может уничтожить два из 1-го, 4-го или 5-го кораблей, а луч Познания может уничтожить любой корабль из отрезка \([1,4]\). Максимальное количество уничтоженных кораблей равно 4, один из возможных планов — SQL-ракета уничтожает 4-й корабль, OMG-базука уничтожает 1-й и 5-й корабли, а луч Познания уничтожает 2-й корабль. | |
![]()
|
|
F. Электрическая схема
Потоки
Паросочетания
*2700
Паша — начинающий техник, но уже поставил себе большую цель собрать собственный компьютер. Первая непростая задача — научиться собирать электрическую схему. Схема, которую собрал Паша, состоит из несколько проводов. Каждый провод — это отрезок, который соединяет две точки на плоскости с целыми координатами, лежащими в диапазоне \([1, 10^9]\). В схеме есть провода двух цветов: - красные провода: эти провода должны иметь вид горизонтального отрезка, то есть если провод соединяет две точки \((x_1, y_1)\) и \((x_2, y_2)\), то выполнено, что \(y_1 = y_2\);
- синие провода: эти провода должны иметь вид вертикального отрезка, то есть если провод соединяет две точки \((x_1, y_1)\) и \((x_2, y_2)\), то выполнено, что \(x_1 = x_2\).
Обратите внимание, что если провод соединяет две одинаковые точки, то он может быть как красным, так и синим. Также в Пашиной схеме никакие два провода одного цвета не могут пересекаться, то есть любые два отрезка проводов одного цвета не могут содержать общих точек. Недоработка Пашиной схемы состоит в том, что его провода не были изолированы, и поэтому в точках пересечения проводов разных цветов возникли искры, которые Паша увидел. Он записал все точки, в которых он увидел искру. У него получилось множество из \(n\) различных точек. После чего он разобрал схему и пошёл спать. Утром, когда Паша увидел на листочке множество из \(n\) точек, в которых он увидел искру, ему стало интересно, сколько проводов он использовал, собрав эту схему. К сожалению, он ничего не запомнил, поэтому он решил узнать, какое минимальное количество проводов он мог использовать в своей схеме. Помогите ему узнать это число, а также расположить эти провода так, чтобы в получившейся схеме искры возникли в тех же самых точках. Выходные данные Выведите описание электрической схемы в следующем формате: Сначала выведите \(h\) — количество горизонтальных красных проводов (\(0 \leq h\)). В следующих \(h\) строках выведите по \(4\) целых числа \(x_1\), \(y_1\), \(x_2\), \(y_2\) — координаты двух точек \((x_1, y_1)\) и \((x_2, y_2)\), которые соединяет очередной красный провод. Поскольку отрезки горизонтальные, должно быть выполнено \(y_1 = y_2\). Также должно быть выполнено \(1 \leq x_1, y_1, x_2, y_2 \leq 10^9\). Потом выведите \(v\) — количество вертикальных синих проводов (\(0 \leq v\)). В следующих \(v\) строках выведите по \(4\) целых числа \(x_1\), \(y_1\), \(x_2\), \(y_2\) — координаты двух точек \((x_1, y_1)\) и \((x_2, y_2)\), которые соединяет синий очередной провод. Поскольку отрезки вертикальные, должно быть выполнено \(x_1 = x_2\). Также должно быть выполнено \(1 \leq x_1, y_1, x_2, y_2 \leq 10^9\). Никакие два отрезка одного цвета не должны иметь общих точек. Множество точек, в которых Паша мог увидеть искру, если бы он построил такую схему, должно совпадать с данным во входных данных множеством точек. Количество отрезков \((h + v)\) должно быть минимально возможным. Можно легко показать, что ответ всегда существует. Если существует несколько возможных ответов, выведите любой. Примечание В первом примере Паша мог собрать такую схему: 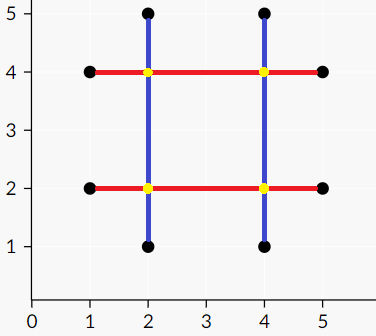 В этой схеме по \(2\) провода каждого цвета: красные из \((5, 2)\) в \((1, 2)\) и из \((1, 4)\) в \((5, 4)\), синие из \((2, 1)\) в \((2, 5)\) и из \((4, 5)\) в \((4, 1)\). Заметим, что он увидит искры ровно в тех точках, которые он записал (обозначены желтым цветом на картинке). Например, искру в точке \((2, 4)\) он увидит, так как в этой точке пересекаются второй красный провод и первый синий. Можно доказать, что нужно не меньше \(4\)-х проводов, чтобы получить схему, нужную Паше. | |
![]()
|
|
E. Ранг случайного леса
Паросочетания
Деревья
математика
дп
*2800
Определим ранг неориентированного графа как ранг его матрицы смежности в \(\mathbb{R}^{n \times n}\). Дано дерево. Каждое из рёбер дерева исчезает с вероятностью \(1/2\) независимо от остальных. Пусть \(E\) — математическое ожидание ранга полученного леса. Найдите остаток от деления \(E \cdot 2^{n-1}\) на \(998244353\) (несложно показать, что \(E \cdot 2^{n-1}\) — целое число). Выходные данные Выведите одно число — ответ на задачу. | |
![]()
|
|
I. Privatization of Roads in Berland
Потоки
Паросочетания
*2400
графы
There are \(n\) cities and \(m\) two-way roads in Berland, each road connecting two distinct cities. Recently the Berland government has made a tough decision to transfer ownership of the roads to private companies. In total, there are \(100500\) private companies in Berland, numbered by integers from \(1\) to \(100500\). After the privatization, every road should belong to exactly one company. The anti-monopoly committee demands that after the privatization each company can own at most two roads. The urbanists of Berland also stated their opinion: each city should be adjacent to the roads owned by at most \(k\) companies. Help the government to distribute the roads between the companies so that both conditions are satisfied. That is, each company gets at most two roads, and each city has roads of at most \(k\) distinct companies adjacent to it. Output Print \(t\) lines: the \(i\)-th line should contain the answer for the \(i\)-th test case. For a test case, print a sequence of integers \(c_1, c_2, \dots, c_m\) separated by space, where \(c_i\) (\(1 \le c_i \le 100500\)) is the company which owns the \(i\)-th road in your plan. If there are multiple solutions, output any of them. If there is no solution for a test case, print \(c_1=c_2=\ldots=c_m=0\). | |
![]()
|
|
F. Вася и бесконечные кредиты
Потоки
Паросочетания
дп
*2600
сортировки
графы
Вася решил купить себе шикарную новую машину. К сожалению, ему немного не хватает денег. Сейчас у него есть 0 бурлей. В местном банке есть \(n\) предложений по кредитам. Каждое предложение описывается тремя числами \(a_i\), \(b_i\) и \(k_i\). Предложения пронумерованы от \(1\) до \(n\). Если Вася пользуется \(i\)-м предложением, то банк выдает ему \(a_i\) бурлей в начале месяца, а потом забирает по \(b_i\) бурлей в конце каждого из \(k_i\) следующих месяцев (включая месяц, в который кредит был взят). Вася может брать предложения в любом порядке. В каждый месяц Вася может брать не более одного кредитного предложения. К тому же каждое кредитное предложение может быть использовано не более одного раза. Несколько кредитов могут быть активны в одно и то же время. Это подразумевает, что Вася платит банку сумму \(b_i\) по всем \(i\) активных кредитов в конце каждого из месяцев. Вася хочет купить машину в середине некоторого месяца. Он просто берет все деньги, которые у него есть на текущий момент, и покупает машину ровно этой цены. Васю не особо заботит, сколько он должен будет заплатить банку после покупки машины. Он просто уедет на своей машине из страны, так что банк не сможет его найти. Какая максимальная цена может быть у новой машины? Выходные данные Выведите одно целое число — максимальную цену машины. Примечание В первом примере оптимальная последовательность взятых кредитов такова: 4 \(\rightarrow\) 3. Количество бурлей у Васи меняется следующим образом: 5 \(\rightarrow\) 32 \(\rightarrow\) -86 \(\rightarrow\) .... Он забирает деньги в середине второго месяца (32 бурля) и покупает машину. Отрицательное число бурлей значит, что Вася должен заплатить банку эту сумму денег. Во втором примере оптимальная последовательность взятых кредитов такова: 3 \(\rightarrow\) 1 \(\rightarrow\) 2. Количество бурлей у Васи меняется следующим образом: 0 \(\rightarrow\) 300 \(\rightarrow\) 338 \(\rightarrow\) 1337 \(\rightarrow\) 236 \(\rightarrow\) -866 \(\rightarrow\) .... | |
![]()
|
|
E. Максимизировать mex
Потоки
Паросочетания
*2400
графы
В колледже учатся \(n\) студентов, также в колледже есть \(m\) клубов, пронумерованных от \(1\) до \(m\). У каждого студента известен его потенциал \(p_i\) и номер клуба \(c_i\), членом которого он является. Изначально каждый студент является членом ровно одного клуба. Скоро в колледже состоится технический фестиваль, который продлится \(d\) дней. Каждый день в рамках фестиваля будет проведено соревнование по программированию. Каждый день утром, ровно один студент решает покинуть свой клуб. После того как студент покинул свой клуб, он больше не присоединится ни к какому клубу снова. Каждый день в полдень, директор колледжа выбирает по одному студенту из каждого клуба (в случае если в каком-то клубе нет ни одного студента, из этого клуба не будет выбран никто) и составляет из них команду на этот день. Силой команды называется mex потенциалов студентов, которые в неё входят. Директор хочет выяснить наибольшую возможную силу команды в каждый из следующих \(d\) дней. Таким образом, каждый день директор выбирает команду так, чтобы максимизировать силу команды. Для мультимножества \(S\), его mex определён как наименьший неотрицательный элемент не входящий в \(S\). Например, mex мультимножества \(\{0, 1, 1, 2, 4, 5, 9\}\) равн \(3\), mex мультимножества \(\{1, 2, 3\}\) равен \(0\), а mex \(\varnothing\) (пустого множества) равен \(0\). Выходные данные Для каждого из \(d\) дней, выведите наибольшую возможную силу команды в этот день. Примечание Рассмотрим первый пример: В первый день студент \(3\) покидает свой клуб. Теперь, остались студенты \(1\), \(2\), \(4\) и \(5\). Мы можем выбрать студентов \(1\), \(2\) и \(4\) чтобы получить максимальную силу команды, равную \(3\). Заметим, что мы не можем выбрать команду из студентов \(1\), \(2\) и \(5\), так как студенты \(2\) и \(5\) состоят в одном клубе. Также мы не можем выбрать команду \(1\), \(3\) и \(4\), так как студент \(3\) уже покинул свой клуб. Во второй день студент \(2\) покидает свой клуб. Теперь, остались студенты \(1\), \(4\) и \(5\). Мы можем выбрать студентов \(1\), \(4\) и \(5\) чтобы получить максимальную возможную силу, то есть \(1\). В третий день, остаются только студенты \(1\) и \(5\). Мы можем выбрать студентов \(1\) и \(5\) чтобы получить наибольшую возможную силу команды, то есть \(1\). В четвёртый день, остался только студент \(1\). Мы можем выбрать студента \(1\), чтобы получить максимальную возможную силу команды, то есть \(1\). В пятый день не осталось ни одного клуба, в котором бы состоял хотя бы один студент, а значит максимальная возможная сила равна \(0\). | |
![]()
|
|
C. Сергей и школьная столовая
Бинарный поиск
Паросочетания
Деревья
Структуры данных
математика
реализация
жадные алгоритмы
*2200
Сергей пришел в школьную столовую и с ужасом обнаружил, что там уже очередь из целых \(m\) человек! Теперь он не уверен, стоит ли дожидаться конца этой очереди, поэтому хочет узнать, какое же блюдо ему достанется, если он это сделает. Так как Сергей устал после занятий, он попросил вас посчитать это за него. Всего в столовой есть \(n\) блюд со стоимостями \(a_1, a_2, \ldots, a_n\). Также есть очередь из \(m\) человек, у которых есть \(b_1, \ldots, b_m\) тугриков (школьники пронумерованы в том же порядке, как они стоят в очереди, то есть \(b_1\) означает, сколько тугриков у школьника, который стоит в очереди первым, а \(b_m\) — сколько у школьника, стоящего последним). Считается, что чем дороже блюдо, тем оно вкуснее, поэтому каждый школьник, когда подходит его очередь, просто покупает самое дорогое блюдо, на которое у него хватит денег (каждое блюдо в столовой есть только в одном экземпляре, поэтому после того, как один школьник купил блюдо, его уже никто не может купить), если же денег не хватает ни на одно из блюд, школьник так и уходит голодным (жестокий капитализм). Но для Сергея деньги не проблема, поэтому, когда подойдет его очередь, он, если еще не уйдет, просто купит самое дорогое из оставшихся блюд. Еще в школе Сергея сейчас нестабильная экономическая ситуация, поэтому, иногда могут изменяться стоимости некоторых блюд или количество денег у некоторых школьников. Поэтому вам нужно обработать \(q\) запросов двух типов: - изменить \(a_i\) на \(x\). То есть стоимость \(i\) блюда становится равна \(x\).
- изменить \(b_i\) на \(x\). То есть у \(i\) школьника становится \(x\) тугриков.
После каждого запроса нужно вывести стоимость блюда, которое получит Сергей, если дождется своей очереди, или \(-1\), если к этому моменту уже ничего не останется. Выходные данные Выведите \(q\) строк, \(i\)-я из которых содержит ответ на вопрос Сергея после \(i\) изменения (стоимость блюда, которое получит Сергей, если дождется своей очереди, или \(-1\), если к этому моменту уже ничего не останется). Примечание В первом примере после первого запроса в столовой есть одно блюдо стоимостью \(100\) тугриков и один школьник с одним тугриком, поэтому Сергей купит блюдо со стоимостью \(100\). Во втором примере после первого запроса есть одно блюдо со стоимостью один тугрик и один школьник, у которого есть \(100\) тугриков, поэтому Сергей ничего не получит. В третьем примере после первого запроса никто не сможет купить блюдо стоимостью \(8\), так что его получит Сергей. После второго запроса все блюда уже будут куплены до того, как настанет очередь Сергея. После третьего запроса запросе третий и пятый школьники купят соответственно первое и второе блюдо, а четвертое уже не купит никто. | |
![]()
|
|
B2. Доктор встречает Вейдера (средняя)
Потоки
Паросочетания
сортировки
графы
*2200
кратчайшие пути
Благодаря помощи Доктора, повстанцам удалось украсть достаточно золота, чтобы запустить полномасштабную атаку на эмперию! Однако Дарт Вейдер ищет возможности отомстить и забрать назад своё золото. Повстанцы спрятали золото на различных базах по всей галактике. Дарт Вейдер и Империя собираются послать свои космические корабли в атаку на эти базы. Галактика может быть представлена как неориентированный граф из \(n\) планет (вершин) и \(m\) червоточин (рёбер), каждая соединяющая две планеты. Всего у империи есть \(s\) космических кораблей, а у повстанцев есть \(b\) баз, расположенных на различных планетах галактики. У каждого космического корабля есть его местоположение \(x\), обозначающее индекс планеты, на которой он находится, его сила атаки \(a\) и определённый уровень топлива \(f\). У каждой базы есть местоположение \(x\) и уровень защиты \(d\). Космический корабль может атаковать базу если выполнены оба следующих условия: - Сила атаки космического корабля больше или равна уровня защиты базы,
- Уровень топлива космического корабля больше или равен кратчайшему расстоянию (количество червоточин) между планетой космического корабля и планетой с базой
Вейдер очень требователен к своим атакующим формациям. Он требует, чтобы каждый космический корабль атаковал не более одной базы, и чтобы каждая база была атакована не более чем одним космическим кораблем. Вейдер знает, что повстанцы спрятали \(k\) золота в каждой базе, так что он назначит космическим кораблям базы для атаки таким образом, чтобы максимизировать число атакованных баз. Таким образом, для каждой атакованной базы повстанцы теряют по \(k\) золота. Однако повстанцы имеют возможность создать произвольное количество фейковых баз. С помощью Доктора, эти базы будут существовать за пределами пространства и времени, так что все корабли смогут достичь и атаковать их. Более того, фейковые базы всегда будут казаться очень заманчивыми, то есть они гарантировано будут атакованы каким-то кораблём. Разумеется, фейковые базы не содержат золота, но создание одной такой базы стоит \(h\) золота. Какое минимальное количество золота повстанцы потеряют, если они создадут оптимальное количество фейковых баз? Выходные данные Выведите одно целое число — минимальную цену в золоте. Примечание Один из способов минимизировать стоимость — это построить \(4\) фейковые базы, тем самым итоговая стоимость равна \(4 \times 3 = 12\). По одному имперскому кораблю будет назначено на атаку каждой фейковой базы, тем самым будет атаковано ноль настоящих баз. | |
![]()
|
|
E. Покраска прямоугольника 2
Потоки
Паросочетания
графы
*2500
Есть клетчатый квадрат размера \(n \times n\). Некоторые клетки квадрата покрашены в черный цвет, остальные клетки покрашены в белый. За одну операцию разрешается выбрать некоторый прямоугольник и перекрасить все его клетки в белый цвет. За перекраску прямоугольника размера \(h \times w\) взимается штраф в размере \(\min(h, w)\). Требуется за минимальный суммарный штраф покрасить все клетки в белый цвет. Квадрат большой, поэтому зададим мы его в сжатом виде. Множество чёрных клеток является объединением \(m\) прямоугольников. Выходные данные Выведите одно число — минимальный суммарный штраф покраски всего квадрата в белый цвет. Примечание На картинке вы можете видеть два примера и некоторые из оптимальных способов их покрасить. 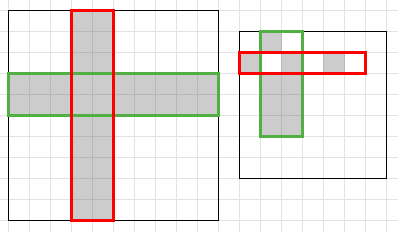 | |
![]()
|
|
H. Краткость — сестра таланта
Паросочетания
*1800
Общаясь с людьми, человек узнает много различной информации. Однако процесс общения занимает очень много времени. Это становится понятным, если обратить внимание на слова, которые мы используем в нашей речи. Можно привести множество примеров простых слов, в которых большое количество букв: «информатика», «клавиатура», «университет», «строительство», «консерватория», «сковородка», «холодильник», «секундомер», «подоконник», «электричество», «государство», «автомобиль» и другие. Разумеется, этот список можно продолжать до бесконечности. К счастью, решение этой проблемы уже было найдено. Для краткости и простоты общения предлагается заменить все слова нашей речи на такие, которые будут похожи на исходные, но в то же время будут заметно короче. Однако реализации этой идеи пока не существует, поэтому было решено поручить вам исправить ситуацию. Рассмотрим следующую формальную модель преобразования слов: будем считать, что в разговоре можно использовать n слов. Для каждого слова введем понятие его сокращенного аналога. Сокращенным аналогом произвольного слова s назовем такое слово t, которое удовлетворяет следующим условиям: - встречается в s в качестве подпоследовательности,
- имеет длину от одного до четырех символов.
Другими словами, слово t состоит хотя бы из одного и не более чем из четырех символов, которые встречаются в том же порядке, но не обязательно подряд, в слове s. Разрешается не сокращать исходное слово, если его длина не превосходит четырех символов. Вашей задачей является для заданного списка из n различных слов получить набор их сокращенных аналогов. Сокращенные аналоги всех слов из списка должны быть различны. Выходные данные Если решение существует, в выходной файл выведите ровно n строк, где i-ая строка является сокращенным аналогом i-го слова исходного набора. Если решений несколько, выведите любое из них. Если решения не существует, выведите -1. | |
![]()
|
|
D. Конкурс котиков
Паросочетания
поиск в глубину и подобное
*2400
графы
2-sat
В Котовице в ближайшие выходные будет проходить конкурс котиков. Для конкурса нужно выбрать жюри и участников. Всего в Котовице \(n\) жителей и \(n\) котиков, у каждого жителя живёт ровно один котик. Жители и котики пронумерованы целыми числами от \(1\) до \(n\), причем у \(i\)-го жителя живёт \(i\)-й котик. Каждый житель Котовице знаком с несколькими котиками, включая, конечно же, своего. Для конкурса нужно выбрать нескольких жителей на роль жюри, и нескольких котиков на роль участников. Для того, чтобы конкурс состоялся, в нём должен принять участие хотя бы один член жюри, и хотя бы один участник. Для того, чтобы конкурс прошёл честно, ни один член жюри не должен быть знаком ни с одним участником. И, наконец, чтобы конкурс прошёл наиболее интересно, было решено, что количество членов жюри плюс количество участников должно равняться \(n\). Помогите жителям Котовице выбрать состав жюри и участников для предстоящего конкурса, либо определите, что это сделать невозможно. Выходные данные Для каждого тестового случая выведите: - «No», если выбрать состав жюри и участников для конкурса невозможно.
- Иначе выведите «Yes».
Во второй строке выведите два целых числа \(j\) и \(p\) (\(1 \le j\), \(1 \le p\), \(j + p = n\)) — количество членов жюри и участников в конкурсе. В третьей строке выведите \(j\) различных целых чисел от \(1\) до \(n\) — номера жителей, которые должны быть выбраны на роль жюри. В четвертой строке выведите \(p\) различных целых чисел от \(1\) до \(n\) — номера котиков, которые должны быть выбраны на роль участников. Если существует несколько корректных ответов, выведите любой из них. Примечание В первом тестовом случае на роль жюри можно выбрать первого и третьего жителя, ни один из них не знаком со вторым котиком, поэтому его можно выбрать на роль участника. Во втором тестовом случае на роль жюри можно выбрать второго жителя, он не знаком ни с первым, ни с третьим котиком, которых можно выбрать на роль участников. В третьем тестовом случае ответа не существует, потому что единственный житель знаком с единственным котиком. Поэтому они не могут участвовать в конкурсе одновременно. Значит, в конкурсе не будет участвовать ни один житель, либо ни один котик. В четвёртом тестовом случае, каждый житель знаком с каждым котиком, поэтому в конкурсе не могут одновременно участие какой-то житель и какой-то котик. | |
![]()
|
|
E. Красивая лига
Потоки
Паросочетания
Конструктив
*2700
Футбольная лига недавно стартовала в Красивой долине. Всего \(n\) команд участвует в этой лиге. Пронумеруем их для удобства целыми числами от \(1\) до \(n\). Всего будет проведено ровно \(\frac{n(n-1)}{2}\) матчей: каждая команда будет играть со всеми оставшимися командами ровно по одному разу. В каждом матче всегда есть победившая и проигравшая команда, ничьих не бывает. После того, как все матчи будут сыграны, организаторы посчитают количество красивых троек. Тройка команд \((A, B, C)\) называется красивой, если команда \(A\) победила команду \(B\), команда \(B\) победила команду \(C\) и команда \(C\) победила команду \(A\). Мы рассматриваем только тройки различных команд, порядок команд внутри тройки имеет значение. Красотой лиги назовем количество красивых троек. В данный момент, \(m\) матчей уже было проведено и их результаты уже известны. Какая максимальная красота лиги может быть в итоге, после проведения оставшихся матчей? Также найдите возможные результаты оставшихся \(\frac{n(n-1)}{2} - m\) матчей, при которых красота лиги максимально возможная. Выходные данные Выведите \(n\) строк, в каждой из них строку, содержащую ровно \(n\) символов. Каждый символ должен быть равен \(0\) или \(1\). Обозначим за \(a_{ij}\) \(j\)-е число в \(i\)-й строке. Для всех \(1 \leq i \leq n\) должно быть выполнено \(a_{ii} = 0\). Для всех пар команд \(i \neq j\) число \(a_{ij}\) обозначает результат матча между командой с номером \(i\) и командой с номером \(j\): - Если \(a_{ij}\) это \(1\), то \(i\)-я команда победила \(j\)-ю команду;
- Иначе \(j\)-я команда победила \(i\)-ю команду;
- Также, должно быть выполнено, что \(a_{ij} + a_{ji} = 1\).
Также заметьте, что результаты \(m\) матчей, которые уже были сыграны, не могут быть изменены в вашей лиге. Красота лиги, представленной в качестве ответа должна быть максимально возможной. Если существует несколько лиг, подходящих под условия и красота которых максимальна, вы можете найти любую из них. Примечание Красота лиги в первом тесте равна \(3\), потому что есть ровно три красивые тройки команд: \((1, 2, 3)\), \((2, 3, 1)\), \((3, 1, 2)\). Красота лиги во втором тесте равна \(6\) потому что существует шесть красивых троек команд: \((1, 2, 4)\), \((2, 4, 1)\), \((4, 1, 2)\), \((2, 4, 3)\), \((4, 3, 2)\), \((3, 2, 4)\). | |
![]()
|
|
F. Новый год и социальная сеть
Паросочетания
Деревья
Структуры данных
математика
графы
*3200
Новая социальная сеть (НСС) от Donghyun содержит \(n\) пользователей с номерами \(1, 2, \ldots, n\). Их сеть представляет собой дерево, поэтому между пользователем существует \(n-1\) прямых соединений. Каждый пользователь может связаться с другим пользователем, используя некоторую последовательность прямых соединений. Мы будем обозначать эту первичную сеть как \(T_1\). Чтобы предотвратить возможную поломку сервера, Donghyun создал резервную сеть \(T_2\), которая соединяет тех же \(n\) пользователей как дерево. Если система выходит из строя, ровно одно ребро \(e \in T_1\) становится непригодным для использования. В этом случае Donghyun защитит ребро \(e\), выбрав другое ребро \(f \in T_2\), и добавит его в существующую сеть. Это новое ребро должно сделать сеть опять связной. Donghyun хочет выбрать заменяющее ребро \(f \in T_2\) для максимально возможного количества ребер \(e \in T_1\). Однако, поскольку резервная сеть \(T_2\) является хрупкой, \(f \in T_2\) может быть выбрано в качестве замещающего ребра для не более одного ребра в \(T_1\). С этим ограничением Donghyun хочет защитить как можно больше ребер в \(T_1\). Формально, пусть \(E(T)\) — множество ребер дерева \(T\). Рассмотрим двудольный граф с двумя долями \(E(T_1)\) и \(E(T_2)\). Для \(e \in E(T_1), f \in E(T_2)\), существует ребро, соединяющее \(\{e, f\}\) тогда и только тогда, когда граф \(T_1 - \{e\} + \{f\}\) — дерево. Вы должны найти максимальное паросочетание в этом двудольном графе. Выходные данные В первой строке выведите целое число \(m\) (\(0 \leq m < n\)), размер максимального по размеру паросочетания. В следующих \(m\) строках выведите по четыре целых числа \(a_i, b_i, c_i, d_i\). Эти четыре целых числа описывают, что ребро \((a_i, b_i)\) из \(T_1\) объединено в пару с ребром \((c_i, d_i)\) из \(T_2\). Все выведенные ребра должны принадлежать соответствующим деревьям, и все выведенные ребра одного дерева должны быть различными. Если убирают ребро \((a_i, b_i)\) из \(T_1\) и добавляют ребро \((c_i, d_i)\) из \(T_2\), то сеть должна оставаться связной. Порядок выведенных пар и порядок вершин внутри ребер не имеет значения. Если есть несколько возможных решений, вы можете вывести любое. | |
![]()
|
|
F. Призыв существ
Потоки
Паросочетания
Конструктив
дп
жадные алгоритмы
сортировки
*2500
Поликарп играет в компьютерную игру. В этой игре игроки призывают армии магических существ и сражаются с армиями существ других игроков. Поликарп может призвать \(n\) разных существ, \(i\)-е существо изначально имеет силу \(a_i\); кроме того, когда Поликарп призывает его, оно увеличивает на \(b_i\) силу всех ранее призванных существ (исключая себя). Поликарп может призывать существ в любом порядке. Однако под контролем Поликарпа может находиться не более \(k\) существ одновременно. Поэтому, помимо призыва существ, он может уничтожать ранее призванных существ. Каждое существо может быть призвано (а, значит, и уничтожено) не более одного раза. Цель Поликарпа — собрать максимально сильную армию существ. Он хочет, чтобы после всех его действий суммарная сила всех призванных (но не уничтоженных) им существ была максимально возможной. Помогите Поликарпу составить оптимальную последовательность действий, чтобы собрать максимально сильную армию! Выходные данные Для каждого набора тестовых данных выведите оптимальную последовательность действий в следующем формате: Сначала выведите \(m\) — количество действий, которые должен совершить Поликарп (\(0 \le m \le 2n\)). После этого выведите \(m\) целых чисел \(o_1\), \(o_2\), ..., \(o_m\), где \(o_i\) описывает \(i\)-е действие следующим образом: если \(i\)-е действие — это «призвать существо \(x\)», то \(o_i = x\), а если \(i\)-е действие — это «уничтожить существо \(x\)», то \(o_i = -x\). Каждое существо может быть призвано не более одного раза и не может быть уничтожено, если оно еще не призвано (или уже уничтожено). После каждого действия под контролем Поликарпа должно быть не более \(k\) существ. Если оптимальных последовательностей действий несколько, выведите любую из них. Примечание Рассмотрим пример из условия. В первом наборе тестовых данных можно сначала вызвать существо \(2\) с силой \(7\), затем призвать существо \(1\), которое увеличит силу предыдущего существа на \(3\), после этого уничтожить существо \(1\) и поставить существо \(5\). В итоге у Поликарпа будут два существа с силой \(10\). Во втором наборе тестовых данных у Поликарпа не может быть более одного существа под контролем, поэтому достаточно выбрать самое сильное существо и призвать его. В третьем наборе тестовых данных Поликарп может призвать всех существ, никого не уничтожая. | |
![]()
|
|
C. Похожие пары
Паросочетания
Конструктив
*1100
жадные алгоритмы
сортировки
Назовем два числа \(x\) и \(y\) похожими, если они имеют одинаковую четность (одинаковый остаток при делении на \(2\)), или если \(|x-y|=1\). Например, в каждой из пар \((2, 6)\), \((4, 3)\), \((11, 7)\) числа похожи между собой, а в парах \((1, 4)\), \((3, 12)\) — нет. Вам дан массив \(a\) из \(n\) (число \(n\) четно) целых положительных чисел. Проверьте, существует ли такое разбиение массива на пары, что каждый элемент массива принадлежит ровно одной паре, и в каждой паре числа похожи между собой. Например для массива \(a = [11, 14, 16, 12]\) существует разбиение на пары \((11, 12)\) и \((14, 16)\). Числа в первой паре похожи, потому что модуль их разности равен единице, а во второй паре — потому что они оба четные. Выходные данные Для каждого набора тестовых данных выведите: - YES, если разбиение существует;
- NO, если разбиения не существует.
Буквы в словах YES и NO можно выводить в любом регистре. Примечание Первый набор тестовых данных примера разобран в условии. Во втором наборе два заданных числа не являются похожими. В третьем наборе подходит любое разбиение. | |
![]()
|
|
G. Изменение дерева
Паросочетания
Деревья
Перебор
Конструктив
*2800
поиск в глубину и подобное
графы
Вам дано дерево с \(n\) вершинами. Вы можете изменить строение дерева с помощью следующей многошаговой операции: - Выберите три вершины \(a\), \(b\) и \(c\) такие, чтобы \(b\) соединена ребром и с \(a\) и с \(c\).
- Для каждой вершины \(d\) кроме \(b\), которая соединена ребром с \(a\), удалите ребро, соединяющее \(d\) и \(a\), и добавьте ребро, соединяющее \(d\) и \(c\).
- Удалите ребро, соединяющее \(a\) и \(b\), и добавьте ребро, соединяющее \(a\) и \(c\).
В качестве примера рассмотрим следующее дерево: 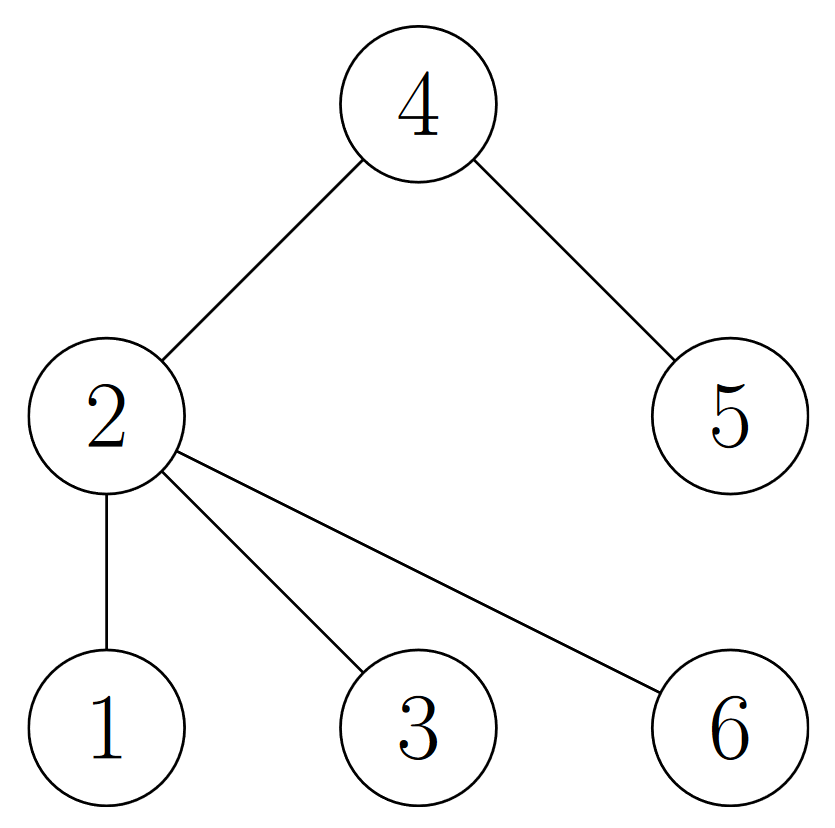 Следующая диаграмма иллюстрирует последовательность шагов, которые происходят, когда мы применяем операцию к вершинам \(2\), \(4\) и \(5\): 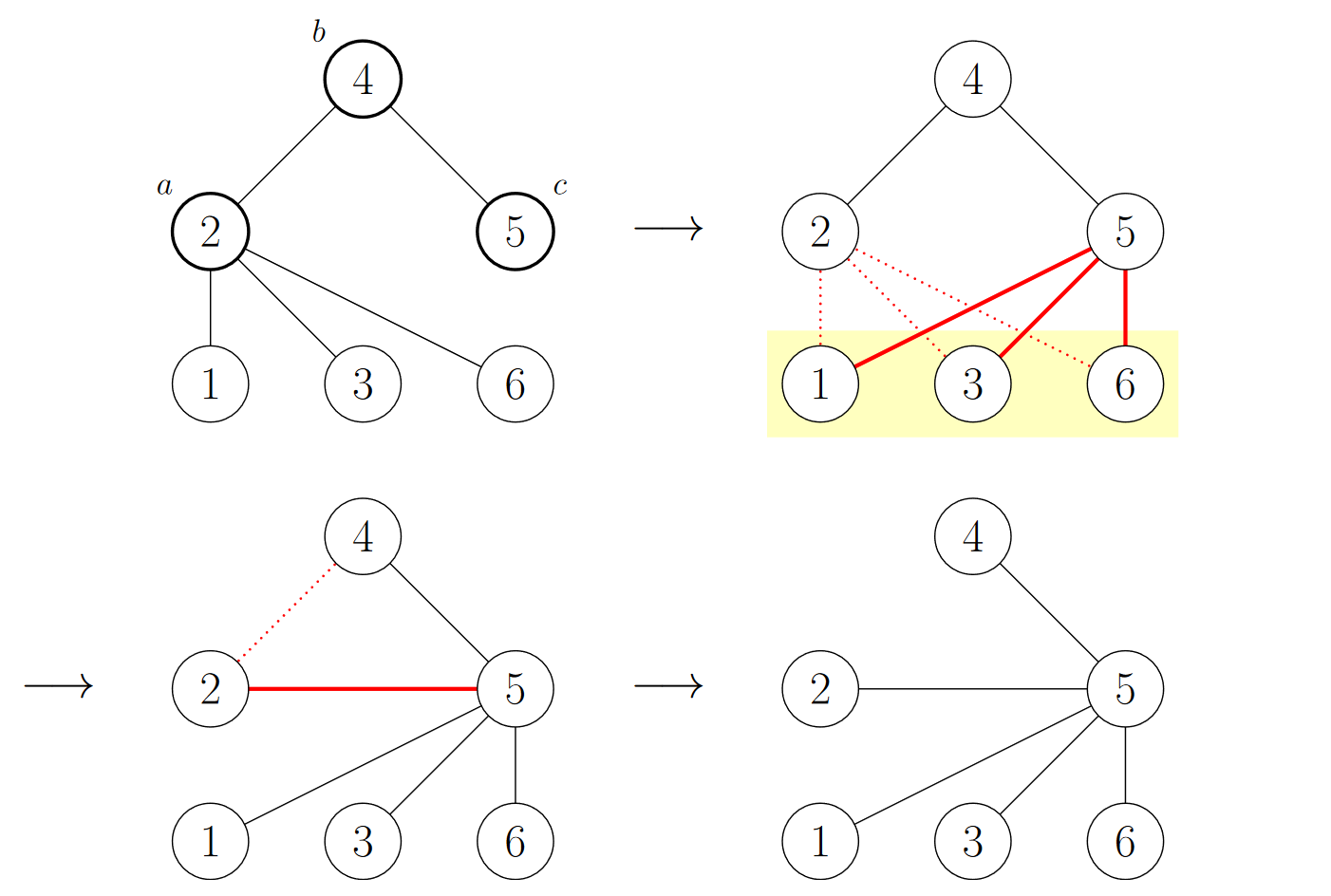 Можно доказать, что после каждой операции полученный граф все еще является деревом. Найдите минимальное количество операций, которые необходимо выполнить, чтобы превратить дерево в звезду. Звезда — это дерево с одной вершиной степени \(n - 1\), называемой его центром, и \(n - 1\) вершинами степени \(1\). Выходные данные Выведите единственное целое число — минимальное количество операций, необходимое для преобразования дерева в звезду. Можно доказать, что при данных ограничениях всегда можно превратить дерево в звезду, используя не более \(10^{18}\) операций. Примечание Первый пример соответствует дереву из условия. Как мы уже видели, мы можем превратить дерево в звезду с центром в вершине \(5\), применив одну операцию к вершинам \(2\), \(4\) и \(5\). Во втором тестовом примере данное дерево уже является звездой с центром в вершине \(4\), поэтому никаких операций выполнять не нужно. | |
![]()
|
|
C. Гениальный шифр
Паросочетания
Конструктив
реализация
жадные алгоритмы
сортировки
*2500
В игре «Гениальный шифр» есть два игрока — Алиса и Боб. У Алисы есть секретный код, который Боб хочет отгадать. Код определяется последовательностью из \(n\) цветов. Всего существует \(n+1\) цвет, они пронумерованы целыми числами от \(1\) до \(n+1\). После того как Боб сделал свою догадку, Алиса говорит ему некоторую информацию о том, насколько его код правильный, в виде двух целых чисел \(x\) и \(y\). Первое число \(x\) равно количеству индексов, в которых цвет кода Боба совпал с правильным цветом в коде Алисы. Второе число \(y\) равно размеру пересечения двух кодов, как мультимножеств. Другими словами, если Боб может поменять порядок цветов в его догадке, \(y\) равно максимальному количеству правильных индексов, которое он сможет получить. Например, допустим \(n=5\), код Алисы будет \([3,1,6,1,2]\) и догадка Боба будет \([3,1,1,2,5]\). В позициях \(1\) и \(2\) цвета совпали, тогда как в других позициях нет. Поэтому \(x=2\). И два кода имеют четыре общих цвета \(1,1,2,3\), поэтому \(y=4\). 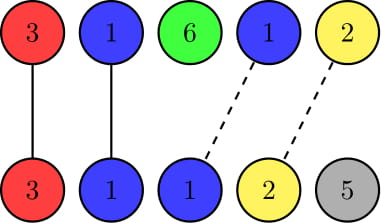 Обычные линии обозначают совпадающие цвета на одинаковых позициях. Пунктирные линии обозначают одинаковые цвета на разных позициях. Тогда \(x\) равно количеству обычных линий и \(y\) равно количеству всех линий. Обычные линии обозначают совпадающие цвета на одинаковых позициях. Пунктирные линии обозначают одинаковые цвета на разных позициях. Тогда \(x\) равно количеству обычных линий и \(y\) равно количеству всех линий. Вам дан код-догадка Боба и два значения \(x\) и \(y\). Можете ли вы найти какой-то возможный загаданный код Алисы, такой что числа \(x\) и \(y\) будут правильными? Выходные данные Для каждого набора входных данных в первой строке выведите «YES», если существует решение или «NO», если не существует ни одного секретного кода Алисы, соответствующего данной ситуации. Вы можете вывести каждый символ в любом регистре (верхнем или нижнем). Если ответ «YES», на следующей строке выведите \(n\) целых чисел \(a_1,\ldots,a_n\) (\(1\le a_i\le n+1\)) — секретный код Алисы, где \(a_i\) равно \(i\)-у цвету этого кода. Если существует несколько возможных решений, выведите любое. Примечание Первый набор входных данных описан в условии. Во втором наборе в входных данных \(x=3\), потому что цвета совпадают на позициях \(2,4,5\). И \(y=4\), потому что цвета \(1,1,1,2\) общие у двух кодов. В третьем наборе входных данных \(x=0\), потому что цвета не совпадают ни в одной из позиций. Но \(y=4\), потому что цвета \(3,3,5,5\) общие у двух кодов. В четвертом наборе входных данных можно показать что ни одного подходящего секретного кода Алисы не существует. | |
![]()
|
|
F. Двухцветные отрезки
Паросочетания
Структуры данных
дп
*2600
сортировки
Вам задано \(n\) отрезков \([l_1, r_1], [l_2, r_2], \dots, [l_n, r_n]\). Каждый отрезок одного из двух цветов: \(i\)-й отрезок покрашен в цвет \(t_i\). Назовем пару отрезков \(i\) и \(j\) плохой, если выполняются два условия: - \(t_i \ne t_j\);
- отрезки \([l_i, r_i]\) и \([l_j, r_j]\) пересекаются, касаются или вкладываются, т. е. существует целое число \(x\), такое, что \(x \in [l_i, r_i]\) и \(x \in [l_j, r_j]\).
Определите, какое максимальное количество отрезков из заданных можно выбрать так, чтобы среди выбранных не было ни одной плохой пары. Выходные данные Выведите максимальное количество отрезков, которые можно выбрать так, чтобы среди выбранных отрезков не было ни одной плохой пары. | |
![]()
|
|
E. Кирпичи
Потоки
Паросочетания
*2800
графы
Кирпич — прямоугольник с целыми сторонами шириной \(1\) или высотой \(1\) (или и то и другое). Дана сетка \(n\times m\), и каждая ячейка окрашена в черный или белый цвет. Замощение — это способ поместить кирпичи на сетку так, чтобы каждая черная ячейка была покрыта ровно одним кирпичом, а каждая белая ячейка не была покрыта кирпичом. Другими словами, кирпичи размещаются только в черных ячейках, покрывают все черные ячейки, и никакие два кирпича не перекрываются. 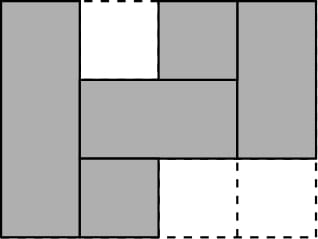 Пример замощения с первого примера с использованием \(5\) кирпичей. Существует также замощение из \(4\) кирпичей. Пример замощения с первого примера с использованием \(5\) кирпичей. Существует также замощение из \(4\) кирпичей. Какое минимальное количество кирпичей необходимо для замощения данной сетки? Выходные данные Выведите единственное целое число — минимальное количество требуемых кирпичей. Примечание Сетка с первого примера может быть замощена \(4\)-мя кирпичами, размещенными вертикально. Сетка с третьего примера может быть замощена такими \(18\) кирпичами: 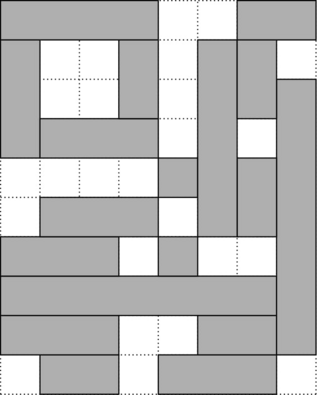 | |
![]()
|
|
F. Понты
Потоки
Паросочетания
реализация
жадные алгоритмы
*3300
В очередной скучный день карантина BThero принялся изучать матрицы размера \(n \times m\). Строки матрицы нумеруются от \(1\) до \(n\) сверху вниз, а столбцы нумеруются от \(1\) до \(m\) слева направо. Клетка в \(i\)-й строке и \(j\)-м столбце обозначается \((i, j)\). Для каждой клетки \((i, j)\) матрицы у BThero были два значения: - ценность данной клетки, которая выражается одним положительным целым числом;
- направление данной клетки, которое выражается одним из символов L, R, D, U. Данные символы означают переходы в соседние клетки \((i, j - 1)\), \((i, j + 1)\), \((i + 1, j)\), \((i - 1, j)\), соответственно. Никакой переход не вел за границу матрицы.
Назовем клетку \((i_2, j_2)\) достижимой из \((i_1, j_1)\), если, начав из клетки \((i_1, j_1)\) и переходя в соседнюю клетку в соответствии с направлением текущей клетки, мы рано или поздно посетим \((i_2, j_2)\). BThero решил создать еще одну матрицу из имеющихся двух. Для клетки \((i, j)\) обозначим \(S_{i, j}\) как множество достижимых из нее клеток (включая саму клетку \((i, j)\)). Значение новой матрицы в клетке \((i, j)\) будет равно сумме ценностей всех клеток из \(S_{i, j}\). Быстро посчитав новую матрицу, BThero разослал ее всем своим друзьям. Однако он не сохранил обе изначальные матрицы! Помогите ему восстановить любые две изначальные матрицы, из которых могла получиться заданная. Выходные данные Для каждого набора, если ответа не существует выведите одну единственную строку NO. Иначе выведите строку YES и две матрицы в таком же формате, как и во вводе. - Первая матрица должна быть матрицей ценностей, а вторая должна быть матрицей направлений.
- Все числа в матрице ценностей должны быть положительными.
- Все буквы в матрице направлений должны быть допустимыми. Никакой переход не должен указывать за границы матрицы.
| |
![]()
|
|
B. Valuable Paper
Бинарный поиск
Потоки
Паросочетания
*1900
графы
The pandemic is upon us, and the world is in shortage of the most important resource: toilet paper. As one of the best prepared nations for this crisis, BubbleLand promised to help all other world nations with this valuable resource. To do that, the country will send airplanes to other countries carrying toilet paper. In BubbleLand, there are \(N\) toilet paper factories, and \(N\) airports. Because of how much it takes to build a road, and of course legal issues, every factory must send paper to only one airport, and every airport can only take toilet paper from one factory. Also, a road can't be built between all airport-factory pairs, again because of legal issues. Every possible road has number \(d\) given, number of days it takes to build that road. Your job is to choose \(N\) factory-airport pairs, such that if the country starts building all roads at the same time, it takes the least amount of days to complete them. Output If there are no solutions, output -1. If there exists a solution, output the minimal number of days to complete all roads, equal to maximal \(d\) among all chosen roads. | |
![]()
|
|
C. Шеф Монокарп
Потоки
Паросочетания
математика
дп
*1800
жадные алгоритмы
сортировки
Шеф Монокарп только что поставил \(n\) блюд на плиту. Он знает, что оптимальное время готовки \(i\)-го блюда равно \(t_i\) минут. В любую положительную целую минуту \(T\) Монокарп может снять не более одного блюда с плиты. Если достать \(i\)-е блюдо в некоторую минуту \(T\), то его испорченность будет равна \(|T - t_i|\) — модуль значения разности между \(T\) и \(t_i\). Как только блюдо снято с плиты, его уже нельзя поставить обратно. Монокарп должен снять все блюда с плиты. Какую минимальную суммарную испорченность он может получить? Выходные данные На каждый набор входных данных выведите одно целое число — минимальную суммарную испорченность блюд, которую может получить Монокарп, когда снимет все блюда с плиты. Помните, что Монокарп может снимать блюда только в положительные целые минуты и не более одного в минуту. Примечание В первом наборе входных данных Монокарп может снять блюда в минуты \(3, 1, 5, 4, 6, 2\). Тогда суммарная испорченность будет равна \(|4 - 3| + |2 - 1| + |4 - 5| + |4 - 4| + |6 - 5| + |2 - 2| = 4\). Во втором наборе входных данных Монокарп может снять блюда в минуты \(4, 5, 6, 7, 8, 9, 10\). В третьем наборе входных данных Монокарп может снять блюдо в минут \(1\). В четвертом наборе входных данных Монокарп может снять блюда в минуты \(5, 1, 2, 4, 3\). В пятом наборе входных данных Монокарп может снять блюда в минуты \(1, 3, 4, 5\). | |
![]()
|
|
D. Странное расселение
Паросочетания
Конструктив
поиск в глубину и подобное
жадные алгоритмы
графы
*2200
В ЛКШ на территории Летово школьники будь жить в домиках. Некоторые пары домиков соединены крытыми переходами, по которым можно перемещаться в обоих направлениях. В некоторых из этих домиках будут жить преподаватели, но из соображений безопасности они не могут быть размещены произвольным образом. А именно, должны выполняться следующие условия: - Каждый переход между домами, ни в одном из которых не живут преподаватели, будет закрыт. Все остальные переходы будут открыты.
- От любого дома до другого должен существовать способ добраться по открытым переходам.
- Преподаватели не могут жить в домах, соединённых переходом.
Помогите организаторам выбрать домики, в которых будут жить преподаватели, так, чтобы выполнялись все требования безопасности, или определите, что это невозможно. Выходные данные Для каждого набора входных данных в первой строке выведите «YES», если организаторы могут поселить преподавателей так, чтобы выполнялись требования безопасности, и «NO» в противном случае. Если ответ «YES», то во второй строке выведите количество домов, в которые нужно поселить преподавателей, а в третьей строке — номера выбранных домов. Примечание Следующая картинка соответствует второму примеру из условия:  | |
![]()
|
|
F. Новогодняя головоломка
Паросочетания
Перебор
*2100
дп
жадные алгоритмы
сортировки
Каждый год Дед Мороз дарит подарки всем детям. Однако в каждой стране есть свои традиции, и этот процесс происходит по разному. Например в Берляндии нужно решить новогоднюю головоломку. Поликарпу досталась следующая задача: дана клетчатая полоска размером \(2 \times n\), некоторые клетки на ней заблокированы. Нужно проверить, можно ли замостить все незаблокированные клетки с помощью дощечек \(2 \times 1\) и \(1 \times 2\). Например, если \(n = 5\) и полоска имеет следующий вид (черные клетки заблокированы):  То ее можно замостить, например, используя две вертикальных и две горизонтальных, как на картинке ниже (разные дощечки обозначаются разным цветом).  А если \(n = 3\) и полоска имеет следующий вид:  То замостить свободные клетки невозможно. Поликарп легко справился с этой задачей и получил свой новогодний подарок. А сможете ли вы решить ее? Выходные данные Для каждого набора входных данных в отдельной строке выведите: - «YES», если можно ли замостить все незаблокированные клетки с помощью дощечек \(2 \times 1\) и \(1 \times 2\);
- «NO» в противном случае.
Вы можете выводить «YES» и «NO» в любом регистре (например, строки yEs, yes, Yes и YES будут распознаны как положительный ответ). Примечание Первые два набора входных данных разобраны в условии. В третьем наборе входных данных полоска выглядит следующим образом  Несложно убедиться, что свободные клетки на ней нельзя замостить | |
![]()
|
|
D. Кресла
Потоки
Паросочетания
дп
*1800
жадные алгоритмы
В ряд стоят \(n\) кресел, пронумерованных от \(1\) до \(n\) слева направо. Некоторые кресла заняты людьми (не более одного человека на кресло), остальные свободны. Количество занятых мест не превосходит \(\frac{n}{2}\). По некоторым причинам вы хотите пересадить людей. Если \(i\)-е кресло занято, а \(j\)-е — нет, вы можете попросить человека, сидящего в \(i\)-м кресле, пересесть в \(j\)-е кресло. Время, которое потребуется на перемещение из \(i\)-го кресла в \(j\)-е, равно \(|i - j|\) минутам. Эту операцию можно проводить любое количество раз, но операции должны выполняться последовательно, то есть вы не можете попросить человека пересесть, пока человек, которого вы попросили в предыдущей операции, еще не закончил перемещение. Вы бы хотели добиться следующей ситуации: все кресла, которые были заняты в самом начале, должны оказаться свободными. За какое минимальное время вы сможете это сделать? Выходные данные Выведите одно целое число — минимальное количество минут, за которое вы можете добиться следующей ситуации: все кресла, которые были заняты в самом начале, должны оказаться свободными. Примечание В первом примере возможна следующая последовательность действий: - попросить человека пересесть из кресла \(1\) в кресло \(2\) за \(1\) минуту;
- попросить человека пересесть из кресла \(7\) в кресло \(6\) за \(1\) минуту;
- попросить человека пересесть из кресла \(4\) в кресло \(5\) за \(1\) минуту.
Во втором примере возможна следующая последовательность действий: - попросить человека пересесть из кресла \(1\) в кресло \(4\) за \(3\) минуты;
- попросить человека пересесть из кресла \(2\) в кресло \(6\) за \(4\) минуты;
- попросить человека пересесть из кресла \(4\) в кресло \(5\) за \(1\) минуту;
- попросить человека пересесть из кресла \(3\) в кресло \(4\) за \(1\) минуту.
В третьем примере ни одно место не занято, поэтому вам не надо тратить время. | |
![]()
|
|
F. Гоблины и гномы
Потоки
Паросочетания
Перебор
дп
*2800
Монокарп играет в компьютерную игру «Гоблины и гномы». В этой игре он управляет подземным городом гномов, защищающимся от орд гоблинов. Подземный город состоит из \(n\) залов и \(m\) односторонних туннелей, соединяющих некоторые пары залов. Структура туннелей такова, что, выйдя из какого-то зала, нельзя вернуться в него обратно по тоннелям. На город готовится \(k\) атак гоблинов, в \(i\)-й атаке город атакуют \(i\) гоблинов. Цель Монокарпа — выдержать все \(k\) атак. \(i\)-я атака происходит следующим образом: сначала \(i\) гоблинов появляются в каких-то залах города и грабят их, при этом в каждом зале появляется не более одного гоблина. После этого гоблины начинают перемещаться из зала в зал по туннелям, попутно грабя каждый зал на своем пути. Гоблины очень жадные и хитрые, а поэтому планируют выбирать свои стартовые залы и пути так, что никакие два гоблина не пройдут через один и тот же зал. При этом, среди всех возможных планов атаки они выбирают такой, что позволяет в сумме разграбить максимальное количество залов. После того как гоблины разграбили максимальное количество залов, они покидают город. Если в результате атаки все залы оказались разграблены — Монокарп проигрывает. Иначе гномам удается восстановить город. Если какой-то зал оказался разграблен в ходе атаки, то в ходе следующих атак он все равно представляет интерес для гоблинов (гномы успевают восстановить его). Перед каждой атакой у Монокарпа есть время для подготовки. Монокарп может готовиться бесконечно долго (он сам решает, когда вызвать каждую атаку), но чем дольше он готовится к атаке, тем меньше очков он получает. Если Монокарп готовился к \(i\)-й атаке \(t_i\) минут, то после нее он получает \(\max(0, x_i - t_i \cdot y_i)\) очков (естественно, если он не проигрывает). Во время подготовки к атаке Монокарп может блокировать туннели. За одну минуту он может заблокировать либо все туннели, ведущие в некоторый зал, либо все туннели, ведущие из некоторого зала. Если Монокарп заблокировал какой-то туннель во время подготовки к атаке, то этот туннель остается заблокированным и во время следующих атак. Помогите Монокарпу выдержать все \(k\) атак гоблинов и набрать максимальное количество очков! Выходные данные Выведите оптимальную последовательность действий Монокарпа в следующем формате: В первой строке выведите целое число \(a\) (\(k \le a \le 2n + k\)) — количество действий, которые совершает Монокарп. Во второй строке выведите сами эти действия в том порядке, в котором Монокарп их выполняет. \(i\)-е действие описывается целым числом \(b_i\) (\(-n \le b_i \le n\)) в следующем формате: - если \(b_i > 0\), то Монокарп блокирует все туннели, ведущие из зала \(b_i\);
- если \(b_i < 0\), то Монокарп блокирует все туннели, ведущие в зал \(|b_i|\);
- если \(b_i = 0\), то Монокарп вызывает очередную атаку гоблинов.
Нельзя повторять одно и то же действие по блокировке \(b_i\) несколько раз. Каждый раз, когда Монокарп вызывает очередную атаку гоблинов, он должен выдержать ее (у гоблинов не должно быть возможности разграбить все залы города). Монокарп должен выдержать ровно \(k\) атак и получить максимально возможное количество очков. Если существует несколько оптимальных последовательностей действий — выведите любую из них. Примечание В первом примере Монокарп сначала блокирует все туннели, ведущие в зал \(2\), а потом — все туннели, ведущие в зал \(3\), после чего вызывает все атаки. Он готовился к атаке \(1\) две минуты, поэтому он получает за нее \(98\) очков. К остальным атакам он не готовился, поэтому получает максимально возможные очки за них (\(200\), \(10\) и \(100\)). Суммарно он набирает \(408\) очков. Во втором примере Монокарп сразу вызывает первую атаку и получает за нее \(100\) очков. Перед второй атакой он блокирует все туннели, ведущие в зал \(3\). Это означает, что он готовится к ней одну минуту и получает \(195\) очков за нее. К третьей атаке Монокарп не готовится и получает \(10\) очков. Перед четвертой атакой он блокирует туннели, ведущие из зала \(1\), это означает, что он готовится к атаке одну минуту и получает за нее \(99\) очков. Суммарно он набирает \(404\) очка. В третьем примере Монокарпу не важно, сделает он одно действие или несколько перед единственной атакой, так как он в любом случае не получит за нее очков. А потому блокирует все туннели в городе, потратив на это целых \(5\) минут и переживает атаку, не получив за нее очков. | |
![]()
|
|
I. Экскурсии
Потоки
Паросочетания
Конструктив
*особая задача
поиск в глубину и подобное
графы
Ирина работает в экскурсионной компании Саратова. Сегодня она собирается организовать экскурсии по городам Саратов и Энгельс. Всего существует \(n_1\) достопримечательность в Саратове и \(n_2\) достопримечательность в Энгельсе. Города разделены рекой, но есть \(m\) автобусных маршрутов, которые проходят по мостам и позволяют туристам добраться из Саратова в Энгельс и обратно. Маршрут \(i\)-го автобуса проходит от \(x_i\)-й достопримечательности в Саратове до \(y_i\)-й достопримечательности в Энгельсе, а также в обратном направлении. Ирина хочет спланировать экскурсии на текущий день. Экскурсионные поездки начинаются в Саратове утром, продолжаются в Энгельсе днем и заканчиваются в Саратове вечером. Каждый турист начинает свой экскурсионный день с какой-нибудь достопримечательности Саратова, \(k_i\) туристов начинают с \(i\)-й достопримечательности. Затем гиды везут их в Энгельс: на каждой достопримечательности Саратова гид выбирает автобусный маршрут, ведущий от этой достопримечательности в Энгельс, и все туристы, отправляющиеся с этой достопримечательности, отправляются в Энгельс по этому автобусному маршруту. После завершения экскурсий в Энгельсе происходит то же самое: для каждой достопримечательности в Энгельсе гид выбирает автобусный маршрут, ведущий от этой достопримечательности в Саратов, и все туристы с этой достопримечательности отправляются в Саратов по этому автобусному маршруту. Этот процесс может привести к такой ситуации, что некоторые туристы вернутся к той же достопримечательности в Саратове, с которой они начали утром. Очевидно, туристам это не нравится, поэтому Ирина хочет выбрать, куда гиды повезут туристов (как по дороге из Саратова в Энгельс, так и по дороге из Энгельса в Саратов), чтобы минимально возможное количество туристов вернулось к той же достопримечательности, с которой они начали. Помогите Ирине найти оптимальный план! Выходные данные Выведите одно целое число — минимально возможное количество туристов, которые вернутся к тому же месту, откуда они начали. | |
![]()
|
|
C. AquaMoon и перестановки
Паросочетания
Перебор
Конструктив
Комбинаторика
*2800
графы
2-sat
Cirno подготовила \(n\) массивов длины \(n\) каждый. Каждый массив — это перестановка из \(n\) целых чисел от \(1\) до \(n\). Эти массивы специальные: для всех \(1 \leq i \leq n\), если мы возьмем \(i\)-й элемент каждого массива и построим другой массив длины \(n\), состоящий из этих элементов, получившийся массив также будет перестановкой \(n\) чисел от \(1\) до \(n\). Другими словами, если эти \(n\) массивов расположить друг под другом, образовав матрицу с \(n\) строками и \(n\) столбцами, эта матрица будет латинским квадратом. После этого Cirno добавила дополнительные \(n\) массивов, каждый массив также является перестановкой из \(n\) целых чисел от \(1\) до \(n\). Для всех \(1 \leq i \leq n\) существует хотя бы одна позиция \(1 \leq k \leq n\), такая что для \(i\)-го и \((n + i)\)-го массивов \(k\)-е элементы совпадают. Обратите внимание, что массивы с индексами от \(n + 1\) до \(2n\) не обязаны образовывать латинский квадрат. Также Cirno убедилась, что среди \(2n\) массивов никакие два не равны, то есть для всех пар индексов \(1 \leq i < j \leq 2n\) существует хотя бы одна позиция \(1 \leq k \leq n\), такая что в \(i\)-м и \(j\)-м массивах \(k\)-е элементы различны. В конце Cirno произвольно поменяла порядок, в котором расположены подготовленные \(2n\) массивов. AquaMoon называет подмножество всех \(2n\) массивов размера \(n\) хорошим, если эти массивы образуют латинский квадрат. AquaMoon хочет узнать, сколько хороших подмножеств существует. Поскольку это количество может быть очень большим, найдите его по модулю \(998\,244\,353\). Также она хочет найти любое хорошее подмножество. Можете ли вы помочь ей? Выходные данные Для каждого набора входных данных выведите две строки. В первой строке выведите количество хороших подмножеств по модулю \(998\,244\,353\). Во второй строке выведите \(n\) индексов от \(1\) до \(2n\) — индексы \(n\) массивов, которые образуют хорошее подмножество (вы можете вывести их в любом порядке). Если существует несколько возможных ответов — выведите любой. Примечание В первом наборе входных данных количество хороших подмножеств равно \(1\). Единственное такое подмножество это подмножество массивов с индексами \(1\), \(2\), \(3\), \(4\), \(5\), \(6\), \(7\). Во втором наборе входных данных количество хороших подмножеств равно \(2\). Эти подмножества это \(1\), \(3\), \(5\), \(6\), \(10\), а также \(2\), \(4\), \(7\), \(8\), \(9\). | |
![]()
|
|
B. Грегор и игра в пешки
Потоки
Паросочетания
реализация
дп
поиск в глубину и подобное
жадные алгоритмы
графы
*800
Дана шахматная доска размера \(n\) на \(n\). Клетка на пересечении \(i\)-й сверху ряду и \(j\)-го слева столбца обозначается как \((i,j)\). На данный момент у Грегора есть несколько пешек в \(n\)-м ряду. Также в \(1\)-м ряду стоят вражеские пешки. За один шаг Грегор перемещает одну из своих пешек. Пешка может ходить на одну клетку вверх (из \((i,j)\) в \((i-1,j)\)), если клетка назначения не занята другой пешкой. В дополнение, пешка может переместиться на одну клетку вверх по диагонали (из \((i,j)\) в \((i-1,j-1)\) или в \((i-1,j+1)\)), если и только если в этой клетке стоит вражеская пешка. Вражеская пешка в таком случае убирается с доски. Грегор хочет узнать, какое максимальное количество его пешек может достичь \(1\)-го ряда. Заметьте, что в этой игре ходит только Грегор, вражеские пешки никогда не перемещаются. Также, когда пешка Грегора достигает \(1\)-го ряда, она останавливается и больше не может перемещаться. Выходные данные Для каждого набора входных данных выведите одно целое число: максимальное количество пешек Грегора, которые могут достичь \(1\)-го ряда. Примечание В первом примере Грегор может просто переместить вперед все его \(3\) пешки. Таким образом, ответ равен \(3\). Во втором примере Грегор может гарантировать, что все его \(4\) пешки достигнут вражеского ряда, следуя раскрашенным путям как показано ниже. Помните — только Грегор делает ходы в этой «игре»! 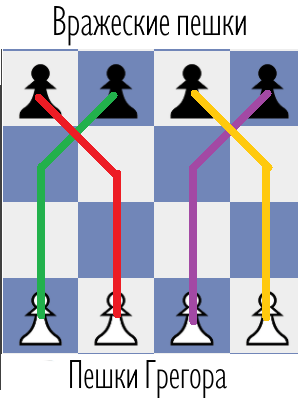 В третьем примере единственная пешка Грегора застряла перед вражеской пешкой и не может достигнуть желаемого ряда. В четвертом примере у Грегора нет пешек, поэтому ответ равен \(0\). | |
![]()
|
|
D. Бридж-клуб
Потоки
Паросочетания
*2800
жадные алгоритмы
графы
В местном бридж-клубе сейчас спорят на \(n\) различных тем, пронумерованных от \(0\) до \(n-1\), и, вот совпадение, в клубе состоят ровно \(2^n\) игроков, пронумерованных от \(0\) до \(2^n-1\). Никакие два игрока не имеют полностью совпадающих взглядов на все \(n\) тем, а именно, у \(i\)-го игрока положительный взгляд на \(j\)-ю тему, если \(i\ \&\ 2^j > 0\), и отрицательный взгляд иначе. Здесь \(\&\) обозначает операцию побитового И. Вы хотите организовать турнир по бриджу, в котором примут участие не более чем \(k\) пар игроков (в бридж играют командами из двух игроков). Вы можете составлять пары игроков произвольным образом (каждый игрок должен быть не более чем в одной паре), но с одним условием: два игрока не могут быть в одной паре, если у них различные взгляды на \(2\) или более из данных \(n\) тем. Вы знаете, что \(i\)-й игрок заплатит вам \(a_i\) долларов, если примет участие в турнире. Вычислите максимальную сумму, которую можно получить, выбрав команды оптимальным образом. Выходные данные Выведите одно целое число: максимальную сумму, которую вы можете получить, если составите команды оптимальным образом. Примечание В первом примере оптимальное решение — поставить в пару \(0\)-го и \(2\)-го игрока, что принесет \(8 + 5 = 13\) долларов. Хотя \(0\)-й и \(5\)-й игроки принесли бы вместе \(8 + 10 = 18\) долларов, мы их не можем объединить в команду, так как их взгляды отличаются в \(2\) из \(3\) тем. Во втором примере можно объединить в команду \(0\)-го и \(1\)-го игрока, а также \(2\)-го и \(3\)-го игрока, что в сумме даст \(7 + 4 + 5 + 7 = 23\) долларов. | |
![]()
|
|
E. Момент цветения
Паросочетания
Деревья
Конструктив
поиск в глубину и подобное
жадные алгоритмы
графы
*2200
Она делает все возможное, чтобы безупречно провести последний обряд человека и сохранить баланс инь и ян в мире. Ху Тао, будучи маленькой проказницей, попыталась напугать вас этой задачей с графом! Вам дан связный неориентированный граф из \(n\) вершин с \(m\) ребрами. У вас также есть \(q\) запросов. Каждый запрос состоит из двух вершин \(a\) и \(b\). Изначально все ребра графа имеют вес \(0\). Для каждого запроса вы должны выбрать простой путь, начинающийся из \(a\) и заканчивающийся в \(b\). Затем к весу каждого ребра вдоль этого пути добавляется \(1\). Определите, возможно ли, чтобы после обработки всех \(q\) запросов все ребра в этом графе имели четный вес. Если да, то выведите выбор путей для каждого запроса. Если это невозможно, определите наименьшее количество дополнительных запросов, которые можно добавить, чтобы это стало возможным. Можно показать, что при заданных ограничениях это число не превысит \(10^{18}\). Простой путь определяется как любой путь, который не посещает вершину более одного раза. Считается, что ребро имеет четный вес, если его значение кратно \(2\). Выходные данные Если можно заставить все веса ребер быть четными, выведите «YES» в первой строке, а затем \(2q\) строк, указывающих выбор пути для каждого запроса в том же порядке, в котором задаются запросы. Для каждого запроса первая строка должна содержать одно целое число \(x\): количество узлов в выбранном пути. Следующая строка должна содержать \(x\) целых чисел \(p_i\), указывающих выбранный путь (\(p_1 = a, p_x = b\) и все числа должны лежать между \(1\) и \(n\)). Этот путь не может содержать одну вершину более одного раза и должен быть корректным простым путем в графе. Если невозможно заставить все веса ребер быть четными, выведите «NO» в первой строке и минимальное количество запросов, которые нужно добавить, во второй строке. Примечание Вот как выглядят запросы для первого примера (красный цвет соответствует 1-му запросу, синий — 2-му, а зеленый — 3-му): 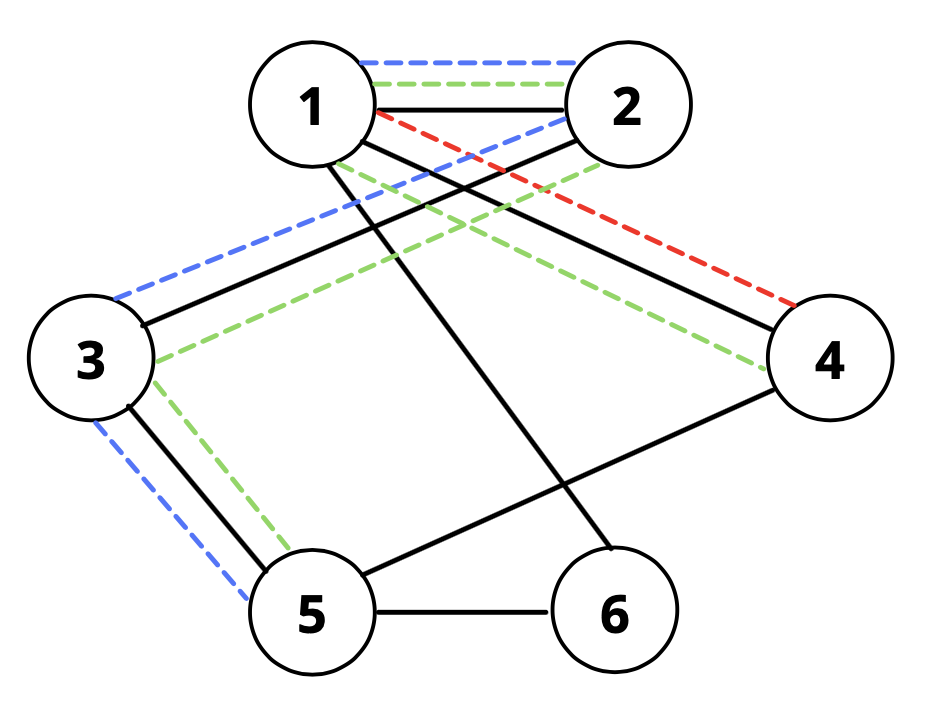 Обратите внимание, что каждое ребро в графе входит либо в \(0\), либо в \(2\) цветных пути. Граф во втором примере выглядит следующим образом: 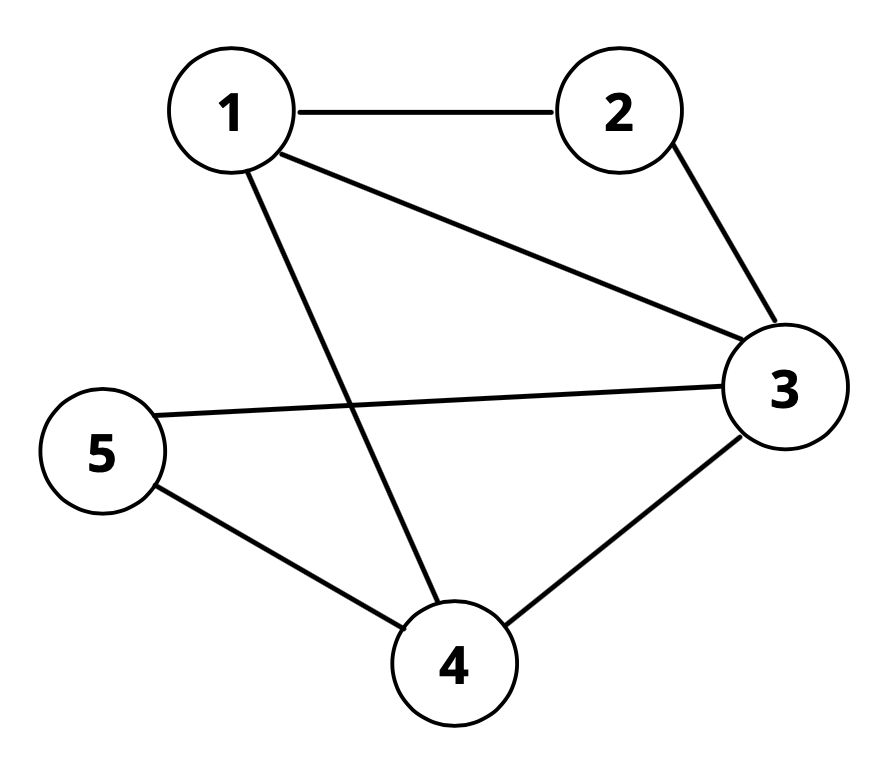 Не существует такого назначения путей, которое заставит все ребра иметь четные веса при заданных запросах. Чтобы получить набор запросов, удовлетворяющих условию, нужно добавить по крайней мере \(2\) новых запроса. | |
![]()
|
|
F2. Алиса и перекрашивание 2
Потоки
Паросочетания
Конструктив
*2800
жадные алгоритмы
Разница между версиями заключается в стоимости операций. Решение для одной версии не будет работать для другой! У Алисы есть таблица размером \(n \times m\), изначально все ее клетки окрашены в белый цвет. Клетка на пересечении \(i\)-й строки и \(j\)-го столбца обозначается как \((i, j)\). Алиса может выполнять следующие операции: Выбрать любой подпрямоугольник, содержащий клетку \((1, 1)\), и инвертировать цвета всех его клеток. (Инвертировать означает изменить цвет клетки с белого на черный или с черного на белый). Эта операция стоит \(1\) монету. Выбрать любой подпрямоугольник, содержащий клетку \((n, 1)\), и инвертировать цвета всех его клеток. Эта операция стоит \(3\) монеты. Выбрать любой подпрямоугольник, содержащий клетку \((1, m)\), и инвертировать цвета всех его клеток. Эта операция стоит \(4\) монеты. Выбрать любой подпрямоугольник, содержащий клетку \((n, m)\), и инвертировать цвета всех его клеток. Эта операция стоит \(2\) монеты.
Напомним, что подпрямоугольник — это все клетки \((x, y)\) с \(x_1 \le x \le x_2\), \(y_1 \le y \le y_2\) для некоторых \(1 \le x_1 \le x_2 \le n\), \(1 \le y_1 \le y_2 \le m\). Алиса хочет получить свою любимую раскраску с помощью этих операций. Какое наименьшее количество монет ей придется потратить? Можно показать, что всегда можно преобразовать исходную таблицу в любую другую. Выходные данные Выведите наименьшее количество монет, которое Алиса должна будет потратить, чтобы получить свою любимую раскраску. Примечание В первом примере оптимально просто применить четвертую операцию один раз к прямоугольнику, содержащему клетки \((2, 2), (2, 3), (3, 2), (3, 3)\). Это обойдется в \(2\) монеты. | |
![]()
|
|
G. Робот и конфеты
Паросочетания
Структуры данных
жадные алгоритмы
*2500
У Поликарпа есть прямоугольное поле размером \(n \times m\) клеток (размер поля \(n \cdot m\) не превышает \(10^6\) клеток, \(m \ge 2\)), в каждой клетке которого может быть конфета. Поле состоит из \(n\) строк и \(m\) столбцов. Обозначим клетку с координатами \(x\) по вертикали и \(y\) по горизонтали за \((x, y)\). Тогда левая верхняя клетка будет обозначаться как \((1, 1)\), а правая нижняя — как \((n, m)\). Если в клетке поля есть конфета, то клетка поля помечена символом «1», иначе — символом «0». Поликарп сконструировал Робота, который может собирать конфеты. Робот может переместиться из клетки \((x, y)\) либо в клетку \((x+1, y+1)\), либо в клетку \((x+1, y-1)\). Если Робот находится в клетке, в которой есть конфета, он её забирает. Пока на поле есть хотя бы одна конфета, выполняется следующий алгоритм: - Поликарп ставит Робота в произвольную клетку первой (верхней) строки поля. Он сам выбирает в какую клетку поставить Робота. Робота можно ставить в одну и ту же клетку несколько раз.
- Робот перемещается по полю и собирает конфеты. Поликарп управляет Роботом. Когда Робот покидает поле, Поликарп подбирает его.
- Если на поле есть хотя бы одна конфета, Поликарп повторяет алгоритм.
Найдите минимальное количество раз, сколько нужно ставить Робота на верхнюю строку поля, чтобы собрать все конфеты. Гарантируется, что Поликарп всегда может собрать все конфеты. Выходные данные Выведите \(t\) строк, каждая из строк должна содержать ответ на соответствующий набор входных данных: минимальное количество раз, которое Поликарпу нужно поставить Робота на верхнюю строку поля, чтобы собрать все конфеты. Примечание В первом наборе Поликарп может вообще не ставить Робота на поле, так что ответ 0 Во втором наборе Поликарпу потребуется два раза ставить робота на поле. Робот может собрать конфеты так: в первый раз Поликарп ставит Робота в клетку \((1, 1)\) соберет конфеты на позициях \((1, 1)\) и \((3, 3)\). Во второй раз Поликарп может снова поставить Робота в клетку \((1, 1)\) и тогда Робот переместится сначала в клетку \((2,2)\), затем в клетку \((3, 1)\) и соберет последнюю конфету. В четвертом наборе можно показать, что за три прохода Робот не сможет собрать все конфеты. | |
![]()
|
|
G. Максимизация пар соседей
Паросочетания
Конструктив
*3300
Вам задан массив \(a\), состоящий из \(n\) неотрицательных целых чисел. Вам нужно заменить каждый \(0\) в \(a\) на целое число от \(1\) по \(n\). Числа \(0\) в различных позициях можно заменять на различные числа. Назовем мерой полученного массива количество чисел \(k\) от \(1\) по \(n\), для которых выполняется следующее условие: существует пара соседних элементов, равных \(k\) (т. е. существует некоторый \(i \in [1, n - 1]\) такой, что \(a_i = a_{i + 1} = k\)). Если для какого-то числа \(k\) существует несколько пар соседей, то число все равно учитывается в мере только один раз. Ваша задача — получить массив с максимально возможной мерой. Выходные данные Выведите \(n\) целых чисел, каждое из которых от \(1\) по \(n\), — массив с максимально возможной мерой. Если существует несколько ответов, выведите любой из них. | |
![]()
|
|
C. Деление на два и перестановка
Потоки
Паросочетания
Конструктив
математика
*1100
жадные алгоритмы
Вам дан массив \(a\), состоящий из \(n\) целых положительных чисел. Над ним вы можете совершать операции. За одну операцию можно заменить любой элемент массива \(a_i\) на \(\lfloor \frac{a_i}{2} \rfloor\), то есть на целую часть от деления \(a_i\) на \(2\) (округление вниз). Проверьте, можно ли за произвольное количество операций (возможно, \(0\)) сделать так, чтобы массив \(a\) стал перестановкой чисел от \(1\) до \(n\) — то есть содержал все числа от \(1\) до \(n\), каждое по одному разу. Например, если \(a = [1, 8, 25, 2]\), \(n = 4\), то ответ положительный. Можно поступить так: - Заменим \(8\) на \(\lfloor \frac{8}{2} \rfloor = 4\), тогда \(a = [1, 4, 25, 2]\).
- Заменим \(25\) на \(\lfloor \frac{25}{2} \rfloor = 12\), тогда \(a = [1, 4, 12, 2]\).
- Заменим \(12\) на \(\lfloor \frac{12}{2} \rfloor = 6\), тогда \(a = [1, 4, 6, 2]\).
- Заменим \(6\) на \(\lfloor \frac{6}{2} \rfloor = 3\), тогда \(a = [1, 4, 3, 2]\).
Выходные данные Для каждого набора входных данных в отдельной строке выведите: - YES, если можно сделать так, чтобы массив \(a\) стал перестановкой чисел от \(1\) до \(n\),
- NO в противном случае.
Вы можете выводить YES и NO в любом регистре (например, строки yEs, yes, Yes и YES будут распознаны как положительный ответ). Примечание Первый тест разобран в тексте условия задачи. Во втором тесте получить искомый массив невозможно. | |
![]()
|
|
F. Сделай его двудольным!
Потоки
Паросочетания
теория чисел
графы
*3400
Дан неориентированный граф, состоящий из \(n\) вершин, пронумерованных от \(1\) до \(n\). Вершина \(i\) имеет значение \(a_i\), все \(a_i\) попарно различны. Между вершинами \(u\) и \(v\) есть ребро, если либо \(a_u\) делит \(a_v\), либо \(a_v\) делит \(a_u\). Найдите минимальное количество вершин, которое нужно удалить, чтобы граф стал двудольным. При удалении вершины удаляются все инцидентные ей ребра. Выходные данные Для каждого набора входных данных выведите одно число — минимальное количество вершин, которое нужно удалить, чтобы граф стал двудольным. | |
![]()
|
|
E. Честный делёж
Паросочетания
Структуры данных
Конструктив
поиск в глубину и подобное
*2400
графы
Even a cat has things it can do that AI cannot. — Fei-Fei Li Вам дано \(m\) массивов целых положительных чисел, длина каждого массива чётна. От вас требуется составить два равных мультимножества \(L\) и \(R\) так, чтобы каждый элемент каждого массива попал ровно в одно мультимножество. Кроме того, для каждого из \(m\) массивов ровно половина его элементов должна попасть в \(L\), а остальные — в \(R\). Приведите пример такого разбиения или определите, что такого разбиения не существует. Выходные данные В случае если ответ существует выведите «YES», а затем выведите \(m\) строк. В каждой строке для каждого элемента выведите букву «L» или «R» (обязательно заглавную, без пробелов) — в какое мультимножество должен попасть данный элемент. Если ответа не существует, в единственной строке выведите «NO». Примечание В первом массиве первый элемент мы добавляем в \(R\), а второй в \(L\). Сейчас \(L = \{2\}\), а \(R = \{1\}\). Во втором массиве первый и третий элемент мы добавляем в \(L\), а остальные в \(R\). Сейчас \(L = \{1, 2, 3\}\) и \(R = \{1, 2, 3\}\). В третьем массиве элементы 2, 3 и 6 мы добавляем в \(L\), а на остальных — в \(R\). В итоге \(L = R = \{1, 1, 2, 2, 3, 3\}\). | |
![]()
|
|
E. Сумма паросочетаний
Паросочетания
Перебор
Конструктив
Комбинаторика
математика
*2600
поиск в глубину и подобное
жадные алгоритмы
Обозначим размер максимального паросочетания в графе \(G\) как \(\mathit{MM}(G)\). Задан двудольный граф. Вершины первой доли пронумерованы от \(1\) до \(n\). Вершины второй доли пронумерованы от \(n+1\) до \(2n\). Степень каждой вершины равна \(2\). Для четверки целых чисел \((l, r, L, R)\), где \(1 \le l \le r \le n\) и \(n+1 \le L \le R \le 2n\), определим \(G'(l, r, L, R)\) как граф, который состоит из всех вершин заданного графа, которые находятся либо в отрезке \([l, r]\), либо в отрезке \([L, R]\), и всех ребер заданного графа таких, что вершины их концов принадлежат одному из этих отрезков. Другими словами, чтобы получить граф \(G'(l, r, L, R)\) из изначального графа, надо удалить все вершины \(i\) такие, что \(i \notin [l, r]\) и \(i \notin [L, R]\), и все инцидентные им ребра. Посчитайте сумму \(\mathit{MM}(G(l, r, L, R))\) по всем наборам целых чисел \((l, r, L, R)\) таких, что \(1 \le l \le r \le n\) and \(n+1 \le L \le R \le 2n\). Выходные данные Выведите одно целое число — сумму \(\mathit{MM}(G(l, r, L, R))\) по всем наборам целых чисел \((l, r, L, R)\), у которых \(1 \le l \le r \le n\) и \(n+1 \le L \le R \le 2n\). | |
![]()
|
|
E. Минимальная покрывающая звездочка
Паросочетания
Комбинаторика
математика
дп
*2200
В данной задаче мы рассматриваем полные неориентированные графы, состоящие из \(n\) вершин со взвешенными ребрами. Вес каждого ребра — это целое число от \(1\) до \(k\). Неориентированный граф называется красивым, если сумма весов всех ребер, инцидентных вершине \(1\), равна весу минимального покрывающего дерева в графе. Минимальное покрывающее дерево — это дерево, состоящее из \(n-1\) ребра графа, которое соединяет все \(n\) вершин и имеет наименьшую сумму среди всех таких деревьев; его вес равен сумме весов ребер в нем. Посчитайте количество полных красивых графов, в которых ровно \(n\) вершин и все веса ребер от \(1\) до \(k\). Так как ответ может быть большим, выведите его по модулю \(998244353\). Выходные данные Выведите одно целое число — количество полных красивых графов, в которых ровно \(n\) вершин и все веса ребер от \(1\) до \(k\). Так как ответ может быть большим, выведите его по модулю \(998244353\). | |
![]()
|
|
D. Обувной магазин
Паросочетания
дп
жадные алгоритмы
сортировки
*2500
На складе вашего магазина находятся n пар обуви, каждая пара характеризуется двумя целыми числами: ценой ci и размером si. Известно, что именно в этот день все числа si различны, то есть каждого размера имеется не более одной пары. В магазин зашли одновременно m покупателей, у покупателя номер i при себе di денег, а размер его ноги равен li. Покупатель номер i может купить себе пару номер j, если cj ≤ di, а также если li = sj или li = sj - 1; то есть необходимо, чтобы у него было достаточно денег чтобы заплатить, а также размер ноги был в точности равен или на 1 меньше, чем размер выбранной пары. Ваша задача — продать некоторым покупателям по паре обуви так, чтобы максимизировать сумму cj проданных пар, то есть прибыль. Гарантируется, что каждый покупатель возьмет не более одной пары, а каждую пару, разумеется, купит не более одного покупателя. Выходные данные В первой строке выведите единственное целое число — максимальную прибыль, которую вы сможете получить от продажи. Во второй строке выведите целое число k — количество пар обуви, которые вы продадите. Далее в k строках выведите описания проданных пар — два целых числа через пробел, где первое число означает номер покупателя, а второе — номер обуви, которую этот покупатель приобретет. Пары чисел «номер покупателя и номер обуви» можно выводить в любом порядке, покупатели и обувь нумеруются с 1 в том порядке, в котором они заданы во входных данных. Если существует несколько оптимальных ответов, то разрешается вывести любой. Пожалуйста, не используйте спецификатор %lld для чтения или записи 64-х битовых чисел на С++, вместо него рекомендуется использовать потоки cin, cout, а также спецификатор %I64d. | |
![]()
|
|
D. Волшебники и дороги
Паросочетания
Структуры данных
жадные алгоритмы
графы
разделяй и властвуй
*3000
В некоторой стране живут волшебники. Они любят строить города и дороги. Раньше в стране было k городов, j-ый (1 ≤ j ≤ k) был расположен в точке (xj, yj). Было решено наколдовать еще n - k городов. Причем i-ый (k < i ≤ n) город колдовался в точку с координатами (xi, yi): - xi = (a·xi - 1 + b) mod (109 + 9)
- yi = (c·yi - 1 + d) mod (109 + 9)
Здесь a, b, c, d — простые числа. Причем a ≠ c, b ≠ d. После постройки всех n городов, волшебники заметили удивительное свойство. Для любых двух различных городов с номерами i и j: xi ≠ xj и yi ≠ yj. Города построены, пора строить дороги! Было решено использовать самое сложное (и, конечно же, самое мощное) заклинание для постройки дорог. C использованием этого заклинания, между городами u, v (yu > yv) проводится дорога тогда и только тогда, когда для любого города w, лежащего строго внутри уголка на точках u, v (см. ниже), есть город s, не лежащий в уголке, который находится по x-координате строго между w и u и при этом ys > yv. Уголком на точках p2(x2, y2), p1(x1, y1) (y2 > y1) называется множество точек (x, y), для которых выполнено хотя бы одно из двух условий: - min(x1, x2) ≤ x ≤ max(x1, x2) и y ≥ y1
- y1 ≤ y ≤ y2 и (x - x2)·(x1 - x2) ≥ 0
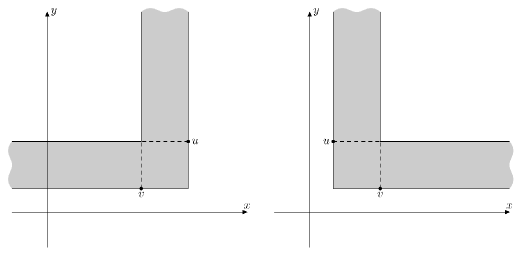 На рисунке изображены примеры уголков На рисунке изображены примеры уголков Для того, чтобы опробовать заклинание, оно будет применено ко всем городам, лежащим по x-координате в отрезке [L, R]. После постройки дорог руководство страны хочет выбрать как можно больше пар городов, соединенных дорогой, так, что никакой город не лежит в двух или более парах. Вам предлагается для каждого из m предложенных вариантов выбора значений L, R посчитать максимальное количество таких пар после постройки дорог. Обратите внимание, что города, не лежащие в отрезке [L, R] по x-координате, никак не влияют на постройку дорог. Выходные данные Для каждой пары чисел Li, Ri выведите ответ на задачу в отдельной строке. Ответы для пар выводите в том порядке, в котором пары заданы во входных данных. Примечание В первом примере дороги соединяют города в цепочку в порядке возрастания x. Во втором примере оставшиеся 5 городов будут построены в точках (5, 11); (20, 263098); (65, 292514823); (200, 76958738); (605, 622120197). | |
![]()
|
|
G. Алгоритм Люсине
Потоки
Паросочетания
Конструктив
математика
теория чисел
*2800
Принято считать, что самый известный алгоритм нахождения наибольшего общего делителя двух чисел придумал Евклид, однако на самом деле этот алгоритм придумала именно Тётя Люсине. Вы, должно быть, уже не удивились, ведь она — величайший ум человечества. И теперь она решила модернизировать этот алгоритм, привнеся в него немного креатива. А в вас есть эта жилка креатива? Рассмотрим алгоритм Люсине для нахождения наибольшего общего делителя, где \(t\) это некоторый список:
function Euclid(a, b):
if a < b:
swap(a, b)
if b == 0:
return a
r = остаток от деления a на b
if r > 0:
добавить r в конец t
return Euclid(b, r)
Существует массив \(p\) пар положительных целых чисел, каждое из них не больше \(m\). Изначально список \(t\) пустой. Описанная выше функция запускается на каждой паре из массива \(p\). После этого вам даётся перестановка элементов \(t\). Вам необходимо найти массив \(p\) любого размера не больше \(2 \cdot 10^4\) такой, что по описанному алгоритму из него получится массив \(t\), или сказать, что это невозможно. Выходные данные - Если ответа не существует, выведите \(-1\).
- Если ответ существует, в первой строке выведите \(k\) (\(1 \le k \le 2 \cdot 10^4\)) — размер массива \(p\), т. е. количество пар в вашем ответе. \(i\)-я из следующих \(k\) строк должна содержать два целых числа \(a_i\) и \(b_i\) (\(1 \le a_i, b_i \le m\)) — \(i\)-я пара массива \(p\).
Если существуют несколько решений, вы можете вывести любой из них. Примечание В первом тесте рассмотрим массив \(t\) для каждой из пар: - \((19,\, 11)\): \(t = [8, 3, 2, 1]\);
- \((15,\, 9)\): \(t = [6, 3]\);
- \((3,\, 7)\): \(t = [1]\).
Тогда в итоге \(t = [8, 3, 2, 1, 6, 3, 1]\), что совпадает с входным массивом \(t\) с точностью до перестановки. Во втором тесте невозможно найти такой массив пар \(p\), в котором все числа не превосходят \(10\) и \(t = [7, 1]\). В третьем тесте для пары \((15,\, 8)\) массив \(t\) будет \([7, 1]\). | |
![]()
|
|
E. Два массива
Бинарный поиск
Паросочетания
*2400
игры
Вам даны два массива целых чисел \(a_1,a_2,\dots,a_n\) и \(b_1,b_2,\dots,b_m\). Алиса и Боб играют в игру. Алиса ходит первой, а затем они ходят по очереди. Они играют на доске \(n \times m\) (\(n\) строк и \(m\) столбцов). Изначально в клетке в первой строке и первом столбце стоит ладья. В свой ход игрок может сделать одну из следующих двух операций: - Переместить ладью в другую клетку в том же ряду или в том же столбце с текущей клеткой. Игрок не может переместить ладью в клетку, которая уже была посещена \(1000\) раз до этого (т. е. ладья может находиться на одной клетке не более \(1000\) раз за всю игру). Обратите внимание, что стартовая клетка считается уже посещенной один раз в начале игры.
- Немедленно закончить игру со счетом \(a_r+b_c\), где \((r, c)\) — координаты текущей клетки (т. е. ладья находится в \(r\)-й строку \(c\)-м столбце).
Боб хочет максимизировать счет игры, а Алиса хочет минимизировать его. Если они оба играют оптимально, каким будет итоговый счет? Выходные данные Выведите одну строку — итоговый счет игры. Примечание В первом примере Алиса передвинет ладью на клетку \((2, 1)\), а Боб передвинет ладью обратно на клетку \((1, 1)\). Этот процесс повторится \(999\) раз, а затем, после хода Алисы, Боб не сможет передвинуть ладью обратно на клетку \((1, 1)\), так как она уже была посещена \(1000\) раз. Поэтому счет игры будет равен \(a_2+b_1=4\). Во втором примере счет игры равен \(a_3+b_5\). | |
![]()
|
|
F. Мадока и первая сессия
Потоки
Паросочетания
Конструктив
реализация
графы
*2500
О нет, на первой же сессии Мадоке попался билет со следующей сложной задачей: Дано число \(n\) и \(m\) пар чисел (\(v_i, u_i\)). А также есть массив \(b_1, b_2, \ldots, b_n\), изначально заполненный нулями. Затем для каждого индекса \(i\), где \(1 \leq i \leq m\), выполняется либо \(b_{v_i} := b_{v_i} - 1\) и \(b_{u_i} := b_{u_i} + 1\), либо \(b_{v_i} := b_{v_i} + 1\) и \(b_{u_i} := b_{u_i} - 1\). Обратите внимание, что ровно одна из этих операций должна быть выполнена для каждого \(i\). Также дан массив \(s\) размера \(n\), состоящий только из \(0\) и \(1\). И массив \(a_1, a_2, \ldots, a_n\), где гарантируется, что если \(s_i = 0\), то \(a_i = 0\). Помогите Мадоке и определите, можно ли выполнить операции выше таким образом, чтобы для каждого \(i\), где \(s_i = 1\), выполнялось \(a_i = b_i\). И если возможно, то как это сделать. Выходные данные Выведите в первой строке «YES», если можно выполнить операции нужным образом, и «NO» в противном случае. Вы можете выводить каждую букву в любом регистре (например, «YES», «Yes», «yes», «yEs» будут распознаны как положительный ответ). В случае, если вы вывели «YES», выведите \(m\) пар целых чисел. Если для пары \((v_i, u_i)\) нужно выполнить \(b_{v_i} := b_{v_i} - 1\) и \(b_{u_i} := b_{u_i} + 1\), выведите \((v_i, u_i)\). Иначе выведите \((u_i, v_i)\). Если существует несколько способов получить правильный ответ, можно вывести любой из них. Пары можно выводить в любом порядке. Примечание В первом примере массив \(b\) будет меняться следующим образом: \([0,0,0,0,0] \rightarrow [-1,0,0,1,0] \rightarrow [-2,0,0,1,1] \rightarrow [-2,0,1,0,1] \rightarrow [-2,0,2,0,0] \rightarrow [-2,0,2,1,-1]\). \(a_i = b_i\) для всех индексов \(i\) от \(1\) до \(5\). Во втором примере нам достаточно, чтобы в конце \(b_2 = 1\), поскольку только \(s_2 = 1\). В третьем примере входных данных нельзя выполнить операции нужным образом. | |
![]()
|
|
D. Перестановка для Бурёнки
Паросочетания
Деревья
Структуры данных
математика
жадные алгоритмы
*3300
Назовем массив \(a\) чистым, если в нем все элементы попарно различны. Например, массив \([1, 7, 9]\) — чистый, а \([1, 3, 3, 7]\) — нет, ведь \(3\) встречается в нем дважды. Чистый массив \(b\) похож на чистый массив \(c\), если их длина \(n\) одинакова, и для всех пар индексов \(l\), \(r\) таких, что \(1 \le l \le r \le n\), выполняется \(\)\operatorname{argmax}([b_l, b_{l + 1}, \ldots, b_r]) = \operatorname{argmax}([c_l, c_{l + 1}, \ldots, c_r]),\(\) где \(\operatorname{argmax}(x)\) — индекс наибольшего элемента в \(x\) (уникального для чистых массивов). Например, \(\operatorname{argmax}([3, 4, 2]) = 2\), \(\operatorname{argmax}([1337, 179, 57]) = 1\). Недавно Тоня узнал, что Бурёнке очень нравится перестановка \(p\) длины \(n\). Тоня решил обрадовать Бурёнку и подарить ей массив \(a\), похожий на \(p\). Он уже зафиксировал некоторые элементы \(a\), но ровно \(k\) элементов отсутствуют (в этих позициях сейчас \(a_i = 0\)). Гарантируется, что \(k \ge 2\). Кроме того, у Тони есть множество \(S\) из \(k - 1\) числа. Тоня понял, что для того, чтобы заполнить пропуски в массиве \(a\) ему не хватает одного числа, поэтому он решил купить его. У него есть \(q\) вариантов покупки. Тоня считает, что число \(d\) подходит ему, если можно заполнить пропуски в \(a\) числами из \(S\) и числом \(d\) так, чтобы \(a\) стал чистым массивом, похожим на \(p\). Для каждого варианта покупки числа \(d\) выведите, подходит ли Тоне это число или нет. Входные данные В первой строке находится единственное целое число \(t\) (\(1 \le t \le 10^4\)) — количество наборов входных данных. Далее следует описание наборов входных данных. В первой строке каждого набора входных данных содержится два целых числа \(n\) и \(q\) (\(1 \le n, q \le 3 \cdot 10^5\)) — длина перестановки и количество вариантов покупки. Во второй строке каждого набора входных данных содержатся \(n\) различных целых чисел \(p_1, p_2, \ldots, p_n\) (\(1 \le p_i \le n\)) — перестановка, которая нравится Бурёнке. В третьей строке каждого набора входных данных содержатся \(n\) целых чисел \(a_1, a_2, \ldots, a_n\) (\(0 \le a_i \le 10^6\)) — элементы массива, где \(0\) означает место, которое нужно заполнить. Гарантируется, что существуют два индекса \(i, j\) \((1 \le i, j \le n, i \ne j)\) такие, что \(a_i = 0, a_j = 0\) из чего следует, что \(k \geq 2\). В четвертой строке каждого набора входных данных содержится \(k - 1\) число \(s_1, s_2, \ldots, s_{k-1}\) (\(1 \le s_i \le 10^6\)) — числа, которые есть у Тони во множестве \(S\). Каждая из следующих \(q\) строк содержит одно целое число \(d\) (\(1 \le d \le 10^6\)) – число, которое планирует купить Тоня. Гарантируется, что для каждого данного \(d\) существует способ заполнить пропуски в \(a\) числами из \(S\) и числом \(d\) так, чтобы получить чистый массив. Гарантируется, что сумма \(n\) и сумма \(q\) по всем тестам не превосходят \(3 \cdot 10^5\). Выходные данные Для каждого набора входных данных выведите \(q\) строк. Для каждого значения \(d\) выведите «YES», если существует способ заполнить массив \(a\), сделав его похожим на \(p\), и «NO» в противном случае. Примечание В первом наборе входных данных для \(d = 9\) можно получить \(a = [5, 9, 7, 6]\), можно доказать, что такое \(a\) похоже на \(p\), для \(d=1\) и \(d=4\) можно доказать, что ответа не существует. Во втором наборе входных данных для \(d = 1\) можно получить \(a = [1, 5, 10, 9, 3]\), для \(d = 8\) можно получить \(a = [3, 5, 10, 9, 8]\), можно доказать, что для \(d = 11\) ответа не существует. | |
![]()
|
|
F. Уменьшение паросочетания
Потоки
Паросочетания
Перебор
Конструктив
*2800
поиск в глубину и подобное
графы
интерактив
Дан двудольный граф с \(n_1\) вершинами в первой доле, \(n_2\) вершинами во второй доле и \(m\) ребрами. Максимальное паросочетание в таком графе — максимальный по размеру набор ребер, такой, что ни одна вершина не инцидентна более чем одному выбранному ребру. Вам нужно обрабатывать запросы двух видов к этому графу: - \(1\) — удалить минимально возможное количество вершин так, чтобы размер максимального паросочетания уменьшился ровно на \(1\), и вывести список удаленных вершин. Затем найти любое максимальное паросочетание в полученном графе и вывести сумму номеров ребер, входящих в это паросочетание;
- \(2\) — запрос этого типа может быть задан только после запроса типа \(1\). В качестве ответа на этот запрос вы должны вывести список номеров ребер, входящих в выбранное в предыдущем запросе паросочетание.
Обратите внимание, что вы должны решить эту задачу в режиме online. Это означает, что вы не можете считать все входные данные сразу. Вы можете считать каждый запрос только после вывода ответа на последний запрос. Используйте функции fflush в C++ и BufferedWriter.flush в Java после каждого вывода в вашей программе. Выходные данные Для запроса типа \(1\) выведите три строки: - в первой строке выведите количество удаляемых вершин;
- во второй строке выведите список вершин, которые вы удаляете, следующим образом: если вы удаляете вершину \(x\) из первой доли, выведите \(x\); если вы удаляете вершину \(y\) из второй доли, выведите \(-y\) (номер со знаком минус);
- в третьей строке выведите сумму номеров ребер, которые принадлежат некоторому максимальному паросочетанию. Ребра нумеруются от \(1\) до \(m\).
Для запроса типа \(2\) выведите две строки: - в первой строке выведите одно число — размер максимального паросочетания;
- во второй строке выведите номера ребер, формирующих максимальное паросочетание. Обратите внимание, что сумма этих номеров должна быть равна числу, которое вы вывели в конце предыдущего запроса типа \(1\);
После вывода ответа на запрос не забудьте сбросить буфер вывода. Протокол взаимодействия В этой задаче вы можете получить вердикт «Решение зависло», так как ее нужно решать в режиме online. Если это случилось, то либо вы не следуете формату вывода, либо нарушаете какое-то из ограничений задачи. Вы можете считать, что это эквивалентно вердикту «Неправильный ответ». Для вашего удобства в примере из условия вывод для запросов разделен строкой ===. Ваше решение не должно выводить эту строку; она добавлена только для того, чтобы было проще понять, где ответ на какой запрос. | |
![]()
|
|
F. Рыбаки
Потоки
Паросочетания
жадные алгоритмы
*3100
С рыбалки вернулось \(n\) рыбаков. \(i\)-й рыбак поймал рыбу размера \(a_i\). Рыбаки выберут какой-то порядок, в котором они будут рассказывать, какого размера они поймали рыбу (порядок — это просто перестановка размера \(n\)). Рыбаки не совсем честны, и во время рассказа могут «увеличить» размер пойманной рыбы. Формально, пусть рыбаки рассказывают про пойманную ими рыбу в порядке \([p_1, p_2, p_3, \dots, p_n]\). Пусть \(b_i\) — размер рыбы, названный \(i\)-м рыбаком в выбранном порядке. Значения \(b_i\) считаются следующим образом: - первый рыбак в выбранном порядке просто честно называет размер пойманной рыбы, то есть \(b_1 = a_{p_1}\);
- каждый следующий рыбак хочет назвать минимальное значение, которое будет строго больше значения, названного предыдущим рыбаком, а также делится на размер пойманной этим рыбаком рыбы. То есть для \(i > 1\) значение \(b_i\) равно минимальному целому числу, которое одновременно строго больше \(b_{i-1}\) и делится на \(a_{p_i}\).
Например, пусть \(n = 7\), \(a = [1, 8, 2, 3, 2, 2, 3]\). Если выбранный порядок рыбаков \(p = [1, 6, 7, 5, 3, 2, 4]\), тогда: - \(b_1 = a_{p_1} = 1\);
- \(b_2\) — минимальное целое число, которое делится на \(2\) и превосходит \(1\), то есть \(2\);
- \(b_3\) — минимальное целое число, которое делится на \(3\) и превосходит \(2\), то есть \(3\);
- \(b_4\) — минимальное целое число, которое делится на \(2\) и превосходит \(3\), то есть \(4\);
- \(b_5\) — минимальное целое число, которое делится на \(2\) и превосходит \(4\), то есть \(6\);
- \(b_6\) — минимальное целое число, которое делится на \(8\) и превосходит \(6\), то есть \(8\);
- \(b_7\) — минимальное целое число, которое делится на \(3\) и превосходит \(8\), то есть \(9\).
Вы хотите выбрать такой порядок, в котором рыбаки будут называть размер пойманной рыбы, чтобы минимизировать значение \(\sum\limits_{i=1}^{n} b_i\). Выходные данные Выведите одно целое число — минимально возможное значение \(\sum\limits_{i=1}^{n} b_i\), если выбрать порядок рыбаков оптимально. | |
![]()
|
|
E. Планирование дома
Паросочетания
Структуры данных
Конструктив
жадные алгоритмы
*2400
В вашем городке есть \(n\) домов, расположенных на числовой прямой в точках \(h_1, h_2, \ldots, h_n\). Вы хотите построить себе новый дом и рассматриваете два варианта, где его разместить: точки \(p_1\) и \(p_2\). Так как вы любите ходить в гости, вы заблаговременно вычислили для обеих точек расстояния до уже существующих домов. Более формально, вы вычислили два массива \(d_1\), \(d_2\): \(d_{i, j} = \left|p_i - h_j\right|\), где \(|x|\) обозначает модуль числа \(x\). Спустя долгое время бездействия вы забыли расположение домов \(h\) и планируемые точки \(p_1\), \(p_2\). Но в вашем дневнике нашлись два массива — \(d_1\), \(d_2\), в подлинности которых вы сомневаетесь. Также значения внутри каждого из массивов могли перемешаться, поэтому значения на одинаковых позициях массивов \(d_1\) и \(d_2\) могут соответствовать разным домам. Обратите внимание, что значения из одного массива не могли попасть в другой, иными словами, все значения в массиве \(d_1\) соответствуют расстоянию от \(p_1\) до домов, а в массиве \(d_2\) — от \(p_2\) до домов. Обратите внимание, что расположения домов \(h_i\) и рассматриваемых вариантов \(p_j\) могли совпадать. Например, корректными являются расположения \(h = \{1, 0, 3, 3\}\), \(p = \{1, 1\}\), которым могли соответствовать уже перемешанные \(d_1 = \{0, 2, 1, 2\}\), \(d_2 = \{2, 2, 1, 0\}\). Проверьте, существуют ли расположение домов \(h\) и планируемые точки \(p_1\), \(p_2\), для которых бы найденные массивы расстояний были корректными. Если такое возможно, найдите подходящее расположение домов и мест строительства. Выходные данные Для каждого набора входных данных выведите одну строку «NO», если ответа не существует. Иначе выведите три строки. Первая строка должна содержать «YES». Вторая строка должна содержать \(n\) целых чисел \(h_1, h_2, \ldots, h_n\). Третья строка должна содержать два целых числа \(p_1\), \(p_2\). Должно выполняться \(0 \le h_i, p_1, p_2 \le 2 \cdot 10^9\). Можно показать, что если существует ответ, то он существует и при заданных ограничениях. Если решений несколько, выведите любое. Примечание На изображении ниже можно видеть решения из примера. Планируемые дома изображены яркими цветами: розовым и фиолетовым. Существующие дома - тусклыми. В \(1\) наборе данных первый планируемый дом расположен в точке \(0\), второй - в точке \(10\). Существующий дом расположен в точке \(5\) и находится на расстоянии \(5\) от обеих планируемых домов.  Можно показать, что не существует решения для \(2\) набора данных.  В \(3\) наборе данных планируемые дома расположены в точках \(33\) и \(69\).  Обратите внимание, что в \(4\) тесте оба плана расположены в точке \(1\), где в то же время находится и один из существующих домов, что является корректным расположением. 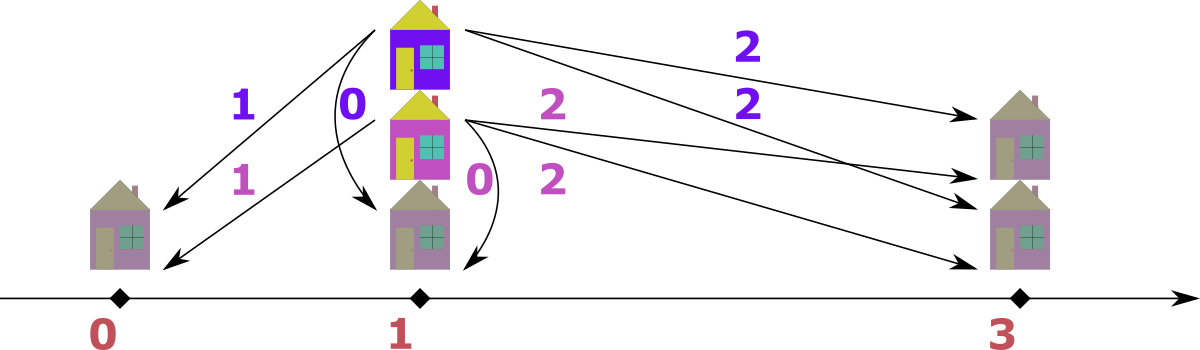 | |
![]()
|
|
A. Access Levels
Потоки
Паросочетания
*2400
битмаски
снм
BerSoft is the biggest IT corporation in Berland, and Monocarp is the head of its security department. This time, he faced the most difficult task ever. Basically, there are \(n\) developers working at BerSoft, numbered from \(1\) to \(n\). There are \(m\) documents shared on the internal network, numbered from \(1\) to \(m\). There is a table of access requirements \(a\) such that \(a_{i,j}\) (the \(j\)-th element of the \(i\)-th row) is \(1\) if the \(i\)-th developer should have access to the \(j\)-th document, and \(0\) if they should have no access to it. In order to restrict the access, Monocarp is going to perform the following actions: - choose the number of access groups \(k \ge 1\);
- assign each document an access group (an integer from \(1\) to \(k\)) and the required access level (an integer from \(1\) to \(10^9\));
- assign each developer \(k\) integer values (from \(1\) to \(10^9\)) — their access levels for each of the access groups.
The developer \(i\) has access to the document \(j\) if their access level for the access group of the document is greater than or equal to the required access level of the document. What's the smallest number of access groups Monocarp can choose so that it's possible to assign access groups and access levels in order to satisfy the table of access requirements? Output The first line should contain a single integer \(k\) — the smallest number of access groups Monocarp can choose so that it's possible to assign access groups and access levels in order to satisfy the table of access requirements. The second line should contain \(m\) integers from \(1\) to \(k\) — the access groups of the documents. The third line should contain \(m\) integers from \(1\) to \(10^9\) — the required access levels of the documents. The \(i\)-th of the next \(n\) lines should contain \(k\) integers from \(1\) to \(10^9\) — the access level of the \(i\)-th developer on each of the access groups. If there are multiple solutions, print any of them. Note In the first example, we assign the documents to different access groups. Both documents have level \(2\) in their access group. This way, we can assign the developers, who need the access, level \(2\), and the developers, who have to have no access, level \(1\). If they had the same access group, it would be impossible to assign access levels to developers \(1\) and \(3\). Developer \(1\) should've had a lower level than developer \(3\) in this group to not be able to access document \(1\). At the same time, developer \(3\) should've had a lower level than developer \(1\) in this group to not be able to access document \(2\). Since they can't both have lower level than each other, it's impossible to have only one access group. In the second example, it's possible to assign all documents to the same access group. | |
![]()
|
|
J. Hero to Zero
Паросочетания
математика
*2900
There are no heroes in this problem. I guess we should have named it "To Zero". You are given two arrays \(a\) and \(b\), each of these arrays contains \(n\) non-negative integers. Let \(c\) be a matrix of size \(n \times n\) such that \(c_{i,j} = |a_i - b_j|\) for every \(i \in [1, n]\) and every \(j \in [1, n]\). Your goal is to transform the matrix \(c\) so that it becomes the zero matrix, i. e. a matrix where every element is exactly \(0\). In order to do so, you may perform the following operations any number of times, in any order: - choose an integer \(i\), then decrease \(c_{i,j}\) by \(1\) for every \(j \in [1, n]\) (i. e. decrease all elements in the \(i\)-th row by \(1\)). In order to perform this operation, you pay \(1\) coin;
- choose an integer \(j\), then decrease \(c_{i,j}\) by \(1\) for every \(i \in [1, n]\) (i. e. decrease all elements in the \(j\)-th column by \(1\)). In order to perform this operation, you pay \(1\) coin;
- choose two integers \(i\) and \(j\), then decrease \(c_{i,j}\) by \(1\). In order to perform this operation, you pay \(1\) coin;
- choose an integer \(i\), then increase \(c_{i,j}\) by \(1\) for every \(j \in [1, n]\) (i. e. increase all elements in the \(i\)-th row by \(1\)). When you perform this operation, you receive \(1\) coin;
- choose an integer \(j\), then increase \(c_{i,j}\) by \(1\) for every \(i \in [1, n]\) (i. e. increase all elements in the \(j\)-th column by \(1\)). When you perform this operation, you receive \(1\) coin.
You have to calculate the minimum number of coins required to transform the matrix \(c\) into the zero matrix. Note that all elements of \(c\) should be equal to \(0\) simultaneously after the operations. Output Print one integer — the minimum number of coins required to transform the matrix \(c\) into the zero matrix. Note In the first example, the matrix looks as follows: You can turn it into a zero matrix using \(2\) coins as follows: - subtract \(1\) from the first row, paying \(1\) coin;
- subtract \(1\) from the third row, paying \(1\) coin.
In the second example, the matrix looks as follows: You can turn it into a zero matrix using \(5\) coins as follows: - subtract \(1\) from the first row, paying \(1\) coin;
- subtract \(1\) from the third row, paying \(1\) coin;
- subtract \(1\) from the third row, paying \(1\) coin;
- subtract \(1\) from \(a_{2,3}\), paying \(1\) coin;
- add \(1\) to the third column, receiving \(1\) coin;
- subtract \(1\) from the first row, paying \(1\) coin;
- subtract \(1\) from \(a_{2,3}\), paying \(1\) coin.
| |
![]()
|
|
D. Косия и игра
Потоки
Паросочетания
Структуры данных
Конструктив
реализация
*2000
поиск в глубину и подобное
графы
снм
игры
Косия и Махиру играют в игру с тремя массивами \(a\), \(b\) и \(c\) длины \(n\). Каждый элемент \(a\), \(b\) и \(c\) — целое число от \(1\) до \(n\) включительно. Игра состоит из \(n\) раундов. В \(i\)-м раунде они делают следующие ходы: - Пусть \(S\) — мультимножество \(\{a_i, b_i, c_i\}\).
- Косия удаляет один из элементов \(S\) по своему выбору.
- Затем Махиру выбирает одно из двух оставшихся в \(S\) чисел.
Пусть \(d_i\) — число, выбранное Махиру в \(i\)-м раунде. Если \(d\) является перестановкой\(^\dagger\), Косия выигрывает. Иначе выигрывает Махиру. Сейчас выбраны только массивы \(a\) и \(b\). Являясь ярым поклонником Косии, вы хотите выбрать массив \(c\) так, чтобы Косия выиграла. Вычислите количество таких \(c\) по модулю \(998\,244\,353\). Обратите внимание, что Косия и Махиру играют оптимально. \(^\dagger\) Перестановкой длины \(n\) является массив, состоящий из \(n\) различных целых чисел от \(1\) до \(n\) в произвольном порядке. Например, \([2,3,1,5,4]\) — перестановка, но \([1,2,2]\) не перестановка (\(2\) встречается в массиве дважды) и \([1,3,4]\) тоже не перестановка (\(n=3\), но в массиве встречается \(4\)). Выходные данные Выведите одно целое число — количество массивов \(c\), при которых выигрывает Косия, по модулю \(998\,244\,353\). Примечание В первом примере есть \(6\) массивов \(c\), при которых выигрывает Косия: \([1, 2, 3]\), \([1, 3, 2]\), \([2, 2, 3]\), \([2, 3, 2]\), \([3, 2, 3]\), \([3, 3, 2]\). Во втором примере можно показать, что нет массивов \(c\), при которых выигрывает Косия. | |
![]()
|
|
F. Двойная сортировка II
Потоки
Паросочетания
поиск в глубину и подобное
графы
*2500
Даны две перестановки \(a\) и \(b\), обе размера \(n\). Перестановка размера \(n\) — это массив из \(n\) элементов, в который каждое целое число от \(1\) до \(n\) входит ровно один раз. Элементы в каждой перестановке пронумерованы от \(1\) до \(n\). Вы можете выполнять следующую операцию любое количество раз: - выбрать целое число \(i\) от \(1\) до \(n\);
- обозначим за \(x\) такое целое число, что \(a_x = i\). Поменять местами \(a_i\) и \(a_x\);
- обозначим за \(y\) такое целое число, что \(b_y = i\). Поменять местами \(b_i\) и \(b_y\).
Вы должны отсортировать обе перестановки в порядке возрастания (то есть должны выполняться условия \(a_1 < a_2 < \dots < a_n\) и \(b_1 < b_2 < \dots < b_n\)) за минимальное количество операций. Обратите внимание, что обе перестановки должны быть отсортированы после того, как вы выполните выбранную вами последовательность операций. Выходные данные Сначала выведите одно целое число \(k\) (\(0 \le k \le 2n\)) — минимальное количество операций, за которое можно отсортировать обе перестановки. Обратите внимание: можно показать, что \(2n\) операций всегда достаточно. Затем выведите \(k\) целых чисел \(op_1, op_2, \dots, op_k\) (\(1 \le op_j \le n\)), где \(op_j\) — значение \(i\), выбранное для \(j\)-й операции. Если ответов несколько, выведите любой из них. | |
![]()
|
|
F. Хороший граф
Паросочетания
реализация
поиск в глубину и подобное
графы
битмаски
*3500
Вам дан двудольный граф \(G\) с множеством вершин в левой доле \(L\), в правой доле \(R\) и \(m\) ребрами, соединяющими эти два множества. Мы знаем, что \(|L| = |R| = n\). Для любого подмножества \(S \subseteq L\), пусть \(N(S)\) обозначает множество всех соседей вершин в \(S\). Мы говорим, что подмножество \(S \subseteq L\) в графе \(G\) является строгим, если \(|S| = |N(S)|\). Мы говорим, что граф \(G\) является хорошим, если \(\forall_{S \subseteq L}, |S| \leq |N(S)|\). Ваша задача — проверить, является ли граф хорошим, и, если да, то оптимизировать его. Если граф не является хорошим, найдите подмножество \(S \subseteq L\) такое, что \(|S| > |N(S)|\). Однако, если граф хороший, ваша задача — найти хороший двудольный граф \(G'\) с тем же набором вершин \(L \cup R\), в котором \(\forall_{S \subseteq L}\) множество \(S\) является строгим в \(G\) тогда и только тогда, когда \(S\) строго в \(G'\). Если таких графов несколько, выберите один с наименьшим возможным числом ребер. Если таких графов по-прежнему несколько, выведите любой из них. Выходные данные Если граф \(G\), заданный на входе, не является хорошим, выведите в первой строке вывода одно слово «NO». Во второй строке вывода выведите число \(k\), а в третьей строке выведите \(k\) чисел \(l_1, l_2, \dots, l_k\), разделенные пробелами. Эти числа должны показать, что для множества \(S = \{l_1, l_2, \dots, l_k\}\) выполняется \(|S| > |N(S)|\). Однако, если граф \(G\), заданный на входе, хороший, выведите одно слово «YES» в первой строке вывода. Во второй строке вывода выведите число \(m'\), обозначающее количество ребер в новом, также хорошем графе \(G'\). Затем, в следующих \(m'\) строках, выведите ребра графа \(G'\) в том же формате, что и во входных данных. Примечание В первом тестовом примере граф \(G\) хороший; таким образом, мы ищем эквивалентный граф с такими же строгими множествами. Единственный строгий набор — это \(\{ 1, 2, 3 \}\), который остается строгим в результирующем графе. Более того, никакое другое множество не является строгим в полученном графе. Можно доказать, что не существует графа с менее чем \(6\) ребрами и такими же строгимимножествами. Во втором тестовом примере граф \(G\) не является хорошим. Множество \(\{ 2, 3 \}\) имеет только одного соседа — вершину \(6\). Таким образом, \(|\{ 2, 3 \}| > |\{ 6 \}|\), что доказывает, что входной граф не является хорошим. | |
![]()
|
|
I. Contingency Plan 2
Паросочетания
*2900
You are working as a manager in The ICPC Company. In the company building, there are \(N\) computers (numbered from \(1\) to \(N\)). There are \(N - 1\) cables, numbered from \(1\) to \(N - 1\), that connect all the computers into a single network. Cable \(i\) connects computer \(U_i\) and \(V_i\). Each cable can be set into emergency mode, where cable \(i\) only transfers data from computer \(U_i\) to computer \(V_i\), but not the other way around. During a disaster, it is mandatory for all cables to be in emergency mode. Through your research, you discover a new way to determine the vulnerability of a network. You want to add zero or more new cables to the current network such that it is not vulnerable during a disaster. Your network is not vulnerable if and only if there is exactly one permutation of \(1\) to \(N\) such that \(u\) appears before \(v\) in the permutation for all cables that connect computer \(u\) and \(v\). In other words, it should have exactly one topological order. The following illustration shows examples of not vulnerable networks and vulnerable networks.  For the not vulnerable networks, the only permutation that satisfies the requirement for the networks on the left and on the right are \([1, 2, 3]\) and \([3, 1, 2]\), respectively. Meanwhile, for the vulnerable networks, there are \(2\) permutations that satisfy the requirement for the network on the left: \([1, 2, 3]\) and \([3, 1, 2]\); while there is no permutation that satisfies the requirement for the network on the right. You are interested in the minimum number of new cables that should be added to the current network such that it is not vulnerable during a disaster. Furthermore, you want to know, which pairs of computers should be connected by using the minimum number of cables. If there are several ways to connect, you can connect in any way of your choice. Under the given constraints, it can be proven that there exists a way to make the network not vulnerable. Output The first line consists of an integer, representing the minimum number of new cables that should be added to the current network such that it is no longer vulnerable during a disaster. Denote this number as \(K\) and the new cables are numbered from \(1\) to \(K\). If \(K\) is not \(0\), then output \(K\) lines. Each of the next \(K\) lines consists of two integers \(A_i\) \(B_i\), representing the computers that are connected by the new cable \(i\). During a disaster, new cable \(i\) only transfers data from computer \(A_i\) to computer \(B_i\), but not the other way around. If there exist several solutions, you can output any of them. Note Explanation for the sample input/output #3 The following illustration shows the original network and the new network with the added cables during a disaster. The only permutation that satisfies the requirement is \([1, 2, 3, 4, 5]\). 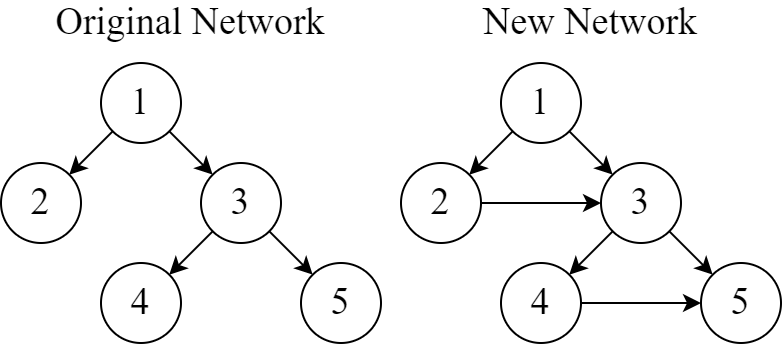 | |
![]()
|
|
F. Соревнование по программированию
Паросочетания
Деревья
дп
поиск в глубину и подобное
жадные алгоритмы
*1900
BerSoft — крупнейшая IT-корпорация в Берляндии. В компании BerSoft работает \(n\) сотрудников, пронумерованных от \(1\) до \(n\). Первый сотрудник является руководителем компании и у него нет начальника. У каждого другого сотрудника \(i\) есть ровно один непосредственный начальник \(p_i\). Сотрудник \(x\) считается начальником (непосредственным или косвенным) сотрудника \(y\), если выполняется одно из следующих условий: - сотрудник \(x\) является непосредственным начальником сотрудника \(y\);
- сотрудник \(x\) является начальником непосредственного начальника сотрудника \(y\).
Структура BerSoft организована таким образом, что руководитель компании является начальником для каждого сотрудника. Скоро будет проведено соревнование по программированию. Для этой цели будут созданы команды из двух человек. Однако, если в команде один сотрудник является начальником другого, им будет некомфортно вместе. Поэтому команды из двух человек должны быть созданы таким образом, что никто не был начальником для другого. Обратите внимание, что никакой сотрудник не может участвовать более чем в одной команде. Ваша задача — посчитать максимально возможное количество команд в соответствии с вышеописанными правилами. Выходные данные Для каждого набора входных данных выведите одно целое число — максимально возможное количество команд в соответствии с вышеописанными правилами. Примечание В первом примере можно создать команду \((3, 4)\). Во втором примере команда не может быть создана, потому что здесь всего \(2\) сотрудника и один является начальником другого. В третьем примере можно создать команду \((2, 3)\). В четвертом примере можно создать команды \((2, 4)\), \((3, 5)\) и \((6, 7)\). В пятом примере можно создать команды \((2, 3)\), \((6, 4)\) и \((5, 7)\). | |
![]()
|
|
F. Замена на подотрезке
Паросочетания
дп
*2500
Вам дан массив \(a_1, a_2, \dots, a_n\), где каждый элемент является целым числом от \(1\) до \(x\). Вы можете выполнять следующую операцию любое количество раз: - выберите три целых числа \(l\), \(r\) и \(k\) таких, что \(1 \le l \le r \le n\), \(1 \le k \le x\) и каждый элемент \(a_i\), для которого \(l \le i \le r\), отличается от \(k\). Затем для каждого \(i \in [l, r]\) замените \(a_i\) на \(k\).
Другими словами, вы выбираете подотрезок массива и целое число от \(1\) до \(x\), которое не встречается в этом подотрезке, и заменяете каждый элемент в подотрезке на это выбранное число. Ваша цель — сделать все элементы в массиве равными. Какое минимальное количество операций вам нужно выполнить? Выходные данные Для каждого теста выведите одно целое число — минимальное количество операций, которые вам нужно выполнить. | |
![]()
|
|
G. MST с паросочетанием
Паросочетания
Деревья
Перебор
битмаски
снм
*3100
Дан неориентированный связный граф, в котором \(n\) вершин. У каждого ребра этого графа есть вес; вес ребра между вершинами \(i\) и \(j\) равен \(w_{i,j}\) (или \(w_{i,j} = 0\), что означает, что между \(i\) и \(j\) нет ребра). Все веса — положительные целые числа. Также дано положительное целое число \(c\). Вы должны построить остовное дерево для этого графа, то есть выбрать ровно \((n-1)\) ребер графа так, чтобы можно было из любой вершины добраться до любой другой по выбранным ребрам. Стоимость остовного дерева — это сумма двух значений: - сумма весов всех выбранных ребер;
- максимальное паросочетание в остовном дереве (то есть максимальный размер множества ребер, такого, что каждое ребро принадлежит остовному дереву и каждой вершине инцидентно не более одного ребра из множества), умноженное на заданное число \(c\).
Найдите любое остовное дерево с минимальной стоимостью. Так как граф связный, у него существует хотя бы одно остовное дерево. Выходные данные Выведите одно целое число — минимальную стоимость остовного дерева. Примечание В первом примере минимальное остовное дерево состоит из ребер \((1, 3)\), \((2, 3)\) и \((3, 4)\). Максимальное паросочетание относительно него равно \(1\). Во втором примере минимальное остовное дерево состоит из ребер \((1, 2)\), \((2, 3)\) и \((3, 4)\). Максимальное паросочетание относительно него равно \(2\). | |
![]()
|
|
I. Disks
Паросочетания
геометрия
*1800
поиск в глубину и подобное
графы
You are given \(n\) disks in the plane. The center of each disk has integer coordinates, and the radius of each disk is a positive integer. No two disks overlap in a region of positive area, but it is possible for disks to be tangent to each other. Your task is to determine whether it is possible to change the radii of the disks in such a way that: - Disks that were tangent to each other remain tangent to each other.
- No two disks overlap in a region of positive area.
- The sum of all radii strictly decreases.
The new radii are allowed to be arbitrary positive real numbers. The centers of the disks cannot be changed. Output Print \(\texttt{YES}\) if it is possible to change the radii in the desired manner. Otherwise, print \(\texttt{NO}\). Note In the first sample, one can decrease the radii of the first and third disk by \(0.5\), and increase the radius of the second disk by \(0.5\). This way, the sum of all radii decreases by \(0.5\). The situation before and after changing the radii is depicted below. 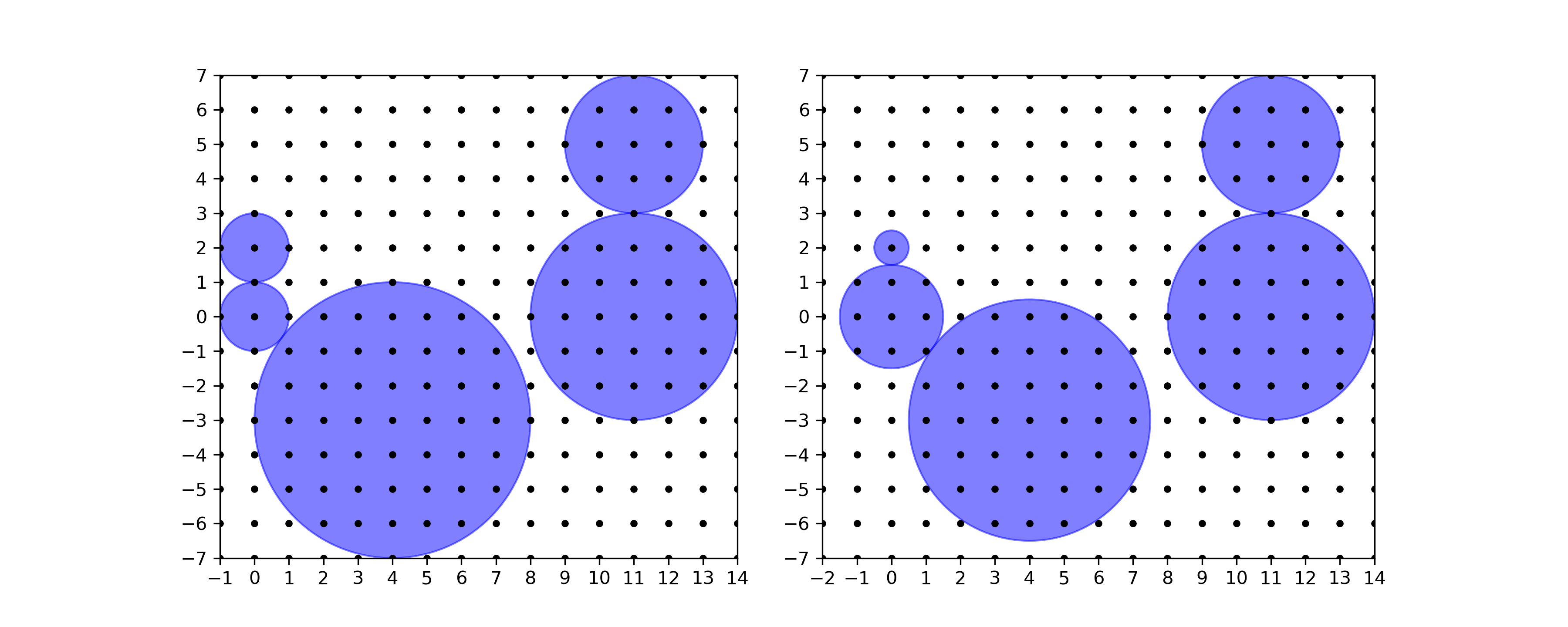 First sample (left) and a valid way to change the radii of the disks (right). First sample (left) and a valid way to change the radii of the disks (right). In the second sample, depicted below, there is no way to change the radii of the disks in the desired manner. 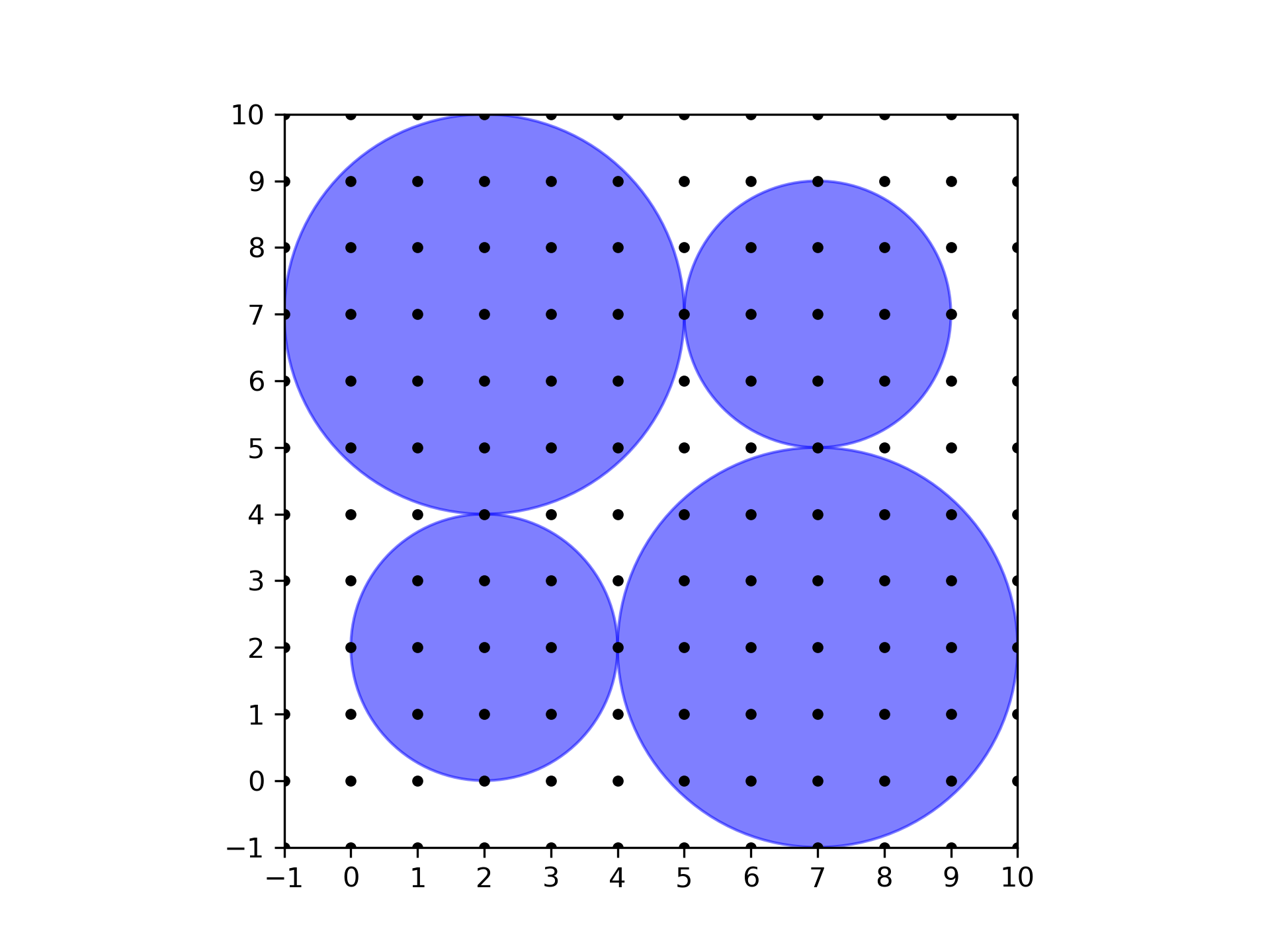 Second sample. Second sample. | |
![]()
|
|
H. Самая безбашенная оборона
Потоки
Паросочетания
Перебор
Конструктив
дп
*2300
кратчайшие пути
битмаски
Вы играете в очень популярную игру в жанре Tower Defense «Runnerfield 2». В ней игрок выставляет защитные башни, которые атакуют врагов, идущих от некоторой начальной точки до базы игрока. Вам дано клетчатое поле размера \(n \times m\), на котором уже расставлены \(k\) башен и проложен маршрут, через который будут идти враги. Клетка на пересечении \(x\)-й строки и \(y\)-го столбца обозначается как \((x, y)\). Каждую секунду башня наносит \(p_i\) единиц урона всем врагам в радиусе её действия. Например, если враг расположен в клетке \((x, y)\), а башня в \((x_i, y_i)\), и её радиус равен \(r\), тогда врагу будет нанесён урон \(p_i\), если \((x - x_i) ^ 2 + (y - y_i) ^ 2 \le r ^ 2\). Враги идут из клетки \((1, 1)\) в клетку \((n, m)\), посещая каждую клетку пути ровно один раз. Враг моментально перемещается на соседнюю по горизонтали или вертикали клетку, однако перед этим он проводит в текущей клетке одну секунду. Если в эту секунду его здоровье стало равно нулю или ниже нуля, то враг больше не может перемещаться. Игрок проигрывает, если враг смог добраться до клетки \((n, m)\) и может сделать ещё одно перемещение. По умолчанию все башни обладают нулевым радиусом действия, но игрок может сделать радиус башни равным целому числу \(r\) (\(r > 0\)) за это здоровье всех врагов увеличится на \(3^r\), однако каждое \(r\) может быть использовано не более чем для одной башни. Допустим, враг имел \(h\) единиц базового здоровья. Если радиусы башен \(2\), \(4\) и \(5\), то его здоровье в начале пути будет \(h + 3 ^ 2 + 3 ^ 4 + 3 ^ 5 = h + 9 + 81 + 243 = h + 333\). Выбор радиусов происходит один раз до появления врагов и не может быть изменён после начала игры. Найдите максимальное количество базового здоровья \(h\), при котором возможно установить радиусы так, чтобы игрок не проиграл при прохождении врага со здоровьем \(h\) (без учёта прибавок за радиусы башен). Выходные данные Для каждого набора входных данных в отдельной строке выведите максимальное количество базового здоровья \(h\), при котором возможно установить радиусы так, чтобы игрок не проиграл при прохождении врага со здоровьем \(h\) (без учёта прибавок за радиусы башен). Если невозможно выбрать радиусы даже для врага с \(1\) единицей базового здоровья, выведите «0». Примечание В первом примере нет смысла увеличивать радиус башни, так как она не сможет нанести достаточное количество урона монстру даже с \(1\) единицей здоровья. Во втором примере радиус башни равен \(1\), она наносит урон монстру в клетках \((1, 1)\) и \((2, 2)\). В третьем примере радиус башни равен \(2\), она наносит урон монстру на всех клетках пути. Если базовое здоровье врага \(1491\), то после прибавки за радиус башни его здоровье будет \(1491 + 3 ^ 2 = 1500\), что в точности будет равно урону, который ему нанесёт башня за три секунды. В четвёртом примере у башни \((1, 2)\) радиус \(1\), а у башни \((3, 1)\) радиус \(2\). | |
![]()
|
|
I. Игра на сетке
Паросочетания
Конструктив
жадные алгоритмы
интерактив
игры
*3500
Это интерактивная задача. Вам дана сетка из \(n\) строк и \(m\) столбцов. Вам нужно заполнить каждую ячейку уникальным целым числом от \(1\) до \(n \cdot m\). После заполнения сетки вы сыграете с интерактором в игру на этой сетке. Игроки по очереди выбирают из сетки ранее не выбранные ячейки, причем интерактор ходит первым. В первый ход интерактор может выбрать любую ячейку из сетки. После этого любая выбранная клетка должна быть соседней по стороне хотя бы с одной ранее выбранной клеткой. Игра продолжается до тех пор, пока не будут выбраны все клетки. Ваша цель состоит в том, чтобы сумма чисел в выбранных вами клетках была строго меньше суммы чисел в клетках, выбранных соперником. Протокол взаимодействия Сначала выведите \(n\) строк, каждая из которых содержит по \(m\) целых чисел — числа, которыми вы заполнили сетку. Каждое целое число от \(1\) до \(n \cdot m\) должно появиться ровно один раз. Затем начинается игра. Интерактор и вы по очереди выводите координаты выбранных ячеек в течение \(n \times m\) ходов, причем интерактор начинает первым. В свой ход каждый игрок (либо вы, либо интерактор) выводит два целых числа \(i\) и \(j\) (\(1 \le i \le n\), \(1 \le j \le m\)), означающие, что игрок выбрал клетку в \(i\)-й строке и \(j\)-м столбце. Эта клетка не должна быть выбрана в предыдущих раундах. Кроме того, если это не первый ход, клетка должна быть смежной по стороне хотя бы с одной ранее выбранной клеткой. Если любой из ваших выводов некорректен, жюри выведет «-1», и вы получите вердикт Неправильный ответ. После всех \(n \cdot m\) ходов, если сумма чисел в выбранных вами клетках не будет строго меньше суммы чисел в клетках, выбранных соперником, жюри выведет «-1» и вы получите вердикт Неправильный ответ. Если ваша программа получила вердикт Неправильный ответ, она должна немедленно завершиться. В противном случае вы можете получить любой вердикт, так как программа продолжит чтение из закрытого потока. После вывода не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте: - fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Взломы в этой задаче отключены. Примечание Обратите внимание, что это пример игры и не обязательно представляет собой оптимальную стратегию для обоих игроков. Сначала мы заполнили сетку \(4 \times 4\) различными целыми числами от \(1\) до \(16\) следующим образом: | \(2\) | \(3\) | \(4\) | \(10\) | | \(12\) | \(6\) | \(11\) | \(15\) | | \(5\) | \(13\) | \(16\) | \(8\) | | \(9\) | \(7\) | \(1\) | \(14\) |
Далее началась игра. - Сначала соперник выбирает клетку \((3, 4)\), в которой находится число \(8\). Во время первого раунда интерактор может выбрать любое число. Начиная со следующего раунда, каждое выбранное число должно быть смежным с любым ранее выбранным числом.
- Мы выбрали клетку \((2, 4)\), в которой находится число \(15\), и которая является соседней с \((3, 4)\).
- Интерактор выбрал клетку \((4, 4)\), в которой находится число \(14\), и которая является смежной с \((3, 4)\).
- Мы выбрали клетку \((4, 3)\), в которой находится число \(1\), и которая является смежной с \((4, 4)\).
- \(\ldots\)
- Это продолжается до тех пор, пока не будут выбраны все числа.
В итоге вы выбрали такие числа: \([15, 1, 16, 5, 4, 2, 11, 13]\), а соперник выбрал \([8, 14, 7, 9, 10, 3, 6, 12]\). Сумма выбранных нами чисел составляет \(67\), что меньше суммы чисел, выбранных соперником: \(69\). Таким образом, мы выиграли эту игру. | |
![]()
|
|
E. Лучшая подпоследовательность
Потоки
Паросочетания
поиск в глубину и подобное
графы
битмаски
*2500
Задан целочисленный массив \(a\) размера \(n\). Скажем, что ценность массива равна его размеру минус количество единичных бит в побитовом ИЛИ всех элементов массива. Например, для массива \([1, 0, 1, 2]\) побитовое ИЛИ равно \(3\) (содержит \(2\) единичных бита), а ценность массива равна \(4-2=2\). Ваша задача — вычислить максимально возможную ценность некоторой подпоследовательности заданного массива. Выходные данные Для каждого набора входных данных выведите максимально возможную ценность некоторой подпоследовательности заданного массива. | |
![]()
|
|
G1. Средняя демоническая задача (легкая версия)
Паросочетания
Деревья
реализация
поиск в глубину и подобное
*1700
графы
Это легкая версия задачи. Ключевое отличие между двумя версиями выделено жирным шрифтом. Группа из \(n\) пауков собралась, чтобы обменяться плюшевыми игрушками. Изначально у каждого паука есть \(1\) плюшевая игрушка. Каждый год, если паук \(i\) имеет хотя бы одну плюшевую игрушку, он отдаст ровно одну плюшевую игрушку пауку \(r_i\). В противном случае он ничего не сделает. Обратите внимание, что все передачи плюшевых игрушек происходят одновременно. В этой версии, если у любого паука в любой момент времени больше \(1\) плюшевой игрушки, он выбросит все, кроме \(1\). Процесс считается стабильным в текущем году, если у каждого паука количество плюшевых игрушек (до обмена в текущем году) совпадает с количеством плюшевых игрушек, которое у него было в предыдущем году (до обмена в предыдущем году). Обратите внимание, что год \(1\) никогда не может быть стабильным. Найдите первый год, в котором процесс становится стабильным. Выходные данные Для каждого набора входных данных выведите целое число в новой строке, первый год, в котором процесс становится стабильным. Примечание Для второго набора входных данных: - В год \(1\) следующий массив показывает количество плюшевых игрушек у каждого паука: \([1, 1, 1, 1, 1]\). Затем происходит обмен в год \(1\).
- В год \(2\) следующий массив показывает количество плюшевых игрушек у каждого паука: \([1, 1, 1, 1, 1]\). Поскольку этот массив такой же, как в предыдущем году, этот год является стабильным.
Для третьего набора входных данных: - В год \(1\) следующий массив показывает количество плюшевых игрушек у каждого паука: \([1, 1, 1, 1, 1]\). Затем происходит обмен в год \(1\).
- В год \(2\) следующий массив показывает количество плюшевых игрушек у каждого паука: \([1, 1, 1, 1, 0]\). Затем происходит обмен в год \(2\). Обратите внимание, что, хотя два паука отдали пауку \(2\) плюшевые игрушки, паук \(2\) может оставить только одну плюшевую игрушку.
- В год \(3\) следующий массив показывает количество плюшевых игрушек у каждого паука: \([1, 1, 0, 1, 0]\). Затем происходит обмен в год \(3\).
- В год \(4\) следующий массив показывает количество плюшевых игрушек у каждого паука: \([1, 1, 0, 0, 0]\). Затем происходит обмен в год \(4\).
- В год \(5\) следующий массив показывает количество плюшевых игрушек у каждого паука: \([1, 1, 0, 0, 0]\). Поскольку этот массив такой же, как в предыдущем году, этот год является стабильным.
| |
![]()
|
|
B. Кис-кис-кис
Паросочетания
Перебор
Конструктив
реализация
*1300
Кошек привлекает «кис-кис-кис», но Эвирир, будучи достойным англоговорящим драконом, отзывается только на «pspspsp» с особыми условиями... Дана строка \(s = s_1s_2\ldots s_n\) длины \(n\), состоящая из символов p, s и . (точка). Определите, существует ли перестановка\(^{\text{∗}}\) \(p\) длины \(n\), такая, что для каждого целого \(i\) (\(1 \le i \le n\)): - Если \(s_i\) равно p, то \([p_1, p_2, \ldots, p_i]\) образует перестановку (длины \(i\));
- Если \(s_i\) равно s, то \([p_i, p_{i+1}, \ldots, p_{n}]\) образует перестановку (длины \(n-i+1\));
- Если \(s_i\) равно ., то дополнительных ограничений нет.
Выходные данные Для каждого набора входных данных в первой строке выведите YES или NO. Выведите YES, если искомая перестановка существует, и NO в противном случае. Вы можете выводить каждую букву в любом регистре (строчную или заглавную). Например, строки «yEs», «yes», «Yes» и «YES» будут приняты как положительный ответ. Примечание Для первого набора входных данных одна подходящая перестановка такова: \(p = [3, 4, 1, 2]\). Для неё выполняются все условия: - \(s_1 =\) s : \([p_1, p_2, p_3, p_4] = [3, 4, 1, 2]\) образует перестановку.
- \(s_2 =\) . : Никаких дополнительных ограничений.
- \(s_3 =\) s : \([p_3, p_4] = [1, 2]\) образует перестановку.
- \(s_4 =\) p : \([p_1, p_2, p_3, p_4] = [3, 4, 1, 2]\) образует перестановку.
Для второго набора входных данных можно доказать, что не существует перестановки, удовлетворяющей всем ограничениям. Для третьего набора входных данных одной перестановкой, удовлетворяющей условиям, является \(p = [1, 2, 3, 4, 5]\). | |
![]()
|
|
C. Обслуживание клиентов
Паросочетания
Перебор
Конструктив
математика
*1600
жадные алгоритмы
сортировки
Никир устроился работать регулировщиком очередей в компанию «Чёрный Контур». Ему нужно будет выбирать порядок обслуживания клиентов. Всего есть \(n\) очередей, в каждой из которых изначально стоит \(0\) человек. В каждый из следующих \(n\) моментов времени происходит два последовательных события: - Во все очереди приходят новые клиенты. Более формально, в \(j\)-й момент времени количество людей в \(i\)-й очереди увеличивается на положительное целое число \(a_{i,j}\).
- Никир выбирает ровно одну из \(n\) очередей, которую будут обслуживать в этот момент времени. Количество клиентов в этой очереди становится равным \(0\).
Пусть количество людей в \(i\)-й очереди после всех событий равно \(x_i\). Никир хочет, чтобы MEX\(^{\dagger}\) набора чисел \(x_1, x_2, \ldots, x_n\) был как можно больше. Помогите ему определить максимальное значение, которое он сможет получить при оптимальном порядке обслуживания очередей. \(^{\dagger}\)Наименьшее исключенное (MEX) набора чисел \(c_1, c_2, \ldots, c_k\) определяется как наименьшее неотрицательное целое число \(y\), которое не встречается в наборе чисел \(c\). Например: - \(\operatorname{MEX}([2,2,1])= 0\), так как \(0\) не принадлежит массиву.
- \(\operatorname{MEX}([3,1,0,1]) = 2\), так как \(0\) и \(1\) принадлежат массиву, а \(2\) нет.
- \(\operatorname{MEX}([0,3,1,2]) = 4\), так как \(0\), \(1\), \(2\) и \(3\) принадлежат массиву, а \(4\) нет.
Выходные данные Для каждого набора входных данных выведите единственное целое число — максимальное значение \(\operatorname{MEX}([x_1, x_2, \ldots, x_n])\), которое можно получить. Примечание В первом наборе входных данных можно обслужить вторую очередь в момент времени \(1\) и первую очередь в момент времени \(2\). В первой очереди останется \(x_1 = 0\) человек, во второй очереди останется \(x_2 = 1\) человек. Тогда ответ равен \(\operatorname{MEX}([0, 1]) = 2\). Во втором наборе входных данных можно оба раза обслужить первую очередь. В первой очереди останется \(x_1 = 0\) человек, во второй очереди останется \(x_2 = 20\) человек. Тогда ответ равен \(\operatorname{MEX}([0, 20]) = 1\). В третьем наборе входных данных можно обслужить третью очередь в момент времени \(1\), вторую очередь в момент времени \(2\) и первую очередь в момент времени \(3\). В первой очереди останется \(x_1 = 0\) человек, во второй очереди останется \(x_2 = 1\) человек, в третьей очереди останется \(x_3 = 2\) человека. Тогда ответ равен \(\operatorname{MEX}([0, 1, 2]) = 3\). | |
![]()
|
|
H1. Кевин и камни (простая версия)
Потоки
Паросочетания
графы
*3500
Это простая версия задачи. Отличие между версиями заключается в том, что в этой версии вам нужно только определить, существует ли корректная последовательность операций. Вы можете делать взломы только в том случае, если решили все версии этой задачи. У Кевина есть неориентированный граф с \(n\) вершинами и \(m\) рёбрами. Изначально некоторые вершины содержат камни, которые Кевин хочет переместить на новые позиции. Кевин может выполнять следующую операцию: - Для каждого камня на \(u_i\) выбрать соседнюю вершину \(v_i\). Одновременно переместить каждый камень из \(u_i\) на соответствующую ему \(v_i\).
В любой момент каждая вершина может содержать не более одного камня. Определите, существует ли корректная последовательность операций, которая перемещает камни из начального состояния в целевое. Выходные данные Для каждого набора входных данных на отдельной строке выведите «Yes» или «No» — существует ли допустимая последовательность операций. Вы можете выводить каждую букву в любом регистре (строчную или заглавную). Например, строки «yEs», «yes», «Yes» и «YES» будут приняты как положительный ответ. | |
![]()
|
|
G. Фабрика перестановок
Потоки
Паросочетания
геометрия
графы
*3500
Даны две перестановки \(p_1,p_2,\ldots,p_n\) и \(q_1,q_2,\ldots,q_n\) длины \(n\). За одну операцию вы можете выбрать два целых числа \(1\leq i,j\leq n,i\neq j\) и поменять местами \(p_i\) и \(p_j\). Стоимость операции равна \(\min (|i-j|,|p_i-p_j|)\). Найдите минимальную стоимость последовательности операций, в результате которых для всех \(1\leq i\leq n\) выполняется равенство \(p_i = q_i\), и выведите последовательность с минимальной стоимостью. Перестановкой длины \(n\) является массив, состоящий из \(n\) различных целых чисел от \(1\) до \(n\) в произвольном порядке. Например, \([2,3,1,5,4]\) — перестановка, но \([1,2,2]\) не перестановка (\(2\) встречается в массиве дважды) и \([1,3,4]\) тоже не перестановка (\(n=3\), но в массиве встречается \(4\)). Выходные данные Для каждого набора входных данных выведите общее количество операций \(k\) (\(0\le k\le n^2\)) в первой строке. Затем выведите \(k\) строк, каждая из которых содержит два целых числа \(i,j\) (\(1\le i,j\le n\), \(i\neq j\)) — операцию обмена \(p_i\) и \(p_j\). Операции выводите в порядке выполнения. Можно показать, что ни одна оптимальная последовательность операций не имеет длину больше \(n^2\). Примечание Во втором наборе входных данных вы можете поменять местами \(p_1,p_3\), что будет стоить \(\min(|1-3|,|1-3|)=2\). Тогда \(p\) станет равно \(q\), а общая стоимость равна \(2\). В третьем наборе входных данных вы можете выполнить следующие операции: Изначально, \(p=[2,1,4,3]\). - Поменять местами \(p_1,p_4\), что будет стоить \(\min(|1-4|,|2-3|)=1\), в результате чего \(p=[3,1,4,2]\).
- Поменять местами \(p_2,p_4\), что будет стоить \(\min(|2-4|,|1-2|)=1\), в результате чего \(p=[3,2,4,1]\).
- Поменять местами \(p_1,p_3\), что будет стоить \(\min(|1-3|,|3-4|)=1\). Тогда \(p\) станет равно \(q\). Общая стоимость равна \(3\).
| |
![]()
|
|
D. Обход графа
Паросочетания
*2400
графы
битмаски
Вам задан взвешенный неориентированный граф. Ваша задача найти наименьшую длину такого цикла, который начинается (и заканчивается) в вершине 1 и проходит по каждому ребру хотя бы раз. Граф может содержать кратные ребра (т.е. несколько ребер между парой вершин) и петли (ребра из вершины в себя). Выходные данные Выведите искомую длину цикла или -1 если такой не существует. | |
![]()
|
|
B. Очередь в школе
Паросочетания
Конструктив
реализация
*800
кратчайшие пути
На перемене в школьной столовой образовалась очередь из n человек, в которой стоят мальчики и девочки. Изначально ребята встали в таком порядке, в котором они забежали в столовую. Однако через некоторое время мальчикам стало неловко, что они стоят в очереди перед девочками, и они стали каждую секунду пропускать девочек вперед. Опишем процесс более точно. Пусть позиции в очереди последовательно пронумерованы целыми числами от 1 до n, причем тот, кто стоит на позиции номер 1 обслуживается первым. Тогда, если в момент времени x на i-ой позиции стоит мальчик, а на (i + 1)-ой — девочка, то в момент времени x + 1 на i-ой позиции будет находиться девочка, а на (i + 1)-ой — мальчик. Моменты времени заданы в секундах. Вам задано расположение ребят в начальный момент времени, определите, как будет выглядеть очередь через t секунд. Выходные данные Выведите строку a, обозначающую расположение ребят в очереди спустя t секунд. Если на i-ой позиции через заданное время будет стоять мальчик, то i-ый символ a должен быть равен «B», иначе он должен быть равен «G». | |
![]()
|
|
C. WTF?
Паросочетания
Деревья
реализация
*особая задача
*1700
HAI
I HAS A TUX
GIMMEH TUX
I HAS A FOO ITS 0
I HAS A BAR ITS 0
I HAS A BAZ ITS 0
I HAS A QUZ ITS 1
TUX IS NOW A NUMBR
IM IN YR LOOP NERFIN YR TUX TIL BOTH SAEM TUX AN 0
I HAS A PUR
GIMMEH PUR
PUR IS NOW A NUMBR
FOO R SUM OF FOO AN PUR
BAR R SUM OF BAR AN 1
BOTH SAEM BIGGR OF PRODUKT OF FOO AN QUZ AN PRODUKT OF BAR BAZ AN PRODUKT OF FOO AN QUZ
O RLY?
YA RLY
BAZ R FOO
QUZ R BAR
OIC
IM OUTTA YR LOOP
BAZ IS NOW A NUMBAR
VISIBLE SMOOSH QUOSHUNT OF BAZ QUZ
KTHXBYE
Выходные данные Выведите единственное вещественное число. Ответ будет считаться правильным, если его абсолютная или относительная погрешность не превышает 10 - 4. | |
![]()
|
|
E. Антицепь
Паросочетания
дп
жадные алгоритмы
*2200
Вам задан ориентированный ациклический граф G, состоящий из n вершин, пронумерованных от 0 до n - 1. В графе имеется n ребер, пронумерованных от 0 до n - 1. Ребро с номером i соединяет вершины i и (i + 1) mod n, при этом может быть ориентировано как в одну сторону, так и в другую. Операция x mod y обозначает взятие остатка от деления числа x на число y. Назовем две вершины u и v в графе G сравнимыми, если существует путь в графе из u в v, либо из v в u. Назовем антицепью множество вершин графа G, в котором любые две различные вершины не являются сравнимыми. Размером антицепи назовем количество вершин в соответствующем множестве. Назовем антицепь максимальной, если в графе нет антицепей с большим размером. Вам требуется найти размер максимальной антицепи в графе G. Выходные данные Выведите единственное целое число — размер максимальной антицепи графа G. Примечание Рассмотрим первый тестовый пример. Ребра графа G: 0 → 1, 1 → 2, 0 → 2. В качестве максимальной антицепи можно выбрать множество вершин [0]. Большую по размеру антицепь выбрать не получится. | |
![]()
|
|
D. Георгий и интересный граф
Паросочетания
*2200
Георгий любит графы. Особенно он любит интересные графы. Будем называть ориентированный граф интересным, если выполнены все следующие условия: - В графе отсутствуют кратные дуги.
- Существует такая вершина v (будем называть ее центром), что для любой вершины графа u в графе содержатся дуги (u, v) и (v, u). При этом стоит отметить, что петля (v, v) должна содержаться в графе.
- Степень исхода каждой вершины кроме центра равна двум, степень захода каждой вершины кроме центра равна двум. Степень исхода вершины u — количество исходящих из u дуг, степень захода вершины u — количество входящих в u дуг. Стоит отметить, что граф может содержать петли.
Однако, не все так просто. Георгию подарили ориентированный граф, состоящий из n вершин и m дуг. В подаренном графе отсутствовали кратные дуги. Поскольку Георгий любит интересные графы, он хочет немного изменить подаренный граф так, чтобы получить интересный. За одно изменение разрешается удалить произвольную существующую дугу в графе, либо добавить произвольную дугу в граф. Георгий интересуется: какое минимальное количество изменений потребуется, чтобы из подаренного графа получить интересный граф? Помогите Георгию и узнайте ответ на поставленный вопрос. Выходные данные Выведите единственное целое число — ответ на поставленный Георгием вопрос. Примечание Если вы не знакомы с ориентированными графами, то можете изучить их здесь: http://ru.wikipedia.org/wiki/Ориентированный_граф В первом примере граф уже является интересным, и его центром является вершина 3. | |
![]()
|
|
B. Два множества
Паросочетания
*2000
поиск в глубину и подобное
жадные алгоритмы
2-sat
снм
У Little X есть n различных целых чисел: p1, p2, ..., pn. Он хочет так разделить все числа на два множества, A и B, чтобы выполнялись условия: - Если число x принадлежит множеству A, то число a - x также должно принадлежать множеству A.
- Если число x принадлежит множеству B, то число b - x также должно принадлежать множеству B.
Помогите Little X разделить числа на два множества или определите, что это невозможно. Выходные данные Если способ разделения чисел на два множества существует, то выведите "YES" в первой строке. Затем выведите n целых чисел: b1, b2, ..., bn (bi равняется либо 0, либо 1), описывающих разделение. Если bi равняется 0, то pi принадлежит множеству A, в противном случае оно принадлежит множеству B. Если это невозможно, выведите "NO" (без кавычек). Примечание Допустимо следующее разбиение: все числа содержатся в одном множестве, а второе множество пустое. | |
![]()
|
|
D. Дерево
Паросочетания
*3100
У Little X есть дерево, состоящее из n вершин, пронумерованных от 1 до n. Для каждого ребра дерева задана его длина — целое положительное число. Определим расстояние между двумя вершинами v и u (обозначим его как d(v, u)) как сумму длин ребер в кратчайшем пути между v и u. Будем называть перестановкой p последовательность из n различных целых чисел p1, p2, ..., pn (1 ≤ pi ≤ n). Little X хочет найти такую перестановку p, что сумма 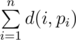 принимает как можно большее значение. При этом, если есть несколько оптимальных перестановок, он хочет найти лексикографически минимальную. Помогите ему найти такую перестановку! принимает как можно большее значение. При этом, если есть несколько оптимальных перестановок, он хочет найти лексикографически минимальную. Помогите ему найти такую перестановку! Выходные данные В первой строке выведите максимально возможное значение описанной суммы. Во второй строке выведите n целых чисел — искомая лексикографически минимальная перестановка. | |
![]()
|
|
E. Перманент
Паросочетания
математика
дп
meet-in-the-middle
*3100
Little X на днях решил #P полную задачу за полиномиальное время. Теперь он задает эту задачу вам! Дана особая матрица A размера n × n, ваша задача — подсчитать ее перманент по модулю 1000000007 (109 + 7). Особое свойство матрицы A заключается в том, что почти все ее элементы равняются 1. Только k элементов имеют заданное значение. Определение перманента можно найти по следующей ссылке: https://ru.wikipedia.org/wiki/Перманент Выходные данные Выведите перманент матрицы по модулю 1000000007 (109 + 7). | |
![]()
|
|
B. Бал в БерлГУ
Паросочетания
дп
поиск в глубину и подобное
жадные алгоритмы
*1200
сортировки
По случаю 100500-летия Берляндского государственного университета совсем скоро состоится бал! Уже n юношей и m девушек во всю репетируют вальс, менуэт, полонез и кадриль. Известно, что на бал будут приглашены несколько пар юноша-девушка, причем уровень умений танцевать партнеров в каждой паре должен отличаться не более чем на единицу. Для каждого юноши известен уровень его умения танцевать. Аналогично, для каждой девушки известен уровень ее умения танцевать. Напишите программу, которая определит наибольшее количество пар, которое можно образовать из n юношей и m девушек. Выходные данные Выведите единственное число — искомое максимальное возможное количество пар. | |
![]()
|
|
C. Расшифровка
Потоки
Паросочетания
*2300
Недавно на уроке во время контрольной Мария Ивановна перехватила записку от Саши к Оле. Мария Ивановна очень хочет знать, что в записке, но, к сожалению, записка зашифрована. Мария Ивановна знает, что её ученики для шифровки заменяют каждую букву исходного сообщения на какую-то другую. Замена происходит таким образом, что одинаковые буквы всегда заменяются одной и той же буквой, а разные — разными. Мария Ивановна подозревает, что записка — это ответы к контрольному тесту (ведь её длина случайно оказалась равной длине строки с правильными ответами). Однако она знает, что ответы Саши не обязательно полностью правильны. На каждый вопрос возможен один из K вариантов ответа. Естественно, Мария Ивановна знает правильные ответы. Мария Ивановна решила расшифровать записку таким способом, чтобы максимизировать количество правильных ответов Саши. Однако, она очень занята, поэтому попросила Вас помочь ей в этом пустяковом деле. Выходные данные В первой строке выведите единственное число — максимально возможное количество правильных ответов у Саши. Во второй строке выведите расшифровку — строчку длины K, где по порядку для каждой буквы из шифра учеников указано, какому ответу она соответствует. Если несколько расшифровок дают правильный ответ, выведите любую. | |
![]()
|
|
C. Массив и операции
Потоки
Паросочетания
*2100
теория чисел
Вы выписали на листок массив из n целых положительных чисел a[1], a[2], ..., a[n] и m хороших пар целых чисел (i1, j1), (i2, j2), ..., (im, jm). Каждая хорошая пара (ik, jk) удовлетворяет условиям: ik + jk — нечетное число и 1 ≤ ik < jk ≤ n. За одну операцию вы можете выполнить последовательность действий: - взять одну из хороших пар (ik, jk) и некоторое целое число v (v > 1), которое делит оба числа a[ik] и a[jk];
- разделить оба числа на v, т. е. выполнить присваивания:
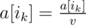 и и 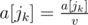 . . Определите, какое максимальное количество операций можно последовательно совершить над данным массивом. Обратите внимание, что одну пару можно использовать несколько раз в описанных операциях. Выходные данные Выведите единственное целое число — ответ на задачу. | |
![]()
|
|
C. Клубы
Паросочетания
Перебор
*2700
битмаски
Обратите внимание на необычное ограничение по памяти в этой задаче. Сотрудники MDCS (Microsoft Development Center Serbia, сербского центра разработок Майкрософта) любят вечеринки. Обычно они ходят в ночные клубы в пятницу и субботу. Всего в MDCS работает N людей, а в городе всего есть N клубов. К сожалению, если в ночном клубе будет больше одного сотрудника Майкрософта, то уровень крутизны этой вечеринки возрастает до небес, и вечеринка заканчивается, так что владельцы клуба никогда не позволяют более, чем одному сотруднику Майкрософта войти в их клуб в течение недели (так, на всякий случай). Вы организуете ночную жизнь сотрудников Майкрософта и у Вас есть статистика о том, насколько каждому сотруднику нравятся вечеринки в пятницу и субботу, для всех клубов. Вам надо распределить людей по клубам, максимизируя общую сумму их довольства (они настолько довольны, насколько им нравится выбранный клуб), при этом половина людей должна пойти клубиться в пятницу, а другая половина — в субботу. Выходные данные Вывод должен содержать единственное целое число — максимальную возможную сумму счастья. Примечание Распределение людей по клубам в примере: Пятница: 1-й человек идет в 4-й клуб (4 единицы довольства), а 4-й человек идет в 1-й клуб (4 единицы довольства). Суббота: 2-й человек идет в 3-й клуб (81 единица довольства), а 3-й человек идет во 2-й клуб (78 единиц довольства). 4 + 4 + 81 + 78 = 167. | |
![]()
|
|
E. День рождения
Строки
Паросочетания
*3200
У маленькой Даши сегодня день рождения — ей исполнилось целых 8 лет! По такому случаю каждый из n её родственников и друзей подарил ей ленточку с праздничным поздравлением, причём, как оказалось, все поздравления отличаются друг от друга. Даша собрала все ленточки вместе и решила выкинуть некоторые из них так, чтобы оставшийся набор стал стильным. Именинница считает набор стильным, если ни одно поздравление не является подстрокой другого. Напомним, что подстрокой строки s называется непрерывный отрезок букв строки s. Помогите Даше оставить как можно больше ленточек, чтобы она могла хвастаться ими всем своим друзьям. Ленточки не разрешается поворачивать и переворачивать, то есть каждое поздравление может быть прочитано единственным способом. Выходные данные В первой строке выведите максимальный размер стильного набора. Во второй строке выведите номера участвующих в нём лент, считая, что они нумеруются с единицы в порядке следования во входных данных. Если стильных наборов максимального размера несколько, то выведите любой из них. Примечание В примере можно было также оставить ленты 3 и 4. | |
![]()
|
|
D. Гамильтоново остовное дерево
Паросочетания
Деревья
дп
поиск в глубину и подобное
жадные алгоритмы
*2200
Группа из n городов связана сетью дорог. Первоначально между любой парой городов есть двунаправленная дорога, таким образом суммарное количество дорог равно 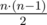 . Чтобы проехать по любой из этих дорог, требуется ровно y секунд. . Чтобы проехать по любой из этих дорог, требуется ровно y секунд. Остовным деревом называется такое подмножество дорог размера n - 1, что между любой парой городов можно проехать, используя только эти дороги. Было выбрано некоторое остовное дерево. После этого время проезда по каждой дороге остовного дерева было изменено с y на x. Обратите внимание, не гарантируется, что x меньше y. Вы хотели бы посетить все города по одному разу, используя кратчайший путь. Вам даны числа n, x, y и описание выбранного остовного дерева. Определите минимальное время, необходимое, чтобы посетить каждый город ровно один раз, если разрешается начать маршрут в любом городе и закончить также в любом городе. Выходные данные Выведите единственное целое число — минимальное количество секунд, которое придётся потратить на путь, проходящий через каждый город ровно один раз. Примечание В первом примере дороги в остовном дереве требуют 2 секунд, в то время как на другие дороги уходит 3 секунды. Один из примеров оптимального пути: 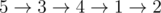 . . Во втором примере нам дано такое же остовное дерево, но дороги в нём требуют 3 секунд, в то время как остальные дороги требуют 2 секунд. Один из примеров оптимального пути: 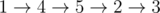 . . | |
![]()
|
|
E. Тане - 5 лет!
Паросочетания
жадные алгоритмы
графы
*3300
расписания
Тане исполнилось 5 лет и все её друзья собрались на праздновании дня рождения. Всего, включая Таню, на празднике присутствуют n детишек. Праздник уже подходит к концу, но напоследок запланированы игровые автоматы. В зале, где проходит праздник, есть m игровых автоматов, которые пронумерованы от 1 до m. Каждый из детей уже составил список тех автоматов, в которые он хочет поиграть. Более того, если ребенок хочет поиграть на каком-то автомате, то он знает точно, сколько ему надо времени, чтобы насладиться игрой на нём. На любом автомате единовременно может играть только один ребенок. Так как праздник уже затянулся, то все взрослые гости уже хотят по домам. Чтобы ускорить процесс вы можете дополнительно заказывать вторые экземпляры автоматов, для того чтобы арендовать второй экземпляр автомата j надо заплатить pj бурлей. Арендовав автомат, его можно использовать до конца праздника. Как скоро все дети смогут поиграть в соответствии со своими пожеланиями, если у вас есть бюджет b бурлей на аренду дополнительных автоматов. Для каждого автомата в наличии есть только один запасной, так что арендовать третий экземпляр автомата нельзя. Дети могут прерываться во время игры произвольным образом. Если i-й ребенок хочет поиграть на j-м автомате, то после аренды еще одного автомата j допустимо, что часть времени он сыграет на основном экземпляре j-го автомата, а часть — на дополнительном (причем любая из этих частей может выродиться в пустую). Переключение между автоматами может происходить мгновенно в целочисленные моменты времени. Конечно, ребенок не может играть на двух автоматах одновременно. Помните, что цели сэкономить нет (на детях не экономят!), требуется минимизировать время окончания игры последнего из детей. Выходные данные В первую строку выведите искомое минимальное время. Во вторую строку выведите строку из нулей и единиц длины m, j-й символ равен '1', если был арендован дубликат j-го автомата. В третью строку выведите g (0 ≤ g ≤ 106) — количество промежутков непрерывной игры всех детей. Далее в g строках выведите сами промежутки в виде четверки чисел i, j, s, d, которая обозначает, что ребенок i без перерыва играл в автомат j с момента времени s (s ≥ 0) в течение d (d ≥ 1) минут. Строки можно выводить в любом порядке. Если ответов несколько, выведите любой из них. | |
![]()
|
|
D. Восстановление функционального графа
Паросочетания
*3400
Функциональный граф — это ориентированный граф, каждая вершина которого имеет исходящую степень 1. Петли разрешены. Некоторые вершины функционального графа лежат на циклах. Из остальных же вершин можно попасть в цикл, сделав конечное число переходов по рёбрам (мы рассматриваем только конечные функциональные графы). Дадим вершинам функционального графа две характеристики. precyclei — количество ребёр, по которым необходимо перейти, начиная из вершины i, чтобы попасть в вершину, принадлежащую циклу (ноль, если вершина уже принадлежит циклу), и cyclei — количество вершин в цикле, в который мы попадём. Вам дана информация о вершинах некоторого функционального графа. Для каждой вершины известны значения precyclei и cyclei, однако вместо некоторых из этих значений могут стоять знаки вопроса. Это означает, что соответствующее значение может быть любым. Восстановите любой функциональный граф, подходящий под заданное описание, либо сообщите, что такого графа не существует. Выходные данные Если искомого графа не существует, на единственной строке выведите -1. В противном случае, выведите n чисел. i-е число — номер вершины, в которую ведёт ребро, исходящее из вершины i. Вершины выведенного графа должны следовать в том же порядке, в котором они были заданы во входных данных. Если существует несколько решений, выведите любое. | |
![]()
|
|
G. Олег и шахматы
Потоки
Паросочетания
Структуры данных
разделяй и властвуй
*3400
Обычный клиент банка Олег решает интересную шахматную задачу: расставить на шахматной доске n × n наибольшее число ладей, чтобы они не били друг друга. Напомним, что ладья, которая стоит в клетке (a, b), бьет ладью, стоящую в клетке (x, y), тогда и только тогда, когда a = x или b = y. К сожалению (или радости?) Олега ответ в этой задаче всегда получался равным n, поэтому вскоре задача ему наскучила. Он решил её усложнить, удалив некоторые клетки из шахматной доски. Удалив клетку, Олег подразумевает, что на нее нельзя ставить ладью, однако, бить «сквозь» удаленные клетки ладьи могут. Олег удаляет клетки группами, а именно, он раз за разом выбирает некоторый прямоугольник по сторонами, параллельными осям координат, и удаляет все клетки в нем. Формально, если он выбрал некоторый прямоугольник, левая нижняя и правая верхняя клетки которого имеют координаты (x1, y1) и (x2, y2), соответственно, то он удаляет все такие клетки (x, y) что x1 ≤ x ≤ x2 и y1 ≤ y ≤ y2. Гарантируется, что никакую клетку два раза Олег удалять не будет, то есть все выбранные прямоугольники не пересекаются. Эту версию задачи Олег решить не смог, а его друг, к которому он часто обращается за советами, — аналитик Игорь — сейчас очень занят на конференции, и не может помочь Олегу. Вы — последняя надежда Олега! Помогите ему: по заданному размеру доски и прямоугольникам, клетки в которых удалены, выясните, какое максимальное число ладей можно расставить на доске так, чтобы никакая ладья не била никакую другую. Выходные данные В единственной строке выведите максимальное число ладей, которое Олег сможет расставить на поле так, чтобы они не били друг друга. Примечание Ниже приведено изображения поля и пример расстановки ладей на нем в первом примере. 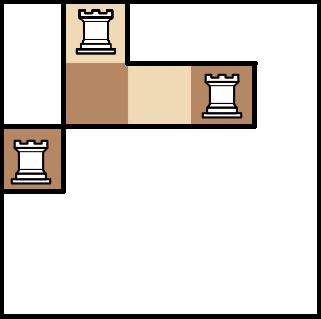
| |
![]()
|
|
D. Путь исследования
Бинарный поиск
Потоки
Паросочетания
*2100
кратчайшие пути
Участники Bubble Cup X собрались после соревнования и обсуждают, как лучше всего узнать страну-организатор и города в ней. После небольшого исследования карты Сербии участники выяснили следующий факт: в стране есть V городов, которые пронумерованы от 1 до V, и E двусторонних дорог, соединяющих города. У каждой дороги есть вес (время, необходимое для прохода по этой дороге). На Bubble Cup есть N команд, поэтому участники придумали следующий план: каждая из N команд начнет свой путь в одном из V городов, возможно, некоторые команды будут иметь одинаковую начальную позицию. Они хотят найти минимальное время T такое, что каждая команда может двигаться в течении этих T минут, и количество различных городов, в которых окажутся команды, как минимум K (потому что они будут исследовать только город, в котором окажутся в конце). Команда не обязана двигаться все время, если им нравится какой-то город, они могут остаться в нем и подождать, пока время пройдет. Помогите участникам определить это минимальное время T такое, что участники закончат в минимум K различных городах, или выведите -1, если решения нет. Обратите внимание, что между некоторыми городами может быть больше одной дороги. Выходные данные Выведите единственное число — минимальное время, в течение которого команды могут двигаться, чтобы закончить в хотя бы K различных городах, или выведите -1, если решения не существует. Если решение существует, результат будет не больше 1731311. Примечание В примере три команды начинают из города 5, две начинают из города 2. Если они будут двигаться 3 минуты, то возможно следующее: две команды в городе 2, одна команда в городе 5, одна команда в городе 3, и одна команда в городе 1. Видно, что всего есть четыре города, в которых команды закончили путешествие. | |
![]()
|
|
B. И снова тетрис
Паросочетания
Конструктив
математика
жадные алгоритмы
*2200
В редких перерывах между поисками теории всего физик Воль играет в расслабляющую игру — модифицированный им тетрис. Компьютер выдает Волю прямоугольное игровое поле n × m, на котором некоторые клетки пустые, остальные же заполнены. Игровая панель рядом с полем содержит изображения всевозможных связных фигурок, содержащих от двух до пяти клеток. Здесь мы рассматриваем только связные по стороне фигурки. Фигурки можно копировать с игровой панели на поле, заполняя ими пустые клетки. Разумеется, каждую фигурку можно использовать сколько угодно раз. Задача Воля — заполнить все поле так, чтобы на нем не осталось пустых клеток. Каждая изначально свободная клетка должна оказаться покрыта ровно одной клеткой некоторой фигурки. Каждая фигурка должна полностью находиться на игровом поле. 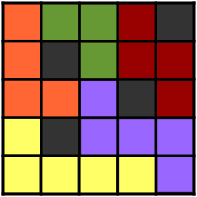 На рисунке черные клетки — изначально заполненные клетки поля, а одноцветные связные области — фигурки. Выходные данные Если поле заполнить невозможно, выведите единственной число «-1» (без кавычек). Иначе выведите любое заполнение поля фигурками в формате, совпадающем с входным, где все «.» (пустые клетки) заменены описанием фигурок следующим образом (см. примеры): каждая фигурка должна быть выведена конкретной цифрой, при этом касающимся по стороне фигуркам должны соответствовать разные цифры. Примечание В третьем примере невозможно заполнить пустую клетку, у которой нет пустых соседей. В четвертом примере ничего заполнять не нужно, поэтому надо вывести исходное поле. | |
![]()
|
|
D. Лень
Паросочетания
Деревья
дп
поиск в глубину и подобное
*3100
Лень — это плохо, не так ли? Поэтому мы решили приготовить задачу, чтобы наказать ленивых. Вам дано дерево, вы должны посчитать количество способов убрать одно ребро, а затем добавить одно ребро так, чтобы получившийся граф был деревом, и в нем существовало совершенное паросочетание. Два способа считаются различными, если удаленные или добавленные ребра не совпадают. Добавленное ребро может совпадать с удаленным. Совершенным паросочетанием называется подмножество ребер такое, что каждая вершина графа является концом ровно одного ребра. Выходные данные Выведите одно целое число — ответ на задачу. Примечание В первом примере имеются 8 вариантов: - ребро между 2 и 3 заменить на ребро между 1 и 3,
- ребро между 2 и 3 заменить на ребро между 1 и 4,
- ребро между 2 и 3 заменить на ребро между 2 и 3,
- ребро между 2 и 3 заменить на ребро между 2 и 4,
- ребро между 1 и 2 заменить на ребро между 1 и 2,
- ребро между 1 и 2 заменить на ребро между 1 и 4,
- ребро между 3 и 4 заменить на ребро между 1 и 4,
- ребро между 3 и 4 заменить на ребро между 3 и 4.
| |
![]()
|
|
F. Круговой марьяж
Бинарный поиск
Паросочетания
жадные алгоритмы
*2500
В прекрасной стране Кругляндии объявили брачный сезон! Страна Кругляндия представляет собой окружность длины \(L\). В стране есть \(n\) кавалеров и \(n\) дам, и кавалеры решили выбрать себе дам в пары. Конечно, каждый кавалер должен выбрать себе в жены ровно одну даму, а каждая дама должна быть выбрана ровно одним кавалером. Все объекты в Кругляндии находятся на окружности, в том числе столица, а также замки кавалеров и особняки дам. Замок \(i\)-го кавалера находится на расстоянии \(a_i\) от столицы при движении по часовой стрелке, а особняк \(i\)-й дамы на расстоянии \(b_i\) от столицы при движении по часовой стрелке. Назовем неудобством женитьбы максимальное расстояние, которое придется пройти даме от своего особняка до замка своего кавалера по кратчайшему пути (по или против часовой стрелки). Помогите кавалерам страны Кругляндия выбрать себе жен так, чтобы неудобство женитьбы было минимально возможным. Выходные данные В единственной строке выведите минимальное возможное неудобство женитьбы, где неудобство равно максимальному расстоянию, которое придется пройти какой-либо даме. Примечание В первом тестовом примере чтобы минимизировать женитьбу первому кавалеру следует жениться на второй даме, а второму кавалеру на первой даме. Таким образом, второй даме до замка первого жениха потребуется пройти расстояние \(1\), и то же расстояние понадобиться пройти первой даме до замка второго жениха. Таким образом, неудобство женитьбы равно \(1\). Во втором примере обозначим за \(p_i\) даму, которая досталась \(i\)-у кавалеру. Тогда одно из \(p\), принимающее минимальное возможное неудобство женитьбы это \((6,8,1,4,5,10,3,2,7,9)\). | |
![]()
|