| | | |
|
Симпатичные узоры
Динамическое программирование на таблицах
Динамическое программирование по профилю
Компания BrokenTiles планирует заняться выкладыванием во дворах у состоятельных клиентов узоров из черных и белых плиток, каждая из которых имеет размер 1 х 1 метр. Известно, что дворы всех состоятельных людей имеют наиболее модную на сегодня форму прямоугольника N х M метров. Однако при составлении финансового плана у директора этой организации появилось целых две серьезных проблемы: во-первых, каждый новый клиент, очевидно, захочет, чтобы узор, выложенный у него во дворе, отличался от узоров всех остальных клиентов этой фирмы, а во-вторых, этот узор должен быть симпатичным.

Как показало исследование, узор является симпатичным, если в нем нигде не встречается квадрата 2 х 2 метра, полностью покрытого плитками одного цвета. Для составления финансового плана директору Васе необходимо узнать, сколько клиентов он сможет обслужить, прежде чем симпатичные узоры данного размера закончатся. Помогите ему!
Входные данные
Вводятся два положительных целых числа N и M (1 ≤ N · M ≤ 30).
Выходные данные
Выведите единственное число – количество различных симпатичных узоров, которые можно выложить во дворе размера N х M. Узоры, получающиеся друг из друга сдвигом, поворотом или отражением, считаются различными.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1 2 |
4 |
| 2 |
2 3 |
50 |
| |
![]()
|
|
Симпатичные узоры возвращаются
Динамическое программирование по профилю
Со времен написания условия предыдущей задачи многое изменилось. Симпатичные узоры (о том, что это такое – см. задачу "Симпатичные узоры") стали очень популярны по всему миру, поэтому люди готовы содержать очень большой участок земли, лишь бы иметь на ней узор, не встречающийся больше нигде.
Теперь компания BrokenTiles является ведущим производителем симпатичных узоров в мире! Для составления плана исполнительному директору Васе по-прежнему необходимо знать, сколько клиентов могут рассчитывать на узор данных размеров.
Так как масштабы буквально мировые, N <= 10100. Однако Вася не любит большие числа, поэтому просит выдать ответ по модулю P.
Входные данные
В первой строке входных данных содержатся три положительных целых числа, разделенные пробелом – N, M и P (1 <= N <= 10100, 1 <= M <= 5, 1 <= P <= 10 000).
Выходные данные
Выведите количество различных симпатичных узоров N x M по модулю P .
| |
![]()
|
|
Треугольная реформа
Динамическое программирование по профилю
Многоугольники. Выпуклые оболочки
Король Полигонии Трианг IV помешан на реформах. Чтобы войти в мировую историю, он решил провести территориальную реформу в своей стране. Страна Полигония имеет форму простого многоугольника, то есть ее граница не имеет самопересечений и самокасаний. В Полигонии большую роль играют внутренние диагонали — отрезки, соединяющие вершины государственной границы и полностью проходящие по территории страны, не касаясь границы. При этом форма Полигонии такова, что никакие две внутренние диагонали не лежат на одной прямой.
Вместо традиционного деления государства на административные округа король Трианг IV решил разделить свою страну на административные треугольники внутренними диагоналями. Для сокращения управляющего аппарата король повелел подготовить такой план деления страны, в котором количество административных треугольников будет минимальным.
Требуется написать программу, выполняющую деление Полигонии внутренними диагоналями на минимально возможное число административных треугольников.
Формат входных данных
В первой строке входных данных задается число N (3 ≤ N ≤ 20) — количество вершин многоугольника, образующего границу Полигонии. В следующих N строках находятся по 2 целых числа, по абсолютной величине не превосходящих 10 000 — координаты вершин в порядке обхода многоугольника против часовой стрелки. Гарантируется, что никакие три последовательные вершины многоугольника не лежат на одной прямой, и он не имеет самопересечений и самокасаний. Также гарантируется, что никакие две диагонали, содержащиеся внутри многоугольника, не лежат на одной прямой.
Формат выходных данных
В первую строку выведите наименьшее количество административных треугольников, на которое можно разбить Полигонию.
Во вторую строку выведите количество различных внутренних диагоналей K, с помощью которых можно произвести данное разбиение.
В каждую из следующих K строк выведите 4 целых числа — координаты начала и конца соответствующей диагонали разбиения, полностью лежащей внутри многоугольника и не проходящей по его границе.
Если искомых разбиений несколько, выведите любое из них.
Примеры
| № |
Входные данные |
Выходные данные |
Рисунок к тесту |
| 1 |
4
0 0
1 0
1 1
0 1 |
2
1
1 1 0 0 |
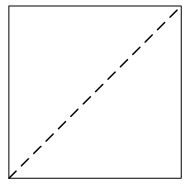 |
| 2 |
10
-6 0
0 2
6 0
3 3
6 4
2 4
0 6
-2 4
-6 4
-3 3 |
4
3
2 4 -2 4
0 2 3 3
-3 3 0 2 |
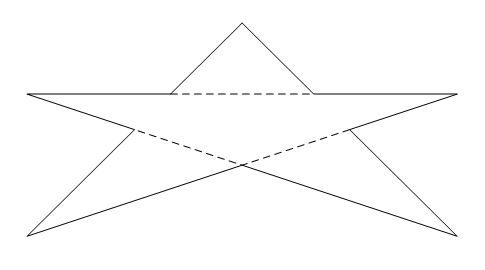 |
| |
![]()
|
|
Узор
Динамическое программирование по профилю
В комнате решили сделать паркетный пол. Причем есть задумка выложить на полу некоторый узор.
Плитки паркета, которыми выкладывается пол комнаты, состоят из квадратиков 1x1, каждый из которых может быть либо белым, либо черным. В свою очередь, комната имеет размеры NxM. На плане комнаты указано, какой квадрат комнаты какого цвета должен быть.
Существует несколько форм паркетных плиток:
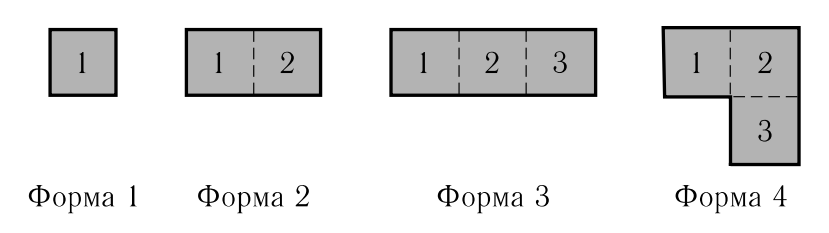
Квадратики одной паркетной плитки могут быть окрашены по-разному. Может существовать несколько типов плиток одинаковой формы, но окрашенных по-разному. Плитки разных типов могут иметь разную стоимость. Количество плиток каждого типа не ограничено. Плитки разрешается как угодно поворачивать (на углы, кратные 90 градусам). Не разрешается разламывать плитки, а также класть их лицевой стороной вниз.
Изначально, какая-то часть пола может уже быть выложена плиткой.
Требуется определить минимальную стоимость плитки, необходимой для того, чтобы замостить оставшуюся часть комнаты.
Входные данные
В первой строке входного файла записаны три числа: N, M (размеры комнаты) и K (количество доступных видов плитки). 1≤N≤8, 1≤M≤8, 1≤K≤10. Далее идет описание желаемой раскраски пола. Описание представляет собой N строчек по M чисел в каждой, где 0 обозначает белый цвет, 1 — черный, 2 — то, что квадрат уже выложен плиткой. В последних K строчках находятся описания доступных типов плитки в следующем формате:
<форма> <стоимость> <окраска>
<Форма> — это число от 1 до 4, описывающее форму плитки (см. рисунок выше)
<Стоимость> — это натуральное число, не превосходящее 10000, задающее стоимость одной плитки такого типа
<Окраска> — это от одного до трех чисел 0 или 1. Количество чисел совпадает с количеством квадратиков, из которых состоит плитка. Числа задают цвета квадратиков плитки в том порядке, в каком квадратики пронумерованы на рисунке.
Выходные данные
В выходной файл выведите единственное число — минимальную стоимость укладки или –1, если требуемым образом уложить плитку невозможно.
| |
![]()
|