| | | |
|
Вложенный тернарный поиск: футбольные ворота
Тернарный поиск
Соня, в отличие от многих студентов мат-меха, спортивна не только в программировании. В один прекрасный день она отправилась поиграть в футбол с друзьями. К сожалению, нигде поблизости не оказалось специально оборудованного футбольного поля, только высокая берёза одиноко красовалась в глубине двора. Покопавшись дома в кладовке, Соня нашла две палки и решила соорудить футбольные ворота из палок и берёзы. Конечно, берёза будет использована как одна из боковых стоек ворот. Осталось сделать из двух палок вторую стойку и перекладину.
Соня, конечно, хочет забить как можно больше голов. Поэтому она решила сделать ворота максимальной площади. Стандартные футбольные ворота имеют прямоугольную форму, но Соня — человек креативный, и она считает, что ворота могут иметь форму произвольного четырёхугольника.
Можно считать, что берёза является отрезком прямой и растёт строго перпендикулярно земле.
Входные данные
В единственной строке записаны целые числа a, b — длины палок (\(1 <= a, b <= 10 000\)). Известно, что суммарная длина палок строго меньше высоты берёзы.
Выходные данные
Выведите максимальную площадь ворот, которые можно соорудить из палок и берёзы. Ответ следует вывести с точностью не менее шести знаков после десятичной точки.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 2 |
4.828427125 |
Источник: Уральская региональная командная олимпиада по программированию 2011
| |
![]()
|
|
Дом у дороги
Тернарный поиск
Вычислительная геометрия
Министерство дорожного транспорта решило построить себе новый офис. Поскольку министр регулярно выезжает с инспекцией наиболее важных трасс, было решено, что офис министерства не должен располагаться слишком далеко от них.
Наиболее важные трассы представляют собой прямые на плоскости. Министерство хочет выбрать такое расположение для своего офиса, чтобы максимум из расстояний от офиса до трасс был как можно меньше.
Требуется написать программу, которая по заданному расположению наиболее важных трасс определяет оптимальное расположение дома для офиса министерства дорожного транспорта.
Входные данные
Первая строка входного файла содержит одно целое число n — количество наиболее важных трасс (1 ≤ n ≤ 104 ).
Последующие n строк описывают трассы. Каждая трасса описывается четырьмя целыми числами x1, y1, x2 и y2 и представляет собой прямую, проходящую через точки (x1, y1) и (x2, y2) . Координаты заданных точек не превышают по модулю 104. Точки (x1 , y1) и (x2 , y2) ни для какой прямой не совпадают.
Выходные данные
Выходной файл должен содержать два разделенных пробелом вещественных числа: координаты точки, в которой следует построить офис министерства дорожного транспорта. Координаты по модулю не должны превышать 109, гарантируется, что хотя бы один такой ответ существует. Если оптимальных ответов несколько, необходимо выведите любой из них.
Ответ должен иметь абсолютную или относительную погрешность не более 10−6, что означает следующее. Пусть максимальное расстояние от выведенной точки до некоторой трассы равно x, а в правильном ответе оно равно y. Ответ будет засчитан, если значение выражения | x − y | / max(1, |y| ) не превышает 10−6.
| Ввод |
Вывод |
|
4
0 0 0 1
0 0 1 0
1 1 2 1
1 1 1 2
|
0.5000000004656613 0.4999999995343387 |
|
7
376 -9811 376 -4207
6930 -3493 6930 -8337
1963 -251 1963 -5008
-1055 9990 -684 9990
3775 -348 3775 1336
7706 -2550 7706 -8412
-9589 8339 -4875 8339
|
4040.9996151750674 12003.999615175067 |
Личные олимпиады, Всероссийская олимпиада школьников, Региональный этап, 2011, 2 день, Задача D
| |
![]()
|
|
Load Balancing
Тернарный поиск
Структуры данных
Дерево отрезков, RSQ, RMQ
Дерево Фенвика
Коровы Фермера Джона стоят в различных точках (x1,y1)…(xn,yn) его поля (1≤N≤100,000, все xi и yi - положительные нечётные целые числа, не превышающие 1,000,000. ФД хочет разделить своё поле изгородью бесконечной длины с севера на юг, описываемой уравнением x=a (a - чётное целое, так обеспечивается, что изгородь не пройдёт через позицию ни одной коровы). Также он хочет построить изгородь бесконечной длины с востока на запад, которая описывается уравнением y=b, где b - чётное целое. Эти две изгороди пересекаются в точке (a,b), и вместе делят поле на четыре региона.
ФД хочет выбрать a и b так, чтобы получить "сбалансированное" количество коров во всех регионах, т.е. чтобы не было региона, который содержит слишком много коров. Пусть M - максимальное количество коров в этих четырёх регионах, ФД хочет, чтобы M было как можно меньше. Помогите ФД определить это минимально возможное значение для M.
ФОРМАТ ВВОДА:
Первая строка ввода содержит одно целое число, N. Каждая из следующих n строк содержит местоположение одной коровы, указанное её координатами x и y.
ФОРМАТ ВЫВОДА:
Выведите минимально возможное значение M, которое может достичь ФД оптимальным расположением изгородей.
| Ввод |
Вывод |
|
7
7 3
5 5
7 13
3 1
11 7
5 3
9 1
|
2 |
| |
![]()
|
|
Вложенный вложенный тернарный поиск: Космические спасатели
Тернарный поиск
В галактике находится n планет, на каждой из которых обитают множество различных живых существ. И каждое из них может оказаться в беде! Космические спасатели прекрасно знают об этом и всегда готовы помочь каждому, кому эта помощь действительно понадобится. Стоит только позвать.
Сейчас космические спасатели планируют построить самую большую в истории галактики спасательную базу, однако месторасположение будущей базы пока еще не определено. Поскольку помощь иногда требуется абсолютно неотложно, спасатели стремятся найти такую точку в галактике, из которой можно было бы добраться до самой удаленной планеты за наименьшее возможное время. Другими словами, необходимо найти такую точку в пространстве, чтобы расстояние от нее до самой удаленной от нее планеты было наименьшим из всех возможных точек в пространстве. К сожалению, они не в силах решить такую задачу.
Поскольку планеты достаточно удалены друг от друга, их можно считать точками в евклидовом трехмерном пространстве. Расстояние между точками (x i, y i, z i) и (x j, y j, z j) вычисляется по формуле:
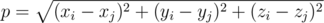
Спасательная база может располагаться в любой точке пространства, в том числе, совпадать с какой либо из планет.
Галактика в опасности! Спасите космических спасателей и укажите им искомую точку.
Входные данные
В первой строке входного файла содержится целое число n — количество планет (1 ≤ N ≤ 100). Каждая из последующих n строк содержит информация о планетах. i-я из этих строк содержит три целых числа xi, yi, zi — координаты i-й планеты ( - 104 ≤ xi, yi, zi ≤ 104, 1 ≤ i ≤ n). Никакие две планеты не совпадают.
Выходные данные
В первой строке выходного файла следует вывести три вещественных числа через пробел x 0, y 0, z 0 — координаты будущей базы. Если существует несколько решений, то разрешается вывести любое. Ответ будет засчитан, если расстояние от данной точки до самой удаленной планеты будет отличаться от результата жюри не более чем на 10 -6 по абсолютному или относительному значению.
| Ввод |
Вывод |
|
5
5 0 0
-5 0 0
0 3 4
4 -3 0
2 2 -2
|
0.000 0.000 0.000 |
| |
![]()
|
|
Архимедова спираль
Тернарный поиск
Дима недавно поступил на работу в НИИ Плоских Кривых. Как следует из названия этого научно- исследовательского института, он занимается различными исследованиями в области плоских кривых. Недавно Димин начальник Георгий столкнулся с весьма интересной кривой, которая, как выяснилось после некоторого исследования, известна под названием Архимедовой спирали. Архимедова спираль плоская кривая, изображающая траекторию точки M, которая равномерно движется вдоль луча OK с началом в O, в то время как сам луч OK равномерно вращается вокруг точки O (см. рисунок). Другими словами, расстояние до начала координат ρ = OM линейно зависит от угла поворота φ луча OK. При этом повороту луча OK на один и тот же угол соответствует одно и то же приращение расстояния ρ.
Движение точки M можно задать с помощью ряда параметров:
• начального угла поворота α луча OK (измеряется в градусах против часовой стрелки относительно положительного направления оси OX);
• угловой скорости вращения ω луча OK (измеряется в градусах за единицу времени);
• начального расстояния R от точки M до начала координат (точки O);
• скорости движения V точки M по лучу OK.
Если, задав эти параметры, не ограничить время движения точки M, то получится бесконечная кривая, исследовать которую достаточно трудно. Поэтому Дима решил ограничиться исследованием некоторой части этой кривой той, которая получается при движении точки M от нулевого момента времени до момента времени T. Задача, которую решает Дима состоит в поиске прямоугольника минимальной площади со сторонами, параллельными осям координат, в который ее можно вписать.
Требуется написать программу, которая найдет искомый прямоугольник
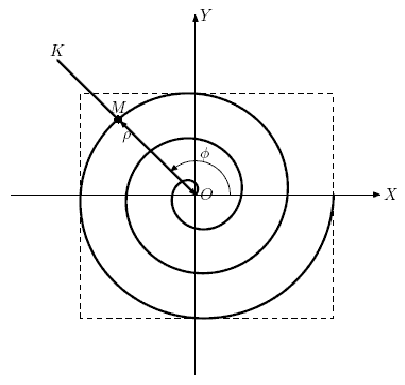
Входные данные
Входной файл содержит четыре целых числа: ω (1 ≤ ω ≤ 100), V (1 ≤ V ≤ 100), R (0 ≤ R ≤ 100) и T (1 ≤ T ≤ 1000). В этой задаче считается, что начальный угол поворота α равен нулю.
Выходные данные
В первой строке выходного файла выведите два вещественных числа — координаты левого нижнего угла искомого прямоугольника, а во второй строке — координаты правого верхнего угла искомого прямоугольника.
Ответ будет считаться правильным, если значение каждой из координат будет отличаться от истинного значения не более чем на 10-5.
| |
![]()
|
|
Про любовь...
Тернарный поиск
Паук и паучиха плывут по озеру на двух веточках. Плавать они не умеют, поэтому смогут встретиться только тогда, когда веточки соприкоснутся.
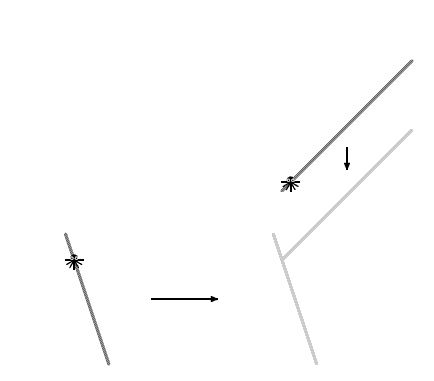
Считая, что веточки имеют форму отрезков, и что они плывут с постоянными скоростями, определите, сколько осталось ждать встречи несчастным членистоногим.
Входные данные
Входной файл содержит 12 чисел: x1, y1, x2, y2, x3, y3, x4, y4, v1x, v1y, v2x, v2y. Координаты вершин первого отрезка: (x1, y1) и (x2, y2), координаты вершин второго отрезка: (x3, y3) и (x4, y4), скорость первого отрезка (v1x, v1y), скорость второго отрезка (v2x, v2y). Все числа целые и не превосходят по модулю 104. В начальный момент времени веточки не соприкасаются. Гарантируется, что веточки имеют ненулевую длину.
Выходные данные
Выведите в выходной файл время до ближайшего момента, когда веточки соприкоснутся, с ошибкой не более 10 −4. Если веточки не соприкоснутся никогда, выведите число -1.
| Ввод |
Вывод |
|
0 0 -1 3
4 4 7 7
3 0
0 -1
|
1.6 |
|
0 0 -1 3
4 4 7 7
1 0
0 -3
|
-1 |
| |
![]()
|
|
Велогонка
Тернарный поиск
Велосипедисты, участвующие в шоссейной гонке, в некоторый момент времени, который называется начальным, оказались в точках, удалённых от места старта на x1, x2, ..., xn метров (n – общее количество велосипедистов). Каждый велосипедист двигается со своей постоянной скоростью v1, v2, ..., vn метров в секунду. Все велосипедисты двигаются в одну и ту же сторону.
Репортёр, освещающий ход соревнований, хочет определить момент времени, в который расстояние между лидирующим в гонке велосипедистом и замыкающим гонку велосипедистом станет минимальным, чтобы с вертолёта сфотографировать сразу всех участников велогонки.
Требуется написать программу, которая по заданному количеству велосипедистов n, заданным начальным положениям велосипедистов x1, x2, ..., xn и их скоростям v1, v2, ..., vn, вычислит момент времени t, в который расстояние l между лидирующим и замыкающим велосипедистом будет минимальным.
Входные данные
Первая строка входного файла содержит целое число n – количество велосипедистов.
В последующих n строках указаны по два целых числа: xi – расстояние от старта до i-го велосипедиста в начальный момент времени (0 ≤ xi ≤ 107 ) и vi – его скорость (0 ≤ vi ≤ 107 ).
Выходные данные
В выходной файл необходимо вывести два вещественных числа: t – время в секундах, прошедшее от начального момента времени до момента, когда расстояние в метрах между лидером и замыкающим будет минимальным, l – искомое расстояние.
Числа t и l должны иметь абсолютную или относительную погрешность не более 10–6, что означает следующее. Пусть выведенное число равно x, а в правильном ответе оно равно y. Ответ будет считаться правильным, если значение выражения |x – y| / max(1, |y| ) не превышает 10–6.
Подзадачи и система оценки
Данная задача содержит четыре подзадачи. Для оценки каждой подзадачи используется своя группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.
| Ввод |
Вывод |
|
3
0 40
30 10
40 30
|
1 30 |
|
5
90 100
100 70
100 70
110 60
120 35
|
0.5 5.000000000000 |
| |
![]()
|
|
D. Заповедник
Бинарный поиск
Тернарный поиск
геометрия
*2200
В лесу, который мы представляем как плоскость, живут \(n\) редких животных. Животное номер \(i\) имеет логово в точке \((x_{i}, y_{i})\). В целях защиты этих животных было решено создать заповедник, имеющий форму круга, в котором должны находиться все логова редких животных. Также через лес протекает единственная река, из которой пьют все животные, в связи с чем она должна иметь хотя бы одну общую точку с заповедником. С другой стороны, по реке постоянно ходят корабли, чему может помешать наличие более чем одной общей точки реки и заповедника. Таким образом, необходимо, чтобы заповедник и река имели ровно одну общую точку. Для вашего удобства ученые уже сделали преобразование координат такое, что теперь река задана уравнением \(y = 0\). Определите, возможно ли построить заповедник и найдите минимальный радиус заповедника, удовлетворяющего заданным условиям. Выходные данные Если заповедник невозможно построить, выведите \(-1\). Иначе выведите одно вещественное число — минимальный радиус заповедника. Ваш ответ будет засчитан, если абсолютная или относительная погрешность вашего ответа не превышает \(10^{-6}\). Формально, пусть ваш ответ равен \(a\), а ответ жюри равен \(b\). Ваш ответ будет зачтен, если \(\frac{|a - b|}{\max{(1, |b|)}} \le 10^{-6}\). Примечание В первом примере оптимально построить заповедник радиуса \(0.5\) с центром в точке \((0,\ 0.5)\). Во втором примере невозможно построить заповедник. В третьем примере оптимально построить заповедник радиуса \(\frac{5}{8}\) с центром в точке \((\frac{1}{2},\ \frac{5}{8})\). | |
![]()
|
|
E. Космические спасатели
Тернарный поиск
геометрия
*2100
В галактике находится n планет, на каждой из которых обитают множество различных живых существ. И каждое из них может оказаться в беде! Космические спасатели прекрасно знают об этом и всегда готовы помочь каждому, кому эта помощь действительно понадобится. Стоит только позвать. Сейчас космические спасатели планируют построить самую большую в истории галактики спасательную базу, однако месторасположение будущей базы пока еще не определено. Поскольку помощь иногда требуется абсолютно неотложно, спасатели стремятся найти такую точку в галактике, из которой можно было бы добраться до самой удаленной планеты за наименьшее возможное время. Другими словами, необходимо найти такую точку в пространстве, чтобы расстояние от нее до самой удаленной от нее планеты было наименьшим из всех возможных точек в пространстве. К сожалению, они не в силах решить такую задачу. Поскольку планеты достаточно удалены друг от друга, их можно считать точками в евклидовом трехмерном пространстве. Расстояние между точками (xi, yi, zi) и (xj, yj, zj) вычисляется по формуле 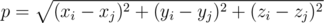 . Спасательная база может располагаться в любой точке пространства, в том числе, совпадать с какой либо из планет. . Спасательная база может располагаться в любой точке пространства, в том числе, совпадать с какой либо из планет. Галактика в опасности! Спасите космических спасателей и укажите им искомую точку. Выходные данные В первой строке выходного файла следует вывести три вещественных числа через пробел x0, y0, z0 — координаты будущей базы. Если существует несколько решений, то разрешается вывести любое. Ответ будет засчитан, если расстояние от данной точки до самой удаленной планеты будет отличаться от результата жюри не более чем на 10 - 6 по абсолютному или относительному значению. | |
![]()
|
|
E. Павел и треугольники
Тернарный поиск
Перебор
дп
жадные алгоритмы
*1900
бпф
У Павла есть набор палок, с длинами равными степеням двойки. У него есть \(a_0\) палок длины \(2^0 = 1\), \(a_1\) палок длины \(2^1 = 2\), ..., \(a_{n-1}\) палок длины \(2^{n-1}\). Павел хочет составить из этих палок наибольшее количество треугольников, с площадью строго больше нуля, каждая палка при этом может содержаться не более чем в одном треугольнике. Запрещено ломать палки, а также каждый треугольник должен состоять из ровно трех палок. Найдеите наибольшее количество треугольников, которое может составить Павел. Выходные данные Выведите одно целое число — максимальное количество невырожденных треугольников, которые может составить Павел. Примечание В первом примере Павел может, например, составить такой комплект треугольников (перечислены длины сторон треугольника): \((2^0, 2^4, 2^4)\), \((2^1, 2^3, 2^3)\), \((2^1, 2^2, 2^2)\). Во втором примере Павел не может составить ни одного треугольника. В третьем примере Павел может, например, составить такой комплект треугольников (перечислены длины сторон треугольника): \((2^0, 2^0, 2^0)\), \((2^1, 2^1, 2^1)\), \((2^2, 2^2, 2^2)\). | |
![]()
|
|
C. Соединение точек
Бинарный поиск
Тернарный поиск
*2000
жадные алгоритмы
сортировки
Вам дан набор точек \(x_1\), \(x_2\), ..., \(x_n\) на числовой прямой. Две точки \(i\) и \(j\) могут быть соединены друг с другом при выполнении следующих условий: - Ни \(i\), ни \(j\) не соединены ни с какими другими точками;
- \(|x_i - x_j| \ge z\).
Какое максимальное количество пар точек вы можете соединить друг с другом? Выходные данные Выведите одно целое число — максимальное количество пар точек, которое вы можете соединить друг с другом. Примечание В первом примере вы можете соединить точку \(1\) с точкой \(2\) (\(|3 - 1| \ge 2\)), и точку \(3\) с точкой \(4\) (\(|7 - 3| \ge 2\)). Во втором примере вы можете соединить точку \(1\) с точкой \(3\) (\(|5 - 10| \ge 5\)). | |
![]()
|
|
E. Минимизация разности
Бинарный поиск
Тернарный поиск
Конструктив
*2000
жадные алгоритмы
сортировки
В данной задаче вам задана последовательность \(a_1, a_2, \dots, a_n\), состоящая из \(n\) целых чисел. Вы можете изменять элементы последовательности. В ходе одной операции изменения, вы можете выбрать произвольную позицию в последовательности и увеличить или уменьшить элемент, находящийся в этой позиции, на единицу. Перед вами стоит задача определить минимально возможную разность между максимальным и минимальным элементами последовательности, которую можно достичь, произведя не более \(k\) описанных операций. Выходные данные Выведите минимально возможную разность между максимальным и минимальным элементами последовательности, которую можно достичь, произведя не более \(k\) операций, описанных в условии. Примечание В первом примере можно дважды увеличить на единицу второе число и дважды уменьшить на единицу третье число. Тогда получим последовательности \([3, 3, 5, 5]\), в которой разность между максимальным и минимальным элементами равна \(2\). При этом останется одна еще операция, но ее можно не использовать, так как не удастся сделать разность между максимальным и минимальным элементами меньше \(2\). Во втором примере можно не использовать ни одной операции, так как все элементы в последовательности одинаковые, а значит разность между максимальным и минимальным элементами равна \(0\). | |
![]()
|
|
B1. Отправьте коробки Алисе (упрощенная версия)
Тернарный поиск
Конструктив
математика
теория чисел
*1800
жадные алгоритмы
Это — упрощённая версия задачи. В этой версии, \(1 \le n \le 10^5\) и \(0 \le a_i \le 1\). Вы можете взламывать эту задачу только тогда, когда решите и заблокируете обе версии. Приближается Рождество, и наш главный герой, Боб, готовит эффектный подарок для своей давней лучшей подруги Алисы. В этом году он решил приготовить \(n\) коробок шоколада, пронумерованных от \(1\) до \(n\). Изначально \(i\)-я коробка содержит \(a_i\) кусочков шоколада. Поскольку Боб — типичный приятный парень, он не отправит Алисе \(n\) пустых ящиков. Другими словами, минимум одно число из \(a_1, a_2, \ldots, a_n\) является положительным. Поскольку Алиса не любит взаимно простые множества, она будет счастлива, только если существует какое-то целое число \(k > 1\), такое, что количество кусочков в каждой коробке делится на \(k\). Обратите внимание, что Алиса не будет возражать, если будут какие-то пустые коробки. Чарли, парень Алисы, также является вторым лучшим другом Боба, поэтому он решает помочь Бобу, переставляя кусочки шоколада. За одну секунду Чарли может взять кусок в \(i\)-й коробке, и поместить его либо в \(i-1\)-ю коробку или \(i+1\)-ю коробку (если такие коробки существуют). Конечно, он хочет помочь своему другу как можно быстрее. Поэтому он просит вас подсчитать минимальное количество секунд, которое понадобится ему, чтобы сделать Алису счастливой. Выходные данные Если Чарли не может сделать Алису счастливой, выведите \(-1\). Иначе выведите \(x\) — минимальное количество секунд, которые нужны Чарли, чтобы помочь Бобу сделать Алису счастливой. | |
![]()
|
|
B2. Отправьте коробки Алисе (усложнённая версия)
Тернарный поиск
Конструктив
математика
*2100
теория чисел
жадные алгоритмы
Это — сложная версия задачи. В ней \(1 \le n \le 10^6\) и \(0 \leq a_i \leq 10^6\). Вы можете взламывать эту версию тогда, когда решите ее (но предыдущую только тогда, когда заблокировали обе версии). Приближается Рождество, и наш главный герой, Боб, готовит эффектный подарок для своей давней лучшей подруги Алисы. В этом году он решил приготовить \(n\) коробок шоколада, пронумерованных от \(1\) до \(n\). Изначально \(i\)-я коробка содержит \(a_i\) кусочков шоколада. Поскольку Боб — типичный приятный парень, он не отправит Алисе \(n\) пустых ящиков. Другими словами, минимум одно число из \(a_1, a_2, \ldots, a_n\) является положительным. Поскольку Алиса не любит взаимно простые множества, она будет счастлива, только если существует какое-то целое число \(k > 1\), такое, что количество кусочков в каждой коробке делится на \(k\). Обратите внимание, что Алиса не будет возражать, если будут какие-то пустые коробки. Чарли, парень Алисы, также является вторым лучшим другом Боба, поэтому он решает помочь Бобу, переставляя кусочки шоколада. За одну секунду Чарли может взять кусок в \(i\)-й коробке, и поместить его либо в \(i-1\)-ю коробку или \(i+1\)-ю коробку (если такие коробки существуют). Конечно, он хочет помочь своему другу как можно быстрее. Поэтому он просит вас подсчитать минимальное количество секунд, которое понадобится ему, чтобы сделать Алису счастливой. Выходные данные Если Чарли не может сделать Алису счастливой, выведите \(-1\). Иначе выведите \(x\) — минимальное количество секунд, которые нужны Чарли, чтобы помочь Бобу сделать Алису счастливой. Примечание В первом примере Чарли может передвинуть все шоколадные кусочки во вторую коробку. Каждая коробка будет делиться на \(17\). Во втором примере Чарли может передвинуть кусочек из \(2\)-й коробки в \(3\)-ю и еще один из \(4\)-й в \(5\)-ю. Каждая коробка делится на \(3\). В третьем примере каждая коробка уже делится на \(5\). В четвертом примере Чарли не может ничего сделать, он не может помочь Бобу сделать Алису счастливой. | |
![]()
|
|
A. Дедлайн
Бинарный поиск
Тернарный поиск
Перебор
математика
*1100
Адилбеку назначили особый проект. Для Адилбека это означает, что у него есть \(n\) дней, чтобы запустить особую программу и представить полученные результаты. Но есть одна проблема: программе нужно работать \(d\) дней, чтобы посчитать результаты. К счастью, Адилбек может оптимизировать программу. Если он потратит \(x\) (\(x\) — целое неотрицательное) дней на оптимизацию, то программа станет работать за \(\left\lceil \frac{d}{x + 1} \right\rceil\) дней (\(\left\lceil a \right\rceil\) — это округление вверх: \(\left\lceil 2.4 \right\rceil = 3\), \(\left\lceil 2 \right\rceil = 2\)). Программу не получится оптимизировать, пока она работает, а потому общее количество потраченных Адилбеком дней будет равняться \(x + \left\lceil \frac{d}{x + 1} \right\rceil\). Успеет ли Адилбек получить результаты за не более, чем \(n\) дней? Выходные данные Выведите \(T\) ответов — по одному на набор входных данных. Для каждого набора выведите YES (регистр не важен), если Адилбек сможет уложиться в \(n\) дней или NO (регистр не важен) в противном случае. Примечание В первом наборе, Адилбек решает совсем не оптимизировать программу, так как \(d \le n\). Во втором наборе, Адилбек может потратить \(1\) день на оптимизацию и программа станет отрабатывать за \(\left\lceil \frac{5}{2} \right\rceil = 3\) дней. Суммарно, он потратит \(4\) дня и уложится в сроки. В третьем наборе, невозможно уложиться в сроки. Например, если Адилбек потратит \(2\) дня на оптимизацию, то программа все равно будет работать еще \(\left\lceil \frac{11}{2+1} \right\rceil = 4\) дня. | |
![]()
|
|
B. День рождения Мотарака
Бинарный поиск
Тернарный поиск
*1500
жадные алгоритмы
Дарк собирается посетить день рождения Мотарака. Дарк решил, что он хочет подарить Мотараку массив \(a\), состоящий из \(n\) неотрицательных целых чисел. Дарк создал этот массив еще \(1000\) лет назад, поэтому некоторые его элементы пропали. Дарк знает, что Мотарак не любит, когда у двух соседних элементов большая абсолютная разница. У него не так много времени, поэтому он хочет выбрать целое число \(k\) (\(0 \leq k \leq 10^{9}\)) и заменить все пропущенные элементы в массиве \(a\) числом \(k\). Обозначим за \(m\) максимальную абсолютную разницу между всеми парами соседних элементов (то есть максимальное значение \(|a_i - a_{i+1}|\) по всем \(1 \leq i \leq n - 1\)) в массиве \(a\) после того, как Дарк заменит все пропавшие элементы на число \(k\). Дарк хочет выбрать число \(k\) так, что \(m\) будет минимально. Можете ли вы помочь ему? Выходные данные Выведите ответы для каждого тестового случая в следующем формате: Вы должны вывести два целых числа, минимальное возможное значение \(m\) и целое число \(k\) (\(0 \leq k \leq 10^{9}\)), которое делает максимальную абсолютную разницу между соседними элементами массива \(a\) равной \(m\). Обратите внимание, что после замены всех пропавших элементов на \(k\) максимальная абсолютная разница между всеми парами соседних элементов должна стать равной \(m\). Если существует более, чем одно подходящее \(k\), вы можете вывести любое из них. Примечание В первом тестовом случае, после замены всех пропавших элементов на \(11\) массив станет равным \([11, 10, 11, 12, 11]\). Абсолютная разница между любой парой соседних элементов равна \(1\). Выбрать такое значение \(k\), чтобы максимальная абсолютная разница между всеми парами соседних элементов стала \(\leq 0\) невозможно, поэтому ответ равен \(1\). В третьем тестовом случае, после замены всех пропавших элементов массива на \(6\) массив станет равным \([6, 6, 9, 6, 3, 6]\). - \(|a_1 - a_2| = |6 - 6| = 0\);
- \(|a_2 - a_3| = |6 - 9| = 3\);
- \(|a_3 - a_4| = |9 - 6| = 3\);
- \(|a_4 - a_5| = |6 - 3| = 3\);
- \(|a_5 - a_6| = |3 - 6| = 3\).
Поэтому максимальная абсолютная разница между всеми парами соседних элементов будет равна \(3\). | |
![]()
|
|
C. Прибавление степеней
Тернарный поиск
математика
реализация
теория чисел
*1400
жадные алгоритмы
битмаски
Представим следующий алгоритм. Есть массив \(v_1, v_2, \dots, v_n\), изначально заполненный нулями. Несколько раз с массивом проделываются похожие операции — на \(i\)-м шаге (в \(0\)-индексации) вы можете: - либо выбрать любую позицию \(pos\) (\(1 \le pos \le n\)) и увеличить \(v_{pos}\) на \(k^i\);
- либо не выбирать позицию и пропустить шаг.
Вы можете выбирать, как алгоритм ведет себя на каждом шаге и когда он будет остановлен. Вопрос в следующем: можно ли сделать массив \(v\) равным некоторому массиву \(a\) (\(v_j = a_j\) для каждого \(j\)) после некоторого шага? Выходные данные Для каждого набора тестовых данных выведите либо YES (регистр не важен), если можно получить массив \(a\) после некоторого шага, либо NO (регистр не важен), если это невозможно. Примечание В первом наборе тестовых данных можно остановить алгоритм до \(0\)-го шага, или не выбирать никакую позицию и остановить алгоритм позже. Во втором наборе можно прибавить \(k^0\) к \(v_1\) и остановить алгоритм. В третьем наборе невозможно получить два элемента, равных \(1\), в массиве \(v\). В пятом наборе можно пропустить \(9^0\) и \(9^1\), прибавить \(9^2\) и \(9^3\) к \(v_3\), пропустить \(9^4\) и, наконец, прибавить \(9^5\) к \(v_2\). | |
![]()
|
|
C. Простые простые
Тернарный поиск
Конструктив
математика
*1800
Это последний класс Профессора R в его карьере преподавателя. Каждый раз, когда Профессор R вел класс, он давал своим ученикам особенную задачу. Как его любимый ученик, вложите всю душу в решение этой задачи в последний раз. Вам даны два многочлена \(f(x) = a_0 + a_1x + \dots + a_{n-1}x^{n-1}\) и \(g(x) = b_0 + b_1x + \dots + b_{m-1}x^{m-1}\), с целыми положительными коэффициентами. Гарантируется, что общий НОД всех коэффициентов равен \(1\) для обоих многочленов. Другими словами, \(gcd(a_0, a_1, \dots, a_{n-1}) = gcd(b_0, b_1, \dots, b_{m-1}) = 1\). Пусть \(h(x) = f(x)\cdot g(x)\). Пусть \(h(x) = c_0 + c_1x + \dots + c_{n+m-2}x^{n+m-2}\). Вам также дано простое число \(p\). Профессор R просит вас найти любое такое \(t\), что \(c_t\) не делится на \(p\). Он гарантирует вам, что при данных ограничениях такое \(t\) всегда существует. Если существует несколько таких \(t\), выведите любое из них. Так как ввод может быть достаточно большим, рекомендуем использовать быстрые способы ввода. Выходные данные Выведите одно число \(t\) (\(0\le t \le n+m-2\)) — подходящая степень \(x\) в \(h(x)\), коэффициент при которой не делится на данное простое \(p\). Если несколько степеней \(x\) удовлетворяют условию, выведите любую. Примечание В первом примере, \(f(x)\) равен \(2x^2 + x + 1\) и \(g(x)\) равен \(x + 2\), их произведение \(h(x)\) равно \(2x^3 + 5x^2 + 3x + 2\), поэтому ответ может быть 1 или 2, так как и 3 и 5 не делятся на 2. Во втором примере, \(f(x)\) равен \(x + 2\) и \(g(x)\) равен \(x + 3\), их произведение \(h(x)\) равно \(x^2 + 5x + 6\), поэтому ответом может быть любая из этих степеней, так как ни один коэффициент не делится на данное простое число. | |
![]()
|
|
C1. Просто вписываем многоугольник
Бинарный поиск
Тернарный поиск
математика
геометрия
*1400
Условие этой задачи почти полностью совпадает с условием задачи C2. Единственное отличие в следующем: в задаче C1 \(n\) всегда четно, а в задаче C2 \(n\) всегда нечетно. Вам задан правильный многоугольник из \(2 \cdot n\) вершин (то есть он выпуклый и имеет равные стороны и углы) и все его стороны имеют длину \(1\). Назовем этот многоугольник \(2n\)-угольником. Ваша задача — найти квадрат минимального размера, такой что в него можно вписать \(2n\)-угольник. \(2n\)-угольник можно вписать в квадрат, если \(2n\)-угольник можно разместить таким образом, что каждая точка, лежащая внутри или на границе \(2n\)-угольника также будет лежать внутри или на границе квадрата. Вы можете вращать \(2n\)-угольник и/или квадрат. Выходные данные Выведите \(T\) действительных чисел — по одному на набор входных данных. Для каждого набора, выведите минимальную длину стороны квадрата, в который можно вписать \(2n\)-угольник. Ваш ответ будет считаться правильным, если его абсолютная или относительная погрешность не превосходит \(10^{-6}\). | |
![]()
|
|
E. Реставрационное расстояние
Бинарный поиск
Тернарный поиск
математика
*2100
жадные алгоритмы
сортировки
Вам нужно отреставрировать стену. Стена состоит из \(N\) столбиков кирпичей, высота \(i\)-го столбика изначально равна \(h_{i}\), высота измеряется количеством кирпичей. После реставрации все \(N\) столбиков должны иметь одинаковую высоту. Вам доступны следующие операции: - положить кирпич на верх одного из столбиков, стоимость этой операции равна \(A\);
- убрать кирпич с верха одного из непустых столбиков, стоимость этой операции равна \(R\);
- переложить один кирпич с верха одного из непустых столбиков на верх другого столбика, стоимость этой операции равна \(M\).
Вы не можете создавать дополнительные столбики или игнорировать какие-то из существующих столбиков, даже если их высота стала равна \(0\). За какую минимальную суммарную стоимость возможно провести реставрацию, то есть сделать высоты всех столбиков равными? Выходные данные Выведите одно целое число — минимальную суммарную стоимость реставрации стены. | |
![]()
|
|
E2. Чтение книг (сложная версия)
Тернарный поиск
Структуры данных
реализация
жадные алгоритмы
сортировки
*2500
Простая и сложная версии на самом деле являются разными задачами, поэтому прочитайте условия обеих задач полностью и внимательно. Летние каникулы начались, поэтому Алиса и Боб хотят играть и веселиться, но... Их мама не согласна с этим. Она говорит, что они должны прочитать ровно \(m\) книг перед всеми развлечениями. Алиса и Боб прочитают каждую книгу вместе, чтобы быстрее закончить это задание. В семейной библиотеке есть \(n\) книг. \(i\)-я книга характеризуется тремя целыми числами: \(t_i\) — количество времени, которое Алиса и Боб должны потратить, чтобы прочитать ее, \(a_i\) (равное \(1\), если Алисе нравится \(i\)-я книга, и \(0\), если не нравится), и \(b_i\) (равное \(1\), если Бобу нравится \(i\)-я книга, и \(0\), если не нравится). Поэтому им нужно выбрать ровно \(m\) книг из имеющихся \(n\) книг таким образом, что: - Алисе нравятся не менее \(k\) книг из выбранного множества и Бобу нравятся не менее \(k\) книг из выбранного множества;
- общее время, затраченное на прочтение этих \(m\) книг минимизировано (ведь они дети и хотят начать играть и веселиться как можно скорее).
Множество, которое они выбирают, одинаковое и для Алисы и для Боба (они читают одни и те же книги), и они читают все книги вместе, таким образом, суммарное время чтения равно сумме \(t_i\) по всем книгам, которые находятся в выбранном множестве. Ваша задача — помочь им и найти любое подходящее множество книг или определить, что такое множество найти невозможно. Выходные данные Если подходящего решения не существует, выведите целое число -1. Если решение существует, выведите \(T\) первой строкой — минимальное суммарное время, необходимое для прочтения подходящего множества книг. Второй строкой выведите \(m\) различных целых чисел от \(1\) до \(n\) в любом порядке — индексы книг, включенных в выбранное вами множество. Если существует несколько подходящих ответов, вы можете вывести любой из них. | |
![]()
|
|
A. Граф
Бинарный поиск
Тернарный поиск
математика
*2100
дп
*особая задача
поиск в глубину и подобное
Дан неориентированный граф, в котором каждое ребро покрашено либо в чёрный цвет, либо в красный цвет. Ваша задача присвоить каждой вершине по вещественному числу таким образом, что: - сумма чисел на обеих концах каждого чёрного ребра равна \(1\);
- сумма чисел на обеих концах каждого красного ребра равна \(2\);
- сумма модулей всех присвоенных чисел наименьшая возможная.
Если это не возможно, выведите, что не существует такого комплекта чисел. Выходные данные Если решение существует, выведите в первой строке слово «YES» и во второй строке выведите \(N\) чисел. Для каждого \(i\) (\(1 \le i \le N\)), \(i\)-е из этих чисел должно равняться числу, присвоенному вершине с номером \(i\). Вывод должен соответствовать следующим ограничениям точности: - сумма чисел на концах каждого ребра должна отличаться от нужной суммы для этого ребра меньше, чем на \(10^{-6}\);
- сумма модулей всех присвоенных чисел отличается от наименьшего возможного меньше, чем на \(10^{-6}\).
Если существует несколько решений, выведите любое из них. Если решения не существует, выведите одно слово «NO». Система оценки Подзадачи: - (5 баллов) \(N \leq 5\), \(M \leq 14\)
- (12 баллов) \(N \leq 100\)
- (17 баллов) \(N \leq 1000\)
- (24 баллов) \(N \leq 10\,000\)
- (42 баллов) Без дополнительных ограничений.
Примечание Примите во внимание, что во втором примере решение не уникальное. | |
![]()
|
|
C. Boboniu и строка
Бинарный поиск
Тернарный поиск
геометрия
*2600
Boboniu определяет BN-строку как строку \(s\) из символов 'B' и 'N'. Он может совершать следующие операции над BN-строкой \(s\): - Удалить один символ из \(s\).
- Удалить подстроку «BN» или «NB» из \(s\).
- Добавить символ 'B' или 'N' в конец \(s\).
- Добавить строку «BN» или «NB» в конец \(s\).
Строка \(a\) является подстрокой строки \(b\) если \(a\) может быть получена из \(b\) удалением нескольких (возможно, нуля или всех) символов из начала и нескольких (возможно, нуля или всех) символов из конца. Boboniu считает, что BN-строки \(s\) и \(t\) похожи если и только если: - \(|s|=|t|\).
- Существует перестановка \(p_1, p_2, \ldots, p_{|s|}\), что для всех \(i\) (\(1\le i\le |s|\)), \(s_{p_i}=t_i\).
Boboniu также определяет \(\text{dist}(s,t)\), расстояние между \(s\) и \(t\), как минимальное число операций, необходимое чтобы сделать \(s\) похожей на \(t\). Теперь Boboniu дал вам \(n\) непустых BN-строк \(s_1,s_2,\ldots, s_n\) и просит вас найти непустую BN-строку \(t\), что максимальное расстояние до строки из \(s\) минимизировано, т.е. вам нужно минимизировать \(\max_{i=1}^n \text{dist}(s_i,t)\). Выходные данные В первой строке, выведите минимальное значение \(\max_{i=1}^n \text{dist}(s_i,t)\). Во второй строке, выведите подходящее \(t\). Если есть несколько возможных \(t\), вы можете вывести любое. Примечание В первом примере \(\text{dist(B,BN)}=\text{dist(N,BN)}=1\), \(\text{dist(BN,BN)}=0\). Таким образом максимальное значение равно \(1\). | |
![]()
|
|
E. Oracle соло мид
Тернарный поиск
математика
*2100
жадные алгоритмы
Меха-Наруто играет в компьютерную игру. У его персонажа есть следующая способность: нанести вражескому герою \(a\) единиц урона, затем восполнять ему \(b\) единиц здоровья в конце каждой секунды, начиная со следующей, на протяжении ровно \(c\) секунд. В частности, если эта способность применяется в момент времени \(t\), то здоровье врага уменьшается на \(a\) в момент времени \(t\), а затем увеличивается на \(b\) в моменты \(t + 1\), \(t + 2\), ..., \(t + c\). У способности есть время перезарядки, равное \(d\) секундам, то есть если Меха-Наруто применяет способность в момент времени \(t\), то в следующий раз он может её применить не раньше момента \(t + d\). По некоторым причинам Меха-Наруто может использовать способность только в целые моменты времени, поэтому все изменения здоровья врага также происходят в целочисленные моменты. Эффекты от разных применений заклинания накладываются друг на друга. В частности, если вражеский герой находится под действием \(k\) заклинаний, применённых ранее и ещё не истёкших, то его здоровье увеличится на \(k\cdot b\). Помимо этого все изменения, которые происходят в один и тот же момент времени, учитываются одновременно. Теперь Меха-Наруто интересно, может ли он убить своего оппонента просто применяя свою способность так часто, как только можно (то есть каждые \(d\) секунд). Герой считается погибшим, если уровень его здоровья становится равным \(0\) или ниже. Предположим, что здоровье вражеского персонажа не изменяется никаким образом, кроме как от применения заклинания. Какое наибольшее количество здоровья может быть у врага, чтобы Меха-Наруто мог его убить? Выходные данные Для каждого теста выведите на отдельной строке \(-1\), если способность может рано или поздно убить любого врага, каким бы большим ни был его уровень здоровья; в противном случае выведите наибольшее число здоровья, при котором оппонент будет убит. Примечание В первом тесте из условия любая единица урона отменяется через секунду, поэтому Меха-Наруто не может нанести больше, чем 1 единицу урона. В четвёртом тесте из условия герой оппонента получает: - \(4\) урона (\(1\)-е применение способности) в момент \(0\);
- \(4\) урона (\(2\)-е применение способности), и \(3\) единицы здоровья восполняются (\(1\)-е применение) в момент \(1\) (всего \(5\) урона к начальному уровню здоровья);
- \(4\) урона (\(3\)-е применение способности), и \(6\) здоровья восполняется (\(1\)-е и \(2\)-е применения) в момент \(2\) (всего \(3\) урона к изначальному здоровью);
- и так далее.
Можно доказать, что ни к какому моменту времени враг не получит суммарно \(6\) или больше урона, поэтому ответ на этот тест есть \(5\). Обратите внимание, как производится пересчёт здоровья: например, если бы у врага было \(8\) здоровья, он бы не умер в момент времени \(1\), как если бы мы сначала вычли из его здоровья \(4\) единицы, а затем сочли бы его мёртвым, не успев добавить \(3\) единицы от лечения. В шестом тесте из условия герой со сколько угодно большим количеством здоровья рано или поздно умрёт. В седьмом тесте из условия ответ не вмещается в 32-битный целочисленный тип. | |
![]()
|
|
H. Побег из тюрьмы
Бинарный поиск
Тернарный поиск
геометрия
игры
*3500
Заключенный хочет сбежать из тюрьмы. Тюрьма является внутренней частью выпуклого многоугольника с вершинами \(P_1, P_2, P_3, \ldots, P_{n+1}, P_{n+2}, P_{n+3}\). Известно, что \(P_1=(0,0)\), \(P_{n+1}=(0, h)\), \(P_{n+2}=(-10^{18}, h)\) и \(P_{n+3}=(-10^{18}, 0)\). 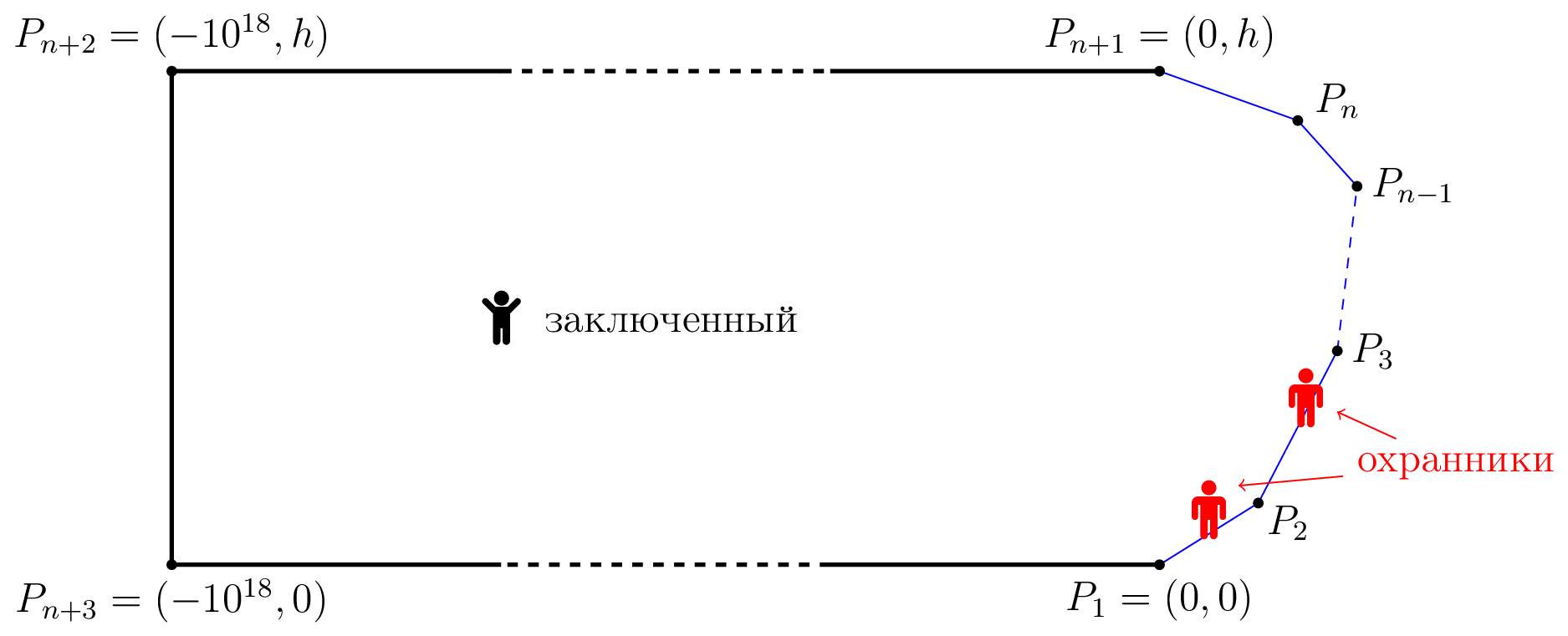 Стены тюрьмы \(P_{n+1}P_{n+2}\), \(P_{n+2}P_{n+3}\) и \(P_{n+3}P_1\) очень высокие, и заключенный не может на них взобраться. Следовательно, его единственный шанс — это достичь точки на одной из стен \(P_1P_2, P_2P_3,\dots, P_{n}P_{n+1}\) и сбежать оттуда. По периметру тюрьмы находятся два охранника. Заключенный движется со скоростью \(1\), в то время как охранники движутся, всегда оставаясь на периметре тюрьмы, со скоростью \(v\). Если заключенный достигает точки на периметре, где есть охранник, охранник убивает заключенного. Если заключенный достигает точки, на которую он может взобраться, и там нет охранника, то он сразу же убегает. Изначально заключенный находится в точке \((-10^{17}, h/2)\), а охранники — в точке \(P_1\). Найдите минимальную скорость \(v\) такую, чтобы охранники могли гарантировать, что заключенный не сбежит (при условии, что и заключенный, и охранники будут двигаться оптимально). Замечания: - В любой момент охрана и заключенный могут видеть друг друга.
- Залезание на стену не занимает времени.
- Вы можете считать, что и заключенный, и охранники могут изменить направление и скорость мгновенно и что они оба имеют идеальные рефлексы (так что они могут мгновенно реагировать на то, что делает другой).
- Оба охранника могут заранее спланировать, как реагировать на передвижения заключенного.
Выходные данные Выведите одно действительное число — минимальную скорость \(v\), которая позволяет охранникам гарантировать, что заключенный не сбежит. Ваш ответ будет считаться правильным, если его относительная или абсолютная погрешность не превысит \(10^{-6}\). | |
![]()
|
|
E. Четыре точки
Тернарный поиск
Потоки
Перебор
Конструктив
математика
реализация
геометрия
жадные алгоритмы
*2400
Вам заданы четыре различные целые точки \(p_1\), \(p_2\), \(p_3\) и \(p_4\) на коодинатной плоскости \(\mathit{XY}\). За один шаг вы можете выбрать одну из точек \(p_i\) и сдвинуть ее в одном из четырех направлений на единицу. Другими словами, если вы выбрали точку \(p_i = (x, y)\), вы можете передвинуть ее в \((x, y + 1)\), \((x, y - 1)\), \((x + 1, y)\) или \((x - 1, y)\). Ваша задача — сдвинуть точки таким образом, чтобы они образовали квадрат со сторонами параллельными осям \(\mathit{OX}\) и \(\mathit{OY}\) (квадрат со стороной \(0\) разрешен). Какое минимальное количество шагов вам нужно, чтобы получить такой квадрат? Выходные данные Для каждого набора входных данных, выведите единственное число — минимальное количество шагов, необходимых для получения квадрата. Примечание В первом наборе входных данных, один из оптимальных ответов изображен ниже:  Каждая точка будет сдвинута два раза, поэтому ответ \(2 + 2 + 2 + 2 = 8\). Во втором наборе, один из оптимальных ответов изображен ниже: 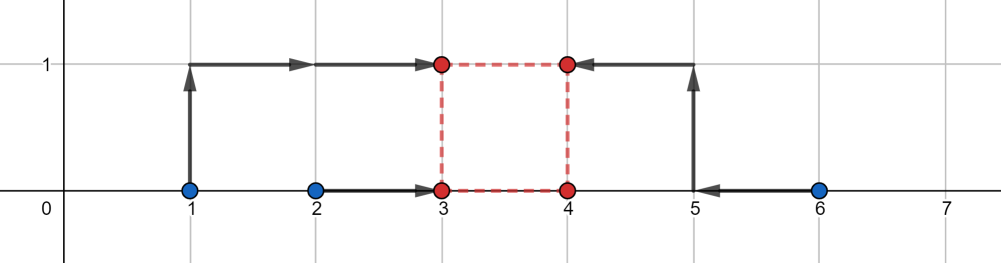 Ответ равен \(3 + 1 + 0 + 3 = 7\). В третьем наборе, один из оптимальных ответов изображен ниже: 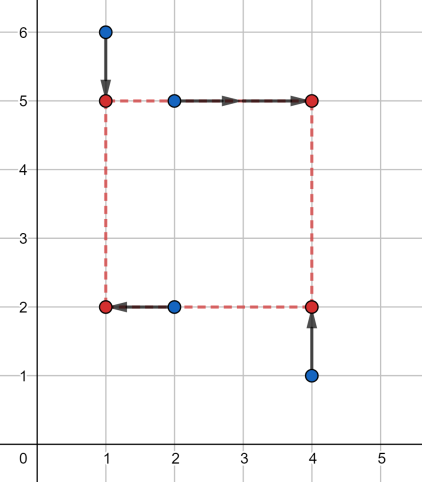 Ответ равен \(1 + 1 + 2 + 1 = 5\). | |
![]()
|
|
A. В поисках локального минимума
Бинарный поиск
Тернарный поиск
*1700
интерактив
Это интерактивная задача. Гомеру очень нравятся массивы, и он хочет поиграть с вами в игру. Гомер загадал перестановку \(a_1, a_2, \dots, a_n\) чисел от \(1\) до \(n\). Вас просят найти любой индекс \(k\) (\(1 \leq k \leq n\)), который является локальным минимумом. Для массива \(a_1, a_2, \dots, a_n\) индекс \(i\) (\(1 \leq i \leq n\)) считается локальным минимумом, если \(a_i < \min\{a_{i-1},a_{i+1}\}\), где \(a_0 = a_{n+1} = +\infty\). Массив называется перестановкой чисел от \(1\) до \(n\), если он содержит все целые числа от \(1\) до \(n\) ровно один раз. Изначально вам дается только значение \(n\) без какой-либо другой информации об этой перестановке. На каждом шаге взаимодействия вы можете выбрать любой индекс \(i\) (\(1 \leq i \leq n\)) и сделать с ним запрос. В ответ вы получите значение \(a_i\). Вы должны найти любой индекс \(k\), который является локальным минимумом, за не более чем \(100\) запросов. Протокол взаимодействия Вы начинаете взаимодействие с чтения целого числа \(n\) (\(1\le n \le 10^5\)) в отдельной строке. Чтобы сделать запрос с индексом \(i\) (\(1 \leq i \leq n\)), необходимо в отдельной строке вывести «? \(i\)». Затем считайте в отдельной строке значение \(a_i\). Количество запросов «?» должно не превышать \(100\). Чтобы вывести индекс \(k\) (\(1 \leq k \leq n\)), который является локальным минимумом, выведите «! \(k\)» в отдельной строке и завершите вашу программу. В случае, если ваш запрос имеет неверный формат, или вы сделали более \(100\) запросов типа «?», вы получите вердикт Неправильный ответ. После вывода запроса не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте: - fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Формат взломов Первая строка взлома должна содержать единственное целое число \(n\) (\(1 \leq n \leq 10^5\)). Вторая строка должна содержать попарно различные целые числа \(n\) \(a_1, a_2, \dots, a_n\) (\(1 \leq a_i \leq n\)). Примечание В примере в первой строке содержится целое число \(5\), указывающее на то, что длина массива составляет \(n = 5\). В примере делается пять запросов «?», после которых мы делаем вывод, что массив равен \(a = [3,2,1,4,5]\) и \(k = 3\) является локальным минимумом. | |
![]()
|
|
G. Подарочный набор
Бинарный поиск
Тернарный поиск
математика
*2100
жадные алгоритмы
У Поликарпа есть \(x\) красных и \(y\) синих конфет. Из них он хочет составить подарочные наборы. Каждый подарочный набор будет содержать либо \(a\) красных конфет и \(b\) синих конфет, либо наоборот — \(a\) синих конфет и \(b\) красных конфет. Помогите Поликарпу понять, какое наибольшее число подарочных наборов он может составить. Например, если \(x = 10\), \(y = 12\), \(a = 5\) и \(b = 2\), то он может составить три подарочных набора: - В первом наборе будет \(5\) красных конфет и \(2\) синие;
- Во втором наборе будет \(5\) синих конфет и \(2\) красные;
- В третьем наборе будет \(5\) синих конфет и \(2\) красные.
У Поликарпа останется одна красная конфета, используя которую, он не сможет собрать еще один подарочный набор. Выходные данные Для каждого набора входных данных выведите одно число — максимальное количество подарочных наборов, которое может собрать Поликарп. | |
![]()
|
|
D. Очередь с приоритетом
Тернарный поиск
Комбинаторика
математика
реализация
дп
*2200
Дана последовательность \(A\), в которой каждый элемент записан в формате + x или -, где \(x\) — целое число. Для последовательности \(S\), в которой каждый элемент записан в формате + x или -, определим \(f(S)\) следующим образом: - Проходим по \(S\) от первого элемента до последнего и поддерживаем мультимножество \(T\), изначально пустое.
- Если элемент последовательности имеет вид + x, добавим \(x\) в \(T\). Иначе удалим наименьший элемент из \(T\) (если \(T\) пусто, ничего делать не нужно).
- После прохода по \(S\) посчитаем сумму всех элементов в \(T\). \(f(S)\) полагается равным этой сумме.
Последовательность \(b\) является подпоследовательностью последовательности \(a\), если \(b\) может быть получена из \(a\) удалением нуля или больше элементов без изменения порядка оставшихся элементов. Для всех подпоследовательностей \(B\) последовательности \(A\) посчитайте сумму \(f(B)\) по модулю \(998\,244\,353\). Выходные данные Выведите одно целое число, равное ответу на задачу по модулю \(998\,244\,353\). Примечание В первом примере все возможные пары \(B\) и \(f(B)\) выглядят так: - \(B=\) {}, \(f(B)=0\).
- \(B=\) {-}, \(f(B)=0\).
- \(B=\) {+ 1, -}, \(f(B)=0\).
- \(B=\) {-, + 1, -}, \(f(B)=0\).
- \(B=\) {+ 2, -}, \(f(B)=0\).
- \(B=\) {-, + 2, -}, \(f(B)=0\).
- \(B=\) {-}, \(f(B)=0\).
- \(B=\) {-, -}, \(f(B)=0\).
- \(B=\) {+ 1, + 2}, \(f(B)=3\).
- \(B=\) {+ 1, + 2, -}, \(f(B)=2\).
- \(B=\) {-, + 1, + 2}, \(f(B)=3\).
- \(B=\) {-, + 1, + 2, -}, \(f(B)=2\).
- \(B=\) {-, + 1}, \(f(B)=1\).
- \(B=\) {+ 1}, \(f(B)=1\).
- \(B=\) {-, + 2}, \(f(B)=2\).
- \(B=\) {+ 2}, \(f(B)=2\).
Сумма этих значений равна \(16\). | |
![]()
|
|
C. Slay the Dragon
Бинарный поиск
Тернарный поиск
жадные алгоритмы
сортировки
*1300
Недавно Петя узнал о новой игре «Slay the Dragon». Как видно из названия, игроку предстоит сражаться с драконами, чтобы победить дракона, необходимо его убить и защитить свой замок. Для этого в распоряжении игрока есть отряд из \(n\) героев, сила \(i\)-го героя равна \(a_i\). По правилам игры убивать дракона должен отправиться ровно один герой, все остальные будут защищать замок. Если защита дракона равна \(x\), то на его убийство можно отправлять героя с силой не менее \(x\). Если сила атаки дракона равна \(y\), то суммарная сила героев, защищающих замок, должна быть хотя бы \(y\). За одну золотую монету игрок может увеличить силу любого из героев на \(1\). Эту операцию можно выполнять любое количество раз. Всего в игре существует \(m\) драконов, у \(i\)-го из них защита \(x_i\), а сила атаки \(y_i\). Пете стало интересно, какое минимальное количество монет ему необходимо потратить, чтобы победить \(i\)-го дракона. Обратите внимание, что задача решается независимо для каждого дракона (улучшения не сохраняются). Выходные данные Выведите \(m\) строк, \(i\)-я из которых содержит одно целое число — минимальное количество монет, которое необходимо потратить, чтобы победить \(i\)-го дракона. Примечание Для победы над первым драконом можно увеличить силу третьего героя на \(1\), тогда силы героев будут равны \([3, 6, 3, 3]\). Для убийства дракона можно выбрать первого героя. Для победы над вторым драконом можно увеличить силы второго и третьего героев на \(1\), тогда силы героев будут равны \([3, 7, 3, 3]\). Для убийства дракона можно выбрать второго героя. Для победы над третьим драконом можно увеличить силы всех героев на \(1\), тогда силы героев будут равны \([4, 7, 3, 4]\). Для убийства дракона можно выбрать четвертого героя. Для победы над четверым драконом можно не улучшать героев и выбрать третьего героя для убийства дракона. Для победы над пятым драконом можно увеличить силу второго героя на \(2\), тогда силы героев будут равны \([3, 8, 2, 3]\). Для убийства дракона можно выбрать второго героя. | |
![]()
|
|
C. Bubble Strike
Тернарный поиск
Теория вероятностей
Комбинаторика
математика
*2000
Little Johnny Bubbles enjoys spending hours in front of his computer playing video games. His favorite game is Bubble Strike, fast-paced bubble shooting online game for two players. Each game is set in one of the N maps, each having different terrain configuration. First phase of each game decides on which map the game will be played. The game system randomly selects three maps and shows them to the players. Each player must pick one of those three maps to be discarded. The game system then randomly selects one of the maps that were not picked by any of the players and starts the game. Johnny is deeply enthusiastic about the game and wants to spend some time studying maps, thus increasing chances to win games played on those maps. However, he also needs to do his homework, so he does not have time to study all the maps. That is why he asked himself the following question: "What is the minimum number of maps I have to study, so that the probability to play one of those maps is at least \(P\)"? Can you help Johnny find the answer for this question? You can assume Johnny's opponents do not know him, and they will randomly pick maps. Output Output contains one integer number – minimum number of maps Johnny has to study. | |
![]()
|
|
K. Pandemic Restrictions
Тернарный поиск
геометрия
After a long time living abroad, you have decided to move back to Italy and have to find a place to live, but things are not so easy due to the ongoing global pandemic. Your three friends Fabio, Flavio and Francesco live at the points with coordinates \((x_1, y_1), (x_2, y_2)\) and \((x_3, y_3)\), respectively. Due to the mobility restrictions in response to the pandemic, meetings are limited to \(3\) persons, so you will only be able to meet \(2\) of your friends at a time. Moreover, in order to contain the spread of the infection, the authorities have imposed the following additional measure: for each meeting, the sum of the lengths travelled by each of the attendees from their residence place to the place of the meeting must not exceed \(r\). What is the minimum value of \(r\) (which can be any nonnegative real number) for which there exists a place of residence that allows you to hold the three possible meetings involving you and two of your friends? Note that the chosen place of residence need not have integer coordinates. Output Print the minimum value of \(r\) which allows you to find a residence place satisfying the above conditions. Your answer is considered correct if its absolute or relative error does not exceed \(10^{-4}\). Formally, let your answer be \(a\), and the jury's answer be \(b\). Your answer is accepted if and only if \(\frac{|a - b|}{\max{(1, |b|)}} \le 10^{-4}\). Note In the first sample, Fabio, Flavio and Francesco live at the points with coordinates \((0,0)\), \((5,0)\) and \((3,3)\) respectively. The optimal place of residence, represented by a green house in the picture below, is at the point with coordinates \((2.3842..., 0.4151...)\). 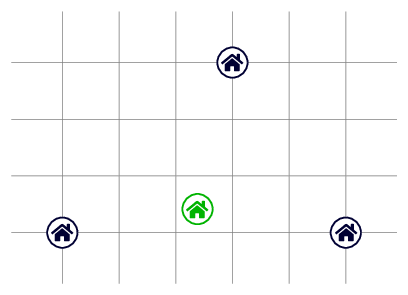 For instance, it is possible for you to meet Flavio and Francesco at the point depicted below, so that the sum of the lengths travelled by the three attendees is at most (and in fact equal to) \(r=5.0686...\). 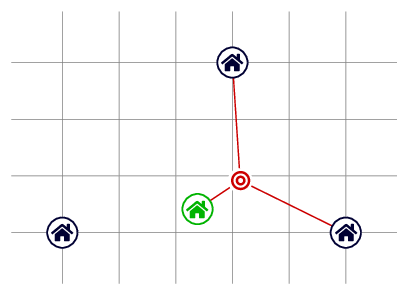 In the second sample, any point on the segment \(\{(x,0):\ -1 \leq x \leq 1 \}\) is an optimal place of residence. | |
![]()
|
|
C. Робот в коридоре
Тернарный поиск
Структуры данных
реализация
дп
*2000
жадные алгоритмы
Задано поле, состоящее из \(2\) строк и \(m\) столбцов. Строки занумерованы от \(1\) до \(2\) сверху вниз. Столбцы занумерована от \(1\) до \(m\) слева направо. Робот начинает в клетке \((1, 1)\). За одну секунду он может проделать любое из двух действий: - перейти в соседнюю по стороне клетку: наверх, направо, вниз или налево;
- остаться в той же клетке.
Роботу запрещено выходить за пределы поля. Изначально все клетки, кроме клетки \((1, 1)\) заблокированы. Каждая клетка \((i, j)\) содержит значение \(a_{i,j}\) — момент, когда данная клетка будет разблокирована. Робот может перейти в клетку \((i, j)\), если до начала хода прошло хотя бы \(a_{i,j}\) секунд. Робот должен посетить все клетки, не входя ни в какую клетку дважды или больше (считается, что робот вошел в клетку \((1, 1)\) на старте). Он может закончить в любой клетке. Какое минимальное время у него это может занять? Выходные данные На каждый набор входных данных выведите одно целое число — минимальное количество секунд, которые могут потребоваться роботу, чтобы посетить все клетки, не входя ни в какую клетку дважды или больше. | |
![]()
|
|
B. Собрание на прямой
Бинарный поиск
Тернарный поиск
математика
реализация
*1600
геометрия
жадные алгоритмы
\(n\) людей живут на координатной прямой, \(i\)-й человек живет в точке \(x_i\) (\(1 \le i \le n\)). Они хотят выбрать точку \(x_0\) для встречи. \(i\)-й человек потратит \(|x_i - x_0|\) минут, чтобы добраться до места встречи. Также \(i\)-му человеку требуется \(t_i\) минут чтобы одеться, поэтому суммарно ему нужно \(t_i + |x_i - x_0|\) минут чтобы добраться до места встречи. Здесь \(|y|\) обозначает модуль числа \(y\). Эти люди просят вас выбрать позицию \(x_0\), которая минимизирует время, через которое все \(n\) людей доберутся до места встречи. Выходные данные Для каждого набора входных данных выведите единственное вещественное число — оптимальная позиция \(x_0\). Можно показать, что существует единственная оптимальная позиция \(x_0\). Ваш ответ будет считаться правильным, если его абсолютная или относительная ошибка не превосходит \(10^{−6}\). Формально, пусть ваш ответ равен \(a\), а ответ жюри равен \(b\). Ваш ответ будет зачтен, если \(\frac{|a−b|}{max(1,|b|)} \le 10^{−6}\). Примечание - В \(1\)-м наборе входных данных есть только один человек, поэтому целесообразно выбрать место встречи в его позиции. Тогда он доберется до него за \(3\) минуты, которые нужны ему, чтобы одеться.
- Во \(2\)-м наборе входных данных есть \(2\) человека, которым не нужно время, чтобы одеться. Чтобы добраться до позиции \(2\), каждому из них потребуется по одной минуте.
- В \(5\)-м наборе входных данных \(1\)-му человеку нужно \(4\) минуты, чтобы добраться до позиции \(1\) (\(4\) минуты, чтобы одеться, и \(0\) минут на сам путь); \(2\)-му человеку нужно \(2\) минуты, чтобы добраться до позиции \(1\) (\(1\) минута, чтобы одеться, и \(1\) минута на сам путь); \(3\)-му человеку нужно \(4\) минуты, чтобы добраться до позиции \(1\) (\(2\) минуты, чтобы одеться, и \(2\) минуты на сам путь).
| |
![]()
|
|
E1. Задача-шутка (простая версия)
Бинарный поиск
Тернарный поиск
Конструктив
интерактив
*2500
Единственная разница между этой задачей и сложной версией — максимальное количество вопросов. Это интерактивная задача! Загадано некоторое целое число \(1 \le x \le n\), которое вам нужно найти. Чтобы найти его, вы можете задать не более \(\mathbf{82}\) вопросов. В каждом вопросе вы можете выбрать непустое множество целых чисел \(S\) и спросить, принадлежит ли \(x\) множеству \(S\) или нет. После каждого запроса, если \(x\) принадлежит \(S\), вы получите «YES», иначе «NO». Проблема в том, что не все ответы обязательно верны (некоторые из них шуточные). Гарантируется, что на каждые два последовательных вопроса хотя бы на один из них дан правильный ответ. Вы также можете сделать не более \(2\) попыток угадать \(x\). Каждый раз, если вы правильно угадаете \(x\), вы получите «:)» и ваша программа должна завершиться, иначе вы получите «:(». Как часть шутки, мы не будем фиксировать значение \(x\) в начале. Наоборот, это значение может изменяться в процессе взаимодействия, но все уже полученные ответы всегда будут корректны с точки зрения описанного выше. Обратите внимание, что на ваши догадки ответа всегда отвечают правильно. Если вы задаете вопрос до и после догадки, по крайней мере на один из этих ваших вопросов будет дан правильный ответ, как обычно. Протокол взаимодействия Для каждого вопроса, если вы хотите спросить о множестве \(S\), сначала выведите символ «?», затем выведите размер множества \(S\), а затем уже элементы \(S\) один за другим. Все элементы должны быть различными целыми числами от \(1\) до \(n\). После каждого вопроса вы получите ответ на него: «YES» или «NO» в соответствии с условием. Вы можете задать не более \(82\) таких запросов. Если вы хотите угадать \(x\), сначала выведите «!», а затем выведите свою догадку. Если вы угадаете \(x\) правильно, вы получите «:)» и ваша программа должна завершиться, иначе вы получите «:(». Вы можете сделать не более \(2\) таких догадок. После вывода запроса не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте: - fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Взломы в этой задаче отключены. Примечание Если бы ответ на первый вопрос был правильным, то \(x\) было бы равно \(6\), но, как мы видим из первого предположения, \(6\) не является ответом. Так что ответ на первый вопрос — шутка. Как мы знаем, ответ хотя бы на один из наших двух вопросов правильный, и так как ответ на первый вопрос был шутливым, ответ на второй вопрос должен быть правильным. Итак, мы понимаем, что \(x\) не равно \(1, 2, 3\) или \(4\), и мы также знаем, что \(x\) не равно \(6\). Следовательно, \(x\) равно \(5\). | |
![]()
|
|
D. Вика и бонусы
Бинарный поиск
Тернарный поиск
Перебор
математика
*2200
В любимом Викином магазине косметики «Золотая груша» новая система бонусов! Работает эта система следующим образом: пусть у покупателя есть \(b\) бонусов. Перед оплатой покупки он может выбрать одну из двух опций: - Получить скидку в размере текущего количества бонусов, при этом бонусы не списываются.
- Накопить дополнительно \(x\) бонусов, где \(x\) — последняя цифра числа \(b\). В результате чего на счету покупателя станет \(b+x\) бонусов.
Например, если у покупателя было \(24\) бонуса, он может как получить скидку в размере \(24\), так и накопить ещё \(4\) бонуса, после чего на его счету станет \(28\) бонусов. На данный момент Вика уже успела накопить \(s\) бонусов. Девушка знает, что за оставшееся время действия бонусной системы она совершит ещё \(k\) покупок в сети магазинов «Золотая груша». Ознакомившись с правилами работы системы бонусов, Вике стало интересно, какую максимальную суммарную скидку она сможет получить. Помогите девушке ответить на этот вопрос. Выходные данные Для каждого набора входных данных выведите одно целое число — максимально возможную суммарную скидку, которую можно получить по бонусной системе. Примечание В первом наборе входных данных Вика может накопить бонусы после первой и второй покупки, после чего получить скидку \(4\). Во втором наборе входных данных Вика может три раза получить скидку \(11\), суммарная скидка составит \(33\). В третьем наборе входных данных независимо от действий Вики у неё всегда будет суммарная скидка \(0\). | |
![]()
|
|
B. Грибные учёные
Тернарный поиск
математика
*1800
Как известно, во всей вселенной принята трёхмерная декартова система координат, в которой каждой точке ставится в соответствие три вещественные координаты (x, y, z). В этой системе координат, расстояние от центра вселенной до точки считается по формуле: 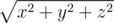 . Грибные ученые, подчиненные Великого Грибного короля, считают, что вселенная не совсем права и что расстояние от центра вселенной до точки равно xa·yb·zc. . Грибные ученые, подчиненные Великого Грибного короля, считают, что вселенная не совсем права и что расстояние от центра вселенной до точки равно xa·yb·zc. Чтобы «завалить» метрику грибных ученых, обычные учёные задали им задачку: найти такие x, y, z (0 ≤ x, y, z; x + y + z ≤ S), что расстояние от центра вселенной до точки (x, y, z) в метрике грибных ученых максимально. Грибные ученые не сильны в математике, поэтому они поручили это задание Вам. Обратите внимание, в этой задаче считается, что 00 = 1. Выходные данные Выведите три вещественных числа — координаты точки, в которой достигается максимум в метрике грибных учёных. Если ответов несколько выведите любой, удовлетворяющий ограничениям. Натуральный логарифм расстояния от центра вселенной до выведенной точки в метрике грибных ученых не должен отличаться от натурального логарифма максимального расстояния более, чем на 10 - 6. Считается, что ln(0) = - ∞. | |
![]()
|
|
F. Анти-прокси посещаемость
Тернарный поиск
Конструктив
дп
интерактив
*3500
Это интерактивная задача! Мистер 1048576 — один из тех преподавателей, который ненавидит тратить время на ведение посещаемости. Вместо того чтобы вести посещаемость традиционным способом, он решил попробовать что-то новое сегодня. В его классе \(n\) студентов с номерами от \(1\) до \(n\). Он точно знает, что сегодня отсутствует ровно \(1\) студент. Чтобы определить, кто отсутствует, он может задать некоторые запросы классу. В каждом запросе он может указать два целых числа \(l\) и \(r\) (\(1\leq l\leq r\leq n\)), и все студенты, чьи номера от \(l\) до \(r\) (включительно), поднимут руки. Затем он подсчитывает их, чтобы определить, лежит ли номер отсутствующего студента между этими значениями. Все было хорошо, пока его ассистент не заметил что-то странное — студенты нечестные! Некоторые студенты, чьи номера находятся в указанном диапазоне, могут не поднимать руки, в то время как другие студенты, чьи номера не находятся в указанном диапазоне, могут поднять руки и дать прокси-посещаемость за кого-то другого. Но они не хотят вызывать подозрений. Таким образом, возможны только следующие \(4\) случая для конкретного запроса \((l,r)\) — - Истинно положительный: присутствуют \(r-l+1\) студент и \(r-l+1\) студент подняли руки.
- Истинно отрицательный: присутствуют \(r-l\) студентов и \(r-l\) студентов подняли руки.
- Ложно положительный: присутствуют \(r-l\) студентов, но \(r-l+1\) студент поднял руку.
- Ложно отрицательный: присутствуют \(r-l+1\) студент, но \(r-l\) студентов поднял руку.
В первых двух случаях студенты считаются отвечающими честно, в то время как в последних двух случаях студенты считаются отвечающими нечестно. Студенты могут взаимно решить свою стратегию, неизвестную мистеру 1048576. Кроме того, студенты не хотят вызывать подозрений и в то же время хотят создать много путаницы. Поэтому их стратегия всегда соответствует следующим двум условиям — - Студенты никогда не будут отвечать честно \(3\) раза подряд.
- Студенты никогда не будут отвечать нечестно \(3\) раза подряд.
Мистер 1048576 раздосадован таким поведением студентов. Поэтому он готов отметить как минимум \(2\) студентов как отсутствующих (хотя он знает, что отсутствует только один). Посещаемость считается успешной, если отсутствующий студент находится среди этих двух. Кроме того, из-за ограниченного времени на занятия, он может задать не более \(\lceil\log_{1.116}{n}\rceil-1\) запросов (странное число, но ладно). Помогите ему завершить успешную посещаемость. Протокол взаимодействия Сначала прочтите строку, содержащую одно целое число \(t\) (\(1\leq t\leq 2048\)), обозначающее количество независимых тестов, которые вы должны решить. Для каждого теста сначала прочтите строку, содержащую одно целое число \(n\) (\(3\leq n\leq 10^5\)). Затем вы можете задать до \(\lceil\log_{1.116}{n}\rceil-1\) запросов. Чтобы задать запрос, напечатайте одну строку в формате "? l r" (без кавычек) \((1\leq l\leq r\leq n)\). Затем прочтите одну строку, содержащую одно целое число \(x\) (\(r-l\leq x\leq r-l+1\)), обозначающее количество студентов, поднявших руки в ответ на запрос. Чтобы отметить студента как отсутствующего, напечатайте одну строку в формате "! a" (без кавычек) \((1\leq a\leq n)\). Затем прочтите одно целое число \(y\) (\(y\in\{0,1\}\)). Если студент с номером \(a\) отсутствовал, \(y=1\), в противном случае, \(y=0\). Обратите внимание, что эта операция не считается запросом, но вы можете выполнить эту операцию не более \(2\) раз. Чтобы завершить тест, напечатайте одну строку в формате "#" (без кавычек). Затем вы должны продолжить решать оставшиеся тесты. Обратите внимание, что если вы зададите больше запросов, или запрос будет невалидным — вы получите вердикт Wrong answer. Гарантируется, что сумма \(n\) по всем тестам не превышает \(10^5\). После вывода ответов не забудьте вывести конец строки и очистить буфер вывода. В противном случае вы получите вердикт Idleness limit exceeded. Чтобы очистить буфер, используйте: - fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- Прочтите документацию для других языков.
Формат ввода для взломов Тесты для этой задачи используют как неадаптивные, так и адаптивные тесты. Вы можете использовать неадаптивный тест для проведения взломов. Первая строка ввода содержит одно целое число \(t\) (\(1\leq t\leq 2048\)). Первая строка каждого теста содержит три целых числа \(g\), \(n\) и \(x\), где \(g=1\) (для идентификации того, что этот тест должен использовать неадаптивный алгоритм), \(n\) (\(3\leq n\leq 10^5\)) означает количество студентов в классе, и \(x\) (\(1\leq x\leq n\)) означает номер студента, который отсутствует. Вы должны учесть, что сумма \(n\) по всем тестам не превышает \(10^5\). Вторая строка каждого теста содержит одну строку \(S\) (\(1\leq\vert S\vert\leq 120, S_i\in \{\texttt{T},\texttt{F}\}\)). Эта строка представляет последовательность истины. Если \(S_{(i-1)\bmod \vert S\vert+1}= \texttt{T}\), студенты будут действовать честно во время \(i\)-го запроса, в противном случае они будут действовать нечестно. Вы также должны учесть, что не должно быть индекса \(i\), для которого \(S_{(i-1)\bmod \vert S\vert+1} = S_{i\bmod \vert S\vert+1} = S_{(i+1)\bmod \vert S\vert+1}\). Примечание Для первого теста отсутствует студент с номером \(2\), и последовательность истины (см. раздел для взломов) — TFFTFTTF. Во время выполнения вашего решения этот тест будет использовать неадаптивный алгоритм. Для второго теста отсутствует студент с номером \(4\), и последовательность истины — FFTFTTFT. Во время выполнения вашего решения этот тест будет использовать адаптивный алгоритм. Таким образом, фактический ответ может измениться в зависимости от ваших запросов, но всегда будет согласован с ответом на предыдущие запросы. | |
![]()
|
|
D. Подземелья Одинокой горы
Тернарный поиск
Перебор
Структуры данных
математика
жадные алгоритмы
*1900
Однажды, люди, эльфы, гномы и другие жители Средиземья собрались отнять у Смога украденные у них сокровища. Во имя этой великой цели они сплотились вокруг сильного эльфа Тимофея и начали планировать свержение правителя Одинокой горы. Армия жителей Средиземья будет состоять из нескольких отрядов. Известно, что каждая пара существ одной расы, которые находятся в разных отрядах, прибавляет \(b\) единиц к суммарной силе армии. Но так как Тимофею будет сложно руководить армией, состоящей из большого числа отрядов, то суммарная сила армии, состоящей из \(k\) отрядов, уменьшается на \((k - 1) \cdot x\) единиц. Обратите внимание, что армия всегда состоит из хотя бы одного отряда. Известно, что в Средиземье проживают \(n\) рас, и количество существ \(i\)-й расы равно \(c_i\). Помогите жителям Средиземья определить максимальную силу армии, которую они могут составить. Выходные данные Для каждого набора входных данных выведите одно целое число — максимальную силу армии, которую могут составить жители Средиземья. Примечание В первом наборе входных данных жители Средиземья могут составить \(3\) отряда. Так как \(x = 0\), то сила армии не уменьшится из-за количества отрядов. Жителей по отрядам можно распределить так: - Единственного представителя первой расы можно отправить в первый отряд.
- Первого представителя второй расы можно отправить в первый отряд, второго представителя второй расы можно отправить во второй отряд. Тогда суммарная сила армии увеличится на \(b = 1\).
- Первого представителя третьей расы можно отправить в первый отряд, второго представителя третьей расы можно отправить во второй отряд, третьего представителя третьей расы можно отправить в третий отряд. Тогда суммарная сила армии увеличится на \(3 \cdot b = 3\), так как они образуют три пары, находящиеся в разных отрядах.
Таким образом, суммарная сила армии равна \(4\). Во втором наборе входных данных жители Средиземья могут составить \(3\) отряда. Так как \(x = 10\), то сила армии уменьшится на \(20\). Жителей по отрядам можно распределить так: - Первого представителя первой расы можно отправить в первый отряд, второго представителя первой расы можно отправить во второй отряд. Тогда суммарная сила армии увеличится на \(b = 5\).
- Первого и второго представителя второй расы можно отправить в первый отряд, третьего и четвёртого представителя второй расы можно отправить во второй отряд, пятого представителя третьей расы можно отправить в третий отряд. Тогда суммарная сила армии увеличится на \(8 \cdot b = 40\).
- Первого представителя третьей расы можно отправить в первый отряд, второго представителя третьей расы можно отправить во второй отряд, третьего представителя третьей расы можно отправить в третий отряд. Тогда суммарная сила армии увеличится на \(3 \cdot b = 15\), так как они образуют три пары, находящиеся в разных отрядах.
Таким образом, суммарная сила армии равна \(5 + 40 + 15 - 20 = 40\). | |
![]()
|
|
E. Оптимальные тренировки
Бинарный поиск
Тернарный поиск
математика
реализация
*1500
Исаак начинает свою тренировку. Доступно \(n\) маршрутов, \(i\)-й маршрут (\(1 \le i \le n\)) состоит из \(a_i\) участков одинаковой длины. Дано целое число \(u\) (\(1 \le u \le 10^9\)), завершение каждого участка может увеличить способности Исаака на определенное значение: - Завершение \(1\)-го участка увеличивает способности Исаака на \(u\).
- Завершение \(2\)-го участка увеличивает способности Исаака на \(u-1\).
- Завершение \(3\)-го участка увеличивает способности Исаака на \(u-2\).
- \(\ldots\)
- Завершение \(k\)-го участка (\(k \ge 1\)) увеличивает способности Исаака на \(u+1-k\). (Значение \(u+1-k\) может быть отрицательным, что означает, что завершение дополнительного участка уменьшает способности Исаака.)
Также дано целое число \(l\). Вы можете выбрать целое число \(r\), такое что \(l \le r \le n\), и тогда Исаак завершит каждый участок каждого маршрута \(l, l + 1, \dots, r\) (то есть, всего \(\sum_{i=l}^r a_i = a_l + a_{l+1} + \ldots + a_r\) участков). Ответьте на следующий вопрос: какое оптимальное значение \(r\) вы можете выбрать, чтобы увеличение способностей Исаака было максимальным? Если существует несколько значений \(r\), которые максимизируют увеличение способностей Исаака, выведите наименьшее значение \(r\). Для увеличения сложности вам нужно ответить на вопрос для \(q\) различных значений \(l\) и \(u\). Выходные данные Для каждого теста выведите \(q\) целых чисел: \(i\)-е целое число содержит оптимальное значение \(r\) для \(i\)-го запроса. Если существует несколько решений, выведите наименьшее из них. Примечание Для \(1\)-го запроса в первом тесте: - Выбрав \(r = 3\), Исаак завершает \(a_1 + a_2 + a_3 = 3 + 1 + 4 = 8\) участков в общей сложности, поэтому его увеличение способностей составляет \(u+(u-1)+\ldots+(u-7)=8+7+6+5+4+3+2+1 = 36\).
- Выбрав \(r = 4\), Исаак завершает \(a_1 + a_2 + a_3 + a_4 = 3 + 1 + 4 + 1 = 9\) участков в общей сложности, поэтому его увеличение способностей составляет \(u+(u-1)+\ldots+(u-8)=8+7+6+5+4+3+2+1+0 = 36\).
Оба варианта дают оптимальное увеличение способностей, однако мы хотим выбрать наименьшее значение \(r\). Поэтому мы выбираем \(r = 3\). Для \(2\)-го запроса в первом тесте, выбрав \(r = 4\), Исаак завершает \(a_2 + a_3 + a_4 = 1 + 4 + 1 = 6\) участков в общей сложности, поэтому его увеличение способностей составляет \(u+(u-1)+\ldots+(u-5)=7+6+5+4+3+2 = 27\). Это оптимальное увеличение способностей. Для \(3\)-го запроса в первом тесте: - Выбрав \(r = 5\), Исаак завершает \(a_5 = 5\) участков в общей сложности, поэтому его увеличение способностей составляет \(u+(u-1)+\ldots+(u-4)=9+8+7+6+5 = 35\).
- Выбрав \(r = 6\), Исаак завершает \(a_5 + a_6 = 5 + 9 = 14\) участков в общей сложности, поэтому его увеличение способностей составляет \(u+(u-1)+\ldots+(u-13)=9+8+7+6+5+4+3+2+1+0+(-1)+(-2)+(-3)+(-4) = 35\).
Оба варианта дают оптимальное увеличение способностей, однако мы хотим выбрать наименьшее значение \(r\). Поэтому мы выбираем \(r = 5\). Таким образом, вывод для первого теста: \([3, 4, 5]\). | |
![]()
|
|
B. Новая булочная
Бинарный поиск
Тернарный поиск
математика
жадные алгоритмы
*800
Боб решил открыть булочную. В день открытия он испёк \(n\) булок, которые может продать. Обычная цена булки равна \(a\) монет, но чтобы привлечь покупателей, Боб организовал следующую акцию: - Боб выбирает некоторое целое число \(k\) (\(0 \le k \le \min(n, b)\)).
- Первые \(k\) булок Боб продаёт по изменённой цене. В таком случае цена \(i\)-й (\(1 \le i \le k\)) проданной булки равна \((b - i + 1)\) монет.
- Оставшиеся \((n - k)\) булок Боб продаёт по \(a\) монет за каждую.
Обратите внимание, что \(k\) может равняться \(0\). В таком случае Боб продаст все булки по \(a\) монет за каждую. Помогите Бобу определить максимальную прибыль, которую он может получить, если продаст все \(n\) булок. Выходные данные Для каждого набора входных данных выведите одно целое число — максимальную прибыль, которую может получить Боб. Примечание В первом наборе входных данных Бобу выгодно выбрать \(k = 1\). Тогда он продаст одну булку за \(5\) монет, и три булки по обычной цене за \(4\) монеты. Тогда прибыль равна \(5 + 4 + 4 + 4 = 17\) монет. Во втором наборе входных данных Бобу выгодно выбрать \(k = 5\). Тогда он продаст все булки по изменённой цене и получит прибыль \(9 + 8 + 7 + 6 + 5 = 35\) монет. В третьем наборе входных данных Бобу выгодно выбрать \(k = 0\). Тогда он продаст все булки по обычной цене и получит прибыль \(10 \cdot 10 = 100\) монет. | |
![]()
|
|
A. Ноги
Бинарный поиск
Тернарный поиск
математика
*800
Снова прекрасный день на ферме Фермера Джона. После того, как Фермер Джон прибыл на свою ферму, он насчитал \(n\) ног. Известно, что на ферме живут только куры и коровы, причем у куриц по \(2\) ноги, а у коров по \(4\). Какое минимальное количество животных может быть у Фермера Джона на его ферме, если он посчитал количество ног у всех животных? Выходные данные Для каждого набора входных данных выведите одно целое число — минимальное количество животных у Фермера Джона на его ферме. | |
![]()
|
|
G2. Линейка (сложная версия)
Бинарный поиск
Тернарный поиск
*1700
интерактив
Это сложная версия задачи. Единственное отличие между двумя версиями заключается в том, что в этой версии вы можете сделать не более \(\mathbf{7}\) запросов. Это интерактивная задача. Если вы не уверены, как работают интерактивные задачи, рекомендуется прочитать руководство для участников. У нас есть секретная линейка, на которой отсутствует одно число \(x\) (\(2 \leq x \leq 999\)). Когда вы измеряете объект длиной \(y\), линейка сообщает следующие значения: - Если \(y < x\), линейка (правильно) измеряет объект как имеющий длину \(y\).
- Если \(y \geq x\), линейка неправильно измеряет объект как имеющий длину \(y+1\).
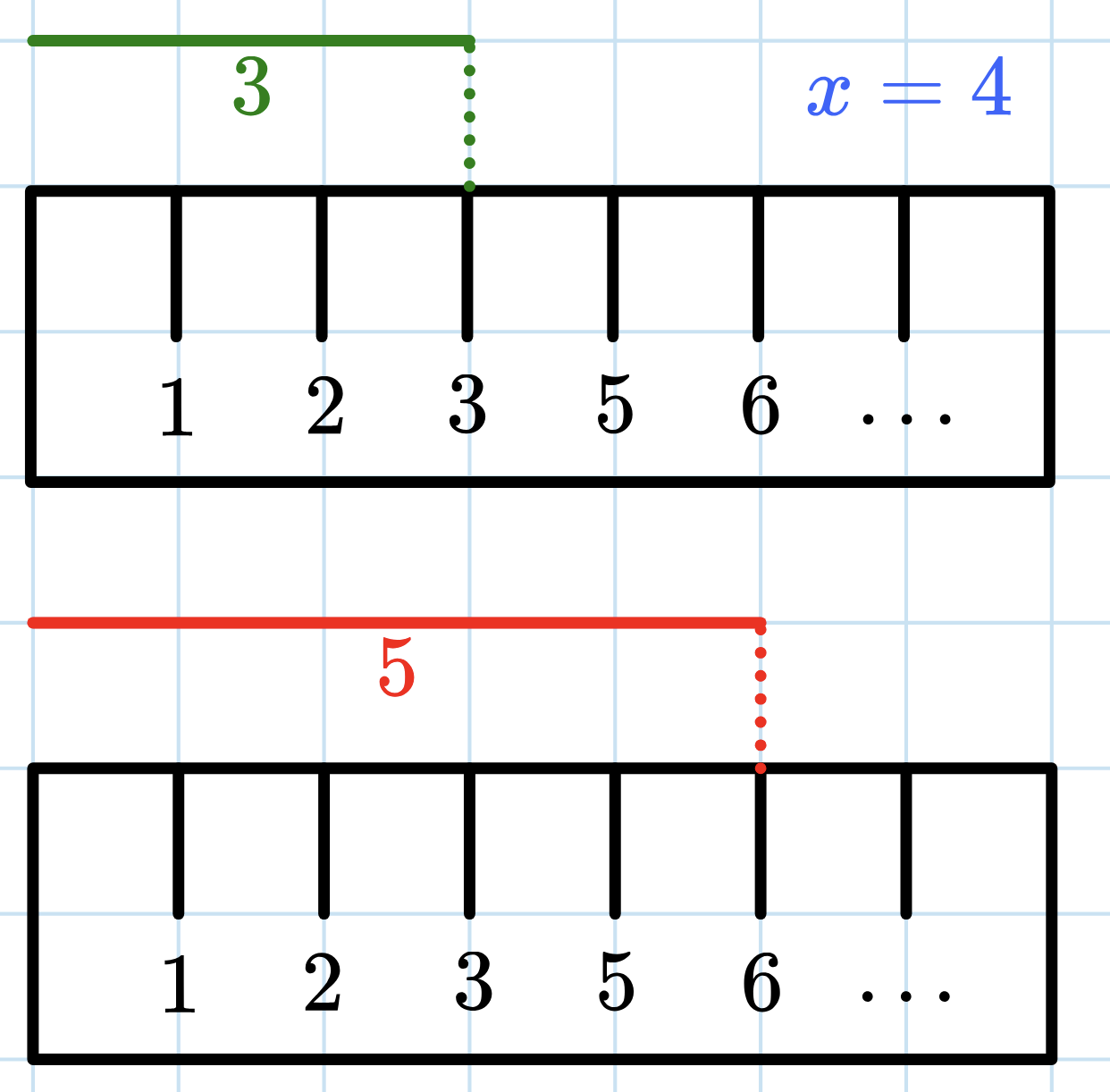 Линейка выше не имеет числа \(4\), поэтому она правильно измеряет первый отрезок как длину \(3\), но неправильно измеряет второй отрезок как длину \(6\), хотя на самом деле он равен \(5\). Вам нужно найти значение \(x\). Для этого вы можете делать запросы следующего вида: - \(\texttt{?}~a~b\) — в ответ мы измерим стороны прямоугольника \(a \times b\) с помощью нашей линейки и умножим результаты, сообщив вам измеренную площадь прямоугольника. Например, если \(x=4\) и вы запрашиваете прямоугольник \(3 \times 5\), мы измерим его стороны как \(3 \times 6\) и сообщим вам \(18\).
Найдите значение \(x\). Вы можете задать не более \(\mathbf{7}\) запросов. Протокол взаимодействия Для каждого набора нет начального ввода. Вы должны начать взаимодействие, задав запрос. Чтобы сделать запрос, выведите одну строку формата \(\texttt{?}~a~b\) (\(1 \leq a, b \leq 1000\)). В ответ вам будет сообщена измеренная площадь прямоугольника согласно нашей секретной линейке. Когда вы будете готовы вывести ответ, выведите одну строку формата \(\texttt{!}~x\) (\(2 \leq x \leq 999\)). После этого продолжайте обрабатывать следующий набор или завершите программу, если это был последний набор. Печать ответа не считается запросом. Интерактор не адаптивен, что означает, что ответ известен до того, как участник задаст запросы, и не зависит от запросов, заданных участником. Если ваша программа сделает более \(7\) запросов для одного набора входных данных, сделает недопустимый запрос или выведет неправильное значение \(x\), то ответ на запрос будет \(-1\). После получения такого ответа ваша программа должна немедленно завершиться, чтобы получить вердикт Неправильный ответ. В противном случае вы можете получить произвольный вердикт, поскольку ваше решение продолжит чтение из закрытого потока. После вывода запроса не забудьте вывести конец строки и сбросить вывод. В противном случае вы можете получить вердикт Превышен лимит бездействия. Для этого используйте: - fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Взломы Чтобы сделать взлом, используйте следующий формат. Первая строка должна содержать одно целое число \(t\) (\(1 \leq t \leq 1000\)) — количество наборов входных данных. Единственная строка каждого набора должна содержать одно целое число \(x\) (\(2 \leq x \leq 999\)) — отсутствующее число на линейке. Примечание В примере взаимодействие происходит следующим образом. | Решение | Жюри | Объяснение | | \(\texttt{2}\) | Есть 2 набора входных данных. | | \(\texttt{? 3 5}\) | \(\texttt{18}\) | Тайно жюри выбрало \(x=4\). Решение запрашивает прямоугольник \(3 \times 5\), и жюри отвечает \(3 \times 6 = 18\), как описано в условии. | | \(\texttt{? 4 4}\) | \(\texttt{25}\) | Решение запрашивает прямоугольник \(4 \times 4\), который жюри измеряет как \(5 \times 5\) и отвечает \(25\). | | \(\texttt{! 4}\) | | Решение каким-то образом определило, что \(x=4\), и выводит его. Поскольку вывод правильный, жюри переходит к следующему набору. | | \(\texttt{? 99 100}\) | \(\texttt{1}\) | Тайно жюри выбрало \(x=100\). Решение запрашивает прямоугольник \(99 \times 100\), который жюри измеряет как \(99 \times 101\) и отвечает \(9999\). | | \(\texttt{! 100}\) | | Решение каким-то образом определило, что \(x=100\), и выводит его. Поскольку вывод правильный и больше нет наборов, жюри и решение завершают работу. |
Обратите внимание, что переносы строк в примерах ввода и вывода сделаны для ясности и не происходят в реальном взаимодействии. | |
![]()
|
|
E. Тракторный институт
Тернарный поиск
математика
реализация
теория чисел
*2400
Пока большинство студентов все еще сдает экзамены, в тракторном институте сессия уже завершилась. В этом институте студенты изучают всего одну дисциплину — искусство тракторного дела. Поэтому за целую сессию в зачетку студента ставится всего одна оценка — тройка, четверка или пятерка. Двоечников, к сожалению, отчисляют. В институте учится n студентов, и, как ни странно, каждый из них может получать стипендию. Каждый семестр размер стипендии меняется. Поскольку сессия толька завершилась, то самое время определить размер стипендии до конца следующего семестра. Месячный бюджет стипендии тракторного института составляет s рублей. Чтобы распределить этот бюджет оптимально, необходимо придерживаться следующих правил: - Студенты, получившие одинаковые оценки за сессию, должны получать одинаковую стипендию;
- Обозначим размер стипендии (в рублях) студентов, получивших оценки 3, 4 и 5 за экзамен, k3, k4 и k5 соответственно. Величины k3, k4 и k5 должны быть целыми числами и удовлетворять неравенствам 0 ≤ k3 ≤ k4 ≤ k5;
- Пусть c3, c4, c5 — количество студентов, получивших оценку за сессию 3, 4 и 5 соответственно. Бюджет стипендии нужно потратить полностью, то есть c3·k3 + c4·k4 + c5·k5 = s;
- Введем функцию
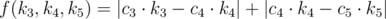 — величину, показывающую насколько хорошо распределена стипендия между студентами. В оптимальном распределении функция f(k3, k4, k5) принимает минимально возможное значение. — величину, показывающую насколько хорошо распределена стипендия между студентами. В оптимальном распределении функция f(k3, k4, k5) принимает минимально возможное значение. Зная результаты сессии и размер бюджета s, от Вас требуется найти оптимальное распределение стипендии. Выходные данные В единственной строке выведите три целых числа k3, k4 и k5 — искомые величины, обозначающие оптимальное распределение размеров стипендии. Если оптимальных ответов несколько, выведите любой из них. Если ответа не существует, выведите -1. | |
![]()
|
|
E. СУПЕР ДУПЕР БОЛЬШОЙ Массив Кли!!!
Бинарный поиск
Тернарный поиск
математика
*1400
У Кли есть массив \(a\) длиной \(n\), содержащий целые числа \([k, k+1, ..., k+n-1]\) в этом порядке. Кли хочет выбрать индекс \(i\) (\(1 \leq i \leq n\)) так, чтобы \(x = |a_1 + a_2 + \dots + a_i - a_{i+1} - \dots - a_n|\) был минимален. Обратите внимание, что для произвольного целого числа \(z\), \(|z|\) представляет собой модуль числа \(z\). Выведите минимально возможное значение \(x\). Выходные данные Для каждого набора входных данных выведите минимальное значение \(x\). Примечание В первом примере \(a = [2, 3]\). При выборе \(i = 1\), \(x = |2-3| = 1\). Можно показать, что это минимально возможное значение \(x\). В третьем примере \(a = [3, 4, 5, 6, 7]\). При выборе \(i = 3\), \(x = |3 + 4 + 5 - 6 - 7| = 1\). Можно показать, что это минимально возможное значение \(x\). | |
![]()
|
|
B. Угадай автомобиль!
Тернарный поиск
математика
*1800
Широко известный в узких кругах белорусский олимпиадник Юра владеет громадным количеством информации об автомобилях. В связи с этим его пригласили поучаствовать в ток-шоу «Угадай автомобиль!». Место проведения ток-шоу представляет собой гигантскую автомобильную стоянку протяженностью 4n метров с севера на юг и 4m метров с запада на восток. На стоянке начерчены n + 1 разделительных полос, проходящих с запада на восток и m + 1 разделительных полос, проходящих с севера на юг, которые разделяют стоянку на n·m квадратов размером 4 на 4 метра. Строго внутри каждого квадрата припаркован автомобиль. Разделительные полосы пронумерованы от 0 до n с севера на юг и от 0 до m с запада на восток. Каждый квадрат имеет координаты (i, j) таким образом, что квадрат в северо-западном углу имеет координаты (1, 1), а квадрат в юго-восточном — координаты (n, m). Смотрите рисунок в примечаниях для уточнения. Перед началом ток-шоу организаторы предлагают Юре занять любую из (n + 1)·(m + 1) точек пересечения разделительных полос, после чего он приступит к угадыванию. После выбора точки Юре будет запрещено перемещаться по стоянке до окончания ток-шоу. Поскольку Юра является автомобильным гуру, то он все равно угадает все предложенные автомобили, это всего лишь вопрос времени. По себе Юра знает, что на угадывание каждой машины ему нужно потратить время, равное квадрату евклидова расстояния между точкой, где он находится, и центром квадрата, в котором находится эта машина, умноженному на некоторый коэффициент, характеризующий «необычность» машины (более редкие машины сложнее угадывать). Более формально, на угадывание автомобиля, имеющего «необычность» c и находящегося в квадрате, от центра которого до Юры d метров, он потратит c·d2 секунд. Временем, которое Юра тратит на повороты головы, можно пренебречь. Так уж вышло, что Юра заранее знает «необычность» каждого автомобиля, находящегося на стоянке. Помогите ему выбрать точку для угадывания таким образом, чтобы суммарное время угадывания всех автомобилей было как можно меньше. Выходные данные В первой строке выведите минимальное суммарное время, за которое Юра угадает все предложенные автомобили. Во второй строке выведите два числа li и lj (0 ≤ li ≤ n, 0 ≤ lj ≤ m) — номера разделительных полос, на пересечении которых Юра должен начинать ток-шоу. В случае, если существует несколько оптимальных стартовых точек, выведите точку с меньшим li. Если и таких точек несколько, выведите точку с меньшим lj. Пожалуйста, не используйте спецификатор %lld для чтения или записи 64-битных чисел на С++. Рекомендуется использовать потоки cin, cout или спецификатор %I64d. Примечание В первом тесте суммарное время вычисляется как 3·8 + 3·8 + 4·8 + 9·8 + 5·40 + 1·40 = 392 Система координат на поле: 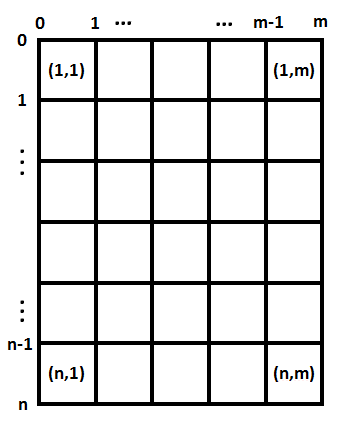 | |
![]()
|
|
C. Битовый баланс
Тернарный поиск
математика
реализация
*1400
хэши
битмаски
расписания
Даны три неотрицательных целых числа \(b\), \(c\) и \(d\). Найдите неотрицательное целое число \(a \in [0, 2^{61}]\), такое что \((a\, |\, b)-(a\, \&\, c)=d\), где \(|\) и \(\&\) обозначают операцию побитового ИЛИ и операцию побитового И соответственно. Если такое \(a\) существует, выведите его значение. Если решения не существует, выведите одно целое число \(-1\). Если существует несколько решений, выведите любое из них. Выходные данные Для каждого набора входных данных выведите значение \(a\) или \(-1\), если решения не существует. Обратите внимание, что \(a\) должно быть неотрицательным и не может превышать \(2^{61}\). Примечание В первом наборе входных данных \((0\,|\,2)-(0\,\&\,2)=2-0=2\). Так что \(a = 0\) является корректным ответом. Во втором наборе входных данных никакое значение \(a\) не удовлетворяет уравнению. В третьем наборе входных данных \((12\,|\,10)-(12\,\&\,2)=14-0=14\). Так что \(a = 12\) является корректным ответом. | |
![]()
|
|
D. Приключения Алисы в картах
Тернарный поиск
Структуры данных
Конструктив
реализация
дп
*2000
жадные алгоритмы
графы
Алиса играет в карты с Дамой Червей, Королем Червей и Валетом Червей. В их карточной игре есть \(n\) различных типов карт. В данный момент у Алисы есть карта типа \(1\), и ей нужна карта типа \(n\), чтобы сбежать из Страны Чудес. У остальных игроков есть по одной карте каждого типа. В этой карточной игре Алиса может обмениваться картами с тремя другими игроками. У каждого игрока есть свои предпочтения среди этих \(n\) типов, которые можно описать перестановками\(^{\text{∗}}\) \(q\), \(k\) и \(j\) для Дамы, Короля и Валета соответственно. Игрок оценивает карту \(a\) больше, чем карту \(b\), если для их перестановки \(p\), \(p_a > p_b\). Тогда этот игрок готов обменять карту \(b\) с Алисой в обмен на карту \(a\). Предпочтения Алисы просты: она оценивает карту \(a\) больше, чем карту \(b\) если \(a > b\), и она будет обмениваться картами только в соответствии с этими предпочтениями. Определите, может ли Алиса обменять карту типа \(1\) на карту типа \(n\), учитывая эти предпочтения. Если это возможно, приведите возможный набор обменов для этого. Выходные данные Для каждого набора входных данных в первой строке выведите одну строку «YES» или «NO» (без кавычек), обозначающую, может ли Алиса обменяться на карту \(n\). Если первая строка была «YES», то на следующей строке выведите \(k\) — количество обменов, которые сделает Алиса. На следующих \(k\) строках выведите через пробел символ \(c\in \{\texttt{q}, \texttt{k}, \texttt{j}\}\) и целое число \(x\), обозначающее, что Алиса обменивается с игроком \(c\), чтобы получить карту \(x\). Должно быть так, что на \(k\)-й строке \(x = n\). Если существует несколько решений, выведите любое из них. Вы можете выводить каждую букву в любом регистре (строчную или заглавную). Например, строки «yEs», «yes», «Yes» и «YES» будут приняты как положительный ответ. То же самое касается символа \(c\), обозначающего игрока в обмене (\(\texttt{Q}, \texttt{K}, \texttt{J}\) будут приняты наряду с их строчными вариантами). Примечание В первом наборе входных данных Алиса может обменяться с Королем, чтобы получить карту \(2\). Затем она может обменяться с Дамой, чтобы получить карту \(3\). Во втором наборе входных данных, хотя Алиса может обменяться с Дамой, чтобы получить карту \(3\), с Королем, чтобы получить карту \(2\), а затем с Валетом, чтобы получить карту \(4\), это не является допустимым решением, так как оно не соответствует предпочтениям Алисы. Мы можем показать, что нет способа для Алисы получить карту \(4\). | |
![]()
|
|
E. Монстр
Бинарный поиск
Тернарный поиск
Перебор
Конструктив
математика
реализация
жадные алгоритмы
*2300
Мужик, этот босс в Genshin такой сложный. Хорошо, что у них есть пополнение на \(6\) монет всего за \( \$4.99\). Мне следует быть осторожнее и не тратить больше, чем нужно, иначе мама меня поймает... Вы сражаетесь с монстром со здоровьем \(z\), используя оружие с уроном \(d\). Изначально \(d=0\). Вы можете выполнять следующие действия. - Увеличить \(d\) — урон вашего оружия на \(1\), потратив \(x\) монет.
- Атаковать монстра, нанеся ему \(d\) урона, потратив \(y\) монет.
Вы не можете выполнять первую операцию более \(k\) раз подряд. Найдите минимальное количество монет, необходимое для того, чтобы победить монстра, нанеся ему хотя бы \(z\) урона. Выходные данные Для каждого набора входных данных выведите минимальное количество монет, необходимое для победы над монстром. Примечание В первом наборе входных данных \(x = 2\), \(y = 3\), \(z = 5\) и \(k = 5\). Вот стратегия, которая обеспечивает наименьшую возможную стоимость в \(12\) монет: - Увеличить урон на \(1\), потратив \(2\) монеты.
- Увеличить урон на \(1\), потратив \(2\) монеты.
- Увеличить урон на \(1\), потратив \(2\) монеты.
- Атаковать монстра, нанеся ему \(3\) урона, потратив \(3\) монеты.
- Атаковать монстра, нанеся ему \(3\) урона, потратив \(3\) монеты.
Вы наносите в общей сложности \(3 + 3 = 6\) урона, побеждая монстра, который имеет \(5\) здоровья. Суммарное количество монет, которое вы потратите, составляет \(2 + 2 + 2 + 3 + 3 = 12\) монет. Во втором наборе входных данных \(x = 10\), \(y = 20\), \(z = 40\) и \(k = 5\). Вот стратегия, которая позволяет достичь наименьшей возможной стоимости в \(190\) монет: - Увеличить урон на \(5\), что стоит \(5\cdot x\) = \(50\) монет.
- Атаковать монстра один раз, нанеся ему \(5\) урона, потратив \(20\) монет.
- Увеличить урон на \(2\), потратив \(2\cdot x\) = \(20\) монет.
- Атаковать монстра \(5\) раз, нанеся \(5\cdot 7 = 35\) урона, потратив \(5\cdot y\) = \(100\) монет.
Всего вы нанесли \(5 + 35 = 40\) урона, победив монстра, у которого ровно \(40\) здоровья. Вы потратили \(50 + 20 + 20 + 100 = 190\) монет. | |
![]()
|
|
C. Искатели приключений
Бинарный поиск
Тернарный поиск
Структуры данных
*2100
жадные алгоритмы
сортировки
Однажды четверо римских торговцев встретились в одном из римских мансионов, чтобы обсудить свои торговые планы. У торговцев была следующая проблема: торговали они одним и тем же видом товара, поэтому, если они занимались торговлей в одном и том же городе, неизбежно терпели убытки. Было решено распределить города, в которых будет вестись торговля, между собой. Карту Рима можно в этой задаче представить как плоскость, на которой в некоторых местах отмечены точки — города Римской империи. Торговцы хотят выбрать некоторую разделяющую точку \((x_0, y_0)\). Затем в городе с координатами \((x_i, y_i)\) будет торговать только - первый торговец, если \(x_0 \le x_i\) и \(y_0 \le y_i\);
- второй торговец, если \(x_0 > x_i\) и \(y_0 \le y_i\);
- третий торговец, если \(x_0 \le x_i\) и \(y_0 > y_i\);
- четвертый торговец, если \(x_0 > x_i\) и \(y_0 > y_i\).
Торговцы хотят выбрать точку \((x_0, y_0)\) так, чтобы максимизировать минимальное количество городов, которое достанется кому-либо из них торговцев (то есть максимально честно). Помогите им найти такую точку. Выходные данные В первой строке выведите одно целое число \(k\) (\(0 \le k \le \frac{n}{4}\)) — максимально возможное количество городов, которое достанется каждому торговцу. Во второй строке выведите два целых числа \(x_0\) и \(y_0\) (\(|x_0|, |y_0| \le 10^9\)) — координаты разделяющей точки. Если подходящих точек может быть несколько, то разрешается вывести любую из них. | |
![]()
|
|
D. Игра с треугольниками
Бинарный поиск
Тернарный поиск
Перебор
Структуры данных
математика
реализация
геометрия
*2000
жадные алгоритмы
Даже маленькому Джону нужны деньги, чтобы купить дом. Но он недавно потерял работу; как же он теперь заработает деньги? Конечно, играя в игру, которая дает ему деньги в качестве награды! Ну, может быть, не в те игры, о которых вы думаете. На плоскости есть \(n+m\) различных точек \((a_1,0), (a_2,0), \ldots, (a_{n},0), (b_1,2), (b_2,2), \ldots, (b_{m},2)\). Изначально ваш счет равен \(0\). Чтобы увеличить свой счет, вы можете выполнить следующую операцию: - Выберите три различные точки, которые не лежат на одной прямой.
- Увеличьте свой счет на площадь треугольника, образованного этими тремя точками.
- Затем удалите три точки с плоскости.
 Пример игры, где операция выполняется дважды. Пример игры, где операция выполняется дважды. Пусть \(k_{\max}\) — максимальное количество операций, которое можно выполнить. Например, если нельзя выполнить эту операцию ни разу, то \(k_\max\) равно \(0\). Кроме того, определим \(f(k)\) как максимальный возможный счет, который можно получить, выполнив операцию ровно \(k\) раз. Здесь \(f(k)\) определено для всех целых чисел \(k\), таких что \(0 \le k \le k_{\max}\). Найдите значение \(k_{\max}\) и найдите значения \(f(x)\) для всех целых чисел \(x=1,2,\ldots,k_{\max}\) независимо. Выходные данные Для каждого набора входных данных, учитывая, что максимальное количество операций равно \(k_{\max}\), вы должны вывести не более двух строк: - Первая строка содержит значение \(k_{\max}\);
- Вторая строка содержит \(k_{\max}\) целых числа, обозначающих \(f(1),f(2),\ldots,f(k_{\max})\). Вы можете опустить эту строку, если \(k_{\max}\) равно \(0\).
Обратите внимание, что в условиях этой задачи можно показать, что все значения \(f(x)\) являются целыми числами, не превышающими \(10^{16}\). Примечание В первом наборе входных данных есть \(1+3=4\) точки \((0,0),(0,2),(1,2),(-1,2)\). Можно показать, что вы не можете выполнить две или более операций. Значение \(k_{\max}\) равно \(1\), и вас просят только о значении \(f(1)\). Вы можете выбрать \((0,0)\), \((-1,2)\) и \((1,2)\) в качестве трех вершин треугольника. После этого ваш счет увеличивается на площадь треугольника, которая равна \(2\). Затем три точки удаляются с плоскости. Можно показать, что максимальное значение вашего счета после выполнения одной операции равно \(2\). Следовательно, значение \(f(1)\) равно \(2\). В пятом наборе входных данных есть \(8+2=10\) точек. Можно показать, что вы не можете выполнить три или более операций. Значение \(k_{\max}\) равно \(2\), и вас просят о значениях \(f(1)\) и \(f(2)\). Чтобы максимизировать счет с помощью только одной операции, вы можете выбрать три точки \((198\,872\,582,0)\), \((-1\,000\,000\,000,2)\) и \((1\,000\,000\,000,2)\). Затем три точки удаляются с плоскости. Можно показать, что максимальное значение вашего счета после выполнения одной операции равно \(2\,000\,000\,000\). Следовательно, значение \(f(1)\) равно \(2\,000\,000\,000\). Чтобы максимизировать счет с помощью ровно двух операций, вы можете выбрать следующую последовательность операций. - Выберите три точки \((-509\,489\,796,0)\), \((553\,177\,666,0)\) и \((-1\,000\,000\,000,2)\). Три точки удаляются.
- Выберите три точки \((-400\,714\,529,0)\), \((564\,040\,265,0)\) и \((1\,000\,000\,000,2)\). Три точки удаляются.
Тогда счет после двух операций становится \(2\,027\,422\,256\). Можно показать, что максимальное значение вашего счета после выполнения ровно двух операций равно \(2\,027\,422\,256\). Следовательно, значение \(f(2)\) равно \(2\,027\,422\,256\). | |
![]()
|
|
B. Пингвин Поло и матрица
Тернарный поиск
Перебор
реализация
дп
*1400
сортировки
У маленького пингвина Поло есть матрица n × m, состоящая из целых чисел. Пронумеруем строки матрицы от 1 до n сверху вниз, а столбцы от 1 до m слева направо. Обозначим через aij элемент матрицы, стоящий на пересечении i-ой строки и j-го столбца. За один шаг пингвин может добавить к любому элементу матрицы или отнять от любого элемента матрицы число d. Найдите минимальное количество шагов, которое требуется для того, чтобы все элементы матрицы были равны между собой. Если описанное невозможно, сообщите об этом. Выходные данные В единственной строке выведите целое число — минимальное количество шагов, которое требуется для того, чтобы все элементы матрицы были равны между собой. Если описанное невозможно, выведите «-1» (без кавычек). | |
![]()
|
|
E. Полицейский патруль
Тернарный поиск
математика
реализация
*2000
жадные алгоритмы
Представьте, что ваш город — бесконечная двухмерная плоскость, с введенной на ней Декартовой системой координат. Единственная дорога, подверженная преступлениям, это ось Ox. На данный момент вдоль этой дороги стоят n преступников. Ни один полицейский участок еще не построен на дороге, поэтому мэр как можно скорее хочет построить участок и избавиться от преступников. Управлять новым участком доверили вам, поэтому вам и выбирать, где он будет находиться. Вы должны так выбрать целочисленную точку для полицейского участка, чтобы операция по поимке всех преступников на оси Ox заняла как можно меньше времени. Поимка преступников оси Ox будет осуществляться только из нового участка. В новом участке будет только одна патрульная машина. На этой машине можно подъезжать к преступникам, арестовывать их, затем сажать их в машину, везти в участок и сажать в тюрьму. В патрульную машину одновременно помещается не больше m преступников. Обратите внимание, что преступники не знают о вашей операции. Поэтому они будут стоять на месте, а не будут убегать. Ваша задача — найти такое место для полицейского участка, что минимальное расстояние, которое придется в сумме проехать, чтобы посадить в тюрьму всех преступников, будет как можно меньше. Обратите внимание, что вы можете построить полицейский участок в точке, где находится один или несколько преступников, в таком случае все эти преступники сразу же будут аррестованы. Выходные данные Выведите единственное целое число, обозначающее минимальное расстояние, которое требуется проехать, чтобы посадить в тюрьму всех преступников, при оптимальном выборе точки для полицейского участка. | |
![]()
|
|
E. Химический эксперимент
Бинарный поиск
Тернарный поиск
Структуры данных
*2200
Как-то раз два студента Гриша и Диана оказались в химической лаборатории университета. В лаборатории ребята нашли n колб c ртутью, пронумерованных от 1 до n, и решили провести эксперимент. Эксперимент состоит из q шагов. На каждом шаге выполняется одно из следующих действий: - Диана выливает все содержимое из колбы номером pi, а затем заливает туда ровно xi литров ртути.
- Рассмотрим все возможные способы долить vi литров воды в колбы; для каждого способа посчитаем, сколько жидкости (вода и ртуть) содержит колба с водой с максимальным количеством жидкости; среди всех вычисленных чисел найдем минимальное. Ребята хотят посчитать описанное значение. При подсчетах ребята ничего никуда не доливают на самом деле. Все подсчеты они делают, не изменяя содержимое колб.
К сожалению, оказалось, что вычисления слишком громоздкие, поэтому ребята обратились за помощью к вам. Помогите ребятам провести описанный эксперимент. Выходные данные Для каждого действия второго вида вам нужно вывести подсчитанное значение. Ответ будет считаться правильным, если относительная или абсолютная погрешность не будет превышать 10 - 4. | |
![]()
|
|
D. Деву и братишка
Бинарный поиск
Тернарный поиск
сортировки
*1700
Деву и его братишка очень любят друг друга. Они супер-гики и предпочитают играть только с массивами. Как-то раз папа подарил им два массива, a и b. Массив a достался Деву, а b — его брату. Деву — пакостник тот еще. Хочется ему, чтобы минимум в массиве a был не меньше максимума массива b. Вам надо помочь Деву добиться описанного. Для этого вы можете выполнять операции с массивами a и b. За одну операцию разрешено уменьшить или увеличить любой элемент любого массива на 1. Обратите внимание, что операцию можно применять несколько раз для любого элемента любого массива. Требуется найти наименьшее количество операций, необходимых для достижения описанного условия. Выходные данные Выведите единственное целое число — минимальное количество операций, необходимых для выполнения желания Деву. Примечание В первом тестовом примере можно увеличить a1 на 1 и уменьшить b2 на 1, затем снова уменьшить b2 на 1. Теперь массив a выглядит так [3; 3], массив b выглядит так [3; 3]. Наименьший элемент a не меньше наибольшего элемента b. Выполнить желание Деву за меньшее количество операций никак не получится. В примере 3 не надо выполнять никаких операций, желание Деву уже выполнено. | |
![]()
|
|
C. Цивилизация
Тернарный поиск
Деревья
*2100
дп
поиск в глубину и подобное
снм
Андрей играет в игру «Цивилизация». Дима помогает ему. В игре «Цивилизация» n городов и m двусторонних дорог. Города пронумерованы целыми числами от 1 до n. Между любой парой городов либо существует единственный путь, либо не существует никакого пути. Путем называется последовательность различных городов v1, v2, ..., vk, в которой между любыми двумя соседними городами vi и vi + 1 (1 ≤ i < k) есть дорога. Длина такого пути равна (k - 1). Давайте говорить, что два города лежат в одной области тогда и только тогда, когда существует путь между этими двумя городами. В процессе игры происходят события двух типов: - Андрей спрашивает у Димы длину самого длинного пути в области, в которой лежит город x.
- Андрей просит Диму объединить область, в которой лежит город x, с областью, в которой лежит город y. Если города лежат в одной области, то объединять области не нужно. Иначе нужно объединить области следующим образом: выбрать город в первой области, город во второй области и связать их дорогой так, чтобы минимизировать длину самого длинного пути в полученной области. Если существует несколько оптимальных способов соединить области, то разрешается выбрать любой.
Диме очень сложно выполнять просьбы Андрея, поэтому он обращается к вам за помощью. Помогите Диме. Выходные данные Для каждого события первого типа выведите ответ на него в отдельной строке. | |
![]()
|
|
E. Артур и вопросы
Тернарный поиск
математика
реализация
жадные алгоритмы
*2200
После скобочных последовательностей Артур увлекся теорией чисел. И у него появилась новая любимая последовательность длины n (a1, a2, ..., an), состоящая из целых чисел, и целое число k, не превышающее n. Эта последовательность обладала следующим свойством. Если выписать суммы всех ее подотрезков, состоящих из k подряд идущих элементов (a1 + a2 ... + ak, a2 + a3 + ... + ak + 1, ..., an - k + 1 + an - k + 2 + ... + an), то элементы выписанной последовательности будут строго возрастать. Например, для следующего примера: n = 5, k = 3, a = (1, 2, 4, 5, 6) последовательность сумм будет иметь вид: (1 + 2 + 4, 2 + 4 + 5, 4 + 5 + 6) = (7, 11, 15), а значит последовательность a удовлетворяет описанному свойству. Очевидно, в последовательности сумм будет n - k + 1 элемент. Кто-то (не будем говорить кто) заменил в последовательности Артура некоторые числа на знаки вопроса (если число заменяется, то ровно на один знак вопроса). Нужно восстановить последовательность, чтобы она удовлетворяла нужному свойству, и при этом минимизировать сумму |ai|, где |ai| — абсолютная величина ai. Выходные данные Если Артур что-то напутал, и последовательности, соответствующей данной информации нет, выведите единственную строку «Incorrect sequence» (без кавычек). В противном случае, выведите в первую строку выходных данных n целых чисел — любимую последовательность Артура. Если таких последовательностей несколько, выведите последовательность с минимальной суммой |ai|, где |ai| — абсолютная величина ai. Если и таких последовательностей несколько, разрешается вывести любую из них. Элементы последовательности следует выводить без лидирующих нулей. | |
![]()
|
|
C. Слабость и бедность
Тернарный поиск
*2000
Вам дана последовательность из n целых чисел a1, a2, ..., an. Определите действительное число x, такое, чтобы слабость последовательности a1 - x, a2 - x, ..., an - x была как можно меньше. Слабость последовательности определяется как максимальное значение бедности по всем отрезкам (непрерывным подпоследовательностям) последовательности. Бедность отрезка определяется как модуль суммы элементов отрезка. Выходные данные Выведите действительное число, обозначающее минимально возможную слабость a1 - x, a2 - x, ..., an - x. Ответ будет засчитан, если его относительная или абсолютная погрешность не превышает 10 - 6. Примечание Для первого примера оптимальное значение x равняется 2, в таком случае последовательность примет вид - 1, 0, 1 и максимальная бедность достигается либо на отрезке "-1", либо отрезке "1". Значение слабости (ответ) равняется в этом случае 1. Во втором примере оптимальное значение x равняется 2.5, в таком случае последовательность принимает вид - 1.5, - 0.5, 0.5, 1.5, а максимальная бедность достигается либо на отрезке "-1.5 -0.5", либо на отрезке "0.5 1.5". Значение слабости (ответ) равняется в этом случае 2. | |
![]()
|
|
A. Петя и снегоуборочная машина
Бинарный поиск
Тернарный поиск
геометрия
*1900
На новый год Пете подарили новую снегоуборочную машину. Конечно, Пете сразу захотелось её испытать. Прочитав инструкцию, он понял, что она работает не так, как обычные снегоуборочные машины. Для того чтобы она работала, нужно привязать её к некоторой точке, которую она не покрывает, после чего включить, и тогда она проедет по окружности вокруг этой точки и уберёт снег со всего своего пути. Более формально, будем считать Петину машину многоугольником на плоскости. Тогда после включения она проедет круг вокруг некоторой точки, к которой Петя её привязал (эта точка находится строго снаружи многоугольника). Таким образом каждая точка внутри или на границе многоугольника пройдёт по окружности с центром в точке, к которой Петя привязал свою машину. Петя решил привязать свою машину к точке P, и теперь ему интересно, какова площадь области, с которой машина уберёт снег. Помогите ему. Выходные данные Выведите одно вещественное число — площадь области, которая будет очищена от снега. ответ на задачу с абсолютной или относительной погрешностью не более 10 - 6. Ваш ответ будет считаться правильным, если его абсолютная или относительная ошибка не будет превосходить 10 - 6. А именно: пусть ваш ответ равен a, а ответ жюри — b. Проверяющая программа будет считать ваш ответ правильным, если 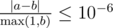 . . Примечание В первом примере из условия снег будет убран с этой территории: 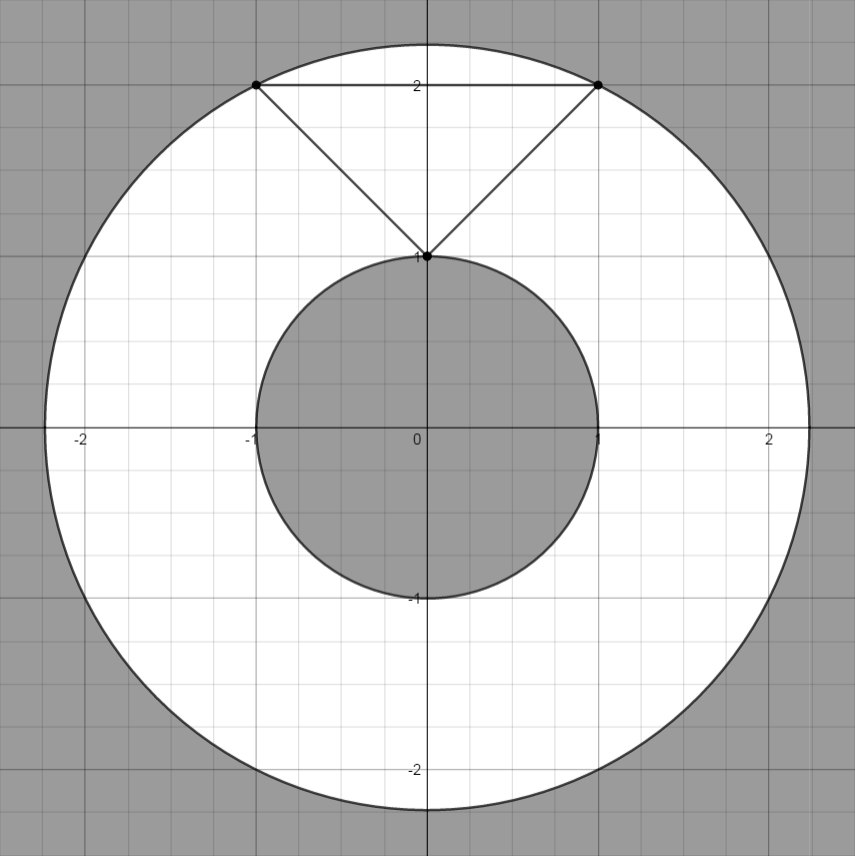 | |
![]()
|
|
E. Простая асимметрия
Бинарный поиск
Тернарный поиск
математика
*2400
Назовём простой асимметрией набора чисел разность (не модуль разности) между средним значением и медианой. Вам дан список из n чисел, необязательно различных. Требуется выбрать какое-то непустое подмножество этих чисел (возможны повторения) с максимальным значением простой асимметрии. Средним значением набора чисел является среднее арифметическое всех его элементов. Медианой набора чисел назовём средний элемент, если набор отсортирован. Для наборов чётного размера медианой будем называть среднее арифметическое двух средних элементов при сортировке. Выходные данные В первой строке выведите число k (1 ≤ k ≤ n) — размер подмножества. Во второй строке выведите k чисел — элементы выбранного подмножества в любом порядке. Если оптимальных ответов несколько, то разрешается вывести любой. Примечание В первом примере оптимальным подмножеством является 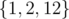 со средним значением 5, медианой 2 и значением простой асимметрии 5 - 2 = 3. со средним значением 5, медианой 2 и значением простой асимметрии 5 - 2 = 3. Во втором примере оптимальным подмножеством является 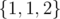 . Обратите внимание, что разрешены одинаковые элементы. . Обратите внимание, что разрешены одинаковые элементы. В последнем примере у любого подмножества среднее значение равно медиане, поэтому максимальная простая асимметрия равна 0. | |
![]()
|
|
F. Медведь и боулинг 4
Бинарный поиск
Тернарный поиск
Структуры данных
геометрия
разделяй и властвуй
*2500
Лимак — старый бурый медведь. Он часто играет в боулинг со своими друзьями. Сегодня он в отличном настроении и хочет побить свой собственный рекорд! За каждый бросок даётся некоторое целое (возможно отрицательное) количество очков. Очки за i-й бросок умножаются на число i и прибавляются к общей сумме. Таким образом, за k бросков с очками s1, s2, ..., sk в сумме даётся 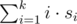 очков. Если бросков не было, общее количество очков равно 0. очков. Если бросков не было, общее количество очков равно 0. Лимак сделал n бросков и получил ai очков за i-й бросок. Он хочет максимизировать общее количество очков, поэтому ему в голову пришла интересная идея. Он может сказать, что некоторое количество первых бросков он разогревался и был рассредоточен во время некоторого количества последних бросков. Формально он может выкинуть некоторый префикс и некоторый суффикс последовательности очков a1, a2, ..., an. Разрешается выкидывать из рассмотрения все броски или же не выкидывать из вовсе. Общее количество очков вычисляется как будто выкинутых бросков не было. Таким образом, за первый невыкинутый бросок количество очков умножается на 1, за второй — на 2 и так далее до последнего невыкинутого броска. Какое максимальное количество очков может получить Лимак? Выходные данные Выведите максимальное суммарное количество очков, которое можно получить выкидыванием некоторых бросков. Примечание В первом примере Лимак должен выкинуть из рассмотрения первые два и последний броски. После этого останутся броски 1, - 3, 7, которые принесут ему 1·1 + 2·( - 3) + 3·7 = 1 - 6 + 21 = 16 очков. | |
![]()
|
|
A. Парк аттракционов
Тернарный поиск
*2100
*особая задача
Школьники решили всем классом пойти в парк аттракционов. Некоторые из них взяли с собой родителей. Всего в парк пришло n человек и все они хотят попасть на самый экстремальный аттракцион и прокатиться на нём ровно по одному разу. Билеты на аттракцион продаются для групп из x человек, причём в группе обязательно должен быть хотя бы один взрослый (возможно, что группа состоит из одного взрослого человека). Стоимость билета для такой группы равна c1 + c2·(x - 1)2 (в частности, если группа состоит из одного человека, то стоимость равна c1). Поэтому все пришедшие в парк школьники и их родители решили разбиться на группы таким образом, чтобы каждый пришедший попал ровно в одну группу, при этом суммарная стоимость посещения самого экстремального аттракциона была минимально возможной. Перед вами стоит задача определить эту минимальную суммарную стоимость. В каждой группе должен быть хотя бы один взрослый. Выходные данные Выведите минимальную стоимость посещения самого экстремального аттракциона для всех пришедших школьников и их родителей. Каждый из них должен прокатнуться на аттракционе ровно по одному разу. Примечание В первом примере нужно пойти на аттракцион одной группой, состоящей из трёх человек. Тогда придётся заплатить 4 + 1 * (3 - 1)2 = 8. Во втором примере выгодно пойти на аттракцион двумя группами. В первой группе должно быть два взрослых (например, первый и второй человек), а во второй группе должен быть один ребёнок и один взрослый (третий и четвертый человек). Тогда каждая группа будет иметь размер два и за каждую придётся заплатить 7 + 2 * (2 - 1)2 = 9. Таким образом, суммарная стоимость для двух групп будет равна 18. | |
![]()
|
|
E. Продажа сувениров
Бинарный поиск
Тернарный поиск
дп
жадные алгоритмы
*2300
После нескольких реформ в Берляндию стали гораздо чаще приезжать туристы, и многие жители Берляндии, смекнув, что в туристическом бизнесе можно очень неплохо заработать, решили сменить место работы. Петя, например, бросил работу в IT-фирме и стал продавать сувениры на рынке. Как и всегда, этим утром Петя собрался на рынок. У Пети дома стоит n различных сувениров; i-й сувенир характеризуется своим весом wi и стоимостью ci. По предыдущим дням Петя понял, что, скорее всего, ему не удастся донести все сувениры до рынка. Поэтому Петя хочет выбрать такое подмножество сувениров, что суммарный вес всех сувениров из подмножества не превышает m, а суммарная стоимость максимальна. Помогите Пете определить максимальную суммарную стоимость. Выходные данные Выведите единственное число — максимальную суммарную стоимость сувениров, которые Петя сможет донести на рынок. | |
![]()
|
|
F. Создание уровней
Бинарный поиск
Тернарный поиск
математика
*2100
Иван разрабатывает свою собственную компьютерную игру. Сейчас Иван хочет создать все уровни игры. Но перед этим он хочет нарисовать каждый уровень на бумаге в виде графа. Иван решил, что в графе i-го уровня должно быть ровно ni вершин, а сам граф должен быть неориентированный. Главная, по мнению Ивана, характеристика графа — количество специальных рёбер, называемых мостами. Ребро, соединяющее вершины u и v, называется мостом, если оно лежит на каждом пути из u в v (и эти вершины окажутся в разных компонентах связности, если ребро стереть). Иван хочет, чтобы в построенном для каждого уровня графе как минимум 50% всех рёбер были бы мостами. Также Иван хочет максимизировать количество рёбер в каждом графе. Итак, задание, которое вам дал Иван, состоит в следующем: по заданным q числам n1, n2, ..., nq для каждого i определить максимальное количество рёбер в графе из ni вершин, если хотя бы 50% рёбер должны быть мостами. Обратите внимание, в графах не может быть петель или кратных рёбер. Выходные данные Выведите q чисел, i-е из которых равно максимальному количеству рёбер в i-м графе. Примечание В примере из условия можно построить следующие графы: - 1 - 2, 1 - 3;
- 1 - 2, 1 - 3, 2 - 4;
- 1 - 2, 1 - 3, 2 - 3, 1 - 4, 2 - 5, 3 - 6.
| |
![]()
|
|
B. Заказ пиццы
Бинарный поиск
Тернарный поиск
сортировки
*1900
Проходит очередной финал Start[c]up, поэтому необходимо заказать пиццу для финалистов, участвующих в соревновании в офисе компании. Существует всего два типа пиццы (конечно нет, но в этой задаче будем считать, что да), все пиццы содержат одинаковое число S кусочков. Известно, что i-й участниц съест si кусочков пиццы, и получит ai единиц счастья от съедания каждого кусочка пиццы первого типа, и bi единиц счастья от съедания каждого кусочка пиццы второго типа. Мы можем заказать любое число пицц первого и второго типов, но мы хотим заказать минимальное число пицц, необходимое для того, чтобы все участники могли съесть необходимое каждому число кусочков. Учитывая это ограничение, какое максимальное суммарное число единиц счастья могут получить участники? Выходные данные Выведите максимальное суммарное счастье, которое могут получить участники. Примечание В первом примере нужно купить лишь одну пиццу. Если это будет пицца первого типа, то суммарное счастье будет равно 3·5 + 4·6 + 5·9 = 84, а если купить пиццу второго типа — то суммарное счастье будет равно 3·7 + 4·7 + 5·5 = 74. | |
![]()
|
|
E. Максимизируй!
Бинарный поиск
Тернарный поиск
*1800
жадные алгоритмы
Выходные данные Выведите ответ на каждую операцию второго типа в том порядке, в котором эти операции шли во входных данных. Каждое число должно располагаться на отдельной строке. Ваш ответ будет считаться правильным, если каждый из ваших ответов имеет абсолютную или относительную ошибку не больше 10 - 6. Формально, пусть ваш ответ равен a, а ответ жюри — b. Ваш ответ будет считаться правильным, если 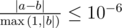 . . | |
![]()
|
|
C. Помогите Гному Грише
Тернарный поиск
геометрия
*2500
В Тридевятом царстве — Тридесятом государстве живет один очень необычный обитатель — Дварф (а на Руси — просто Гном) Гракула. Однако необычное имя — не главная его странность (тем более, что местные жители с незапамятных времен кличут его Гномом Гришей). Главные странности состоят в том, что живет Гном Гриша уже более 200 лет, причем живет он в склепе на заброшенном кладбище, и днем его еще никто ни разу не видел. Так же точно, как никто не видел, что Гном Гриша покупает себе еду. Поэтому никто особо не удивился, когда после трагической гибели Змея Горыныча с лугов не перестал пропадать скот — местные жители давно были убеждены, что причина пропаж — совсем не безобидный Горыныч, который давно признавался, что склонен к вегетарианству. Но самое плохое во всей этой истории даже не это. Самое плохое то, что буквально несколько минут назад Гном Гриша каким-то непостижимым образом оказался у вас дома, и попросил помощи в разрешении одного вопроса. Дело в том, что совсем недавно Гриша решил заказать себе новый гроб (зная его странности, эта новость вас ничуть не удивила). Но вот незадача — в Гришин склеп ведет очень длинный в обоих направлениях Г-образный коридор, через который удастся пронести не любой гроб. Поэтому он и обратился за помощью к вам. 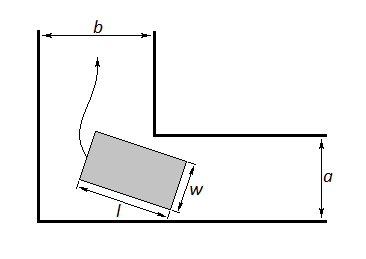 Вы формализовали задачу на плоскости следующим образом: пусть ширина коридора до и после поворота равна соответственно a и b (см. рисунок), коридор поворачивает строго под прямым углом, гроб суть прямоугольник с длиной и шириной соответственно l и w (l ≥ w). Гном Гриша уже определил длину гроба (l), исходя из своего роста, ваша задача — определить максимально возможную ширину гроба (w), при которой его можно будет внести в склеп. При этом в силу большой массы (чистый мрамор!) гроб оснащен вращающимися колесиками, поэтому его невозможно оторвать от земли, однако он может совершать произвольные перемещения и вращения в рассматриваемой плоскости. Гроб разрешено развернуть произвольным образом и до внесения в склеп и перемещения по коридору. Гриша пообещал, что если вы поможете ему — он наградит вас бессмертием (интересно, как?), а если нет — то лучше вам не знать, что произойдет... Выходные данные Выведите максимально возможную ширину гроба с абсолютной или относительной погрешностью не более 10 - 7, либо сообщение «My poor head =(» (без кавычек), если никакого гроба с заданной длиной и положительной шириной, удовлетворяющего условию задачи, не существует. Гарантируется, что в случае наличия положительного ответа он окажется не меньше 10 - 7. Все взломы также будут проверяться на соответствие этому условию. Примечание В первом примере ответ к задаче ограничен длиной гроба (вспомните — ширина гроба должна быть не больше его длины). Во втором примере гроб возможно пронести через коридор благодаря вращающимся колесикам: сначала двигаем его одной стороной вперед до тех пор, пока гроб не упрется в стену, затем двигаем перпендикулярно первоначальному направлению движения соседней стороной вперед (вспомните — возможны произвольные перемещения и вращения гроба в плоскости). | |
![]()
|