| | | |
|
Имена на Тау Кита
Сортировка подсчетом
На далекой планете Тау Кита есть непонятные нам обычаи. Например, таукитяне очень необычно для землян выбирают имена своим детям. Родители так выбирают имя ребенку, чтобы оно могло быть получено как удалением некоторого набора букв из имени отца, так и удалением некоторого набора букв из имени матери. Например, если отца зовут «abacaba», а мать — «bbccaa», то их ребенок может носить имена «a», «bba», «bcaa», но не может носить имена «aaa», «ab» или «bbc». Возможно, что имя ребенка совпадает с именем отца и/или матери, если оно может быть получено из имени другого родителя удалением нескольких (возможно, ни одной) букв.
Пусть отец по имени X и мать по имени Y выбирают имя своему новорожденному ребенку. Так как в таукитянских школах учеников часто вызывают к доске в лексикографическом порядке имен учеников, то есть в порядке следования имен в словаре, то они хотят выбрать своему ребенку такое имя, чтобы оно лексикографически следовало как можно позже.
- Формально, строка S лексикографически больше строки T, если выполняется одно из двух условий: строка T получается из S удалением одной или более букв с конца строки S;
- первые (i - 1) символов строк T и S не различаются, а буква в i-й позиции строки T следует в алфавите раньше буквы в i-й позиции строки S.
Требуется написать программу, которая по именам отца и матери находит лексикографически наибольшее имя для их ребенка.
Входные данные
Первая строка входного файла содержит X — имя отца. Вторая строка входного файла содержит Y — имя матери. Каждое имя состоит из строчных букв латинского алфавита, включает хотя бы одну букву и имеет длину не более 105 букв.
Выходные данные
Выходной файл должен содержать искомое лексикографически наибольшее из возможных имен ребенка. В случае, если подходящего имени для ребенка не существует, выходной файл должен быть пустым.
Примеры
входные данные
abcabca
abcda
выходные данные
ca
входные данные
ccba
accbbaa
выходные данные
ccba
| |
![]()
|
|
Драгоценные камни
Сортировка подсчетом
В одной далекой восточной стране до сих пор по пустыням ходят караваны верблюдов, с помощью которых купцы перевозят пряности, драгоценности и дорогие ткани. Разумеется, основная цель купцов состоит в том, чтобы подороже продать имеющийся у них товар. Недавно один из караванов прибыл во дворец одного могущественного шаха.
Купцы хотят продать шаху n драгоценных камней, которые они привезли с собой. Для этого они выкладывают их перед шахом в ряд, после чего шах оценивает эти камни и принимает решение о том, купит он их или нет. Видов драгоценных камней на Востоке известно не очень много всего 26, поэтому мы будем обозначать виды камней с помощью строчных букв латинского алфавита. Шах обычно оценивает камни следующим образом. Он заранее определил несколько упорядоченных пар типов камней: (a1, b1), (a2, b2), ..., (ak, bk). Эти пары он называет красивыми, их множество мы обозначим как P. Теперь представим ряд камней, которые продают купцы, в виде строки S длины n из строчных букв латинского алфавита. Шах считает число таких пар (i,j), что 1 ≤ i < j ≤ n, а камни Si и Sj образуют красивую пару, то есть существует такое число 1 ≤ q ≤ k, что Si=aq и Sj=bq.
Если число таких пар оказывается достаточно большим, то шах покупает все камни. Однако в этот раз купцы привезли настолько много камней, что шах не может посчитать это число. Поэтому он вызвал своего визиря и поручил ему этот подсчет. Напишите программу, которая находит ответ на эту задачу.
Входные данные
Первая строка входного файла содержит целые числа n и k (1 ≤ n ≤ 100000, 1 ≤ k ≤ 676) число камней, которые привезли купцы и число пар, которые шах считает красивыми. Вторая строка входного файла содержит строку S, описывающую типы камней, которые привезли купцы.
Далее следуют k строк, каждая из которых содержит две строчных буквы латинского алфавита и описывает одну из красивых пар камней.
Выходные данные
В выходной файл выведите ответ на задачу — количество пар, которое должен найти визирь.
Примеры
входные данные
7 1
abacaba
aa
выходные данные
6
входные данные
7 3
abacaba
ab
ac
bb
выходные данные
7
| |
![]()
|
|
Расшифровка письменности МАйя
Сортировка подсчетом
Расшифровка письменности Майя оказалась более сложной задачей, чем предполагалось ранними исследованиями. На протяжении более чем двух сотен лет удалось узнать не так уж много. Основные результаты были получены за последние 30 лет.
Письменность Майя основывается на маленьких рисунках, известных как значки, которые обозначают звуки. Слова языка Майя обычно записываются с помощью этих значков, которые располагаются рядом друг с другом в некотором порядке.
Одна из проблем расшифровки письменности Майя заключается в определении этого порядка. Рисуя значки некоторого слова, писатели Майя иногда выбирали позиции для значков, исходя скорее из эстетических взглядов, а не определенных правил. Это привело к тому, что, хотя звуки для многих значков известны, археологи не всегда уверены, как должно произноситься записанное слово.
Археологи ищут некоторое слово W. Они знают значки для него, но не знают все возможные способы их расположения. Поскольку они знают, что Вы приедете на IOI ’06, они просят Вас о помощи. Они дадут Вам g значков, составляющих слово W, и последовательность S всех значков в надписи, которую они изучают, в порядке их появления. Помогите им, подсчитав количество возможных появлений слова W.
Задание
Напишите программу, которая по значкам слова W и по последовательности S значков надписи подсчитывает количество всех возможных вхождений слова W в S, то есть количество всех различных позиций идущих подряд g значков в последовательности S, которые являются какой-либо перестановкой значков слова W .
Ограничения
1 ≤ g ≤ 3 000, g – количество значков в слове W
g ≤ |S| ≤ 3 000 000 где |S| – количество значков в последовательности S
Входные данные
На вход программы поступают данные в следующем формате:
СТРОКА 1: Содержит два числа, разделенных пробелом – g и |S|.
СТРОКА 2: Содержит g последовательных символов, с помощью которых записывается слово W . Допустимы символы: ‘a’-‘z’ и ‘A’-‘Z’; большие и маленькие буквы считаются различными.
СТРОКА 3: Содержит |S| последовательных символов, которые представляют значки в надписи. Допустимы символы: ‘a’-‘z’ и ‘A’-‘Z’; большие и маленькие буквы считаются различными.
Выходные данные
Единственная строка выходных данных программы должна содержать количество возможных вхождений слова W в S.
Важно для программирования на PASCAL
По умолчанию во FreePascal переменная типа string имеет ограничение размера в 255 символов. Если Вы хотите использовать более длинные строки, Вы должны добавить директиву {$ H +} в ваш код, сразу после строки program ...;.
Примеры
входные данные
4 11
cAda
AbrAcadAbRa
выходные данные
2
| |
![]()
|
|
Списки по классам
Сортировка подсчетом
Входные данные
В каждой строке сначала записан номер класса (число, равное 9, 10 или 11), затем (через пробел) — фамилия ученика.
Выходные данные
Необходимо вывести список школьников по классам: сначала всех учеников 9 класса, затем — 10, затем — 11. Внутри одного класса порядок вывода фамилий должен быть таким же, как на входе.
Примеры
входные данные
9 Ivanov
10 Petrov
11 Sidorov
9 Grigoryev
9 Sergeev
10 Yakovlev
выходные данные
9 Ivanov
9 Grigoryev
9 Sergeev
10 Petrov
10 Yakovlev
11 Sidorov
| |
![]()
|
|
Гистограмма
Сортировка подсчетом
Вовочка ломает систему безопасности Пентагона. Для этого ему понадобилось узнать, какие символы в секретных зашифрованных посланиях употребляются чаще других. Для удобства изучения Вовочка хочет получить графическое представление встречаемости символов. Поэтому он хочет построить гистограмму количества символов в сообщении. Гистограмма – это график, в котором каждому символу, встречающемуся в сообщении хотя бы один раз, соответствует столбик, высота которого пропорциональна количеству этих символов в сообщении.
Входные данные
Входной файл содержит зашифрованный текст сообщения. Он содержит строчные и прописные латинские буквы, цифры, знаки препинания («.», «!», «?», «:», «-», «,», «;», «(», «)»), пробелы и переводы строк. Размер входного файла не превышает 104 байт. Текст содержит хотя бы один непробельный символ. Все строки входного файла не длиннее 200 символов.
Выходные данные
Для каждого символа c кроме пробелов и переводов строк выведите столбик из символов «#», количество которых должно быть равно количеству символов c в данном тексте. Под каждым столбиком напишите символ, соответствующий ему. Отформатируйте гистограмму так, чтобы нижние концы столбиков были на одной строке, первая строка и первый столбец были непустыми. Не отделяйте столбики друг от друга. Отсортируйте столбики в порядке увеличения кодов символов.
Пример
| Входные данные |
Выходные данные |
Hello, world!
|
#
##
#########
!,Hdelorw
|
Twas brillig, and the slithy toves
Did gyre and gimble in the wabe;
All mimsy were the borogoves,
And the mome raths outgrabe.
|
#
#
#
#
#
# #
# # #
# # ### ####
## ###### ####
##############
############## ##
# # ############## ###
########################
,.;ADTabdeghilmnorstuvwy
|
| |
![]()
|
|
Жребий Крижановского
Сортировка подсчетом
Петя играет с друзьями в игру, которую иногда называют "Жребий Крижановского". Правила игры следующие: в каждом туре каждый игрок загадывает произвольное натуральное число. После этого игрок, загадавший минимальное число, которое не повторяется, выигрывает в этом туре, причем его выигрыш равен этому числу. Например, если играют 6 человек и были загаданы числа 3, 2, 1, 1, 4 и 2, то выиграл первый игрок, причем его выигрыш равен 3. Если все загаданные числа повторяются, то тур считается ничейным и никто баллов не получает.
Общий выигрыш игрока за игру равен сумме баллов за все сыгранные туры.
Петя с друзьями при игре просто называют по очереди загаданные ими числа, а потом определяют, кто выиграл, и подсчитывают баллы. Однако при таком формате игры в принципе можно сжульничать, не загадывая число заранее, а, уже зная числа, названные предыдущими игроками, выбрать себе оптимальное "загаданное" число. Этим и пользуется Петя. Он называет число последним и старается выбрать число так, чтобы максимизировать свой выигрыш.
Идет последний тур игры. Известны очки всех игроков перед этим туром и названные игроками числа. Выясните, какое число следует назвать Пете, чтобы по результатам игры у как можно большего числа игроков количество баллов было меньше, чем у него. Если таких чисел несколько, то Петя хочет назвать минимальное возможное.
Входные данные
В первой строке вводится число n - количество игроков (2 <= n <= 100). Вторая строка содержит n чисел - баллы игроков перед последним туром (неотрицательные целые числа, не большие 100). Баллы перечислены в том порядке, в котором игроки обычно называют числа (то есть Петины баллы указаны последними). В третьей строке задано (n-1) число - числа, названные игроками в последнем туре (числа не превышают 100), в том порядке, в котором они их называли.
Выходные данные
Выведите число, которое следует назвать Пете.
Пояснения
Во втором примере Петя не может выиграть в последнем туре. Однако, назвав число 2, Петя не позволяет выиграть первому игроку, и ,тем самым, остается вторым по итогам всей игры. У четырех игроков баллы меньше, чем у Пети.
| Ввод |
Вывод |
6
0 0 0 0 0 0
2 3 4 5 6 |
1 |
6
8 3 12 5 0 9
2 1 3 1 4 |
2 |
| |
![]()
|
|
Мегавзлом
Сортировка подсчетом
У Егора очень старый телефон. Слава отправил Егору кодовую фразу от Серёжиного банковского счёта, чтоб его ограбить, но телефон Егора настолько стар, что не умеет принимать длинные сообщения. Он разбивает их на несколько маленьких случайной длины, и приходят они ему в случайном порядке.
Когда Егор получил все эти сообщения, он по-настоящему расстроился. Он проклинал телефон, кидал его об стену. К несчастью, телефон оказался обидчивым и перемешал ещё и все буквы в каждом сообщении, хоть и склеил при этом все сообщения в одно. Егор знал, что Серёжа любит такие строки, что в них все буквы идут по убыванию (в обратном алфавитном порядке). Помогите Егору и Славе и найдите кодовую фразу от Серёжиного банковского счёта по единственному оставшемуся сообщению в телефоне.
Входные данные
Единственная строка входных данных содержит строку s — сообщение в телефоне Егора (1 ≤ |s| ≤ 105). Гарантируется, что s содержит только маленькие латинские буквы.
Выходные данные
Выведите кодовую фразу от Серёжиного банковского счёта.
Примеры
входные данные
qwerty
выходные данные
ywtrqe
входные данные
onehundredseventynine
выходные данные
yvutsronnnnniheeeeedd
| |
![]()
|
|
Арифметика Саши и Кати
Сортировка подсчетом
Саша и Катя учатся в начальной школе. Для изучения арифметики при этом используются карточки, на которых написаны цифры (на каждой карточке написана ровно одна цифра). Однажды они пришли на урок математики, и Саша, используя все свои карточки, показал число A, а Катя показала число B. Учитель тогда захотел дать им такую задачу, чтобы ответ на нее смогли показать и Саша, и Катя, каждый используя только свои карточки. При этом учитель хочет, чтобы искомое число было максимально возможным.
Входные данные
Вводятся два целых неотрицательных числа A и B (каждое число в одной строке). Длина каждого из чисел не превосходит 100 000 цифр.
Выходные данные
Выведите одно число — максимальное целое число, которое можно составить используя как цифры первого числа, так и цифры второго числа. Если же ни одного такого числа составить нельзя, выведите -1.
Примеры тестов
входные данные
280138
798081
выходные данные
8810
входные данные
123
456
выходные данные
-1
| |
![]()
|
|
Головоломка
Сортировка подсчетом
Петя разгадывает головоломку, которая устроена следующим образом. Дана квадратная таблица размера NxN, в каждой клетке которой записана какая-нибудь латинская буква. Кроме того, дан список ключевых слов. Пете нужно, взяв очередное ключевое слово, найти его в таблице. То есть найти в таблице все буквы этого слова, причем они должны быть расположены так, чтобы клетка, в которой расположена каждая последующая буква слова, была соседней с клеткой, в которой записана предыдущая буква (клетки называются соседними, если они имеют общую сторону — то есть соседствуют по вертикали или по горизонтали). Например, на рисунке ниже показано, как может быть расположено в таблице слово olympiad.
| P |
O |
L |
T |
E |
| R |
W |
Y |
M |
S |
| O |
A |
I |
P |
T |
| B |
D |
A |
N |
R |
| L |
E |
M |
E |
S |
Когда Петя находит слово, он вычеркивает его из таблицы. Использовать уже вычеркнутые буквы в других ключевых словах нельзя.
После того, как найдены и вычеркнуты все ключевые слова, в таблице остаются еще несколько букв, из которых Петя должен составить слово, зашифрованное в головоломке.
Помогите Пете в решении этой головоломки, написав программу, которая по данной таблице и списку ключевых слов выпишет, из каких букв Петя должен сложить слово, то есть какие буквы останутся в таблице после вычеркивания ключевых слов.
Входные данные
В первой строке записаны два числа N (1 ≤ N ≤ 10) и M ( 0 ≤ M ≤ 200). Следующие N строк по N заглавных латинских букв описывают ребус. Следующие M строк содержат слова. Слова состоят только из заглавных латинских букв, каждое слово не длиннее 200 символов. Гарантируется, что в таблице можно найти и вычеркнуть по описанным выше правилам все ключевые слова.
Выходные данные
В единственную строку выведите в любом порядке буквы, которые останутся в таблице.
Примеры
входные данные
5 3
POLTE
RWYMS
OAIPT
BDANR
LEMES
OLYMPIAD
PROBLEM
TEST
| |
![]()
|
|
Автобусы
Сортировка подсчетом
Сканирующая прямая
Жадный алгоритм
Новый Президент Тридевятой республики начал свою деятельность с полной ревизии системы общественного транспорта страны. В результате на основе социологических опросов населения было составлено идеальное ежедневное расписание движения междугородних автобусов, утвержденное Парламентом республики.
Более того, было решено заменить весь автобусный парк одинаковыми новыми, очень дорогими, но гораздо более надежными, красивыми и удобными машинами.
Автобусная сеть страны охватывает N городов, занумерованных целыми числами от 1 до N.
Идеальное расписание содержит M ежедневных рейсов, i-й рейс начинается в городе Fi в момент времени Xi и заканчивается в некотором другом городе Gi в момент времени Yi. Продолжительность каждого рейса ненулевая и строго меньше 24 часов. Рейс i выполняется одним из автобусов, находящихся в момент времени Xi в городе Fi.
Новые автобусы не требуют ремонта и могут работать круглосуточно, поэтому автобус, прибывший в некоторый момент времени в некоторый город, всегда готов в тот же самый момент времени или позже отправиться в путь для обслуживания любого другого рейса из данного города. Автобус может выехать из города, только выполняя какой-либо рейс из расписания.
Предполагается, что расписание будет действовать неограниченное время, поэтому может оказаться так, что его невозможно обслужить никаким конечным числом автобусов.
Определите наименьшее количество новых автобусов, достаточное для обеспечения движения по расписанию в течение неограниченного периода времени.
Входные данные
В первой строке задаются целые числа N и М (1 ≤ N, M ≤ 100 000) — количество городов и рейсов автобусов соответственно.
В каждой из следующих M строк содержится описание рейса автобуса: номер города отправления Fi, время отправления Xi, номер города назначения Gi (Fi ≠ Gi), время прибытия Yi, отделенные друг от друга одним пробелом. Время прибытия и отправления задается в формате HH:MM, где HH — часы от 00 до 23, MM — минуты от 00 до 59.
Выходные данные
Выведите одно число — минимально необходимое количество автобусов. Если расписание невозможно обслуживать в течение неограниченного периода времени конечным числом автобусов, выведите число -1.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 6
1 10:00 2 12:00
1 10:00 3 09:00
3 12:00 4 23:00
2 11:00 4 13:00
4 12:00 1 11:00
4 12:00 1 10:30 |
8 |
| |
![]()
|
|
Пожиратель карт
Сортировка подсчетом
Конструктив
Ушан решил сыграть в карточную игру. У него есть колода, состоящая из N съедобных карт. На i-й карте сверху написано целое число Ai. Ушан выполняет описанную ниже операцию ноль или более раз, так что значения, записанные на оставшихся карточках, будут попарно различны.
Найдите максимально возможное количество оставшихся карт. Здесь N нечетное, что гарантирует сохранение хотя бы одной карты.
Операция: вынуть из колоды три произвольные карты. Из этих трех карт съешьте две: одну с наибольшим значением, а другую с наименьшим значением. Затем верните оставшуюся одну карту в колоду.
Входные данные
В первой строке записано нечетное число N (\(3<=N<=10^5\)). Во второй строке записаны N чисел Ai (\(1<=A_i<=10^5\))
Выходные данные
Выведите максимально возможное количество оставшихся карт.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснения |
| 1 |
5
1 2 1 3 7 |
3 |
Оптимальное решение - выполнить операцию один раз, вынув две карты с 1 и одну карту с 2. Одна карта с 1 и другая с 2 будут съедены, а оставшаяся карта с 1 будет возвращена в колоду.
Тогда значения, написанные на оставшихся картах в колоде, будут попарно различными: 1, 3 и 7. |
| 2 |
15
1 3 5 2 1 3 2 8 8 6 2 6 11 1 1 |
7 |
|
| |
![]()
|
|
Новый аэропорт
Сортировка подсчетом
Сканирующая прямая
ЕГЭ_информатика
ЕГЭ-26. Обработка массива целых чисел. Сортировка
В аэропорту города Че начал работать новый аэропорт. В первые сутки работы был записан файл с временем прилета и вылета самолетов. Самолеты, которые улетали на следующие сутки в файл не были записаны. Определите максимальное число самолетов, которые находились в аэропорту одновременно и в течении какого максимального промежутка времени (в минутах) находилось в аэропорту такое число самолетов. Учитываются только самолеты, информация о которых записана в файле.
Входные данные
Первая строка содержит число N - общее количество самолетов за весь день. В каждой из следующих N строк содержится пара значений, где первое значение в паре показывает время прилета самолета, а второе значение - время вылета (время прилета и вылета находится в диапазоне от 00:00 до 23:59, причем гарантируется, что время прилета меньше времени вылета) . Все данные в строках разделены одним пробелом.
При совпадающем времени считается, что прилет происходит раньше вылета.
В ответе запишите два целых числа через пробел: сначала максимальное количество самолетов, которые находились в аэропорту одновременно, затем максимальный промежуток времени (в минутах), в течении которого в аэропорту было такое число транзитных самолетов.
Если самолет прилетел в 12:00, а вылетел в 12:01, то считается, что он пробыл в аэропорту 2 минуты.
Файл к заданию
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
6
09:00 10:07
10:20 11:35
12:00 17:00
11:00 11:30
11:20 12:30
11:30 18:15 |
4 1 |
| |
![]()
|
|
Гимнастические ленты. Тренировочное задание - 3
Сортировка подсчетом
ЕГЭ_информатика
Для выступления гимнастки используют ленты, которые после выступления кладут на стол. Папа самой лучшей гимнастки Анны К. в ожидании награждения решил записывать координаты начала и конца лент. У вас есть файл с данной информацией. Определите в скольки точках стола получилась самая большая толщина покрытия и чему она равна. Стол имеет длину Lмм. По окончании выступления всех гимнасток, на столе оказалось N лент. Никакая лента не вылезает за границы стола. Все ленты лежат горизонтально. Ленты складываются друг на друга.
Входные данные
В первой строке файла записаны два числа - L, N (1 <= L <= 10000, 1 <= N <= 10000). В слеующих N строках записаны по 2 числа - l, r (1 <= l <= r <= L) - левые и правые концы лент относительно левого края стола.
В ответе укажите два числа через пробел - максимальную толщину ленточного покрытия стола и количество точек с такой толщиной.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
39 4
3 21
3 15
2 20
3 17
|
4 13 |
Файл к заданию
| |
![]()
|
|
Гимнастические ленты
Сортировка подсчетом
ЕГЭ_информатика
ЕГЭ-26. Обработка массива целых чисел. Сортировка
Для выступления гимнастки используют ленты, которые после выступления кладут на стол. Папа самой лучшей гимнастки Анны К., в ожидании награждения, решил записывать координаты начала и конца лент. Если лента свисала с левого края стола, то он ставил левую координату равной нулю, если лента свисала с правого конца стола, то он ставил правую координату равной нулю. Если лента свисала с двух сторон, то он записывал обе координаты равной нулю. У вас есть файл с данной информацией. Определите, в скольки точках стола получилась самая большая толщина покрытия и чему она равна. Стол имеет длину Lмм. По окончании выступления всех гимнасток, на столе оказалось N лент. У некоторых лент свисает со стола только один конец, у некоторых оба. Все ленты лежат горизонтально. Ленты складываются друг на друга.
Входные данные
В первой строке файла записаны два числа - L, N (1 <= L <= 10000, 1 <= N <= 10000). В слеующих N строках записаны по 2 числа - l, r (1 <= l <= r <= L) - левые и правые концы лент относительно левого края стола.
В ответе укажите два числа через пробел - максимальную толщину ленточного покрытия стола и количество точек с такой толщиной.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
39 4
3 21
3 15
2 20
3 17
|
4 13 |
Файл к заданию
| |
![]()
|
|
Носки
Сортировка подсчетом
Имеется стол длины L. На столе разложено N носков так, что никакой носок не вылезает за границы стола. Далее имеется умный мальчик Васёк, который хочет (сугубо в корыстных целях) замерить толщину покрытия стола носками в M точках.
Формат входных данных
Во входном файле даны сначала L, N, M (1 ≤ L ≤ 10000, 1 ≤ N ≤ 10000, 1 ≤ M ≤ 100000). Далее идут N пар чисел l ≤ r от 1 до L – левые и правые концы носков. Затем идут M чисел от 1 до L интересующие Васька точки.
Формат выходных данных
Выведите M чисел – толщину носкового покрытия в каждой точке.
| |
![]()
|
|
Самая частая сумма
Сортировка подсчетом
Дан набор из N целых положительных чисел. Для каждого числа вычисляется сумма двух последних цифр в его десятичной записи (для однозначных чисел предпоследняя цифра считается равной нулю). Необходимо определить, какая сумма при этом получается чаще всего. Если таких сумм несколько, необходимо вывести наибольшую из них.
Напишите эффективную по времени и по памяти программу для решения этой задачи.
Программа считается эффективной по времени, если при увеличении количества исходных чисел N в k раз время работы программы увеличивается не более чем в k раз.
Программа считается эффективной по памяти, если память, необходимая для хранения всех переменных программы, не превышает 1 Кбайт и не увеличивается с ростом N.
Формат входных данных
В первой строке входных данных задаётся количество чисел N (1 ≤ N ≤ 1000). В каждой из последующих N строк записано одно натуральное число, не превышающее 10 000.
Формат выходных данных
Выведите одно число - искомый ответ.
| |
![]()
|
|
Относительная сортировка
Сортировка подсчетом
Даны два массива arr1 и arr2. Элементы массива arr2 различны, и при этом все элементы arr2 содержатся в arr1.
Отсортируйте элементы массива arr1 таким образом, чтобы относительный порядок элементов в массиве arr1 был таким же, как в массиве arr2. Элементы, которых нет в массиве arr2 должны располагаться в конце массива arr1 в порядке возрастания.
Входные данные
Первая строка входных данных содержит целое число n - количество элементов в массиве arr1, вторая строка содержит n целых чисел - элементы массива arr1. Третья строка содержит целое число m - количество элементов в массиве arr2, четвертая строка содержит m целых чисел - элементы массива arr2.
Ограничения на входные данные
1 <= n, m <= 1060 <= arr1[i], arr2[i] <= 1000- Все элементы массива
arr2 различны.
- Каждый элемент массива
arr2[i] содержится в массиве arr1.
Выходные данные
Выведите, отсортированный по условию задачи, массив arr1.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
11
2 3 1 3 2 4 6 7 9 2 19
6
2 1 4 3 9 6 |
2 2 2 1 4 3 3 9 6 7 19 |
| 2 |
6
28 6 22 8 44 17
4
22 28 8 6 |
22 28 8 6 17 44 |
| |
![]()
|
|
Первый уникальный
Строки
Сортировка подсчетом
Символ называется уникальным, если он встречается в строке один раз. Первый уникальный символ - это уникальный символ с наименьшим индексом.
Дана строка s. Найдите первый уникальный символ в данной строке. Выведите его индекс. Если в строке нет уникальных символов, выведите -1.
Входные данные
Программа получает на вход последовательность непробельных символов s.
Ограничения
'a' <= s[i] <= 'z'
0 <= i <= 255
Выходные данные
Выведите ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
silvertests
|
1 |
| 2 |
sstt
|
-1 |
| |
![]()
|
|
Сортировка строки по частоте букв
Строки
Сортировка подсчетом
Дана строка s. Отсортируйте символы данной строки в порядке убывания частоты встречаемости. Частота встречаемости символа - это количество раз, которое данный символ встречается в строке.
Выведите отсортированную строку. Если два символа встречаются одинаковое количество раз, то они должны идти в лексикографическом порядке.
Входные данные
Программа получает на вход
Ограничения
1 <= s.length <= 5 * 105 (s.length - длина строки s)
s содержит большие и маленькие английские буквы и цифры.
Выходные данные
Выведите отсортированную строку.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
tree
|
eert
|
| 2 |
cccaaa
|
aaaccc
|
| 3 |
Aabb
|
bbAa
|
| |
![]()
|
|
Клавиатура
Сортировка подсчетом
Всем известно, что со временем клавиатура изнашивается, и клавиши на ней начинают залипать. Конечно, некоторое время такую клавиатуру еще можно использовать, но для нажатий клавиш приходиться использовать большую силу.
При изготовлении клавиатуры изначально для каждой клавиши задается количество нажатий, которое она должна выдерживать. Если знать эти величины для используемой клавиатуры, то для определенной последовательности нажатых клавиш можно определить, какие клавиши в процессе их использования сломаются, а какие – нет.
Требуется написать программу, определяющую, какие клавиши сломаются в процессе заданного варианта эксплуатации клавиатуры.
Входные данные
Первая строка входного файла содержит целое число n (1 ≤ n ≤ 100) – количество клавиш на клавиатуре. Вторая строка содержит n целых чисел – с1, с2, … , сn, где сi (1 ≤ сi ≤ 100000) – количество нажатий, выдерживаемых i-ой клавишей. Третья строка содержит целое число k (1 ≤ k ≤ 100000) – общее количество нажатий клавиш, и последняя строка содержит k целых чисел pj (1 ≤ pj ≤ n) – последовательность нажатых клавиш.
Выходные данные
В выходной файл необходимо вывести n строк, содержащих информацию об исправности клавиш. Если i-ая клавиша сломалась, то i-ая строка должна содержать слово “yes” (без кавычек), если же клавиша работоспособна – слово “no”.
| Ввод |
Вывод |
|
5
1 50 3 4 3
16
1 2 3 4 5 1 3 3 4 5 5 5 5 5 4 5
|
yes
no
no
no
yes
|
Личные олимпиады, Всероссийская олимпиада школьников, Региональный этап, 2009, 2 день, Задача A
| |
![]()
|
|
Артур Числовский и его массив
Сортировка подсчетом
Артур Числовский получил на свой день рождения массив из N целых чисел в подарок. Но ему он не понравился. Артур Числовский хочет сделать этот массив красивым. Числовский считает массив A1, A2, A3 ... AN красивым, если A1 > AN. Чтобы сделать его красивым, Артур Числовский может поменять местами любые два числа в массиве. Кроме того, Артур Числовский может выполнять эту операцию любое количество раз над смежными парами целых чисел в массиве A. Найдите количество способов, которыми Артур Числовский может сделать этот массив красивым. Два способа считаются одинаковыми, если итоговый массив после всех обменов имеет одинаковые значения A1 и AN.
Формат входных данных
Первая строка ввода содержит целое число N, обозначающее количество элементов в массиве A. Следующая строка ввода содержит N разделенных пробелом целых чисел, обозначающих A1,A2,A3 ... AN соответственно.
Ограничения
1 ≤ N ≤ 106
1 ≤ Ai ≤ 106
Формат выходных данных
Выведите одно число - количество способов, с помощью которых можно сделать данный массив красивым.
Примечание
В приведенном примере общее количество способов равно (5,1),(4,1),(3,1),(2,1),(5,2),(4,2),(3,2),(5,3),(4,3),(5,4). Первое число в приведенной выше паре - A[1], а второе - A[N]. Заметим, что два способа считаются одинаковыми, если A[1] и A[N] в результирующем массиве после обмена совпадают.
| |
![]()
|
|
Подсчет пар
Словари
Сортировка подсчетом
Вам дан массив A из N чисел. Найдите количество различных пар (i, j), таких, что j>=i и A[i] = A[j].
Формат входных данных
Первая строка входных данных содержит количество тестовых случаев T. Каждый тестовый случай состоит из двух строк, первая строка - число N, за ней следует строка, состоящая из N целых чисел, которые являются элементами массива A.
Ограничения
1 <= T <= 10
1 <= N <= 106
-106 <= A[i] <= 106
0 <= i < N
Формат выходных данных
Для каждого тестового случая выведите количество различных пар.
| |
![]()
|
|
Игра "Банковские карты"
Разные системы счисления
Сортировка подсчетом
После четвёртого сезона Шерлок и Мориарти осознали бессмысленность баталии, развернувшейся между ними, и решили дальше соревноваться в мирную игру “Банковские карты”.
Правила у этой игры предельно просты: каждый игрок приносит свою любимую банковскую карту с \(n\)-значным номером. Далее оба игрока по очереди называют последовательные цифры из банковской карты. Если цифры не совпадают, то участник, цифра которого оказывается меньше, получает щелбан от другого игрока. Например, если \(n=3\) и у Шерлока номер карты \(123\), а у Мориарти \(321\), то сначала Шерлок называет число \(1\), а Мориарти называет число \(3\) и Шерлок получает щелбан. Затем и Шерлок и Мориарти называют число \(2\), и щелбан не получает никто. Наконец на третьем шаге, Шерлок называет \(3\), а Мориарти называет \(1\) и получает щелбан.
Шерлок, конечно, будет играть честно, но Мориарти, как настоящий злодей, подсмотрел номер карты Шерлока и теперь хочет называть цифры своей банковской карты не последовательно, а в некотором другом порядке (однако количество каждой из цифр он не изменяет). Например в случае выше, Мориарти мог бы назвать цифры в последовательности \(3\), \(2\), \(1\) и не получил бы щелбанов вообще, а мог назвать \(2\), \(3\) и \(1\) и выдать Шерлоку целых два щелбана.
Вам поручено вычислить, какое минимальное количество щелбанов Мориарти точно получит и какое максимальное число Мориарти может дать Шерлоку. Обратите внимание, что это две разные цели, и они могут достигаться при использовании разных порядков.
Формат входных данных
В первой строке находится одно целое число \(n\) (\(1 \leqslant n \leqslant 1000\)) — количество цифр в банковских картах Шерлока и Мориарти.
Во второй строке записана последовательность из \(n\) цифр — номер кредитной карточки Шерлока.
В третьей строке записана последовательность из \(n\) цифр — номер кредитной карточки Мориарти.
Формат выходных данных
В первой строке выведите одно число — минимальное число щелбанов, которое обязательно получит Мориарти.
Во второй строке выведите так же одно число — максимальное число щелбанов, которое Мориарти может дать Шерлоку.
Замечание
Первый примерс овпадает с примером разобранным в условии задачи. Во втором примере Мориарти никак не сможет избежать двух щелбанов
В данной задаче 50 тестов, помимо тестов из условия, каждый из них оценивается в 2 балла. Результаты работы ваших решений на первых 30 тестах будут доступны во время соревнования. Результаты работы на остальных 20 будут доступны после окончания соревнования.
Решения, корректно работающие при \(1 \leq n \leq 3\), наберёт не менее \(10\) баллов.
Решения, корректно работающие при \(1 \leq n \leq 8\), наберет не менее \(30\) баллов.
| |
![]()
|
|
Банковские карты
Разные системы счисления
Сортировка подсчетом
Банк «Кисловодск» переходит на новый вид банковских карт. Для этого производятся одинаковые заготовки, на которых есть специальное место для идентификации клиента. Изначально на этом месте записывается кодовое число X. В банке с помощью специального прибора можно стирать некоторые цифры числа X. Оставшиеся цифры, будучи записанными подряд, должны образовывать номер счета клиента. Например, при X = 12013456789 номера счетов 5, 12, 17 или 12013456789 получить можно, а номера 22 или 71 получить нельзя.
Способ распределения номеров счетов в банке очень прост. Счетам присваиваются последовательно номера 1, 2, … Очевидно, что при таком способе в какой-то момент впервые найдется номер счета N, который нельзя будет получить из цифр X указанным выше способом. Руководство банка хочет знать значение N.
Напишите программу, которая находила бы N по заданному X.
Формат входных данных
Вводится натуральное число X без ведущих нулей (1 ≤ X ≤ 101000).
Формат выходных данных
Выведите искомое N без ведущих нулей.
| |
![]()
|
|
Разнообразный куб
Сортировка подсчетом
Даны восемь символов из диапазона от "A" до "Z". Некоторые из них могут совпадать. Требуется определить, можно ли расположить эти символы в вершинах куба таким образом, чтобы на соседних (т. е. соединенных ребром) вершинах оказались разные символы
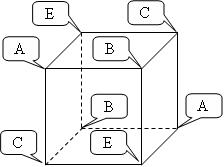
Входные данные
Во входном файле находится строка из восьми заглавных латинских букв.
Выходные данные
Выходной файл должен содержать целое число 1, если расположение возможно, и 0 (нуль) в противном случае.
| |
![]()
|
|
Форум
Сортировка подсчетом
Клуб Юных Хакеров организовал на своем сайте форум. Форум имеет следующую структуру: каждое сообщение либо начинает новую тему, либо является ответом на какое-либо предыдущее сообщение и принадлежит той же теме.
После нескольких месяцев использования своего форума юных хакеров заинтересовал вопрос - какая тема на их форуме наиболее популярна. Помогите им выяснить это.
Входные данные
В первой строке вводится целое число N - количество сообщений в форуме (1 <= N <= 1000). Следующие строки содержат описание сообщений в хронологическом порядке.
Описание сообщения, которое представляет собой начало новой темы, состоит из трех строк. Первая строка содержит число 0. Вторая строка содержит название темы. Длина названия не превышает 30 символов. Третья строка содержит текст сообщения.
Описание сообщения, которое является ответом на другое сообщение, состоит из двух строк. Первая строка содержит целое число - номер сообщения, ответом на которое оно является. Сообщения нумеруются, начиная с единицы. Ответ всегда появляется позже, чем сообщение, ответом на которое он является. Вторая строка содержит текст сообщения.
Длина каждого из сообщений не превышает 100 символов.
Выходные данные
Выведите название темы, к которой относится наибольшее количество сообщений. Если таких тем несколько, то выведите первую в хронологическом порядке
| Ввод |
Вывод |
|
2
0
topic 1
body of message 1
0
topic 2
body of message 2
|
topic 1 |
| |
![]()
|
|
Триангуляция
Сортировка подсчетом
Сканирующая прямая
Вася нарисовал выпуклый N-угольник и провел в нем несколько диагоналей таким образом, что никакие две диагонали не пересекаются внутри N-угольника. Теперь он утверждает, что весь N-угольник оказался разбит на треугольники. Напишите программу, которая проверяет истинность Васиного утверждения.
Входные данные
Сначала вводятся числа N - количество вершин N-угольника (3 <= N <= 1000) и M - количество диагоналей, проведенных Васей. Далее на вход программы поступают M пар чисел, задающих диагонали (каждая диагональ задается парой номеров вершин, которые она соединяет). Гарантируется, что каждая пара чисел задает диагональ (то есть две вершины различны и не являются соседними), а также что никакие две пары не задают одну и ту же диагональ. Никакие две диагонали не пересекаются внутри N-угольника. Вершины N-угольника нумеруются числами от 1 до N.
Выходные данные
Если Васино утверждение верно, то программа должна выводить единственное число 0. В противном случае необходимо вывести сначала число K - количество вершин в какой-нибудь не треугольной части. Далее должно быть выведено K чисел - номера вершин исходного N-угольника, которые являются вершинами этой K-угольной части в порядке обхода этой части.
| |
![]()
|
|
Палиндром
Сортировка подсчетом
Палиндром - это строка, которая читается одинаково как справа налево, так и слева направо.
На вход программы поступает набор больших латинских букв (не обязательно различных). Разрешается переставлять буквы, а также удалять некоторые буквы. Требуется из данных букв по указанным правилам составить палиндром наибольшей длины, а если таких палиндромов несколько, то выбрать первый из них в алфавитном порядке.
Входные данные
В первой строке входных данных содержится число N (1 <= N <= 100000). Во второй строке задается последовательность из N больших латинских букв (буквы записаны без пробелов).
Выходные данные
В единственной строке выходных данных выдайте искомый палиндром.
| Ввод |
Вывод |
|
3
AAB
|
ABA |
|
6
QAZQAZ
|
AQZZQA |
|
6
ABCDEF
|
A |
| |
![]()
|