Двоичная система счисления

Рассмотрим натуральное число \(x\). Требуется прибавить к нему минимальное возможное целое неотрицательное число \(y\), чтобы двоичная запись получившегося числа \(x+y\) имела ровно \(k\) единиц.

Формат входных данных
Первая строка ввода содержит натуральное число \(x\) (\(1 \le x \le 10^{18}\)).

Вторая строка ввода содержит натуральное число \(k\) (\(1 \le k \le 60\)).

Формат выходных данных
Выведите минимальное возможное целое неотрицательное число \(y\), такое что двоичная запись числа \(x+y\) имеет ровно \(k\) единиц.

Современные компьютеры состоят из микроскопических транзисторов (электронных переключателей). Каждый из них может быть в двух состояниях:

• 1 (ВКЛ) — есть ток → True

• 0 (ВЫКЛ) — нет тока → False

Какое число соответствует True в двоичном коде?

В мире двоичных чисел решили разобраться, почему некоторые числа не дружат друг с другом, потому после ряда проведённых экспериментов было выявлено, что точно не дружат друг с другом те числа, которые нельзя поставить рядом так, чтобы в их последовательности не было двух и более единиц подряд, а также не было трёх и более нулей подряд.
Помогите понять жителям двоичного мира, сколько пар чисел от 1 до N нельзя точно никак подружить.
Например: есть два числа 4 и 5, в двоичной системе счисления они представлены как 100 и 101. Если их поставить как 101 и 100, получится 101100, что даёт две единицы подряд в строке, значит дружить они не будут, но если поставим наоборот 100 и 101 = 100101, то двух единиц подряд нет, а также нет трёх и более нулей подряд, значит числа могут подружиться.
Формат входных данных
На первой строке подаётся число N (1 <= N <= 10⁵) – количество чисел в двоичном мире от 1 до N (включительно).
Формат выходных данных
Вывести на первой строке количество пар чисел, которые никак нельзя будет подружить друг с другом. Рассматриваются все числа от 1 до N, но все числа уникальны, потому не рассматриваются пары одинаковых чисел и повторяющиеся пары (если нельзя подружить число x с числом y, то пара (x, y) и (y, x) считается одной парой чисел).

В мире двоичных чисел произошёл масштабный сбой, теперь двоичные числа разучились складываться друг с другом. Притом спустя часть времени была выявлена закономерность новых правил сложения, она оказалась следующей:

• 1 + 1 = 0
• 1 + 0 = 1
• 0 + 1 = 0
• 0 + 0 = 1

Таким образом было выявлено, что также порядок слагаемых имеет значение (первое слагаемое число верхнее, второе – нижнее). Так как все эти правила теперь запомнить было очень сложно, то попросили разработать алгоритм, который будет принимать два двоичных числа одинаковой длины и возвращать результат суммы этих двух чисел в столбик.

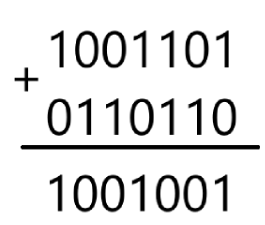
Формат входных данных
На первой строке подаётся первое слагаемое – двоичное число без значащих нулей длины N (1 <= N <= 10⁵).
На второй строке подаётся второе слагаемое – двоичное число без значащих нулей также длины N.

Формат выходных данных
Вывести на первой строке результат суммы двух двоичных чисел. Если в результате есть незначащие нули, то выводить без них. Если получился 0, то вывести просто 0.

Злым числом в математике называется неотрицательное целое число с чётным числом единиц в его двоичной записи (например, число 5 — злое, в его двоичной записи две единицы). Они используются в теории чисел при исследовании последовательности Морса–Туэ и применяются в алгоритмах фрактального сжатия изображений. Натуральное число будем называть очень злым, если само оно чётное и количество единиц в его двоичной записи также чётное. Это такие числа, как 6, 10, 12, 18, 20 и так далее. По данному n определите количество очень злых чисел, не превосходящих n.

Формат входных данных
Единственная строка входного файла содержит натуральное число n (1 ≤ n ≤ 10⁹ ).

Формат выходных данных
Выведите одно неотрицательное целое число — количество очень злых натуральных чисел, не превосходящих n.

Дана запись некоторого числа в двоичном дополнительном коде. Выведите десятичную запись этого числа.

Входные данные
Программа получает на вход строку из нулей и единиц. Длина строки не меньше 2 и не больше 16.

Выходные данные
Программа должна вывести десятичную запись числа, записанного в этой строке в двоичном дополнительном коде.

Напишите программу, которая по данным числам A и n записывает представление числа A в n-разрядном двоичном дополнительном коде.

Входные данные
Первая строка входных данных содержит число A, вторая строка –– число n, при этом    2 ≤ n ≤ 16,  −2^n-1 ≤ A ≤  2 ^n-1−1 .

Выходные данные
Программа должна вывести строку из n символов, содержащих запись числа A в n-разрядном двоичном дополнительном коде, первый символ –– старший знаковый разряд.

Преобразуйте дробь.

Входные данные
Дана запись двоичной дроби, как в задаче "Binary periodical fraction to decimal", но в целых числах точки может не быть. Необходимо представить ее в виде несократимой рациональной дроби n/m.

Выходные данные
Программа должна вывести значения n и m .

Дано рациональное число. Запишите его в виде двоичной периодической дроби.

Входные данные
На вход программа получает два натуральных числа n и m, каждое из которых не превосходит 1000.

Выходные данные
Программа должна вывести значение n/m, записанное в виде двоичной периодической дроби, при этом длина непериодической дробной части и длина периода должны быть минимально возможными. Если данное число является конечной двоичной дробью, периодическую часть выводить не надо.

Преобразуйте двоичное число.

Входные данные
Дана запись целого двоичного числа или двоичной периодической дроби, которая включает в себя:

1. Необязательную целую часть.
2. Необязательный символ точки, отделяющий целую часть от дробной. 

3. Необязательную дробную непериодическую часть. 

4. Необязательную периодическую дробную часть, записываемую в круглых скобках.

Выходные данные
Необходимо определить значение этой дроби, сохранить его в переменной типа double и вывести на экран с точностью не менее 12 знаков. Общая длина входной строки не превосходит 30 символов.

Переведите десятичное число в двоичную систему.

Входные данные
Дано действительное неотрицательное число, не превосходящее 100, записанное в десятичном виде. Целые числа при этом могут не содержать точку.

Выходные данные
Необходимо представить число в виде двоичной дроби с фиксированной точкой и вывести это представление. Ответ должен отличаться от правильного не более, чем на 2 − 32 , то есть необходимо вывести не менее 32 двоичных цифр после точки.

Переведите число из двоичной системы счисления в десятичную.

Входные данные
Дано число, представленное в виде двоичной дроби: запись длиной не более 30 символов, содержащая цифры 0 и 1 и, возможно, одну точку.

Выходные данные
Необходимо вывести данное число в виде десятичной дроби (тип переменной double с точностью не менее 12 знаков).

Переведите натуральное число из двоичной системы в десятичную (в двоичном числе не более 10 цифр).

Входные данные
Вводится натуральное число, записанное в двоичной системе.

Выходные данные
Выведите число, записанное в десятичной системе.

Будем называть числа круглыми, если они содержат в своей записи только цифры 0 и 5. Составим последовательность неотрицательных целых круглых чисел в порядке возрастания: 0, 5, 50, 55, 500, 505 и так далее.

Написать программу, которая находит K-е по порядку в этой последовательности круглое число.

Входные данные
Вводится одно натуральное число K- номер круглого числа в порядке возрастания.

Выходные данные
Программа должна вывести  круглое число с заданным номером.

Переведите число {1} из 10-й СС в двоичную СС
 

В гостинице для жирафов администрация хочет запастись подушкам так, чтобы удовлетворить потребности любого своего возможного постояльца. Известно, что жирафам в зависимости от длины их шеи нужно сложить стопку подушек (в стопке одна или несколько подушек) толщиной от \(1\) до \(n\) сантиметров. При этом администрация хочет обойтись как можно меньшим числом подушек, а среди наборов подушек, удовлетворяющих этим требованиям, администрация выберет набор минимальной суммарной толщины, чтобы он занимал минимальный объём в шкафу.

Помогите администрации составить нужный набор подушек, позволяющий получить стопку любой высоты от \(1\) до \(n\) сантиметров включительно.

Формат входных данных
Во входных данных записано единственное целое число \(n\) — максимально возможная длина шеи жирафа (\(1 \leq n \leq 10^9\)).

Формат выходных данных
В единственной строке через пробел выведите толщину каждой подушки в этом наборе в произвольном порядке. Если ответов несколько, выведите любой из них.

Замечание

В примере из условия необходимо подобрать такой набор из минимального числа подушек, чтобы используя данные подушки удавалось сложить стопку любой целочисленной толщины от \(1\) до \(9\) см. Таким набором является набор из подушек толщиной \(1\), \(2\), \(3\), \(3\) см. Действительно, стопку толщины \(1\), \(2\), \(3\) см можно сложить из одной подушки. Оставшиеся числа получены так: \(4=1+3\), \(5=2+3\), \(6=3+3\), \(7=1+3+3\), \(8=2+3+3\), \(9=1+2+3+3\). Возможны и другие варианты ответа с тем же количеством подушек и их суммарной толщиной. Выполнить условие задачи, используя только три подушки, нельзя.

Тимофей готовится к ЕГЭ. Для отработки навыка скорости и точности поиска ответов на задания по теме «Системы счисления» ему часто приходится решать примеры типа «сколько значащих нулей (или единиц) содержит двоичная запись значения выражения 2^a + 2^b − 2^c?». Значащими называются все цифры, кроме нулей в начале числа (которые обычно и не записываются). Например, десятичное число 20 в двоичной системе счисления записывается как 10100, и в этой записи две значащие цифры «1» и три значащие цифры «0».

Помогите Тимофею по известным a, b и c узнать ответ на задачу.

Входные данные

Программа получает на вход четыре целых неотрицательных числа: a, b, c и d, записанные в отдельных строках. Числа a, b и c соответствуют показателям степеней двоек в задании (0 ≤a, b, c, ≤10⁹). При этом гарантируется, что 2^a + 2^b − 2^c > 0 и a ≠ b.

Число d равно либо 0, либо 1 — цифра, количество которых в значении выражения нужно узнать.

Выходные данные

Программа должна вывести одно неотрицательное целое число — ответ на задачу.

Пример

Ввод	Вывод	Пояснение
4 3 2 1	2	Нужно узнать количество единиц в двоичной записи значения выражения 24 + 23 − 22. Вычислим: 16 + 8 - 4 = 20. 2010 = 101002. Всего две единицы. Такой же результат можно получить, выполнив действия в столбик, не переводя числа в десятичную систему счисления (см. ниже).

 10000
+ 1000
 -----
 11000

 11000
-  100
 -----
 10100

Переведите {1}  из десятичной системы счисления в двоичную систему счисления.

 

Примеры

№	Входные данные	Выходные данные
1	1	YES
2	4	YES
3	5	NO

По данному натуральному числу N выведите такое наименьшее целое число k, что \(2^k >= N\).

Входные данные
Программа получает на вход натуральное число N.

Выходные данные
Выведите ответ на задачу.
 
 

Примеры

№	Входные данные	Выходные данные
1	10	4