Дано дерево на n вершинах с корнем в вершине 1.
Скажем, что в вершине u содержится k-ичная куча глубины m, если выполняется следующее:
- При m = 1 вершина u сама является k-ичной кучей глубины 1.
- При m > 1 вершина u является k-ичной кучей глубины m, если хотя бы k из ее детей являются k-ичными кучами глубины не менее m - 1.
Определим dpk(u) как максимальную глубину k-ичной кучи по всем вершинам в поддереве u (включая u). Требуется посчитать значение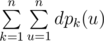 
.
Выходные данные
В единственной строке выведите одно число — ответ на задачу.
Примечание
Рассмотрим первый пример.
Для k ≥ 3 все значения dpk будут равны 1.
При k = 2 dpk равняется 2 при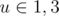 
и 1 в противном случае.
При k = 1 значения dpk равны (3, 1, 2, 1).
Таким образом, сумма равняется 4·1 + 4·1 + 2·2 + 2·1 + 3 + 1 + 2 + 1 = 21.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
4
1 3
2 3
4 3
|
21
|
|
2
|
4
1 2
2 3
3 4
|
22
|