Олимпиадный тренинг

Задача . F. Безумие


Задача

Темы: Деревья Конструктив поиск в глубину и подобное *2500

В университете Павлополиса начинается второй семестр. После отдыха в Вичкополисе Нура вынуждена вернуться в Павлополис и продолжить обучение.

Иногда (или достаточно часто) встречаются преподаватели, которым вы не нравитесь. Вот и у Нуры есть такой. Зовут его Юрий Дмитриевич и он преподает теорию графов. Нура совсем не нравится Юрию Дмитриевичу, поэтому он всегда даёт девушке самые сложные задания. Так случилось и на этот раз.

Преподаватель даёт Нуре дерево из n вершин. Вершины пронумерованы целыми числами от 1 до n. Длины всех ребер этого дерева равны 1. Нура выбирает некоторое множество простых путей, которые попарно не пересекаются по ребрам. При этом каждая вершина должна принадлежать хотя бы одному из выбранных путей.

Для каждого из выбранных путей выполняется следующее:

  1. Выбирается ровно одно ребро (u, v), которое принадлежит пути.
  2. На выбранном ребре (u, v) отмечается точка на некотором выбранном расстоянии x от вершины u и расстоянии 1 - x от вершины v. При этом расстояние x выбирается Нурой произвольно, то есть может быть различным для разных ребер.
  3. Выбирается одна из вершин u или v — именно к выбранной вершине точка начнет свое движение.

Поясним, как происходит движение точки на примере. Пусть путь состоит из двух ребер (v1, v2) и (v2, v3), точка изначально стоит на ребре (v1, v2) и начнет свое движение к вершине v1. Достигнет v1, затем «развернётся», так как был достигнут конец пути, начнет движение к v2, оттуда к v3, там снова «развернётся», переместится к v2 и так далее. При этом скорость движения точек равна 1 ребро в секунду. Например, за 0.5 секунды точка перемещается на длину половины ребра.

В каждую вершину дерева помещается секундомер. Время, которое показывают секундомеры в начальный момент времени, равно 0 секунд. Затем в начальный момент времени все точки одновременно начинают движения с выбранных позиций в выбранные направления по выбранным путям, а секундомеры одновременно запускаются. Когда какая-то из точек достигает вершины v, секундомер в вершине v автоматически обнуляется, то есть начинает считать время с нуля.

Обозначим за resv — максимальное время, которое покажет секундомер в вершине v, если процесс движения точек будет продолжаться бесконечно. Нуру просят выбрать пути и точки на них так, чтобы res1 было минимально возможным. Если вариантов сделать это несколько, необходимо минимизировать res2, затем res3, res4, ..., resn.

Помогите Нуре выполнить задание преподавателя.

Для лучшего понимания условия задачи смотрите пояснение к примерам.

Входные данные

В первой строке строке задано одно целое число n (2 ≤ n ≤ 100) — количество вершин в заданном преподавателем дереве.

В последующих n - 1 строках заданы по два целых числа u и v (1 ≤ u, v ≤ n, u ≠ v) — вершины, связанные очередным ребром дерева.

Гарантируется, что входные данные задают корректное дерево.

Выходные данные

В первой строке выведите одно целое число paths — количество путей, которые вы хотите выбрать.

В последующих paths строках выведите описания путей:

  1. Одно целое число len — количество ребер в текущем пути.
  2. len целых чисел — номера ребер, входящих в текущий путь. Ребра нумеруются от 1 до n - 1 в том порядке, в котором они следуют во входном файле.
  3. Два целых числа u и v — это будет означать, что вы поставили точку на ребро между вершинами u и v (очевидно, что оно должно принадлежать пути) и точка начнет движение по направлению к вершине v. Обратите внимание, что важен порядок, в котором вы выведите эти два числа. Например, если вы выведите «1 2» (без кавычек), то точка начнет движение по направлению к вершине с номером 2; если же вывести «2 1» (без кавычек), то точка начнет движение по направлению к вершине с номером 1.
  4. Одно вещественное число x (0 ≤ x ≤ 1) — расстояние между точкой и вершиной u (той самой, номер которой вы вывели первым в пункте 3).
Система оценки

Система проверки сгенерирует массив res по выходным данным, предоставленным участником. Кроме того, система проверки сгенерирует массив resOptimal по ответу жюри. Ваше решение будет считаться корректным, если для каждого целого i (1 ≤ i ≤ n) .

Примечание

Рассмотрим пример.

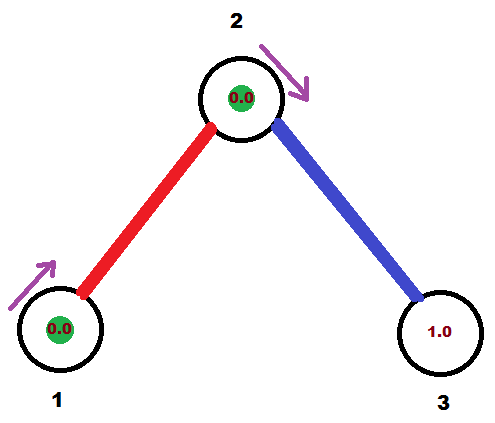
В начальный момент времени точки расположены следующим образом:

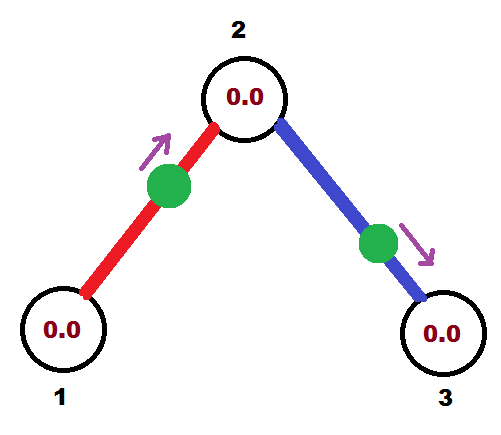
Красным выделен первый путь, синим — второй, зеленые круги обозначают выбранные точки, а коричневые числа внутри вершин — текущее значение секундомера. Фиолетовые стрелочки показывают направление, куда будет двигаться точка.

Через 0.(3) секунд точки будут расположены следующим образом (до обнуления секундомеров):

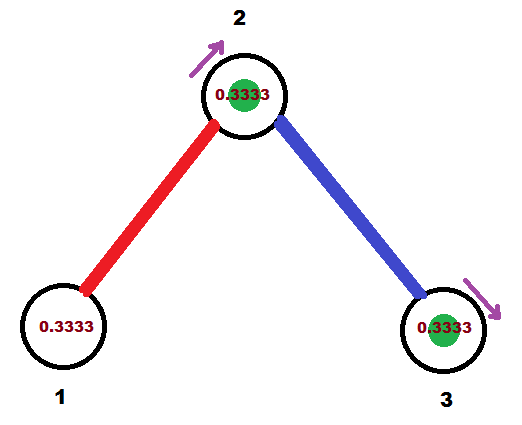
После обнуления секундомеров:

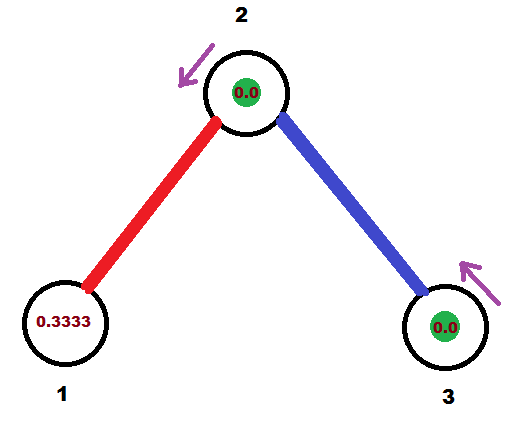
Через 1.0 секунду после начала движения:

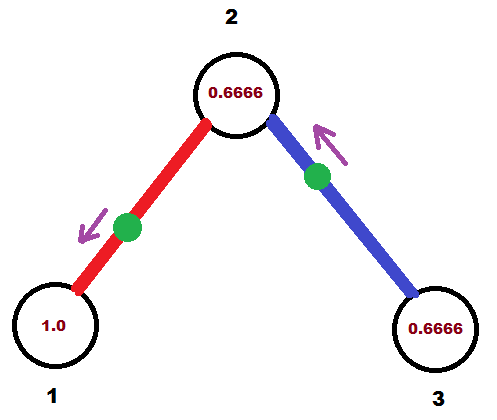
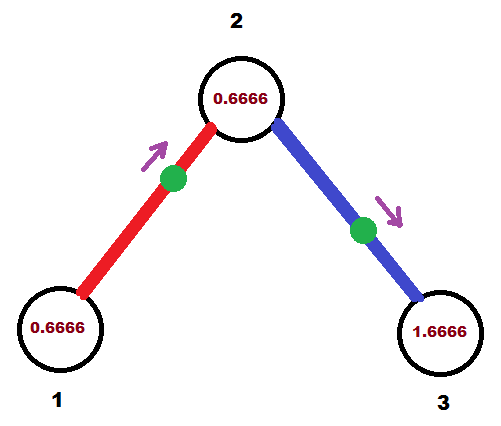
Через 1.(3) секунд после начала движения (после обнуления секундомеров):

Наконец, через 2 секунды после начала движения точки вернутся на исходные позиции:

Такой процесс движения будет продолжаться бесконечно.


Примеры
№Входные данныеВыходные данные
1 3
1 2
2 3 
2
1 1 1 2 0.6666666666
1 2 2 3 0.6666666666

time 2000 ms
memory 256 Mb
Правила оформления программ и список ошибок при автоматической проверке задач

Статистика успешных решений по компиляторам
 Кол-во
С++ Mingw-w644
Комментарий учителя

Ваш ответ

выберите язык и введите исходный код


Для отправки решения задачи необходимо зарегистрироваться или авторизоваться!
     

Загруженные файлы
Нет