Древляндия — это страна в которой n городов, соединенных n - 1 двусторонней дорогой так, что из любого города можно проехать в любой другой по дорогам.
В Древляндии 2k университетов, расположенных в разных городах.
Недавно Президент подписал указ о соединении университетов высокоскоростной сетью. Министерство образования по своему поняло этот указ, решив что для экономии усилий достаточно каждый университет соединить кабелем с некоторым другим. Формально, указ окажется выполнен!
Для того, чтобы в бюджет заложили максимальную сумму в министерстве решили так разбить университеты на пары, что суммарная длина потраченного кабеля будет максимальна. Иными словами, сумма расстояний между университетами в k парах должна быть как можно больше.
Помогите министерству найти искомую максимальную сумму расстояний. Конечно, каждый университет должен попасть ровно в одну пару. Считайте, что все дороги равны по длине между собой и имеют длины равные 1.
Выходные данные
Выведите искомую максимальную сумму расстояний при делении университетов на пары.
Примечание
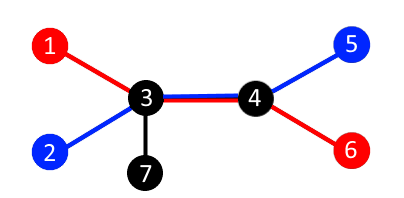
На рисунке ниже представлено одно из возможных оптимальных разбиений на пары для первого тестового примера. Если соединить кабелем университеты номер 1 и 6 (отмечены красным цветом) и университеты номер 2 и 5 (отмечены синим цветом), то суммарное расстояние будет равно 6, что является максимальной суммой для данного примера.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
7 2
1 5 6 2
1 3
3 2
4 5
3 7
4 3
4 6
|
6
|
|
2
|
9 3
3 2 1 6 5 9
8 9
3 2
2 7
3 4
7 6
4 5
2 1
2 8
|
9
|