Drazil и Varda — дождевые черви. Они хотят подыскать хорошее местечко, чтобы растить детей. И вот нашли они подходящую почву с хорошей природной норой. Нора состоит из множества комнат, некоторые пары которых соединены маленькими туннелями, по которым могут перемещаться черви.
Рассмотрим комнаты и туннели как вершины и ребра в графе. Этот граф представляет собой дерево. Иными словами, между любой парой вершин существует единственный простой путь.
Каждая комната, являющаяся листом этого дерева, соединена с поверхностью вертикальным туннелем. Здесь, под листом мы подразумеваем вершину, смежную ровно с одним ребром в дереве.
В каждой комнате хватает места для проживания не более одного червя. Дождевой червь не может жить в туннеле.
Drazil и Varda подумывают воспитывать своих деток по следующему плану. Им хочется, чтобы все их дети сразу после подъема делали утреннюю зарядку!
Когда наступает утро, все червячки просыпаются в одно и то же время, затем каждый из них выбирает самый длинный путь к поверхности на собрание (как и любые дети, они ленятся делать зарядку, поэтому им всем хочется приступить к упражнениям как можно позже).
Drazil и Varda хотят, чтобы разница между моментами появления на поверхности первого и последнего червячка не превышала l (в противном случае детишки расползутся по земле и их будет сложно собрать на зарядку).
Есть дополнительное условие — комнаты, которые занимают детки, должны формировать связное множество. Иными словами, для любых двух комнат, которые занимают червячки, все комнаты, лежащие на пути из одной комнаты в другую, тоже должны быть заняты червячками.
Какое максимальное количество детей может быть у Drazil и Varda, чтобы удовлетворить всем вышеприведенным условиям? Drazil и Varda хотят знать ответ для многих различных вариантов l.
(Drazil и Varda не живут в одной норке со своими детьми)
Примечание
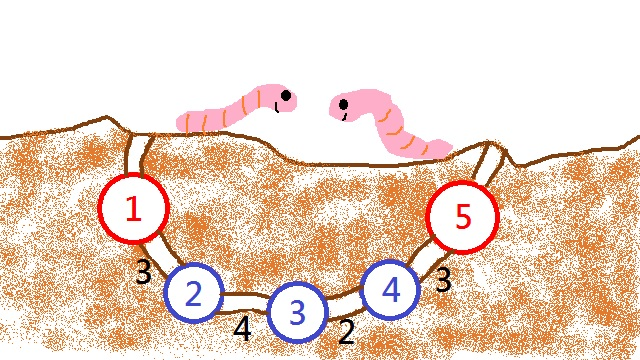
В первом примере нора выглядит следующим образом. Комнаты 1 и 5 представляют из себя листы, так что в них содержится по вертикальному туннелю, связывающему их с поверхностью. Длины наидлиннейшего пути из комнат 1 – 5 наружу равняются 12, 9, 7, 9, 12, соответственно.
При l = 1 мы можем выбрать любую одну комнату.
При l = 2..4 мы можем выбрать в качестве ответа комнаты 2, 3, и 4.
При l = 5 мы можем выбрать все комнаты.