Вам дан связный неориентированный граф, вершины которого пронумерованы целыми числами от \(1\) до \(n\). Ваша задача минимизировать количество пар вершин \(1 \leq u < v \leq n\), между которыми существует путь в этом графе. Для этого вы можете удалить ровно одно любое ребро из графа.
Найдите это наименьшее количество пар вершин!
Выходные данные
Для каждого набора входных данных выведите наименьшее количество пар достижимых друг из друга вершин, если можно удалить ровно одно ребро.
Примечание
В первом наборе входных данных мы удалим единственное ребро \((1, 2)\) и единственная пара вершин \((1, 2)\) станет не достижима друг из друга.
Во втором наборе входных данных какое бы ребро мы не удалили, все вершины будут достижимы друг из друга.
В четвертом наборе входных данных так выглядит граф изначально.
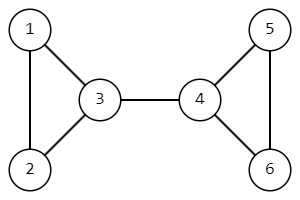
Мы удалим ребро \((3, 4)\) и тогда достижимы друг из друга будут только пары вершин \((1, 2)\), \((1, 3)\), \((2, 3)\), \((4, 5)\), \((4, 6)\), \((5, 6)\).
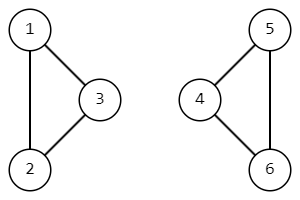
В шестом наборе входных данных так выглядит граф изначально.
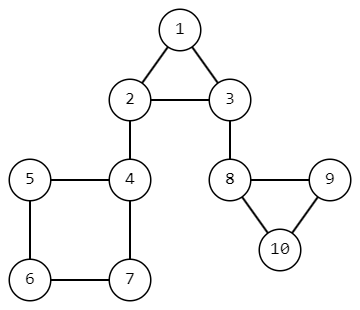
После удаления ребра \((2, 4)\) граф будет выглядеть следующим образом. Таким образом, будет \(21\) пара достижимых друг из друга вершин.
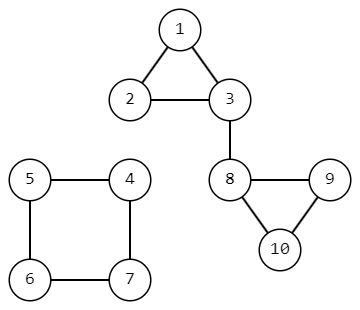
Примеры
| № | Входные данные | Выходные данные |
|
1
|
6
2 1
1 2
3 3
1 2
2 3
1 3
5 5
1 2
1 3
3 4
4 5
5 3
6 7
1 2
1 3
2 3
3 4
4 5
4 6
5 6
5 5
1 2
1 3
2 3
2 4
3 5
10 12
1 2
1 3
2 3
2 4
4 5
5 6
6 7
7 4
3 8
8 9
9 10
10 8
|
0
3
4
6
6
21
|