У вас есть дерево из \(n\) вершин, некоторые вершины которого помечены. Дерево — это связный неориентированный граф без циклов.
Обозначим за \(f_i\) максимальное расстояние от вершины с номером \(i\) до какой-то из помеченных вершин.
Ваша задача — найти минимальное значение \(f_i\) среди всех вершин.
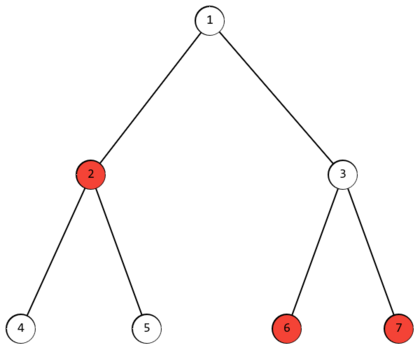
Например, в дереве из примера раскрашены вершины с номерами \(2\), \(6\) и \(7\). Тогда массив \(f(i) = [2, 3, 2, 4, 4, 3, 3]\). \(f_i\) минимальна для вершин с номерами \(1\) и \(3\).
Выходные данные
Для каждого набора входных данных выведите одно целое число — минимальное значение \(f_i\) по всем вершинам.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
6
7 3
2 6 7
1 2
1 3
2 4
2 5
3 6
3 7
4 4
1 2 3 4
1 2
2 3
3 4
5 1
1
1 2
1 3
1 4
1 5
5 2
4 5
1 2
2 3
1 4
4 5
10 8
1 2 3 4 5 8 9 10
2 10
10 5
5 3
3 1
1 7
7 4
4 9
8 9
6 1
10 9
1 2 4 5 6 7 8 9 10
1 3
3 9
9 4
4 10
10 6
6 7
7 2
2 5
5 8
|
2
2
0
1
4
5
|
|
2
|
3
6 1
3
1 2
1 3
3 4
3 5
2 6
5 3
1 2 5
1 2
1 3
2 4
3 5
7 1
2
3 2
2 6
6 1
5 6
7 6
4 5
|
0
2
0
|