Миша был забанен в шахматах за использование компьютера. Он отправился на пенсию и решил стать ксолдуном.
Однажды, гуляя в парке, Миша наткнулся на корневое дерево с вершинами, пронумерованными от \(1\) до \(n\). Корнем дерева является вершина с номером \(1\).
Для всех \(1\le i\le n\) в вершине \(i\) лежат \(a_i\) камней. Миша недавно выучил новое заклинание на уроке ксолдовства и хочет его опробовать. Заклинание состоит из нескольких шагов:
- Выбрать некоторую вершину \(i\) (\(1 \leq i \leq n\)).
- Вычислить побитовое исключающее ИЛИ \(x\) всех \(a_j\) таких, что вершина \(j\) лежит в поддереве вершины \(i\) (\(i\) принадлежит своему поддереву).
- В значения \(a_j\) для всех вершин \(j\) в поддереве \(i\) присвоить \(x\).
Миша может выполнить не более \(2n\) заклинаний и хочет, чтобы в дереве не осталось камней. Более формально, он хочет, чтобы выполнялось \(a_i=0\) для всех \(1\leq i \leq n\). Можете помочь ему выполнить заклинания?
Деревом из \(n\) вершин называется связный ациклический граф из \(n-1\) ребра. Поддеревом вершины \(i\) является множество всех вершин \(j\) таких, что \(i\) лежит на простом пути от \(1\) (корня) к \(j\). В этой задаче \(i\) принадлежит собственному поддереву.
Выходные данные
Если нет подходящей последовательности заклинаний, выведите \(-1\).
Иначе в первой строке выведите одно целое число \(q\) (\(0 \leq q \leq 2n\)) — количество заклинаний в вашем решении.
Во второй строке выведите последовательность целых чисел \(v_1,v_2,\ldots,v_q\) (\(1 \leq v_i \leq n\)): \(i\)-е заклинание будет выполнено к поддереву вершины \(v_i\). Обратите внимание, что здесь важен порядок.
Если существует несколько решений, выведите любое из них. Вам не нужно минимизировать число операций.
Примечание
Рисунок ниже объясняет третий пример. Показаны только первые \(4\) заклинания, так как последние \(2\) ничего не меняют. Первый рисунок показывает начальное дерево, число камней в каждой вершине написано над вершиной зеленым. Изменения от заклинаний показаны красным.
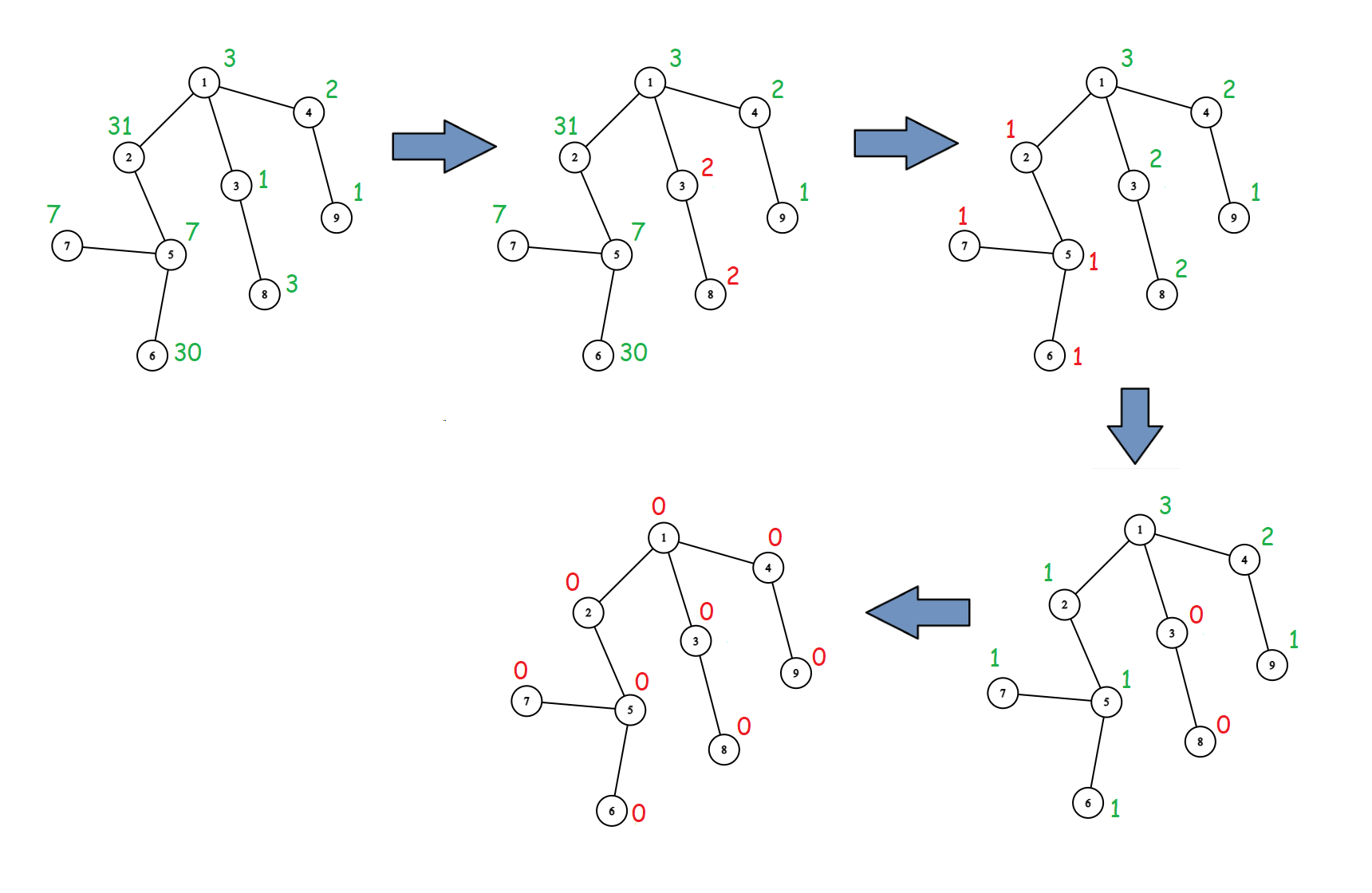
Примеры
| № | Входные данные | Выходные данные |
|
1
|
2
13 13
1
|
1
1
|
|
2
|
7
5 2 8 3 4 1 31
1 1 2 2 3 3
|
-1
|
|
3
|
9
3 31 1 2 7 30 7 3 1
1 1 1 2 5 5 3 4
|
6
3 2 3 1 2 2
|