Вам дан неориентированных, связный граф из \(n\) вершин и \(m\) ребер. Все вершины \(u\) графа удовлетворяют следующему условию:
- Пусть \(S_u\) это множество вершин принадлежащих длиннейшему простому циклу начинающемуся и заканчивающемуся в \(u\).
- Пусть \(C_u\) это объединение множеств вершин всех простых циклов начинающихся и заканчивающихся в \(u\).
- \(S_u = C_u\).
Вы должны ответить на \(q\) запросов.
Для каждого запроса вам будет дана вершина \(a\) и вершина \(b\). Для всех ребер принадлежащих любому простому пути из \(a\) в \(b\), посчитайте число ребер таких, что если вы удалите их, \(a\) и \(b\) останутся достижимы друг из друга.
Выходные данные
Для каждого запроса выведите одно целое число — ответ на запрос.
Примечание
Граф в первом примере:
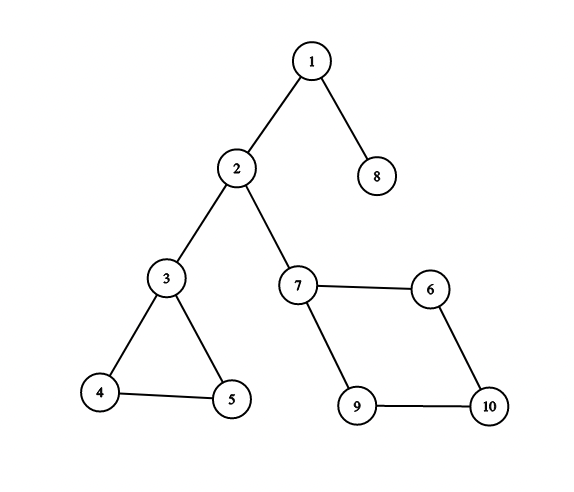
Первый запрос это \((1, 4)\). Тут всего \(5\) ребер принадлежат любому простому пути из \(1\) в \(4\). Ребра \((3, 4), (4, 5), (5, 3)\) будут посчитаны как ответ на запрос.
Четвертый запрос \((2, 8)\). Тут только один простой путь из \(2\) в \(8\), причем ни одно ребро не будет посчитано в ответ.
Пятый запрос \((7, 10)\). Тут всего \(4\) ребра принадлежат любому простому пути из \(7\) в \(10\), все они будут посчитаны в ответе.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
10 11
1 2
2 3
3 4
4 5
5 3
2 7
7 9
9 10
10 6
6 7
1 8
5
1 4
5 10
3 5
2 8
7 10
|
3
7
3
0
4
|
|
2
|
13 15
1 2
2 3
3 4
4 1
2 4
3 5
5 6
6 7
6 8
7 9
9 10
8 7
10 11
10 12
10 13
6
9 11
1 5
1 8
5 2
5 12
12 13
|
0
5
8
5
3
0
|