Олимпиадный тренинг

Задача . G. Префиксы путей

Задача

Темы: Бинарный поиск Деревья поиск в глубину и подобное Структуры данных *1700

Вам задано корневое дерево. Оно содержит $n$ вершин, которые пронумерованы от $1$ до $n$. Корнем является вершина $1$.

У каждого ребра есть две положительных целых стоимости. Таким образом, для каждого ребра заданы два положительных целых числа $a_j$ и $b_j$.

Выведите $n-1$ число $r_2, r_3, \dots, r_n$, где $r_i$ определяется следующим образом.

Рассмотрим путь из корня (вершины $1$) в $i$ ($2 \le i \le n$). Пусть сумма стоимостей $a_j$ вдоль этого пути равна $A_i$. Тогда $r_i$ равно длине максимального такого префикса этого пути, что сумма $b_j$ вдоль этого префикса не превосходит $A_i$.

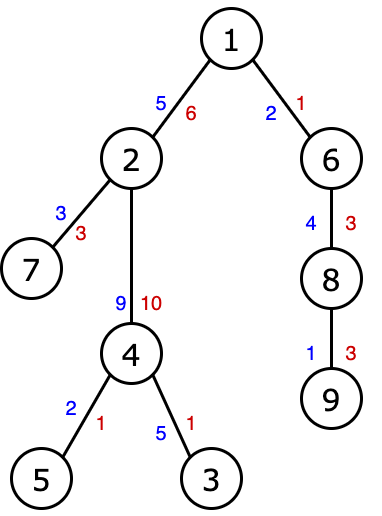$\text{[math]}$ Пример для $n=9$. Синим цветом изображены стоимости $a_j$, а красным изображены стоимости $b_j$.

Рассмотрим пример. В этом случае:

$r_2=0$, так как путь до $2$ имеет сумму по $a_j$ равную $5$, только префикс этого пути длины $0$ имеет меньшую или равную сумму по $b_j$;
$r_3=3$, так как путь до $3$ имеет сумму по $a_j$ равную $5+9+5=19$, префикс длины $3$ этого пути имеет сумму по $b_j$ равную $6+10+1=17$ (число $17 \le 19$);
$r_4=1$, так как путь до $4$ имеет сумму по $a_j$ равную $5+9=14$, префикс длины $1$ этого пути имеет сумму по $b_j$ равную $6$ (это самый длинный подходящий префикс, так как префикс длины $2$ уже имеет сумму по $b_j$ равную $6+10=16$, что больше $14$);
$r_5=2$, так как путь до $5$ имеет сумму по $a_j$ равную $5+9+2=16$, префикс длины $2$ этого пути имеет сумму по $b_j$ равную $6+10=16$ (это самый длинный подходящий префикс, так как префикс длины $3$ уже имеет сумму по $b_j$ равную $6+10+1=17$, что больше $16$);
$r_6=1$, так как путь до $6$ имеет сумму по $a_j$ равную $2$, префикс длины $1$ этого пути имеет сумму по $b_j$ равную $1$;
$r_7=1$, так как путь до $7$ имеет сумму по $a_j$ равную $5+3=8$, префикс длины $1$ этого пути имеет сумму по $b_j$ равную $6$ (это самый длинный подходящий префикс, так как префикс длины $2$ уже имеет сумму по $b_j$ равную $6+3=9$, что больше $8$);
$r_8=2$, так как путь до $8$ имеет сумму по $a_j$ равную $2+4=6$, префикс длины $2$ этого пути имеет сумму по $b_j$ равную $1+3=4$;
$r_9=3$, так как путь до $9$ имеет сумму по $a_j$ равную $2+4+1=7$, префикс длины $3$ этого пути имеет сумму по $b_j$ равную $1+3+3=7$.

Входные данные

В первой строке записано целое число $t$ ($1 \le t \le 10^4$) — количество наборов входных данных в тесте.

Далее следуют описания наборов входных данных.

Каждое описание начинается строкой, которая содержит целое число $n$ ($2 \le n \le 2\cdot10^5$) — количество вершин в дереве.

Далее следует $n-1$ строка, каждая из которых содержит три числа $p_j, a_j, b_j$ ($1 \le p_j \le n$; $1 \le a_j,b_j \le 10^9$) — предок вершины $j$, первая и вторая стоимости ребра, которое ведёт из $p_j$ в $j$. Величина $j$ пробегает все значения от $2$ до $n$ включительно. Гарантируется, что в каждом наборе входных данных задано корректное подвешенное дерево с корнем в вершине $1$.

Гарантируется, что сумма значений $n$ по всем наборам входных данных не превосходит $2\cdot10^5$.

Выходные данные

Для каждого набора входных данных выведите $n-1$ целое число в одной строке: $r_2, r_3, \dots, r_n$.

Примечание

Первый пример разобран в условии.

Во втором примере:

$r_2=0$, так как путь до $2$ имеет сумму по $a_j$ равную $1$, только префикс этого пути длины $0$ имеет меньшую или равную сумму по $b_j$;
$r_3=0$, так как путь до $3$ имеет сумму по $a_j$ равную $1+1=2$, префикс длины $1$ этого пути имеет сумму по $b_j$ равную $100$ ($100 > 2$);
$r_4=3$, так как путь до $4$ имеет сумму по $a_j$ равную $1+1+101=103$, префикс длины $3$ этого пути имеет сумму по $b_j$ равную $102$, .

Примеры

№	Входные данные	Выходные данные
1	4 9 1 5 6 4 5 1 2 9 10 4 2 1 1 2 1 2 3 3 6 4 3 8 1 3 4 1 1 100 2 1 1 3 101 1 4 1 100 1 2 1 1 3 1 101 10 1 1 4 2 3 5 2 5 1 3 4 3 3 1 5 5 3 5 5 2 1 1 3 2 6 2 1	0 3 1 2 1 1 2 3 0 0 3 1 2 2 0 1 2 1 1 2 2 1 1

time 3000 ms
memory 256 Mb
Правила оформления программ и список ошибок при автоматической проверке задач

Статистика успешных решений по компиляторам

	Кол-во
С++ Mingw-w64	5

Комментарий учителя

Ваш ответ

выберите язык и введите исходный код

Для отправки решения задачи необходимо зарегистрироваться или авторизоваться!

Загруженные файлы

Нет