Василий приехал на посвященную криптовалютам конференцию. Для того, чтобы быть в курсе всех самых важных новостей из мира криптовалют, нужно постоянно заводить новые знакомства или пользоваться знакомствами своих друзей.
В конференции участвует \(n\) человек, которые изначально не знакомы между собой. Василий может познакомить двух любых людей \(a\) и \(b\), которые не были знакомы до этого.
У Василия есть \(d\) условий, \(i\)-е из которых требует, чтобы человек \(x_i\) имел связь с человеком \(y_i\). Формально два человека \(x\) и \(y\) имеют связь, если найдется цепочка \(p_1=x, p_2, p_3, \dots, p_k=y\) такая, что для всех \(i\) от \(1\) до \(k - 1\) известно, что люди под номерами \(p_i\) и \(p_{i + 1}\) знакомы.
Василий хочет, чтобы для каждого \(i\) (\(1 \le i \le d\)) вы рассчитали, какое максимальное количество знакомств может иметь один человек при условии, что Василий выполнил все условия от \(1\) до \(i\) включительно, произведя при этом ровно \(i\) знакомств. Проверка условий происходит после того, как Василий провел \(i\) знакомств. Ответ для каждого \(i\) необходимо найти независимо. То есть, когда вы вычисляете ответ для \(i\), вы должны считать, что никто из людей еще не был знаком.
Выходные данные
Выведите \(d\) целых чисел. \(i\)-е число должно быть равно количеству знакомств у человека с наибольшим возможным количеством знакомств, если Василий провел \(i\) знакомств и выполнил первые \(i\) условий.
Примечание
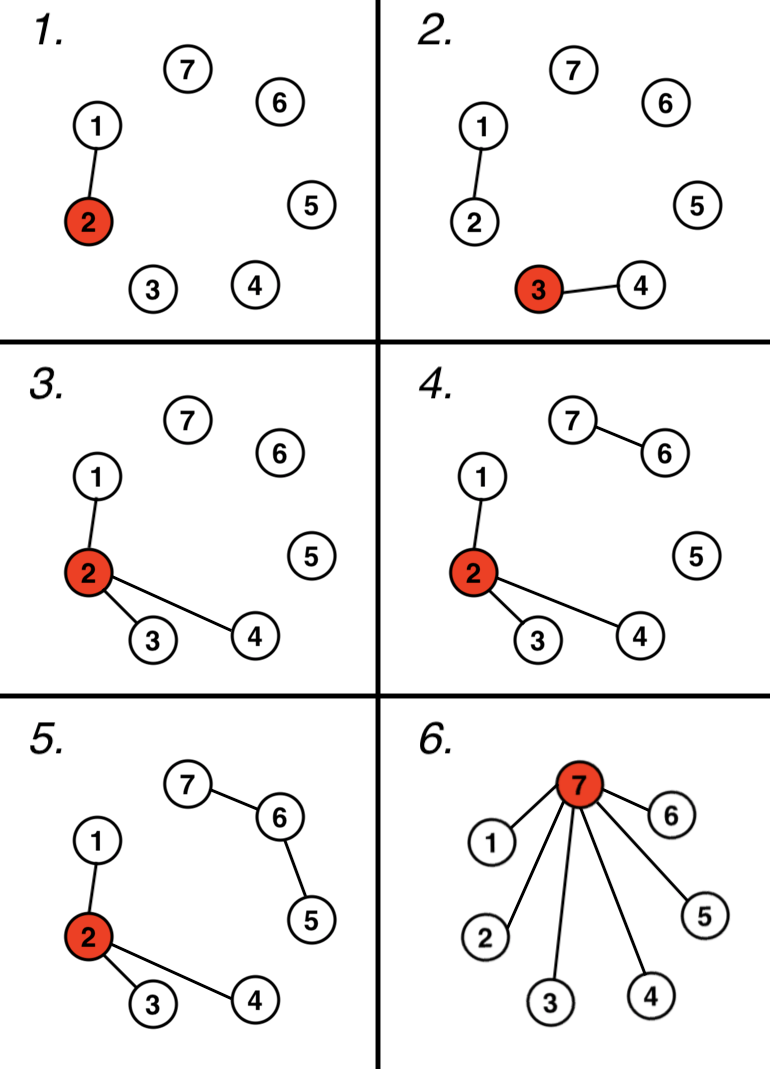
Пояснение для первого тестового примера:
В этом пояснении круг и вписанное число обозначают человека с соответствующим номером. Линии, соединяющие людей, обозначают то, что эти люди знакомы между собой. Человек, отмеченный красным цветом, имеет наибольшее количество знакомых. Данные способы познакомить людей не являются единственными правильными.