Задано целое число \(k\) и неориентированное дерево, состоящее из \(n\) вершин.
Длина простого пути (пути, в котором каждая вершина встречается не более одного раза) между некоторой парой вершин равна количеству ребер в данном пути. Диаметр дерева равен максимальной длине пути между всеми парами вершин в дереве.
Вы планируете удалить множество ребер из дерева. Когда ребра удаляются, дерево распадается на несколько меньших деревьев. Множество ребер считается корректным, если у всех полученных деревьев диаметр меньше либо равен \(k\).
Два множества ребер считаются различными, если существует такое ребро, что оно встречается только в одном из множеств.
Посчитайте количество корректных множеств ребер по модулю \(998\,244\,353\).
Выходные данные
Выведите одно целое число — количество корректных множеств ребер по модулю \(998\,244\,353\).
Примечание
В первом примере диаметр заданного дерева уже меньше либо равен \(k\). Поэтому можно выбрать любое множество ребер, и в полученных деревьях диаметры будут меньше либо равны \(k\). Всего есть \(2^3\) множеств, включая пустое.
Во втором примере нужно удалить единственное ребро. Иначе диаметр будет \(1\), что больше \(0\).
Деревья для третьего и четвертого примеров:
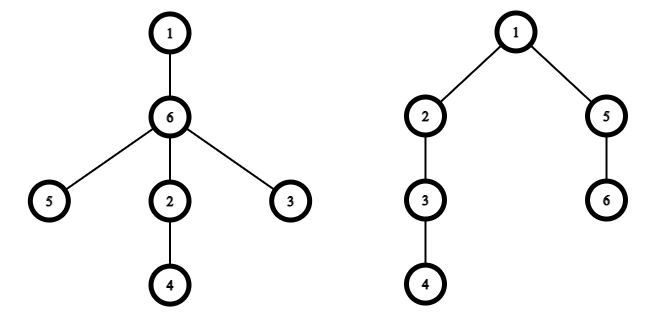
Примеры
| № | Входные данные | Выходные данные |
|
1
|
4 3
1 2
1 3
1 4
|
8
|
|
2
|
2 0
1 2
|
1
|
|
3
|
6 2
1 6
2 4
2 6
3 6
5 6
|
25
|
|
4
|
6 3
1 2
1 5
2 3
3 4
5 6
|
29
|