Вам дано \(n - 1\) целое число \(a_2, \dots, a_n\) и корневое дерево с \(n\) вершинами, подвешенное в вершине \(1\). Все листья находятся на одинаковом расстоянии \(d\) от корня.
Деревом называется связный неориентированный граф без циклов. Расстоянием между парой вершин называется количество ребер на простом пути между ними. Все некорневые вершины, имеющие степень \(1\), называются листьями. Если вершины \(s\) и \(f\) соединены ребром, и \(f\) находится на расстоянии от корня большем, чем \(s\), то \(f\) называется сыном \(s\).
Изначально в вершине \(1\) находятся красная и синяя фишки. Давайте обозначим за \(r\) вершину, в которой находится красная фишка, и за \(b\) вершину, в которой находится синяя фишка. Вы должны сделать \(d\) ходов. Ход состоит из трех шагов:
- Переместить красную фишку в любого сына \(r\).
- Переместить синюю фишку в любую вершину \(b'\) такую, что \(dist(1, b') = dist(1, b) + 1\). Здесь \(dist(x, y)\) обозначает длину кратчайшего пути между \(x\) и \(y\). Обратите внимание, что \(b\) и \(b'\) не обязательно соединены ребром.
- Вы можете, если хотите, поменять две фишки местами (или пропустить этот шаг).
Обратите внимание, что \(r\) и \(b\) могут быть равны в любой момент времени, а в корне дерева не записано никакое число.
После каждого хода вы получаете \(|a_r - a_b|\) очков. Какое максимальное количество очков вы можете получить после \(d\) ходов?
Выходные данные
Для каждого набора входных данных выведите единственное целое число: максимальное количество очков, которое вы можете получить после \(d\) ходов.
Примечание
В первом наборе входных данных оптимальное решение — это:
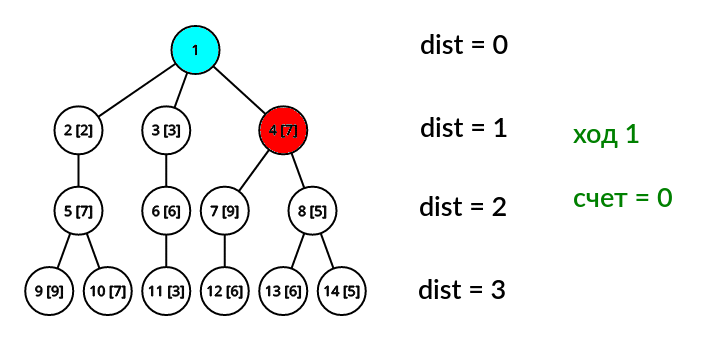
- ход \(1\): \(r = 4\), \(b = 2\); нет замены;
- ход \(2\): \(r = 7\), \(b = 6\); замена (после нее \(r = 6\), \(b = 7\));
- ход \(3\): \(r = 11\), \(b = 9\); нет замен.
Общее количество очков равно \(|7 - 2| + |6 - 9| + |3 - 9| = 14\).
Во втором наборе входных данных оптимальное решение — это:
- ход \(1\): \(r = 2\), \(b = 2\); нет замены;
- ход \(2\): \(r = 3\), \(b = 4\); нет замены;
- ход \(3\): \(r = 5\), \(b = 6\); нет замены.
Общее количество очков равно \(|32 - 32| + |78 - 69| + |5 - 41| = 45\).
Примеры
| № | Входные данные | Выходные данные |
|
1
|
4
14
1 1 1 2 3 4 4 5 5 6 7 8 8
2 3 7 7 6 9 5 9 7 3 6 6 5
6
1 2 2 3 4
32 78 69 5 41
15
1 15 1 10 4 9 11 2 4 1 8 6 10 11
62 13 12 43 39 65 42 86 25 38 19 19 43 62
15
11 2 7 6 9 8 10 1 1 1 5 3 15 2
50 19 30 35 9 45 13 24 8 44 16 26 10 40
|
14
45
163
123
|