Ли потратил так много времени на создание хорошей div.2 D задачи, чтобы сбалансировать недавний контест, но задача продолжает ощущаться неподходящей. Ли придумывал ее так мучительно долго, что заработал фобию div.2 D задач. И теперь он прячется в кустах...
Назовем Корневым Сухим Кустом (КСК) уровня \(n\) корневое дерево, построенное согласно правилам ниже.
Корневой Сухой Куст уровня \(1\) — это одна вершина. Для построения КСК уровня \(i\), сначала построим КСК уровня \(i-1\) и далее для каждой вершины \(u\):
- если у \(u\) нет детей, то подвесим к ней одного сына;
- если у \(u\) есть один сын, то подвесим к ней еще двух детей;
- если у \(u\) есть более одного сына, то пропустим ее.
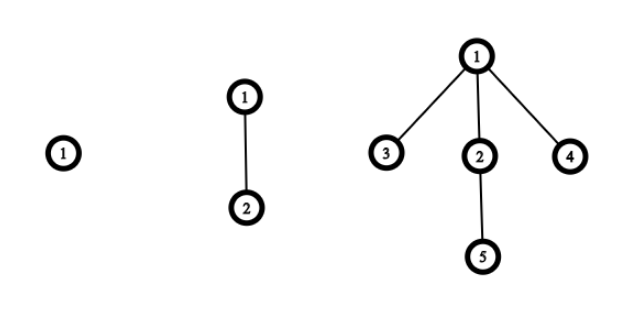Корневые Сухие Кусты уровня \(1\), \(2\) и \(3\). Назовем лапой корневое дерево из четырех вершин: одна корневая вершина (также называется центром) и три ребенка. Оно напоминает лапу:
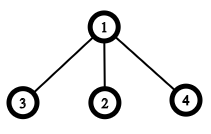Центром лапы является вершина с номером \(1\). У Ли есть Корневой Сухой Куст уровня \(n\). Первоначально все вершины КСК зеленого цвета.
За один шаг, он может выбрать лапу в КСК и, если все вершины в ней зеленые и все вершины лапы являются детьми ее центра, покрасить вершины лапы в в желтый.
Ли хочет узнать максимальное количество желтых вершин, которое он сможет получить. Так как ответ может быть очень большим, выведите его по модулю \(10^9+7\).
Выходные данные
Для каждого набора входных данных выведите единственное целое число — максимальное количество желтых вершин, которые может получить Ли, по модулю \(10^9 + 7\).
Примечание
Несложно заметить, что ответ для КСК уровня \(1\) или \(2\) равен \(0\).
Ответ для КСК уровня \(3\) равен \(4\), так как есть только одна лапа, которую можно выбрать: \(\{1, 2, 3, 4\}\).
Ответ для КСК уровня \(4\) равен \(4\), так как мы можем выбрать либо одну лапу \(\{1, 3, 2, 4\}\) или одну лапу \(\{2, 7, 5, 6\}\). Других лап в КСК уровня \(4\) нет (например, мы не можем выбрать \(\{2, 1, 7, 6\}\), так как \(1\) не является ребенком вершины-центра \(2\)).
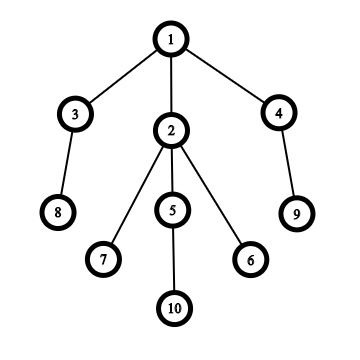Корневой Сухой Куст уровня 4.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
7
1
2
3
4
5
100
2000000
|
0
0
4
4
12
990998587
804665184
|