Олимпиадный тренинг

Задача . E. Запросы на дереве

Задача

Темы: графы Деревья поиск в глубину и подобное *1900

Вам дано корневое дерево, состоящее из $n$ вершин, пронумерованных от $1$ до $n$. Корень дерева находится в вершине с номером $1$.

Дерево — это связный неориентированный граф с $n-1$ ребром.

Вам заданы $m$ запросов. $i$-й запрос состоит из множества $k_i$ различных вершин $v_i[1], v_i[2], \dots, v_i[k_i]$. Ваша задача — определить, существует ли путь от корня до некоторой вершины $u$ такой, что каждая из заданных $k$ вершин или принадлежит этому пути, или расположена на расстоянии $1$ от некоторой вершины на этом пути.

Входные данные

Первая строка теста содержит два целых числа $n$ и $m$ ($2 \le n \le 2 \cdot 10^5$, $1 \le m \le 2 \cdot 10^5$) — количество вершин в дереве и количество запросов.

Каждая из следующих $n-1$ строк описывает ребро дерева. Ребро $i$ задается двумя целыми числами $u_i$ и $v_i$ — номерами вершин, которые это ребро соединяет $(1 \le u_i, v_i \le n, u_i \ne v_i$).

Гарантируется, что заданные ребра формируют дерево.

Следующие $m$ строк описывают запросы. $i$-я строка описывает $i$-й запрос и начинается с целого числа $k_i$ ($1 \le k_i \le n$) — количества вершин в текущем запросе. Затем следуют $k_i$ целых чисел: $v_i[1], v_i[2], \dots, v_i[k_i]$ ($1 \le v_i[j] \le n$), где $v_i[j]$ — это $j$-я вершина в $i$-м запросе.

Гарантируется, что все вершины в одном запросе различны.

Также гарантируется, что сумма всех $k_i$ не превосходит $2 \cdot 10^5$ ($\sum\limits_{i=1}^{m} k_i \le 2 \cdot 10^5$).

Выходные данные

Для каждого запроса выведите ответ — «YES», если существует путь от корня до некоторой вершины $u$ такой, что каждая из $k$ заданных вершин или принадлежит этому пути, или расположена на расстоянии $1$ от какой-либо вершины на этом пути, и «NO» в противном случае.

Примечание

Изображение, относящееся к примеру:

$\text{[math]}$

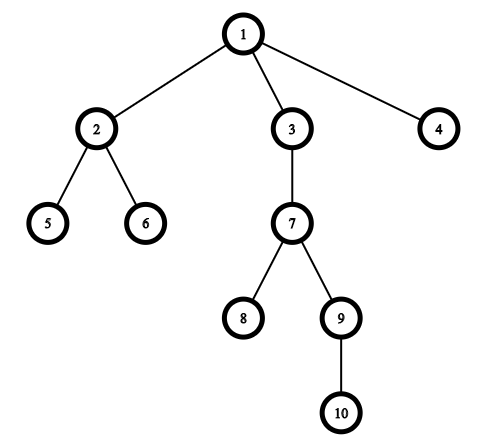
Рассмотрим запросы.

Первый запрос — $[3, 8, 9, 10]$. Ответ — «YES», так как вы можете выбрать путь от корня $1$ до вершины $u=10$. Тогда вершины $[3, 9, 10]$ принадлежат пути от $1$ до $10$ и вершина $8$ расположена на расстоянии $1$ от вершины $7$, которая также принадлежит этому пути.

Второй запрос — $[2, 4, 6]$. Ответ — «YES», так как вы можете выбрать путь до вершины $u=2$. Тогда вершина $4$ находится на расстоянии $1$ от вершины $1$, которая принадлежит этому пути, а вершина $6$ находится на расстоянии $1$ от вершины $2$, которая принадлежит этому пути.

Третий запрос — $[2, 1, 5]$. Ответ — «YES», так как вы можете выбрать путь до вершины $u=5$ и все вершины из запроса будут принадлежать этому пути.

Четвертый запрос — $[4, 8, 2]$. Ответ — «YES», так как вы можете выбрать путь до вершины $u=9$, и вершины $2$ и $4$ расположены на расстоянии $1$ от вершины $1$, которая принадлежит этому пути, а вершина $8$ расположена на расстоянии $1$ от вершины $7$, которая принадлежит этому пути.

Ответ и на пятый, и на шестой запросы — «NO», потому что вы не можете выбрать подходящую вершину $u$.

Примеры

№	Входные данные	Выходные данные
1	10 6 1 2 1 3 1 4 2 5 2 6 3 7 7 8 7 9 9 10 4 3 8 9 10 3 2 4 6 3 2 1 5 3 4 8 2 2 6 10 3 5 4 7	YES YES YES YES NO NO

time 2000 ms
memory 256 Mb
Правила оформления программ и список ошибок при автоматической проверке задач

Статистика успешных решений по компиляторам

	Кол-во
С++ Mingw-w64	5

Комментарий учителя

Ваш ответ

выберите язык и введите исходный код

Для отправки решения задачи необходимо зарегистрироваться или авторизоваться!

Загруженные файлы

Нет