Вам дано дерево, состоящее из \(n\) вершин. Вы хотите написать какие-то числа на ребрах дерева, чтобы выполнялись следующие условия:
- Каждое написанное число является целым числом от \(0\) до \(n-2\) включительно.
- Все написанные числа различны.
- Наибольшее значение среди \(MEX(u,v)\) среди всех пар вершин \((u,v)\) минимально возможно.
Здесь \(MEX(u,v)\) обозначает наименьшее неотрицательное целое число, которое не записано ни на одном ребре уникального простого пути между вершинами \(u\) и \(v\).
Выходные данные
Выведите \(n-1\) целых чисел. \(i\)-е из них должно быть равно числу, записанным на \(i\)-м ребре (в порядке ввода).
Примечание
Дерево с второго примера:
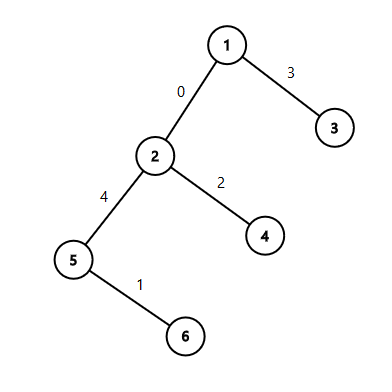
Примеры
| № | Входные данные | Выходные данные |
|
1
|
3
1 2
1 3
|
0
1
|
|
2
|
6
1 2
1 3
2 4
2 5
5 6
|
0
3
2
4
1
|