Олимпиадный тренинг

Задача . E. Построить бинарное дерево

Задача

Вам даны два целых числа $n$ и $d$. Нужно построить корневое бинарное дерево из $n$ вершин с корнем в вершине $1$ с суммой глубин всех вершин равной $d$.

Дерево — это связный граф без циклов. Корневое дерево имеет специальную вершину — корень. Родитель вершины $v$ — это последняя отличная от $v$ вершина на пути от корня к вершине $v$. Глубина вершины $v$ — это длина пути от корня к вершине $v$. Дети вершины $v$ — все вершины, для которых $v$ является родителем. Бинарное дерево — это такое дерево, в котором ни одна вершина не имеет более $2$ детей.

Вам нужно ответить на $t$ независимых наборов входных данных.

Входные данные

Первая строка теста содержит одно целое число $t$ ($1 \le t \le 1000$) — количество наборов входных данных.

Единственная строка каждого набора содержит два целых числа $n$ и $d$ ($2 \le n, d \le 5000$) — количество вершин в дереве и требуемую сумму глубин всех вершин.

Гарантируется, что сумма всех $n$ и сумма всех $d$ не превышают $5000$ ($\sum n \le 5000, \sum d \le 5000$).

Выходные данные

Для каждого набора входных данных выведите ответ на него.

Если невозможно построить такое дерево, выведите «NO» (без кавычек) первой строкой. Иначе выведите «{YES}» первой строкой. Затем выведите $n-1$ целое число $p_2, p_3, \dots, p_n$ второй строкой, где $p_i$ — родитель вершины $i$. Обратите внимание: последовательность родителей, которую вы выведете, должна описывать некоторое бинарной дерево.

Примечание

Изображения, соответствующие первому и второму наборам входных данных из примера:

$\text{[math]}$

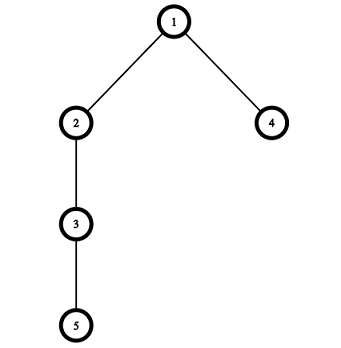
Примеры

№	Входные данные	Выходные данные
1	3 5 7 10 19 10 18	YES 1 2 1 3 YES 1 2 3 3 9 9 2 1 6 NO

time 2000 ms
memory 256 Mb
Правила оформления программ и список ошибок при автоматической проверке задач

Статистика успешных решений по компиляторам

Комментарий учителя

Ваш ответ

выберите язык и введите исходный код

Для отправки решения задачи необходимо зарегистрироваться или авторизоваться!

Загруженные файлы

Нет