Ги-Мануэль и Тома планируют \(144\) кругосветных путешествия.
Вам дан простой взвешенный неориентированный связный граф из \(n\) вершин и \(m\) рёбер со следующим ограничением: не существует простого цикла (т. е. цикла, проходящего через каждую вершину не больше раза) длины больше \(3\), проходящего через вершину \(1\). Стоимостью пути (необязательно простого) в этом графе является XOR весов всех рёбер, входящих в этот путь, причём каждое ребро считается столько, сколько раз через него проходит путь.
Однако, путешествия стоимостью \(0\) их не устраивают.
Вы можете выбрать любое подмножество рёбер, инцидентных вершине \(1\), и удалить их. Сколько существует таких множеств, что при их удалении в полученном графе нет нетривиального цикла (необязательно простого) стоимостью \(0\), проходящего через вершину \(1\)? Цикл называется нетривиальным, если существует ребро, через которое он проходит нечётное количество раз. Так как ответ может быть большим, выведите его по модулю \(10^9+7\).
Выходные данные
В единственной строке выведите ответ по модулю \(10^9+7\).
Примечание
На рисунках представлены графы из примеров.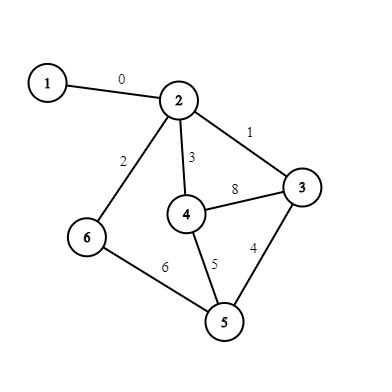 
В первом примере в графе нет нетривиальных циклов со стоимостью \(0\), так что мы можем как удалить единственное ребро, инцидентное вершине \(1\), так и не удалять. 
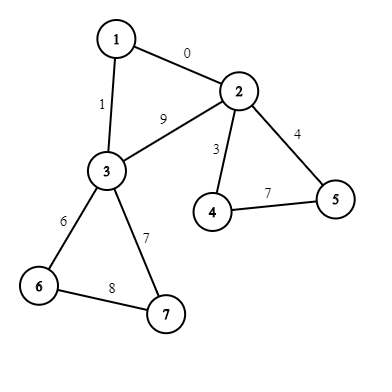Во втором примере если мы не удаляем ребро \(1-2\), то в графе будет цикл \(1-2-4-5-2-1\) со стоимостью \(0\); аналогично, если мы не удаляем ребро \(1-3\), то в графе будет цикл \(1-3-2-4-5-2-3-1\) со стоимостью \(0\). Единственный вариант — удалить оба ребра. 
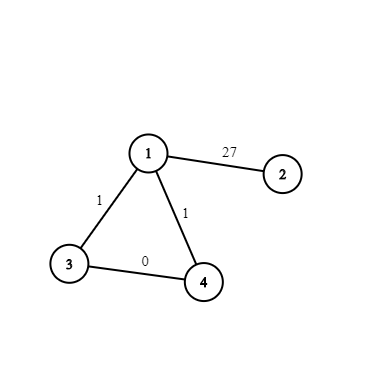В третьем примере подходят все подмножества, кроме тех двух, при которых остаются оба ребра \(1-3\) и \(1-4\).
Примеры
| № | Входные данные | Выходные данные |
|
1
|
6 8
1 2 0
2 3 1
2 4 3
2 6 2
3 4 8
3 5 4
5 4 5
5 6 6
|
2
|
|
2
|
7 9
1 2 0
1 3 1
2 3 9
2 4 3
2 5 4
4 5 7
3 6 6
3 7 7
6 7 8
|
1
|
|
3
|
4 4
1 2 27
1 3 1
1 4 1
3 4 0
|
6
|