Древляндия состоит из \(n\) городов и \(n-1\) двусторонних дорог, соединяющих некоторые пары городов. Из любого города можно добраться до любого другого города. Вы правы — система городов и дорог в Древляндии образует неориентированное дерево.
Правительство объявило тендер на модернизацию инфраструктуры городов, при этом допустимо модернизировать произвольное подмножество \(S\) городов (возможно, все города), которое удовлетворяет следующим требованиям:
- подмножество городов должно быть «связным», то есть из любого города подмножества \(S\) можно доехать до любого другого города подмножества \(S\) по дорогам, перемещаясь только по городам из \(S\);
- количество «тупиковых» городов в \(S\) должно быть равно заданному числу \(k\). Город является тупиковым, если он является единственным городом в \(S\), либо связан ровно с одним другим городом из \(S\).
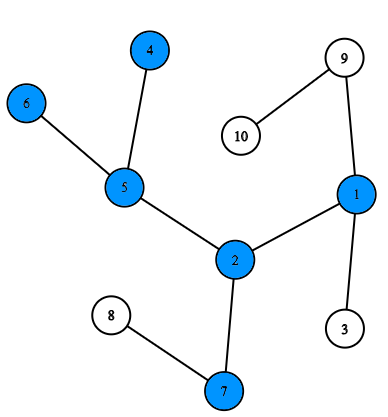Здесь изображён один из возможных способов выбрать \(S\) (синие вершины) для заданной конфигурации и \(k=4\). Тупиковыми вершинами являются вершины с номерами \(1\), \(4\), \(6\) и \(7\). Помогите Древляндии с модернизацией — найдите любое из возможных подмножеств \(S\) или определите, что такого подмножества не существует.
Выходные данные
Для каждого набора входных данных выведите Yes или No (в любом регистре), в зависимости от того, существует ответ или нет. Если ответ существует, то далее выведите \(m\) (\(1 \le m \le n\)) — количество городов в найденном подмножестве. Затем выведите \(m\) различных чисел от \(1\) до \(n\) — номера городов, которые составляют найденное подмножество. Номера городов можно выводить в любом порядке. Если решений несколько, то выведите любое из них.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
4
10 4
4 5
5 2
2 1
1 3
1 9
9 10
2 7
7 8
5 6
4 3
1 2
2 3
3 4
5 3
1 2
1 3
1 4
1 5
4 1
1 2
2 4
2 3
|
Yes
9
1 2 4 5 6 7 8 9 10
No
Yes
4
1 3 4 5
Yes
1
4
|