Новая пешеходная зона в центре Москвы состоит из \(n\) площадей, соединённых друг с другом с помощью \(n - 1\) пешеходных дорожек. Простым путём называется такая последовательность площадей, что никакая площадь не встречается в последовательности дважды, и любые две соседние в последовательности площади напрямую соединены пешеходной дорожкой. Размером простого пути будем называть количество площадей в образующей его последовательности. Дорожки спроектированы таким образом, что между любой парой различных площадей существует ровно один простой путь.
В рамках подготовки к празднованию дня города московская мэрия планирует обновить плитку на всех \(n\) площадях. Всего существует \(k\) видов плитки разных цветов, пронумерованных от \(1\) до \(k\). Для каждой площади нужно выбрать ровно один вид плитки, который будет там уложен в процессе обновления. Чтобы сделать прогулки по центру Москвы более увлекательными, было решено назначить типы плиток площадям таким образом, чтобы для любого возможного простого пути размера ровно \(k\), при прогулке вдоль этого пути встречались бы все \(k\) различных типов плитки.
Определите, можно ли уложить плитку подходящим образом или нет.
Выходные данные
Выведите «Yes», если уложить плитку возможно, и «No» иначе.
В случае если ваш ответ «Yes», выведите \(n\) целых чисел от \(1\) до \(k\) — цвет плитки для каждой площади.
Примечание
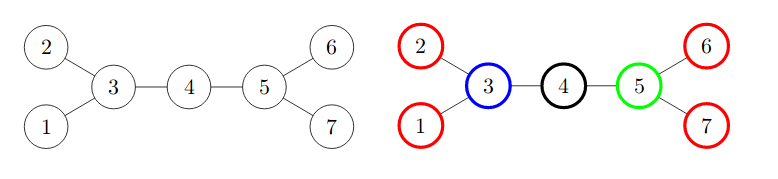
Ниже изображена карта пешеходной зоны из первого и второго примеров, а также корректный выбор типов плитки для \(k = 4\).
Примеры
| № | Входные данные | Выходные данные |
|
1
|
7 4
1 3
2 3
3 4
4 5
5 6
5 7
|
Yes
1 1 2 3 4 1 1
|
|
2
|
7 3
1 3
2 3
3 4
4 5
5 6
5 7
|
No
|