Олимпиадный тренинг

Задача . B. Динамический диаметр

Задача

Темы: *особая задача Деревья поиск в глубину и подобное разделяй и властвуй Структуры данных

Вам дано взвешенное неориентированное дерево с $n$ вершинами, а также список из $q$ обновлений. Каждое обновление меняет вес одного ребра. Ваша задача — вычислить диаметр дерева после каждого обновления.

(Расстоянием между двумя вершинами называется сумма весов ребер на единственном простом пути между этими двумя вершинами. Диаметр дерева — наибольшее из этих расстояний.)

Входные данные

Первая строка содержит три разделенных пробелом целых числа $n$, $q$ и $w$ ($2 \leq n \leq 100,000, 1 \leq q \leq 100,000$, $1 \leq w \leq 20,000,000,000,000$) – число вершин в дереве, число обновлений и ограничение на вес ребер. Вершины пронумерованы от $1$ до $n$.

Следующие $n-1$ строк описывают изначальное дерево. $i$-я из этих строк содержит три целых числа $a_i$, $b_i$, $c_i$ ($1 \leq a_i, b_i \leq n$, $0 \leq c_i < w$), обозначающих, что изначально есть ребро между вершинами $a_i$ и $b_i$ с весом $c_i$. Гарантируется, что эти $n-1$ строк описывают дерево.

Последние $q$ строк описывают обновления. $j$-я из этих строк содержт два целых числа $d_j$, $e_j$ ($0 \leq d_j < n - 1, 0 \leq e_j < w$). Эти два числа вы должны изменить следующим образом:

$d'_j = (d_j + last) \bmod (n - 1)$,
$e'_j = (e_j + last) \bmod w$,

где $last$ — диаметр дерева после предыдущего обновления (изначально $last=0$). Пара $(d'_j, e'_j)$ обозначает, что в данном обновлении вес $d'_j+1$-го ребра становится равным $e'_j$.

Выходные данные

Выведите $q$ строк. Для всех возможных $i$ строка $i$ должна содержать диаметр дерева после $i$-го обновления.

Система оценки

Подзадача 1 (11 баллов): $n,q \leq 100$ и $w \leq 10,000$

Подзадача 2 (13 баллов): $n,q \leq 5,000$ и $w \leq 10,000$

Подзадача 3 (7 баллов): $w \leq 10,000$, и все ребра дерева имеют вид $\{1, i\}$ (То есть граф имеет вид «звезды» с центром в вершине 1.)

Подзадача 4 (18 баллов): $w \leq 10,000$, и все ребра дерева имеют вид $\{i, 2i\}$ и $\{i, 2i+1\}$ (То есть если мы подвесим дерево за вершину 1, то оно будет иметь вид сбалансированного бинарного дерева.)

Подзадача 5 (24 балла): гарантируется, что после каждого обновления по крайней мере один из наидлиннейших простых путей проходит через вершину $1$

Подзадача 6 (27 баллов): нет дополнительных ограничений

Примечание

Первый пример показан на рисунке ниже. Рисунок слева показывает изначальное дерево. Каждый следующий рисунок показывает ситуацию после очередного обновления. Вес обновленного ребра показан зеленым, а диаметр — красным.

$\text{[math]}$

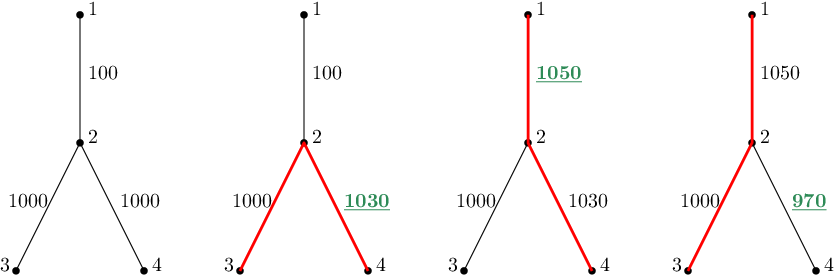
Первое обновление меняет вес $3$-го ребра, т.е. $\{2, 4\}$, на $1030$. Наибольшее расстояние между какой-либо парой вершин равно $2030$ — расстояние между $3$ и $4$.

Так как ответ равен $2030$, то для второго обновления d'_2 = (1 + 2030) \bmod 3 = 0 e'_2 = (1020 + 2030) \bmod 2000 = 1050 Поэтому вес ребра $\{1, 2\}$ меняется на $1050$. Теперь наибольшее расстояние между вершинами $\{1, 4\}$, оно равно $2080$.

Для третьего обновления имеем d'_3 = (1 + 2080) \bmod 3 = 2 e'_3 = (890 + 2080) \bmod 2000 = 970 Теперь, так как вес ребра $\{2, 4\}$ уменьшается до $970$, наиболее удаленная пара вершин, внезапно, $\{1, 3\}$, а расстояние — $2050$.

Примеры

№	Входные данные	Выходные данные
1	4 3 2000 1 2 100 2 3 1000 2 4 1000 2 1030 1 1020 1 890	2030 2080 2050
2	10 10 10000 1 9 1241 5 6 1630 10 5 1630 2 6 853 10 1 511 5 3 760 8 3 1076 4 10 1483 7 10 40 8 2051 5 6294 5 4168 7 1861 0 5244 6 5156 3 3001 8 5267 5 3102 8 3623	6164 7812 8385 6737 6738 7205 6641 7062 6581 5155

time 6000 ms
memory 1024 Mb
Правила оформления программ и список ошибок при автоматической проверке задач

Статистика успешных решений по компиляторам

Комментарий учителя

Ваш ответ

выберите язык и введите исходный код

Для отправки решения задачи необходимо зарегистрироваться или авторизоваться!

Загруженные файлы

Нет