Обратите внимание, что это вторая задача из двух похожих задач. Вы можете взламывать эту задачу тогда, когда решите ее. Но предыдущую только тогда, когда решите обе задачи.
Вам дано дерево с \(n\) вершинами. Изначально на каждом ребре написан \(0\). За одну операцию вы можете выбрать любые \(2\) различных листа \(u\), \(v\) и любое целое число \(x\), и прибавить \(x\) ко всем числам записанных на ребрах на простом пути с \(u\) до \(v\). Обратите внимание, что в предыдущей подзадаче \(x\) могло быть любым действительным, теперь оно должно быть целым.
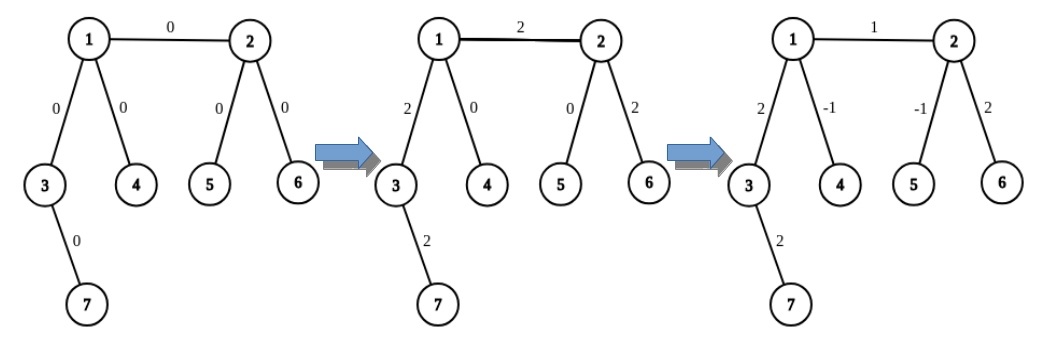
Для примера на изображении ниже показан результат применения двух операций к графу: прибавления \(2\) на пути от \(7\) до \(6\), а потом прибавления \(-1\) на пути от \(4\) до \(5\).
Вам дана некоторая конфигурация из неотрицательных целых, попарно различных, четных чисел, записанных на ребрах. Для заданной конфигурации необходимо сказать, можно ли получить ее с помощью данных операций, и, если это возможно, вывести последовательность операций, которая приводит к заданной конфигурации. Ограничения на операции смотрите в формате вывода.
Лист это вершина степени \(1\). Простой путь это путь, не содержащий ни одну вершину дважды.
Выходные данные
Если требуемой последовательности операций не существует, в первой строке выведите «NO».
Если же она существует, в первой строке выведите «YES». Во второй строке выведите \(m\) — количество операций, которое вы собираетесь применить (\(0 \le m \le 10^5\)). Заметьте, что минимизировать количество операций не требуется!
В следующих \(m\) строках выведите операции в следующем формате:
\(u, v, x\) (\(1 \le u, v \le n\), \(u \not = v\), \(x\) — целое число, \(-10^9 \le x \le 10^9\)), где \(u, v\) — листья, \(x\) — прибавляемое число.
Гарантируется, что если существует последовательность операций, дающая заданную конфигурацию, то существует и последовательность операций, дающая ее, которая удовлетворяет всем заданными ограничениям.
Примечание
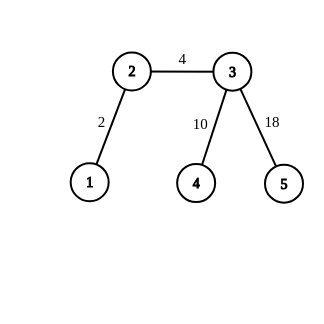
Конфигурация с первого примера нарисована ниже, и ее невозможно достичь.
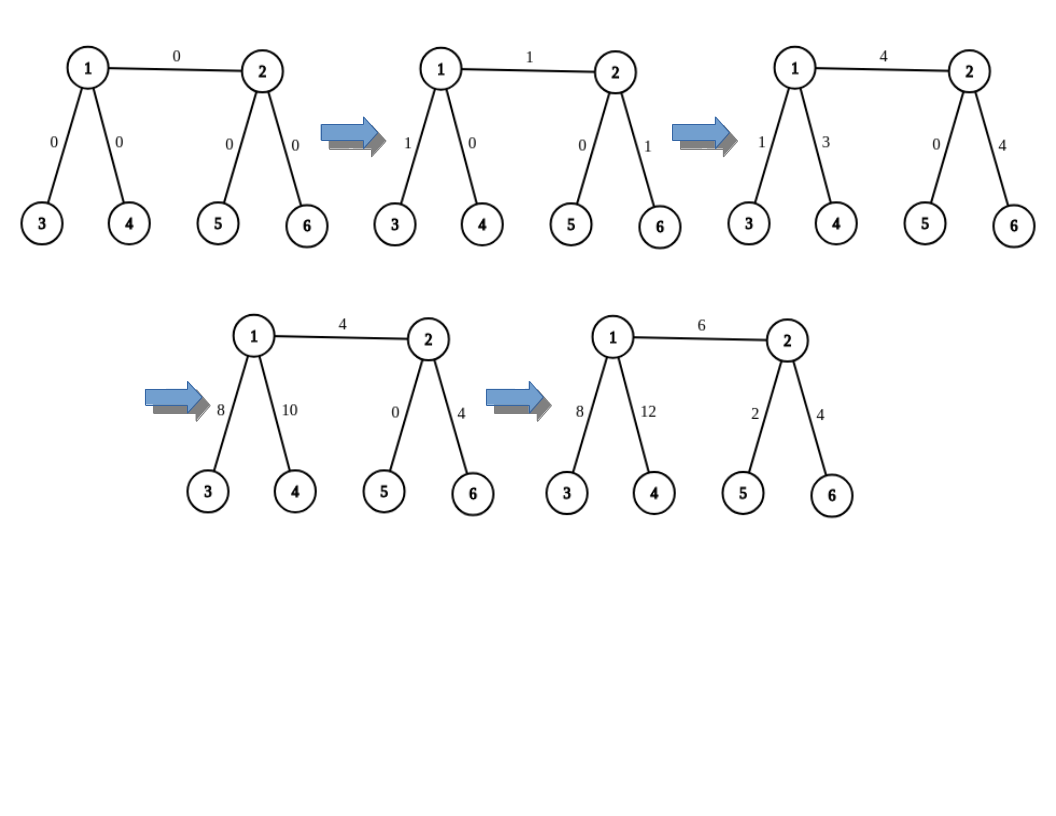
Последовательность операций с второго примера иллюстрирована ниже.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
5
1 2 2
2 3 4
3 4 10
3 5 18
|
NO
|
|
2
|
6
1 2 6
1 3 8
1 4 12
2 5 2
2 6 4
|
YES
4
3 6 1
4 6 3
3 4 7
4 5 2
|