Вам дан неориентированный граф специального вида. Он состоит из \(2n\) вершин, пронумерованных от \(1\) до \(2n\). Граф обладает следующими свойствами:
- в нем ровно \(3n-2\) ребра: \(n\) ребер соединяют вершины с четными номерами и вершины с нечетными номерами, \(n - 1\) ребер соединяют вершины с нечетными номерами друг с другом, и \(n - 1\) ребер соединяют вершины с четными номерами друг с другом;
- для каждого ребра \((u, v)\) между вершинами с нечетными номерами существует ребро \((u + 1, v + 1)\), и наоборот;
- для каждого нечетного числа \(u \in [1, 2n - 1]\) существует ребро \((u, u + 1)\);
- граф является связным; более того, если мы удалим все четные вершины и ребра, инцидентные им, граф станет деревом (то же самое произойдет, если удалить все нечетные вершины).
Граф можно представить как два дерева с одинаковой структурой, и дополнительно \(n\) ребер, соединяющих соответствующие вершины в различных деревьях.
Ребра графа являются взвешенными. Длина простого пути в этом графе определяется как сумма весов всех ребер, по которым проходит путь.
Вам даны \(q\) запросов к графу; в каждом запросе требуется подсчитать длину кратчайшего пути между какой-то парой вершин. Можете ли вы справиться со всеми запросами?
Выходные данные
Выведите \(q\) целых чисел, \(i\)-е из которых должно быть ответом на \(i\)-й запрос.
Примечание
Граф в первом тесте выглядит следующим образом:
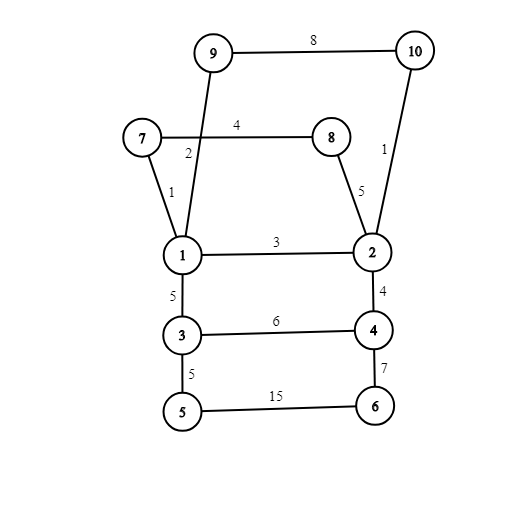
Примеры
| № | Входные данные | Выходные данные |
|
1
|
5
3 6 15 4 8
1 2 5 4
2 3 5 7
1 4 1 5
1 5 2 1
3
1 2
5 6
1 10
|
3
15
4
|