Вам дано дерево (связный неориентированный граф без циклов), состоящее из \(n\) вершин. Каждое из \(n - 1\) рёбер дерева покрашено в чёрный или красный цвет.
Вам также дано целое число \(k\). Рассмотрим последовательности из \(k\) вершин. Скажем, что последовательность \([a_1, a_2, \ldots, a_k]\) является хорошей, если она удовлетворяет следующему:
- Мы пройдём некоторый путь в дереве (возможно посещающий несколько раз одну и ту же вершину или ребро), начинающийся в \(a_1\) и заканчивающийся в \(a_k\).
- Начнём в \(a_1\), затем перейдём в \(a_2\) по кратчайшему пути между \(a_1\) и \(a_2\), затем перейдём в \(a_3\) аналогичным образом, и так далее, пока наконец не пройдём кратчайший путь из \(a_{k-1}\) в \(a_k\).
- Если в результате такого процесса мы пройдём хотя бы по одному чёрному ребру, то последовательность является хорошей.
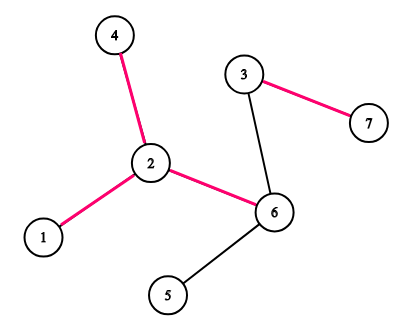
Рассмотрим дерево, изображенное на рисунке. Если \(k=3\), то следующие последовательности являются хорошими: \([1, 4, 7]\), \([5, 5, 3]\) и \([2, 3, 7]\). Следующие последовательности не являются хорошими: \([1, 4, 6]\), \([5, 5, 5]\), \([3, 7, 3]\).
Всего есть \(n^k\) последовательностей вершин, посчитайте сколько из них являются хорошими. Так как это число может быть очень большим, выведите его по модулю \(10^9+7\).
Примечание
В первом примере все последовательности (\(4^4\)) длины \(4\) являются хорошими, кроме следующих:
- \([1, 1, 1, 1]\)
- \([2, 2, 2, 2]\)
- \([3, 3, 3, 3]\)
- \([4, 4, 4, 4]\)
Во втором примере, все рёбра красные, а значит нет ни одной хорошей последовательности.