Олимпиадный тренинг

Задача . G. Крестики-нолики на дереве

Задача

Игра в крестики-нолики начинается на дереве из $n$ вершин. Некоторые вершины уже окрашены в белый цвет, а остальные пока бесцветны.

Есть два игрока — белый и чёрный. Игроки ходят по очереди, белый игрок начинает игру. В свой ход игрок выбирает ещё не покрашенную вершину и красит её в свой цвет.

Игрок выигрывает, если он покрасит какой-нибудь путь из трёх вершин в свой цвет. В случае, если все вершины становятся покрашенными, а никакой игрок так и не выиграл, то игра заканчивается вничью.

Не могли бы вы выяснить, кто выиграет эту игру или закончится ли она в ничью, если оба игрока играют оптимально?

Входные данные

Первая строка содержит одно целое число $T$ ($1 \le T \le 50\,000$) — количество тестовых случаев. Далее следуют описания $T$ тестовых случаев.

Первая строка каждого тестового случая содержит одно целое число $n$ ($1 \le n \le 5 \cdot 10^5$) — количество вершин в дереве.

Каждая из следующих $n - 1$ строк содержит целые числа $v$ и $u$ ($1 \le v, u \le n$), означающие, что вершины $u$ и $v$ соединены очередным ребром.

Последняя строка теста содержит строку длины $n$, состоящую из букв «W» и «N». Покрашенные в белый цвет вершины отмечены как «W».

Гарантируется, что заданные рёбра образуют дерево, что есть хотя бы одна неокрашенная вершина и что пути, состоящего из трёх белых вершин, нет.

Гарантируется, что сумма $n$ по всем тестовым случаям не превосходит $5 \cdot 10^5$.

Выходные данные

Для каждого тестового случая выведите «White», «Draw» или «Black» в зависимости от того, кто выиграет (соответственно белый, ничья или черный).

Примечание

В первом примере вершина $4$ уже изначально покрашена в белый. Белый игрок может выиграть покрасив своим первым ходом вершину $1$ и покрасив оставшуюся вершину своим следующим ходом. Этот процесс изображен на картинках ниже.

$\text{[math]}$

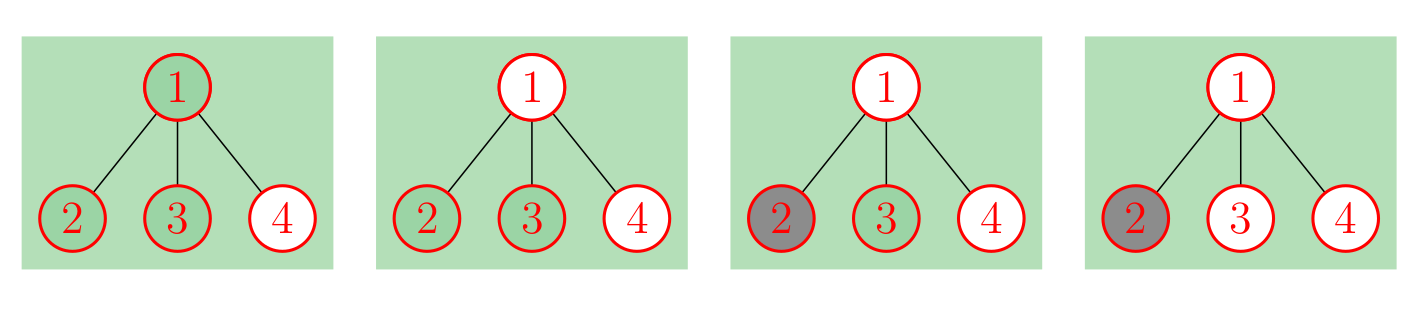
Во втором примере можно показать, что ни один игрок не может гарантировать себе победу.

Примеры

№	Входные данные	Выходные данные
1	2 4 1 2 1 3 1 4 NNNW 5 1 2 2 3 3 4 4 5 NNNNN	White Draw

time 3000 ms
memory 256 Mb
Правила оформления программ и список ошибок при автоматической проверке задач

Статистика успешных решений по компиляторам

	Кол-во
С++ Mingw-w64	4

Комментарий учителя

Ваш ответ

выберите язык и введите исходный код

Для отправки решения задачи необходимо зарегистрироваться или авторизоваться!

Загруженные файлы

Нет