Однажды, во время пары Саше стало скучно и он решил поговорить со своими друзьями. Тут он увидел Кефу. О Кефе можно говорить бесконечно, поэтому делать мы этого не будем. Разговор ребят зашёл о графах. Кефа пообещал рассказать Саше один интересный факт из теории графов, если тот, в свою очередь, поможет Кефе посчитать количество красивых деревьев.
В данной задаче деревом называется взвешенный связный граф, состоящий из \(n\) вершин и \(n-1\)-го ребра, такой, что веса всех рёбер — целые числа от \(1\) до \(m\). Красоту дерева Кефа оценивает следующим образом: он находит в дереве две свои любимые врешины — вершины с номерами \(a\) и \(b\), и считает расстояние между ними. Расстоянием между двумя вершинами \(x\) и \(y\) назовём сумму весов всех рёбер на простом пути из \(x\) в \(y\). Если расстояние от вершины \(a\) до вершины \(b\) равно \(m\), то дерево красивое.
Саша очень любит теорию графов, а ещё больше Саша любит интересные факты, поэтому Саша согласился помочь. К счастью, Саша знаком с вами, лучшим программистом Байтландии. Помогите Саше посчитать количество красивых деревьев для Кефы. Два дерева считаются различными, если существует хотя бы одно ребро, принадлежащее одному из этих деревьев и не принадлежащее другому. Вес ребра имеет значение.
Кефа предупредил Сашу, что красивых деревьев очень много, поэтому достаточно будет вычислить их количество по модулю \(10^9 + 7\).
Примечание
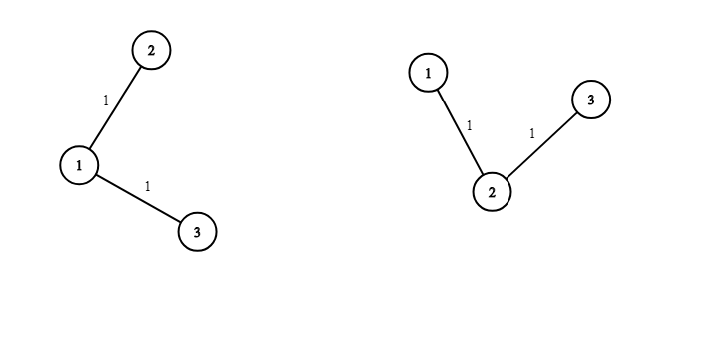
В первом примере существует \(5\) красивых деревьев:

Во втором примере красивыми являются следующие деревья: