Погуляв по заснеженному лесу, Миша очень полюбил деревья и решил нарисовать своё!
Это дерево состоит из \(n\) вершин, пронумерованных различными целыми числами от \(1\) до \(n\). В этом дереве вершина \(1\) является корнем, а у любой другой вершины \(i\) есть непосредственный предок \(p_{i}\) (при этом \(i\) — непосредственный потомок \(p_{i}\)).
Вершина \(u\) лежит в поддереве вершины \(v\), если переходя по непосредственным предкам из вершины \(u\) (\(u\), \(p_{u}\), \(p_{p_{u}}\), ...), можно попасть в вершину \(v\). В частности, любая вершина \(v\) лежит в поддереве самой себя. Число вершин в поддереве вершины \(v\) называется размером поддерева. Миша рассматривает только те деревья, в которых все вершины лежат в поддереве вершины \(1\).
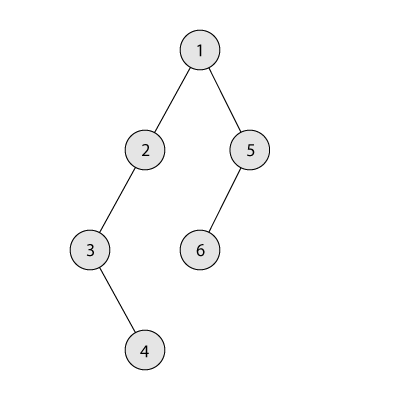
На рисунке ниже изображено дерево из \(6\) вершин. Поддерево вершины \(2\) состоит из вершин \(2\), \(3\), \(4\), \(5\). Таким образом, размер поддерева этой вершины равен \(4\).
Назовём разветвлённостью дерева максимальное количество непосредственных потомков какой-то из его вершин. Так, разветвлённость дерева на рисунке выше равна 2. Помогите Мише построить дерево из \(n\) вершин, в котором сумма размеров всех поддеревьев равна в точности \(s\), а разветвлённость — минимально возможная.
Выходные данные
Если требуемого дерева не существует, выведите «No». Иначе в первой строке выходных данных выведите «Yes», а в следующей строке выведите числа \(p_2\), \(p_3\), ..., \(p_n\), где вершина с номером \(p_i\) является непосредственным предком вершины с номером \(i\).
Примечание
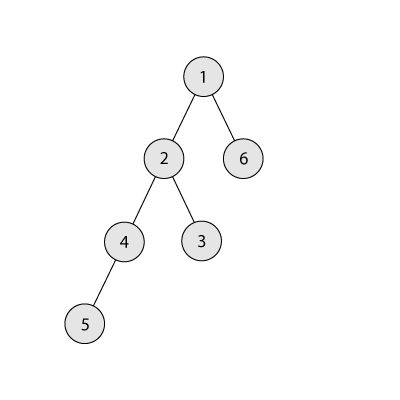
Для первого примера одним из оптимальных деревьев изображено ниже. Сумма размеров поддеревьев в этом дереве равна \(3 + 1 + 1 = 5\), а разветвлённость равна \(2\).
Для третьего примера одним из оптимальных деревьев изображено ниже. В этом дереве сумма размеров поддеревьев равна \(6 + 3 + 2 + 1 + 2 + 1 = 15\), а разветвлённость равна \(2\).