Олимпиадный тренинг

Задача . E. Достижимость из столицы

Задача

Темы: графы жадные алгоритмы поиск в глубину и подобное *2000

В Берляндии $n$ городов и $m$ дорог, каждая из дорог соединяет пару городов. Дороги в Берляндии — односторонние.

Какое наименьшее количество новых дорог надо построить, чтобы из столицы Берляндии по дорогам стали достижимы все города страны?

Построенные новые дороги тоже будут односторонними.

Входные данные

В первой строке задано три целых числа $n$, $m$ и $s$ ($1 \le n \le 5000, 0 \le m \le 5000, 1 \le s \le n$) — количество городов, количество дорог и номер столицы. Города пронумерованы от $1$ до $n$.

В следующих $m$ строках заданы дороги: $i$-я дорога задается парой номеров соединяемых городов $u_i$ и $v_i$ ($1 \le u_i, v_i \le n$, $u_i \ne v_i$). Для каждой пары городов $(u, v)$ может быть не более одной дороги из $u$ в $v$, но существование встречных дорог (из $u$ в $v$ и одновременно из $v$ в $u$) допустимо. Все дороги в Берляндии — односторонние.

Выходные данные

Выведите одно целое число — минимальное количество дорог, которое необходимо построить, чтобы из города $s$ стали достижимы все остальные города. Если во входных данных уже все города достижимы из $s$, то выведите 0.

Примечание

Первый пример изображен на следующем рисунке:

$\text{[math]}$

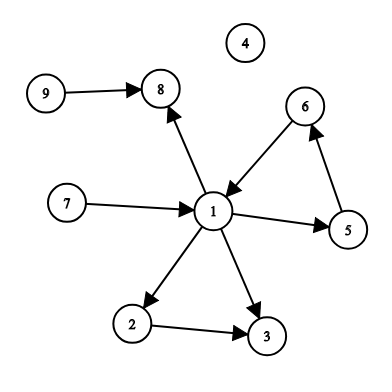
Для того, чтобы все города стали достижимы из $s = 1$, можно добавить, например, дороги ($6, 4$), ($7, 9$), ($1, 7$).

Второй пример:

$\text{[math]}$

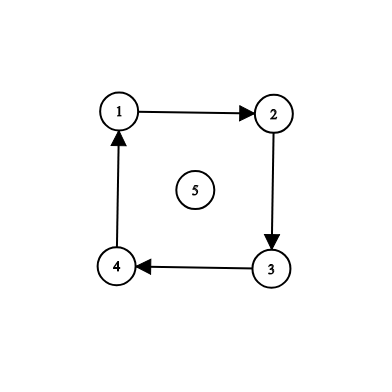
В этом примере можно добавить любую из дорог ($5, 1$), ($5, 2$), ($5, 3$), ($5, 4$), чтобы все остальные города стали достижимы из $s = 5$.

Примеры

№	Входные данные	Выходные данные
1	9 9 1 1 2 1 3 2 3 1 5 5 6 6 1 1 8 9 8 7 1	3
2	5 4 5 1 2 2 3 3 4 4 1	1

time 2000 ms
memory 256 Mb
Правила оформления программ и список ошибок при автоматической проверке задач

Статистика успешных решений по компиляторам

	Кол-во
С++ Mingw-w64	5

Комментарий учителя

Ваш ответ

выберите язык и введите исходный код

Для отправки решения задачи необходимо зарегистрироваться или авторизоваться!

Загруженные файлы

Нет