Представьте себе бильярдный стол размера \(n \times m\) с четырьмя лузами в углах. Введем систему координат относительно левого нижнего угла стола (см. картинку).
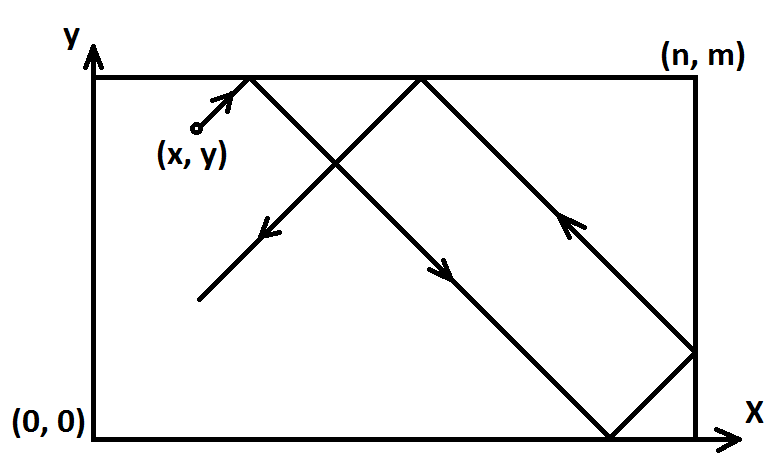
На столе один шар, который стоит в точке с координатами \((x, y)\). В один момент к столу подошел Макс, ярый любитель бильярда, и ударил по шару. Оказалось, что шар начал двигаться по прямой, которая либо параллельна осям координат, либо образует с ними угол в \(45^{\circ}\). Будем считать, что:
- углы, которые траектория шара образует со стенкой до и после соударения, равны,
- шар двигается бесконечно долго, пока не попадет ни в какую лузу,
- шар можно представить точкой, он попадает в лузу, только если его координаты точно совпадают с координатами какой-то лузы,
- в начальный момент времени шар не находится в лузе.
Обратите внимание, шар может катиться вдоль какой-то стенки, в таком случае считается, что соударений со стенкой не происходит, и шар в итоге попадет в лузу в конце стенки.
Ваша задача — определить попадет ли шар когда-либо в лузу, и если да, то в какую.
Выходные данные
Выведите координаты лузы, в которую попадет шар, или \(-1\), если такого не произойдет.
Примечание
Первый тест:
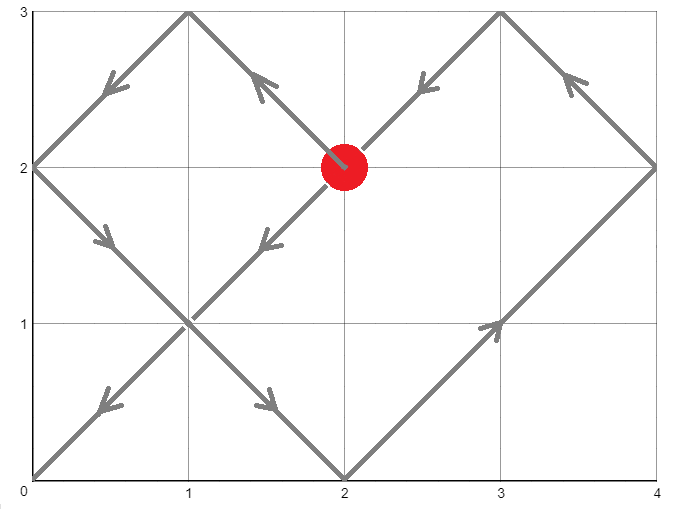
Второй тест:
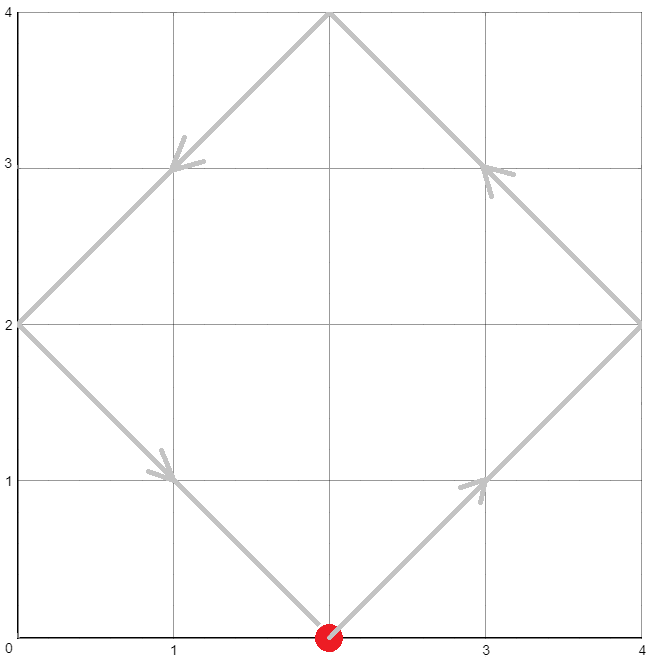
В третьем тестовом примере \(y\) координата не меняется, соответственно шар не попадет в лузу.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
4 3 2 2 -1 1
|
0 0
|
|
2
|
4 4 2 0 1 1
|
-1
|
|
3
|
10 10 10 1 -1 0
|
-1
|