Призраки «живут» в мире и гармонии, путешествуя сквозь пространство с одной лишь целью — пугать тех, кто находится у них на пути.
Во вселенной \(n\) призраков. Они двигаются в плоскости \(OXY\) с постоянной скоростью каждый: \(\overrightarrow{V} = V_{x}\overrightarrow{i} + V_{y}\overrightarrow{j}\), где \(V_{x}\) — скорость призрака в проекции на ось \(x\), а \(V_{y}\) — в проекции на ось \(y\).
Призрак \(i\) обладает опытом \(EX_i\), равным числу раз, которое он был испуган другими призраками в прошлом. Два призрака пугают друг друга, если они находятся в одной точке на плоскости в один момент времени.
Из-за того, что скорости призраков постоянны, после какого-то момента времени призраки больше не будут пугать друг друга (какое облегчение!). Тогда суммарный опыт призраков \(GX = \sum_{i=1}^{n} EX_i\) перестанет увеличиваться.
Красный гигант Тамим сфотографировал декартову плоскость в момент времени \(T\), и волшебным образом все призраки на фотографии находились на прямой \(y = a \cdot x + b\). Вам необходимо выяснить, чему будет равен суммарный опыт призраков \(GX\) после того, как он перестанет увеличиваться.
Обратите внимание, в момент времени, когда Тамим сделал фотографию, опыт \(GX\) может уже быть больше \(0\), так как призраки могли пугать друг друга в моменты времени в интервале \([-\infty, T]\).
Выходные данные
Выведите одно число полный опыт всех призраков \(GX\) в бесконечном будущем.
Примечание
В первом примере есть четыре встречи \((1,2,T-0.5)\), \((1,3,T-1)\), \((2,4,T+1)\), \((3,4,T+0.5)\), где \((u,v,t)\) означает встречу между призраками \(u\) и \(v\) в момент времени \(t\). В момент каждой встречи оба встречающихся призрака получают по единице опыта, поэтому \(GX = 4 \cdot 2 = 8\).
В втором примере, все призраки встретятся в момент времени \(t = T + 1\).
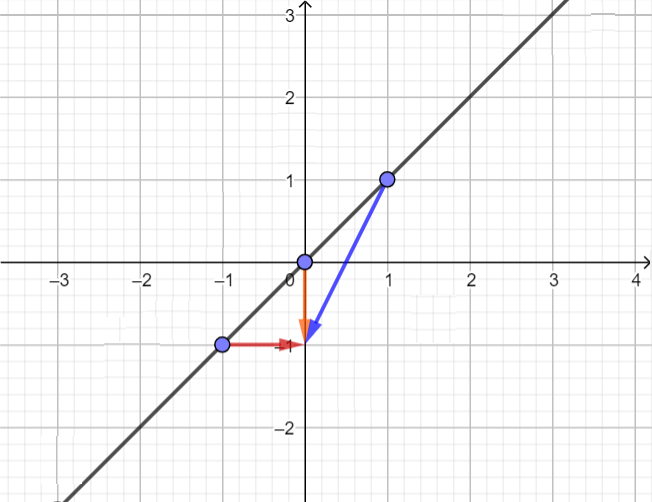
Красная стрелка обозначает скорость первого призрака, оранжевая — второго, а синяя — третьего.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
4 1 1
1 -1 -1
2 1 1
3 1 1
4 -1 -1
|
8
|
|
2
|
3 1 0
-1 1 0
0 0 -1
1 -1 -2
|
6
|
|
3
|
3 1 0
0 0 0
1 0 0
2 0 0
|
0
|