Изначально на доске написано целое число x. Вы повторяете следующую операцию некоторое число раз:
- взять число x, которое сейчас написано на доске и стереть его,
- выбрать целое число равновероятно случайным образом из отрезка [0, x] включительно, и написать его на доску.
По данному распределению вероятностей начального числа и количеству операций определите распределение вероятностей для конечного числа.
Выходные данные
Выведите одну строку с N + 1 целыми числами, где Ri описывает вероятность того, что число после M шагов равно i. Можно доказать, что искомая вероятность всегда можно представить в виде несократимой дроби P / Q. Вам нужно вывести 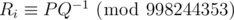 .
.
Примечание
В первом примере мы начинаем с числа 2. После одного шага число на доске будет 0, 1 или 2 с вероятностью 1/3 каждая.
Во втором примере число останется 2 с вероятностью 1/9. С вероятностью 1/9 оно остается равным 2 в первом раунде, и изменяется на 1 во втором, и с вероятностью 1/6 изменяется на 1 в первом раунде и остается таким же во втором. Во всех остальных случаях конечное число равно 0.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
2 1
0 0 1
|
332748118 332748118 332748118
|
|
2
|
2 2
0 0 1
|
942786334 610038216 443664157
|
|
3
|
9 350
3 31 314 3141 31415 314159 3141592 31415926 314159265 649178508
|
822986014 12998613 84959018 728107923 939229297 935516344 27254497 413831286 583600448 442738326
|