Имп очень благодарен вам за оказанную помощь. Впрочем, если вы решите последнюю задачу, его радость возрастет многократно.
Определим
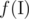
для некоторого множества
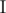
как число таких пар
a,
b во множестве
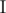
, что:
- a строго меньше b;
- a делит b без остатка.
Необходимо найти такое множество 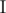, которое является подмножеством множества {1, 2, ..., n} (т. е. множества всех положительных целых чисел, не превосходящих n), что 
.
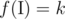Выходные данные
Если ответ не существует, выведите одно слово «No».
В противном случае в первой строке выведите «Yes», во второй — число m, размер множества 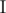, а в третьей строке — m чисел, составляющих множество 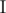. Если возможных ответов несколько, выведите любой.
Для лучшего понимания формата вывода смотрите примеры.
Примечание
Во втором примере подходящими парами являются (1, 2), (1, 4), (1, 5), (1, 6), (2, 4), (2, 6). Таким образом,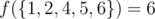 
.
В третьем примере подходящими парами являются (2, 4), (4, 8), (2, 8). Таким образом,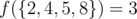 
.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
3 3
|
No
|
|
2
|
6 6
|
Yes
5
1 2 4 5 6
|
|
3
|
8 3
|
Yes
4
2 4 5 8
|