В городе Нормгород проходит шахматный турнир. n игроков были приглашены для участия в нём. Турнир проходит по следующим правилам:
- Каждый игрок играет с каждым другим одну партию, ничьих не бывает;
- После этого организаторы строят полный ориентированный граф, вершинами которого являются игроки. Для каждой пары игроков в графе есть одно ребро, начало которое идет от победителя игры между ними к проигравшему;
- После этого граф конденсируется. Так как исходный граф полный, то его конденсация — ацикличный полный ориентированный граф, в котором есть единственный гамильтонов путь из компонент сильной связности исходного графа A1 → A2 → ... → Ak;
- Игроки из первой компоненты сильной связности A1 занимают первые
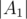 мест, игроки из компоненты A2 занимают следующие
мест, игроки из компоненты A2 занимают следующие 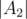 мест, и так далее;
мест, и так далее; - Для того, чтобы определить, кто какое место занял внутри каждой компоненты сильной связности, все шаги с 1 по 5 повторяются рекурсивно для каждой компоненты, то есть, для всех i = 1, 2, ..., k все игроки из компоненты Ai снова играют друг с другом партию, и так далее.
- Если компонента сильной связности состоит из одного человека, то ему больше не с кем играть, его место уже однозначно определено, и процесс останавливается.
Игроки пронумерованы числами от 1 до n. Нумерация была выполнена по результатам прошлого турнира. Известно, что игрок с номером i побеждает игрока с номером j с вероятностью p при i < j.
Вам поручено помочь с организацией турнира. Найдите математическое ожидание суммарного количества партий, сыгранных всеми игроками.
Можно показать, что ответ может быть выражен как 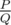 , где P и Q — взаимно простые целые числа, а
, где P и Q — взаимно простые целые числа, а 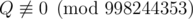 . Выведите значение P·Q - 1 по модулю 998244353.
. Выведите значение P·Q - 1 по модулю 998244353.
Если вы не знакомы с понятиями теории графов, используемыми выше, вы можете ознакомиться с ними по ссылке.
Выходные данные
В единственной строке выведите математическое ожидание суммарного количества партий в игре в формате, приведенном выше.
Примечание
В первом примере математическое ожидание равно 4.
Во втором примере математическое ожидание равно 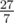 .
.
В третьем примере математическое ожидание равно 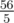 .
.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
3
1 2
|
4
|
|
2
|
3
4 6
|
142606340
|
|
3
|
4
1 2
|
598946623
|