Пока Гриша встречает Новый Год в компании Деда Мороза, Миша дарит Саше небольшой прямоугольный прудик размера n × m, поделенный на клеточки размера 1 × 1, в которых обитают маленькие злобные рыбки (не более одной рыбки на клеточку, иначе они подерутся!).
Вместе с прудиком в комплекте идет квадратный сачок размера r × r, предназначенный для рыбной ловли. Так, если поместить левый нижний угол сачка клеточку с координатами (x, y), будут пойманы все рыбки в квадрате (x, y)...(x + r - 1, y + r - 1). Отметим, что в процессе сачок должен полностью находиться внутри прудика.
К сожалению, Саша совсем не искушена в благородном искусстве рыбной ловли, поэтому закидывает сачок случайным образом. Чтобы та не расстраивалась из-за плохих результатов, Миша решил выпустить в различные клеточки изначально пустого прудика k рыбок так, чтобы математическое ожидание количества пойманных сачком рыбок было бы максимально. Помогите ему этого достигнуть и обрадовать Сашу! А именно, расположите k рыбок в различных клетках так, чтобы при забрасывании сачка в случайное из (n - r + 1)·(m - r + 1) положений среднее количество рыбок в сачке было максимально возможным.
Выходные данные
Выведите одно число — максимально возможное математическое ожидание числа пойманных рыбок.
Ваш ответ будет зачтен, если его относительная или абсолютная ошибка не превосходит 10 - 9. А именно, пусть ваш ответ равен a, а ответ жюри — b. Ваш ответ будет зачтен, если 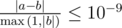 .
.
Примечание
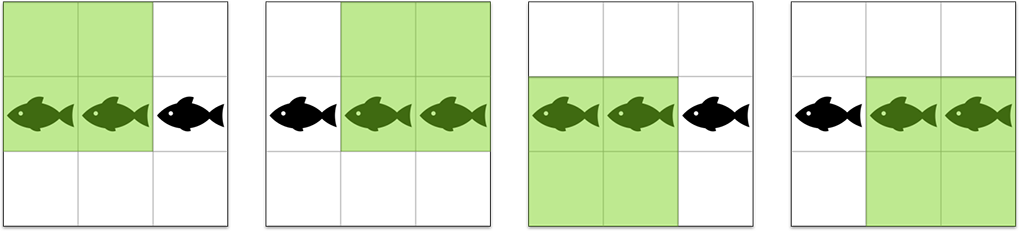
В первом примере можно выпустить рыбок в клетки (2, 1), (2, 2), (2, 3). В таком случае для любой из четырех возможных конфигураций сачка (выделены салатовым) количество рыбок внутри будет равняться двум, как и математическое ожидание.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
3 3 2 3
|
2.0000000000
|
|
2
|
12 17 9 40
|
32.8333333333
|