Вам даны три целых числа k, pa и pb.
Вы будете строить последовательность в соответствии со следующим алгоритмом. Изначально у вас есть пустая последовательность. Раз в секунду вы делаете следующее. С вероятностью pa / (pa + pb) вы добавляете «a» в конец последовательности. Иначе (с вероятностью pb / (pa + pb)) вы добавляете «b» в конец последовательности.
Вы останавливаетесь, как только в вашей последовательности есть хотя бы k подпоследовательностей «ab». Определите математическое ожидание числа подпоследовательностей «ab» в итоговой строке. Можно показать, что это число может быть выражено как P / Q, где P и Q — взаимно простые целые числа, а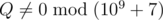 
. Выведите значение 
.
Выходные данные
Выведите одно целое число — ответ на задачу.
Примечание
В первом примере мы будем добавлять к последовательности букву, пока не получим хотя бы одну подпоследовательность «ab». Среди прочего, мы можем получить последовательность «ab» с вероятностью 1/4, «bbab» с вероятностью 1/16, и «aab» с вероятностью 1/8. Обратите внимание, невозможно получить строку «aabab», так как мы бы остановились, как только получили префикс «aab».
Математическое ожидание числа подпоследовательностей «ab» равно 2.
Во втором примере ответ равен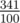 
.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
1 1 1
|
2
|
|
2
|
3 1 4
|
370000006
|