Дано положительное целое число n. Построим граф на вершинах 1, 2, ..., n так, чтобы ребро между вершинами u и v существовало тогда и только тогда, когда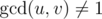 
. Пусть d(u, v) — кратчайшее расстояние между u и v или 0, если между ними нет пути. Посчитайте сумму d(u, v) для всех 1 ≤ u < v ≤ n.
gcd или НОД (наибольший общий делитель) двух натуральных чисел — такое наибольшее натуральное число, которое делит оба этих числа нацело.
Выходные данные
Выведите сумму d(u, v) для всех 1 ≤ u < v ≤ n.
Примечание
Все кратчайшие пути в первом примере:
Между остальными парами вершин путь не существует.
Суммарное расстояние 2 + 1 + 1 + 2 + 1 + 1 = 8.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
6
|
8
|
|
2
|
10
|
44
|