Илья работает в компании по производству роботов. Илья пишет программы для игровых моделей, его текущий проект «Боб» — игровой робот нового поколения. Начальник Ильи интересуется его продвижениями в работе. В частности он хочет узнать, насколько Боб лучше предыдущей модели, «Алисы».
Теперь Илья хочет сравнить навыки своих роботов в простой игре «1-2-3». Эта игра похожа на «Камень-ножницы-бумага»: роботы втайне друг от друга выбирают число из набора {1, 2, 3} и одновременно произносят свое число. Если роботы сказали одно и то же число, тогда объявляется ничья и никто не получает очки. Но если числа различны, то один из роботов зарабатывает очко: робот, назвавший 3, побеждает робота, назвавшего 2, 2 побеждает 1 и 1 побеждает 3.
Программы роботов выбирают числа таким образом, что их выбор в (i + 1)-й игре зависит только от их выбора в i-й игре.
Илья знает, что роботы сыграют ровно k игр, Алиса выберет число a в первой игре, а Боб выберет число b в первой игре. Также он знает программы обоих роботов и может сказать, какое число выберет робот на основе выбора в предыдущей игре. Илья не хочет ждать, пока все k игр будут сыграны, и он просит вас подсчитать количество очков, которое наберет каждый из роботов после финальной игры.
Выходные данные
Выведите два числа. Первое — количество очков, набранное Алисой, второе — количество очков, набранное Бобом, после k игр.
Примечание
Во втором примере игра идет следующим образом:
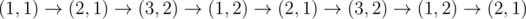
В четвертой и седьмой игре побеждает Боб, в первой игре ничья, а во всех остальных побеждает Алиса.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
10 2 1
1 1 1
1 1 1
1 1 1
2 2 2
2 2 2
2 2 2
|
1 9
|
|
2
|
8 1 1
2 2 1
3 3 1
3 1 3
1 1 1
2 1 1
1 2 3
|
5 2
|
|
3
|
5 1 1
1 2 2
2 2 2
2 2 2
1 2 2
2 2 2
2 2 2
|
0 0
|