Билл — известный математик в стране. Благодаря его революционным открытиям в области математики, он заработал достаточно денег, чтобы построить прекрасный дом. К сожалению, за неуплату налогов на собственность, суд решил наказать Билла, убрав некоторые части он его дома
Дом Билла может быть представлен как выпуклый правильный 2n-угольник A0 A1... A2n - 1 A2n, A2n = A0, каждая сторона имеет длину ровно 1 метр.
Суд постановил следующие правила для удаления частей дома:
- Разделим каждую сторону Ak Ak + 1, k = 0... 2n - 1 на n равных частей длины 1 / n точками P0, P1, ..., Pn - 1
- На каждом ребре A2k A2k + 1, k = 0... n - 1 суд выберет одну точку B2k = Pi для некоторого i = 0, ..., n - 1 такую, что
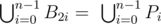
- На каждом ребре A2k + 1A2k + 2, k = 0...n - 1 Билл выберет одну точку B2k + 1 = Pi для некоторого i = 0, ..., n - 1 такую, что
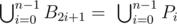
- Биллу останется часть дома, ограниченная 2n-угольником B0 B1... B2n - 1
Билл узнал, какие точки B2k выбрал суд. Несмотря на то, что он великий математик, его дом очень большой и ему сложно все рассчитать. Поэтому он просит вас помочь ему выбрать точки так, чтобы максимизировать площадь дома, которая ему останется.
Выходные данные
Выведите n различных целых чисел, описывающих точки B1, B3, ..., B2n - 1, которые Билл должен выбрать, чтобы оставить себе максимально возможную площадь дома.
Примечание
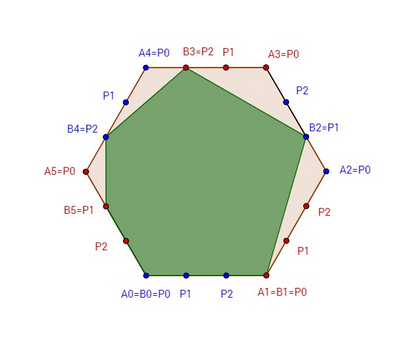
Чтобы максимизировать площадь в примере, Билл должен выбрать следующие точки: B1 = P0, B3 = P2, B5 = P1
Примеры
| № | Входные данные | Выходные данные |
|
1
|
3
0 1 2
|
0 2 1
|