У Майка есть последовательность A = [a1, a2, ..., an] длины n. Он считает последовательность B = [b1, b2, ..., bn] красивой, если gcd всех её элементов больше чем 1, то есть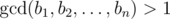 
.
Майк хочет изменить последовательность, чтобы сделать её красивой. За один ход он может выбрать позицию i (1 ≤ i < n), удалить числа ai, ai + 1 и вставить числа ai - ai + 1, ai + ai + 1 на их место в таком порядке. Он хочет сделать как можно меньше ходов. Найдите минимальное количество ходов, которое необходимо сделать, чтобы последовательность A стала красивой, иначе сообщите ему, что это невозможно.
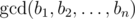— наибольшее натуральное число d, такое что d делит bi для всех i (1 ≤ i ≤ n).
Выходные данные
В первой строке выведите «YES» (без кавычек), если возможно последовательность A сделать красивой, выполнением ходов, описанных выше. Или выведите «NO» (без кавычек) иначе.
Если выведенный ответ был «YES», тогда выведите минимальное количество ходов необходимое для того, чтобы сделать последовательность A красивой.
Примечание
В первом тестовом примере достаточно сделать только один ход, чтобы получить последовательность [0, 2] с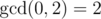 
.
Во втором тестовом примере gcd последовательности изначальное больше чем 1.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
2
1 1
|
YES
1
|
|
2
|
3
6 2 4
|
YES
0
|
|
3
|
2
1 3
|
YES
1
|