Одним из подарков Тимофею на день рождения была раскраска. Она была устроена следующим образом: плоскость, на которой отмечены n прямоугольников со сторонами, параллельными осям координат. Все прямоугольники имеют стороны нечетной длины. Никакие два прямоугольника не пересекаются, но могут касаться.
Помогите Тимофею раскрасить все прямоугольники в 4 цвета так, чтобы никакие два касающихся сторонами не были одного цвета, или скажите, что это невозможно.
Два прямоугольника пересекаются, если их пересечение имеет ненулевую площадь. Два прямоугольника касаются сторонами, если пересечение некоторой пары их сторон имеет ненулевую длину.
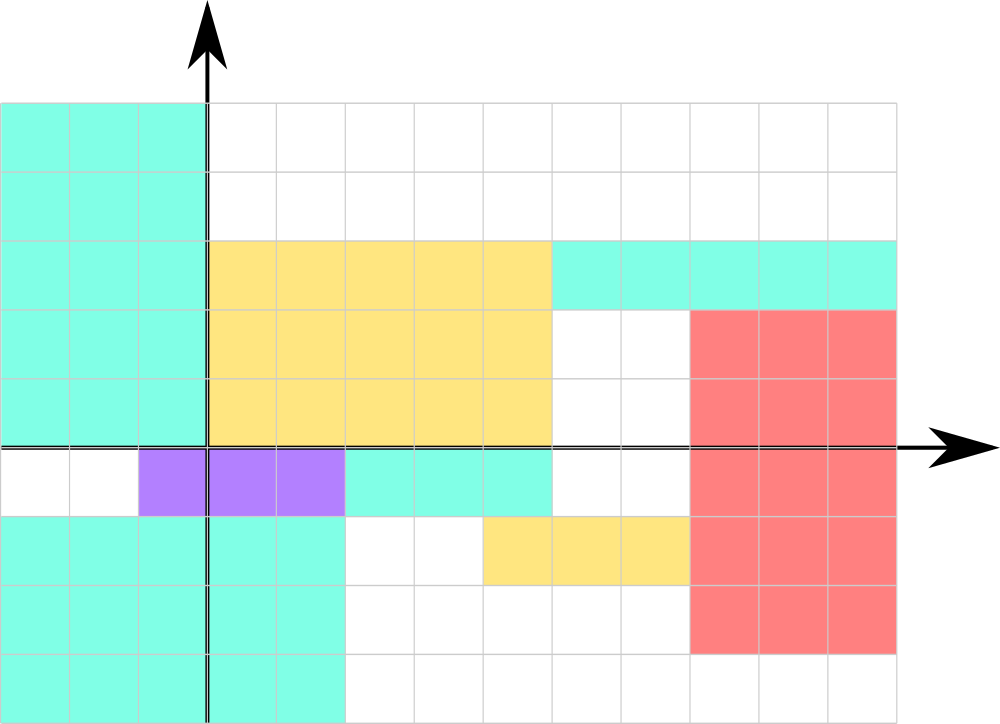Рисунок соответствует первому тесту из условия Выходные данные
В первой строке выведите «NO», если невозможно покрасить прямоугольники в 4 цвета так, чтобы никакие два касающихся не были одного цвета.
В противном случае выведите в первой строке «YES». Далее выведите n строк, в i-й из них выведите одно натуральное число ci (1 ≤ ci ≤ 4) — цвет i-ого прямоугольника.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
8
0 0 5 3
2 -1 5 0
-3 -4 2 -1
-1 -1 2 0
-3 0 0 5
5 2 10 3
7 -3 10 2
4 -2 7 -1
|
YES
1
2
2
3
2
2
4
1
|