К сожалению, в этой задаче не удалось написать достаточно короткую формальную постановку, поэтому пришлось придумать легенду.
Исследовательский зонд, наконец, достиг поверхности Марса и готов выполнить свою миссию. К сожалению, из-за сбоя навигационной системы, зонд приземлился не в той точке, в которой планировалось.
Участок, на котором высадился зонд, можно представить в виде клетчатого поля, состоящего из n строк и m столбцов. Будем обозначать через (r, c) клетку, расположенную в строке r и столбце c. Из каждой клетки зонд может продолжить движение только в клетки по соседству с текущей по стороне.
Зонд высадился в клетке с координатами (1, 1) и должен отправиться в клетку с координатами (n, m). Для этого зонд выберет произвольный кратчайший маршрут, соединяющий начальную и конечную клетки. Каждый возможный маршрут зонд выберет с равной вероятностью.
В грузовом отсеке зонда находится батарея, которая понадобится зонду для проведения исследований в конечной точке его маршрута. Изначально заряд батареи равен s единицам энергии.
В некоторых клетках данного поля находятся аномалии. Каждый раз, когда зонд оказывается в клетке с аномалией, батарея теряет половину своего заряда, округлённую вниз, то есть если до попадания в аномалию заряд был равен x, то после попадания он будет равен 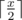 .
.
Пока зонд перебирает все возможные маршруты своего путешествия, посчитайте математическое ожидание заряда батареи в момент, когда робот достигнет клетки (n, m). Если в клетках (1, 1) и (n, m) также есть аномалии, то они тоже изменяют заряд батареи.
Примечание
В первом примере зонд может выбрать один из шести маршрутов:
-
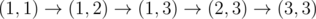 , после прохождения клетки (2, 3) заряд становится равным 6.
, после прохождения клетки (2, 3) заряд становится равным 6. -
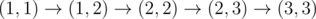 , после прохождения клетки (2, 3) заряд становится равным 6.
, после прохождения клетки (2, 3) заряд становится равным 6. -
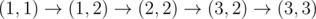 , заряд батареи остаётся равным 11.
, заряд батареи остаётся равным 11. -
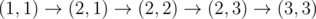 , после прохождения клеток (2, 1) и (2, 3) заряд становится равным сначала 6, а затем 3.
, после прохождения клеток (2, 1) и (2, 3) заряд становится равным сначала 6, а затем 3. -
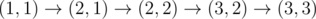 , после прохождения клетки (2, 1) заряд становится равным 6.
, после прохождения клетки (2, 1) заряд становится равным 6. -
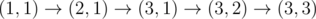 , после прохождения клетки (2, 1) заряд становится равным 6.
, после прохождения клетки (2, 1) заряд становится равным 6.
Математическое ожидание заряда батареи в конце пути в данном случае считается по формуле: 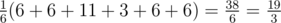 .
.
Таким образом, P = 19, а Q = 3.
3 - 1 по модулю 109 + 7 равно 333333336.
19·333333336 = 333333342 (mod 109 + 7)