Кодер ZS недавно узнал об интересной идее, так называемом Парадоксе дней рождения. Он утверждает, что среди произвольной группы из 23 человек с примерно 50% вероятностью найдутся двое, дни рождения которых совпадают. Кодер ZS нашел это очень интересным, и решил проверить это на жителях Удайлэнда.
Продолжительность года в Удайлэнде равна 2n дням. Кодер ZS хочет расспросить k жителей Удайлэнда, день рождения каждого из которых совпадает с одним из 2n дней (с равной вероятностью). ZS'а интересует вероятность того, что хотя бы двое из них родились в один и тот же день.
Кодер ZS знает, что ответ можно записать в виде несократимой дроби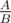 
. Он хочет найти значения A и B (ему не нравится работать с вещественными числами). Поможете ему?
Выходные данные
Если вероятность того, что хотя бы двое из k людей имеют совпадающий день рождения в году продолжительностью 2n дней, равняется 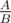(A ≥ 0, B ≥ 1, 
), выведите A и B в единственной строке.
Так как эти числа могут быть очень большими, выведите остатки от их деления на 106 + 3. Заметьте, что A и B должны быть взаимно простыми до того, как берутся их остатки от деления на 106 + 3.
Примечание
В первом примере из условия, продолжительность года в Удайлэнде равна 23 = 8 дней. Вероятность того, что 2 человека имеют день рождения в один и тот же день среди группы из 2 человек, очевидно равна 
, поэтому A = 1, B = 8.
Во втором примере из условия, в Удайлэнде всего 21 = 2 дня в году, но группа состоит из 3 человек, поэтому в любом случае у двоих из них совпадут дни рождения. Таким образом, вероятность равна 1 и A = B = 1.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
3 2
|
1 8
|
|
2
|
1 3
|
1 1
|
|
3
|
4 3
|
23 128
|